On the directionality and non-linearity of halogen and hydrogen bonds

Abstract

Benchmark quality structures and interaction energies have been produced using explicitly correlated coupled cluster methods for a systematic series of hydrogen and halogen bonded complexes: B⋯HCCH, B⋯HCl and B⋯ClF, with six different Lewis bases B. Excellent agreement with experimental structures is observed, verifying the method used to deduce the equilibrium deviation from collinearity of the intermolecular bond via rotational spectroscopy. This level of agreement also suggests that the chosen theoretical method can be employed when experimental equilibrium data are not available. The application of symmetry adapted perturbation theory reveals differences in the underlying mechanisms of interaction for hydrogen and halogen bonding, providing insights into the differences in non-linearity. In the halogen bonding case it is shown that the dispersion term is approximately equal to the overall interaction energy, highlighting the importance of choosing the correct theoretical method for this type of interaction.

---

I. Introduction

The intermolecular hydrogen bond is of well-established importance in a great number of scientific disciplines,¹ and over the last decade interest has also grown in the purportedly similar halogen bond.² The applications of the latter are varied and include drug design,³ crystal engineering⁴ and supramolecular chemistry.⁵ In general, strong analogies between hydrogen and halogen bonding have been drawn due to similarities in the structures of such intermolecular complexes, which has also led to a widespread belief that halogen bonds can be described purely through electrostatic interactions in a manner similar to that successfully employed for hydrogen bonding.⁶ This can be rationalised through what is termed a σ-hole model by Politzer and co-workers.⁷ However, Stone has recently demonstrated that while electrostatics are the largest attractive term in halogen bonding, the propensity of halogen bonds to be linear is dominated by exchange-repulsion.⁸

Investigations by rotational spectroscopy of the non-covalent interactions of simple Lewis bases B with Lewis acids (such as the hydrogen halides HX or homo- and hetero-dihalogen molecules XY) have the advantage that the properties of B⋯HX and B⋯XY determined in this way refer to the isolated complex in the gas phase. Such properties are therefore uncomplicated by perturbations resulting from nearby molecules, unlike those determined in the liquid and solid phases. In that sense, gas-phase results for simple complexes of the type B⋯HX and B⋯XY are best compared with those from high-level ab initio calculations.

Parallels between the properties of the hydrogen bond in B⋯HX and those of (what is now referred to as) the halogen bond in B⋯XY complexes have been identified through systematic investigations^9–12 by rotational spectroscopy conducted over an extended period. For example, it was noted in the early studies^13–15 of complexes B⋯Cl₂ that two generalisations, previously enunciated for complexes B⋯HX (X = F, Cl, Br or I), also applied to B⋯Cl₂, namely rules for rationalising the angular geometries¹⁶ and a simple relationship involving intermolecular stretching force constants.¹⁷ Subsequently, these (and other) generalisations were found to apply^12,18,19 to all B⋯XY, where XY is one of F₂, ClF, Cl₂, BrCl, Br₂, or ICl. Parallels involving hydrogen and halogen bonds have also been reviewed by Grabowski,²⁰ and Resnati and co-workers.²¹

The rules for predicting angular geometries for B⋯HX and B⋯XY are relevant to the subject of this article. They state simply that, in the equilibrium geometry of the complex B⋯HX or B⋯XY, the subunit HX or XY lies along the symmetry axis of either a non-bonding electron (n) pair (drawn in the conventional exaggerated form commonly used by chemists) or, in the absence of n-pairs, a π electron pair. When both n and π pairs are present on B, the n pair takes precedence (except in a few well-understood cases involving the series of heteroaromatic molecules pyridine, furan or thiophene as the Lewis base¹²).

In those B⋯HCl for which the arrangement Z⋯H–Cl (Z is the H-bond acceptor atom or centre in B) is not constrained by symmetry to be collinear, significantly nonlinear hydrogen bonds have been identified in complexes isolated in the gas phase. The precise placing of the hydrogen bond H atom is required to establish a nonlinear hydrogen bond and this is difficult for two reasons. First, the H atom makes only a small contribution to the moments of inertia of the complex and, secondly, it undergoes large amplitude displacements in the zero-point mode. Fortunately, a method²² based on the complete Cl nuclear quadrupole coupling tensor can locate the HCl internuclear axis within the principal inertia axis system of the complex. If the molecule has C_s symmetry, with the principal inertia plane ab, for example, as the symmetry plane, the only nonzero off-diagonal element of the coupling tensor is χ_ab(Cl). Then the angle α_az between the principal inertia axis a and the HCl axis z is given by

Moreover, it can be shown^22,23 that the angle α_az so obtained is the equilibrium value and it leads, under the assumption of unperturbed monomer geometries, in good approximation to the equilibrium value of the angular deviation θ of the Z⋯H–Cl system from collinearity. This is convenient for comparison with angles θ calculated ab initio, as in this article.

Fig. 1 defines the angles φ and θ used here and elsewhere to discuss details of the angular geometry of complexes B⋯HX or B⋯XY, with reference to the case when the Lewis base is a cyclic ether, such as 2,5-dihydrofuran or oxirane. The values of these angles obtained using the procedure based on the Cl-nuclear quadrupole coupling tensor to locate the HCl subunit in 2,5-dihydrofuran⋯HCl²³ are φ = 54.3(3)° and θ = 9.5(1)° and the results for oxirane⋯HCl²⁴ are φ = 69.1(1)° and θ = 16.5(1)°. The increase in φ is readily understood on the basis of the rules for rationalising angular geometries because the angle between the n pairs on O increase as the COC ring angle decreases from ∼108° in 2,5-dihydrofuran to ∼60° in oxirane.

Fig. 1 Definition of the angles φ (associated with angular geometry) and θ (intermolecular interaction nonlinearity) for oxirane⋯HCl.

The same procedure can be used for the complexes 2,5-dihydrofuran⋯ClF²⁵ and oxirane⋯ClF.²⁶ The results for φ are 53.0(3)° and 67.3(1)°, respectively, which are very similar to their values in the corresponding B⋯HCl complexes. On the other hand, the results for θ are 2.0(2)° and 2.9(1)°, respectively, indicating that the Z⋯Cl–F system barely deviates from collinearity in 2,5-dihydrofuran⋯ClF and oxirane⋯ClF. The propensity for hydrogen bonds to be significantly nonlinear while the corresponding halogen bonds remain collinear has been noted in other pairs of B⋯HCl and B⋯ClF complexes, namely those in which B = formaldehyde,^27,28 thiirane,^29,30 vinyl fluoride^31,32 and methylenecyclopropane.^33,34 This difference can be understood by imagining a hypothetical mechanism in which the HCl molecule initially approaches B along the direction of an n-pair on O, followed by a secondary interaction between Cl and an electrophilic region of B, thereby leading to nonzero values of θ. Evidently, the energy cost of bending ClF at Cl when a similar process is imagined in B⋯ClF complexes is greater than that gained by the secondary interaction; hence the much smaller θ values. This difficulty in bending at Cl in B⋯ClF complexes is what Stone has identified as being due to large increases in exchange-repulsion as θ is varied from its equilibrium value.⁸

One way of testing the secondary interaction hypothesis for nonlinearity is to weaken the hydrogen bond. According to the criterion of the intermolecular stretching force constant, ethyne forms weaker hydrogen bonds than HCl.¹⁷ Several complexes B⋯HCCH (B = formaldehyde,³⁵ 2,5-dihydrofuran,³⁶ oxirane,³⁷ thiirane³⁸ and vinyl fluoride³⁹) capable of exhibiting nonlinear Z⋯HCCH hydrogen bonds were therefore investigated by means of their rotational spectra. The HCCH molecule in the complex cannot be located by the method involving a nuclear quadrupole coupling tensor, but its larger moment of inertia than HCl and rigid character mean that it can be placed within the complex B⋯HCCH by the more conventional (but probably less accurate) method involving only zero-point principal moments of inertia. The experimental result is that the order of θ is B⋯ClF < B⋯HCl < B⋯HCCH for the various Lewis bases B.

In recent years high accuracy ab initio calculations have become more practical for molecular complexes of the sizes described above due to the development of explicitly correlated (F12) methods.^40,41 This ensures that ‘gold-standard’ quantum chemical methods such as coupled cluster with single, double and perturbative triple excitations [CCSD(T)]⁴² no longer require very large basis sets to produce excellent results. Preliminary comparisons of experiment with explicitly correlated coupled cluster results for halogen and hydrogen bonded complexes have demonstrated a direct proportionality between the theoretical intermolecular dissociation energy and the experimental intermolecular quadratic stretching force constants.^43,44 A rigorous comparison of gas-phase geometries will provide a stern test of the agreement between theory and rotational spectroscopy for both halogen and hydrogen bonding.

In this article, we present benchmark quality CCSD(T)-F12 calculations for the three series B⋯HCCH, B⋯HCl and B⋯ClF, where B is formaldehyde, vinyl fluoride, oxirane, thiirane, 2,5-dihydrofuran and methylenecyclopropane. The aim is to test: (1) whether the use of the Cl nuclear quadrupole coupling tensor to determine equilibrium values of θ does indeed lead to values in agreement with theory in the cases of the B⋯HCl and B⋯ClF, (2) whether in the B⋯HCCH complexes the experimental zero-point values of θ are usefully close to the ab initio equilibrium values, and (3) whether the observed (zero-point) angular geometries (as defined by φ) agree with the calculated equilibrium values in all three series of complexes. Symmetry adapted perturbation theory (SAPT) calculations are carried out in order to partition the interaction energy into chemically meaningful terms and thus establish the differences in the underlying mechanisms that determine the equilibrium geometries of hydrogen- and halogen-bonded complexes.

II. Computational details

Geometry optimisations and single point energy calculations were carried out using the explicitly correlated [approximation b with the 3C(fix) ansatz] coupled cluster with single, double and perturbative triple excitations [CCSD(T)-F12b]^45,46 method in the MOLPRO package of ab initio programs.^47,48 Geometry optimisations used numerical gradients and the aug-cc-pV(T+d)Z basis set for the elements Cl and S,⁴⁹ which contains an additional ‘tight’ d-type basis function. The aug-cc-pVTZ basis was used for all other elements,^50,51 but the combination shall be referred to as aug-cc-pV(T+d)Z herein. The density fitting of the Fock and exchange matrices was performed using the cc-pVTZ/JKFit auxiliary basis set (ABS),⁵² with aug-cc-pVTZ/MP2Fit used for the remaining two electron electron-repulsion integrals.⁵³ Resolution-of-the-identity for the many electron integrals used the complementary ABS+ (CABS+) procedure as implemented in MOLPRO,^45,54,55 along with the aug-cc-pV(T+d)Z/OptRI ABS.⁵⁶ CABS singles relaxation of the Hartree–Fock energy was included throughout, and the geminal Slater exponent was set to 1.2 a₀⁻¹.

In order to examine the basis set convergence and estimate the complete basis set (CBS) limit, single point CCSD(T)-F12b calculations were also carried out using the aug-cc-pV(D+d)Z, aug-cc-pV(T+d)Z and aug-cc-pV(Q+d)Z basis sets with matching ABSs. The quadruple-zeta calculations were carried out on triple-zeta optimised geometries, with all others using the same basis for optimisation and single point energies. The geminal Slater exponent was set to 1.0, 1.2 and 1.4 a₀⁻¹ for the respective basis sets. The counterpoise (CP) correction of Boys and Bernardi was applied for all of the single point energy calculations.⁵⁷ The CBS interaction energy was estimated using a Schwenke type extrapolation of the correlation energy and the parameters of Hill et al. according to the expression:^58,59

E^corr_CBS = (E^corr_QZ − E^corr_TZ)F + E^corr_TZ,

where F = 1.416422 for the CCSD-F12b contribution and 1.663388 for (T). The reference energy was chosen as QZ HF with CABS singles relaxation.

The degree of charge transfer on complex formation was determined by the natural bond orbital (NBO) method, comparing the charges on each nuclear centre in the interacting complex and as well-separated fragments. The NBOs were calculated from the Møller–Plesset second-order perturbation theory (MP2) density matrix with the aug-cc-pV(T+d)Z basis, using the NBO6 program interfaced to MOLPRO.⁶⁰

Symmetry adapted perturbation theory (SAPT) calculations were carried out to decompose the interaction energy into chemically meaningful terms.⁶¹ This was performed at the SAPT2+(3)δMP2/aug-cc-pV(T+d)Z level, where a CP-MP2 correction is applied. This level of SAPT has recently been shown to produce very accurate non-covalent interaction energies.⁶² All of the SAPT calculations were performed with the Psi4 (beta 5)⁶³ program using density fitting and MP2 natural orbitals,^64,65 and were assembled into a “chemist's grouping” of electrostatic, exchange-repulsion, induction and dispersion terms:⁶⁶

E_{electrostatic} = E⁽¹⁰⁾_elst + E⁽¹²⁾_elst,resp + E⁽¹³⁾_elst,resp

E_exchange = E⁽¹⁰⁾_exch + E⁽¹¹⁾_exch + E⁽¹²⁾_exch

E_induction = E⁽²⁰⁾_ind,resp + E⁽²⁰⁾_{exch-ind,resp} + E⁽³⁰⁾_ind + E⁽³⁰⁾_exch-ind + ^tE⁽²²⁾_ind + ^tE⁽²²⁾_exch-ind + δE⁽³⁾_HF + [δE_MP2]

E_dispersion = E⁽²⁰⁾_disp + E⁽³⁰⁾_disp + E⁽²¹⁾_disp + E⁽²²⁾_disp + E⁽²⁰⁾_disp-exch.

Interested readers are directed to ref. 61 for further explanation of the individual SAPT components.

III. Results and analysis of results

The results of the equilibrium geometry optimisations are summarised in graphical form in Fig. 2, with full Cartesian coordinates presented in the ESI.† All minimum energy structures located possess C_s symmetry. The angle θ, which indicates the deviation from collinearity of the hydrogen or halogen bond, is displayed as the theoretical value in black, with the experimental angle taken from the literature in red. It is immediately apparent that the agreement between theory and experiment is excellent for the B⋯HCl and B⋯ClF complexes, with mean absolute deviations (MAD) of 1.6° and 0.6°, respectively. The experimental results for these structures are produced with the aid of the Cl nuclear quadrupole tensor using eqn (1) and should be directly comparable to those from ab initio computation as equilibrium values. The small deviations in the angle may be due, in part, to the assumption of unperturbed monomer geometries upon complex formation in the experimental approach, whereas the ab initio geometry optimisations relaxed all degrees of freedom. This excellent level of agreement with highly accurate theoretical deviations from collinearity validates the experimental approach to producing equilibrium values and provides some context for the comparison of theory with zero-point B⋯HCCH structures. With a MAD of 3.3°, the agreement for the B⋯HCCH complexes is slightly worse than the B⋯HCl and B⋯ClF cases, but remains at a reasonably good level and is reassuring in terms of the experimental structure being usefully close to that from ab initio calculation. As the chosen high-level theoretical method is capable of producing accurate gas-phase equilibrium structures, a full comparison of the deviation from collinearity in all of the complexes considered could use the theoretical angles for the B⋯HCCH complexes along with the experimental data for B⋯HCl and B⋯ClF. This would ensure comparable accuracy of equilibrium structures in all cases.

Fig. 2 Geometries of the B⋯HCl (left column), B⋯HCCH (centre column) and B⋯ClF (right column) complexes. Black text denotes the theoretical CCSD(T)-F12b deviations from collinearity (θ), red text (lower) are experimental.^{12,19,24,26,29,32–36,38,39}

While the deviation from collinearity is an intriguing difference between hydrogen and halogen bonds that is well reproduced by CCSD(T)-F12b, the angular geometry φ and the intermolecular bond lengths provide additional areas of comparison for theory and experiment. However, it must be noted that all experimental data in this regard are for zero-point structures where unperturbed monomer geometries are assumed, hence the level of agreement is expected to be less than in the case of θ. Even taking this into consideration, the concurrence in φ for both B⋯HCl and B⋯ClF should be superior to B⋯HCCH as obtaining the Cl nuclear quadrupole tensor fixes the orientation of the HCl or ClF subunit in the principal inertia axis system of the complex, while the process for placing HCCH is not so accurate. Table 1 displays the calculated and literature experimental values of φ, with this angle defined visually for each complex in the ESI.† The trends for φ mirror those for θ, with an excellent theory/experiment agreement for B⋯ClF (MAD = 0.6°), very good for B⋯HCl (MAD = 2.6°) and useful for B⋯HCCH (MAD = 7.5°). These trends are those to be expected from the amplitude of the zero-point motion of the components in the complexes, which is likely to be B⋯HCCH > B⋯HCl > B⋯ClF. The directionality of halogen bonding was recently investigated in terms of a σ-hole model that proposed minor modifications to the nomenclature relating to the size and magnitude of the σ-hole.⁶⁷ Perhaps unsurprisingly, an increase in the size of the sigma-hole was found to decrease the directionality of a resulting halogen bond as the area in which an attractive electrostatic approach can be made was increased.

Table 1 CCSD(T)-F12b optimised angular geometries φ (°). Values in square brackets refer to experimental values from the literature

Lewis base B	B⋯HCl	B⋯HCCH	B⋯ClF
Formaldehyde	73.8 [70.0(10)]^27	80.0 [92.0(16)]^35	69.7 [69.1(7)]^28
Vinyl fluoride	121.0 [123.7(1)]^68	119.7 [122.7(4)]^39	124.4 [125.7(3)]^32
Oxirane	71.9 [69.1(1)]^36	77.9 [90.4(12)]^36,37	67.3 [67.3(1)]^26
Thiirane	94.6 [94.5(20)]^29	99.1 [96.0(5)]^38	84.9 [85.0(2)]^30
Methylenecyclopropane	87.0 [89.2(6)]^33	81.6 [N/A]	91.9 [92.5(5)]^34
2,5-Dihydrofuran	58.1 [54.3(3)]^23	64.6 [57.8(18)]^36	53.9 [53.0(3)]^25

---

The theoretical equilibrium and experimental zero-point intermolecular distances are shown in Table 2, where it can be seen that, on average, the experimental distances are 0.079 Å longer than those from theory. This improves to 0.055 Å if only the halogen bonding complexes are considered. In all cases the ab initio distances are shorter than those from experiment, with the equilibrium/zero-point comparison likely to be the main cause of the difference. A previous CCSD(T)-F12 theoretical study has shown that upon formation of H₃N⋯ClF the ClF bond distance increases by 0.057 Å (see Table 3 of ref. 43) indicating that such rearrangements will also contribute to the difference between experimental and theoretical intermolecular distances in B⋯ClF complexes. Comparing hydrogen and halogen bond lengths, B⋯HCl is always shorter than B⋯ClF for any given B. The increase in hydrogen bond distance for B⋯HCCH compared to B⋯HCl may be expected as ethyne forms weaker hydrogen bonds than HCl.¹⁷

Table 2 CCSD(T)-F12b optimised equilibrium intermolecular hydrogen and halogen bond distances (Å). Values in square brackets refer to zero-point experimental values from the literature

Lewis base B	B⋯HCl	B⋯HCCH	B⋯ClF
Formaldehyde	1.885 [1.968(10)]^27	2.245 [2.39(2)]^35	2.466 [2.523(7)]^28
Vinyl fluoride	2.066 [2.123(1)]^36	2.341 [2.441(4)]^39	2.687 [2.719(5)]^32
Oxirane	1.773 [1.841(1)]^22	2.154 [2.392(20)]^36,37	2.383 [2.437(2)]^26
Thiirane	2.258 [2.329(28)]^29	2.691 [2.76(5)]^38	2.483 [2.542(3)]^30
Methylenecyclopropane	2.278 [2.323(11)]^33	2.660 [N/A]	2.620 [2.675(10)]^34
2,5-Dihydrofuran	1.714 [1.798(5)]^23	2.088 [2.127(8)]^36	2.351 [2.422(5)]^25

---

Benchmark quality interaction energies for the optimised geometries were produced using an extrapolation scheme to estimate the complete basis set (CBS) limit and using the CP correction to account for the basis set superposition errors (BSSE) that occur for intermolecular complexes in finite basis sets. These interaction energies are displayed in Table 3. It is important to note that at the true CBS limit the CCSD(T) and CCSD(T)-F12b energies would be identical. The attractions in B⋯HCCH are considerably weaker than for the B⋯HCl (or B⋯ClF) cases, demonstrating that any additional CH⋯π interaction does not fully compensate for the large reduction in hydrogen bond strength from making HCCH the donor, or for any other secondary interactions between B and Cl. With two notable exceptions (see below), the interaction energies of B⋯HCl and B⋯ClF are roughly equivalent for any given Lewis base, thus it is apparent that the deviation from collinearity is not simply related to the overall strength of the interaction. The individual interaction energies from the various basis sets used in the CBS extrapolations are tabulated in the ESI,† along with the magnitude of the BSSE for each complex. The average BSSE with the aug-cc-pV(T+d)Z basis sets used in the geometry optimisations is 0.26 kcal mol⁻¹, which is small enough that attempting CP corrected geometry optimisations would have a very small effect on the structures, incommensurate with the large increase in computational cost this would require.

Table 3 CCSD(T)/CBS interaction energies (kcal mol⁻¹) for the hydrogen and halogen bonding complexes

Lewis base B	B⋯HCl	B⋯HCCH	B⋯ClF
Formaldehyde	−5.72	−3.21	−6.02
Vinyl fluoride	−3.12	−2.05	−2.93
Oxirane	−7.43	−3.92	−7.82
Thiirane	−6.48	−3.57	−13.22
Methylenecyclopropane	−4.33	−2.67	−6.70
2,5-Dihydrofuran	−8.23	−3.95	−8.72

---

The methylenecyclopropane⋯ClF complex has an interaction energy that is 2.37 kcal mol⁻¹ larger in magnitude than the analogous HCl complex. In the set of Lewis bases chosen, methylenecyclopropane is notable as the only one that leads to a hydrogen or halogen bond forming with a π system, in this case a C–C double bond, which may account for the discrepancy in the relative interaction energies. The more surprising difference in the interaction energies occurs when thiirane acts as a Lewis base. Table 3 shows that the halogen bond is slightly more than twice as strong as the hydrogen bond, yet for oxirane the two interactions are roughly comparable in energy. This unusually strong interaction was the subject of a recent communication, where it was suggested that the underlying mechanism features significantly greater charge transfer and that thiirane⋯ClF should be described as a so-called Mulliken inner complex,⁶⁹ a conclusion also arrived at from a consideration of the experimental Cl nuclear quadrupole coupling tensor of thiirane⋯ClF.³⁰

In order to produce some insight into the differences in the interactions that determine the structure of the complexes and, in particular, the directionality of the hydrogen and halogen bonds, SAPT calculations have been carried out to partition the interaction energies into a “chemist's grouping”. How the resulting electrostatic, exchange, dispersion and induction contributions change as a function of θ is displayed for all 18 complexes in Fig. 3, where φ, the hydrogen or halogen bond distance and the monomer geometries are all fixed at their equilibrium values. The individual SAPT terms for the CCSD(T)-F12b optimised geometries are tabulated in the ESI,† where it can be seen that there is excellent agreement between the total SAPT interaction energy and the benchmark values in Table 3, lending a great deal of confidence to the accuracy of the individual SAPT terms. The charge transfer on complex formation in terms of fractional electrons was calculated using the natural bond orbital (NBO) method in order to supplement the SAPT analysis. Full details of these calculations and a data table are provided in the ESI,† where it can be seen that charge transfer is relatively small for all complexes, with the exception of thiirane⋯ClF (see above).

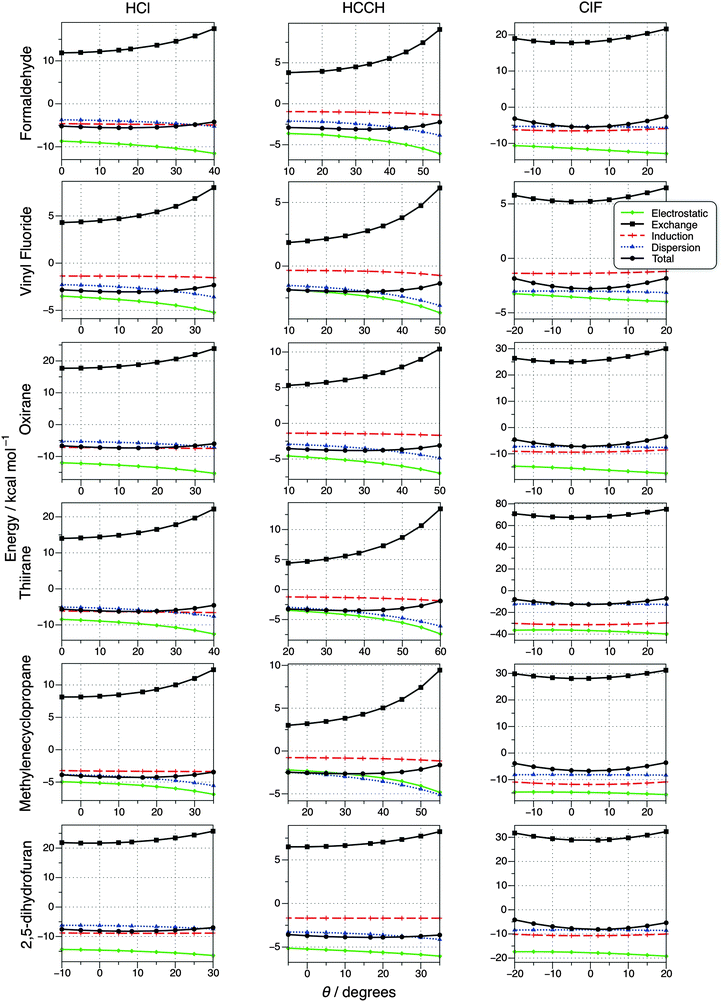Fig. 3 Variation of SAPT interaction energy components with the deviation from collinearity (θ) for hydrogen- and halogen-bonded complexes.

Fig. 3 shows that the total interaction energy with respect to θ is relatively flat for the hydrogen bonding complexes, but there is significantly more pronounced curvature for halogen bonding. While this does indicate stronger directionality in halogen bonding, appreciable interaction energies are still observed when the nonlinearity is varied. For example, in oxirane⋯ClF when θ = 25° the interaction energy is still −3.48 kcal mol⁻¹, which is comparable to the interaction in the B⋯HCCH complexes. As previously noted by Stone,⁸ the minimum in the interaction energy for the halogen bonding complexes is strongly connected to the minimum in the exchange-repulsion contribution, although the two minima do not exactly coincide. It is obvious that this is not the case for hydrogen bonding, where the minimum in the exchange occurs at an angle far removed from that for the overall interaction energy.

For all of the complexes considered (with the exception of methylenecyclopropane⋯HCCH) Fig. 3 illustrates that the strongest attractive component is due to electrostatics, but the other components all contribute in a non-negligible fashion. For halogen bonding the dispersion term is effectively flat with respect to angle, but it is interesting that at the equilibrium geometry it acts as a good approximation of the overall interaction energy, i.e., all of the other contributions effectively cancel out. This suggests that one should be very careful to include an accurate description of dispersion when more approximate computational chemistry is used to investigate halogen bonding, especially MP2 and basic DFT methods. This reinforces the study of Kozuch and Martin, who found that an accurate description of halogen bonding with DFT requires functionals that account for dispersion and have a long-range correction, such as ωB97XD.⁷⁰ A previous SAPT investigation of halogen bonding in formaldehyde⋯halomethane complexes also concluded that dispersion was a very important component of the interaction energy, in some cases representing a significantly larger contribution than electrostatics.⁷¹ The SAPT dispersion term in the case of methylenecyclopropane⋯ClF is 1.43 kcal mol⁻¹ more attractive than the total interaction energy, slightly disrupting the trend outlined above. As the Lewis base in this case is a π-system, the increased dispersion contribution appears logical and accounts for some of the additional stability when methylenecyclopropane⋯ClF is compared with methylenecyclopropane⋯HCl.

A number of studies have demonstrated a direct correlation between strength of halogen bonding and charge transfer,^20,43,72 hence it is not so surprising that the induction term (where charge transfer would contribute in SAPT) is shown to be a relatively large contribution here. A recent study combining modern valence bond and block-localised wavefunction theories also concluded that charge transfer was one of the driving forces for halogen bonding.⁷³ As briefly mentioned above, for thiirane⋯ClF the larger degree of charge transfer, and thus induction, compared to other halogen bonding complexes has been the subject of a recent communication. Therefore, a full analysis of the differences between the thiirane and oxirane halogen bonding complexes can be found in ref. 69 and the details are not repeated here. There is a degree of controversy over the role of charge transfer in intermolecular interactions, with some groups claiming that charge transfer and polarisation are both charge redistribution on complex formation (see, for example, ref. 74) and are indistinguishable. Many theoretical descriptions of charge-transfer are also very closely related to the definition of BSSE,⁷⁵ further muddying the issue. However, the view taken by Shaik and co-workers is that experiment can distinguish between the sub-units of a complex and hence polarisation within an individual sub-unit should be distinguished from charge transfer between them.⁷³ In SAPT polarisation and charge transfer are both grouped within the induction energy, and although it is possible to separate charge transfer from the total induction energy this is basis set dependent procedure and has not been carried out in the present investigation.^76,77

When considering the hydrogen bonded complexes in Fig. 3 there is greater curvature to the dispersion term than for halogen bonding, and it becomes more attractive as the deviation from linearity is increased from the equilibrium position, i.e., as θ becomes larger. In addition to the weaker hydrogen bond interaction, the B⋯HCCH complexes have different secondary interactions compared to B⋯HCl, which are considered to be important in terms of deviation from collinearity in hydrogen bonds. As detailed in the Introduction, for B⋯HCl this secondary interaction can be pictured as being between Cl and an electrophilic region of B. Considering the SAPT components as θ is increased from zero, i.e., as any secondary interactions are increased, it can be seen that a subtle interplay between the different terms results; the exchange-repulsion increases, but so do the attractive electrostatic and dispersion terms. Induction remains roughly constant, perhaps suggesting that this contribution is related to the primary H-bond interaction. The induction term is significantly smaller for all of the B⋯HCCH complexes, correlating well with the reduced NBO charge transfer.

A theoretical study based on NBO analysis and the Quantum Theory of Atoms in Molecules by Grabowski also examined the underlying mechanisms of hydrogen and halogen bonding, with the conclusion that the mechanisms were the same; driven/steered by electrostatic interaction and followed by an “electron charge shift”.²⁰ While at first glance this appears to contradict the current findings, there is a significant area of overlap between the two. Firstly it is important to note that the complexes considered by Grabowski do not feature any strong secondary interactions that promote the deviation from collinearity in hydrogen bonding and were probed in terms of intermolecular distance rather than angle, meaning a comparison is not entirely straightforward. Although the present work and that of Stone⁸ clearly demonstrates that it is exchange-repulsion that is responsible for the enhanced collinearity of halogen bonding, electrostatics are generally the most attractive component and are likely to be responsible for the initial attraction between the donor and acceptor. Finally, it is obvious from both investigations that shifts of the electron charge are important contributions to the overall interaction, regardless of whether this is expressed in Grabowski's terms of hyperconjugation and rehybridisation, or the ‘induction’ favoured in the current work.

IV. Conclusions

Rotational spectroscopy has been used for several decades to investigate small molecular clusters bound by hydrogen or halogen bonds. The capability of the method to consider isolated complexes in the gas phase makes for a natural comparison with highly accurate ab initio data. However, producing such theoretical data in a computationally practical manner is a relatively recent development, made feasible by advances in explicitly correlated (F12) wavefunctions. The current work presents the results of F12 geometry optimisations on a systematic series of complexes and compares the resulting equilibrium structures to those elucidated through rotational spectroscopy. The primary aim of this comparison is to establish whether the quadrupole coupling tensor and rigid monomer approach used experimentally provides good approximations to the angles defining the directionality and linearity of the hydrogen and halogen bonds. On the whole there is excellent agreement and it is especially striking for the intermolecular interaction nonlinearity (θ) of all the B⋯HCl and B⋯ClF complexes, confirming that using the Cl nuclear quadrupole coupling tensor (as described in the Introduction) does indeed produce a good approximation of the equilibrium value of θ. As expected, the agreement between the zero-point experimental and equilibrium theoretical structures for B⋯HCCH is at a lower level, but still usefully close. Based on the excellent agreement for the systems where it was possible to use the nuclear quadrupole tensor method, it is suggested that the theoretical structure for B⋯HCCH would make for a more accurate comparison with the experimental data for B⋯HCl and B⋯ClF.

Geometrical parameters other than θ also show a reasonable level of agreement, and it is especially good for the angular geometry (φ) of the B⋯ClF series. As the experimental method leads to zero-point (rather than equilibrium) geometries and assumes no distortion of the sub-unit geometries on complex formation, it is perhaps unsurprising that the experimental intermolecular distances are, on average, around 0.08 Å longer than those from theory. However, the trends are all preserved, with the general order of the distance being B⋯HCl < B⋯HCCH < B⋯ClF for the various Lewis bases. Benchmark quality interaction energies have been calculated for all of the complexes and, in general, the interaction in B⋯HCl is roughly the same strength as B⋯ClF for a given B. The major exception to this is when B is thiirane, as the halogen bond is approximately twice as strong as the comparable hydrogen bond. It has been proposed that the underlying mechanism of halogen bonding is different in this case, with significantly greater charge transfer.⁶⁹ The high accuracy theoretical structures and interaction energies detailed in this article could be used as a benchmark set/database for more approximate methods such as DFT or molecular mechanics, perhaps aiding in future developments, but this is beyond the scope of the present study.

A SAPT analysis of the variation in the electrostatic, exchange-repulsion, induction and dispersion components of the interaction energy with respect to deviation from collinearity was carried out to provide some insights into the underlying mechanisms of interaction for the different complexes. The first conclusion is that the SAPT terms show a striking difference between hydrogen and halogen bonding and it is obvious that the exchange-repulsion is responsible for the smaller deviation from linearity in the latter, adding further weight to previous work by Stone.⁸ Electrostatics generally represent the most important attractive term, but as dispersion is a good approximation to the total interaction energy its importance in halogen bonding cannot be discounted. Comparing the two hydrogen bond donors indicates that B⋯HCCH has significantly less induction (which contains any charge transfer contribution along with polarisation) than B⋯HCl, contributing to the weaker interaction. Although secondary interactions between the H-bond donor and the Lewis base are thought to be important in determining the nonlinearity, SAPT reveals this to be a subtle interplay of different components. It was also observed that even when θ is significantly displaced from the minimum energy structure, halogen bonding can still result in appreciable interaction energies.

Notes and references

1. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, New York, 1999.
2. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711.
3. M. R. Scholfield, C. M. Vander Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22, 139.
4. P. Metrangolo and G. Resnati, Cryst. Growth Des., 2012, 12, 5835.
5. F. Meyer and P. Dubois, CrystEngComm, 2013, 15, 3058.
6. A. D. Buckingham, P. W. Fowler and A. J. Stone, Int. Rev. Phys. Chem., 1986, 5, 107.
7. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748.
8. A. J. Stone, J. Am. Chem. Soc., 2013, 135, 7005.
9. A. C. Legon and D. J. Millen, Chem. Rev., 1986, 86, 635.
10. A. C. Legon, Chem. Soc. Rev., 1990, 19, 197.
11. A. C. Legon, Chem. Soc. Rev., 1993, 22, 153.
12. A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686.
13. A. C. Legon and H. E. Warner, J. Chem. Phys., 1993, 98, 3827.
14. A. C. Legon and J. C. Thorn, J. Chem. Soc., Faraday Trans., 1993, 89, 4157.
15. H. I. Bloemink, K. Hinds, A. C. Legon and J. C. Thorn, Chem. Phys. Lett., 1994, 223, 162.
16. A. C. Legon and D. J. Millen, Faraday Discuss. Chem. Soc., 1982, 73, 71.
17. A. C. Legon and D. J. Millen, J. Am. Chem. Soc., 1987, 109, 356.
18. A. C. Legon, Chem. – Eur. J., 1998, 4, 1890.
19. A. C. Legon, Phys. Chem. Chem. Phys., 2010, 12, 7736.
20. S. J. Grabowski, Phys. Chem. Chem. Phys., 2013, 15, 7249.
21. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386.
22. A. C. Legon, Faraday Discuss., 1994, 97, 19.
23. A. C. Legon and J. C. Thorn, Chem. Phys. Lett., 1994, 227, 472.
24. A. C. Legon, C. A. Rego and A. L. Wallwork, J. Chem. Phys., 1992, 97, 3050.
25. S. A. Cooke, G. K. Corlett, C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1997, 275, 269.
26. H. I. Bloemink, C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1996, 251, 275.
27. A. C. Legon, J. Chem. Soc., Faraday Trans., 1996, 92, 2677.
28. S. A. Cooke, G. K. Corlett, C. M. Evans, A. C. Legon and J. H. Holloway, J. Chem. Phys., 1998, 108, 39.
29. C. M. Evans and A. C. Legon, Chem. Phys., 1995, 198, 119.
30. C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1996, 255, 119.
31. Z. Kisiel, P. W. Fowler and A. C. Legon, J. Chem. Phys., 1990, 93, 3054.
32. J. B. Davey, J. H. Holloway, A. C. Legon and E. R. Waclawik, Phys. Chem. Chem. Phys., 1999, 1, 2415.
33. Z. Kisiel, P. W. Fowler and A. C. Legon, J. Chem. Phys., 1994, 101, 4635.
34. S. A. Cooke, J. H. Holloway and A. C. Legon, J. Chem. Soc., Faraday Trans., 1997, 93, 4253.
35. N. W. Howard and A. C. Legon, J. Chem. Phys., 1988, 88, 6793.
36. G. C. Cole, R. A. Hughes and A. C. Legon, J. Chem. Phys., 2005, 122, 134311.
37. A. C. Legon, Chem. Phys. Lett., 1995, 247, 24.
38. R. C. Batten, G. C. Cole and A. C. Legon, J. Chem. Phys., 2003, 119, 7903.
39. G. C. Cole and A. C. Legon, Chem. Phys. Lett., 2003, 369, 31.
40. C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4.
41. L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75.
42. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
43. J. G. Hill and X. Hu, Chem. – Eur. J., 2013, 19, 3620.
44. A. C. Legon, Phys. Chem. Chem. Phys., 2014, 16, 12415.
45. T. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
46. G. Knizia, T. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
47. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushchenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, see http://https://molpro.net.
48. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242.
49. T. H. Dunning Jr, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244.
50. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007.
51. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
52. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285.
53. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143.
54. E. F. Valeev, Chem. Phys. Lett., 2004, 395, 190.
55. G. Knizia and H.-J. Werner, J. Chem. Phys., 2008, 128, 154103.
56. K. E. Yousaf and K. A. Peterson, Chem. Phys. Lett., 2009, 476, 303.
57. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
58. D. Schwenke, J. Chem. Phys., 2005, 122, 014107.
59. J. G. Hill, K. A. Peterson, G. Knizia and H.-J. Werner, J. Chem. Phys., 2009, 131, 194105.
60. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, USA.
61. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
62. T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106.
63. J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556.
64. E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 014101.
65. E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 104107.
66. E. G. Hohenstein and C. D. Sherrill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 304.
67. M. Kolář, J. Hostaš and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 9987.
68. A. C. Legon and P. Ottaviani, Phys. Chem. Chem. Phys., 2002, 4, 4103.
69. J. G. Hill, Phys. Chem. Chem. Phys., 2014 10.1039/c4cp03412k.
70. S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918.
71. K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2008, 4, 232.
72. P. Ramasami and T. A. Ford, Comput. Theor. Chem., 2012, 990, 227.
73. C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput. DOI:10.1021/ct500422t.
74. P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278.
75. A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, 2nd edn, 2013.
76. A. J. Stone, Chem. Phys. Lett., 1993, 211, 101.
77. A. J. Stone and A. J. Misquitta, Chem. Phys. Lett., 2009, 473, 201.

---

Footnote

† Electronic supplementary information (ESI) available: Convergence of interaction energies, tabulated SAPT energies, NBO charge transfer, definition of angular geometries and Cartesian coordinates of optimised structures. See DOI: 10.1039/c4cp03376k

---