Open Access Article
Open Access ArticleMultiscale study of the influence of cationic surfactants on amorphous calcium phosphate precipitation†
A.
Selmani
a,
I.
Coha
b,
K.
Magdić
b,
B.
Čolović
c,
V.
Jokanović
c,
S.
Šegota
b,
S.
Gajović
d,
A.
Gajović
e,
D.
Jurašin
f and
M.
Dutour Sikirić
*f
aDepartment of Chemistry, Faculty of Science, University of Zagreb, Horvatovac 102a, 10000 Zagreb, Croatia
bDivision for Marine and Environmental Research, Ruđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia
cVinča Institute of Nuclear Sciences, University of Belgrade, Mike Petrovića Alasa 11-14, 11001 Belgrade, Serbia
dCroatian Institute for Brain Research, School of Medicine, University of Zagreb, Šalata 3, 10000 Zagreb, Croatia
eDivision of Materials Physics, Ruđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia
fDivision of Physical Chemistry, Ruđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia. E-mail: sikiric@irb.hr; Web: http://www.irb.hr/eng/People/Maja-Dutour-Sikiric Tel: +385 1 456 0941
First published on 7th October 2015
Abstract
The influence of monomeric and micellar concentrations of the cationic monomeric, dodecyltrimethylammonium bromide (DTAB), and the corresponding dimeric, bis(N,N-dimethyl-N-dodecyl)ethylene-1,2-diammonium dibromide (12-2-12), surfactants on the formation and transformation of amorphous calcium phosphate (ACP) was investigated. The combination of microscopy (AFM and TEM) and light scattering techniques (size and zeta potential measurements) enabled, for the first time, the simultaneous monitoring of the effect that additives exert on different length scales during CaP formation in solution – from prenucleation clusters and ACP particles to the crystalline phase. Depending on their aggregation state (monomers or micelles) and the geometry of the aggregate (spherical or elongated micelles), DTAB and 12-2-12 have exhibited different effects on the rate of ACP transformation, as well as on the morphology of the amorphous and crystalline phases. It was shown that the effect of surfactants on the precipitation process observed on the microscale could be a result of different pathways on the nanoscale. The obtained results may have implications for the understanding of the general mechanism of inorganic–organic interactions underlying the biomineralization processes, as well as for materials science.
Introduction
Amorphous calcium phosphate (ACP) is the initial solid phase formed during calcium phosphate (CaP) precipitation from basic and neutral solutions.1,2 Its excellent biological properties3 and the mounting evidence that its formation is the first step by which hard tissue in vertebrates are formed4,5 lately motivate interest for the investigation of ACP formation and its further transformation, as well as for application in different types of biomaterials.6First to propose that the formation of ACP is the first step in the precipitation of CaPs was Posner7 in 1965. Posner also proposed that the basic structural unit of ACP is a spherical Ca9(PO4)6 cluster, later named Posner's cluster, about 9.5 Å in diameter.8 A large number of these clusters are randomly close packed in spheres 30–100 nm in diameter, which in turn assemble into chain-like aggregates.9,10 Although the existence of Posner's clusters was accepted, only the recent development of experimental techniques (cryogenic transmission electron microscopy (cryo-TEM), atomic force microscopy (AFM) and dynamic light scattering (DLS)) revealed their formation under different experimental conditions.11–14 However, as was noted by Dey et al.,13 the agreement in size between prenucleation clusters (PNCs) observed in different systems and Posner's clusters should not be taken as proof of their chemical and structural identity. Upon contact with the mother liquor, ACP is prone to transform into more stable crystalline phases such as octacalcium phosphate [OCP, Ca8(HPO4)2(PO4)4·5H2O], calcium hydrogen phosphate dihydrate (DCPD, CaHPO4·2H2O), calcium-deficient apatite [CDHA, Ca10−x(HPO4)x(PO4)6−x(OH)2−x, 0 < x < 2] and/or hydroxyapatite [HAP, Ca10(PO4)6(OH)2].10,15–18 Therefore, in order to be successfully applied, ACP should be stabilized. In organisms, ACP is stabilized by specific proteins, like amelogenin and enamelin in teeth.19 Despite the considerable interest for ACP, the mechanism of its formation and transformation on the nanoscale, as well as the role of organic molecules, has not yet been fully elucidated.
Surfactants, due to their ability to self-assemble in different supramolecular structures and ready availability in many different designs, lend themselves as ideal model systems for systematic studies of the effect of organic molecules on the formation and transformation of ionic crystals.20 Moreover, they can be used as models even for complex systems such as proteins and biomembranes.21 The surfactants typically used for the control of precipitation processes are the conventional ones composed of one hydrophilic headgroup and one hydrophobic tail, i.e. monomeric surfactants. In the past three decades, dimeric surfactants, consisting of two molecules of monomeric surfactants covalently linked at the level of the headgroups or close to them with a flexible or rigid, hydrophobic or hydrophilic spacer, have drawn considerable attention in both fundamental research and application.22–25 The reason lies in their superior physicochemical properties in comparison to those of the corresponding monomeric surfactants. Among the dimeric surfactants, bisquaternary ammonium surfactants, due to the relative ease of their synthesis and enhanced surface properties, have received much attention. In addition, bisquaternary ammonium surfactants possess antibacterial properties and have been used in the synthesis of porous materials,22 making them also of potential interest in the design and preparation of biomaterials. While dimeric surfactants can be found in cosmetic and pharmaceutical products,25 the investigation of their possible use in controlling precipitation processes is scarce.
The aim of this paper was to assess the influence that monomers and micelles of monomeric dodecyltrimethylammonium bromide (DTAB) and the corresponding dimeric bis(N,N-dimethyl-N-dodecyl)ethylene-1,2-diammonium dibromide (12-2-12) quarternary ammonium surfactant (Scheme 1) exert on the formation and transformation of ACP in solution, in order to contribute to the understanding of the factors governing the first stages of CaP formation in complex systems. Although both surfactants have the same headgroup(s) and the same alkyl chain lengths, connecting two DTAB molecules at the level of headgroups with an ethylene spacer results in markedly different 12-2-12 properties. It is known that 12-2-12 is more surface-active than DTAB and has peculiar micellization properties.22,26 Due to the geometric constraints, dimeric surfactants with short ethylene spacers tend, unlike DTAB, to aggregate in elongated and worm-like micelles at relatively low surfactant concentrations even without an added electrolyte.22,26 Such a choice of surfactants enabled the assessment of the influence of different surfactant molecular (different number of headgroups and alkyl chains) and aggregate structures (spherical and elongated micelles) on CaP precipitation while keeping the additive chemical functionality and composition the same. The combination of different experimental techniques, microscopy (AFM and TEM) and light scattering techniques (size and zeta potential measurement) enabled, for the first time, the simultaneous monitoring of the effect that additives exert on different length scales during CaP formation in solution, from PNCs and ACP particles to the final crystalline phase. Understanding interactions in such complex systems is of interest in materials science for the design of new organic–inorganic materials and it also contributes to the understanding of principal factors governing the precipitation processes in biological environments.
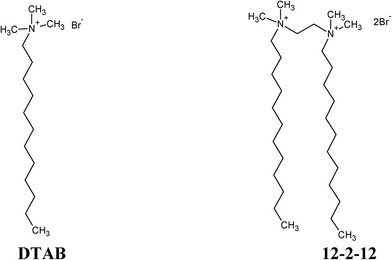 | ||
| Scheme 1 Molecular structures of monomeric, dodecyltrimethylammonium bromide (DTAB), and its corresponding dimeric, bis(N,N-dimethyl-N-dodecyl)ethylene-1,2-diammonium dibromide (12-2-12) surfactants. | ||
Experimental section
Materials
Analytical grade chemicals including calcium chloride (CaCl2), sodium hydrogen phosphate (Na2HPO4) and dodecyltrimethylammonium bromide (DTAB) were obtained from Sigma Aldrich, Germany. The dimeric surfactant, bis(N,N-dimethyl-N-dodecyl)ethylene-1,2-diammonium dibromide (12-2-12), was synthesized and characterized as described elsewhere.24 The purity of surfactants was tested by surface tension measurements, i.e. no minima in the surface tension isotherm confirmed the high purity of both surfactants. Milli-Q water (Millipore) was used in all experiments.CaCl2 and Na2HPO4 stock solutions were prepared from the analytical grade chemicals which were dried overnight in a desiccator over silica gel. The pH of sodium hydrogen phosphate stock solution was adjusted to 7.4 with HCl. Each stock solution contained 0.05% sodium azide to prevent bacterial contamination. Stock solutions of DTAB and 12-2-12 were prepared by weighting dried surfactants and dissolving them in water.
Surfactant/Na2HPO4 systems
The presence of an electrolyte can significantly alter the interfacial and micellization properties of ionic surfactants.27 Therefore, in order to determine the monomer and micellar surfactant concentrations under the given experimental conditions, DTAB and 12-2-12 solutions at an electrolyte concentration corresponding to that in the precipitation system, c(Na2HPO4) = 3 mmol dm−3 and pH = 7.4 were prepared for surface tension measurements (for details of surface tension measurement, please see the methods section).Preparation of precipitation systems
The control precipitation system was prepared by fast mixing of equal volumes of equimolar CaCl2 and Na2HPO4 solutions. Anionic and cationic reactant solutions used for precipitation experiments were diluted from the respective stock solutions. The initial concentrations in the precipitation system were c(CaCl2) = c(Na2HPO4) = 3 × 10−3 mol dm−3 at pH = 7.4. In the control system, the resulting saturation indices of HAP, OCP and ACP were 13.5, 5.2 and 3.7, respectively. Precipitation systems containing surfactants with monomer and micellar concentrations were prepared by adding the respective surfactant solutions to the phosphate solution before mixing the reactant solutions and readjusting the pH if necessary. Surfactant concentrations for precipitation systems below and above the corresponding cmc as well as, in the case of 12-2-12, above the 2nd break observed in the surface tension isotherm were chosen. In this way, investigation of the influence of surfactant monomers and different micellar structures on ACP formation and transformation was possible. The solution composition of the investigated precipitation systems is given in Table 1.| System | c(CaCl2)/mmol dm−3 | c(Na2HPO4)/mmol dm−3 | c(DTAB)/mmol dm−3 | c(12-2-12)/mmol dm−3 | |
|---|---|---|---|---|---|
| CS – control system, MS – monomeric surfactant, DS – dimeric surfactant. | |||||
| CS | 3 | 3 | |||
| MS1 | 3 | 3 | 0.1 | Monomers | |
| MS2 | 3 | 3 | 30 | Micelles | |
| DS1 | 3 | 3 | 0.01 | Monomers | |
| DS2 | 3 | 3 | 0.5 | Micelles | |
| DS3 | 3 | 3 | 3 | Micelles | |
The precipitation experiments were performed at 25 ± 0.1 °C without additional stirring. The precipitation of calcium phosphate was followed by continuously monitoring pH changes (Metrohm 701 pH/ion meter). Samples for further analysis were taken after 10 and 30 minutes, as well as after 24 hours of aging time. These time periods were chosen based on pH measurements to enable precipitate characterization at different precipitation stages.
Methods
Data interpretation
The maximum surface excess of surfactant molecules (Γmax) at the air/solution interface was calculated from the maximal slope (dγ/dlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) in the surface tension vs. concentration curve using the Gibbs adsorption equation:27
c) in the surface tension vs. concentration curve using the Gibbs adsorption equation:27 | (1) |
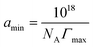 | (2) |
Values of the critical micelle concentration (cmc) were determined from the intersection of the two straight lines drawn in the low and high concentration regions of the surface tension curves (γ vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) using linear regression analysis.
c) using linear regression analysis.
The ion activities in the control precipitation system were calculated by VMINTEQ 3.0 (freely available at http://vminteq.lwr.kth.se/download/). Activity coefficients were calculated using the Davies approximation of the Debye–Hückel equation (b = 0.3). Saturation index (SI), defined as:
SI = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IAP − log IAP − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ksp Ksp | (3) |
Results and discussion
Properties of surfactant/Na2HPO4 systems
It is well established that the presence of an electrolyte in an aqueous solution of an ionic surfactant can significantly alter its interfacial and micellization behavior due to screening of the ionic headgroup charge. As a result, the electrostatic repulsions between surfactant headgroups within the adsorbed monolayer and micelles are reduced.27 Therefore, DTAB and 12-2-12 interfacial and micellization properties were determined in the presence of an actual phosphate concentration in the precipitation system. Detailed description and discussion of the obtained results are given in the ESI.† Here, a brief description of the main findings is presented.Surface tension and dynamic light scattering measurements revealed the difference in DTAB and 12-2-12 interfacial and micellization properties (Fig. S2 and S3,†Table 2). As expected,22,24 12-2-12 was more efficient in lowering the surface tension and had much lower cmc in comparison with DTAB (Fig. S2,†Table 2). In addition, 12-2-12 molecules occupied a larger area at the air/solution interface than DTAB.
| Surfactant | Γ max /mol m−2 | a min /nm2 | cmc/mmol dm−3 |
|---|---|---|---|
| a Values in brackets are expressed per alkyl chain in the molecule of the dimeric surfactant. | |||
| DTAB | 1.93 | 0.86 | 14.6 |
| 12-2-12 | 0.96 (1.9) | 1.74 (0.87) | 0.36 |
The difference in micellization behavior indicated by the shape of the surface tension isotherms of DTAB and 12-2-12 was confirmed by DLS and zeta potential measurements. At a concentration above the cmc, only small DTAB micelles with an average hydrodynamic diameter of 3.6 ± 0.3 nm (Fig. S3a†) and a ζ potential of 29.6 ± 2.5 mV were detected. Unlike DTAB, DLS measurements revealed that the value of the hydrodynamic diameter of the 12-2-12 micelles increased with increasing surfactant concentration from 4.7 ± 0.5 nm immediately above the cmc to 10.9 ± 0.4 nm at concentrations above the 2nd break in the surface tension isotherm (Fig. S3b†). In addition, at concentrations above the 2nd break, a bimodal distribution of the ζ potential of 12-2-12 micelles was observed (peaks at 14.2 ± 4.8 and 37.7 ± 7.3 mV). Based on these results and literature data for DTAB22,24,31 and 12-2-12,22,32 it is reasonable to assume the existence of spherical micelles in the investigated DTAB and 12-2-12 systems at concentrations immediately above the cmc, and the coexistence of spherical and elongated micelles at 12-2-12 concentrations above the 2nd break.
Based on these results, surfactant concentrations for the precipitation experiments were chosen (Table 1) below (MS1 and DS1) and above (MS2 and DS2) the corresponding cmc values, as well as above the second break (DS3) observed in the surface tension vs. concentration curve of 12-2-12 (Fig. S2b†). In this way, it was possible to assess how the different charge and rigidity of monomer molecules, as well as the different charge density and distribution, size, shape and curvature of micelles, affected the ACP formation and transformation. It should be noted that in micellar surfactant solutions, monomers and micelles coexist in dynamic equilibrium.27
The influence of monomeric and dimeric surfactants on ACP precipitation
As Bleek and Taubert have recently pointed out, different investigations of the influence of additives on CaP formation and transformation are carried out under a wide range of experimental conditions and therefore, their results cannot be fully compared.33 In order to be able to compare the results obtained in this study with literature data to a larger extent, the conditions corresponding to the study of the influence of anionic and cationic polyelectrolytes (PEs) on ACP formation (Bar-Yosef Ofir et al.10) were chosen. The choice was motivated by parallels that can be drawn between the behavior of PEs and surfactants in precipitation systems. Unlike small molecular additives, surfactants included, PEs can, depending on their solution concentration, exhibit a dual role in the precipitation process, i.e. they can act as promoters or as inhibitors. The explanation for such a behavior is that at low concentrations, polyelectrolytes can act as heterogeneous nucleation centers, while at high concentrations, they can inhibit the growth of nascent nuclei.20 Studies of the influence of surfactants on the formation of different biominerals (CaPs, calcium oxalates and carbonates) have shown that surfactant micelles can act as templates for the formation of a solid phase, facilitating nucleation and/or initial growth.20 In addition, as an explanation for the observed changes in the crystallizing polymorph or crystal hydrate, preferential adsorption of the surfactants on the nuclei of one phase was suggested as a possible mechanism.20 The mode of adsorption, consequently the effect on the nascent solid phase, of PEs10 as well as surfactants34,35 depends on their concentration and molecular structure.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.64) and as a result, the pH decreased. Subsequent pH increase, previously explained by the formation of ion clusters,30,36 was followed by a stage in which the pH slightly decreased (section 2a, Fig. 1a). This stage is associated with the formation of ACP, during which the changes in pH and calcium concentrations are small or absent.10,16,30,36,38 As can be seen from Fig. 1c, except in the presence of DTAB monomers (MS1), the initial pH drop in systems containing surfactants is smaller than that in the control system. Studies of cetyltrimethylammonium bromide surface and micellization properties in the presence of PO43− ions have shown that phosphate ions can replace bromide ions on the surface of the micelle.39 Based on this result, it could be assumed that phosphate ions bind to the surface of DTAB and 12-2-12 micelles in the investigated systems, in that way, influencing the initial pH change. However, due to the lack of relevant equilibrium data for the micelle/phosphate systems, it is not possible to quantify this influence following the approach of Wang et al.30 for the control system. The explanation of pH changes in precipitation systems containing monomers is not straightforward and needs more investigation of DTAB and 12-2-12 monomer interaction with phosphate ions. In DTAB and 12-2-12 solutions at surfactant concentrations below the cmc, both monomers are considered to be fully dissociated,22 which cannot account for the observed changes in the initial pH. The slopes of section 2a of the pH curves did not differ much, indicating similar rates of ACP formation in all systems.
0.64) and as a result, the pH decreased. Subsequent pH increase, previously explained by the formation of ion clusters,30,36 was followed by a stage in which the pH slightly decreased (section 2a, Fig. 1a). This stage is associated with the formation of ACP, during which the changes in pH and calcium concentrations are small or absent.10,16,30,36,38 As can be seen from Fig. 1c, except in the presence of DTAB monomers (MS1), the initial pH drop in systems containing surfactants is smaller than that in the control system. Studies of cetyltrimethylammonium bromide surface and micellization properties in the presence of PO43− ions have shown that phosphate ions can replace bromide ions on the surface of the micelle.39 Based on this result, it could be assumed that phosphate ions bind to the surface of DTAB and 12-2-12 micelles in the investigated systems, in that way, influencing the initial pH change. However, due to the lack of relevant equilibrium data for the micelle/phosphate systems, it is not possible to quantify this influence following the approach of Wang et al.30 for the control system. The explanation of pH changes in precipitation systems containing monomers is not straightforward and needs more investigation of DTAB and 12-2-12 monomer interaction with phosphate ions. In DTAB and 12-2-12 solutions at surfactant concentrations below the cmc, both monomers are considered to be fully dissociated,22 which cannot account for the observed changes in the initial pH. The slopes of section 2a of the pH curves did not differ much, indicating similar rates of ACP formation in all systems.
In the control system and MS1, stage 2a is followed by an abrupt decrease in the pH of the system as a consequence of deprotonation of H2PO4− and HPO42− ions associated with the formation of mineral precipitates,38i.e. secondary precipitation of the crystalline phase upon ACP (section 3, Fig. 1a). However, in the precipitation system containing micellar DTAB solution (MS2) and in the systems with 12-2-12 as the additive (DS1, DS2 and DS3) between section 2a and the abrupt decrease in pH (section 3), a region was detected in which a gradual decrease in pH occurred (section 2b, Fig. 1a and b), indicating the difference in the pathway of ACP/crystalline phase transformation compared to those of the control system and MS1.17,40
The abrupt pH decrease in section 3 of the pH curve is associated with the secondary precipitation of the crystalline phase upon ACP.10,38 Unlike in other systems, the drop of pH in section 3 in the MS2 system is slow. A similar behavior was observed in the studies of ACP-mediated HAP nucleation kinetics41 and ACP stabilization by citrate.42 This slow change of pH is attributed to the reduced rate of ACP transformation.30 In the final stage, solution-mediated growth and phase transformation occur (section 4, Fig. 1), followed by a slight pH change.10,38
Recent studies of the influence of different additives (amino acids (Asp, Lys and Gly),43 magnesium36,43 and citrate42 ions, phosphorylated osteopontin peptides,38 cationic and anionic PEs10) on ACP formation and transformation showed that in their presence, the mineralization pathway remains the same as compared to the control. While interactions of small molecular additives and ions with the nascent solid phase are dominated by electrostatic forces, the surfactant adsorption behavior is governed by two opposing interactions, electrostatic and hydrophobic, which could be the origin of their more complex role in the precipitation process. Not only do 12-2-12 monomers have a higher positive charge than DTAB monomers (in the solutions, 12-2-12 monomers are considered to be fully dissociated22), but the presence of two alkyl chains affects the hydrophobic interactions during adsorption. As a consequence, 12-2-12 monomers exhibit a stronger influence on the precipitation processes than DTAB at much lower concentrations, resulting in an effect similar to those of the DTAB and 12-2-12 micelles.
The different rate of pH change in the stages of ACP and crystalline phase formation allows the induction time for nucleation of the crystalline phase (ti) to be determined, from the intersection of the tangents drawn on the second and third sections of the pH vs. time curve.10,42 For MS2, DS1, DS2 and DS3 systems, the intersection of tangents drawn on sections 2b and 3 of the pH curve was used to calculate ti. The induction time is frequently used as an indicator of ACP stability, i.e. the longer it is, the more stable the ACP is considered to be.10,42
The induction time, obtained from the free drift experiments, depended on both the surfactant concentration and the structure of the micelles (Table 3). Monomer concentrations of both surfactants, as well as micellar DTAB concentration, have a negligible effect on induction time. However, the induction time is significantly shorter in the presence of 12-2-12 micelles, with a more prominent effect observed in the presence of smaller, spherical micelles (DS2). Considering the importance of electrostatic forces in precipitate/additive interactions,20,33 it seems that the difference in the overall charge of monomers and micelles and charge distribution at the micelle/solution interface could be the origin of the observed effects. Surfactant monomers have a lower charge in comparison with their aggregates and therefore it can be expected that they influence ti to a much smaller extent.
| System | t i/min | SD |
|---|---|---|
| CS | 45.2 | 1.8 |
| MS1 | 46.1 | 5.2 |
| MS2 | 43.8 | 4.1 |
| DS1 | 43.3 | 3.6 |
| DS2 | 22.8 | 1.6 |
| DS3 | 34.9 | 5.1 |
The influence of DTAB (MS2) and 12-2-12 (DS2 and DS3) micelles on ti was very different. Small, spherical DTAB micelles didn't affect ti at all, while somewhat larger, spherical 12-2-12 micelles were the most effective in promoting ACP/crystalline transformation (the shortest ti). Not only do the DTAB and 12-2-12 micelles have different sizes and ζ potentials (as described in the previous section), but it is also known that they have different distributions of headgroup distances at the micelle/solution interface, i.e. different charge distribution. The distribution of the headgroup distances at the DTAB micelle/solution interface is monomodal peaked at a thermodynamic equilibrium distance determined by the opposite forces at play in micelle formation.22,26 On the other hand, in the case of 12-2-12 micelles, the distribution is bimodal, with an additional peak at the distance corresponding to the fully extended ethylene spacer.22,26 Micelles are not rigid structures and it can be expected that they can adapt to a certain extent to the ionic structure of the nascent solid, i.e. act as efficient promoters of crystalline phase formation. The observed difference in ti between spherical DTAB (MS2) and 12-2-12 micelles (DS2) could mean that bimodal charge distribution enabled 12-2-12 micelles to more easily adapt to the structure of crystalline CaP. The 12-2-12 spherical micelles (DS2) are also more effective than 12-2-12 elongated micelles (DS3) in reducing ti. Although the charge distribution at the micelle/solution interface is bimodal for both types of micelles, in general, elongated micelles have lower surface charge density than the spherical22 ones and therefore exhibit a less pronounced effect on ti. In support of this conclusion is the observation that present at low concentrations, poly-L-lysine (PLL), poly-L-glutamic acid (PGA) and polystyrene sulfonate (PSS) promote ACP transformation, with high molecular weight polyelectrolytes being more effective in decreasing ti than low molecular weight ones, probably due to the higher number of the charged group present in the molecule.10 However, when discussing the influence of the molecular weight of polyelectrolytes, it should be taken into account that PEs with different molecular weights can adopt different conformations. High molecular weight PEs can adopt a less flexible conformation and/or a conformation in which not all functional groups are available for interaction with the solid phase. As a result, the effect of high molecular weight PEs can be less strong than that of low molecular weight PEs, e.g. like in the case of poly(acrylic acid).44
To reveal the nature of processes observed in the pH curves, samples collected after 10 and 30 minutes, as well as after 24 hours of aging time, were subjected to further analysis.
Precipitation systems after 10 min of aging time. In the control system, after 10 min of reaction time, AFM and TEM micrographs revealed the coexistence of the PNCs (Fig. 2a), spherical ACP particles and chain-like aggregates of spherical particles (Fig. 3a). The corresponding FTIR spectra (Fig. S5†) showed phosphate and hydroxyl bands characteristic of amorphous calcium phosphate.6
The average height of small particles in the control system (height ~ 1.4 nm), imaged by AFM, was attributed to PNCs (Table 4). Previous studies have shown that the size of PNCs can vary depending on the supersaturation, pH and the presence of a template. Clusters with sizes in the range 0.70–1.00 nm were detected in SBF by DLS.11 This was confirmed by cryo-TEM13 which has shown that isolated PNCs with an average size of 0.87 ± 0.2 nm form in SBF. In the presence of amelogenin, clusters of ~1 nm were observed by TEM.29 Additionally, cryo-TEM and TEM studies revealed that PNCs can exist as polymeric assemblies.13,29,40 According to the definition of prenucleation clusters by Gebauer et al.,47 PNCs are solutes without an interface and therefore there is no driving force for their aggregation. This means that only discrete, non-aggregated clusters can be considered as PNCs. On the other hand, clusters that form polymeric assemblies have an interfacial surface which drives aggregation and should be considered as nanophases.47 The distribution of PNC sizes was asymmetric with a small population of clusters having larger sizes (up to 4.7 nm). Similarly, an asymmetric size distribution of calcium carbonate clusters with the majority of particles in the range from 0.6 to 1.1 nm and a small population of larger clusters (up to 4.5 nm) was observed by cryo-TEM.48 The presence of larger nanoclusters was ascribed to the onset of the aggregation process leading to nucleation.48
| t | 10 min | 30 min | ||||||
|---|---|---|---|---|---|---|---|---|
| System | Height/nm | SD | min/nm | max/nm | Height/nm | SD | min/nm | max/nm |
| Control system (CS), DTAB monomers (MS1), DTAB micelles (MS2), 12-2-12 monomers (DS1), 12-2-12 spherical (DS2) and 12-2-12 elongated micelles (DS3). | ||||||||
| CS | 1.4 | 0.3 | 1.0 | 4.7 | 1.0 | 0.1 | 0.8 | 1.1 |
| MS1 | 1.0 | 0.3 | 0.6 | 3.1 | 1.1 | 0.2 | 0.8 | 2.0 |
| MS2 | 1.2 | 0.9 | 0.6 | 6.2 | 2.2 | 1.0 | 1.6 | 12.7 |
| DS1 | 1.4 | 0.4 | 1.0 | 7.4 | 0.7 | 0.3 | 0.4 | 1.4 |
| DS2 | 1.5 | 0.6 | 1.0 | 4.3 | 2.7 | 1.3 | 1.0 | 8.0 |
| DS3 | 2.0 | 0.8 | 1.6 | 7.1 | 2.7 | 0.8 | 2.0 | 6.8 |
Due to the small amount of the sample used for AFM imaging, it was possible that, although present, polymeric assemblies of nanoclusters were not detected. Therefore, DLS was conducted to verify the AFM data. Larger ACP particles were removed from the control system after 10 and 30 min of aging time by centrifugation. PNCs and polymeric assemblies were not detected after 10 min, probably due to low concentration. However, after 30 min of aging time, particles of sizes ranging from around 1.3 nm to several hundred nms were detected. Below 20 nm, particles in size categories of around 1.5 nm, 5.6 nm, 10 nm and 15 nm were detected, confirming the existence of both individual PNCs and polymeric assemblies of CaP clusters (Fig. S7†).
Spherical ACP particles formed in the control system after 10 min have an average size of 127 ± 55.8 nm as measured from TEM micrographs (Fig. 3a, Table 5), similar to the sizes reported in other studies.10,15,20 The size distribution of spherical particles was broad, indicating a polydispersed sample (Fig. S9a†). Information about the extent of their aggregation was obtained from the volume size distribution measured by DLS (Fig. S10a†) which showed the coexistence of two particle populations. A population of smaller particles with a hydrodynamic diameter of 1856 nm at peak maximum was present in larger volume% (Table 6). In addition, a population of larger particles with the hydrodynamic radius around 5300 nm at peak maximum was observed. The hydrodynamic diameters greater by one order of magnitude (Table 6) than the sizes of spherical particles obtained from TEM micrographs (Table 5) indicate that the measured hydrodynamic diameters correspond to chain-like aggregates of spherical particles. It seems that the percentage of non-aggregated spherical ACP particles in the control system is too low to be detected by DLS. The volume size distribution was broad, which is typical for this kind of system.30ζ potential measurements showed that particles in the control system after 10 min of reaction time bear an overall slightly negative charge (ζ = −2.7 ± 0.7 mV).
| t | 10 min | 30 min | ||||||
|---|---|---|---|---|---|---|---|---|
| System | d/nm | SD | min | max | d/nm | SD | min | max |
| Control system (CS), DTAB monomers (MS1), DTAB micelles (MS2), 12-2-12 monomers (DS1), 12-2-12 spherical (DS2) and 12-2-12 elongated micelles (DS3). | ||||||||
| CS | 127.0 | 55.8 | 18.3 | 282.2 | 55.5 | 10.9 | 37.6 | 82.9 |
| MS1 | 151.2 | 44.1 | 51.6 | 294.2 | 73.8 | 13.5 | 44.3 | 109.9 |
| MS2 | 67.5 | 26.8 | 30.0 | 156.6 | 49.9 | 16.9 | 21.2 | 112.9 |
| DS1 | 83.0 | 18.6 | 36.3 | 140.1 | ||||
| DS2 | 150.1 | 31.3 | 56.4 | 222.9 | ||||
| DS3 | 149.4 | 45.5 | 75.1 | 225.9 | ||||
| Peak I | Peak II | |||||
|---|---|---|---|---|---|---|
| System | d h/nm | SD | Mean vol% | d/nm | SD | Mean vol% |
| Control system (CS), DTAB monomers (MS1), DTAB micelles (MS2), 12-2-12 monomers (DS1), 12-2-12 spherical (DS2) and 12-2-12 elongated micelles (DS3). | ||||||
| CS | 1855.7 | 148.1 | 69.4 | 5272.0 | 686.0 | 30.6 |
| MS1 | 1889.0 | 166.5 | 92.3 | 5097.7 | 103.0 | 7.7 |
| MS2 | 1346.3 | 281.6 | 99.3 | 5312.0 | 147.1 | 0.7 |
| DS1 | 1854.7 | 259.6 | 96.9 | 5243.0 | 302.6 | 3.1 |
| DS2 | 1541.0 | 319.5 | 83.3 | 4855.3 | 732.8 | 16.7 |
| DS3 | 205.1 | 14.2 | 100 | |||
In general, the dominant mechanism in the formation of ACP is aggregation. Calcium and phosphate ions associate forming PNCs, which aggregate to spherical ACP particles, which in turn assemble into chain-like aggregates.6,9,10,29 Therefore, the processes that occur at the solution/precipitate interface are of utmost importance for the stability of ACP. This was recently confirmed in the studies of ACP stabilization by citrate and magnesium ions, in which it was shown that the surface adsorbed ions, and not the incorporated ones, play a decisive role.36,42 The main driving forces in adsorption of the additive molecule on the precipitate/solution interface can range from purely electrostatic to highly specific recognition of crystal faces by the additive.20,33 The adsorption behavior of simple additives is generally uncomplicated and can be modeled accurately on the basis of the interactions between the adsorbing species and the surface of the substrate.34 The adsorption behavior of surfactants differs very much from that of small molecules due to their amphiphilic nature. At low surfactant concentrations, electrostatic interactions have a dominant role in the adsorption of ionic surfactants on the charged crystal faces (charged solids in general). As a result, surfactant monomers adsorb with their headgroups facing towards the substrate. With increasing concentration, as a consequence of the hydrophobic interaction between surfactant tails, surfactant molecules tend to form aggregates at the solid/liquid interface, so-called hemi-micelles.34,35 This process is similar to the formation of the surfactant aggregates in the solution. Hydrophobic interactions become a major driving force of adsorption at concentrations when the crystal surface becomes electrically neutral due to the adsorption. At concentrations above the cmc, surfactants adsorb with their headgroups facing towards the solution and a bilayer is formed. When maximum adsorption density is reached, the increase in the surfactant concentration contributes only to the micellization in the solution.34,35 In addition, the micelles formed in solution can be adsorbed directly on the substrate surface.34
As in the control system, after 10 minutes of reaction time in all precipitation systems containing the DTAB (Fig. 2b, c and 3b, c) and 12-2-12 surfactants (Fig. 2d–f and 3d–f), PNCs, spherical ACP particles and their chain-like aggregates were formed. Therefore, the effect that surfactants exerted on these three length scales will be discussed.
The difference in the effect that DTAB and 12-2-12 exhibited on the properties of the amorphous phase was observed already at monomer concentrations. While in the presence of DTAB monomers (MS1), smaller PNCs and larger spherical particles compared to those in the control system were obtained, only the size of the spherical particles was affected by the presence of 12-2-12 monomers (DS1). However, the monomers of both surfactants had a negligible effect on the size of chain-like aggregates (Table 6), although the percentage of larger aggregates was reduced in both cases. The difference in the behavior of DTAB and 12-2-12 monomers on the nanoscale could be a consequence of their different adsorption behaviors due to the difference in their molecular structure and geometry. Based on the studies of DTAB and 12-2-12 adsorption on different substrates,22,34 it is unexpected that DTAB monomers exhibited a stronger effect on PNCs than 12-2-12 monomers. The great affinity of 12-2-12 monomers to adsorb on solid surfaces was also affirmed in the AFM micrograph of the DS1 system (Fig. 2d). A featureless bilayer typical for 12-2-12 (ref. 34) was observed on mica, despite sample washing. These observations indicate that the geometrical factor has an important role in the adsorption of surfactant molecules on ACP particles of different sizes. Due to their different molecular structures, DTAB and 12-2-12 molecules occupy a different minimum area at the solid/solution interface. The values of minimum area that the molecules of these two surfactants occupy at the air/solution interface (Table 1) point out that 12-2-12, as a result of an additional headgroup and dodecyl chain in its molecular structure, will occupy a larger surface area than DTAB at the ACP/solution interface as well. In addition, the rigidity of the ethylene spacer in the 12-2-12 molecule prevents it from enveloping around small PNCs when adsorbing. Therefore, DTAB molecules can be more easily accommodated at the solid ACP/solution interface preventing further growth of nanosized clusters. In addition, the effect of DTAB monomers on PNCs could have been more pronounced because they were present in much higher concentration (c = 1 × 10−4 mol dm−3) than 12-2-12 (c = 1 × 10−5 mol dm−3).
Since spherical particles are much larger than PNCs, the 12-2-12 molecules are more easily accommodated at the ACP/solution interface and the difference in DTAB and 12-2-12 adsorption efficiency becomes more pronounced. The ζ potential of the ACP particles obtained in the presence of DTAB monomers (ζ = 4.6 ± 1.4 mV) was slightly more positive than that of the particles formed in the presence of 12-2-12 monomers (ζ = −0.7 ± 0.2 mV). At low surfactant concentration, adsorption on the solid surface is due to the electrostatic interactions between ions in the solid phase and ionic headgroups of the surfactants. This head-on adsorption on solid surfaces results in the hydrophobic tails of the surfactants protruding into the solution.34,35 Considering that a 12-2-12 molecule contains two charged headgroups and two alkyl chains and DTAB consists of only one, more pronounced steric stabilization of ACP particles could be achieved by adsorption of 12-2-12. This prevents growth of spherical ACP particles in the DS1 system, but not in MS1. Previous studies have shown that in the presence of different additives e.g. magnesium ions and amino acids,43 phosphorylated osteopontin peptides38 and PEs,10 the size of spherical ACP particles is reduced.
DTAB and 12-2-12 micelles exhibited different effects of different length scales. While the sizes of PNCs, obtained by AFM, in the presence of spherical DTAB (MS2) and 12-2-12 micelles (DS2) were not significantly different from the ones in the control system, the clusters obtained in the presence of elongated 12-2-12 micelles (DS3) were larger (Table 4). In addition, height minimum and maximum values were also higher. The micelles formed in these systems differ not only in charge density and distribution, but also in curvature. Elongated 12-2-12 micelles (DS3), which had the most pronounced effect, have the lowest curvature. It was found that the Langmuir monolayer of arachidic acid promotes further aggregation and growth of PNCs in SBF.13 These findings point to the conclusion that the templates of lower curvature promote aggregation of PNCs, most probably due to the fact that the surface of lower curvature enables better contact between clusters.
The micelles exhibited a pronounced effect on the morphology and size of spherical ACP particles. The smallest spherical ACP particles were obtained in the presence of DTAB micelles. In addition, their appearance (Fig. 3c) was different from the well-delimited particles formed in other investigated systems. On the other hand, in the presence of 12-2-12 micelles (DS2 and DS3), spherical ACP particles, larger than those in the control and MS2 systems, were detected after 10 min of aging time (Fig. 3e and f, Table 5). In addition, in the presence of spherical 12-2-12 micelles (DS2), an interesting morphology was observed. The obtained spherical particles were similar to the hollow ACP spheres found in microemulsions containing the anionic asymmetric double-chained bis(2-ethylhexyl)sulfosuccinate (AOT).49 Both 12-2-12 and AOT contain two alkyl chains, confirming that hydrophobic interactions have a major role in determining the final ACP morphology. The observed difference in the size and morphology of spherical ACP particles formed in the presence of DTAB and 12-2-12 micelles demonstrates how changing micelle properties, charge density and distribution, as well as curvature, could be used for achieving different effects on the precipitation process.
Unlike monomers, both DTAB and 12-2-12 micelles exhibited a pronounced effect on chain-like aggregates. In the presence of spherical DTAB (MS2) and 12-2-12 micelles (DS2), the value of the major peak maximum was shifted towards lower values and the percentage of larger particles was reduced, as compared to the control system and systems containing surfactant monomers. Contrary to other investigated systems, at higher micellar 12-2-12 concentration, at which elongated micelles were present (DS3), a monomodal size distribution was observed. In addition, a notably smaller particle hydrodynamic diameter (dh ~ 205.1 nm) was measured in the DS3 system, indicating that elongated 12-2-12 micelles are the most efficient in preventing the aggregation of spherical ACP particles. The fact that the most pronounced effect on aggregation processes was observed in the presence of elongated 12-2-12 micelles (DS3) indicates that, in addition to concentration, the curvature of the aggregate has a considerable influence, as mentioned before.
Precipitation systems after 30 min of reaction time. The presence of DTAB and 12-2-12 monomers and micelles in the precipitation systems affected the kinetics and pathway of ACP transformation in different ways, as can be seen from the pH vs. time curves (Fig. 1). As a consequence, after 30 min of reaction time, the precipitation process was at different stages in the different investigated systems. In the control system and the system containing monomer DTAB concentration (MS1), the precipitation process was still at stage 2a (Fig. 1), i.e. transformation of ACP has not yet begun. Contrary to this, in the system with lower micellar 12-2-12 concentration (DS2), ACP/crystalline phase transformation has already begun (stage 3, Fig. 1), confirmed also by splitting of the ν4 PO4 band in the FTIR spectra of the formed precipitate (Fig. S5†). In all other precipitation systems after 30 minutes of reaction time, a change in the precipitate morphology was observed. The AFM and TEM micrographs of the precipitates formed in the investigated systems after 30 minutes are shown in Fig. 4 and 5, respectively.
In the control system, the size of PNCs and spherical particles decreased with aging time (Fig. 4a and 5a, Tables 4 and 5). It is known that calcium carbonate clusters are present even after nucleation, i.e. at later stages of the precipitation process.48 The study of calcium carbonate nucleation has shown that long-lived precritical clusters grow by colliding and coalescing,50 so if carbonate clusters are stable with respect to the solution state, they would grow larger.14 The same conclusion could be drawn for CaP PNCs. Analysis of the AFM micrographs showed that in the control system, the average height of the PNCs, as well as the maximum observed height, decreased after 30 min of reaction time. The decrease in size indicates that PNCs in the control system were not stable with respect to the solution. The size of spherical ACP particles as well as their chain-like aggregates also decreased with time. DLS measurements of the chain-like ACP particles showed the existence of only one population of chain-like particles with the peak maximum at 1792 nm (Table 7). A second, i.e. larger, population of aggregated particles was not detected as opposed to the results obtained after 10 min.
| t | 30 min | |||||
|---|---|---|---|---|---|---|
| Peak I | Peak II | |||||
| System | d h/nm | SD | Mean vol% | d/nm | SD | Mean vol% |
| Control system (CS), DTAB monomers (MS1), DTAB micelles (MS2), 12-2-12 monomers (DS1), 12-2-12 spherical (DS2) and 12-2-12 elongated micelles (DS3). | ||||||
| CS | 1792.5 | 521.1 | 100 | |||
| MS1 | 1405.0 | 82.0 | 50.9 | 4363.0 | 148.5 | 49.1 |
| MS2 | 1568.0 | 209.3 | 98.6 | 5443.5 | 43.1 | 1.4 |
| DS1 | 2183.3 | 154.9 | 91.7 | 5216.0 | 272.9 | 8.3 |
| DS2 | 2490.3 | 463.7 | 69.5 | 4147.0 | 113.1 | 30.5 |
| DS3 | 514.7 | 20.4 | 100 | |||
Although the shape of the pH curves suggest that ACP transformation in the CS and MS1 systems proceeds via the same pathway, the properties of ACP particles changed somewhat differently than those in the control system. Contrary to the control system, at monomer DTAB concentration (MS1), the average size of PNCs remained unchanged after 30 minutes of aging time. However, as in the control system, the sizes of spherical particles decreased compared to the particles formed after 10 min in the same systems (Fig. 5b, Table 5). On the other hand, in the MS1 system, a bimodal distribution of the chain-like aggregates of spherical particles was observed similar to that detected after 10 min (Table 7). However, the values of peak maxima were shifted towards lower values.
In the presence of 12-2-12, a change in ACP morphology was observed. As in the control system, the average height of the PNCs, as well as the maximum observed height, decreased after 30 min of aging time. The decrease in size indicates that PNCs, as in the control system, were not stable with respect to the solution. As was pointed out in the discussion of the sizes of PNCs obtained after 10 min of reaction time, the tendency of 12-2-12 to adsorb at various interfaces is known. However, due to the small sizes of PNCs and the molecular structure of 12-2-12, adsorption of the dimeric surfactant was geometrically constrained. Therefore, the PNCs were not stabilized by 12-2-12 monomers. TEM micrographs revealed the coexistence of a small amount of spherical ACP particles and a dense precipitate. DLS measurements reflected the ongoing change of morphology. The obtained volume size distribution revealed the coexistence of two particle populations (Table 7, Fig. S13†). The value of the peak maximum of smaller particles was shifted toward a larger value, while the volume percentage of larger particles increased, as compared to the results obtained after 10 min (Tables 6 and 7), confirming the observed change.
After 30 minutes of aging time, changes in the ACP morphology were also detected in the presence of spherical DTAB (MS2) and elongated 12-2-12 micelles (DS3). In these systems, a significant increase in the average size of the clusters, as well as height minimum and maximum values, was observed after 30 min of aging time. The increase in the sizes of PNCs in the presence of micellar concentration of both surfactants indicates that surfactant micelles stabilized PNCs even after a longer aging time. In the presence of micellar DTAB concentration (MS2), a denser phase, with a morphology different from the one formed in DS1, was observed (Fig. 5c) in addition to spherical ACP particles. A similar dense phase was observed by Xie et al.51 who proposed that it is ACP-II formed by partial dehydration of ACP-I. Size analysis of spherical particles showed the reduction of their sizes as compared to the particles formed after 10 min in the same system. However, DLS results for particles on a larger length scale showed an opposite trend (Table 7, Fig. S13c†). The volume size distribution obtained in the presence of spherical DTAB micelles (MS2) showed the existence of two particle populations, similar to that observed after 10 min, with the corresponding peak maxima shifted to higher values. In the presence of elongated 12-2-12 micelles (DS2), a floccular precipitate and a small amount of spherical particles were observed. The volume size distribution of particles obtained in the presence of higher micellar 12-2-12 concentration (DS3) remained monomodal, but the peak maximum value increased.
Although the ACP-to-crystalline phase transformation has commenced after 30 minutes in the DS2 system, PNCs were still detected. As in the case of MS2 and DS3 systems, a significant increase in the size of the clusters was observed. TEM micrographs revealed that along with a small percentage of spherical ACP particles, a sheet-like precipitate was formed confirming that the ACP/crystalline phase transformation has progressed the most in the DS2 system. Splitting of the ν4 phosphate band in the FTIR spectra confirmed the increased crystallinity of the precipitate (Fig. S14†). Similar results were reported by Ding et al.,36 who observed the coexistence of spherical ACP particles and sheet-like HAP crystallites at the onset of the rapid pH drop (stage 3, Fig. 1), as well as at latter precipitation stages. The obtained volume size distributions in the system containing 12-2-12 spherical micelles revealed the coexistence of two particle populations (Table 7). The value of the peak maximum of smaller particles was shifted toward a larger value, while the volume percentage of larger particles increased, as compared to the results obtained after 10 min (Table 6).
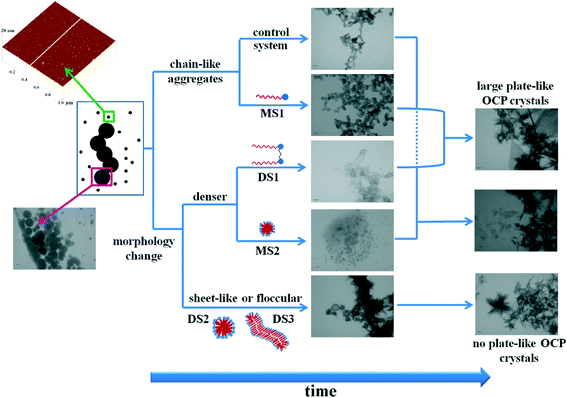
In summary, different effects of monomers and micelles of DTAB and 12-2-12 surfactants on the properties of ACP were observed at different aging times and on different length scales. In the control system and in the presence of DTAB monomers (MS1), ACP transformation was direct. In contrast, in the presence of DTAB micelles (MS2), 12-2-12 monomers (DS1) and elongated micelles (DS3), a change in the morphology of the precipitate was observed. In addition, the morphology of the precipitate was different in each system, indicating that interactions of surfactants with ACP were not the same in different systems. These diverse effects on ACP transformation can be ascribed to the difference in the molecular structure of the surfactants and their aggregation state. In addition to the difference in charge density and distribution, the rigidity of the headgroup and curvature of the aggregates should be taken into account. Interestingly, it seems likely that the effect of additives on the precipitation process observed on the microscale could be a result of different pathways on the nanoscale.
The influence of monomeric and dimeric surfactants on the properties of the crystalline phase
| Wavenumber/cm−1 | Peak assignment | Ref. | |||||
|---|---|---|---|---|---|---|---|
| CS | MS1 | MS2 | DS1 | DS2 | DS3 | ||
| Control system (CS), DTAB monomers (MS1), DTAB micelles (MS2), 12-2-12 monomers (DS1), 12-2-12 spherical (DS2) and 12-2-12 elongated micelles (DS3). | |||||||
| 3700–3000 | 3677–3000 | 3650–3300 | 3655–3055 | 3650–3200 | 3677–3100 | Water vibration | 52 |
| 3645 | 3734 | ν s stretching mode of O–H | 52 | ||||
| 2970–2840 | 2970–2840 | Asymmetric and symmetric stretching of 12-2-12 C–H groups | 53 | ||||
| 2919 | Asymmetric stretching of DTAB CH2 groups | 54 | |||||
| 2852 | Symmetric stretching of DTAB CH2 groups | 54 | |||||
| 1643 | 1643 | 1635 | 1641 | 1641 | 1652 | Water vibration | 52 |
| 1488 | ν 3 stretching mode of CO32− in CaP | 52 | |||||
| 1450 | 1467 | 1459 | 1459 | ν 3 or ν4 bending mode of CO32− | 52 | ||
| 1420 | 1423 | 1392 | ν 3 stretching mode of CO32− | 55 | |||
| 1281 | 1282 | 1284 | 1284 | 1284 | 1284 | HPO32− OH in-plane bending | 56 |
| 1113 | 1114 | 1114 | 1120 | 1109 | 1115 | ν 3a triply degenerate asymmetric stretching mode of PO43− (P–O bond) | 52 |
| 1028 | 1026 | 1030 | 1030 | 1029 | 1030 | ν 3c triply degenerate asymmetric stretching mode of PO43− (P–O bond) | 52 |
| 956 | 963 | 962 | 967 | 962 | 962 | ν 1 nondegenerate symmetric stretching mode of PO43− (P–O bond) | 52 |
| 870 | 867 | 872 | 865 | 866 | 866 | HPO42− | 55 |
| 752 | ν 4 in-plane deformation bending mode of CO32− (O–C–O bond) | 57 | |||||
| 695 | ν 4 in-plane deformation bending mode of CO32− (O–C–O bond) | 57 | |||||
| 645 | ν L librational mode of OH (O–H bond) | 52 | |||||
| 600 | 602 | 605 | 600 | 605 | 600 | ν 4 triply degenerate bending mode of PO43− (O–P–O bond) | 52 |
| 561 | 561 | 560 | 560 | 560 | 560 | ν 4 triply degenerate bending mode of PO43− (O–P–O bond) | 52 |
| 469 | 472 | 463 | 463 | 470 | ν 2 doubly degenerate bending mode of PO43− (O–P–O bond) | 52 | |
Similar to PEs,10 surfactants didn't have an influence on the composition of the formed precipitates. All FTIR spectra contained bands characteristic of OCP and apatitic phase (Fig. 6, Table 8). In the spectra of the precipitates obtained in micellar DTAB (MS2) and 12-2-12 solutions (DS2 and DS3), bands attributed to asymmetric and symmetric stretching of DTAB CH2 and 12-2-12 C–H groups were observed, respectively (Fig. 6b and c). Considering that the precipitates were thoroughly washed, this finding indicates that the surfactants were tightly bound. In the case of 12-2-12, the intensity of the bands increased with 12-2-12 concentration, indicating its progressive incorporation into the precipitate. The XRD patterns (Fig. 7) revealed that, in addition to OCP and HAP in all investigated systems, DCPD was formed (due to the small amount of precipitate formed in the MS2 system, not all OCP and HAP reflections observed in the patterns of other systems are present). Considering that no characteristic DCPD bands could be discerned in the FTIR spectra and that only the most intense reflection (020) was present in the XRD patterns, it could be assumed that the amount of precipitated DCPD is small.
However, TEM micrographs showed that surfactants affected the precipitate morphology. In the control system, a heterogeneous mixture of small, thin, plate-like crystals and poorly crystalline sheet-like precipitate was formed, as visualized by TEM (Fig. 8a). Selected area electron diffraction (SAED) of the crystals showed a pattern characteristic of OCP,10 but a diffuse ring characteristic of an amorphous material was also observed (inset in Fig. 8a).
The TEM images of the precipitates formed in the presence of DTAB (Fig. 8b and c) and 12-2-12 (Fig. 8d–f) show that monomers and micelles differently affected the morphology of the crystalline phase. In precipitation systems with DTAB and 12-2-12 monomers (MS1 and DS1) after 24 hours of aging time, a heterogeneous mixture of crystals and sheet-like precipitate was formed (Fig. 8b and d). However, contrary to the control system where only small OCP crystals were formed, large, well-developed, thin plate-like crystals were observed. These crystals have an OCP structure, as confirmed by SAED (inset in Fig. 8b). In the case of the precipitate formed in the DS1 system, the SAED pattern indicated a mixture of smaller and larger OCP crystals obtained in different orientations (Fig. 8d). However, no change in OCP morphology was observed compared to MS1 (Fig. 8b and d).
Under the same experimental conditions, polyelectrolytes, PLL, PGA and PSS also affected the OCP crystal morphology.10 In the presence of PEs, affected OCP crystals appeared smaller and thinner, with rounded edges. This nonspecific inhibition of crystal growth in all directions is due to the adsorption of the flexible PEs at all active sites.10 The answer to the question why larger OCP crystals appeared in the presence of the DTAB and 12-2-12 monomers in such a complex system, where several CaP phases are simultaneously formed, is not straightforward. On the one hand, it could mean that surfactant monomers promoted OCP crystal growth and the crystal grew larger. An example is the growth of larger calcium oxalate monohydrate crystals (COM) in the presence of nephrocalcin isoforms with lower surface activity. However, these isoforms also promoted COM aggregation.58 On the other hand, larger and more regular crystals can be obtained if the nucleation rate is reduced, due to e.g. lowering of supersaturation.59 Lower supersaturation with respect to OCP could be achieved if DTAB and 12-2-12 monomers promote the growth of other CaP phases.
Small, spherical DTAB micelles (MS2) didn't influence the morphology of the CaP precipitate formed after 24 hours. Only a small amount of precipitate with a morphology similar to that in the control system was formed (Fig. 8c). The SAED pattern shown in the inset of Fig. 8c indicates that the precipitate is poorly crystalline, since a diffuse ring characteristic of an amorphous material was observed. In addition, rings characteristic of small crystals in different orientations were visible (rings observed in the SAED pattern consist of low intensity spots).
In the presence of 12-2-12 micelles (DS2 and DS3), no large OCP crystals were observed. Sheet-like crystallites were observed on the TEM micrographs (Fig. 8e and f). Diffuse rings characteristic of an amorphous material and nanocrystals in different orientations were observed in the SAED patterns (insets in Fig. 8e and f). A possible explanation for the observed effect is the nonspecific interaction of surfactant micelles with all growing faces of OCP crystals, which prevents the formation of large, well-developed plate-like crystals.
In summary, neither surfactant monomers nor micelles influenced the composition of the precipitate. In all systems, a mixture of OCP, HAP and DCPD was formed. However, the surfactant molecular structure and aggregation state had decisive roles in determining the influence of surfactants on the morphology of the crystalline phase, as well as on the pathway of its formation (Scheme 2). In the presence of DTAB and 12-2-12 monomers, OCP crystals larger than those in the control system were observed. 12-2-12 monomers exhibited their influence on the precipitate morphology at the earlier stage of the precipitation process compared to DTAB monomers, most probably due to their higher tendency of adsorption. In the presence of both spherical (DS2) and elongated 12-2-12 micelles (DS3), no plate-like OCP crystals were observed. On the other hand, in the presence of DTAB micelles, small OCP crystals, similar to those obtained in the control system, were formed. The difference in the effect on ACP formation and transformation between DTAB and 12-2-12 surfactants demonstrates how changes in the molecular structure can have a profound impact on the precipitation process even though the chemistry of the molecule was not changed. Chemically linking two DTAB molecules into 12-2-12 resulted in different charge density and flexibility of the molecules. As a consequence, both adsorption and aggregation processes of DTAB and 12-2-12 monomers are greatly affected.22 This results in diverse effects observed in the precipitation systems and points to the charge density and distribution, as well as the geometry of the micelles, as the principle factors responsible for the observed effects.
Conclusions
The combination of microscopy (AFM and TEM) and light scattering (DLS and ζ potential measurements) techniques enabled the simultaneous monitoring of the influence that DTAB and 12-2-12 monomers and micelles exhibit on the formation and transformation of ACP at different stages and on different length scales of the precipitation process. Depending on their aggregation state (monomers or micelles) and the geometry of the aggregate (spherical or elongated micelles), DTAB and 12-2-12 have exhibited different effects on the rate of ACP transformation, as well as on the properties of ACP and the crystalline phase. The difference in the charge density and distribution of the monomers and micelles, which is a consequence of their different molecular structures, as well as the presence of geometrical constraints in the 12-2-12 molecule, affects both the efficiency of their adsorption on different sized substrates and the templating ability of their micelles. Unlike small molecular additives, for which the main driving forces in solid phase/additive interactions are electrostatic, for surfactants, hydrophobic interactions play an important role in addition to electrostatic interactions. Moreover, the effect of surfactants on the precipitation process observed on the microscale could be a result of different pathways on the nanoscale. The obtained results may have implications for the understanding of the general mechanism of inorganic–organic interactions underlying the biomineralization processes, as well as for materials science, especially for the control of materials preparation on the nanoscale.Acknowledgements
We are indebted to Dr. N. Filipović-Vinceković for helpful discussions and reading of the manuscript. Financial support from the Croatian Ministry of Science (Grant 098-0982915-2949), the Croatian Science Foundation (Grant HRZZ-5055) and EU FP7 grant GlowBrain (REGPOT-2012-CT2012-316120) is greatly acknowledged.References
- S. Dorozhkin, Calcium Orthophosphates. Application in Nature, Biology and Medicine, Pan Stanford Publishing, Singapore, 2012 Search PubMed.
- L. Wang and G. H. Nancollas, Chem. Rev., 2008, 108, 4628–4669 CrossRef CAS PubMed.
- J. Zhao, Y. Liu, W.-B. Sun and H. Zhang, Chem. Cent. J., 2011, 5, 40, DOI:10.1002/jbm.a.10426.
- J. Mahamid, A. Sharir, L. Addadi and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12748–12753 CrossRef CAS PubMed.
- E. Beniash, R. A. Metzler, R. S. K. Lam and P. U. P. A. Gilbert, J. Struct. Biol., 2009, 166, 133–143 CrossRef CAS PubMed.
- C. Combes and C. Rey, Acta Biomater., 2010, 6, 3362–3378 CrossRef CAS PubMed.
- E. D. Eans, I. H. Gillesen and A. S. Posner, Nature, 1965, 208, 365–367 CrossRef PubMed.
- A. S. Posner and F. Betts, Acc. Chem. Res., 1975, 8, 273–281 CrossRef CAS.
- L. Brečević, V. Hlady and H. Füredi-Milhofer, Colloids Surf., 1987, 28, 301–313 CrossRef.
- P. Bar-Yosef Ofir, R. Govrin-Lippman, N. Garti and H. Füredi-Milhofer, Cryst. Growth Des., 2004, 4, 177–183 Search PubMed.
- K. Onuma and A. Ito, Chem. Mater., 1998, 10, 3346–3351 CrossRef CAS.
- A. Oyane, K. Onuma, T. Kokubo and A. Ito, J. Phys. Chem. B, 1999, 103, 8230–8235 CrossRef CAS.
- A. Dey, P. H. H. Bomans, F. A. Müller, J. Will, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1010–1014 CrossRef CAS PubMed.
- L. Wang, S. Li, E. Ruiz-Agudo, C. V. Putnis and A. Putnis, CrystEngComm, 2012, 14, 6252–6256 RSC.
- L. Brečević and H. Füredi-Milhofer, Calcif. Tissue Res., 1972, 10, 82–90 CrossRef.
- R. Despotović, N. Filipović-Vinceković and H. Füredi-Milhofer, Calcif. Tissue Res., 1975, 18, 13–26 CrossRef.
- J. Christoffersen, M. R. Christoffersen, W. Kibalczyc and F. A. Andersen, J. Cryst. Growth, 1989, 94, 767–777 CrossRef CAS.
- H. Pan, X.-Y. Liu, R. Tang and H.-Y. Xu, Chem. Commun., 2010, 46, 7415–7417 RSC.
- M. Iijima, D. Fan, K. M. Bromley, Z. Sun and J. Moradian-Oldak, Cryst. Growth Des., 2010, 10, 4815–4822 CAS.
- M. Dutour Sikirić and H. Füredi-Milhofer, Adv. Colloid Interface Sci., 2006, 128, 135–158 CrossRef PubMed.
- M. Ramanathan, L. K. Shrestha, T. Mori, Q. Ji, J. P. Hill and K. Ariga, Phys. Chem. Chem. Phys., 2013, 15, 10580–10611 RSC.
- R. Zana, Adv. Colloid Interface Sci., 2002, 97, 205–253 CrossRef CAS.
- M. Sikirić, I. Primožič, Y. Talmon and N. Filipović-Vinceković, J. Colloid Interface Sci., 2005, 281, 473–481 CrossRef PubMed.
- D. Jurašin, I. Habuš and N. Filipović-Vinceković, Colloids Surf., A, 2010, 368, 119–128 CrossRef PubMed.
- J. Xia and R. Zana, in Gemini Surfactants, Synthesis, Interfacial and Solution – Phase Behaviour and Applications, ed. R. Zana and J. Xia, Marcel Dekker, New York, 2004, ch. 13, pp. 296–315 Search PubMed.
- D. Danino, Y. Talmon and R. Zana, Langmuir, 1995, 11, 1448–1456 CrossRef CAS.
- M. J. Rosen, Surfactants and Interfacial Phenomena, Wiley Interscience, Hoboken, New Jersey, 3rd edn, 2004 Search PubMed.
- J. R. de Bruyn, M. Goiko, M. Mozaffari, D. Bator, R. L. Dauphinee, Y. Liao, R. L. Flemming, M. S. Bramble, G. K. Hunter and H. A. Goldberg, PLoS One, 2013, 8, e56764, DOI:10.1371/journal.pone.0056764.
- X. Yang, L. Wang, Y. Qin, Z. Sun, Z. J. Henneman, J. Moradian-Oldak and G. H. Nancollas, J. Phys. Chem. B, 2010, 114, 2293–2300 CrossRef CAS PubMed.
- C.-G. Wang, J.-W. Liao, B.-D. Gou, J. Huang, R.-K. Tang, J.-H. Tao, T.-L. Zhang and K. Wang, Cryst. Growth Des., 2009, 9, 2620–2626 CAS.
- C. K. Liu and G. Warr, Langmuir, 2012, 28, 11007–11016 CrossRef CAS PubMed.
- M. Pisárčik, M. Dubničková, F. Devínsky, I. Lacko and J. Škvarla, Colloids Surf., A, 1998, 143, 69–75 CrossRef.
- K. Bleek and A. Taubert, Acta Biomater., 2013, 9, 6283–6762 CrossRef CAS PubMed.
- R. Atkin, V. S. J. Craig, E. J. Wanless and S. Biggs, Adv. Colloid Interface Sci., 2003, 103, 219–304 CrossRef CAS.
- R. Zhang and P. Somasundaran, Adv. Colloid Interface Sci., 2006, 123–126, 213–229 CrossRef CAS PubMed.
- H. Ding, H. Pan, X. Xu and R. Tang, Cryst. Growth Des., 2014, 14, 763–769 CAS.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 2004 Search PubMed.
- S. Li and L. Wang, CrystEngComm, 2012, 14, 8037–8043 RSC.
- J. Yao, W. Tjandra, Y. Z. Chen, K. C. Tam, J. Ma and B. Soh, J. Mater. Chem., 2003, 13, 3053–3057 RSC.
- W. J. E. M. Habraken, J. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. H. Bomans, P. M. Frederik, J. Laven, P. van der Schoot, B. Aichmayer, G. de With, J. J. DeYoreo and N. A. J. M. Sommerdijk, Nat. Commun., 2013, 4, 1507 CrossRef PubMed.
- S. Jiang, Y. Chen, H. Pan, Y.-J. Zhang and R. Tang, Phys. Chem. Chem. Phys., 2013, 15, 12530 RSC.
- Y. Chen, W. Gu, H. Pan, S. Jiang and R. Tang, CrystEngComm, 2014, 16, 1864–1867 RSC.
- X. Yang, B. Xie, L. Wang, Y. Qin, Z. J. Henneman and G. H. Nancollas, CrystEngComm, 2011, 13, 1153–1158 RSC.
- A. Bigi, E. Boanini, G. Cojazzi, G. Falini and S. Panzavolta, Cryst. Growth Des., 2001, 1, 239–244 CAS.
- R. F. Domingos, M. A. Baalousha, Y. Ju-Nam, M. M. Reid, N. Tufenkji, J. R. Lead, G. G. Leppard and K. J. Wilkinson, Environ. Sci. Technol., 2009, 43, 7277–7284 CrossRef CAS.
- H. Kato, in Nanomaterials: Processing and Characterization with Lasers, ed. S. C. Singh, H. Zeng, C. Guo and W. Cai, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2012, ch. 8, pp. 535–554 Search PubMed.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
- E. M. Pouget, P. H. H. Bormans, J. A. C. M. Goos, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Science, 2009, 323, 1455–1458 CrossRef CAS PubMed.
- C. E. Fowler, M. Li, S. Mann and H. C. Margolis, J. Mater. Chem., 2005, 15, 3317–3325 RSC.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
- B. Xie, T. J. Halter, B. M. Borah and G. H. Nancollas, Cryst. Growth Des., 2014, 14, 1659–1665 CAS.
- S. Koutsopulos, J. Biomed. Mater. Res., 2002, 62, 600–612 CrossRef PubMed.
- B. Brycki, I. Kowalczyk and A. Kozirog, Molecules, 2011, 16, 319–335 CrossRef CAS PubMed.
- R. B. Viana, A. B. F. Da Silva and A. S. Pimentel, Adv. Phys. Chem., 2012, 903272 Search PubMed.
- C. Mochales, R. M. Wilson, S. E. P. Dowker and M.-P. Ginebra, J. Alloys Compd., 2011, 509, 7389–7394 CrossRef CAS PubMed.
- J. V. Rau, M. Fosca, V. S. Komlev, I. V. Fadeeva, V. R. Albertini and S. M. Barinov, Cryst. Growth Des., 2010, 10, 3824–3834 CAS.
- F. A. Andersen and L. Brečević, Acta Chem. Scand., 1995, 45, 1018–1024 CrossRef.
- J. W. Kurutz, M. Carcalho and Y. Nakagawa, J. Cryst. Growth, 2003, 255, 392–402 CrossRef CAS.
- H. E. L. Madsen and J. B. Pedersen, in Advances in Crystal Growth Inhibition Technologies, ed. Z. Amjad, Kluwer Academic Publisher, New York, 2002, ch. 1, pp. 1–15 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of surfactant/Na2HPO4 system characterization, FTIR spectra of precipitates formed in the control and DS2 system after different aging times, AFM images of large ACP particles and micelles, DLS measurements of PNCs and polymeric assemblies of nanoclusters, and ACP particle size distributions obtained from AFM and TEM micrographs and DLS measurements. See DOI: 10.1039/c5ce01516b |
| This journal is © The Royal Society of Chemistry 2015 |