Intermolecular interactions in crystalline 1-(adamantane-1-carbonyl)-3-substituted thioureas with Hirshfeld surface analysis

Abstract

The conformationally congested species 1-(adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea has been prepared and fully characterized by elemental analyses, FTIR, ¹H NMR, ¹³C NMR and mass spectrometry. Its crystal structure was determined by single-crystal X-ray diffraction. The dihedral angle between the plane of the 2,4,6-trimethylphenyl group and the plane of the thiourea fragment was optimized by theoretical calculations applying the B3LYP/6-311++G(d,p) level for the purpose of investigating the conformational effects on the stabilization of the crystal packing. A detailed analysis of the intermolecular interactions in a series of six closely related phenylthiourea species bearing the 1-(adamantane-1-carbonyl) group has been performed based on the Hirshfeld surfaces and their associated two-dimensional fingerprint plots. The relative contributions of the main intermolecular contacts as well as the enrichment ratios derived from the Hirshfeld surface analysis establish the 1-acyl thiourea synthon to be a widespread contributor.

---

1. Introduction

1-Acyl substituted thiourea species have been known for a long time, in which the preparation of CH₃C(O)NHC(S)NH₂ was reported by Neucki as early as 1873.¹ The current and continuously increasing interest in these compounds is probably twofold: (1) potential applications in a wide range of fields are being investigated and (2) these compounds are relatively easy to prepare. Most promising applications include the use of 1-acyl thioureas as collectors in froth flotation processes,^2,3 as ionophores in ion-selective electrodes,^4–6 and as precursors of metal sulfide nanoparticles.^7,8 1-Acyl substituted thiourea species are versatile reagents for the synthesis of a variety of heterocyclic and organosulfur compounds.⁹ Furthermore, the biological importance of this kind of compound has been highlighted recently.^10,11 In particular, substituted 1-(benzoyl)-3-(phenyl) thioureas have been evaluated for antitumor activity with promising results.¹²

As has been recognized, the structural and conformational properties of 1-acyl thioureas are linked to the achievement of many of these applications. In particular, the formation of appropriate hydrogen bonds with particular receptors is a key factor which plays a role in many fields, such as analytical applications of 1-acyl thioureas as chemosensors for selective and sensitive naked-eye recognition of anions^13–16 as well as in chemical biology and drug design.^17–20

Increasing attention has been paid to the study of non-covalent interactions acting on the crystal structure and packing of sulfur-containing compounds,²¹ a topic of interest not only in organic chemistry,²² but also in transition metal complexes.²³ Very recently, Eccles et al.^24,25 have demonstrated the versatility of the thioamide functional group [–C(S)NH₂] as a key moiety for crystal engineering. The supramolecular arrangement of 1,2,4-triazole-5-(4H)-thione derivatives involves the formation of a short centrosymmetric R²₂(8) N–H⋯S synthon in the solid state.^26,27 It has been shown that the formation of a centrosymmetric N–H⋯S=C hydrogen bond dimer in thiosemicarbazone is favored by the high polarizability of the electron density of the lone pair formally located at the sulfur atom.²⁸

The crystal packing of 1-acyl thiourea compounds, with the possibility of different donor and acceptor groups, is usually dominated by hydrogen bonds, mostly determined to be both N–H⋯O=C and N–H⋯S=C interactions.^29,30 Bifurcated hydrogen bonds are usually observed,^31–33 the N–H group forming both intramolecular and intermolecular N–H⋯O hydrogen bonds.³⁴ As reported recently,³⁵ 440 crystal structures for 1-acyl thioureas were searched in the Cambridge Structural Database, the majority (236 structures) displaying a characteristic intermolecular pattern forming dimers via N–H⋯S hydrogen bonding adopting an R²₂(8) motif.³⁶ In combination with other patterns, very versatile structures are attainable, including infinite chains,³⁷ 2-dimensional sheets³⁸ or 3-dimensional networks.³⁹ By using periodic system electron density, topological and NBO analyses, we recently showed that strong hyperconjugative lpS → σ*(N–H) remote interactions – between the molecules forming the dimeric arrangement – are responsible for the intermolecular interactions in the simple 1-(2-chlorobenzoyl)thiourea species.⁴⁰

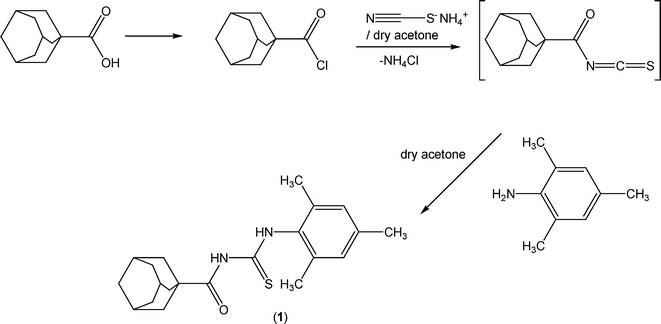
In this article, as part of our ongoing project^41,42 aimed at understanding the structural features of 1-(adamantane-1-carbonyl)-3-substituted thioureas (see Scheme 1), a novel derivative – namely, 1-(adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea – has been synthesized and characterized by single-crystal X-ray diffraction, infrared and nuclear magnetic resonance (NMR) spectroscopy and mass spectrometry. The influence of steric impediment induced by 2,6-dimethyl substitution on the conformational properties was analyzed by quantum chemical calculations at the B3LYP/6-311++G(d,p) level. The study of the X-ray crystal structure of six adamantane-based acylthioureas reveals that hydrogen bonding and other weaker forces such as π⋯π and C–H⋯π interactions participate in a cooperative way to control the supramolecular architectures. Although π-interactions have been widely investigated during the past two decades,⁴³ an increased number of theoretical and experimental studies have been recently carried out to understand the true nature of π⋯π and C–H⋯π interactions.^44–46 These non-covalent interactions could be used as tools in crystal engineering for the design of crystalline adamantane-based thioureas. To obtain a better understanding of the contribution of intermolecular interactions to the crystal packing, Hirshfeld surface analysis^47–49 of a series of six closely related 1-(adamantane-1-carbonyl)-3-substituted-phenyl thioureas has been performed. Thus, the surfaces of all compounds are mapped by using d_norm, whereas the shape index and curvedness are the properties mapped on the surfaces in order to facilitate more detailed identification of the π–π interactions experienced by molecules in various studied compounds.⁴⁴ The present study allowed us to investigate the effect of the molecular conformation adopted by the substituted-phenyl thiourea group on the stabilization of the crystal packing in these compounds, as well as to quantify the propensity of the intermolecular interactions to form the supramolecular assembly.

Scheme 1 Representation of 1-(adamantane-1-carbonyl)-3-substituted thioureas.

2. Experimental

2.1. Instrumentation

Melting points were recorded using a digital Gallenkamp (SANYO, model MPD.BM 3.5) apparatus and are uncorrected. ¹H and ¹³C NMR spectra were acquired in CDCl₃ at 300 MHz and 75.4 MHz, respectively, using a Bruker spectrophotometer. Fourier transform infrared (FTIR) spectra were recorded on an FTS 3000 MX spectrophotometer (Pakistan). Infrared spectra were recorded in KBr pellets with a resolution of 2 cm⁻¹ in the 4000–400 cm⁻¹ range on a Bruker EQUINOX 55 FTIR spectrometer (Argentina). Mass spectrometry (EI, 70 eV) on a GC-MS instrument (Agilent Technologies) and elemental analyses were conducted using a LECO-183 CHNS analyzer.

2.2. Synthesis of 1-(adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea

The reaction sequence leading to the formation of the thioureas is depicted in Scheme 2. The starting material 1-adamantanecarbonyl chloride was obtained via the reaction of 1-adamantanecarboxylic acid with thionyl chloride at room temperature according to the standard procedure.¹ A solution of adamantane-1-carbonyl chloride (10 mmol) in dry acetone (50 ml) was treated with an equimolar quantity of ammonium thiocyanate (10 mmol) in dry acetone (30 ml) and the reaction mixture was refluxed for 30 minutes under nitrogen to afford adamantane-1-isothiocyanate as an intermediate. An equimolar quantity of 2,4,6-trimethylaniline (10 mmol) in acetone (10 ml) was added and the reaction mixture was refluxed for 4 h. On completion (TLC control), the reaction mixture was poured into cold water and the precipitated thiourea (1) was recrystallized from aqueous ethanol.

Scheme 2 Synthetic route to 1-(adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea.

1-(Adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea (1). Yield 87%, mp 196 °C. FT-IR (ν, cm⁻¹): 3336, 3034, 2909, 2849, 1675, 1575, 1457, 1370; ¹H NMR (300 MHz, CDCl₃): δ 12.81 (br s, 1H, NH, D₂O exchangeable), 8.73 (br s, 1H, NH, D₂O exchangeable), 7.63 (d, 2H, Ar), 2.31 (s, 3H, ArCH₃), 2.11 (s, 6H, ArCH₃ (×2)), 2.12 (br s, 3H, adamantane-CH), 2.03 (s, 6H, adamantane-CH₂), 1.81 (q, 6H, adamantane-CH₂, J = 8.6 Hz); ¹³C NMR (75.5 MHz, CDCl₃): 179.1 (C=S), 176.9 (C=O), 134.1 (Ar), 128.6, 126.9, 125.3, 123.6, 121.6 (ArCs), 41.9, 41.9, 39.2, 38.6, 36.1, 36.0, 31.6, 28.0, 27.8 (adamantane-C), 22.3 (ArCH₃), 18.7 (ArCH₃). Anal. calcd. for C₂₁H₂₈N₂OS (356.53): C, 70.75; H, 7.92; N, 7.86; S, 8.99%; found: C, 71.21; H, 7.89; N, 7.90; S, 8.94%. EIMS m/z: 356.1 (M⁺, 41%).

2.3. Quantum chemical calculations

Geometry optimization was accomplished within the framework of the density functional theory^50,51 using the hybrid functional with non-local exchange due to Becke⁵² and the correlation functional due to Lee, Yang and Parr⁵³ (B3LYP), as implemented in the Gaussian 03 package.⁵⁴ Contracted Gaussian basis sets of triple-zeta quality plus polarized and diffuse functions 6-311++G(d,p) for all atoms were used throughout the present work.⁵⁵ The corresponding vibrational analyses were performed for the optimized geometries to verify whether they are local minima or saddle points on the potential energy surface of the molecule. Calculated normal modes were also used as an aid in the assignment of experimental frequencies.

2.4. X-ray data collection and structure refinement

The crystal and refinement data for compound 1 are listed in Table 1. Data for compound 1 were collected at 173(2) K on a STOE IPDS II two-circle diffractometer using Mo Kα radiation. The structure was solved by direct methods⁵⁶ and refined with full-matrix least-squares techniques on F². All non-hydrogen atoms were refined anisotropically, and all H atoms bonded to C were placed in their calculated positions and then refined using the riding model. The H atoms bonded to N were freely refined. The geometry of the molecule was calculated using WinGX⁵⁷ and PARST^58,59 software. XP in SHELXTL-Plus,⁵⁶ ORTEP-3⁶⁰ and Mercury⁶¹ programs were used for molecular graphics.

Table 1 Crystal data and structure refinement for compound 1

Empirical formula	C21H28N2OS
Formula weight	356.51
Temperature/K	173(2)
Crystal system	Triclinic
Space group	P1̄
Unit cell dimensions	a = 7.6584(7) Å
	b = 10.2121(8) Å
	c = 13.1295(11) Å
	α = 108.228(6)°
	β = 97.789(7)°
	γ = 92.502(7)°
Volume/Å^3	962.26(15)
Z	2
ρ calc./mg mm^−3	1.230
μ/mm^−1	0.179
F(000)	384
Crystal size/mm^−3	0.35 × 0.29 × 0.27
Theta range for data collection	3.30 to 27.62°
Index ranges	−9 ≦ h ≦ 9, −12 ≦ k ≦ 13, −17 ≦ l ≦ 17
Reflections collected	18 032
Independent reflections	4399 [R(int) = 0.061]
Data/restraints/parameters	4399/0/238
Goodness-of-fit on F^2	1.054
Final R indexes [I > 2σ(I)]	R 1 = 0.0409, wR2 = 0.1064
Final R indexes [all data]	R 1 = 0.0434, wR2 = 0.1084
Largest diff. peak/hole/e Å^−3	0.316/−0.290

---

Full crystallographic data for compound 1 have been deposited with the Cambridge Crystallographic Data Centre (CCDC 1410273).

2.5. Hirshfeld surface computational method

Hirshfeld surfaces and their associated two-dimensional fingerprint plots^62–65 were generated using CrystalExplorer 3.1 software.⁶⁶ The d_norm (normalized contact distance) surface and the breakdown of the two-dimensional fingerprint plots were used for decoding and quantifying the intermolecular interactions in the crystal lattice.^67–69 The d_norm is a symmetric function of distances to the surface from the nuclei inside and outside the Hirshfeld surface (d_i and d_e, respectively), relative to their respective van der Waals radii. A color scale of red (shorter than vdW separation)–white (equal to vdW separation)–blue (longer than vdW separation) was used to visualize the intermolecular contacts. The 3D d_norm surfaces were mapped over a fixed color scale of −0.24 (red) to 0.93 Å (blue), the shape index in the color range of −1.0 au (concave) to 1.0 au (convex) Å, and curvedness in the range of −4.0 au (flat) to 0.01 au (singular). The 2D fingerprint plots were displayed by using the translated 0.6–2.6 Å range and including reciprocal contacts.

3. Results and discussion

3.1. Conformational properties

Previous structural studies on 1-(adamantane-1-carbonyl)-3-monosubstituted thioureas have shown that a local planar structure of the acyl thiourea group is preferred, with opposite orientation between the C=O and C=S double bonds (“S-shape”).^41,42,70 In the present case, a similar conformational behaviour has been computationally determined for 1-(adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea, with the 1-acyl thiourea group adopting the S-shape and the substituted phenyl ring nearly perpendicular to the mean plane defined by the 1-acyl thiourea group. It is worth noting that the molecule isolated in vacuum displays nearly perfect C_s symmetry.

For comparison purposes, similar calculations have been carried out for the related 1-(adamantane-1-carbonyl)-3-(phenyl)thiourea. For this species, the most stable form displays the same S-shaped conformation, but on the contrary, the phenyl ring is coplanar with the 1-acyl thiourea group. Thus, it becomes apparent that the conformation adopted by the 2,4,6-trimethyl group is determined by strong steric impediment caused by the interaction between the C=S bond with the methyl groups occupying the 2,6-positions. The computed molecular structure is in very good agreement with the experimental one (see section 3.3).

3.2. Vibrational properties

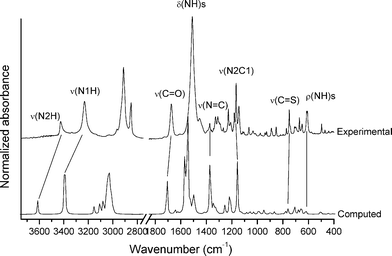
Determination of the vibrational properties of the 1-acyl thioureas has shown to be a powerful tool for analyzing conformational and structural features in the solid state.³⁶ The FTIR spectrum of 1 has been measured and compared with the calculated [B3LYP/6-311++G(d,p)] harmonic frequencies. The experimental and simulated spectra are shown in Fig. 1. Two well-defined absorptions are observed in the infrared spectrum at 3426 and 3231 cm⁻¹, the last one with a higher intensity, which can be associated with the ν(N–H) stretching modes.⁷¹ This spectral region is well reproduced by quantum chemical calculations with the corresponding harmonic frequencies computed at 3613 (56.6) and 3393 (366.5) cm⁻¹ (computed intensities, in km mol⁻¹, are given). The formation of the intramolecular N1–H⋯O1=C hydrogen bond is responsible for the impressive red-shift and strong intensification of the ν(N1–H) normal mode as compared with the second ν(N2–H) stretching mode, in agreement with previous data for related species.⁷² This interaction also affects the force constant of the ν(C=O) stretching mode,⁷³ which is observed as an intense and symmetric band at 1674 cm⁻¹ in the infrared spectrum, in good agreement with the computed value (1707 cm⁻¹).

Fig. 1 Computed [B3LYP/6-311++G(d,p)] and experimental (FTIR) infrared spectra of 1.

The most intense absorption is observed as a rather broad band at 1511 cm⁻¹ in the infrared spectrum, which can be assigned to the δ(N–H) deformation modes, in agreement with previously reported values for 1-acyl-3-monosubstituted thioureas.^74,75 The computed spectrum shows two intense absorptions at similar frequency values [1567 (350.9 km mol⁻¹) and 1546 (628.6 km mol⁻¹) cm⁻¹] that are associated with the δ(N1–H) and δ(N2–H) normal modes, respectively.

The medium-intensity absorptions observed at 772 and 751 cm⁻¹ are assigned to the characteristic “breathing mode” of the adamantane group⁷⁶ and the ν(C=S) stretching mode, respectively. The latter assignment is in agreement with previously studied thiourea derivatives^75,77 and suggests that the C=S group acts as a H-bond acceptor. It is well-known that the formation of intermolecular C=S⋯H–X hydrogen bonds affects the frequency of the ν(C=S) mode.⁷⁸

Thus, based on the analysis of the main features of the infrared spectra, it is concluded that compound 1 forms strong intra- and inter-molecular interactions in the solid state, most probably due to the formation of hydrogen bonds involving the N1–H group as a donor and the carbonyl and thiocarbonyl groups as acceptors.

3.3. Crystal structure determination

The X-ray geometrical parameters around the central 1-acyl thiourea moiety of compound 1, together with the computed [B3LYP/6-311++G(d,p)] values, are listed in Table S1 in the ESI.† The ORTEP view of the X-ray structure – with atomic labeling – is shown in Fig. 2, together with the computed molecular structure. The geometric parameters of hydrogen bonds for compound 1 are shown in Table 2. An intramolecular N–H⋯O hydrogen bond (H⋯O = 2.08(2) Å, N⋯O = 2.723(2) Å, ∠N–H⋯O = 134°) is present, forming a six-membered ring commonly observed in this type of compound,⁷⁹ which confirms the results for the vibrational data. The central –C(O)–NH–C(S)–NH– fragment is planar, with the C=O and C=S bonds in opposite orientation, adopting an “S-shape”, in agreement with the structures of similar 1-acyl-3-monosubstituted thioureas.³² The observed C=S and C=O double bonds, as well as the shortened C–N bond lengths (Table S1†), are typical of thiourea compounds.⁸⁰ The dihedral angle between the best planes through the thiourea moiety CNC(S)N and the 2,4,6-trimethyl group is 89.56(5)°, in agreement with the theoretical calculations (see section 3.1). This value is also similar for related structures with the same nature of substituents on the 2,4,6-trisubstituted group.⁸¹ The ring puckering parameters⁸² for the cyclohexane rings of the adamantane group are given in Table S2 in the ESI.† The q(3) puckering amplitude values are much higher than the corresponding q(2) amplitude values, which are very close to zero. The q(3) values are also very similar to the total puckering amplitudes QT with an average value of 0.625 Å, which lies only slightly under the QT value of 0.63 Å for an ideal cyclohexane chair.⁸² These results indicate that all cyclohexane rings in the adamantane group adopt a very slightly distorted chair conformation.

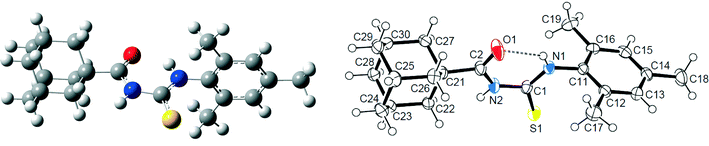Fig. 2 Computed (left) and X-ray (right) molecular structures of 1 with displacement ellipsoids plotted at 50% probability level. Intramolecular N–H⋯O hydrogen bond is shown as a dashed line.

Table 2 Hydrogen bonding geometrical parameters for compounds 1–6 (Å, °)

Compound	D–H⋯A	d(D–H)	d(H⋯A)	d(D⋯A)	∠(D–H⋯A)	Label (Fig. 3)
Symmetry codes for 1: (i) 1 − x, −y, 1 − z; (ii) 1 − x, 1 − y, 1 − z; for 2: (i) x, y, z; (ii) −1/2 + x, 1/2 − y, − 1/2 + z; (iii) 3 − x, 1 − y, 1 − z; (iv) 2.5 − x, −1/2 + y, 1/2 − z; for 3: (i) 1 − x, 1 − y, −z; (ii) x, 1.5 − y, −1/2 + z; (iii) −x, 1/2 + y, −1/2 − z; (iv) −x, 1 − y, −z; for 4: (i) 1 − x, 1 − y, 2 − z; (ii) −1 + x, y, 1 + z; (iii) 1 − x, 1 − y, 1 − z; (iv) x, 1.5 − y, −1/2 + z; for 5: (i) 1 − x, y, 1/2 − z; (ii) x, 1 + y, z; (iii) 1 + x, y, z; (iv) 1 − x, −y, 1 − z; for 6: (i) 2 − x, 1 − y, 1 − z; (ii) 1 − x, −y, 2 − z; (iii) 2 − x, −y, 1 − z; (iv) 3 − x, −y, 2 − z; (v) −1 + x, y, z.a The A⋯H reciprocal interaction.
1
	N1–H1⋯O1^i	0.83(2)	2.40(2)	3.041(2)	132	1
	C27–H27B⋯S1^ii	0.99	2.986(1)	3.916(1)	157	6
2
	N102–H102⋯S2^i	0.83	2.77(2)	3.576(2)	162	1
	C110–H11B⋯S2^i	0.99	2.7031(5)	3.652(2)	161	2
	S1⋯H21J^i	—	2.7110(5)^a	—	—	3
	S1⋯H202^i	—	2.75(2)^a	—	—	4
	C105–H10B⋯O202^ii	0.99	2.544(1)	3.412(2)	152	5
	C112–H11E⋯O203^iii	0.99	2.404(1)	3.380(2)	169	9
	C106–H10C⋯C112^iv	0.95	2.843(2)	3.649(2)	143	10
3
	N2–H2⋯S1^i	0.89	2.66(1)	3.499(1)	157	1
	C14–H14A⋯S1^i	0.99	2.7829(4)	3.710(1)	156	2
	C6–H6A⋯O2^ii	0.95	2.482(2)	3.077(2)	121	3
	C14–H14B⋯O3^iii	0.99	2.646(1)	3.526(2)	148	4
4
	N2–H2⋯S1^i	0.80	2.84(2)	3.592(1)	155	1
	C22–H22B⋯S1^i	0.99	2.7744(5)	3.704(2)	157	2
	C26–H26A⋯S1^i	0.99	2.9861(4)	3.865(2)	148	3
	C29–H29A⋯Cl2^ii	0.99	2.834(1)	3.715(2)	149	4
	C22–H22A⋯C16^iii	0.99	2.895(2)	3.812(3)	154	5
5
	N1–H1⋯O1^i	0.88	2.30(3)	3.038(4)	141	1
	C13–H13⋯F2^ii	—	2.380(2)	—	—	2
	C23–H23⋯F1^iii	1.00	2.661(2)	3.624(4)	161	3
	C26–H26A⋯S1^iv	0.99	2.9123(9)	3.830(3)	154	4
	C27–H27A⋯S1^iv	0.99	2.9650(9)	3.867(3)	152	5
6
	N1–H1⋯O2^i	0.79(3)	2.52(3)	3.184(3)	142	1
	O1–H10⋯S1^ii	0.86(3)	2.36(3)	3.212(2)	169	3
	C14–H14A⋯S1^iii	0.97	2.8411(7)	3.761(2)	159	4
	C3–H3⋯O1^iv	0.93	2.628(2)	3.504(3)	157	5
	C14–H14B⋯F1^v	0.97	2.449(2)	3.354(3)	155	6

---

In the crystal packing of 1, intermolecular N–H⋯O and non-conventional C–H⋯S hydrogen bonds link the molecules into centrosymmetric dimers stacked along the direction of the b axis (Fig. 3), giving R²₂(12) and R²₂(14) graph-set motifs, respectively.

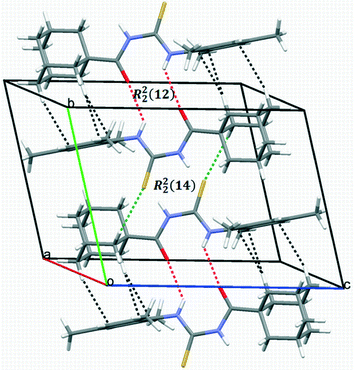Fig. 3 A packing diagram of compound 1 showing centrosymmetric dimers stacked along the b-axis. Intra- and inter-molecular hydrogen bonds are shown as dashed lines.

3.4. Hirshfeld surface analysis

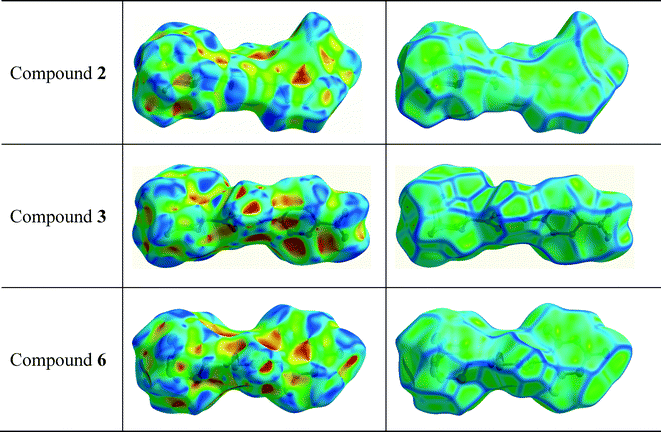
Hirshfeld surface analysis was carried out for the purpose of studying the nature of the intermolecular contacts and their quantitative contributions to the supramolecular assembly of 1, as well as to other five mono-substituted adamantyl phenylthiourea derivatives recently reported.^41,42,83 The selected structures are labelled here as 2 (1-(adamantane-1-carbonyl)-3-(3-nitrophenyl)thiourea), 3 (1-(adamantane-1-carbonyl)-3-(4-nitrophenyl)thiourea), 4 (1-(adamantane-1-carbonyl)-3-(2,4-dichlorophenyl)thiourea), 5 (1-(adamantane-1-carbonyl)-3-(2-bromo-4,6-difluorophenyl)thiourea), and 6 (1-(adamantane-1-carbonyl)-3-(2,6-difluoro-4-hydroxyphenyl)thiourea). The geometric parameters of hydrogen bonds for compounds 1–6 are shown in Table 2.

The Hirshfeld surfaces of compounds 1–6 are shown in Fig. 4. The d_norm map of compound 1 indicates that H⋯O reciprocal contacts are distinguished relative to the other interactions by a pair of adjacent deep-red regions, labelled 1, attributed to strong N–H⋯O hydrogen bonds (Table 2) forming R²₂(12) dimers as described in Fig. 3. The same type of interaction was only observed (labelled 1) for structures 5 and 6. A pair of pale blue to white spots for structures 1 (labelled 6), 5 (labelled 4) and 6 (labelled 4) represents H⋯S contacts that indicate C⋯H contacts associated with two T-shaped C–H⋯π interactions as described in Table 3. The distances between the involved H-atoms (H13 and H22A) and the nearest carbon atom in the corresponding benzene ring are in agreement with theoretical calculations for related compounds.⁸⁴ For structures 2, 3 and 4 (labelled 1), this motif is combined with N–H⋯S hydrogen bonds forming typical centrosymmetric R²₂(8) loops. It is worthwhile to highlight here that the dihedral angles of 65.22(2) and 71.61(3)° between the plane of the central thiourea group and the plane of the 2,4,6-trisubstituted phenyl ring for structures 5 and 6, respectively, are the closest to the one obtained for structure 1. The corresponding angles for structures 2, 3 and 4 measure 51.15(1), 37.22(2) and 39.38(1)°, respectively. The differences in the dihedral angle of structures 5 and 6 in relation to that of structure 1 could be attributed to the presence of two types of substituents in the phenyl ring. For compound 1, the supramolecular arrangement is further controlled by two T-shaped C–H⋯π interactions involving the H26B and H29B atoms of the adamantane group and the C11–C16 benzene ring [centroid Cg(1); symmetry: 1 − x, −y, 1 − z]. The shorter interaction⁸⁵ is found with H26B⋯Cg(1) as described in Table 4. The distance of 2.820(1) Å between the H26B atom and the nearest carbon atom in the benzene ring is in agreement with theoretical calculations.⁸⁴

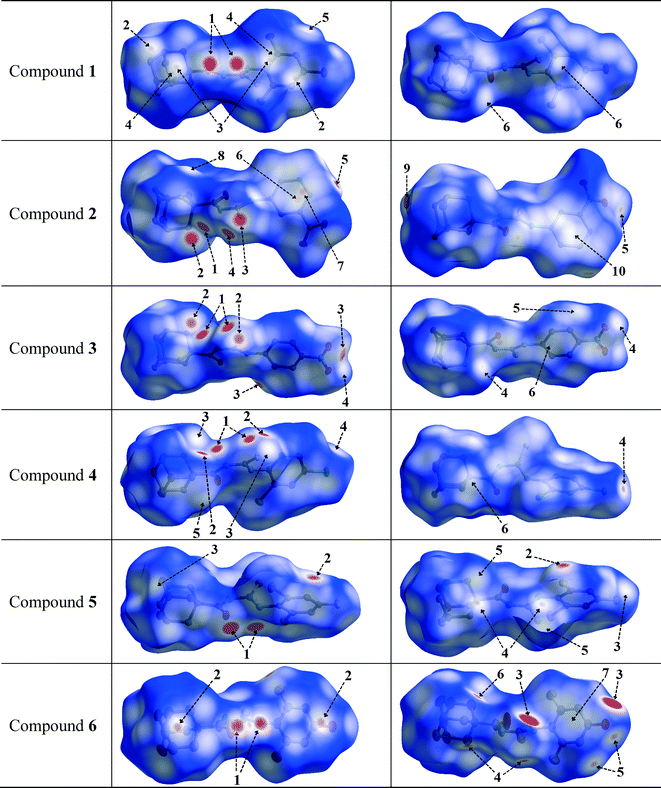Fig. 4 Views of the Hirshfeld surfaces in two orientations for compounds 1–6 with thermal ellipsoids plotted at 50% probability level. The surfaces in column 3 are rotated by 180° around the horizontal axis of the plot. H-atoms are omitted. Numbered arrows are described either in Table 2 or in the text.

Table 3 Geometrical parameters of the π-stacking moieties involved in the π⋯π interactions for compounds 2, 3 and 6 (Å, °)

Rings I–J^a	R c	R 1v	R 2v	α	β	γ	Symmetry
a Cg(1) and Cg(2) are the centroids of the rings C102–C107 and C202–C207 for 2, respectively, and C1–C6 for 3 and 6. b Centroid distance between ring I and ring J. c Vertical distance from ring centroid I to ring J. d Vertical distance from ring centroid J to ring I. e Dihedral angle between mean planes I and J. f Angle between the centroid vector Cg(I)⋯Cg(J) and the normal to plane I. g Angle between the centroid vector Cg(I)⋯Cg(J) and the normal to plane J.
Compound 2
Cg(1)⋯Cg(2)	3.656(1)	3.291(1)	3.317(1)	2.03	24.9	25.8	1.5 − x, −1/2 + y, 1/2 − z
Cg(1)⋯Cg(2)	3.784(1)	3.371(1)	3.332(1)	2.03	28.3	27.0	2.5 − x, −1/2 + y, 1/2 − z
Compound 3
Cg(1)⋯Cg(2)	4.670(1)	3.324(2)	3.324(2)	0.00	44.6	44.6	−x, 1 − y, −z
Compound 6
Cg(1)⋯Cg(2)	4.101(2)	3.371(2)	3.371(2)	0.00	18.3	18.3	2 − x, −y, 2 − z

---

Table 4 Geometrical parameters of C–H⋯π interactions* for compounds 1 and 4 (Å, °)

C–H⋯Cg(J)^a	H⋯Cg1	H-perp^b	γ	∠C–H⋯Cg(J)	H⋯C^d	Symmetry
*(H⋯Cg1 < 3.0 Å, γ < 30.0°).a Centroid of benzene ring.b Perpendicular distance of H to ring plane J.c Angle between the Cg–H vector and ring J normal.d Distance between H-atom and the nearest carbon atom in the benzene ring. R1 denotes a puckered ring of the adamantane group, and R2 of the benzene ring.
Compound 1
C26–H26B⋯Cg(1)	2.70	2.66	10.7	162	2.820(1)	1 − x, −y, 1 − z
Compound 4
(R1)C13–H13⋯Cg(1)	2.85	2.84	3.50	135	3.090(2)	x, 1.5 − y, −1/2 + z
(R2)C22–H22A⋯Cg(1)	2.87	2.80	14.72	127	2.895(2)	1 − x, 1 − y, 1 − z

---

N–H⋯S, C–H⋯S and C–H⋯O hydrogen bonds are present in structures 2 and 3, and can be seen as deep-red spots labelled 1, 2 and 5, respectively, with similar values for the corresponding H⋯A distances (Table 2). However, when the nitro group is at the meta position on the phenyl ring (structure 2), the d_norm map shows H⋯C contacts (labelled 10) attributed to C–H⋯C hydrogen bonds, involving the hydrogen at position 5 on the phenyl ring. In addition, this hydrogen atom forms H⋯O and H⋯H contacts which are not visible in the two selected orientations of the d_norm map. These interactions are responsible for the increase in the dihedral angle between the plane of the thiourea fragment and the plane of the 3-nitrophenyl ring in comparison to that for the 4-nitrophenyl conformation in structure 3 (values are given above).

In the halophenylthioureas 4 and 5, X–H⋯S (X = N, C) contacts are manifested as deep-red spots (labelled 1 and 2) for the former, whereas deep-red regions (labelled 1) are attributed to the presence of N–H⋯O hydrogen bonds for the latter. H⋯D (D = Cl, F) contacts are visible as small red spots, labelled 3 and 2, associated with C–H⋯Cl and C–H⋯F hydrogen bonds, respectively. Unlike that for structure 5, the d_norm map for structure 4 shows a red spot (labelled 5) associated with a C–H⋯C hydrogen bond. For all the six compounds, the existence of H⋯H contacts with red to white regions in the Hirshfeld surfaces is common. In the case of structure 6, two deep-red regions (labelled 3) correspond to strong O–H⋯S hydrogen bonds associated with the presence of hydroxyl groups. In the d_norm surfaces of 1, 2, 3 and 4, there are red to white spots labelled 5, 8, 5 and 6, respectively, due to H⋯H contacts with distances ranging from 2.325 to 2.391 Å, according to the structural determination.

The red to white areas marked as 6 and 7 for the surface of 2, and 7 for the surface of 6 are C⋯C contacts representative of π⋯π stacking interactions (Table 3). The pattern of adjacent red and blue triangles that appears on the shape index surfaces of 2 and 6, as well as a relatively large and flat green region at the same side of the molecule on the corresponding curvedness surfaces, confirms the presence of π⋯π interactions (Fig. 5). The largest region of flat curvedness appears for compound 2. This type of intermolecular contact is also evident in 3 due these properties mapped on its surface as shown in Fig. 5, but its geometric parameters given in Table 3, particularly R_c, β and γ, indicate a weaker interaction, in comparison with those on the surfaces of 2 and 6. In addition, a relatively smaller region of flat curvedness on the surface of 3 allows us to estimate the existence of π⋯π stacking with minor overlapping of adjacent molecules.

Fig. 5 Hirshfeld surfaces mapped with shape index and curvedness for compounds 2, 3 and 6.

The fingerprint plots of the main intermolecular contacts for all the six structures are shown in Fig. 6. For structure 1, the shortest contacts correspond to the very close H⋯H contacts, showing a sharp spike (labelled 1) centred near a (d_e + d_i) sum of 2.1 Å. The O⋯H (labelled 2) and C⋯H contacts (labelled 3), with sharp pairs of spikes centered near a (d_e + d_i) sum of 2.3 and 2.9 Å, correspond to N–H⋯O and C–H⋯C hydrogen bonds, respectively. In addition, we observe S⋯H contacts (labelled 4), with less sharper spikes centered around a (d_e + d_i) of 2.8 Å, attributed to C–H⋯S hydrogen bonding (Table 2). The H⋯H contacts are the shortest for each of the compounds, and O⋯H, S⋯H and C⋯H intermolecular contacts are present in all the structures. In the case of structures 3 and 4, the distances of C⋯H and O⋯H contacts, respectively, are longer than the sum of their van der Waals radii. Unlike compound 1, there are O⋯H reciprocal contacts with an asymmetric pair of spikes for structure 2, indicating H⋯O and O⋯H contacts with significantly different (d_e + d_i) distances near 2.3 and 2.5 Å, respectively. C⋯C contacts (labelled 5) attributed to π⋯π interactions between phenyl rings were observed for structures 2 and 6, with centroid-to-centroid distances of 3.656(2) and 4.101(3) Å, respectively. The corresponding fingerprint plots clearly depict a green area on the diagonal at approximately 1.8 Å, which is characteristic of π⋯π interactions. The pairs of spikes (labelled 6 and 7) in the halophenylthioureas 4 and 5 correspond to Cl⋯H and F⋯H contacts, respectively. The fingerprint of structure 5 reveals the occurrence of weak Br⋯H interactions (labelled 8), which are not visible in the Hirshfeld surfaces due to fact that the distances are longer than the sum of the van der Waals cutoff radii.

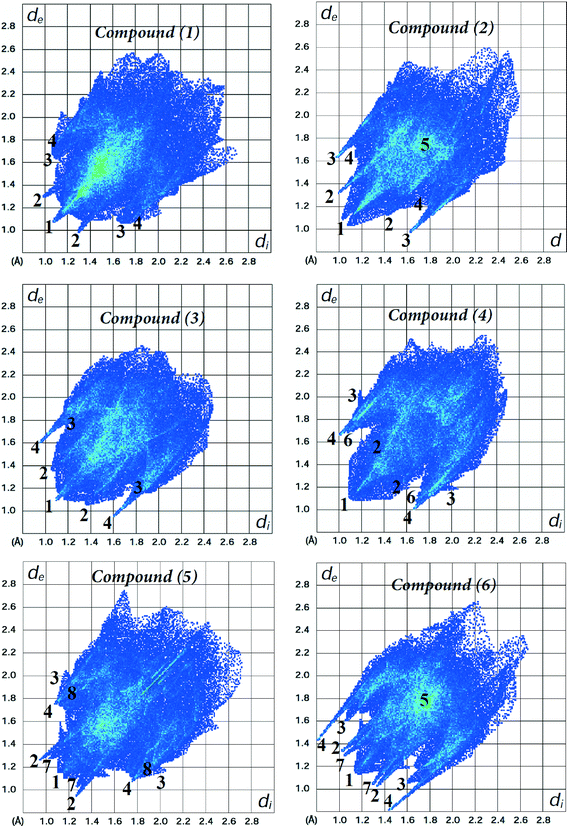Fig. 6 Fingerprint plots of compounds 1–6. Close contacts are labelled as: (1) H⋯H, (2) O⋯H, (3) C⋯H, (4) S⋯H, (5) C⋯C, (6) Cl⋯H, (7) F⋯H and (8) Br⋯H.

The relative contributions to the Hirshfeld surface area due to the main intermolecular contacts for compounds 1–6 are shown as a histogram in Fig. 7. It is clear that the nature, number and position of the substituents on the phenyl ring play a key role in the participation of each type of contact. For all the structures, the H⋯H interactions (labelled 1) have the most important contribution to the total Hirshfeld surface. In structure 1, the major presence of eleven hydrogen atoms on the phenyl group notably increases the contribution from H⋯H contacts over the Hirshfeld surface (72.0%) in relation to the other five structures. However, according to the crystal structure determination, the lowest percentage of H⋯H contacts for structure 5 (33.9%) is a result of interactions involving the adamantane and phenyl groups. For the contacts associated with hydrogen bonds, the contributions of S⋯H contacts are very similar (9.5–12.8%) due to the fact that all the six structures contain only one sulfur atom involved in the formation of dimers through C–H⋯S hydrogen bonds. The percentages of C⋯H contacts present a less close interval of 8.3–14.2%. In the case of structures 2 and 3, the O⋯H interactions show the highest contributions to the Hirshfeld contact surface of 26.4 and 17.9%, respectively. N⋯H contacts are only visible for compounds 2 and 3, with the smallest fingerprint contributions of 4.6 and 3.6%, respectively. Other types of intermolecular contacts with the most important percentages occur such as C⋯C (3.4%) for compound 2, and C⋯O (3.0%), N⋯O (2.2%) and O⋯O (2.4%) for compound 3.

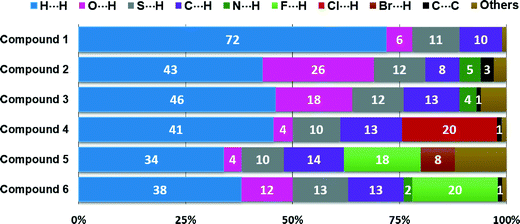Fig. 7 Relative contributions of intermolecular contacts to the Hirshfeld surface area for compounds 1–6.

In this study, we have calculated the enrichment ratios⁸⁶ of the main intermolecular contacts for compounds 1–6 in order to analyze the propensity of two chemical species (X and Y) to be in contact. The enrichment ratio E_XY is a descriptor derived from the Hirshfeld surface analysis, and is defined as the ratio between the proportion of actual contacts C_XY in the crystal and the theoretical proportion of random contacts R_XY. The percentages of Hirshfeld surface contacts C_XY are acquired using CrystalExplorer 3.1.⁶⁶ The proportion S_X of different chemical species on the molecular surface is obtained from C_XX and C_XY values. The random contact R_XY values are calculated from the corresponding S_X and S_Y proportions by using the probability products. The value of E_XY is expected to be generally larger than unity for pairs of elements with a high propensity to form contacts in crystals, while pairs that tend to avoid contacts are associated with E_XY values lower than unity.

Table 5 shows the enrichment ratios of the main intermolecular interactions for compounds 1–6 (complete information is provided in Table S3†). The H⋯H contacts can be considered as favoured in all structures because the enrichment ratios are very close to unity (E_HH = 0.90–0.98), and constitute most of the interaction surface (33.9–72.0%). The E_SH values are larger than unity (1.12–1.49) for all the structures, indicating that S⋯H contacts have an increased propensity to form in the crystal packing, with similar random contacts ranging from 8.1 to 9.4%. The E_CH ratios ranging from 1.10 to 1.37 (except for structure 2) indicate that C⋯H contacts have a high propensity to form in the crystal packing, as a result of the abundant S_H proportion of hydrogen atoms (61.4–85.6%) at the molecular surfaces. The O⋯H contacts of all the structures are much enriched (except for structure 3), with the highest propensity for structures 2 and 6. Despite the lower contribution of O⋯H contacts to the Hirshfeld surface (C_OH = 11.9%) for compound 6 than that for structure 3 (C_OH = 17.9%), the proportion of oxygen atoms on the molecular surface of the former is significantly smaller (S_O = 6.5%), decreasing the value of the random contacts (R_OH = 8.7%). This allows us to explain the higher propensity of the O⋯H contacts to form in structure 6 (E_OH = 1.37) in comparison with that in structure 3.

Table 5 Enrichment ratios E_XY of the main intermolecular interactions for compounds 1–6

Interaction	1	2	3	4	5	6
E XY values for random contacts RXY lower than 0.7% were not calculated.
H⋯H	0.98	0.91	0.97	0.98	0.90	0.84
C⋯H	1.17	0.73	1.10	1.12	1.37	1.20
N⋯H	0.83	1.21	0.90	0.19	/	1.15
O⋯H	1.15	1.35	0.93	1.02	1.16	1.37
S⋯H	1.12	1.44	1.46	1.14	1.19	1.49
F⋯H	—	—	—	—	1.44	1.35
Cl⋯H	—	—	—	1.07	—	—
Br⋯H	—	—	—	—	0.77	—
C⋯C	—	4.86	0.71	1.00	—	/
C⋯O	—	0.58	1.30	—	—	—
N⋯O	—	1.00	2.72	—	—	—
O⋯O	—	—	1.20	—	—	—

---

The E_FH values of 1.44 and 1.35 for the halophenylthioureas 5 and 6, respectively, as well as the E_ClH value of 1.07 for structure 4 reveal that F⋯H and Cl⋯H contacts are highly favoured, with the highest proportion of S_F (10.3 and 10.8%) and S_Cl (14.2%), respectively, apart from the S_H values. This indicates that the weak fluorine and chlorine hydrogen-bonding interactions are comparable in importance to the characteristic strong N–H⋯O hydrogen bonds^86–88 in acylthiourea derivatives. Other types of contacts that appear in structure 6 involving fluorine atoms such as C⋯F, N⋯F and O⋯F contacts are very impoverished. N⋯H contacts are highly favoured for structures 2 and 6 (E_NH = 1.21 and 1.15), slightly favoured for structures 1 (E_NH = 0.83) and 3 (E_NH = 0.90), and impoverished for compounds 4 and 5 with E_NH ratios of 0.19 and 0.06, respectively. No correlation has been found between the E_NH ratios and the corresponding random contacts.

Although the random contacts with values lower than 0.9% are considered insignificant, we have computed the enrichment ratio of C⋯C, N⋯O and O⋯C short contacts for compounds 1–4. It can be interestingly observed in these compounds that the C⋯C contacts are highly enriched (E_CC = 4.86) for compound 2, enriched for structure 4 (E_CC = 1.00), and slightly impoverished for structure 3 (E_CC = 0.71), with the percentage of R_CC being 0.7 for the three compounds. This indicates that the E_CC and S_C values show no correlation for structures 2, 3 and 4. On the other hand, the high value of E_CC for structure 2 helps to explain the exceptionally low propensity of the C⋯H contacts to form (E_CH = 0.73) as both C⋯C and C⋯H contacts are presumably in competition. In the case of structure 3, the high probability to form O⋯O, C⋯O and N⋯O short contacts with enrichment ratios ranging from 1.20 to 2.72 is another reason which can explain the reduced value of E_OH (0.93), in comparison with the other structures. The X⋯Y intermolecular contacts, which are completely avoided with E_XY = 0.00, are not included in Table 5.

4. Conclusions

The molecular structure of 1-(adamantane-1-carbonyl)-3-(2,4,6-trimethylphenyl)thiourea has been characterized by single-crystal X-ray diffraction. The dihedral angle between the plane of the 2,4,6-trimethylphenyl fragment and the plane of the thiourea moiety is 92.6° for the vacuum-isolated molecule, a value very similar to that (89.56(5)°) obtained in the crystal structure determination. All the cyclohexane rings in the adamantane group adopt a slightly distorted chair conformation as reflected by the q(3) value of 0.625 Å. The Hirshfeld surfaces, fingerprint plots and enrichment ratios were found to be very useful in the study of the intermolecular interactions and their quantitative contributions to the crystal packing of a series of six 1-(adamantane-1-carbonyl)-3-substituted-phenyl thioureas. The results revealed remarkable relative contributions of H⋯H interactions more than the other contacts. Compounds 1, 5 and 6 have structural similarities, such as the presence of N–H⋯O and C–H⋯S hydrogen bonds forming centrosymmetric R²₂(12) and R²₂(14) dimers, respectively, related to the nature of substituents on the tri-substituted phenyl ring. According to the enrichment ratios, the H⋯H contacts are favoured, and the S⋯H contacts have a high propensity to form in the crystals for all the structures. The O⋯H and C⋯H contacts displayed a high propensity to occur in five structures. The presence of the less common C–H⋯F and C–H⋯Cl hydrogen bonds, as well as π⋯π and C–H⋯π contacts, showed to be as important as the conventional interactions in directing the packing of the molecules. These results could be applied in crystal engineering for the design of supramolecular arrangements using the 1-(adamantane-1-carbonyl) thiourea synthon.

Acknowledgements

MFE is a member of the Carrera del Investigador of CONICET (República Argentina). The Argentinian author thanks the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), the ANPCYT and the Facultad de Ciencias Exactas, Universidad Nacional de La Plata for financial support.

References

1. E. Neucki, Ber. Dtsch. Chem. Ges., 1873, 6, 598–600.
2. G. A. Hope, R. Woods, S. E. Boyd and K. Watling, Colloids Surf., A, 2004, 232, 129–137.
3. L. Guang-yi, Z. Hong, X. Liu-yin, W. Shuai and X. Zheng-he, Miner. Eng., 2011, 24, 817–824.
4. E. Otazo-Sanchez, L. Pérez-Marin, O. Estevez-Hernandez, S. Rojas-Lima and J. Alonso-Chamarro, J. Chem. Soc., Perkin Trans. 2, 2001, 2211–2218.
5. D. Wilson, M. Á. Arada, S. Alegret and M. del Valle, J. Hazard. Mater., 2010, 181, 140–146.
6. A. I. Daud, W. M. Khairul, H. Mohamed Zuki and K. KuBulat, J. Sulfur Chem., 2014, 35, 691–699.
7. M. Afzaal, M. A. Malik and P. O'Brien, J. Mater. Chem., 2010, 20, 4031–4040.
8. J. C. Bruce, N. Revaprasadu and K. R. Koch, New J. Chem., 2007, 31, 1647–1653.
9. A. Saeed, U. Flörke and M. F. Erben, J. Sulfur Chem., 2014, 35, 318–355.
10. A. Solinas, H. Faure, H. Roudaut, E. Traiffort, A. Schoenfelder, A. Mann, F. Manetti, M. Taddei and M. Ruat, J. Med. Chem., 2012, 55, 1559–1571.
11. C. Li, W. Yang, H. Liu, M. Li, W. Zhou and J. Xie, Molecules, 2013, 18, 15737–15749.
12. G. Hallur, A. Jimeno, S. Dalrymple, T. Zhu, M. K. Jung, M. Hidalgo, J. T. Isaacs, S. Sukumar, E. Hamel and S. R. Khan, J. Med. Chem., 2006, 49, 2357–2360.
13. M. Boiocchi, L. Del Boca, D. E. Gomez, L. Fabbrizzi, M. Licchelli and E. Monzani, J. Am. Chem. Soc., 2004, 126, 16507–16514.
14. M. Bonizzoni, L. Fabbrizzi, A. Taglietti and F. Tiengo, Eur. J. Org. Chem., 2006, 2006, 3567–3574.
15. H.-L. Chen, Z.-F. Guo and Z.-L. Lu, Org. Lett., 2012, 14, 5070–5073.
16. S. Li, X. Cao, C. Chen and S. Ke, Spectrochim. Acta, Part A, 2012, 96, 18–23.
17. C. Limban, A.-V. Missir, I. C. Chirita, A. F. Neagu, C. Draghici and M. C. Chifiriuc, Rev. Chim., 2011, 62, 168–173.
18. C. Limban, A.-V. Missir, I. C. Chirita, C. D. Badiceanu, C. Draghici, M. C. Balostescu and O. Stamatoiu, Rev. Roum. Chim., 2008, 53, 595–602.
19. J. Müller, C. Limban, B. Stadelmann, A. V. Missir, I. C. Chirita, M. C. Chifiriuc, G. M. Nitulescu and A. Hemphill, Parasitol. Int., 2009, 58, 128–135.
20. J. Sun, S. Cai, H. Mei, J. Li, N. Yan, Q. Wang, Z. Lin and D. Huo, Chem. Biol. Drug Des., 2010, 76, 245–254.
21. F. F. Ferreira, A. C. Trindade, S. G. Antonio and C. de Oliveira Paiva-Santos, CrystEngComm, 2011, 13, 5474–5479.
22. R. Custelcean, N. L. Engle and P. V. Bonnesen, CrystEngComm, 2007, 9, 452–455.
23. J. Huang, R. L. Ostrander, A. L. Rheingold and M. A. Walters, Inorg. Chem., 1995, 34, 1090–1093.
24. K. S. Eccles, R. E. Morrison, A. R. Maguire and S. E. Lawrence, Cryst. Growth Des., 2014, 14, 2753–2762.
25. K. S. Eccles, R. E. Morrison, A. S. Sinha, A. R. Maguire and S. E. Lawrence, Cryst. Growth Des., 2015, 15, 3442–3451.
26. D. Dey, T. P. Mohan, B. Vishalakshi and D. Chopra, Cryst. Growth Des., 2014, 14, 5881–5896.
27. I. Wawrzycka-Gorczyca, J. Struct. Chem., 2014, 55, 520–524.
28. S. B. Novaković, B. Fraisse, G. A. Bogdanović and A. Spasojević-de Biré, Cryst. Growth Des., 2007, 7, 191–195.
29. B. M. Yamin and U. M. Osman, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, o1286.
30. W. Zhu, W. Yang, W. Zhou, H. Liu, S. Wei and J. Fan, J. Mol. Struct., 2011, 1004, 74–81.
31. O. Estévez-Hernández, J. Duque, J. Ellena and R. S. Correa, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, o1157.
32. A. Okuniewski, J. Chojnacki and B. Becker, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2012, 68, o619–o620.
33. X. Zhang, H. He, M. Xu and P. Zhong, J. Chem. Res., 2011, 35, 323–325.
34. N. Gunasekaran, R. Karvembu, S. W. Ng and E. R. T. Tiekink, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, o2113.
35. H. Pérez, R. S. Correa, A. M. Plutin, B. O'Reilly and M. B. Andrade, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2012, 68, o19–o22.
36. L. R. Gomes, L. M. N. B. F. Santos, J. A. P. Coutinho, B. Schroder and J. N. Low, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2010, 66, o870.
37. A. Saeed and U. Flörke, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, o2403–o2405.
38. G. Binzet, F. M. Emen, U. Flörke, T. Yesilkaynak, N. Külcü and H. Arslan, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o81–o82.
39. M. K. Rauf, A. Badshah and U. Flörke, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, o3823–o3825.
40. A. Saeed, A. Khurshid, M. Bolte, A. C. Fantoni and M. F. Erben, Spectrochim. Acta, Part A, 2015, 143, 59–66.
41. A. Saeed, M. F. Erben and M. Bolte, Spectrochim. Acta, Part A, 2013, 102, 408–413.
42. A. Saeed, U. Flörke and M. F. Erben, J. Mol. Struct., 2014, 1065–1066, 150–159.
43. C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896.
44. S. K. Seth, D. Sarkar and T. Kar, CrystEngComm, 2011, 13, 4528–4535.
45. S. K. Seth, P. Manna, N. J. Singh, M. Mitra, A. D. Jana, A. Das, S. R. Choudhury, T. Kar, S. Mukhopadhyay and K. S. Kim, CrystEngComm, 2013, 15, 1285–1288.
46. P. Manna, S. K. Seth, M. Mitra, A. Das, N. J. Singh, S. R. Choudhury, T. Kar and S. Mukhopadhyay, CrystEngComm, 2013, 15, 7879–7886.
47. S. K. Seth, I. Saha, C. Estarellas, A. Frontera, T. Kar and S. Mukhopadhyay, Cryst. Growth Des., 2011, 11, 3250–3265.
48. S. K. Seth, D. Sarkar, A. D. Jana and T. Kar, Cryst. Growth Des., 2011, 11, 4837–4849.
49. S. K. Seth, CrystEngComm, 2013, 15, 1772–1781.
50. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
51. W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138.
52. A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
53. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004.
55. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
56. G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
57. L. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838.
58. M. Nardelli, Comput. Chem., 1983, 7, 95–98.
59. M. Nardelli, J. Appl. Crystallogr., 1995, 28, 659.
60. J. L. Farrugia, J. Appl. Crystallogr., 1997, 30, 565.
61. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.
62. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816.
63. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
64. M. A. Spackman, Phys. Scr., 2013, 87, 048103.
65. J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668.
66. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer (Version 3.1), University of Western Australia, 2012.
67. S. K. Seth, D. Sarkar, A. Roy and T. Kar, CrystEngComm, 2011, 13, 6728–6741.
68. S. K. Seth, Inorg. Chem. Commun., 2014, 43, 60–63.
69. P. Manna, S. K. Seth, A. Das, J. Hemming, R. Prendergast, M. Helliwell, S. R. Choudhury, A. Frontera and S. Mukhopadhyay, Inorg. Chem., 2012, 51, 3557–3571.
70. H. M. Abosadiya, E. H. Anouar, S. A. Hasbullah and B. M. Yamin, Spectrochim. Acta, Part A, 2015, 144, 115–124.
71. D. M. Gil, M. E. Defonsi Lestard, O. Estévez-Hernández, J. Duque and E. Reguera, Spectrochim. Acta, Part A, 2015, 145, 553–562.
72. M. Atiş, F. Karipcin, B. Sarıboğa, M. Taş and H. Çelik, Spectrochim. Acta, Part A, 2012, 98, 290–301.
73. M. S. M. Yusof, R. H. Jusoh, W. M. Khairul and B. M. Yamin, J. Mol. Struct., 2010, 975, 280–284.
74. A. Saeed, M. F. Erben and U. Flörke, J. Mol. Struct., 2010, 982, 91–99.
75. O. Estévez-Hernández, E. Otazo-Sánchez, J. L. Hidalgo-Hidalgo de Cisneros, I. Naranjo-Rodríguez and E. Reguera, Spectrochim. Acta, Part A, 2005, 62, 964–971.
76. L. Bistricic, G. Baranovic and K. Mlinaric-Majerski, Spectrochim. Acta, Part A, 1995, 51, 1643–1664.
77. W. Yang, W. Zhou and Z. Zhang, J. Mol. Struct., 2007, 828, 46–53.
78. P. P. Tadbuppa and E. R. T. Tiekink, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, o1779–o1780.
79. A. Saeed, A. Khurshid, J. P. Jasinski, C. G. Pozzi, A. C. Fantoni and M. F. Erben, Chem. Phys., 2014, 431–432, 39–46.
80. Z. Weiqun, L. Baolong, Z. Liming, D. Jiangang, Z. Yong, L. Lude and Y. Xujie, J. Mol. Struct., 2004, 690, 145–150.
81. M. K. Rauf, A. Badshah and M. Bolte, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, o2444–o2445.
82. D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358.
83. S. K. Mohamed, A.-A. M. Jaber, S. Saeed, K. S. Ahmad and W.-T. Wong, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2012, 68, o1597.
84. R. Kumar, M. Elango, R. Parthasarathi, D. Vijay and V. Subramanian, J. Chem. Sci., 2012, 124, 193–202.
85. A. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
86. C. Jelsch, K. Ejsmont and L. Huder, IUCrJ, 2014, 1, 119–128.
87. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, Oxford, 1999.
88. C. Jelsch, S. Soudani and C. Ben Nasr, IUCrJ, 2015, 2, 327–340.

---

Footnote

† Electronic supplementary information (ESI) available: Tables S1 and S2 list the selected bond distances/angles and ring puckering parameters, respectively, for compound 1. Relevant data from the Hirshfeld analysis (including C_XY, S_X (%), R_XY and E_XY values) of the main intermolecular interactions for compounds 1–6 are given in Table S3.

---