Gearing motion in cogwheel pairs of molecular rotors: weak-coupling limit

Abstract

Variable-temperature (VT) crystal structures, VT ¹H spin–lattice relaxation in static crystals, and DFT modelling of the rotational barriers of BCP rotators in crystalline arrays of a rod-like molecule containing two 1,3-bis(ethynyl)bicyclo[1.1.1]pentane (BCP) units demonstrate that a correlated gearing motion occurs in the limit of a weak coupling between two rotors in a pair.

---

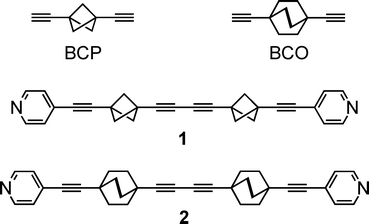
Understanding the mechanism of motion in crystalline arrays of molecular rotors with complex dynamics¹ is a key step that will foster the development of molecular machines capable of performing useful work.^2–8 The present investigation of the topology and dynamics of solid state assemblies of the rod-like molecule bis(3-(pyrid-4-ylethynyl)bicyclo[1.1.1]pent-1-yl)buta-1,3-diyne (1) that contains two 1,3-bis(ethynyl)bicyclo[1.1.1]pentane (BCP) rotators linked by a diyne fragment (Chart 1),⁹ was prompted (i) by our recent report¹⁰ of a correlated gearing motion in cogwheel pairs of a similar rod (2) with 1,4-bis(ethynyl)bicyclo[2.2.2]octane (BCO) rotators⁸ instead; and (ii) the demonstration that, in keeping with the one-dimensional topology of 2, a 4 Å shift of the rotor axles with respect to each other in the thermodynamic polymorph of 2 effectively suppresses the gearing motion.¹¹ Another, yet different, example of correlated rotational motion in a pair is reported here for 1. The latter is shown to be a structural isomer of 2 where the BCP rotators do not rub against each other as much as the BCO rotators in the kinetic polymorph of 2, thereby defining a weak-coupling limit for the gearing motion in cogwheel pairs of molecular rotors.

Chart 1

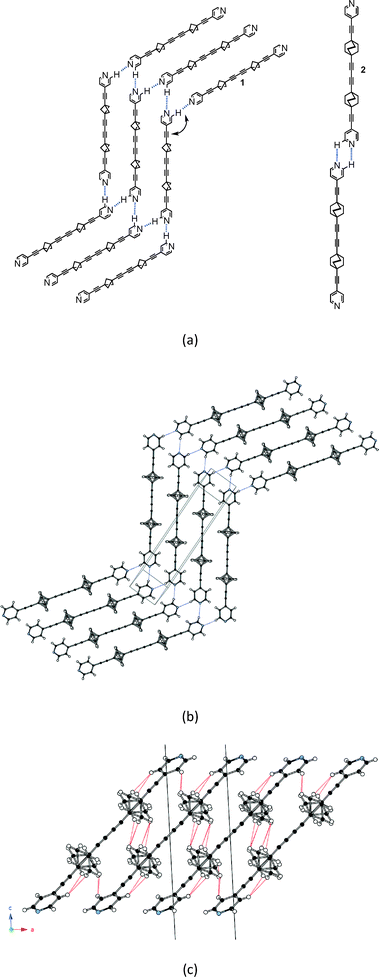
Self-assembly by C–H⋯N hydrogen bonds in layers of parallel zig-zag strings of rods

The molecular rod 1 was synthesized as reported earlier.⁹ Plate-like colourless crystals were obtained by slow cooling of an ethyl acetate solution and their structure was determined by X-ray diffraction at 293 K and 120 K.‡§

As exemplified in Fig. 1, a striking feature distinguishes the patterns of self-assembly, and thus the topologies, of crystalline arrays of 1 and 2. Instead of two parallel C–H⋯N hydrogen bonds connecting successive rods in 2 into infinite one-dimensional strings, the same two hydrogen bonds (Table S1†) connect three rods in 1, creating infinite zig-zag strings with successive rod axles at an angle of 120° (Fig. 1a) and directing the formation of layers of parallel zig-zag strings of 1 (Fig. 1b). The latter are stacked at a canted angle along a (Fig. 1c).

Fig. 1 (a) The two motifs of C–H⋯N hydrogen bonds in 1 and 2; (b) a layer of parallel zig-zag strings in 1; (c) the layers are stacked at a canting angle along a. The dotted red lines are H⋯H interactions (<2.8 Å) identifying pairs of rotators across layers. Note that the two equilibrium positions are drawn in b and c.

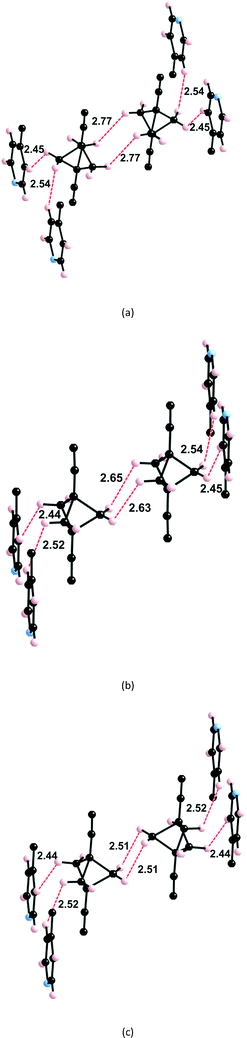
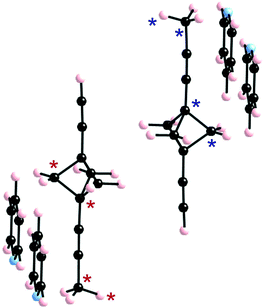
The BCP rotators are located at a single crystallographic site, distributed over two equilibrium positions whose occupancies are unbalanced (0.62 and 0.38 at 293 K; 0.66 and 0.34 at 120 K), but to a lesser extent than in the kinetic polymorph of 2 (0.88 and 0.12 at 293 K).¹⁰ The dotted red lines in Fig. 1c show the inventory of H⋯H interactions shorter than 2.8 Å. It is of interest to note that there is no such contact between BCP rotators in a layer (Fig. 1b). Instead, interacting BCP rotators in a pair are identified in the (a, c) plane as a result of the stacking of layers along a (Fig. 1c). The H⋯H distances associated with the three possible rotor–rotor interactions corresponding to the occupancies of the two equilibrium positions on a single site, i.e. Majority–Majority (2.770 Å (×2)), minority–minority (2.506 Å (×2)) and Majority–minority (2.630 and 2.650 Å), are shown in Fig. 2. In view of such data and our previous work on 2 (ref. 10) we anticipate the possibility of two different rotational barriers associated with: (i) a well-correlated synchronous motion of the two adjacent rotors and (ii) a higher energy asynchronous motion in which two blades of adjacent rotors rub against each other. However, there is an important difference between the two systems: whereas in 2 the H⋯H contacts in the minority–minority situation were as short as 2.1–2.2 Å, in 1 such H⋯H contacts are kept relatively long. Consequently, the two barriers should be relatively close in the present case.

Fig. 2 H⋯H contacts shorter than 2.8 Å in (a) the Majority–Majority, (b) the Majority–minority and (c) the minority–minority occupancies of the two adjacent rotor sites according to the 120 K structure of 1.

Variable-temperature ¹H spin–lattice relaxation identifies two relaxation processes

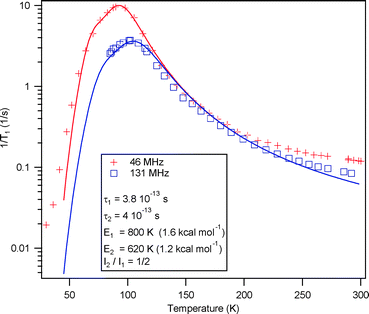
Variable-temperature (35–300 K) proton spin–lattice relaxation experiments were carried out at two fields (with ¹H Larmor frequencies of 46 and 131 MHz) on a static crystalline sample, as described in earlier work.^8,10–12 The correlation time τ_c is obtained by the fit of the ¹H T₁⁻¹ data (Fig. 3) to the Kubo–Tomita formula, τ_c = τ₀ exp(E_a/k_T), with two relaxation processes for the same spin temperature to yield rotational barriers of 1.23 kcal mol⁻¹ = 620 K and 1.59 kcal mol⁻¹ = 800 K, and τ₀ of 4.0 × 10⁻¹³ s and 3.8 × 10⁻¹³ s, for the low and high energy processes, respectively. The occurrence of two relaxation processes for a rotator with two equilibrium positions with unbalanced occupancies on a single crystallographic site has been observed for the kinetic polymorph of 2 and attributed to the dynamic characteristics of a gearing motion within correlated cogwheel pairs.¹⁰ Note however that in 2, in agreement with the analysis above, the energy barriers are typically larger, especially for the high energy process (E_a = 6.1 kcal mol⁻¹ = 3078 K).

Fig. 3 Variable-temperature proton spin–lattice relaxation time, ¹H T₁⁻¹, at two fields for 1.

Modelling the energy barriers

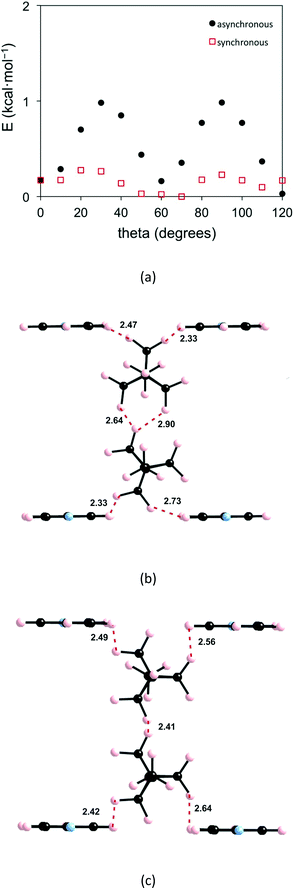
As discussed above (see Fig. 1c) the H atoms of a rotor in 1 are implicated in H⋯H contacts shorter than 2.8 Å with an adjacent rotor and two pyridine substituents. Consequently, the appropriate model to study the rotational motion in this solid is a couple of neighbouring rotors surrounded with four pyridine fragments, as shown in Fig. 4. This model was used in order to estimate the rotational barriers in the solid. The rotors have been modelled as a BCP unit (Chart 1) mimicking the situation in the solid whose triple bonds have been capped in the following manner: 1) by a H atom on the side of the ethynyl group; 2) by a H₃C– on the side of the pyridine. The four neighbouring pyridines, which show relatively short contacts with the blades of the rotors, have been simply considered as pyridine molecules (Fig. 2). As in previous studies,^8,10,11 density functional theory¹³ (DFT) calculations were carried out with the M06-2X functional¹⁴ using the Gaussian 09 code.¹⁵ Basis sets of the type 6-31-G(d,p) were used for C, N and H.¹⁶

Fig. 4 Model used to study the correlated motion of two adjacent BCP rotators. For the synchronous motion, we fix the dihedral angle θ₁ defined by the atoms labelled by a red asterisk and change it every 10°. For the asynchronous motion, we also fix the dihedral angle defined by the atoms labelled with a blue asterisk (θ₂) at the same value as the θ₁ angle. θ = 0° corresponds to the dihedral angle of the crystal structure with the majority occupation on the BCP site.

We have estimated the two rotational barriers for the synchronous and asynchronous motion of the two BCP rotators in a pair searching for the lowest-energy path by means of partial geometry optimizations. In our calculations, the outer H₃C–C≡C– and –C≡CH groups of the two rotators are always kept fixed. For the synchronous motion, we fix the dihedral angle (θ₁) defined by the atoms labelled with a red asterisk in Fig. 4 and change it every 10°. The coordinates for the two neighbouring rotators have been fully optimized within these restrictions. For the asynchronous motion, the dihedral angle defined by the atoms labelled with a blue asterisk in Fig. 4 were also fixed at the same value of the θ₁ angle. The coordinates of the two rotators have been fully optimized within these restrictions. In both cases the four surrounding pyridine molecules were kept fixed at their crystallographic positions. We have verified that the associated H⋯H contacts never become too short and that this assumption is justified.

The calculated barriers are reported in Fig. 5. That for the synchronous motion is very small, 0.28 kcal mol⁻¹ = 141 K, whereas that for the asynchronous motion is larger yet not very high, 0.98 kcal mol⁻¹ = 493 K. These values of the DFT barriers are about 1 kcal mol⁻¹ lower than those obtained by the fit of the spin–lattice relaxation data. This is not unexpected in view of such small barriers, particularly since our discrete model does not take into account long-range contributions. The important result is that the energy difference between the two barriers is relatively small in both the spin–lattice relaxation experiments and the DFT calculations. These barriers mostly originate from the variation of the rotor–rotor H⋯H contacts. The optimized geometries for the higher energy structure of the two types of rotational motions are also shown in Fig. 5. It is clear that the rotor–rotor H⋯H contacts stay considerably long, which is the reason why the barriers are low, as expected. Thus, a picture emerges from this combined experimental and theoretical analysis of the motion of the rotors in a pair where adjacent rotors move gently in a synchronous, well correlated way as long as H⋯H contacts around 2.4 Å occurring in the asynchronous motion are avoided, which according to previous work^10,11 is the onset for the development of repulsive, gear-slipping interactions.

Fig. 5 (a) Computed energy profiles (in kcal mol⁻¹) for the synchronous and asynchronous rotation of two adjacent rotators; (b) calculated structure of the higher energy structure for the synchronous and (c) asynchronous rotations.

Conclusions

We have shown that the rod-like molecule 1 containing two 1,3-bis(ethynyl)bicyclo[1.1.1]pentane (BCP) rotators, linked by a diyne fragment, self-assembles by C–H⋯N hydrogen bonds in a crystalline array that proved to be a structural isomer of the analogous rod, 2, carrying 1,4-bis(ethynyl)bicyclo[2.2.2]octane (BCO) rotators instead. As a result, the rod axles are shifted in 1 in such a way that the rotor–rotor interactions defining strong correlated cogwheel pairs in 2 are rather weakened, that is, the rotors do not rub against each other as much as in 1. Our investigation of the rotor dynamics by VT crystal structures and VT spin–lattice relaxation on static crystals, ¹H T₁⁻¹, and DFT modelling of the rotational barriers reveals two low rotational barriers differing by 0.4–0.7 kcal mol⁻¹, whose energies are rather lower that those in 2 (1.8 and 6.1 kcal mol⁻¹), and concludes that the very same type of correlated gearing motion occurs at thermodynamic equilibrium yet in the limit of a weak coupling between two rotors in a pair, exemplified by a much smaller difference in energy between the low-energy gearing relaxation process and a higher-energy gear-slipping relaxation process.

Acknowledgements

JK and JM gratefully acknowledge financial support from the European Research Council under the European Community's Framework Programme (FP7/2007-2013) ERC grant agreement no. 227756 and the Institute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic (RVO: 61388963). This material is based upon the work supported by the National Science Foundation under Grant No. CHE-1265922. Work at Orsay was supported by the CNRS. Work at Angers was supported by the CNRS, the joint CNRS-Russian Federation grants PICS 6028 and RFBR-CNRS 12-03-91059 (Chernogolovka), and by the Région des Pays de la Loire Grant MOVAMOL. Work in Bellaterra and Tarragona was supported by the Spanish Ministerio de Economía y Competitividad (Projects FIS2012-37549-C05-05 and CTQ2014-52774-P) and Generalitat de Catalunya (2014GR301 and 2014GR199).

Notes and references

1. B. Rodríguez-Molina, S. Peŕez-Estrada and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2013, 135, 10388; B. Rodríguez-Molina, N. Farfán, M. Romero, J. M. Méndez-Stivalet, R. Santillan and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2011, 133, 7280; M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10771; T.-A. V. Khuong, J. E. Nunez, C. E. Godinez and M. A. Garcia-Garibay, Acc. Chem. Res., 2006, 39, 413; S. D. Karlen, H. Reyes, R. E. Taylor, S. I. Khan, M. F. Hawthorne and M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14973; V. Vogelsberg and M. A. Garcia-Garibay, Chem. Soc. Rev., 2012, 41, 1892.
2. B. L. Feringa, Acc. Chem. Res., 2001, 34, 504; D. Horinek and J. Michl, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14175; G. S. Kottas, L. I. Clarke, D. Horinek and J. Michl, Chem. Rev., 2005, 105, 1281; E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2007, 46, 72; K. Skopek, M. C. Hershberger and J. A. Gladysz, Coord. Chem. Rev., 2007, 251, 1723; L. Kobr, K. Zhao, Y. Shen, R. K. Shoemaker, C. T. Rogers and J. Michl, Cryst. Growth Des., 2014, 14, 559.
3. W. Setaka and K. Yamaguchi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9271; W. Setaka and K. Yamaguchi, J. Am. Chem. Soc., 2012, 134, 17932.
4. W. Zhang and R.-G. Xiong, Chem. Rev., 2012, 112, 1163; W. Zhang, H.-Y. Ye, R. Graf, H. W. Spiess, Y.-F. Yao, R.-Q. Zhu and R.-G. Xiong, J. Am. Chem. Soc., 2013, 135, 5230.
5. S. Horiuchi, Y. Tokunaga, G. Giovanetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789; T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S. I. Noro, H. Takahashi, R. Kumai, Y. Tokura and T. Nakamura, Nat. Mater., 2009, 8, 342.
6. S. Yamamoto, H. Iida and E. Yashima, Angew. Chem., Int. Ed., 2013, 52, 6849.
7. Q.-C. Zhang, F.-T. Wu, H.-M. Hao, H. Xu, H.-X. Zhao, L.-S. Long, R.-B. Huang and L.-S. Zheng, Angew. Chem., Int. Ed., 2013, 52, 12602.
8. C. Lemouchi, H. M. Yamamoto, R. Kato, S. Simonov, L. Zorina, A. Rodriguez-Fortea, E. Canadell, P. Wzietek, K. Iliopoulos, D. Gindre, M. Chrysos and P. Batail, Cryst. Growth Des., 2014, 14, 3375; C. Lemouchi, C. S. Vogelsberg, S. Simonov, L. Zorina, P. Batail, S. Brown and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2011, 133, 6371.
9. J. Kaleta, P. I. Dron, K. Zhao, Y. Shen, I. Císařová, C. T. Rogers and J. Michl, J. Org. Chem., 2015, 80, 6173; M. Cipolloni, J. Kaleta, M. Mašát, P. I. Dron, Y. Shen, K. Zhao, C. T. Rogers, R. K. Shoemaker and J. Michl, J. Phys. Chem. C, 2015, 119, 8805; J. Kaleta, M. Nečas and C. Mazal, Eur. J. Org. Chem., 2012, 25, 4783; J. Kaleta, J. Michl and C. Mazal, J. Org. Chem., 2010, 75, 2350; C. Mazal, O. Škarka, J. Kaleta and J. Michl, Org. Lett., 2006, 8, 749; P. F. H. Schwab, B. C. Noll and J. Michl, J. Org. Chem., 2002, 67, 5476; M. D. Levin, P. Kaszynski and J. Michl, Chem. Rev., 2000, 100, 169; P. Kaszynski and J. Michl, [n]Staffanes, in Advances in Strain in Organic Chemistry, IV, ed. B. Halton, JAI Press Inc., Greenwich, CT, 1995, p. 283; M. D. Levin, S. J. Hamrock, P. Kaszynski, A. B. Shtarev, G. A. Levina, B. C. Noll, M. E. Ashley, R. Newmark, G. G. I. Moore and J. Michl, J. Am. Chem. Soc., 1997, 119, 12750; A. B. Shtarev, E. Pinkhassik, M. D. Levin, I. Stibor and J. Michl, J. Am. Chem. Soc., 2001, 123, 3484.
10. C. Lemouchi, K. Iliopoulos, L. Zorina, S. Simonov, P. Wzietek, T. Cauchy, A. Rodríguez-Fortea, E. Canadell, J. Kaleta, J. Michl, D. Gindre, M. Chrysos and P. Batail, J. Am. Chem. Soc., 2013, 135, 9366.
11. G. Bastien, C. Lemouchi, M. Allain, P. Wzietek, A. Rodríguez-Fortea, E. Canadell, K. Iliopoulos, D. Gindre, M. Chrysos and P. Batail, CrystEngComm, 2014, 16, 1241.
12. See also: A. Comotti, S. Bracco, T. Ben, S. Qiu and P. Sozzani, Angew. Chem., Int. Ed., 2014, 53, 1043; A. Comotti, S. Bracco, A. Yamamoto, M. Beretta, T. Hirukawa, N. Tohnai, M. Miyata and P. Sozzani, J. Am. Chem. Soc., 2014, 136, 618.
13. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864; W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
14. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B1, Gaussian Inc., Wallingford CT, 2009.
16. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
17. A. J. M. Duisenberg, L. M. J. Kroon-Batenburg and A. M. M. Schreurs, J. Appl. Crystallogr., 2003, 36, 220; CrysAlisPro, Version 1.171.37.34c, Agilent Technologies.
18. G. M. Sheldrick, SADABS, University of Göttingen, Germany, 1996; SCALE3ABSPACK, Version 1.171.37.34c, Agilent Technologies.
19. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.

---

Footnotes

† Electronic supplementary information (ESI) available: Table S1. CCDC 1412010–1412011. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ce01372k

‡ Crystallography. Single crystal X-ray diffraction data were collected with MoKα (0.71073 Å) radiation on a Bruker Kappa CCD diffractometer at room temperature and with an Oxford Diffraction Gemini-R diffractometer at 120 K (in a cooled nitrogen gas stream). The 293 and 120 K data were processed using the EvalCCD and CrysAlisPro software,¹⁷ respectively; empirical absorption correction was applied with the programs SADABS and Scale3AbsPack.¹⁸ The structure was solved by direct methods followed by Fourier syntheses and refined by the full-matrix least-squares method in an anisotropic approximation for all non-hydrogen atoms using the program SHELX-97.¹⁹ H atoms were refined in a riding model with U_iso(H) = 1.2 U_eq(C). The small thickness of the plate-type crystal and twinning resulted in rather high values of the reliability factors after the structure refinement.

§ Crystal data for 1 at 293 K: C₂₈H₂₀N₂, M = 384.46, monoclinic P2₁/c, a = 5.7123(19), b = 5.7076(17), c = 33.016(18) Å, β = 93.68(5)°, V = 1074.2(8) ų, Z = 2, μ = 0.70 cm⁻¹, 2Θ_max = 54.2°, 7162 reflections measured, 2400 unique (R_int = 0.165), 790 with I > 2σ(I), 166 parameters refined, R(F²) = 0.0769, wR(F²) = 0.1598, GOF = 0.861. At 120 K: monoclinic P2₁/c, a = 5.6780(10), b = 5.6456(7), c = 32.491(12) Å, β = 93.09(2)°, V = 1040.0(4) ų, Z = 2, μ = 0.72 cm⁻¹, 2Θ_max = 56.7°, 4203 reflections measured, 2332 unique (R_int = 0.0617), 1635 with I > 2σ(I), 165 parameters refined, R(F²) = 0.0954, wR(F²) = 0.2314, GOF = 1.020.

---