Anisotropic displacement parameters from dispersion-corrected DFT methods and their experimental validation by temperature-dependent X-ray diffraction

Abstract

In chemical crystallography, the thermal motion of scattering centres is commonly described by anisotropic displacement parameters (ADPs). Very recently, it has been shown that ADPs are not only accessible by diffraction experiments but also via theory: this emerging approach seems promising but must be thoroughly tested. In this study, we have performed specifically tailored X-ray diffraction (XRD) experiments in fine steps between 100 and 300 K which allow detailed comparison to ab initio data from dispersion-corrected density functional theory (DFT) combined with periodic lattice-dynamics. The compound chosen for this study, crystalline pentachloropyridine (C₅NCl₅), is well suited for this purpose: it represents a molecular crystal without H atoms, thus posing no challenge to XRD; its solid-state structure is controlled by dispersion and halogen-bonding interactions; and the ADPs associated with the peripheral Cl atoms show strong temperature dependence. Quality criteria in direct and in reciprocal space prove that ADPs are predicted with high confidence for the temperature range between 100 and 200 K, and that several economic dispersion corrections to DFT can be reliably employed for this purpose. Within the limits we have explored here, the ab initio prediction of ADPs appears to be a facile and complementary tool, especially in those cases where diffraction data cannot provide a straightforward model for thermal motion.

---

Introduction

Crystal engineering requires the understanding of intermolecular interactions to design new materials with desired properties.¹ These contacts between molecular residues comprise directional interactions between individual atoms, such as hydrogen or halogen bonds, and also non-directional attraction due to the correlated movements of the electrons in adjacent molecules, so-called dispersion interactions.

Often, it is the synergy of diffraction experiments and complementary computations which allow for new insight into crystalline materials. While the traditional “workhorses” of solid-state theory, that is, density-functional theory (DFT) methods, face trouble when it comes to describing dispersion (and are hence occasionally eyed upon with some suspicion), the recent years have seen significant progress of dispersion-corrected DFT methods.² This is reflected, for example, in the correct energetic ranking of inorganic polymorphs,³ in successful cohesive energy calculations⁴ and in ab initio crystal-structure predictions.⁵

Previous work from our laboratories and others⁶ has tried to build such bridges between experiment and theory. For example, some of us have been able to correlate results from theory and experimental charge density for the covalency of hydrogen bonds, one of the core interactions in crystal engineering.^6b

The above-mentioned encouraging results underline the good match between minimum energy and optimised structure from periodic DFT calculations on the one and experimental crystal structures and charge densities on the other side. There is, however, more information from high-quality diffraction experiments: in addition to mean atomic positions, displacements from these mean positions can be obtained and thermal motion becomes visible.⁷ In the most popular Gaussian approximation, the components of a symmetric second-order tensor are refined and usually referred to as anisotropic displacement parameters (ADPs).⁸

Recently, the ab initio calculation of ADPs based on experimentally determined lattice parameters and atomic sites became available. Currently, ADPs for molecular crystals can be derived from (1) cluster-models combined with multi-level simulations (ONIOM model),⁹ (2) molecular dynamics trajectories,¹⁰ and (3) periodic lattice-dynamics calculations with atom-centered¹¹ or plane-wave based¹² basis sets. Very recently, some of us have used dispersion-corrected DFT to calculate ADPs based on the latter approach for a set of molecular solids which represent prototypes of hydrogen-bonded and salt-like crystals, respectively.¹²

Our previous results from theory have been validated by comparison to data derived from neutron-diffraction experiments since the compounds contained hydrogen atoms. By contrast, when laboratory-grade X-ray diffraction (XRD) data are interpreted in the conventional way using spherical scattering factors, they can in general not provide sufficiently precise values for hydrogen atoms. Aspherical scattering factors based on invarioms can improve this situation,¹³ but anisotropic refinement of peripheral hydrogen atoms will still result in large standard uncertainties.

In this work, we now take the next step on a compound that has purposefully been chosen to not contain hydrogen atoms. Thereby, we broaden the methodological scope of our investigations: several methods and types of dispersion correction are applied to predict ADPs, and we perform quantitative comparisons of these results with experimental data based on temperature-dependent XRD. In view of the limited data collection time for neutron-diffraction experiments, our previous comparisons between experimental and calculated ADPs had to rely on a few temperatures only. In contrast, in-house XRD equipment allows for fine-grained temperature variation and can thus provide information concerning the temperature range in which ADPs can be reliably calculated from periodic lattice-dynamics calculations and the harmonic approximation.

We chose pentachloropyridine (Cl₅py, Scheme 1) as a suitable test case due to a number of advantages: it exclusively contains atoms for which ADPs may reliably be obtained by XRD; in contrast to many organic and organometallic compounds, the molecular periphery is not dominated by hydrogen but rather by the most relevant scattering centers. Even better: due to large amplitude motions, the most interesting test atoms are usually located in the periphery; for the ADPs of such peripheral atoms pronounced temperature dependence can be expected. In Cl₅py, they correspond to the most electron-rich atom type chlorine for which ADPs can be assessed with very good accuracy. The melting point of the title compound amounts to ca. 120 °C and hence calls for low-temperature data collection, in agreement with common practice nowadays: ca. 60% of the structures which were included in the Cambridge Structural Database¹⁴ during 2014 were derived from intensity data collected at 200 K or lower. And, finally, Cl₅py exhibits simplicity and complexity at the same time: there is only one type of substituent on the aromatic ring, and yet the chlorine atoms are all symmetry-inequivalent and show subtle variations in their ADPs. Can theory capture those?

Scheme 1 Pentachloropyridine, Cl₅py.

Results and discussion

Crystal structure of monoclinic Cl₅py

The dimorphism of Cl₅py has been described in 1973 by Rossell and Scott.¹⁵ We chose the monoclinic polymorph for which crystals of high quality can be reliably obtained. We can confirm the lattice parameters published by Rossell and Scott but we must correct the space group: based on the absence of zonal extinctions for reflections h0l, the original authors described the monoclinic form of Cl₅py in space group P2₁ and found disorder. Inspection of the lattice parameters displayed in Table 1 shows, however, that the unit cells for the Pc and the Pn setting of space group no. 7, related by the matrix operation
are metrically very similar at 100 K. At room temperature, the unit cells associated with both settings are even degenerate within experimental error.

Table 1 Comparison of the lattice parameters for the alternative space group settings Pn and Pc at 100 K

Setting	Pn	Pc
a/Å	5.3122(2)	5.3122(2)
b/Å	5.1770(2)	5.1770(2)
c/Å	14.9058(6)	14.8307(6)
β/°	101.086(2)	99.493(2)

---

Batches of monoclinic Cl₅py (see Experimental section) contain many crystals featuring domains related by the above operation. These crystals correspond to pseudomerohedral twins: their diffraction image can readily be indexed with a single orientation matrix, but the different domain orientations hide the presence of the glide plane and hence the correct extinction symbol. The original authors Rossell and Scott¹⁵ therefore assumed space group P2₁, devoid of any zonal extinctions. Fortunately, our crystallisation experiments did not only afford twinned but also single crystals of Cl₅py; for the results discussed in this article, intensity data collected on single crystals were used. Structure solution and refinement in the correct space group Pc did not give any indication for major disorder. In the monoclinic form of Cl₅py, neighbouring molecules subtend a N⋯Cl halogen bond of ca. 3 Å (dashed lines in Fig. 1).

Fig. 1 Packing in Cl₅py; projection along the crystallographic a axis.

This halogen bond matches the commonly accepted criteria: N1⋯Cl3 amounts to 2.93 Å and hence is significantly shorter than the sum of the van-der-Waals distances¹⁶ (3.3 Å); the almost linear arrangement C–Cl⋯N (179°) corresponds to a close contact between the lone pair on nitrogen and the σ-hole¹⁷ on the halogen atom. The halogen bond represents the only intermolecular contact shorter than van-der-Waals distances: nearest neighbours perpendicular to the direction of the halogen bonds involve Cl⋯C interactions of 3.42 Å (Fig. 2).

Fig. 2 N⋯Cl halogen bond (red dashed line) and closest Cl⋯C interlayer contact (green dashed lines) in Cl₅py.

As outlined in the introduction, we considered monoclinic Cl₅py a suitable test structure for the validation of ADPs obtained from calculations and for their temperature dependence. As preparation for what is to follow, we therefore collected intensity data at 100, 150, 200, 250 and 300 K; the lattice parameters obtained for all data points are compiled in Table 2. In the range from 100 to 300 K, the unit cell parameters increase smoothly with temperature; no phase transition was encountered.

Table 2 Crystal data and convergence results for XRD experiments on Cl₅py at 100, 150, 200, 250 and 300 K

Temperature/K	100(2)	150(2)	200(2)	250(2)	300(2)
a/Å	5.3122(2)	5.3191(16)	5.3290(14)	5.3426(15)	5.359(4)
b/Å	5.1770(2)	5.1827(16)	5.1935(13)	5.2051(15)	5.224(4)
c/Å	14.8307(6)	14.894(5)	14.949(4)	15.021(4)	15.101(13)
β/°	99.493(2)	99.704(5)	99.833(5)	100.003(6)	100.228(18)
V/Å^3	402.28(3)	404.7(2)	407.66(8)	411.4(2)	416.1(6)
Unique refls	2426	1849	1926	1939	1936
R 1 (all data)	0.0326	0.0426	0.0638	0.0821	0.1006
R[F^2 > 2σ(F^2)]	0.0314	0.0387	0.0474	0.0490	0.0525
wR2	0.0725	0.0898	0.0897	0.0855	0.1126
GOF	1.048	1.071	0.992	1.008	0.959

---

ADPs from theory (I): a first test

We then proceeded to compare the experimental data to the outcome of DFT-based lattice-dynamics calculations. Some of us have used such an approach before to calculate ADPs for urea, guanidine, and the rubidium salt of the latter.¹² Thereby, the DFT calculations had been performed at the PBE+D2/PAW level of theory.¹⁸ Being one of many different dispersion corrections developed over the last 15 years,^2,19 the D2 correction is a pairwise correction added a posteriori to the DFT energy:

The damping function f_damp(R_ij) is needed to account for double-counting effects and the R_ij⁻⁶ divergence.

To motivate the use of dispersion corrections for Cl₅py in the first place, we compare the lattice parameters from structures optimised at the uncorrected PBE level and at the PBE+D2 level of theory, respectively, to our experimental data at 100 K (Table 2). The lattice parameters computed without dispersion correction differ from the experiment by up to 15%; PBE+D2 is unsurprisingly better because it differs only by up to 2%. These differences can be clearly attributed to the neglect of dispersion in GGA-type exchange–correlation functionals.

The D2 correction was an obvious choice for the present work since it was used in our previous publication on thermal ellipsoids,¹² and there it gave highly satisfactory results. In Fig. 3, we compare ADPs from experiment to ADPs at the PBE+D2 level of theory at 100 K by means of an ORTEP drawing. We had to handle some numerical difficulties during this calculation: small real frequencies in the phonon band structure forced us to cut off a trace amount of low frequencies for the ADP calculation. This and the other computational details are discussed in the technical details below.

Fig. 3 Experimentally obtained (left) and calculated (PBE+D2 level, right) displacement ellipsoid plots at the 90% level for a molecule of Cl₅py at 100 K.

ADPs from theory (II): a broader range of methods

These initially promising ADPs by PBE+D2 encouraged us to investigate the performance of different dispersion corrections more in depth.

We employed a number of alternative pairwise dispersion corrections added a posteriori to the DFT energy to evaluate the harmonic approximation for the ADP calculation. The dispersion corrections differ in the scaling of the C₆ and R₀ parameters, in the origin of the C₆ parameters, and in the damping function f_damp(R_ij). Grimme's subsequently proposed “D3” correction includes higher order summands of the London dispersion correction (−C_8ij/R₈), and the C_6ij and C_8ij parameters are based on ab initio TDDFT calculations; furthermore, the parameters are scaled due to fractional coordination numbers.²¹ The D3(BJ) correction²² differs only in its damping function from the initially proposed D3 method (the former is occasionally referred to as “zero-damping” variant since the dispersion energy reaches zero in the R_ij → 0 (united atom) limit). The advantage of the BJ damping is that it does not lead to artificial repulsive interatomic forces at short distances which could obviously lead to larger errors during the ADP calculation.²² In the Tkatchenko–Scheffler (TS) correction, finally,²³ the C₆ parameters are derived from free-atom reference data. Moreover, the C₆ parameters and the damping function depend on the electron density due to a Hirshfeld partitioning. These corrections were all applied to DFT calculations with the PBE functional since all parameters for the dispersion correction are already included in the VASP code.

All methods mentioned thus far constitute pairwise, additive corrections, simple to execute but a posteriori by their very nature. For comparison, we also employed a different approach, namely, a direct correction to the correlation functional itself, which is the functional principle of the vdW-DF2 method.²⁴ Thereby, the exchange–correlation functional is extended by a beyond-LDA contribution to the correlation energy; the exchange functional is revPW86.^2,24b As one can see from Table 2, the lattice parameters from all levels of theory—except for PBE without dispersion correction—fit well to the experimental ones at 100 K. To include the positions of the atoms in our comparison, we inspected the root mean square of the Cartesian deviations (rms) between the computed and the experimental structures:^6c,20 the smaller the values, the better the agreement between the experimental and the theoretical structure. Again, the dispersion-corrected methods are better than pure PBE (rightmost column in Table 3).

Table 3 Calculated lattice parameters at different levels of theory compared to the experimental ones at 100 K and the root mean square (rms) of the Cartesian deviations^6c,20 between the calculated structures and the experimental one at 100 K. The acronyms for the different theoretical methods are explained in the main text

	a/Å	b/Å	c/Å	β/°	rms/Å
Exp	5.3122(2)	5.1770(2)	14.8307(6)	99.493(2)	—
PBE	5.629	5.580	17.073	107.44	0.47
PBE+D2	5.351	5.192	15.058	99.58	0.03
PBE+TS	5.353	5.227	15.546	100.35	0.12
PBE+D3	5.381	5.209	15.394	100.82	0.13
PBE+D3(BJ)	5.327	5.176	15.188	100.27	0.05
vdW-DF2	5.371	5.218	15.117	100.09	0.04

---

How is the performance of the different dispersion corrections for the prediction of ADPs? To assess this question in a systematic way, we now inspect the principal-axes components of the ADP matrices U₁, U₂, U₃ for all symmetry-inequivalent chlorine atoms in the title compound, all referring to a temperature of 100 K for the moment. This comparison enables us to judge the quality of the different dispersion corrections for ADPs at 100 K (Fig. 4): ADPs from almost all dispersion-corrected methods compare favourably to the experimental values, with the deviations smaller than 0.003 Ų; PBE+D3 with zero-damping represents the only exception. The marginally less satisfactory agreement may be explained with the zero-damping function and the above-mentioned problems with artificial interatomic forces. We do not present any ADPs from PBE without dispersion correction, because they are erroneously more than twice as large; a dispersion correction is clearly necessary. Another quality indicator—a shape criterion as used previously¹²—is given by the ratios of the main-axis components of the displacement matrix, viz. U₁/U₂, U₁/U₃, and U₂/U₃, as shown in the ESI.†U₁ tends to be too small in comparison to both U₂ and U₃ for all theoretical methods, but the overall shape matching is still good. To conclude, theory can capture the differences between the symmetry-inequivalent chlorine atoms in Cl₅py.

Fig. 4 Comparison of the main-axis components of the thermal displacement parameters calculated at several levels of theory with the experiment at 100 K.

ADPs from theory (III): temperature dependence of ADPs

The close agreement between calculated and experimental ADPs at 100 K encouraged us to investigate the quality of ADPs from theory at higher temperatures, as in our previous publication¹² but this time in a more fine-grained manner. We start by visual inspection of the displacement ellipsoid plots. Exemplarily, we compare plots of the experimental ADPs to those calculated at the PBE+D3(BJ) level of theory in Fig. 5. In contrast to the good match at 100 K, the calculated ADPs are visibly too small when compared to the experimental ones at 200 and 300 K.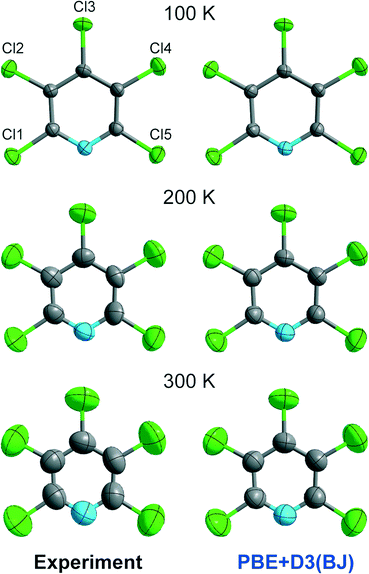

Fig. 5 Graphical comparison of the experimental ADPs and the theoretically derived ones at the PBE+D3(BJ) level of theory at the 90% level.

In Fig. 6, we broaden our methodological perspective again and begin with a comparison of all dispersion corrections to the experiment at higher temperatures. For this purpose, we investigate the temperature dependence of the ADP matrix diagonal elements U₁₁, U₂₂, U₃₃ of Cl3, the chlorine atom involved in the putative C–Cl⋯N halogen bond. At 100 K, displacement parameters from all theoretical methods match the experimental ADPs almost perfectly. The agreement becomes less satisfactory at 150 K, and Fig. 6 suggests a systematic underestimation by theory. This is probably due to neglect of anharmonic motion and thermal expansion of cell parameters with growing temperature in the calculations; the latter has been discussed in detail in our previous work.¹² However, guanidine could be studied at 100 K and 273 K only: while theory provides data over the entire temperature range (continuous lines in Fig. 6), the experiment is naturally limited to a finite number of data points, especially so if expensive neutron-diffraction data are collected. This problem is less severe for Cl₅py, which can be reliably explored by XRD, and so we chose to measure its ADPs in fine increments to judge more reliably at which temperature anharmonic contributions become relevant. (In other words: we simply needed more fine-grained experimental data points in plots—they have been provided in Fig. 6). As the discrepancy between theory and experiment increases with temperature, the following discussion will only refer to the range between 100 and 200 K. The deviation of the calculated ADPs becomes too large above 200 K since none of the calculated values lies within the threefold standard deviation of the experimental values. We expect that future applications of the method will also be focused on the temperature regime up to 200 K—a range that is still conveniently accessible even for “household” diffraction experiments.

Fig. 6 Temperature dependence of the thermal displacement matrix elements U₁₁, U₂₂, U₃₃ and their deviation from experiment ΔU₁₁, ΔU₂₂, ΔU₃₃ for Cl3, the atom involved in the C–Cl⋯N halogen bond. The error bars in the ΔU plots indicate the threefold standard deviations of the experimental values.

Evaluating the DFT results with crystallographers' tools

How to evaluate the competing methods for dispersion correction in terms of usability in refinements of experimental diffraction data? For our evaluation, we have been inspired by previous studies^9,11 in the field of calculated ADPs. The agreement between calculated and experimental structure factor amplitudes represents a straightforward approach, yet at the same time a challenging one. A state-of-the-art diffraction experiment should provide significantly better agreement factors for a structure model with anisotropic displacement parameters than for an isotropic model.

Global quality indicators such as R₁ and wR₂ admittedly have to be used with caution; within their appropriate limits, however, they offer a fast and simple way to judge the match between a structure model and experimental data. The weighted agreement factor based on intensities, wR₂, in particular, represents a rather sensitive criterion. Table 4 compares results based on experiment and theory. Agreement factors for refinement of anisotropic and isotropic structure models against experimental data are given in the first two rows; these models clearly differ with respect to wR₂. The results listed in the lower part of the Table refer to structure factor calculations rather than refinements: fractional coordinates and ADPs were calculated with the various dispersion-corrected DFT methods, and the theoretical structure factors thus calculated were compared to the observed ones; only an overall scale factor (FVAR in SHELX terminology) was refined. The residual results achieved with these models are remarkably good; regardless of the specific dispersion correction, the anisotropic structure models based on calculated ADPs and refinement of only a scale factor represent a significant improvement over an isotropic fit to the experimental structure factors and pass automatic controls such as the popular CheckCIF routine provided by the IUCr without major alerts.²⁵ In contrast, even consistent ADPs with very wrong absolute values will cause visible CheckCIF alerts with respect to the usual crystallographic agreement factors such as R₁, wR₂, GOF or to the resulting electron density in a difference Fourier map.

Table 4 Agreement factors between structure model and experimental data for Cl₅py at 100, 150 and 200 K; see text for further explanation

	100 K		150 K		200 K
	R 1	wR2^d	R 1	wR2	R 1	wR2
a Experimental results of anisotropic refinement. b Experimental results of isotropic refinement. c R 1 = (∑|ΔF|)/(∑|Fo|) = (∑||Fo| − |Fc||)/(∑|Fo|). d .
Aniso^a (Exp)	0.027	0.073	0.039	0.095	0.047	0.098
Iso^b (Exp)	0.052	0.150	0.064	0.154	0.081	0.171
PBE+TS	0.034	0.087	0.053	0.126	0.072	0.152
PBE+D2	0.031	0.083	0.050	0.119	0.064	0.136
PBE+D3	0.031	0.088	0.044	0.107	0.053	0.111
PBE+D3(BJ)	0.030	0.081	0.047	0.113	0.062	0.130
vdW-DF2	0.036	0.090	0.059	0.139	0.080	0.169

---

The quality of a structure model can not only be expressed in the agreement between measured and calculated diffraction pattern, i.e. in reciprocal space, but also in direct space: a good match is reflected in small fluctuations in a final difference Fourier synthesis; ideally, the remaining local density maxima should be mainly associated with valence electrons located at the covalent bonds. We will only focus on the most promising comparison between experimental and DFT-calculated ADPs, those referring to 100 K. The difference Fourier synthesis based on refined ADPs may be taken as benchmark, with insignificant average fluctuations and low residual maxima and minima of unaccounted electron density. On the one hand, the difference Fourier synthesis based on ADPs from all dispersion-corrected DFT calculations gave higher values, thus indicating less suitable models for the electron density distribution in real space. On the other hand, ADPs calculated with any of these roughly equivalent methods represent a significant improvement with respect to an isotropic structure model based on experimental data.

Traditional DFT methods show very good function in intramolecular forces, while dispersion-corrected DFT also demonstrates promising results in simulating intermolecular interactions. In solid Cl₅py, such intermolecular interactions are considerably weaker than intramolecular forces. In the absence of conformational degrees of freedom, Cl₅py molecules in the crystal will therefore essentially perform rigid body motion.²⁶ Technically spoken, good agreement with overall rigid body motion is reflected in small residuals R = ∑|ΔU|/∑|U_obs| (with ΔU = U_obs − U_calc) for the refined ADPs. Rigid-body motion with a variable degree of translational, librational, and screw coupling mode is a necessary, but not a sufficient condition for experimental as well as calculated ADPs. As expected, we find low residuals for the experimentally derived ADPs, with increasing values for the translational and librational tensor components at higher temperature. Not surprisingly, all DFT-based methods correctly identify the Cl₅py molecule in its molecular crystal.

Conclusions

In this work, we have explored how well DFT-based methods can predict anisotropic thermal motion, and thus displacement ellipsoids for molecular crystals “from scratch”. For the first time to our knowledge, we have probed the transition between excellent predictions (at 100 K) and notable deviations (above room temperature), and we have also systematically explored a number of popular (yet inexpensive) dispersion corrections for the purpose of computing ADPs. Remarkably, all these methods give reasonable individual displacement tensors, good quantitative agreement for the different components of motion with the experimental data, and acceptable difference Fourier syntheses. Neither validation in reciprocal nor in real space suggests a unique ranking among the different dispersion correction methods. Such satisfactory results are, however, clearly limited to the temperature range in which harmonic motion prevails. For the test case Cl₅py, 200 K represents the upper limit for good agreement between experimentally derived and dispersion-corrected DFT-based ADPs. Neither this temperature range nor the relative performance of individual correction methods should be over-interpreted based on these results for a single compound. Work on van-der-Waals-dominated solids of different chemical composition is in progress.

We may speculate about the future of calculated ADPs. They can be helpful in those cases in which free refinement of these quantities can be hampered by parameter correlation due to pseudo-inversion,²⁷ by a low ratio between observations and variables or by unfavourable contrast. The latter case occurs, for example, when electron density is associated with symmetric tops such as a tertiary butyl group in the molecular periphery of a heavy-atom metal complex. Structure determination of molecular compounds by powder diffraction represents another area of application; in such systems ADPs are usually not refined, but calculated ADPs could well be taken into account. This study, our initial one¹² and previous studies of others^9–11,28 on ADPs lay the groundwork for such future applications.

Technical details

Chemical and reagents

Cl₅py was purchased from Merck. Crystals of the monoclinic from were grown by slow (ca. 2 d) evaporation of a solution (ca. 40 mmol L⁻¹) in dichloromethane at room temperature. Powder diffraction confirmed that only the monoclinic form was obtained under these conditions (see ESI,† Tables S1 and S2).

Single-crystal analysis

Single-crystal X-ray diffraction experiments were carried out on a Bruker SMART APEX diffractometer with a CCD area detector using Mo-Kα radiation, λ = 0.71073 Å; the radiation source was an INCOATEC microsource with multilayer optics. The temperature was controlled by an Oxford Cryosystems 700 instrument. Intensities were collected in the ω scan mode. Crystal data: C₅Cl₅N, f_w = 251.31 g mol⁻¹, monoclinic space group Pc (no. 7), Z = 2. The same single crystal with approximate dimensions 0.26 × 0.24 × 0.06 mm³ was used for data collections at 50 K intervals, from 100 to 300 K. The intensity data collection at 100 K extended to higher resolution and hence comprised more independent reflections than those at higher temperatures (cf.Table 1). The intensities were integrated with the help of the program SAINT+, and a multi-scan absorption correction was applied with SADABS.²⁹ The structure was solved with direct methods³⁰ and refined using full-matrix least squares on F² (SHELXL2013 (ref. 31)).

During refinement, all atoms were assigned anisotropic displacement parameters, with a total of 100 parameters. The most relevant intermolecular contact is automatically detected by CheckCIF and is associated with the N⋯Cl contact of ca. 3 Å, cf.Fig. 1. Lattice parameters and convergence results for the three different data collection temperatures have been compiled in Table 2.

Computational methods

We performed electronic-structure calculations based on density-functional theory with the Vienna ab initio simulation package (VASP).³² The projector augmented-wave method was applied,^18c,d and the kinetic energy cutoff of the plane-wave expansion was 500 eV. The different exchange–correlation functionals and dispersion corrections are discussed in the main text.

Initial optimisation of the structures concerning forces was performed with convergence criteria of 5 × 10⁻³ eV Å⁻¹ for the forces and 10⁻⁶ eV per cell for the energy.

The calculation of the ADPs was performed with the help of Phonopy,³³ following the same route as in our previous study.¹² Forces were calculated with VASP using a super-cell expansion of 4 × 4 × 2 unit cells. The super-cell size is discussed in detail in the ESI.† The convergence criterion for the structure optimisation based on which the ADPs were calculated was at least 10⁻⁵ eV per cell, and that for the electronic structure was 10⁻⁷ eV per cell. The corresponding lattice parameters are provided in Table 3. The reciprocal-space meshes for these calculations were converged, as shown in the ESI.†

Not only did we have to converge the reciprocal-space meshes for the electronic-structure (k-point meshes) calculations but also for the ADP calculations within Phonopy (q-point meshes). To arrive at ADPs which are convergent with an increasing q-point mesh size for the ADP calculation—that means convergent with an increasing number of points in the reciprocal space at which we evaluate the ADPs, we had to cut off some lower phonon modes (<5 cm⁻¹). This convergence problem is by no means general: the ADPs of diamond calculated at PBE level of theory do converge with the q-point mesh size (ESI†). These numerical difficulties stem from small real modes in the PDOS of Cl₅py. The latter seem to correlate with spurious imaginary modes in the PDOS which are in general neglected in the ADP calculation and other statistical-thermodynamics integrations. Such imaginary modes are quite common in the calculation of the PDOS and have a negligible impact on thermodynamic data such as the free energy, the entropy or the heat capacity.^3d Besides the lacking convergence with the q-point mesh size, some levels of theory without cutoff resulted in ADPs more similar to the experiment at 300 K than at 100 K, which is unexpected and even unphysical. Some others fit well at smaller q-point meshes. We show the influence of the cutoff of the frequencies on the ADPs of all levels of theory in the ESI.† Moreover, we tested the influence of the cutoff of small real frequencies on the thermodynamic data: there is only a negligible influence. We also present these data in the ESI.† We used a 70 × 70 × 28 q-point mesh for all ADP calculations.

Finally, due to the non-orthogonal basis vectors of the unit cell of Cl₅py, the ADPs calculated with Phonopy^12,33 (referring to a Cartesian coordinate system by default) had to be converted to the ADPs used in the CIF format, as described in ref. 34. In doing so, the crystal lattice was taken from the fully optimized structures on which the ADP calculations were based. This conversion was done with a custom-made program.

Acknowledgements

We thank Prof. Atsushi Togo for helpful remarks for the ADP calculations. Financial support by Fonds der Chemischen Industrie (fellowship for J. G.), China Scholarship Council (fellowship for A. W.) and RWTH Aachen University is gratefully acknowledged. Moreover, we thank the Jülich–Aachen Research Alliance (JARA-HPC) and the IT Centre at RWTH Aachen University for large amounts of computing time (project: jara0069).

References

1. G. R. Desiraju, Crystal engineering: the design of organic solids, Elsevier, 1989.
2. A. D. Becke, J. Chem. Phys., 2014, 140, 18A301.
3. (a) J. C. Conesa, J. Phys. Chem. C, 2010, 114, 22718–22726; (b) D. Forrer and A. Vittadini, Chem. Phys. Lett., 2011, 516, 72–75; (c) P. A. Guńka, M. Dranka, J. Piechota, G. Z. Żukowska, A. Zalewska and J. Zachara, Cryst. Growth Des., 2012, 12, 5663–5670; (d) V. L. Deringer, R. P. Stoffel and R. Dronskowski, Cryst. Growth Des., 2014, 14, 871–878; (e) F. Bachhuber, J. von Appen, R. Dronskowski, P. Schmidt, T. Nilges, A. Pfitzner and R. Weihrich, Angew. Chem., Int. Ed., 2014, 53, 11629–11633.
4. J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621.
5. (a) J. van de Streek and M. A. Neumann, CrystEngComm, 2011, 13, 7135–7142; (b) D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551.
6. (a) V. L. Deringer, F. Pan, J. George, P. Müller, R. Dronskowski and U. Englert, CrystEngComm, 2014, 16, 135–138; (b) V. L. Deringer, U. Englert and R. Dronskowski, Chem. Commun., 2014, 50, 11547–11549; (c) J. van de Streek and M. A. Neumann, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 544–558; (d) J. van de Streek and M. A. Neumann, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 1020–1032.
7. K. N. Trueblood, H.-B. Burgi, H. Burzlaff, J. D. Dunitz, C. M. Gramaccioli, H. H. Schulz, U. Shmueli and S. C. Abrahams, Acta Crystallogr., Sect. A: Found. Crystallogr., 1996, 52, 770–781.
8. W. F. Kuhs, International Tables of Crystallography, 2006, vol. D, 1st online edition, ch. 1.9.
9. B. Dittrich, S. Pfitzenreuter and C. B. Hübschle, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 110–116.
10. (a) A. M. Reilly, D. A. Wann, C. A. Morrison and D. W. H. Rankin, Chem. Phys. Lett., 2007, 448, 61–64; (b) A. M. Reilly, D. A. Wann, M. J. Gutmann, M. Jura, C. A. Morrison and D. W. H. Rankin, J. Appl. Crystallogr., 2013, 46, 656–662.
11. A. Ø. Madsen, B. Civalleri, M. Ferrabone, F. Pascale and A. Erba, Acta Crystallogr., Sect. A: Found. Crystallogr., 2013, 69, 309–321.
12. V. L. Deringer, R. P. Stoffel, A. Togo, B. Eck, M. Meven and R. Dronskowski, CrystEngComm, 2014, 16, 10907–10915.
13. (a) B. Dittrich, C. B. Hübschle, M. Messerschmidt, R. Kalinowski, D. Girnt and P. Luger, Acta Crystallogr., Sect. A: Found. Crystallogr., 2005, 61, 314–320; (b) B. Dittrich, P. Munshi and M. A. Spackman, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, o633–o635; (c) J. Lübben, C. Volkmann, S. Grabowsky, A. Edwards, W. Morgenroth, F. P. A. Fabbiani, G. M. Sheldrick and B. Dittrich, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, 309–316.
14. C. R. Groom and F. H. Allen, Angew. Chem., Int. Ed., 2014, 53, 662–671.
15. H. J. Rossell and H. G. Scott, J. Cryst. Mol. Struct., 1973, 3, 259–270.
16. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
17. (a) T. Clark, WIREs Comput. Mol. Sci., 2013, 3, 13–20; (b) P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294.
18. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799; (c) P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979; (d) G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775; (e) T. Bučko, J. Hafner, S. Lebègue and J. G. Ángyán, J. Phys. Chem. A, 2010, 114, 11814–11824.
19. J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
20. J. George, V. L. Deringer and R. Dronskowski, Inorg. Chem., 2015, 54, 956–962.
21. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
22. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
23. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
24. (a) G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102; (b) K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101; (c) J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201; (d) J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
25. Accessible on http://journals.iucr.org/services/cif/checking/checkform.html..
26. (a) D. Cruickshank, Acta Crystallogr., 1956, 9, 754–756; (b) D. Cruickshank, Acta Crystallogr., 1956, 9, 1005–1009; (c) V. Schomaker and K. N. Trueblood, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 63–76.
27. (a) B. Calmuschi and U. Englert, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2002, 58, m545–m548; (b) W. Raven, I. Kalf and U. Englert, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2012, 68, m223–m225; (c) W. Raven, I. Kalf and U. Englert, Crystals, 2015, 5, 244–251.
28. N. J. Lane, S. C. Vogel, G. Hug, A. Togo, L. Chaput, L. Hultman and M. W. Barsoum, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214301.
29. G. M. Sheldrick, SADABS (Version 2.03). A Program for Empirical Absorption Correction, University of Göttingen, Germany, 2004.
30. G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
31. G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
32. (a) G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561; (b) G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269; (c) G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186; (d) G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
33. (a) A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106; (b) L. Chaput, A. Togo, I. Tanaka and G. Hug, Phys. Rev. B, 2011, 84, 094302.
34. R. W. Grosse-Kunstleve and P. D. Adams, J. Appl. Crystallogr., 2002, 35, 477–480.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and simulated powder patterns, shape criterion for the ADPs, convergence tests for the k-, q-point meshes, and the super-cell size, influence of the cutoff on the free energy at 300 K, all structures in VASP input format, CheckCIF results for the computed ADPs. The CIF files for the refinements at 100, 150, 200, 250 and 300 K were deposited at the Cambridge Crystallographic Data Centre and allocated the numbers: CCDC 1400034, 1400028, 1400022, 1402263 and 1402264. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ce01219h

---