Co-crystals and molecular salts of carboxylic acid/pyridine complexes: can calculated pK_a's predict proton transfer? A case study of nine complexes

Abstract

A series of nine complexes and 109 literature examples containing a carboxylic acid functional group and a pyridine functional group on separate molecules follow the ΔpK_a rule such that proton transfer occurs at values above 3 to form a molecular salt and none at values below 0 to form a co-crystal. In the intermediate range, there is a predominance of molecular salt over co-crystal formation. The complexes discussed show that calculated pK_a's are good predictors of the outcome.

---

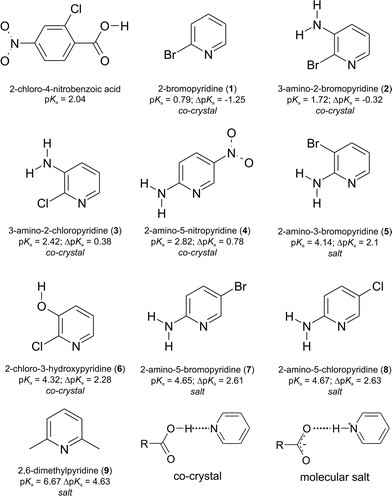
Crystal engineering is about the control of the assembly of organic and inorganic components to a desired structure or a desired property.¹ Organic components can be used either in their unimolecular state² or in their bimolecular state with a predictable combination of different molecules.³ Complexes between two or more organic compounds that remain neutral result in a multi-component molecular complex.⁴ This scenario is often referred to as a co-crystal (or cocrystal!).⁵ In a binary situation, an additional scenario is for the two components to undergo an intermolecular proton transfer, with complimentary acid and basic functional groups.⁶ Such complexes are known as molecular salts⁵ as they do not contain inorganic acids or bases. The interactions between the neutral and ionised species are often governed by a variety of intermolecular interactions,⁷ and their strength can be dependent on the covalent or electrostatic component. In summary, hydrogen bonding interactions as seen in co-crystals have longer intermolecular distances compared to hydrogen bonds seen in molecular salts.⁸ The key for the crystal engineer, who wants to be able to predict and hence control the assembly of his multi-component complex, is to know if in solution proton transfer will or will not take place. This depends on the basicity and acidity of the functional groups that will partake in the hydrogen bonding.⁹ An easy route of obtaining a qualitative answer comes from looking at the difference in pK_a values of the acid and basic functional groups. There exists a “rule of 3” that states that for values of ΔpK_a = pK_a (protonated base) − pK_a (acid) less than 0 a co-crystal forms (all components in their neutral states), and for differences greater than 3, a molecular salt forms (all components are charged, but the overall complex is neutral of course).¹⁰ For an intermediate value, no accurate prediction can be made on the outcome.¹¹ These calculations are often based solely on calculated pK_a's given for species in water solutions. In this report, we want to put these predictions to the test by preparing a series of nine complexes that have a range of calculated ΔpK_a's from less than 0 to greater than 3 and then observing the outcome in their solid state form. The choice of molecules was dependent on the type of functional groups, which need to be able to display hydrogen bonding both in their neutral and charged forms. Hence, molecules with a pyridine group and a carboxylic acid group on the second molecule have been chosen. The hydrogen bonds expected for a co-crystal and a molecular salt are COO–H⋯N_pyr and COO⁻⋯H–N_pyr⁺, respectively. An additional reason was that these functional groups are often found in drug molecules, and a current avenue of research in solid-state organic chemistry is the design of complexes that have neutral or charged components, as this can influence the bio-availability and solubility of the drug component.¹²

To simplify the study, the same molecule with the carboxylic acid group is used, and the second molecule contains the pyridine having a number of different substituents to form a series of nine related molecules with amine, bromo, chloro, nitro, and phenol groups. These substituents influence the basicity of the pyridine group, as shown in Scheme 1. The molecule with the carboxylic acid group is 2-chloro-4-nitrobenzoic acid, which is also a potential anti-HIV molecule that has been used in crystal engineering studies before.¹³ The pK_a values were calculated using the predictor functionality in Sci-Finder, using the programme Advanced Chemistry Development.¹⁴ The calculation of pK_a values for drug discovery and formulation has been used by various researchers^15a,b as well as in a similar study to that presented here for a matrix of 4-substituted benzoic acids and 4-substituted pyridines.^15c Nine complexes (1–9) are formed. Experimentally, the same crystallization procedure was used, where a stoichiometric 1 : 1 ratio was used and dissolved in methanol.‡ Single crystal diffraction data for all compounds was done at −100 °C.‡ To put the results of the series of complexes into context, a database analysis of 109 complexes having these two functional groups was undertaken.‡

Scheme 1 The structural diagrams of the carboxylic acid and nine pyridines used in this study, as well as the primary hydrogen bonding motif expected for co-crystal and salt formation. The pK_a values and resulting ΔpK_a's are given for all the complexes based on calculated values.

The nine different pyridines used have a range of pK_a's from 0.79 to 6.67. The carboxylic acid used has a pK_a of 2.04. Hence, we have been able to synthesize complexes that have a ΔpK_a < 0 (co-crystals 1 and 2), 0 < ΔpK_a < 3 (co-crystals 3, 4, and 6; salts 5, 7, and 8), and lastly ΔpK_a > 3 (salt 9). This is summarized in Scheme 1. The intermediate values too between 0 and 3 do indeed show that either a salt or a co-crystal can form. The most commonly seen hydrogen bonding motifs are shown in Fig. 1 and have been observed in previous work with hydroxybenzoic acids and aminopyridines.¹⁶ The heterosynthon¹⁷ COO–H⋯N_pyr formed between a carboxylic acid donor and a pyridine acceptor is observed in all the co-crystals 1–4 and 6. In 3 and 6, there is an R²₁(6) ring formed between one of the amine H and phenol H, respectively. In the molecular salt structures, proton transfer has occurred to the pyridinium base to form a COO⁻⋯H–N_pyr⁺ hydrogen bond. In addition, a hydrogen bond from the ortho amine to the carboxylate group forms an 8-membered R²₂(8) ring¹⁸ motif, where the two carboxylate O atoms act as hydrogen bond acceptors and two hydrogen atoms (pyridium-H and amine-H) as donors. In addition, an eight membered R²₄(8) motif is observed that joins two R²₂(8) motifs together. This pattern is seen in 5, 7 and 8. A possible reason for this commonality is the amine group ortho to the pyridinium group in those three structures, enabling the formation of a robust 2-aminopyridinium-carboxylate heterosynthon.¹⁹ The molecular salt with 2,6-dimethylpyridine is the only one in the series that is predicted to form a salt, and that is observed. The hydrogen bonding here is simply a COO⁻⋯H–N_pyr⁺ hydrogen bond. There are no other hydrogen bonding functional groups present. There are of course further intermolecular interactions, but these are not included in the description for the sake of brevity. By looking at the average D⋯A distances, there is a greater range for the salt compounds 5, 7–9 of 2.64(8) Å than for the co-crystal ones at 2.67(4) Å. The shortest D⋯A distance is found in 9 (2.58(2) Å) with the greatest ΔpK_a = 4.63. There are no other trends identifiable with regard to hydrogen bonding and ΔpK_a, and there was no intermediate COO–H⋯N_pyr/COO⁻⋯H–N_pyr⁺ hydrogen bonding observed. All compounds were characterized by powder X-ray diffraction and confirm bulk purity.

Fig. 1 A selection of the most commonly observed hydrogen bonding interactions in complexes 1–5 and 9 together with the starting material pyridine used.

The database analysis of similar complexes was undertaken to identify first all the structures that have a carboxylic acid group and a pyridine, respectively, on separate molecules. Additionally, no solvated complexes were taken into consideration. A total of 109 complexes were ultimately selected and categorized as either a co-crystal or a salt. From calculated ΔpK_a's, predictions were made according to the ΔpK_a rule on what type of complex should be observed and then compared to the observed result. The analysed data in a spreadsheet are given in the ESI.†Fig. 2 shows the results of the calculated ΔpK_a and the observed complex formed. In the upper range ΔpK_a > 3 onwards, there are 38 molecular salts and no co-crystals. The range with ΔpK_a < 0 shows 22 co-crystals and no molecular salts, again as expected. In the intermediate range between 0 and 3, there are 15 co-crystals and 34 molecular salts. In fact, there are the same number of co-crystals with 0 < ΔpK_a < 1.5 as there are in 1.5 < ΔpK_a < 3. The unpredictability can be seen especially when one looks at what complex is formed close to the end points of the intermediate range (in a range of 0.5): there are three co-crystals and two salts within 0.07 < ΔpK_a < 0.47 and two co-crystals and three salts within 2.52 < ΔpK_a < 2.93. Hence, there is no trend of having significantly more co-crystals closer to zero and more salts closer to 3. It must also be noted that the molecular environment and the number and types of species in solution can alter the outcome.²⁰

Fig. 2 The 109 complexes found in the CSD, plotted as a function of ΔpK_a and the observed co-crystal or salt complex.

Similar studies where a range of complexes was made using pyridine derivatives as acceptors have been done (Table 1). Bhogala et al. looked at di- and tricarboxylic acids together with 4,4′-bipyridines and isonicotianmide.²¹ The pK_a values were from known literature values, and the authors found that the pK_a range can be extended from 3 to 3.75. Stilinović et al.²² studied co-crystals and salts of gentisic acid (pK_a = 2.82) with 20 different pyridines (spanning a range of −0.7 < ΔpK_a < 4.7) and obtained 22 complexes. Their pK_a values were determined experimentally in aqueous solution, and their crystallizations were done using an ethanol–water solution. They found that proton transfer did not occur for ΔpK_a's < 2 and always occurred for ΔpK_a > 2.5. Hence, the range of uncertainty is 0.5 unit and could be indicative of the larger range required to make accurate predictions from calculated instead of experimentally determined pK_a values. Another study was by Childs et al.²³ looking at 2-aminopyrimidine complexes with a variety of carboxylic acids. The pK_a's in their study were calculated using the same program as in our study. The authors found that in the range 0 < ΔpK_a < 2, eight co-crystals and seven salts were formed. It was found that the intermediate range, where either co-crystal or salt can form, should be delineated by a transition range, and not fixed values like 0 or 3. The authors account for the unpredictability of the intermediate range not only on a poor correlation between pK_a values and proton transfer but also the molecular environment, similarly to how a pK_a value can change with a change in solvent.²⁴ By also using theophylline in their study, which is amphoprotic, complexes using a series of carboxylic acids and amines showed that the ranges of ΔpK_a can be specific for the system under investigation.

Table 1 Studies of other carboxylic acid–pyridine complexes

Acid/pyridine	pKa values	ΔpKa range	Complexes	Rule	Ref.
4-Substituted benzoic acids/4-substituted pyridines	Calculated from ACD Labs	−2.94 to 6.1	22 cc, 11 salts	−1 < ΔpKa < 4	15c
Di- and tricarboxylic acids/bipyridines and isonicotinamide	Literature	−2.95 to 2.90	13 cc, 3 salts	0 < ΔpKa < 3.75	21
Gentisic acid/21 pyridines	Aqueous solutions	−0.7 to 4.7	5 cc, 16 salts	2 < ΔpKa < 2.5	22
29 Acids/2-aminopyrimidine	Calculated from ACD Labs	−1.08 to 3.77	17 cc, 8 salts	0 < ΔpKa < 2	23
Pyridine and 4-dimethylaminopyridine/5 dicarboxylic acids	Aqueous solutions	1.68 to 7.78	2 cc, 7 salts	0 < ΔpKa < 3	25

---

The most related work that also clearly illustrates the complexity of co-crystal versus salt observations according to the ΔpK_a rule is a study by Mohamed et al.²⁵ that used a matrix of pyridine and 4-dimethylpyridine with 5 carboxylic acids. The pK_a values were obtained from the literature in aqueous solutions and corrected for activity effects. The complexes with pyridine formed both co-crystals and salts and the neutral COO–H⋯N_pyr or ionic COO⁻⋯H–N_pyr⁺ variants of hydrogen bonds are observed, and for 4-dimethylpyridine, only salts were formed. This is in exact agreement with the ΔpK_a rule as used in this study. However, for the combination of fumaric acid with 4-dimethylaminopyridine, the molecular salt formed with fumarate also has a neutral fumaric acid molecule in the crystal structure. The difference in pK_a is 6.68 and thus shows that the solid state complex that is formed can violate the empirical rules being used.

In conclusion, this study, looking at a limited matrix of one carboxylic acid with 9 pyridines, corresponds exactly with the ΔpK_a rule, forming co-crystals below 0 and salt above 3 and the intermediate range favourable for both. A further study of already known complexes featuring carboxylic acids and pyridine complexes shows that the lower and upper limits are in perfect agreement for the functional groups. Complexes approaching the 0 and 3 endpoints show no favouritism to co-crystals over salts.

Acknowledgements

This material is based on the work supported financially by the University of the Witwatersrand Friedel Sellschop grant and by the Molecular Sciences Institute. The National Research Foundation National Equipment Programme (UID: 78572) is thanked for financing the purchase of the single-crystal diffractometer.

Notes and references

1. (a) J.-P. Zhang, P.-Q. Liao, H.-L. Zhou, R.-B. Lin and X.-M. Chen, Chem. Soc. Rev., 2014, 43, 5789–5814; (b) K. Biradha and R. Santra, Chem. Soc. Rev., 2013, 42, 950–967; (c) P. Erk, H. Hengelsberg, M. F. Haddow and R. Van Gelder, CrystEngComm, 2004, 6, 474–483.
2. (a) I. Giannicchi, B. Jouvelet, B. Isare, M. Linares, A. D. Cort and L. Boutellier, Chem. Commun., 2014, 50, 611–613; (b) J. S. Brooks, Chem. Soc. Rev., 2010, 39, 2667–2694.
3. (a) D. Braga, L. Maini and F. Grepioni, Chem. Soc. Rev., 2013, 42, 7638–7648; (b) C. B. Aakeröy, K. N. Epa, S. Forbes and J. Desper, CrystEngComm, 2013, 15, 5946–5949; (c) C. B. Aakeröy, J. Desper, B. A. Helfrich, P. Metrangelo, T. Pilati, G. Resnati and A. Stevenazzi, Chem. Commun., 2007, 4236–4238.
4. E. R. T. Tiekink, Chem. Commun., 2014, 50, 11079–11082.
5. S. Aitipamula, et al. , Cryst. Growth Des., 2012, 12, 2147–2152.
6. (a) G. Bolla and A. Nangia, Cryst. Growth Des., 2012, 12, 6250–6259; (b) A. Lemmerer and M. A. Fernandes, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2012, 68, o188–o194; (c) V. R. Hathwar, R. Pal and T. N. G. Row, Cryst. Growth Des., 2010, 10, 3306–3310; (d) C. L. Cooke, R. J. Davey, S. Black, C. Muryn and R. G. Pritchard, Cryst. Growth Des., 2010, 10, 5270–5278.
7. (a) J.-R. Wang, C. Zhou, X. Yu and X. Mei, Chem. Commun., 2014, 50, 855–858; (b) C. B. Aakeröy, P. D. Choapde, C. Ganser and J. Desper, Chem. Commun., 2011, 47, 4688–4690; (c) A. Bagno and G. Scorrano, Acc. Chem. Res., 2000, 33, 609–616.
8. (a) G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, 1997; (b) G. R. Desiraju, Acc. Chem. Res., 2002, 35, 565–573.
9. (a) M. K. Stanton, S. Tufekcic, C. Morgan and A. Bak, Cryst. Growth Des., 2009, 9, 1344–1352; (b) C. B. Aakeröy, M. E. Fasulo and J. Desper, Mol. Pharm., 2007, 4, 317–322.
10. A. J. Cruz-Cabeza, CrystEngComm, 2012, 4, 6362–6365.
11. A. Delori, P. T. A. Galek, E. Pidcock, M. Patni and W. Jones, CrystEngComm, 2013, 15, 2916–2928.
12. (a) L. Rajput, P. Sanphui and G. R. Desiraju, Cryst. Growth Des., 2013, 13, 3681–3690; (b) B. Sarma, R. Thakuria, N. K. Nath and A. Nangia, CrystEngComm, 2011, 13, 3232–3240.
13. (a) I. Barsky, J. Bernstein, P. W. Stephens and K. H. Stone, New J. Chem., 2008, 32, 1747–1753; (b) S. Aitipamula, P. S. Chowa and R. B. H. Tan, CrystEngComm, 2011, 13, 1037–1045; (c) A. Lemmerer, C. Esterhuysen and J. Bernstein, J. Pharm. Sci., 2010, 99, 4054–4071.
14. Calculated using Advanced Chemistry Development (ACD/Labs) Software V11.02 (© 1994–2014 ACD/Labs).
15. (a) D. T. Manallack, R. J. Prankerd, E. Yuriev, T. I. Oprea and D. K. Chalmers, Chem. Soc. Rev., 2013, 42, 485–496; (b) D. T. Mallanack, Perspect. Med. Chem., 2007, 1, 25–38; (c) A. Mukherjee and G. R. Desiraju, Cryst. Growth Des., 2014, 14, 1375–1385.
16. B. Sarma, N. K. Nath, B. R. Bhogala and A. Nangia, Cryst. Growth Des., 2009, 9, 1546–1557.
17. A. Lemmerer and J. Bernstein, CrystEngComm, 2010, 12, 2029–2033.
18. J. Bernstein, R. E. Davis, L. Shimoni and N.-L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555.
19. J. A. Bis and M. J. Zaworotko, Cryst. Growth Des., 2005, 5, 1169–1179.
20. C. C. Seaton, N. Blagden, T. Munshi and I. J. Scowen, Chem. – Eur. J., 2013, 19, 10663–10671.
21. B. R. Bhogala, S. Basavoju and A. Nangia, CrystEngComm, 2005, 7, 551–562.
22. V. Stilinović and B. Kaitner, Cryst. Growth Des., 2012, 12, 5763–5772.
23. S. L. Childs, G. P. Stahly and A. Pak, Mol. Pharm., 2007, 4, 323–338.
24. C. S. Seaton, CrystEngComm, 2014, 16, 5878–5886.
25. S. Mohamed, D. A. Tocher, M. Vickers, P. G. Karamertzanis and S. L. Price, Cryst. Growth Des., 2009, 9, 2881–2889.

---

Footnotes

† Electronic supplementary information (ESI) available: Labelled Ortep diagrams, crystallographic refinements and hydrogen bonding tables, CCDC depositions, CSD analysis summary, PXRD patterns and complete citation for ref. 5. CCDC 1034733, 1034735, 1034737, 1034739, 1034741, 1034743, 1034745, 1034747, and 1034749. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ce00102a

‡ (i) A typical example of the synthesis of the complexes is given for 1: 0.100 g of 2-chloro-4-nitrobenzoic acid (0.496 mmol) and 0.078 g of 2-bromopyridine (0.496 mmol) was dissolved in 5 ml of AR-grade methanol and dissolved by gentle heating. Crystals were grown by slow evaporation. (ii) Data were collected using a Bruker Venture D8 Photon CMOS diffractometer with graphite-monochromated MoKα₁ (λ = 0.71073 Å) radiation at −100 °C. H atoms involved in hydrogen bonding were located from the difference Fourier Map. (iii) All searches were done on the Version 5.34 with the November 2012 database. The search query used was any pyridine/pyridium and COOH/COO⁻ functional groups on a phenyl ring on separate molecules, with general molecular formula C₁₂₋₁₈H₁₀₋₃₀N₁₋₄O₂₋₈ and excluding any methanol or water solvates. This gave 173 hits, which was reduced to 109 after removing duplicate entries, unimolecular compounds, sulfonate salts, dicarboxylic molecules, dipyridines, esters, ammonium cations, amides, N-oxides molecules, and compounds with both functional groups on the same molecule. The filters applied to the search are: 3D coordinates determined, no powder structures, not disordered, no errors, R factor < 0.05, only organics. The conquest search query file with the 173 hits and pdf and the cif file containing the final 109 entries are provided in the ESI.†

---