Electroclinic effect in a chiral carbosilane-terminated 5-phenylpyrimidine liquid crystal with ‘de Vries-like’ properties

Abstract

The chiral carbosilane-terminated liquid crystal 2-[(2S,3S)-2,3-difluorohexyloxy]-5-[4-(12,12,14,14,16,16-hexamethyl-12,14,16-trisilaheptadecyloxy)phenyl]pyrimidine (QL32-6) undergoes a smectic A*-smectic C* phase transition with a maximum layer contraction of only 0.2%. It exhibits an electroclinic effect (ECE) comparable to that reported for the ‘de Vries-like’ liquid crystal 8422[2F3] and shows no appreciable optical stripe defects due to horizontal chevron formation.

---

The chiral smectic A (SmA*) liquid crystal phase is characterized by an analog electro-optical effect known as the electroclinic effect that makes it possible to generate a gray scale in display applications on a much faster time scale than a nematic LCD.¹ The SmA* phase has a diffuse lamellar structure described by a density wave with a period d corresponding to the layer spacing;² the director n corresponding to the average orientation of long molecular axes is coincident with the layer normal z. Garoff and Meyer showed that an electric field E applied parallel to the SmA* layers induces a uniform molecular tilt relative to z in a direction orthogonal to E.³ This electroclinic effect (ECE) is described by a phenomenological model derived from Landau theory that predicts a linear dependence of the induced tilt angle θ on E at low field strengths; this relationship deviates from linearity when the temperature approaches the transition point T_AC from the orthogonal SmA* phase to the tilted SmC* phase.^4,5

In conventional SmA* materials, the ECE causes a contraction of the smectic layers that scales with the cosine of θ and results in a buckling of the layers into a horizontal chevron structure,⁶ which is manifested optically by the appearance of periodic stripe patterns that severely degrade the optical contrast.⁷ To solve this problem, a number of groups have investigated the ECE of liquid crystals with ‘de Vries-like’ properties,⁸ which undergo a SmA*–SmC* transition with minimal layer contraction.^9–14 This behavior was explained by de Vries using a ‘diffuse cone’ model in which mesogens in the SmA* phase have a tilted orientation and a degenerate azimuthal distribution,¹⁵ although recent theoretical and experimental studies suggest that ‘de Vries-like’ behavior generally results from an unusual combination of high lamellar order and low orientational order.^16–20 Liquid crystals with ‘de Vries-like’ properties tend to have unusually large electroclinic susceptibilities, with the field-induced electroclinic tilt accompanied by a significant increase in birefringence that is consistent with an ordering of azimuthal and/or orientational distribution(s).^12,14,21 The ECE of two such materials with first-order SmA*–SmC* transitions was recently explained using a generalized Langevin–Debye model, which assumes a random azimuthal distribution of molecules on a fixed tilt cone of angle θ, with an orientational distribution in which the tilt θ is allowed to vary with the applied field over a prescribed range.¹⁴

Three SmA* materials known to have large electroclinic susceptibilities may be considered as bona fide ‘de Vries-like’, i.e., materials that undergo a SmA*–SmC* phase transition with an increase in birefringence and a maximum layer contraction of <1%. These are the siloxane-terminated mesogen TSiKN65 and its carbosilane-terminated analogue W599,^10,14 and the 2-phenylpyrimidine mesogen 8422[2F3] from 3M with a chiral perfluoroether chain.¹² The electroclinic susceptibilities of TSiKN65 and W599 are remarkably high: tilt angles θ of 31° and 25°, respectively, are induced by an electric field of 5 V μm⁻¹ at T−T_AC = +1 K. This ECE is accompanied by an increase in birefringence (ΔΔn = 0.025 for TSiKN65)²¹ that is consistent with ‘de Vries-like’ behavior. Despite the high electroclinic susceptibilities of these compounds, there are structural limitations to their applicability in electro-optical devices. The siloxane end-group in TSiKN65 is hydrolytically and electrochemically labile,²⁵ and the lateral nitro group in both compounds is associated with higher rotational viscosities and higher levels of ionic impurities. The electroclinic susceptibility of 8422[2F3] is somewhat lower than those of TSiKN65 and W599 (vide infra), but it is chemically inert and the only ‘de Vries-like’ SmA* material reported thus far that may be suitable for electro-optical devices based on the electroclinic effect.

We recently developed a molecular design of ‘de Vries-like’ liquid crystals that combines a nanosegregating carbosilane end-group as SmC-promoting element with either a chloro-terminated alkyl chain or a 5-phenylpyrimidine core as SmA-promoting element.^20,26 For example, the 5-phenylpyrimidine mesogen QL16-6 undergoes a SmA–SmC transition with a maximum layer contraction of only 0.5% and has a reduction factor R of 0.23 at the point of maximum layer contraction (T−T_AC = −6 K),²⁷ which makes it one of the best ‘de Vries-like’ liquid crystals reported heretofore. The profile of relative layer spacing d/d_ACvs. T−T_AC exhibited by these materials typically shows a pronounced negative thermal expansion in the SmA phase that persists on cooling into the SmC phase and counteracts the layer contraction caused by tilting to such an extent that the layer spacing at the SmA–SmC transition is restored. In the case of QL16-6, we recently showed that ‘de Vries-like’ behavior is due to the combined effect of an increase in orientational order and a decrease in bilayer interdigitation with decreasing temperature.²⁰ In this communication, we report a chiral variant of QL16-6 that includes a (S,S)-2,3-difluorohexyloxy chain, which is known to induce high spontaneous polarizations in FLC mixtures without increasing rotational viscosity.²⁸ This new mesogen (QL32-6) forms SmA* and SmC* phases and is comparable to 8422[2F3] in terms of electroclinic susceptibility and chemical inertness, but is unprecedented in terms of ‘de Vries-like’ properties.

The chiral mesogen QL32-6 was prepared by a modification of the synthesis reported for QL16-6, as shown in Scheme 1.²⁰ The chiral (S,S)-2,3-difluorohexan-1-ol (4) was derived from the chiral epoxide 2, which was obtained from E-2-hexen-1-ol via a Sharpless asymmetric epoxidation reaction in 95% ee.²² The chiral alcohol 4 and the carbosilane-terminated 2-chloro-5-phenylpyrimidine precursor 6 were then combined via a nucleophilic aromatic substitution reaction to give QL32-6 (see ESI† for all synthetic details). Characterization by polarized optical microscopy (POM) and differential scanning calorimetry (DSC) showed that QL32-6 forms chiral SmA* and SmC* phases at the following temperatures (measured on heating in °C; enthalpies of transition in kJ mol⁻¹ are in parentheses):

crystal 53 (10) SmC* 62 SmA* 77 (7.4) isotropic

The second-order SmA*–SmC* transition was observed by POM as the appearance of a Schlieren texture in the homeotropic domain of the SmA* phase (see Fig. S1 in ESI†). The fan texture of the SmA* phase turned to a characteristic broken fan texture with a pronounced interference color change that is consistent with an increase in birefringence, as shown in Fig. 1.⁸ The SmC* phase persisted on cooling down to 47 °C.

Scheme 1 Reagents and conditions: (a) (−)-Diethyl-D-tartrate, Ti(OiPr)₄, t-BuOOH, DCM;²² (b) p-TsCl, pyridine, THF; (c) 70% HF·pyridine, DCM; (d) XtalFluor-E, Et₃N·3HF, Et₃N, DCM;²³ (e) SmI₂, THF;²⁴ (f) 1-Bromo-12,12,14,14,16,16-hexamethyl-12,14,16-trisilaheptadecane, Cs₂CO₃, acetone; (g(i)) 4, NaH, THF, (ii) 6.

Fig. 1 Polarized photomicrographs of QL32-6 at 63 °C in the SmA* phase (left) and at 61 °C in the SmC* phase (right).

Measurements of the layer spacing d as a function of temperature were carried out by small angle X-ray scattering (SAXS). The profile of relative layer spacing d/d_ACvs. T−T_AC for QL32-6 is compared to that of QL16-6 in Fig. 2, and shows the same degree of negative thermal expansion in the SmA* phase, but a less pronounced layer contraction in the SmC* phase, to the extent that the layer spacing at T_AC is restored at T−T_AC = −7 K; the maximum layer contraction of QL32-6 upon SmA*–SmC* phase transition is only 0.2%. The two compounds have comparable tilt angles (θ = 25° vs. 27° at T−T_AC = −10 K, see Fig. S2 in ESI†), which suggests that QL32-6 is more ‘de Vries-like’ than QL16-6. Indeed, at the point of maximum layer contraction (T−T_AC = −3 K), QL32-6 has a R value of only 0.17. By comparison, the 3M material 8422[2F3] has a maximum layer contraction of 0.8% and a R value of 0.36 at the point of maximum layer contraction (T−T_AC = −10 K).¹²

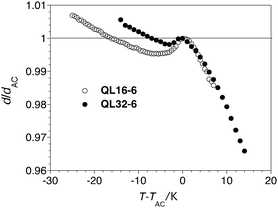Fig. 2 Relative layer spacing d/d_ACvs. reduced temperature T−T_AC for compounds QL32-6 (●) and QL16-6 (○, from ref. 20) measured on cooling from the isotropic phase.

The compound QL32-6 was aligned in an ITO glass cell with a rubbed nylon alignment substrate and a cell gap of 3 μm. The optical birefringence Δn and electroclinic tilt θ were measured as a function of temperature with a rotating analyzer setup described by Langhoff and Giesselmann.²⁹ The sample was switched by applying alternately a positive and negative electric dc field and the corresponding optical signals were evaluated in terms of phase shift and amplitude to determine the tilt angle and the birefringence simultaneously (see ESI† for details).

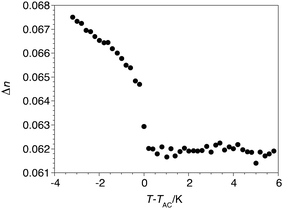
The birefringence was first measured at E = 0 over a relatively narrow temperature range about the SmA*–SmC* phase transition in order to precisely set T_AC as reference point for all the experiments. As shown in Fig. 3, the birefringence is approximately invariant in the SmA* phase and increases sharply at T_AC, which is consistent with the interference color change observed by POM. Measurements of the electroclinic tilt θ in the SmA* phase were performed at five different temperatures above T_AC, from T−T_AC = +0.2 to +5 K, with an electric field E ranging from 0.1 to 20 V μm⁻¹. As shown in Fig. 4, the θ(E) plot is linear at T−T_AC = +5 K, but increasingly deviates from linearity as T approaches T_AC; at T−T_AC = +0.2 K, θ reaches values close to 21°. The electroclinic susceptibility of QL32-6 is about half that of TSiKN65 but it is comparable to that of 8422[2F3]: both compounds give a tilt of 15° at 3 V μm⁻¹ and T−T_AC = +0.2 K.¹²

Fig. 3 Birefringence Δn vs. reduced temperature T−T_AC for QL32-6 measured at E = 0.

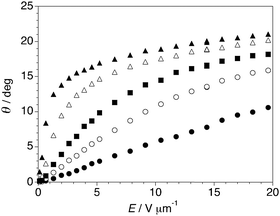Fig. 4 Electroclinic tilt angle θ vs. electric field E measured in the SmA* phase formed by QL32-6 at T−T_AC = +0.2 K (▲), +0.8 K (△), +2 K (■), +3 K (○) and +5 K (●).

The electroclinic tilt observed in the SmA* phase of QL32-6 is accompanied by an increase in birefringence (see Fig. S3 in ESI†). As shown in Fig. 5, the birefringence increases non-linearly with the electroclinic tilt angle θ and is invariant of temperature, so that the Δn(θ) data sets recorded at five different temperatures fall approximately on the same curve; this behavior, as well as the low absolute values of Δn, were observed for the other three ‘de Vries-like’ materials described herein.^12,14,21 The unprecedented ‘de Vries-like’ character of QL32-6 is reflected by the optical quality of the ECE when compared to 8422[2F3]. Optical stripe patterns were generated under the same conditions at T−T_AC = +0.2 K by applying a 105 Hz square wave ac field across 3 μm films at a voltage giving rise to the most intense patterns (7.3 V μm⁻¹ for QL32-6 and 3.7 V μm⁻¹ for 8422[2F3]).³⁰ As shown in Fig. 6, the optical stripe pattern generated by the ECE of QL32-6 is very subtle, and even less pronounced than the pattern generated by the ECE of 8422[2F3]. Similar results were obtained on heating the sample to T−T_AC = +1 and +2 K (see Fig. S4 in ESI†). Further heating of the sample up to T−T_AC = +10 K resulted in the gradual appearance of a stripe pattern at E = 0, which may be ascribed to a contraction of the smectic layers, viz.Fig. 2. Application of a high field of 15 V μm⁻¹ caused the stripe pattern to disappear (see Fig. S5 in ESI†).³⁰

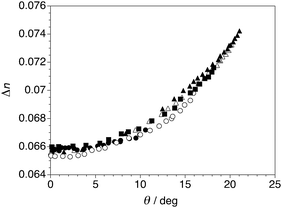Fig. 5 Birefringence Δn vs. electroclinic tilt angle θ measured in the SmA* phase formed by QL32-6 at T−T_AC = +0.2 K (▲), +0.8 K (△), +2 K (■), +3 K (○) and +5 K (●).

Fig. 6 Polarized photomicrographs of QL32-6 (top) and 8422[2F3] (bottom) in 3 μm ITO glass cells with a rubbed nylon alignment substrate at T−T_AC = +0.2 K at E = 0 (left) and with an applied 105 Hz square wave ac field of 7.3 V μm⁻¹ (QL32-6) and 3.7 V μm⁻¹ (8422[2F3]).

In conclusion, we have shown that a chiral variant of the ‘de Vries-like’ carbosilane-terminated mesogen QL16-6 exhibits an electroclinic susceptibility that is comparable to that of the 3M material 8422[2F3]. Measurements of smectic layer spacing as a function of temperature revealed that it undergoes a SmA*–SmC* phase transition with a maximum layer contraction of 0.2%, which corresponds to an R value of only 0.17. This is reflected by an ECE with improved optical quality over that of 8422[2F3], showing no appreciable optical stripe patterns over prolonged electroclinic switching. Given its chemical inertness and lack of a polar nitro group, QL32-6 is currently the best ECE material suitable for device applications and represents a promising new lead in the development of materials for fast analog electro-optical applications. Ongoing efforts are focused on increasing the electroclinic susceptibility of QL32-6via structural modifications and mixture formulation that can broaden the temperature range of the SmA* phase,³¹ and will be reported in due course.

We thank the Natural Sciences and Engineering Research Council of Canada and the Deutsche Forchungsgemeinschaft (NSF/DFG Materials World Network program DFG Gi 243/6) for support of this work. We also thank Prof Andy Evans for the use of his chiral phase HPLC instrument.

Notes and references

1. (a) C. Bahr, in Chirality in Liquid Crystals, ed. H.-S. Kitzerow and C. Bahr, Springer-Verlag, New York, 2001, p. 223; (b) N. A. Clark and S. T. Lagerwall, in Ferroelectric Liquid Crystals: Principles, Properties and Applications, ed. J. W. Goodby, R. Blinc, N. A. Clark, S. T. Lagerwall, M. A. Osipov, S. A. Pikin, T. Sakurai, K. Yoshino and B. Zeks, Gordon & Breach, Philadelphia, 1991, p. 84.
2. W. L. McMillan, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 1238–1246.
3. S. Garoff and R. B. Meyer, Phys. Rev. Lett., 1977, 38, 848–851.
4. I. Abdulhalim and G. Moddel, Liq. Cryst., 1991, 9, 493–518.
5. F. Giesselmann and P. Zugenmaier, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 1762–1772.
6. (a) G. P. Crawford, R. E. Geer, J. Naciri, R. Shashidhar and B. R. Ratna, Appl. Phys. Lett., 1994, 65, 2937–2939; (b) A. G. Rappaport, P. A. Williams, B. N. Thomas, N. A. Clark, M. B. Ros and D. M. Walba, Appl. Phys. Lett., 1995, 67, 362–364; (c) R. E. Geer, S. J. Singer, J. V. Selinger, B. R. Ratna and R. Shashidhar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 3059–3062; (d) A. Iida, Y. Takahashi and Y. Takanishi, Liq. Cryst, 2010, 37, 1091–1096.
7. (a) J. Pavel and M. Glogarova, Liq. Cryst., 1991, 9, 87–93; (b) K. Skarp, G. Andersson, T. Hirai, A. Yoshizawa, K. Hiraoka, H. Takezoe and A. Fukuda, Jpn. J. Appl. Phys., 1992, 31, 1409–1413; (c) R. Shao, P. C. Willis and N. A. Clark, Ferroelectrics, 1991, 121, 127–136.
8. J. P. F. Lagerwall and F. Giesselmann, ChemPhysChem, 2006, 7, 20–45.
9. F. Giesselmann, P. Zugenmaier, I. Dierking, S. T. Lagerwall, B. Stebler, M. Kaspar, V. Hamplova and M. Glogarova, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 598–602.
10. M. S. Spector, P. A. Heiney, J. Naciri, B. T. Weslowski, D. B. Holt and R. Shashidhar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 1579–1584.
11. R. Shao, J. E. Maclennan, N. A. Clark, D. J. Dyer and D. M. Walba, Liq. Cryst., 2001, 28, 117–123.
12. J. P. F. Lagerwall, F. Giesselmann and M. D. Radcliffe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031703.
13. N. A. Clark, T. Bellini, R.-F. Shao, D. Coleman, S. Bardon, D. R. Link, J. E. Maclennan, X.-H. Chen, M. D. Wand, D. M. Walba, P. Rudquist and S. T. Lagerwall, Appl. Phys. Lett., 2002, 80, 4097–4099.
14. Y. Shen, L. Wang, R. Shao, T. Gong, C. Zhu, H. Yang, J. E. Maclennan, D. M. Walba and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062504.
15. A. de Vries, J. Chem. Phys., 1979, 71, 25–31.
16. M. V. Gorkunov, M. A. Osipov, J. P. F. Lagerwall and F. Giesselmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051706.
17. K. Saunders, D. Hernandez, S. Pearson and J. Toner, Phys. Rev. Lett., 2007, 98, 197801.
18. S. T. Lagerwall, P. Rudquist and F. Giesselmann, Mol. Cryst. Liq. Cryst., 2009, 510, 148–157.
19. D. Nonnenmacher, S. Jagiella, Q. Song, R. P. Lemieux and F. Giesselmann, ChemPhysChem, 2013, 14, 2990–2995.
20. C. P. J. Schubert, A. Bogner, J. H. Porada, K. Ayub, T. Andrea, F. Giesselmann and R. P. Lemieux, J. Mater. Chem. C, 2014, 2, 4581–4589.
21. J. V. Selinger, P. J. Collings and R. Shashidhar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061705.
22. T. I. Richardson and S. D. Rychnovsky, Tetrahedron, 1999, 55, 8977–8996.
23. A. L'Heureux, F. Beaulieu, C. Bennett, D. R. Bill, S. Clayton, F. LaFlamme, M. Mirmehrabi, S. Tadayon, D. Tovell and M. Couturier, J. Org. Chem., 2010, 75, 3401–3411.
24. T. Ankner and G. Hilmersson, Org. Lett., 1999, 11, 503–506.
25. R. J. Mandle, E. J. Davis, C.-C. A. Voll, D. J. Lewis, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2015, 3, 2380–2388.
26. Q. Song, D. Nonnenmacher, F. Giesselmann and R. P. Lemieux, J. Mater. Chem. C, 2013, 1, 343–350.
27. The ‘de Vries-like’ character of a smectic liquid crystal may be quantified on a scale of 0 (perfect ‘de Vries’) to 1 (conventional SmA–SmC transition) at a temperature T below T_AC by the reduction factor R according to the equation: R = δ(T)/θ_opt(T) = cos⁻¹ [d_C(T)/d_AC]/θ_opt(T), where δ is the tilt angle required to give the observed layer contraction d_C(T)/d_AC assuming a model of hard spherocylinders in which the layer contraction scales with the cosine of the tilt angle, and θ_opt is the optical tilt angle measured by POM. Y. Takanishi, Y. Ouchi, H. Takezoe, A. Fukuda, A. Mochizuki and M. Nakatsuka, Jpn. J. Appl. Phys., 1990, 2, L984–L986.
28. W. N. Thurmes, M. D. Wand, R. T. Vohra, K. M. More and D. M. Walba, Liq. Cryst., 1993, 14, 1061–1068.
29. A. Langhoff and F. Giesselmann, ChemPhysChem, 2002, 3, 424–432.
30. The intensity of the optical stripe pattern increased with the applied voltage up to an optimum value, and then decreased with further increasing E up to a value of 15 V μm⁻¹, at which point the stripes vanished (see Fig. S4 in ESI†). This may be due to a weakening of surface anchoring that forces the horizontal chevrons to adopt a quasi-bookshelf structure.
31. C. S. Hartley, N. Kapernaum, J. C. Roberts, F. Giesselmann and R. P. Lemieux, J. Mater. Chem., 2006, 16, 2329–2337.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures for compound QL32-6, POM textures, tilt angle and birefringence measurements. See DOI: 10.1039/c5cc05212b

---