The molecular motion of bovine serum albumin under physiological conditions is ion specific

Abstract

Specific ion effects on the Brownian molecular motion of BSA protein under physiological conditions are investigated. New useful insights into Hofmeister phenomena related to electrolyte–protein interactions are presented.

---

There is at present an extraordinary interest toward ion specific ‘Hofmeister’ phenomena.^1–3 In 1888 Franz Hofmeister studied the effect of salt addition on the aggregation of egg white proteins.⁴ He ordered the salts, with the same cation but different anions, according to their ability in promoting the precipitation (salting-out) or the solubility (salting-in) of a protein in aqueous solution. A conventional ‘Hofmeister series’ is:

HPO₄²⁻ > SO₄²⁻ > F⁻ > Cl⁻ > Br⁻ > NO₃⁻ > ClO₄⁻ > SCN⁻

The ‘salting-out’ anions (left side of the series) are strongly hydrated, while ‘salting-in’ anions (right side) are only weakly hydrated. A similar series for cations was also observed:

Cs⁺ > NH₄⁺ > Rb⁺ > K⁺ > Na⁺ > Li⁺ > Mg²⁺

The ‘conventional’ cation series has a substantial difference compared to the case of anions.⁵ Indeed, salting-out cations are weakly hydrated (i.e. Cs⁺) and salting-in cations are strongly hydrated (i.e. Li⁺ and Mg²⁺). Substantially, anions and cations behave in the opposite way. In fact, there is experimental evidence that the cations follow more complicated trends.^5–7 Nonetheless, the understanding of the specific cation behaviour is even more interesting than that of anions, because many cations (i.e. Na⁺, K⁺, Mg²⁺, and Ca²⁺) play a crucial role in fundamental biological systems. The stability of protein solutions against aggregation is important in a range of diseases which are affected by protein aggregation phenomena such as thrombosis in the cardiovascular system,⁸ cold cataract formation in the visual system,⁹ neurodegenerative disorders (i.e. Alzheimer's¹⁰ and Parkinson's¹¹ diseases), etc. Moreover, protein aggregation constitutes a crucial problem in liquid formulations based on concentrated therapeutic proteins such as monoclonal antibodies.¹² Besides salt type and concentration, protein aggregation depends on other intensive properties such as temperature and pH.^13,14

Proteins, depending on concentration and pH, often show remarkably different behaviours. Hence, the choice of concentration is quite important if the experiments must be related to physiological environments. As an example, the concentration of serum albumin (whose physiological function is the transport of hormones, fatty acids, etc. and the regulation of pH and osmotic pressure) ranges, for healthy individuals, between 35 and 50 mg mL⁻¹.¹⁵

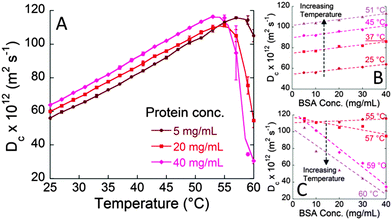
Here we investigated the specific effect of salts on the molecular motion of a concentrated solution of a model protein (bovine serum albumin, BSA) under physiological conditions. Before presenting the results of our experiments, it should be noticed that at pH 7, BSA is negatively charged since its pI (isoelectric point) is around 4.7.¹⁶ To investigate the subtle molecular protein–electrolyte interactions the ‘Brownian’ diffusion coefficient, D_c, obtained through dynamic light scattering (DLS) measurements is an extremely sensitive and convenient parameter. Fig. 1A shows the diffusion coefficient of BSA at different protein concentrations (pH 7 and 0.1 M NaCl) determined as a function of temperature. D_c increases upon increasing the temperature in the range 25–50 °C (Fig. 1A). At higher temperatures (51–57 °C) a maximum value of the diffusion coefficient (D_max) is reached, and then the diffusion coefficient decreases to very low values. The initial part of the D_c/T curve is a straight line in agreement with the Stokes–Einstein equation that, for a spherical particle, is: D₀ = k_BT/6πηR_H, where D₀ represents the diffusion coefficient of the particle at infinite dilution, k_B is the Boltzmann constant, η is the viscosity, and R_H is the hydrodynamic radius of the diffusing particle. Differently, the steep decrease of D_c observed at T > 55 °C is very likely caused by BSA unfolding and resulting aggregation. The temperature ranges at which BSA aggregates start to form are consistent with the values found in the literature for similar conditions.¹⁷Fig. 1A also shows that the increase of BSA concentration from 5 to 40 mg mL⁻¹, in the temperature range 25–51 °C, leads to an increase of the diffusion coefficient (D_c). The linear trend of D_c as a function of BSA concentration, at constant temperature (shown in Fig. 1B) can be described by the equation,¹²

D_c = D₀ [1 + k_Dc_BSA] (1)

where k_D is an interaction parameter and c_BSA is the concentration of BSA (mg mL⁻¹). According to the literature^18,19 the interaction parameter k_D is expected to behave as the ‘second virial coefficient’ (B₂₂) obtained by static light scattering measurements. k_D was indeed used to determine and predict the aggregation of concentrated protein solutions.^12,18,20 The increase of BSA concentration, moreover, produces a shift of the D_max values toward lower temperatures (see Fig. S1 in the ESI†). The value of D_max for the solution containing 5 mg mL⁻¹ of BSA occurs at 57 °C and decreases to 51 °C for the solution at 40 mg mL⁻¹. The increase of D_c with increasing c_BSA is apparently counterintuitive since a higher viscosity, and hence a slower diffusion, would be expected.²¹ The explanation of the observed trend can be found considering the interactions acting among BSA proteins when c_BSA increases. Despite the increase of the viscosity of the solution, the increase of c_BSA may enhance the electrostatic repulsion among BSA molecules (at pH 7 a BSA molecule carries 10 negative charges),²² thus D_c increases. In order to confirm that electrostatic interactions affect the diffusion process, the effect of ionic strength was investigated at the fixed BSA concentration of 40 mg mL⁻¹. Fig. 2A shows that an increase of NaCl concentration results in a decrease of D_c. The important effect of electrostatic repulsion on the diffusion process of BSA molecules can be highlighted by plotting D_cversus NaCl concentration. The trends shown in Fig. 2B confirm that an increase of ionic strength screens the electrostatic repulsion among protein molecules, and thus lowers the diffusion coefficients at all temperatures. We go now to the main purpose of the present work, that is the investigation of ion specific effects on the molecular motion of BSA at the physiological protein concentration of 40 mg mL⁻¹.

Fig. 1 Diffusion coefficients (D_c) of BSA as a function of temperature, in 10 mM phosphate buffer solutions at pH 7 and 100 mM NaCl. (A) Different D_c/T curves for different BSA concentrations (5–40 mg mL⁻¹). (B) D_c/c_BSA (concentration of BSA) at temperatures below the maximum (25–51 °C). (C) D_c/c_BSA at temperatures above the maximum (55–60 °C).

Fig. 2 Effect of NaCl concentrations (0, 50, 100, and 300 mM) on the diffusion coefficient (D_c) of BSA (40 mg mL⁻¹) in 10 mM phosphate buffer solutions at pH 7. (A) D_c/T curves. (B) D_c/NaCl concentration curves.

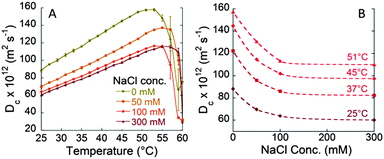
Fig. S2A (ESI†) shows the values of BSA diffusion coefficients as a function of temperature in the presence of different 0.1 M sodium salts. At each temperature the diffusion coefficients increase according to the typical Hofmeister sequence for anions (SCN⁻ > I⁻ > Br⁻ > Cl⁻ > F⁻), usually observed for pH > pI.^23,24Fig. 3A shows the anion specific D_c values at the physiological temperature of 37 °C. The observed trend is consistent with specific anion adsorption on the BSA surface, despite its negative net charge at pH 7. The higher negative charge induced by SCN⁻ adsorption at the BSA surface strengthens the repulsion among protein molecules and, hence, higher D_c values are measured. The marked anion specific effect between BSA molecules is confirmed by the values of D_max that occur at 51 °C for NaF and increase up to more than 60 °C for NaSCN (see Fig. S3 in the ESI†). The increased stability of BSA solution against aggregation is about 10 °C. These striking findings highlight furthermore the importance of the nature of electrolytes at physiological concentrations.

Fig. 3 Specific ion effects on the diffusion coefficient of BSA (40 mg mL⁻¹) in 10 mM phosphate buffer solutions at pH 7, and 100 mM salt concentration. (A) Effect of anions on D_c values at 37 °C. (B) Effect of cations on D_c values at 37 °C.

The effect of different cations was then studied by collecting D_c/T values for BSA solutions (40 mg mL⁻¹) at pH 7 in the presence of different 0.1 M chloride salts, as shown in Fig. S2B (ESI†). As observed elsewhere, the specific effect of cations is less marked than that of anions.⁶ This is in apparent contrast with what was expected from electrostatics. Due to the net negative charge of BSA at pH 7, cations should produce a more marked effect than anions. Nonetheless, we again observe a cation-specific trend at the physiological temperature of 37 °C (Fig. 3B). However, different from the anion case, here the D_c values do not follow a monotonic series but, rather, a “bell-shaped” trend: Rb⁺ ∼ K⁺ > Na⁺ > Cs⁺ ∼ Li⁺. This is a remarkable result. Indeed, cesium and lithium, two cations that are considered to be at the opposite sides of the Hofmeister series, behave very similarly giving rise to the lowest values of D_c. Rubidium and potassium, instead, increase BSA motion, while sodium is in between the two extremes. A similar “bell-shaped” series for cations was previously observed for other protein systems.^6,7,25

At the present time, several approaches are being used to explain these peculiar Hofmeister effects.² Among them, the empirical rule proposed by Collins known as the “law of matching water affinities” (LMWA)²⁶ is worthy of consideration. LMWA is based on the classification of the ions as a function of the hydration degree (kosmotropic and chaotropic) and on the observation of the volcano plots. A theoretical approach due to Ninham explains ion–water, ion–ion and ion–surface specific interactions as the outcome of a delicate interplay between electrostatic and non-electrostatic (dispersion) forces.²⁷

The most recent developments of Ninham's theory explain how to include Collins' rules.²⁸ Here, in order to understand how ions affect the Brownian motion of BSA molecules we will consider the ‘interaction parameter’ k_D introduced in eqn (1),^12,29 calculated at 37 °C. k_D values reported versus BSA concentration (see Fig. S4A in the ESI†) show, for 27 °C and 37 °C, a positive slope, which means that the repulsion among BSA molecules increases with increasing protein concentration. However, at 57 °C k_D becomes negative (see Fig. S4B in the ESI†). This reflects the occurrence of non-electrostatic attractive forces likely due to the partial unfolding of BSA that leads to aggregation.

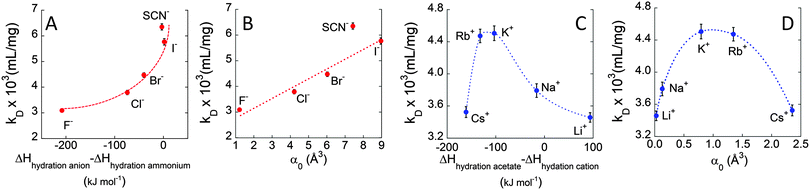
In order to investigate the molecular origin of the Hofmeister effect in protein systems, we propose in Fig. 4 the correlation of the interaction parameter k_D, calculated at 37 °C, with either the difference in hydration enthalpies (ΔH_{hydration anion} − ΔH_{hydration cation}) or the static polarisabilities of anions and cations (α₀). Hydration enthalpies are related to LMWA,³⁰ whereas ion polarisabilities are related to the theory of ion dispersion forces.²Fig. 4A shows a plot of k_D as a function of difference in hydration enthalpies between the different anions and ammonium cation (taken as a reference cation due to its similarity to the amine groups of surface residues of protein). Similarly, k_D was related to anion static polarisability α₀ in Fig. 4B. We notice a quite good correlation between k_D and both the difference in hydration enthalpies and α₀ values. k_D follows a monotonic increasing trend from F⁻ to I⁻ (SCN⁻ does not follow the correlation trend likely because it is the only non-spherical ion and its polarisability is not isotropic). What emerges from the correlations is that both parameters seem to play a role in affecting ion specific BSA diffusion. Indeed, according to LMWA, the positive charges at the protein surface (due to amino, imidazole, or guanidinium groups) are classified as ‘chaotropes’ and thus would prefer to interact with chaotropic anions. That is, the interaction would decrease along the series: SCN⁻ > I⁻ > Br⁻ > Cl⁻> F⁻. But (without considering SCN⁻) this is also the order of decreasing polarisability. Hence, we may argue that both parameters are at work and operate in the same direction. A higher adsorption of highly polarisable anions at the protein surface, indeed, would result in a stronger repulsion among BSA molecules. The same correlation was then evaluated for cations. In this case, k_D was related to the difference in hydration enthalpies using the ΔH_hydration of acetate (taken as a reference anionic group due to its similarity with carboxylates of protein surface residues) and those of the different cations, as well as with static polarisability, as shown in Fig. 4C and D. Different from the monotonic series observed for anions, cations again show a “bell-shaped” trend for both correlations (cf. Fig. 4D). If LMWA is the only mechanism at work, the strength of interaction between cations and negatively charged carboxylates (classified as kosmotropes) would decrease in going from the kosmotropic lithium to the chaotropic cesium. The order would be reversed if polarisability is accounted as the main factor. In fact, the observed trends agree neither with LMWA (D_c would have to decrease in the order: Cs⁺ > Rb⁺ > K⁺ > Na⁺ > Li⁺) nor with the polarizability order (D_c would have to decrease in the order: Li⁺ > Na⁺ > K⁺ > Rb⁺ > Cs⁺). The cation specific “bell-shaped” trend is a clear indication that both mechanisms are at work and operate in opposite directions. Similar findings were recently obtained by studying the ion specific aggregation of haemoglobin as a function of pH.⁶Scheme 1 represents the influence of ion specific interactions on the molecular motion of BSA protein, and deserves some important comments. In the case of anions, we notice that D_c is higher for I⁻ than for F⁻ because the former anion adsorbs on the BSA surface at a larger extent than the latter. This fact would make the BSA surface more negative and thus would increase the repulsion among protein molecules. In the case of cations we notice that D_c is lower for Li⁺ and Cs⁺ than for K⁺. Possibly, Li⁺ and Cs⁺ adsorb on the BSA surface at a larger extent than K⁺, making the surface less negative and thus decreasing the repulsion among protein molecules. It can be suggested that Li⁺ mainly interacts with carboxylates by ion-pairing according to LMWA, whereas Cs⁺ adsorbs on the uncharged patches of the protein, driven by its high polarisability according to the theory of ion dispersion forces.

Fig. 4 The interaction parameter k_D (pH = 7, salt concentration = 0.1 M, T = 37 °C) vs. hydration enthalpy and polarisability. Effect of anions: (A) k_Dvs. ΔH_hydration difference between the anions and ammonium ion (ΔH_{hydration ammonium} = −307 kJ mol⁻¹); (B) k_Dvs. anion static polarisability (α₀). Effect of cations: (C) k_Dvs. ΔH_hydration difference between the acetate ion (ΔH_{hydration acetate} = −425 kJ mol⁻¹) and the cations; (D) k_Dvs. static polarisability (α₀). The dotted curves are guides for the eye.

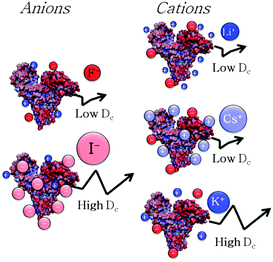Scheme 1 The molecular motion of BSA is ion specific. The arrow represents the molecular Brownian motion.

In conclusion we have shown that ion specific phenomena modulate the molecular motion and the interactions among proteins under physiological conditions of temperature, pH, salt and protein concentration. This was only partially acknowledged, since only seldom Hofmeister related studies used high protein concentrations.²³ In addition, most studies considered very high salt concentrations (up to 1 and 2 M). Here, we have confirmed that above the isoelectric point of the protein, anions (coions) still adsorb on the negatively charged protein surface to a higher extent than cations (counterions). This would be counterintuitive only if electrostatics is considered. These results can only be rationalised calling into play additional polarisability-dependent dispersion forces. Definitely, while for anions both hydration and polarisability work cooperatively thus producing a monotonic Hofmeister series, for cations the two mechanisms operate in opposite directions thus giving rise to a “bell-shaped” Hofmeister series.

MIUR, PRIN 2010–2011 grant number 2010BJ23MN-002, is thanked for financial support.

References

1. P. Jungwirth and P. S. Cremer, Nat. Chem., 2014, 6, 261–263.
2. A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377.
3. P. Lo Nostro and B. W. Ninham, Chem. Rev., 2012, 112, 2286–2322.
4. W. Kunz, J. Henle and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37.
5. N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2013, 29, 2602–2614.
6. L. Medda, C. Carucci, D. F. Parsons, B. W. Ninham, M. Monduzzi and A. Salis, Langmuir, 2013, 29, 15350–15358.
7. C. Carucci, P. Haltenort, M. Salazar, A. Salis and E. Magner, ChemElectroChem, 2015 DOI:10.1002/celc.201402412.
8. C. A. Haynes and W. Norde, Colloids Surf., B, 1994, 2, 517–566.
9. S. Finet, Curr. Opin. Colloid Interface Sci., 2004, 9, 112–116.
10. K. Blennow, M. J. de Leon and H. Zetterberg, Lancet, 2006, 368, 387–403.
11. W. Dauer and S. Przedborski, Neuron, 2003, 39, 889–909.
12. D. Roberts, R. Keeling, M. Tracka, C. F. Van Der Walle, S. Uddin, J. Warwicker and R. Curtis, Mol. Pharmaceutics, 2015, 12, 179–193.
13. G. Yohannes, S. K. Wiedmer, M. Elomaa, M. Jussila, V. Aseyev and M.-L. Riekkola, Anal. Chim. Acta, 2010, 675, 191–198.
14. V. Vetri, F. Librizzi, M. Leone and V. Militello, Eur. Biophys. J., 2007, 36, 717–725.
15. D. C. Carter and J. X. Ho, Adv. Protein Chem., 1994, 45, 153–203.
16. A. Salis, M. Boström, L. Medda, F. Cugia, B. Barse, D. F. Parsons, B. W. Ninham and M. Monduzzi, Langmuir, 2011, 27, 11597–11604.
17. B. Jachimska, M. Wasilewska and Z. Adamczyk, Langmuir, 2008, 24, 6866–6872.
18. M. E. Young, P. A. Carroad and R. L. Bell, Biotechnol. Bioeng., 1980, 22, 947–955.
19. D. Brune and S. Kim, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 3835–3839.
20. A. Saluja, R. M. Fesinmeyer, S. Hogan, D. N. Brems and Y. R. Gokarn, Biophys. J., 2010, 99, 2657–2665.
21. C. Tanford and J. G. Buzzell, J. Phys. Chem., 1956, 60, 225–231.
22. L. Medda, B. Barse, F. Cugia, M. Boström, D. F. Parsons, B. W. Ninham, M. Monduzzi and A. Salis, Langmuir, 2012, 28, 16355–16363.
23. Y. Zhang and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15249–15253.
24. A. Salis, F. Cugia, D. F. Parsons, B. W. Ninham and M. Monduzzi, Phys. Chem. Chem. Phys., 2012, 14, 4343–4346.
25. L. Medda, A. Salis and E. Magner, Phys. Chem. Chem. Phys., 2012, 14, 2875–2883.
26. K. D. Collins, Methods, 2004, 34, 300–311.
27. B. W. Ninham and V. Yaminsky, Langmuir, 1997, 13, 2097–2108.
28. T. T. Duignan, D. F. Parsons and B. W. Ninham, Chem. Phys. Lett., 2014, 608, 55–59.
29. R. A. Curtis, C. Steinbrecher, M. Heinemann, H. W. Blanch and J. M. Prausnitz, Biophys. Chem., 2002, 98, 249–265.
30. J. Kherb, S. C. Flores and P. S. Cremer, J. Phys. Chem. B, 2012, 116, 7389–7397.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details and additional experimental data. See DOI: 10.1039/c5cc01538c

---