Oscillatory growth for twisting crystals

Abstract

We demonstrate the oscillatory phenomenon for the twisting growth of a triclinic crystal through in situ observation of the concentration field around the growing tip of a needle by high-resolution phase-shift interferometry.

---

In nature, twists, which are observed everywhere in different sizes, are basically composed of fluids or flexible soft matter. However, twisting morphologies have been occasionally observed on solid crystals, which are usually faceted with straight edges.¹ The formation of twisting morphologies is a particularly interesting phenomenon of rigid crystals. Although several models have been proposed, the formation mechanism of the fascinating shapes is still a mystery. The formation of twisting crystals has been frequently regarded as the result of intrinsic features such as dislocation stress or distortion of crystal structures. On the other hand, the particular growth in concentration or temperature fields has not been directly observed. In the present work, we demonstrate for the first time the oscillatory phenomenon for the twist of a triclinic crystal (K₂Cr₂O₇) by in situ high-resolution interferometry techniques for the quantitative measurement of the concentration field. The formation of the particular twist architecture was associated with a periodic change in the growth direction of a needle crystal synchronised with an oscillatory concentration field. Extremely high supersaturation levels, as high as ∼120%, are capable of periodic nucleation on top of the needles. The huge supersaturation value was achieved by cooling the solution stabilised by the gel medium. The possibility of structural rotation of the nuclei around the growth axis is due to the low crystallographic symmetry.

Eshelby twists observed in the whiskers of metal oxides are deduced to originate from screw dislocation.² Lamellar twists of polymer crystals are suggested to be derived from the surface stress caused by the tilt of the molecular chain.³ A consecutive rotation of the crystallographic orientation in the lateral crystallisation of NH₄Cl on a substrate was reported to derive from the asymmetric surface energies at the growth front.^1o Asymmetric attachment of small units was deduced to be another mechanism for the formation of the helical structures.^1q According to a recent review article,^1p the twisting crystals mainly arise from internal stress driven by chemical and structural inhomogeneities. The chemical environment and growth conditions strongly affect the inhomogeneities associated with the presence of specific impurities or on the structural state of the surface. In these models, the origin of twisting is attributed to internal dislocations and strains or variation of the interfacial energies on the ordered crystalline lattice. The formation of twisting crystals has been regarded as the result of the intrinsic conditions. However, the particular growth behaviour including variation of the concentration or temperature field has not been clarified by in situ observation.

Our research group has proposed that the presence of a concentration field in a gel-like viscous matrix is correlated with the morphogenesis of crystals with a low crystallographic symmetry, such as the triclinic system.^1j–n In general, the diffusion field causes morphological instability that yields various shapes, such as hoppers, dendrites, diffusion-limited aggregates, and dense branching morphologies.^1j However, the influence of the concentration gradient around the crystal on the twisting growth has not been studied on the basis of experimental evidence. Non-contact and non-destructive methods for real-time observation of solutal concentration are required for a better understanding of the particular crystal growth process.⁴ In the current study, the twist of a crystal in a viscous matrix was found to be associated with the oscillation of a diffusion field on the basis of in situ observation. This particular architecture is constructed through twisted stacking of tilted units with periodic nucleation that is synchronised with the oscillation of solutal concentration at extremely high supersaturation.

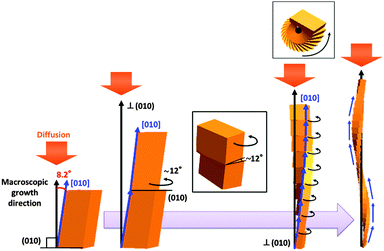
We observed the crystal growth of K₂Cr₂O₇ (space group P1̄) in a gelatine matrix to investigate the twisting architectures. The helical crystals of K₂Cr₂O₇ have been obtained in various kinds of viscous aqueous media containing gelatine, agar, pectin, and poly(acrylic acid).^1k,l Here, gelatine was utilised as a growth medium to perform the in situ observation. We can observe the specific growth easily because relatively large-sized helical crystals are slowly produced in the gelatine system with moderate viscosity.^1b,e–h,j,k A precursor solution was prepared by dissolving 30 g of K₂Cr₂O₇ and 30 g of gelatine in 100 g of purified water at ∼80 °C. The twisting growth of K₂Cr₂O₇ was observed in the gelatine gel at 25 °C using an optical microscope (Keyence VH-Z50LSPA). The macroscopic concentration field around the twisting crystal was observed using a reflection from the backside of the glass window of the cell by a Michelson interferometer (Nikon M Plan 2.5 TI). Fig. 1a shows a time course of the interferograms of a twisting crystal grown in a supersaturated gelatine matrix. The growing tip is found to meander in cycles of ca. 40 min duration with a decrease in the solutal concentration in front of the tip. Fig. 1b shows typical scanning electron microscopy (SEM) images of the backbone of the twisting architectures. As reported in our previous article,^1k the backbone consisted of the tilted planer units of K₂Cr₂O₇ (Fig. 1d), which were twisted with a rotation of ca. 12° on the (010) face. The stacking structure and the sinuous movement of the growing tip suggest that the crystal enters a 360° roll through a rotation of the units along a spiral path around the growth axis as illustrated in Fig. 1c. Although the platy unit of K₂Cr₂O₇ basically elongates in the [010] (b axis), the macroscopic growth orientation of the whole architecture is perpendicular to the (010) plane (Fig. 1d). Based on the lattice structure of K₂Cr₂O₇, the difference between the microscopic growth direction of the unit and the macroscopic direction of the whole architecture is estimated to be 8.2° (Fig. 1d-2).

Fig. 1 Successive pictures of Michelson interferometer images (a), typical SEM images (b), and schematic illustrations (c) of the backbone of a twisting K₂Cr₂O₇ crystal grown in a supersaturated gelatin matrix. The unit of the backbone is illustrated with the growth directions in (d). The bending fringes in (a) indicate a decrease in the solutal concentration in front of the growing tip. Dotted and solid lines in (a) indicate the macroscopic growth line of the twisting architecture and the direction of the growing tip, respectively. For the in situ observation, the precursor solution was cast in the growth cell whose diameter and depth were 10 mm and 0.2 mm, respectively.

As shown in Fig. 2, the microscopic concentration field around the growing tip was observed using a laser confocal phase-shift interferometer (LC-PSI).^4a The precursor solution, cast in a thin cell (25 mm × 25 mm × 0.2 mm), was put on a thermostated stage kept at 25 °C. In the phase-shift interferogram, each pixel of the image possesses the refractive index information. Thus, detailed 2D mapping of the concentration of the solution in front of the twisting crystal can be performed using this technique.

Fig. 2 Time-lapse interference images captured using an LC-PSI (a₁–d₁) and the supersaturation in front of the growing tip (a₂–d₂). A typical variation of the supersaturation around the tip (e). Temporal change in the supersaturation (f) and the growth rate (g) at the tip. The interference images were taken every 10 s. Points a, b, c, and d in (f) indicate time for panels (a₁, a₂), (b₁, b₂), (c₁, c₂), and (d₁, d₂), respectively. The refractive index around the tip was estimated from the brightness variation with a reference of the standard aqueous solution of K₂Cr₂O₇ that contained the same concentration of gelatine. The intensity of the interference in each pixel is directly transformed into the refractive index.⁵ Thus, variation of the refractive index around the tip was calculated from the interferogram with an 8-bit resolution. The solutal concentration or the supersaturation is linearly related to the refractive index obtained from the interferogram. Since the thickness of the growth cell is sufficiently small as compared with the lateral size of the concentration field perpendicular to the growth direction (>1000 μm), we assumed that the concentration was almost homogeneous along the thickness direction. The supersaturation was calculated by σ = (C − C_S)/C_S × 100, C: concentration, C_S: saturated concentration (13.8 g/100 g water at 25 °C⁶). Since the concentration of K₂Cr₂O₇ in the precursor solution was 30.0 g/100 g of water, the initial supersaturation was estimated to be 117% at the working temperature of 25 °C. 3D nucleation was suppressed by the presence of the gel matrix.

Fig. 2a₁–d₁ shows typical interference images around the growing tip of the twisting crystal. Fig. 2a₂–d₂ shows the possible gradients of the supersaturation (σ) obtained from the interference images in front of the growing tip. As shown in Fig. 2e, we found a symmetric concentration field around the growing tip. The lowest value of the supersaturation at the growing tip was ∼95%, which is extremely high for conventional solution growth. (The supersaturation of the growth solution is commonly less than 10%,⁷ in which twisting has never been observed.) The high supersaturation is achieved through suppression of 3D nucleation due to high viscosity in the presence of the gelatine matrix. This suggests that extremely high supersaturation is needed for the twisting of the crystal in the matrix. Because the 3D nucleation frequently occurs at the high degree of supersaturation in solution, the twisting has not been observed in the conventional solution systems.

Fig. 2f shows a time-lapse supersaturation at the tip. The supersaturation at the tip oscillated for a period of ca. 60 s. We also monitored the growth rate at the tip from the interference images (Fig. 2g). The oscillation of the diffusion field synchronised with the change in the growth rate. Fig. 3 shows successive optical micrographs of the growing tip with the oscillation of the growth rate in a cycle of 40–60 s. Since the unit crystal was gradually enlarged at the tip, the growth rate gradually decreased in the blue region. When the supersaturation exceeded ∼103% (Fig. 2f), we observed the start of nucleation at the top of the column and subsequent rapid growth of a newly formed daughter crystal in the orange region. Therefore, the growth-rate oscillation is ascribed to the rapid growth of the daughter unit through periodic nucleation followed by gentle growth with continuous enlargement of the unit. As shown in Fig. 3, the growth direction of the daughter unit deviated from that of the basal crystal. This means that the deviating daughter unit was formed through eccentric nucleation on the top face of the basal unit.

Fig. 3 Successive optical micrographs of the growing tip with oscillation of the growth rate. White solid and dotted lines indicate that the directions of the daughter unit and the basal crystal, respectively.

In the current study, the oscillation of the supersaturation was found to be synchronised with the periodic change in the growth rate through nucleation (Fig. 2 and 3) at extremely high supersaturation. The surface supersaturation gradually increases with decreasing growth rate (Region I). In this region, the tip is gradually enlarged. When the supersaturation exceeds a critical value, the growth rate is boosted after nucleation (Region II). Here, the growth is determined by nucleation and subsequent elongation of the tip. A rapid decrease in the supersaturation follows the continuous increase in the growth rate due to a delay in the solute diffusion. After the drop of the surface supersaturation, the growth rate decreases again with a gradual increase in the supersaturation (Region I). The decrease in the growth rate of the tip is associated with the lateral enlargement of the unit crystal (Fig. 3). When the supersaturation falls below the critical value, the growth behaviour at the tip will change. The growth suppression is also attributable to an increase in the strain of the crystal lattice or the accumulation of impurity molecules at the growing front.⁸ In this case, the growth gradually slows down because of the inhibitory action. The supersaturation then increases in an attempt to reach the bulk value. A fresh daughter crystal that is not contaminated is formed on the basal unit when the supersaturation exceeds a critical value. The growth rate increases again after nucleation.

The cyclic nucleation accompanied by the oscillatory diffusion field leads to the construction of the unit crystals composing the twisting architecture. Consequently, the formation of the particular 3D winding morphologies is correlated with a periodic change in the growth direction through the cyclic nucleation synchronised with an oscillatory diffusion field. As mentioned above, the crystal enters a 360° roll with 30 units through a rotation of 12° along a spiral path. The duration of the 360° roll, about 40 min, roughly agrees with the time of 30 oscillations.

As illustrated in Fig. 4, the twisting architecture, consisting of the small units, is constructed through a periodic change in the growth direction with the cyclic nucleation accompanied by an oscillatory diffusion field. Although the tip of the unit crystal basically elongates in [010] (b axis), the macroscopic growth orientation of the whole architecture is deduced to be perpendicular to (010). This difference in directions due to the low crystallographic symmetry of the triclinic system is adjusted through a periodic change in the growth direction with a rotation of ∼12° on the (010) plane. The eccentric nucleation on the top, shown in Fig. 3, can be explained by the adjustment of the growth direction. The rotation of the unit would be induced by the lattice distortion with impurities or the presence of a coincidence-site lattice on the (010) plane. The distortion with the accumulation of impurities is suggested by the decrease in the growth rate before periodic nucleation. Unfortunately, the origin of the rotation of ∼12° has not been clarified. In fact, a high degree of the supersaturation in the diffusion field causes the cyclic nucleation on the top face to adjust the macroscopic growth direction. Finally, the geometry optimisation occurs with the rotation of the nuclei. By repetition of this procedure, the backbone consisting of the units is formed through periodic nucleation accompanied by the oscillatory diffusion field in the viscous matrix. However, the detailed mechanism of the change in the direction cannot be explained simply by the shape, size, or oscillation of the diffusion field. The interferometry revealed that the interface supersaturation at the tip of the gel was surprisingly high (σ > 90%) as compared to a low value (σ < 10%) for the growth process in solution. Although 3D nucleation in solution at such high supersaturation is usually expected to occur, the gel media may suppress the nucleation and thus an unexpectedly high supersaturated condition is achieved. On the other hand, the chemical structure of gelatine is not essential for the oscillatory growth because the helical crystals are produced in other kinds of viscous aqueous media containing agar, pectin, and poly(acrylic acid).^1k,l The accumulation of strain due to the impurity adsorbed at the growing front must be investigated to discuss the origin of the oscillation and structural rotation. Therefore, further investigation of the particular rotation during periodic growth is required to clarify the detailed mechanism of the direction change with the cyclic nucleation.

Fig. 4 Schematic illustration of formation of the twisting backbone through periodic formation of tilted units with rotation on (010). The growth direction is periodically adjusted through cyclic nucleation along a spiral path.

Twisting crystals were found to be constructed through the periodic change in the growth direction and rate through eccentric nucleation synchronised with the oscillation of the supersaturation at extremely high supersaturation. The factors controlling twist could be extremely high supersaturation capable of nucleation at the growing tip and structural rotation of the nuclei around the growth axis due to a low crystallographic symmetry. Our findings are important for a better understanding of crystal growth and could be utilised for self-organised production of advanced functional materials with complex shapes.

This work was partially supported by Grant-in-Aid for Scientific Research (No. 22107010) on Innovative Areas of “Fusion Materials: Creative Development of Materials and Exploration of Their Function through Molecular Control” (No. 2206) from the Ministry of Education, Culture, Sports, Science and Technology. K.T. was supported by Grant-in-Aid for Scientific Research (No. 22244066) from the Japan Society for the Promotion of Science (JSPS).

Notes and references

1. (a) F. Wallerant, Bull. Soc. Fr. Mineral., 1907, 30, 43–60; (b) A. G. Shtukenberg, E. Gunn, M. Gazzano, J. Freudenthal, E. Camp, R. Sours, E. Rosseeva and B. Kahr, ChemPhysChem, 2011, 12, 1558–1571; (c) J. M. García-Ruiz, J. Cryst. Growth, 1985, 73, 251–262; (d) J. M. García-Ruiz, S. T. A. M. Carnerup, A. G. Christy, M. J. Van Kranendonk and N. J. Welham, Science, 2003, 302, 1194–1197; (e) J. Suda and M. Matsushita, J. Phys. Soc. Jpn., 1995, 64, 348–351; (f) J. Suda, T. Nakayama, A. Nakahara and M. Matsushita, J. Phys. Soc. Jpn., 1996, 65, 771–777; (g) J. Suda, T. Nakayama and M. Matsushita, J. Phys. Soc. Jpn., 1998, 67, 2981–2983; (h) J. Suda, M. Matsushita and K. Izumi, J. Phys. Soc. Jpn., 2000, 69, 124–129; (i) L. A. Gower and D. A. Tirrell, J. Cryst. Growth, 1998, 191, 153–160; (j) Y. Oaki and H. Imai, Cryst. Growth Des., 2003, 3, 711–716; (k) H. Imai and Y. Oaki, Angew. Chem., Int. Ed., 2004, 43, 1363–1368; (l) Y. Oaki and H. Imai, J. Am. Chem. Soc., 2004, 126, 9271–9275; (m) Y. Oaki and H. Imai, Langmuir, 2005, 21, 863–869; (n) H. Imai and Y. Oaki, CrystEngComm, 2010, 12, 1679–1687; (o) M. Wang, D. W. Li, D. J. Shu, P. Bennema, Y. W. Mao, W. Pan and N. B. Ming, Phys. Rev. Lett., 2005, 94, 125505; (p) A. G. Shtukenberg, Y. O. Punin, A. Gujral and B. Kahr, Angew. Chem., Int. Ed., 2014, 53, 672–699; (q) S. H. Yu, H. Cölfen, K. Tauer and M. Antonietti, Nat. Mater., 2005, 4, 51–55; (r) T. Terada, S. Yamabi and H. Imai, J. Cryst. Growth, 2003, 253, 435–444; (s) O. Giraldo, S. L. Brock, M. Marquez, S. L. Suib, H. Hillhouse and M. Tsapatsis, Nature, 2000, 405, 38; (t) O. Giraldo, M. Marquez, S. L. Brock, S. L. Suib, H. Hillhouse and M. Tsapatsis, J. Am. Chem. Soc., 2000, 122, 12158–12163.
2. J. D. Eshelby, J. Appl. Phys., 1953, 24, 176–179.
3. (a) H. D. Keith and F. J. Padden Jr., Polymer, 1984, 25, 28–42; (b) A. Toda, M. Okamura, K. Taguchi, M. Hikosaka and H. Kajioka, Macromolecules, 2008, 41, 2484–2493; (c) Y. Li, D. Yan, S. Z. D. Cheng, F. Bai, T. He, L. C. Chien, F. W. Harris and B. Lotz, Macromolecules, 1999, 32, 524–527.
4. (a) A. Srivastava, K. Tsukamoto, E. Yokoyama, K. Murayama and M. Fukuyama, J. Cryst. Growth, 2010, 12, 2254–2262; (b) S. Maruyama, T. Shibata and K. Tsukamoto, Exp. Therm. Fluid Sci., 1999, 19, 34–48; (c) J. F. Torres, A. Komiya, E. Shoji, J. Okajima and S. Maruyama, Opt. Lasers Eng., 2012, 50, 1287–1296; (d) K. Nagashima and Y. Furukawa, J. Cryst. Growth, 2000, 209, 167–174; (e) W. B. Houa, A. B. Kudryavtseva, T. L. Braya, L. J. DeLucasa and W. W. Wilsonb, J. Cryst. Growth, 2001, 232, 265–272; (f) M. Wang and N. Ming, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 2493–2498; (g) K. Onuma, K. Tsukamoto and S. Nakadate, J. Cryst. Growth, 1993, 129, 706–718.
5. K. Tsukamoto, in Handbook of Crystal Growth, ed. T. Nishinaga, Elsevier, Amsterdam, 2015, vol. 1, pp. 1031–1060.
6. Solubilities of inorganic and organic compounds, ed. H. Stephen and T. Stephen, Pergamon Press, Oxford, 1963, vol. 1, p. 166.
7. (a) A. I. Malkin, A. A. Chernov and I. V. Alexeev, J. Cryst. Growth, 1989, 97, 765–769; (b) A. A. Chernov, Contemp. Phys., 1989, 30, 251–276; (c) X. Y. Liu, K. Maiwa and K. Tsukamoto, J. Chem. Phys., 1997, 106, 1870–1879.
8. H. Miura and K. Tsukamoto, Cryst. Growth Des., 2013, 13, 3588–3595.

---