Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of hydrogen-bonding and its interplay with octahedral tilting in CH3NH3PbI3
Jung-Hoon
Lee
a,
Nicholas C.
Bristowe
b,
Paul D.
Bristowe
*a and
Anthony K.
Cheetham
*a
aDepartment of Materials Science and Metallurgy, University of Cambridge, 27 Charles Babbage Road, Cambridge, CB3 0FS, UK. E-mail: akc30@cam.ac.uk; pdb1000@cam.ac.uk
bDepartment of Materials, Imperial College London, Exhibition Road, London, SW7 2AZ, UK
First published on 5th March 2015
Abstract
First principles calculations on the hybrid perovskite CH3NH3PbI3 predict strong hydrogen-bonding which influences the structure and dynamics of the methylammonium cation and reveal its interaction with the tilting of the PbI6 octahedra. The calculated atomic coordinates are in excellent agreement with neutron diffraction results.
CH3NH3(MA)PbI3 is one of the most extensively studied hybrid halide perovskites due to its impressive power conversion efficiency for solar cell applications.1 In spite of numerous studies on its structural properties,2–8 relatively little progress has been made in our understanding on the role of hydrogen-bonding in the orthorhombic phase (o-MAPbI3). In this study we have used density functional theory (DFT) calculations to examine the thermodynamic consequences of hydrogen-bonding and its interplay with the octahedral rotations that are ubiquitous in perovskites. The computed atomic positions, including those of the hydrogen atoms, are compared to a recent powder neutron diffraction study.9
The DFT calculations were performed using the generalized gradient approximation (GGA) and projector augmented wave (PAW)10 pseudopotentials as implemented in the Vienna ab initio Simulation Package (VASP).11–13 The effects of spin–orbit coupling and van der Waals (vdW) interactions14 were included during structural and electronic relaxation. We adopted (i) a 4 × 3 × 4 Monkhorst–Pack k-point mesh centered at Γ,15 (ii) a 500 eV plane-wave kinetic energy cutoff, and (iii) the tetrahedron method with the Blöchl corrections for the Brillouin zone integrations.16 We explicitly treated 14 valence electrons for Pb (5d106s26p2), 7 for I (5s25p5), 4 for C (2s22p2), 5 for N (2s22p3), and 1 for H (1s1). The ions were relaxed until the forces on them were less than 0.01 eV Å−1. The experimentally observed ratio of the orthorhombic unit cell vectors2 was imposed when we optimized the lattice parameters by calculating the Kohn–Sham (K–S) energy as a function of volume.17
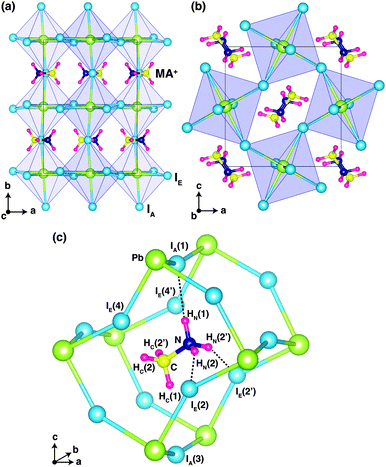
Fig. 1 shows the optimized crystal structure of o-MAPbI3 with space group Pnma. The computed lattice parameters are a = 8.844 Å, b = 12.592 Å, and c = 8.563 Å, in good agreement with the experimental values at 100 K (a = 8.8362 Å, b = 12.5804 Å, and c = 8.5551 Å for the X-ray study2 and a = 8.8657 Å, b = 12.6293 Å, and c = 8.5769 Å for the neutron study9). Note that the calculated values lie between the experimental ones. The perovskite structure exhibits corner-linked PbI6 octahedra forming a three-dimensional network. The Pnma phase displays a particular pattern of rotations of the octahedra involving either in-phase or out-of-phase rotations around the three I–Pb–I octahedral axes, denoted by a−b+a− in Glazer's notation.18 Regarding the organic MA ion, the C–N bonds are aligned approximately along the [101] and [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] directions with a head-to-tail configuration as shown in Fig. 1. Our optimized atomic positions for this structure are listed in Table 1, where H atoms that are connected to N atoms are denoted by HN, and H atoms that are connected to C atoms are denoted by HC. The subscripts A and E on the iodine atoms refer to axial and equatorial configurations, respectively, as shown in Fig. 1(c). Our optimized atomic positions agree very well with the previous experimental values. In particular, the coordinates of the H atoms are in very good agreement with the recent powder neutron diffraction study.9
] directions with a head-to-tail configuration as shown in Fig. 1. Our optimized atomic positions for this structure are listed in Table 1, where H atoms that are connected to N atoms are denoted by HN, and H atoms that are connected to C atoms are denoted by HC. The subscripts A and E on the iodine atoms refer to axial and equatorial configurations, respectively, as shown in Fig. 1(c). Our optimized atomic positions agree very well with the previous experimental values. In particular, the coordinates of the H atoms are in very good agreement with the recent powder neutron diffraction study.9
| Wyckoff site | This work | Experiment | ||||||
|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | |||
| Pb | 4b | 0.500 | 0.000 | 0.000 | ND | 0.500 | 0.000 | 0.000 |
| XD | 0.500 | 0.000 | 0.000 | |||||
| IA(1) | 4c | 0.476 | 0.250 | 0.938 | ND | 0.484 | 0.250 | 0.944 |
| XD | 0.486 | 0.250 | 0.947 | |||||
| IE(2) | 8d | 0.176 | 0.017 | 0.172 | ND | 0.189 | 0.015 | 0.184 |
| XD | 0.190 | 0.017 | 0.186 | |||||
| N | 4c | 0.953 | 0.750 | 0.023 | ND | 0.942 | 0.750 | 0.030 |
| XD | 0.932 | 0.750 | 0.029 | |||||
| C | 4c | 0.908 | 0.250 | 0.075 | ND | 0.937 | 0.250 | 0.058 |
| XD | 0.913 | 0.250 | 0.061 | |||||
| HC(1) | 4c | 0.941 | 0.250 | 0.198 | ND | 0.937 | 0.250 | 0.187 |
| HC(2) | 8d | 0.842 | 0.178 | 0.048 | ND | 0.866 | 0.170 | 0.029 |
| HN(1) | 8d | 0.111 | 0.183 | 0.003 | ND | 0.128 | 0.189 | −0.009 |
| HN(2) | 4c | 0.978 | 0.750 | 0.142 | ND | 0.954 | 0.750 | 0.146 |
Fig. 1(c) shows the ground-state configuration of the H atoms in the surrounding inorganic Pb–I cage. The positions of the H atoms conform with the Pnma space group. If we assume that hydrogen-bonding is important when H⋯I < 3 Å, there are three hydrogen-bonds in the Pb–I cage between HN(1), HN(2), and HN(2′) and IA(1), IE(2), and IE(2′), respectively.
These three H⋯I bonds per MA ion are controlled by both the particular inorganic a−b+a− tilt pattern and the organic MA conformation. Among these, the HN(1)⋯IA(1) hydrogen bond is the shortest (2.565 Å) and presumably the strongest. Accordingly, the N–HN(1)⋯IA(1) angle is almost 180° (Table 2). These results are in good agreement with the recent powder neutron diffraction study, as well as the structure of ammonium iodide (NH4I)19 where hydrogen-bonding is known to play a key role in structural stabilization.20 Details of the computed bond lengths and bond angles for the principal interactions are given in Table 2 and compared with the experimental neutron diffraction values. The N⋯I distances are much shorter than those of C⋯I and also the angle of C–HC(1)⋯IA(3) is smaller than that of N–HN(1)⋯IA(1). Accordingly, the hydrogen-bond interactions mainly originate from H atoms on nitrogen.
| This work | NH4I19 | Experiment9 | |
|---|---|---|---|
| Bond type (Å) | |||
| HN(1)⋯IA(1) | 2.565 | 2.454 | 2.613 |
| HN(2)⋯IE(2) | 2.611 | 2.808 | |
| HC(1)⋯IA(3) | 3.137 | 3.190 | |
| HC(2)⋯IE(4) | 3.094 | 3.006 | |
| N⋯IA(1) | 3.606 | 3.473 | 3.611 |
| N⋯IE(2) | 3.566 | 3.681 | |
| C⋯IA(3) | 4.221 | 4.298 | |
| C⋯IE(4) | 4.032 | 4.090 | |
| Angle type (°) | |||
| N–HN(1)⋯IA(1) | 177 | 178 | 174 |
| N–HN(2)⋯IE(2) | 152 | 146 | |
| C–HC(1)⋯IA(3) | 170 | 172 | |
| C–HC(2)⋯IE(4) | 144 | 148 | |
| Pb–IA(1)–Pb | 159 | 162 | |
| Pb–IE(2)–Pb | 145 | 151 | |
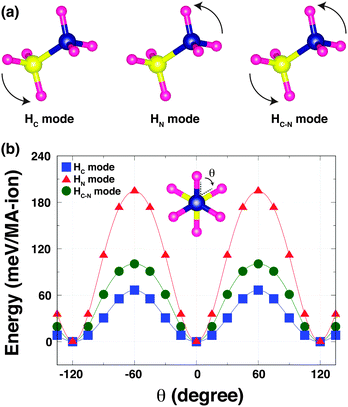
To understand the strength of the hydrogen-bonding in o-MAPbI3, we have examined the energetics as a function of the H positions. The most stable structure shows that the MA cation adopts a staggered conformation [Fig. 2(b) inset], as expected and in agreement with the neutron results; this is denoted by θ = 0° in the following calculations in which we rotate the NH3 and CH3 groups around the C–N axis for all four MA-ions in the unit cell. We have calculated the Kohn–Sham (K–S) energies as a function of the torsion angle θ, fixing all other atoms, for three rotational modes as shown in Fig. 2(a): (i) in the HC mode, the NH3 group is held rigid while the CH3 group is rotated around the C–N bond axis. This mode reveals the stability of the staggered conformation at θ = 0° compared with the eclipsed conformation at θ = 60° [Fig. 2(b)]. The staggered conformation is ∼66 meV per MA-ion more stable than the eclipsed structure. This suggests that the methyl groups may be rotating at high temperatures, but becomes ordered when the material is cooled to lower temperatures, as is seen in [(CH3)2NH2]Mn(HCOO)3.21 (ii) In the HN mode, the NH3 group rotates around the C–N bond axis. This mode reflects the stability of both the staggered conformation and the hydrogen-bonding [Fig. 2(b)], and is the stiffest mode. (iii) In the third mode, HC–N, the MA cation is held in the staggered conformation and rotated around the C–N axis. This mode is dominated by the strength of the hydrogen-bonding, which represents ∼102 meV per MA-ion. This value is quite close to that obtained by NMR for the corresponding rotation in the dimethylammonium perovskite formates (88 meV per DMA-ion).21 Note that the difference in the energy barriers between the HN and HC modes is similar to the energy barrier for the HC–N mode. The three K–S energy curves plotted as a function of the torsion angle θ for the three rotational modes have 120° periodicity in common. This is because the most stable structure represents not only the staggered conformation but also the optimised hydrogen-bonding in the Pb–I cage.
We have also examined the relationship between hydrogen-bonding and the octahedral tilting in o-MAPbI3. We began by fixing the HC–N modes at θ = 0° (hydrogen bonding maximised) and 60° (hydrogen bonding minimised) but allowing the inorganic Pb–I cage to relax. We found that the resulting structure and octahedral rotations were almost unaltered. This suggests, unsurprisingly in perovskites with tolerance factors less than 1,22,23 that the octahedral rotations are robust.
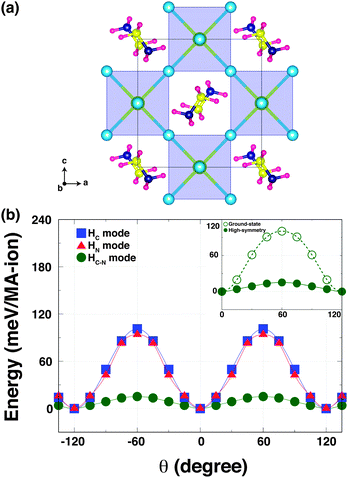
To understand how the robust octahedral rotations (which change amplitude and pattern with temperature), can affect the hydrogen bonding, we performed a second computational experiment. Here, we computed the K–S energies as a function of the torsion angle θ for the same three rotational modes but in a hypothetical high-symmetry structure. This high-symmetry structure is characterized by no octahedral tilting, but with the MA ions in the same configuration as the orthorhombic phase [Fig. 3(a)]. When we calculated the energy of the high-symmetry structure, we relaxed only the MA units within this configuration to optimise any hydrogen-bonding in the Pb–I cage.
In the high-symmetry structure, interestingly, the strength of hydrogen-bonding is remarkably reduced. This is seen for the HN and HC–N modes where the energy barriers are significantly shallower in the high-symmetry structure [Fig. 3(b)]. The energy barrier of the HN mode is ∼90 meV per MA-ion, while that of HC–N mode is ∼12 meV per MA-ion. The latter is an order of magnitude smaller than the corresponding barrier in the orthorhombic (ground state) phase with octahedral tilting [Fig. 3(b) inset]. On the other hand, the energy barrier of the HC mode (∼96 meV per MA-ion) of the high-symmetry structure slightly increases. This suggests that the MA cation is held in the staggered conformation and easily rotated around the C–N axis in the high-symmetry structure without invoking the octahedral tilting, in agreement with NMR results.24 Thus, one can conclude that the octahedron tilting is strongly correlated with the hydrogen-bonding interaction. Our findings are consistent with a recent report of a stiffening of the lattice of a hybrid metal–organic formate [NH4][Zn(HCOO)3] when cooling through a hydrogen bond ordering transition, as revealed by Resonant Ultrasound Spectroscopy.25 Our results could also explain why the MA-ion ordering does not appear above the orthorhombic transition, but is coincident with the phase transition driven by the robust octahedral rotations.
As a way of visualising the hydrogen-bonding in o-MAPbI3, we present in Fig. 4 the non-covalent interaction isosurfaces calculated using the Critic2 code26,27 for the ground-state and high-symmetry structures at θ = 0°. The ground-state case in Fig. 4(a) shows non-covalent interaction density located between three H atoms [HN(1), HN(2), and HN(2′)] and three I atoms [IA(1), IE(2), and IE(2′)], which is consistent with hydrogen bonding in the energy minimised structure. On the other hand, there is only one non-covalent interaction density contour between HN(1) and IA(1) in the high-symmetry structure. The octahedron tilting is clearly coupled to the strength of the hydrogen-bonding. To further quantify this strength we have calculated the hydrogen bond strength index28 from the N–H stretching frequencies of the MA molecule in isolation and in the perovskite. For the HN(1)⋯IA(1) bond, for example, this index is 0.11 in the ground-state structure but only 0.03 in the high-symmetry structure. For the HN(2)⋯IE(2) bond the values are 0.05 and 0.02 respectively. The 11% softening of the N–H stretching frequency in o-MAPbI3 is comparable to the softening of the O–H stretching frequency in ice,29 suggesting similar strengths of hydrogen bonding in both cases.
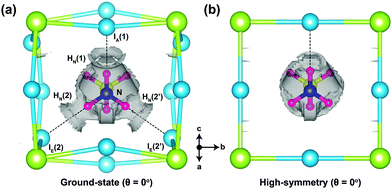 | ||
| Fig. 4 Non-covalent interaction density isosurfaces for (a) the ground-state (θ = 0°) and (b) high-symmetry structures (θ = 0°). The reduced gradient density cut-off is 1.0 au. | ||
We have calculated precise positions for the H atoms in o-MAPbI3 and found excellent agreement with a recent powder neutron diffraction study.9 We have also explored the role of hydrogen bonding in relation to the behaviour of the MA cations and the tilting of the PbI6 octahedra. The MA cation adopts a staggered conformation in the optimised structure. It is shown that rotation of the staggered MA cation around its C–N bond is quite hindered, with an activation energy of ∼102 meV per MA-ion, due to the strong hydrogen-bonding. The strength of the hydrogen-bonding is found to be highly correlated with the octahedral rotations in MAPbI3, providing an explanation for why the MA-ordering transition is coincident with the tilting phase transition temperature.
Funding from the Winton Programme for the Physics of Sustainability at the University of Cambridge is gratefully acknowledged. NCB acknowledges financial support from the Royal Commission for the Exhibition of 1851 for a fellowship at Imperial College London. The calculations were performed at the Cambridge HPCS and the UK National Supercomputing Service. Access to the latter was obtained via the UKCP consortium and funded by EPSRC Grant No. EP/K014560/1.
Notes and references
- http://www.nrel.gov/ncpv/images/efficiency_chart.jpg .
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641 CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- Y. Wang, T. Gould, J. F. Dobson, H. Zhang, H. Yang, X. Yao and H. Zhao, Phys. Chem. Chem. Phys., 2014, 16, 1424–1429 RSC.
- J. Feng and B. Xiao, J. Phys. Chem. Lett., 2014, 5, 1278–1282 CrossRef CAS.
- J. M. Frost, K. T. Butler and A. Walsh, APL Mater., 2014, 2, 081506 CrossRef PubMed.
- E. Menéndez-Proupin, P. Palacios, P. Wahnón and J. Conesa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045207 CrossRef.
- W. Geng, L. Zhang, Y.-N. Zhang, W.-M. Lau and L.-M. Liu, J. Phys. Chem. C, 2014, 118, 19565–19571 CAS.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- D. A. Egger and L. Kronik, J. Phys. Chem. Lett., 2014, 5, 2728–2733 CrossRef CAS.
- A. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- D. P. Kozlenko, B. N. Savenko, V. P. Glazkov, V. A. Somenkov and S. Hull, Physica B, 2000, 276–278, 226–227 CrossRef CAS.
- A. M. Heyns, K. R. Hirsch and W. B. Holzapfel, J. Chem. Phys., 1980, 73, 105–119 CrossRef CAS PubMed.
- T. Besara, P. Jain, N. S. Dalal, P. L. Kuhns, A. P. Reyes, H. W. Kroto and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6828–6832 CrossRef.
- V. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- R. E. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- Z. Zhang, W. Li, M. A. Carpenter, C. J. Howard and A. K. Cheetham, CrystEngComm, 2015, 17, 370–374 RSC.
- A. Otero-de-la-Roza, M. A. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018 CrossRef CAS PubMed.
- X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- B. Santra, J. Klines, D. Alfe, A. Tkatchenko, B. Slater, A. Michaelides, R. Car and M. Scheffler, Phys. Rev. Lett., 2011, 107, 185701 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |