Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measurements of the effect of membrane asymmetry on the mechanical properties of lipid bilayers†
Yuval
Elani‡
a,
Sowmya
Purushothaman‡§
*a,
Paula J.
Booth
b,
John M.
Seddon
a,
Nicholas J.
Brooks
a,
Robert V.
Law
a and
Oscar
Ces
*a
aDepartment of Chemistry, Imperial College London, Exhibition Road, London, SW7 2AZ, UK. E-mail: sp736@cam.ac.uk; o.ces@imperial.ac.uk
bDepartment of Chemistry, Kings College London, Britannia House, 7 Trinity Street, London, SE1 1DB, UK
First published on 13th March 2015
Abstract
We detail an approach for constructing asymmetric membranes and characterising their mechanical properties, leading to the first measurement of the effect of asymmetry on lipid bilayer mechanics. Our results demonstrate that asymmetry induces a significant increase in rigidity compared to symmetric membranes. Given that all biological membranes are asymmetric our findings have profound implications for the role of this phenomenon in biology.
Biological membranes are almost universally asymmetric: there is a compositional difference in the lipids that are present in their inner and outer leaflets. This feature is found across all life classes, cell types and organelles, from plasma membranes and golgi apparatus through to endosomal membranes.1
Membrane asymmetry exists in cells despite the stochastic flipping of lipids between the leaflets (known as flip-flop) which would normally lead to an equilibrated symmetric bilayer.2 The cell devotes significant resources in order to maintain asymmetric membranes via the ATP dependent operation of specialised proteins known as flipases – a strong indication that asymmetry plays important roles in cellular events.3,4 Processes thought to be associated with membrane asymmetry include: endocytosis,5 vesicle budding and trafficking,4 signal-transduction,6,7 membrane curvature,8 modulation of protein channel opening,9 and the regulation of membrane associated enzyme activity.10
Asymmetry is thought to influence many core biological functions by altering the membrane's global biophysical properties.6,9,11,12 One such property is the bending rigidity,13 which characterises the ability of membranes to bend under low stress. This property, first described by Helfrich in 197314 and elaborated upon elsewhere,15 is analogous to the bilayer stiffness and is related to how much energy is needed to deform it. It is thought to influence protein conformation due to its relation to the lateral-pressure profile,9,12 and is one of the core parameters in the field of membrane biophysics. However due to the lack of methods to generate asymmetric GUVs, only the bending rigidities of symmetric GUVs have been studied.16–18 As a result the role that asymmetry plays in cell biology remains qualitative and is largely restricted to how compositional asymmetry varies across organelles, and to how flip-flop rates vary with lipid chemical structure.1 Unlocking the link between membrane asymmetry and membrane mechanical properties therefore has the potential to transform our understanding of membrane structure, protein stability, protein folding, protein binding and protein activity.10,19–28
The recent innovation of phase transfer platforms capable of generating asymmetric giant unilamellar vesicles (GUVs) has opened up the possibility of overcoming this technological bottleneck.29–33 The phase transfer method of vesicle generation has been shown to be capable of generating asymmetric vesicles, yet it has seen most of its use away from the field of membrane biophysics. Instead, due to its high encapsulation efficiency and the ability to exert control over vesicle size, lamellarity,34 and compartmentalization,35,36 it is increasingly being used in bottom-up synthetic biology,37–42 where it has been credited as one of the key technical developments responsible for the rapid expansion of this research area.43
Due to the crucial but as-of-yet poorly understood role of asymmetry and the increasing use of phase transfer methodologies, it is essential to study the properties of symmetric and asymmetric GUVs formed by this method, and to compare them to those formed by more conventional means.44 In this paper we generate asymmetric GUVs using the phase transfer approach, validate their asymmetry and simultaneously undertake bending rigidity determination via fluctuation analysis. This has enabled us to successfully perform the first experimental measurement of the effect of membrane asymmetry upon the mechanical properties of lipid bilayers. We show that (i) symmetric membranes formed via phase transfer have comparable rigidities to those formed via the gold-standard method of electroformation and (ii) asymmetric membranes have rigidities that are significantly higher than their symmetric counterparts.
The phase transfer technique of GUV production involves a two-step process where the individual monolayers are sequentially assembled, shown in Fig. 1 (see ESI,† for full experimental details). Briefly, using density differences, lipid-coated water-in-oil droplets are passed through a water–oil column with an interfacial monolayer. This transforms the droplets into GUVs. By having different lipid compositions in the oil phases used in the two steps an asymmetric distribution of lipids is achieved.
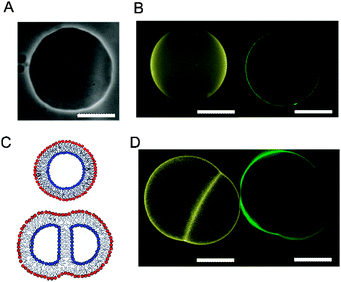
The asymmetry of vesicles formed via this method have been confirmed by several researchers using fluorescence quenching29,30 and protein binding experiments,30 and by domain formation studies.31 We add to these demonstrations by conducting fluorescent microscopy experiments on asymmetric hemifused GUVs. This occurs when two water-in-oil droplets stochastically descend through the interface together, as opposed to simply a single droplet.
The bilayer separating the two halves of the hemifused vesicle pair will only be composed of the inner-leaflet lipid, without the presence of outer-leaflet lipid (Fig. 2C). By introducing different fluorescent lipids in each leaflet this distribution can be observed using fluorescent microscopy. We formed asymmetric GUVs composed of POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine), with different fluorescent lipids in their two leaflets. The inner leaflet comprised of 1 mol% NBD-PE (1,2-diphytanoyl-sn-glycero-3-phosphoethanolamine-N-(7-nitro-2-1,3-benzoxadiazol-4-yl) (ammonium salt)), and the outer of 1 mol% Rh-PE (1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt)). The two fluorophores were imaged using FITC and TRITC filters respectively. Such vesicles were only rarely seen, but on the occasion where it was formed, the distribution of lipids was successfully observed. Indeed, outer leaflet Rh-PE was not observed in the middle bilayer, therefore validating the presence of asymmetry (Fig. 2D).
To determine GUV bending rigidities we used the fluctuation analysis technique described in detail in the ESI.† In short, it relies on the observation that the vesicle membrane exhibits thermal fluctuations, or flickering (see Fig. 2A). GUVs were observed under phase contrast mode and the fluctuations were recorded. For each vesicle ca. 4000 contours were processed to extract the edges and their fluctuations. For small deformations the distance from the membrane edge to the center of the vesicle about the mean edge position can be Fourier transformed (FT) to give a power spectrum, giving the amplitudes of the constituent modes. Using the equipartition theorem, the mean square amplitude 〈h2〉 associated with each mode (qx) at the vesicle equator (y = 0) is related to the bending rigidity, κ, by:45
 | (1) |
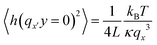 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 vesicle contours (20 individual vesicles) for each composition, apart from DOPC inner, POPC outer, as this gave particularly low yield of fluctuating vesicles. For this composition, 16
000 vesicle contours (20 individual vesicles) for each composition, apart from DOPC inner, POPC outer, as this gave particularly low yield of fluctuating vesicles. For this composition, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 vesicle contours were analyzed.
000 vesicle contours were analyzed.
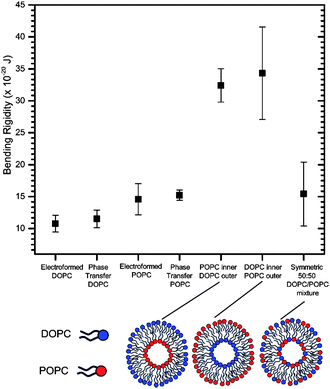
We first wanted to establish the quality and integrity of GUVs formed by phase transfer compared to those generated via the gold-standard of electroformation using the bending rigidity as a proxy (see ESI† for electroformation methods). This was done for symmetric one-component vesicles composed of two lipid compositions, 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and POPC, which differ in the degree of saturation of the tail region and the chain length. Both these lipids are well-characterized and widely used in model membrane systems. The bending rigidity values obtained in the two methods were comparable to one another within error, and to those found in the literature18,47 (Fig. 3).
This indicates that the phase transfer generation strategy does not alter vesicle mechanical properties. This result is crucial in the context of the debate of how much oil is trapped in phase transfer vesicles, by suggesting that if there is trapped oil it is not in substantial enough quantities to influence their mechanical properties. It therefore shows the suitability of these vesicles for studies involving embedded proteins which are affected by bilayer mechanics and the potential presence of oil, and for studying lipid flip-flop. In addition, it offers potential for the incorporation of mechanically-modulated components, such as mechanosensitive channels and mechanoresponsive membranes in functional artificial cells.
Subsequently we investigated the effects of introducing asymmetry upon the bending rigidities of these vesicular systems. We measured the bending rigidities of two types of asymmetric vesicle formed with phase transfer: the first with DOPC in the inner leaflet and POPC in the outer, and the second where this is reversed. Both of these bending rigidities were nearly 250% higher than the values obtained for their symmetric counterparts (Fig. 3), which were composed of a homogenous 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of both lipids. Within error the direction of asymmetry did not affect the bending rigidity. These are surprising empirical results, given that the asymmetry had been generated by varying the distribution of lipids solely with respect to hydrocarbon tail type, with no overall modification to the distribution of headgroup types or charge.
50 mixture of both lipids. Within error the direction of asymmetry did not affect the bending rigidity. These are surprising empirical results, given that the asymmetry had been generated by varying the distribution of lipids solely with respect to hydrocarbon tail type, with no overall modification to the distribution of headgroup types or charge.
The results can be explained by the fact that DOPC and POPC have different spontaneous curvatures48 and so their distribution across the bilayer is likely to impact on its bending energetics. A simple model for the curvature energy associated with changes in mean bilayer curvature can be established by considering bending of the two monolayers separately (see ESI† for full details). This predicts that the curvature energy associated with flat bilayer with constant bilayer composition but varying distribution of lipids between the two monolayers reaches a minimum when the bilayer is symmetric (Fig. S4, ESI†), which is consistent with our experimental measurements.
The indication that asymmetry has a stark effect on membrane mechanical properties has immediate consequences for the study of membrane protein folding,49,50 the behavior of integral-membrane proteins (particularly mechanosensitive pores),51,52 as well as membrane-associated proteins which may be regulated by membrane mechanics.10 It may have crucial implications on the causal mechanisms and biophysics behind processes such as membrane trafficking, and endo- and exocytosis. As in silico simulations of lipid bilayers, both coarse grained and atomistic, are increasingly capable of measuring and predicting the properties of large bilayer systems it will be possible to explore the link between changes in leaflet coupling and lateral pressure resulting from asymmetry with variations in bending rigidity. In parallel our strategy has opened up the possibility in the future of being able to systematically measure how asymmetric distributions of charge, chain type and headgroup type control the mechanics of lipid bilayers.
In conclusion, we form asymmetric vesicles and validate their asymmetry by fluorescence imaging of hemifused vesicles. By combining fluctuation analysis techniques to phase transfer technologies we show that such vesicles have similar bending rigidities to those formed via other traditional methods. Significantly, we obtain the first empirical measurement of a mechanical property of asymmetric vesicles, a result which indicates that asymmetry significantly affects a membrane's bending rigidity. This has notable consequences in understanding the role of membranes in cells, the majority of which are asymmetric and demonstrates that asymmetry must be included as a key variable in studies of protein-membrane and protein-small molecules interactions that are almost exclusively conducted using symmetric lipid bilayer structures. This breakthrough shows that is possible to use asymmetric GUVs to fill the void in our knowledge of the precise role that asymmetry plays in cells, and paves the way for further studies into the role of asymmetry on membrane mechanics.
This work was supported by EPSRC grants EP/J017566/1 and EP/G00465X/1, BBSRC Grant BB/F013167/1, EPSRC Centre for Doctoral Training Studentship from the Institute of Chemical Biology (Imperial College London) and EPSRC Doctoral Prize Fellowship awarded to YE.
Notes and references
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS PubMed.
- F. Contreras, L. Sánchez-Magraner, A. Alonso and F. M. Goñi, FEBS Lett., 2010, 584, 1779–1786 CrossRef CAS PubMed.
- T. Pomorski and A. Menon, Cell. Mol. Life Sci., 2006, 63, 2908–2921 CrossRef CAS PubMed.
- D. L. Daleke, J. Biol. Chem., 2007, 282, 821–825 CrossRef CAS PubMed.
- T. Pomorski, R. Lombardi, H. Riezman, P. F. Devaux, G. van Meer and J. C. Holthuis, Mol. Biol. Cell, 2003, 14, 1240–1254 CrossRef CAS PubMed.
- K. Charalambous, P. J. Booth, R. Woscholski, J. M. Seddon, R. H. Templer, R. V. Law, L. M. Barter and O. Ces, J. Am. Chem. Soc., 2012, 134, 5746–5749 CrossRef CAS PubMed.
- J. M. Boon and B. D. Smith, Med. Res. Rev., 2002, 22, 251–281 CrossRef CAS PubMed.
- T. R. Graham and M. M. Kozlov, Curr. Opin. Chem. Biol., 2010, 22, 430–436 CrossRef CAS PubMed.
- E. Perozo, A. Kloda, D. M. Cortes and B. Martinac, Nat. Struct. Mol. Biol., 2002, 9, 696–703 CAS.
- G. S. Attard, R. H. Templer, W. S. Smith, A. N. Hunt and S. Jackowski, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 9032–9036 CrossRef CAS PubMed.
- W. L. Hwang, M. Chen, B. d. Cronin, M. A. Holden and H. Bayley, J. Am. Chem. Soc., 2008, 130, 5878–5879 CrossRef CAS PubMed.
- P. J. Booth, Curr. Opin. Struct. Biol., 2005, 15, 435–440 CrossRef CAS PubMed.
- D. Marsh, Chem. Phys. Lipids, 2006, 144, 146–159 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1973, 28, 693 CAS.
- W. Helfrich and R.-M. Servuss, Il Nuovo Cimento D, 1984, 3, 137–151 CrossRef.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- W. Rawicz, K. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- R. S. Gracià, N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482 RSC.
- H. Hong and L. K. Tamm, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 4065–4070 CrossRef CAS PubMed.
- A. M. Seddon, M. Lorch, O. Ces, R. H. Templer, F. Macrae and P. J. Booth, J. Mol. Biol., 2008, 380, 548–556 CrossRef CAS PubMed.
- J. K. Nagy, W. L. Lonzer and C. R. Sanders, Biochemistry, 2001, 40, 8971–8980 CrossRef CAS PubMed.
- P. J. Booth and J. Clarke, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 3947–3948 CrossRef CAS PubMed.
- D. Miller, K. Charalambous, D. Rotem, S. Schuldiner, P. Curnow and P. J. Booth, J. Mol. Biol., 2009, 393, 815–832 CrossRef CAS PubMed.
- P. J. Booth, Biochim. Biophys. Acta, Bioenerg., 2000, 1460, 4–14 CrossRef CAS.
- J. R. Lewis and D. S. Cafiso, Biochemistry, 1999, 38, 5932–5938 CrossRef CAS PubMed.
- J. Bigay, J. F. Casella, G. Drin, B. Mesmin and B. Antonny, EMBO J., 2005, 24, 2244–2253 CrossRef CAS PubMed.
- G. Attard, W. Smith, R. Templer, A. Hunt and S. Jackowski, Biochem. Soc. Trans., 1998, 26, S230 CAS.
- K. Charalambous, D. Miller, P. Curnow and P. J. Booth, BMC Biochem., 2008, 9, 31 CrossRef PubMed.
- S. Pautot, B. J. Frisken and D. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10718–10721 CrossRef CAS PubMed.
- P. C. Hu, S. Li and N. Malmstadt, ACS Appl. Mater. Interfaces, 2011, 3, 1434–1440 CAS.
- T. Hamada, Y. Miura, Y. Komatsu, Y. Kishimoto, M. d. Vestergaard and M. Takagi, J. Phys. Chem. B, 2008, 112, 14678–14681 CrossRef CAS PubMed.
- S. Matosevic and B. M. Paegel, J. Am. Chem. Soc., 2011, 133, 2798–2800 CrossRef CAS PubMed.
- H. Ito, T. Yamanaka, S. Kato, T. Hamada, M. Takagi, M. Ichikawa and K. Yoshikawa, Soft Matter, 2013, 9, 9539–9547 RSC.
- S. Matosevic and B. M. Paegel, Nat. Chem., 2013, 5(11), 958–963 CrossRef CAS PubMed.
- Y. Elani, A. Gee, R. V. Law and O. Ces, Chem. Sci., 2013, 4, 3332–3338 RSC.
- Y. Elani, R. V. Law and O. Ces, Nat. Commun., 2014, 5, 5305, DOI:10.1038/ncomms630.
- P. Carrara, P. Stano and P. L. Luisi, ChemBioChem, 2012, 13, 1497–1502 CrossRef CAS PubMed.
- P. Stano, G. Rampioni, P. Carrara, L. Damiano, L. Leoni and P. L. Luisi, BioSystems, 2012, 109, 24–34 CrossRef CAS PubMed.
- V. Noireaux and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17669–17674 CrossRef CAS PubMed.
- V. Noireaux, Y. T. Maeda and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3473–3480 CrossRef CAS PubMed.
- Z. Zhang, Z. Li, W. Yu, K. Li, Z. Xie and Z. Shi, Nanotechnology, 2013, 24, 185103 CrossRef PubMed.
- M. Hadorn, E. Boenzli, K. T. Sørensen, D. De Lucrezia, M. M. Hanczyc and T. Yomo, Langmuir, 2013, 29, 15309–15319 CrossRef CAS PubMed.
- P. Stano, P. Carrara, Y. Kuruma, T. P. de Souza and P. L. Luisi, J. Mater. Chem., 2011, 21, 18887–18902 RSC.
- P. Walde, K. Cosentino, H. Engel and P. Stano, ChemBioChem, 2010, 11, 848–865 CrossRef CAS PubMed.
- J. Pécréaux, H.-G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef PubMed.
- Y. Z. Yoon, J. P. Hale, P. G. Petrov and P. Cicuta, J. Phys.: Condens. Matter, 2010, 22, 062101 CrossRef PubMed.
- J. Henriksen, A. C. Rowat and J. H. Ipsen, Eur. Biophys. J., 2004, 33, 732–741 CrossRef CAS PubMed.
- B. Kollmitzer, P. Heftberger, M. Rappolt and G. Pabst, Soft Matter, 2013, 9, 10877–10884 RSC.
- P. J. Booth, R. H. Templer, W. Meijberg, S. J. Allen, A. R. Curran and M. Lorch, Crit. Rev. Biochem. Mol. Biol., 2001, 36, 501–603 CrossRef CAS PubMed.
- P. J. Booth, M. L. Riley, S. L. Flitsch, R. H. Templer, A. Farooq, A. R. Curran, N. Chadborn and P. Wright, Biochemistry, 1997, 36, 197–203 CrossRef CAS PubMed.
- G. Chang, R. H. Spencer, A. T. Lee, M. T. Barclay and D. C. Rees, Science, 1998, 282, 2220–2226 CrossRef CAS.
- E. Perozo and D. C. Rees, Curr. Opin. Struct. Biol., 2003, 13, 432–442 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and analytical procedures, further discussion of results. See DOI: 10.1039/c5cc00712g |
| ‡ These authors contributed equally. |
| § Current address: Cavendish Laboratory, University of Cambridge, JJ Thomson Avenue, Cambridge, CB3 0HE, UK. |
| This journal is © The Royal Society of Chemistry 2015 |