An analyst's guide to precision

Abstract

Precision is defined in VIM3 as the closeness of agreement between indications or measured quantity values obtained by replicate measurements on the same or similar objects under specified conditions—a crucial idea for analytical chemists. But precision as such is not quantified. Standard deviation is a quantitative concept and therefore handier in practice. But standard deviation is a measure of dispersion, which is the inverse of precision. Accordingly it is necessary in careful writing to avoid using precision as a synonym for standard deviation.

---

For analytical chemists, however, it's the conditions of measurement that are all-important. Analysts use different conditions for different quality-related activities—method validation, internal quality control, collaborative trials, proficiency tests, instrument development, etcetera. Standard deviation varies markedly among these measurement conditions for the same determination so it is essential not to get them muddled. We must also bear in mind that dispersion varies with the concentration of the analyte and furthermore is basic to defining detection capability. Finally, precision is related to, but must not be confused with, uncertainty. Let's examine these features in more detail.

‘Instrumental conditions’

In the process of developing or testing analytical equipment, analysts often make replicate measurements on a single aliquot, with no adjustments, in the shortest possible time. The resulting standard deviation simply describes the short-term behaviour of the instrument alone and should not be used in any other context. These instrumental standard deviations are often found in instrument brochures but tend grossly to underestimate the standard deviation derived from complete analytical procedures. Such ‘real-life’ analysis involves many operations preceding the instrumental measurement stage, and these introduce further and usually much greater variation in the final result.

Repeatability conditions

Repeatability conditions occur when separate test portions of a single test sample are analysed by the same procedure, same equipment, same analyst, in the same environment, and within a short time period. A ‘short’ time period implies that environmental and other factors that affect the measurement do not change. Of course the conditions always do change to some degree. The temperature of the laboratory and instruments may change over a working day, reagents may deteriorate and—dare we say it?—analysts get tired. A ‘run’ of analysis can be defined as the period during which we conventionally regard the effect of changing conditions as negligible, for example, the period between re-calibration events.

To estimate analytical repeatability standard deviation (σ_r) realistically we have to take into account all sources of variation within a run. That means firstly that the whole procedure must be replicated, from the selection and weighing of the test portion to the recording of the final result. Furthermore, the test sample used for replication should be in the same state of preparation as a typical test sample and not, for example, more finely ground. The concentration of the analyte should be appropriate, usually close to a critical decision level. Then for runs typically comprising many test materials, the replicates should be scattered at random among other typical test materials rather than treated in an unbroken sequence. This ensures that both systematic changes within-run and memory effects are included within the estimate. Any deviation from this prescription may result in an under-estimated σ_r, and this shortfall may be the cause of the frequently-disappointing performance obtained from procedures taken from the literature. A convenient way to estimate σ_r is via within-run duplication of typical test materials.

Intermediate conditions

We encounter intermediate conditions (sometimes regrettably called within-laboratory reproducibility conditions) primarily in statistical internal quality control (IQC). The goal of IQC is to ensure as far as possible that the data quality associated with a validated procedure is maintained every time the procedure is used. The relevant intermediate standard deviation (σ_br) describes the between-run dispersion of results on the control material when the analysis is replicated in successive runs. Clearly σ_br subsumes and is greater than σ_r, because it includes run-to-run effects, such as brought about by new batches of reagents, restarting equipment from an overnight shutdown, different laboratory temperatures, different analysts, and many others. The value of σ_br is used to set up control charts in order to identify out-of-control runs and take the appropriate action. The value of σ_r is clearly too small for setting up IQC control charts, as its use would result in an unduly high proportion of apparently out-of-control runs. (Note: σ_br is definitely not a standard uncertainty—it is likely to be substantially smaller. The purpose of statistical IQC is simply to demonstrate long-term consistency in the execution of a procedure, not fitness for purpose.)

Careful planning is needed to obtain a realistic estimate of σ_br. As before, the control material should be typical of the test materials in composition. Test portions of the control material should be analysed at random positions within the sequence of test materials in the run. Again, the replication needs to be done under real-life conditions, that is, when the procedure is in actual use, to avoid under-estimation. Obtaining a realistic estimate by conducting a one-off validation is therefore impracticable. This implies that an initial control chart should be set up with provisional limits, to be updated when enough experience of the analytical process has accumulated.

Reproducibility conditions

Reproducibility standard deviation (σ_R) originally referred to the dispersion of results from a collaborative trial (CT), that is, a number (n ≥ 8) of laboratories analysing the same test materials according to a single detailed procedure. The materials are effectively homogenised before splits are distributed to the participant laboratories. A value of σ_R estimated from a collaborative trial is regarded as a crucial measure of the performance of a particular procedure, and is usually about twice the value of σ_r obtained in the same study. Nowadays the meaning of reproducibility has been broadened to include results from different laboratories when the material is analysed by any variant of a method, or even by different methods, as when results are obtained in proficiency testing (PT). This broadened definition of σ_R is, however, numerically often surprisingly close to the original collaborative trial values, at least in the analysis of foodstuffs where on average σ_R(PT) ≈ 1.06σ_R(CT). The key feature of σ_R is that it accounts for variation of any kind among the collected results, effects caused by repeatability variation and bias in individual results, heterogeneity between the distributed portions of the test material, short-term instability and a host of hidden causes.

Precision and uncertainty

The concept of uncertainty is based on the idea that all known causes of bias have been removed from the measurement procedure. If that proviso is fulfilled, and there are a reasonable number of results replicated under suitable conditions, then the standard deviation from the analytical procedure must be closely related to the standard uncertainty. But what conditions of measurement should apply to the replication? Repeatability standard deviation (even when estimated properly) is too small: it does not capture variation due to various hidden causes such as unrecognised laboratory biases, between-bottle heterogeneity and many other variable factors. However, we usually find that σ_R ≈ 2σ_r, and this greater reproducibility variation is caused by all of the hidden factors, even the unknown ones. It is this comprehensive nature of σ_R that makes it in most instances a good general benchmark for the uncertainty stemming from a given procedure. Estimates of σ_R obtained by robust statistics from proficiency test results are a valuable resource in this respect.

Of course it is perfectly possible for a laboratory to produce results with uncertainties smaller than a typical σ_R by using great care, but this extra vigilance effectively defines a new and different procedure with different performance characteristics (σ′_r and σ′_R). Even so, σ′_r derived from the more careful procedure will still under-estimate the uncertainty of its results—if the new procedure were used in an interlaboratory study, we would still find σ′_r < σ′_R.

Precision and concentration

For a given class of matrix, the dispersion of the results depends markedly on the concentration of the analyte, under any given replication conditions. When results are likely to be restricted to a narrow range, this will cause no extra difficulty. When results fall unpredictably over a wide range, this dependency has to be taken into account when attributing uncertainty to an analytical result. We may need to estimate standard deviation at several different concentrations and interpolate between them. Unfortunately neither constant standard deviation nor constant relative standard deviation is always an appropriate assumption for this interpolation. Several alternative functional relationships may be useful to aid this interpolation. The well-known Horwitz function, σ_H = 0.02c^0.8495 describes well the trend of σ_R in food analysis over mass fractions in the range 10⁻⁷ < c < 10⁻¹ where the analyte concentration is well above the detection limit. This applies to many types of chemical measurement. Generalised versions of the function (that is, σ = θ₁c^θ₂ with adjustable parameters θ₁, θ₂) have been found relevant in other application sectors. The function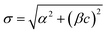 , for concentration c with adjustable parameters α, β, has been found to fit standard deviations from particular procedures in many different types of analysis and conditions of measurement.

Number of observations

Standard deviations estimated from a small number of results are themselves very variable. The commonly-used sample size of ten results is ‘small’ in this context: it gives standard deviations with their own relative standard error of 22%, so estimates could easily be as low as 0.5 times, or as high as 1.5 times, the true value. Standard deviations calculated from even smaller numbers of results should be treated with suitable caution.

Postscript

Most of the issues raised in this Brief are covered in more detail in a critical survey of precision in Analytical Methods, 2012, 4, 1598–1611, and in various issues of AMC Technical Briefs. ‘VIM3’ refers to the International vocabulary of basic and general terms in metrology (VIM), 3rd Edition, JCGM 200:2008. (Free download from http://www.bipm.org/vim.) Meanwhile it seems fit to finish with a quotation from Aristotle: “It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible”.

This Technical Brief was prepared by the Statistical and Validation Subcommittees, and approved for publication by the Analytical Methods Committee on 17/08/15.

---