Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Broadscale resolving power performance of a high precision uniform field ion mobility-mass spectrometer†
Jody C.
May
*a,
James N.
Dodds
a,
Ruwan T.
Kurulugama
b,
George C.
Stafford
b,
John C.
Fjeldsted
b and
John A.
McLean
*a
aDepartment of Chemistry, Center for Innovative Technology, Institute for Chemical Biology, Institute for Integrative Biosystems Research and Education, Vanderbilt University, Nashville, TN 37235-1822, USA. E-mail: jody.c.may@vanderbilt.edu; john.a.mclean@vanderbilt.edu
bAgilent Technologies, Santa Clara, CA 95051, USA
First published on 10th July 2015
Abstract
An extensive study of two current ion mobility resolving power theories (“conditional” and “semi-empirical”) was undertaken using a recently developed drift tube ion mobility-mass spectrometer. The current study investigates the quantitative agreement between experiment and theory at reduced pressure (4 Torr) for a wide range of initial ion gate widths (100 to 500 μs), and ion mobility values (K0 from 0.50 to 3.0 cm2 V−1 s−1) representing measurements obtained in helium, nitrogen, and carbon dioxide drift gas. Results suggest that the conditional resolving power theory deviates from experimental results for low mobility ions (e.g., high mass analytes) and for initial ion gate widths beyond 200 μs. A semi-empirical resolving power theory provided close-correlation of predicted resolving powers to experimental results across the full range of mobilities and gate widths investigated. Interpreting the results from the semi-empirical theory, the performance of the current instrumentation was found to be highly linear for a wide range of analytes, with optimal resolving powers being accessible for a narrow range of drift fields between 14 and 17 V cm−1. While developed using singly-charged ion mobility data, preliminary results suggest that the semi-empirical theory has broader applicability to higher-charge state systems.
Introduction
In the early ion mobility literature, the term “resolving power” was used to characterize the precision and accuracy of an ion mobility spectrometer and was based on the sharpness of a single peak.1,2 In its initial use, resolving power was a qualitative metric used to compare the relative capabilities of one ion mobility technique or instrument to another. Following the commercialization and development of ambient pressure, uniform field ion mobility spectrometry (IMS) in the 1970s,3–5 there were several attempts at quantifying the IMS separation efficiency including the use of theoretical plate numbers,6 two-peak resolution,8,9 and single-peak resolving power.7,10,11 Of these, the single peak resolving power was widely adopted and is currently the conventional means by which the separation efficiency of IMS is quantified.12,13 The experimentally measured ion mobility resolving power (Rm) is a dimensionless ratio defined as the mobility drift time (td) divided by the width of the peak (Δtd):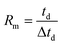 | (1) |
Here, the drift time is measured from the centroid of the ion mobility peak and the peak width is determined using the full width at half maximum (FWHM) definition. The single peak resolving power can be used to directly compare the achievable resolution of different IMS instruments utilizing the same ion mobility technique. Thus, a temporal resolving power definition can directly assess the separation performance between uniform field instruments, but an alternative definition such as a cross-section based resolving power may be more applicable to compare, for example, a uniform field drift tube to a traveling-wave instrument.14
The theoretical drift time of an ion in a uniform electric field is described by a rearrangement of the ion mobility proportionality equation:15
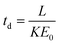 | (2) |
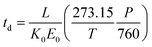 | (3) |
Here, T and P are the temperature (in K) and pressure (in Torr), respectively, of the drift tube. Eqn (3) provides a direct theoretical prediction of the drift time of an ion with a known reduced mobility value under conditions in which the electric field and drift length are well-characterized, such as the case in uniform field IMS.
A theoretical expression for peak width, necessary to predict the denominator in eqn (1), is somewhat more complicated. Revercomb and Mason derived a peak width expression which includes considerations for ion diffusion and the width of the initial ion packet (gate width, tg):7
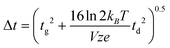 | (4) |
Here, kB is the Boltzmann constant (1.3806488 × 10−23 kg m2 s−2 K−1), e is the elementary charge (1.602176565 × 10−19 C), z is the ion charge state (unitless), T is the drift gas temperature (in K), and V is the drift voltage (in V). The coefficient terms (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) arise from the conventional definition of the FWHM as it relates to the standard deviation of a Gaussian distribution. This expression is similar to one derived at the same time by Spangler and Collins.6 Combining eqn (3) and (4) with eqn (1) yields a theoretical expression termed the conditional resolving power (Rc):13
2) arise from the conventional definition of the FWHM as it relates to the standard deviation of a Gaussian distribution. This expression is similar to one derived at the same time by Spangler and Collins.6 Combining eqn (3) and (4) with eqn (1) yields a theoretical expression termed the conditional resolving power (Rc):13
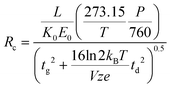 | (5) |
Previous uniform field IMS studies have demonstrated that eqn (4) underestimates the magnitude of the peak width by as much as 30%.6,10–12,16 More recent studies have demonstrated qualitatively good correlation between eqn (5) and experimental results for ambient pressure IMS, but quantitative agreement varied based on the initial gate width and the specific ion being measured.13,18 In some cases the conditional resolving power equation overpredicted the experimental resolving power by as much as 80%.13
Efforts to improve the peak width theory for IMS have involved the addition of correction terms to eqn (4), including a “Townsend factor” for ion heating,6 component error functions for detector effects in stand-alone IMS,16 ion-neutral reaction chemistry occurring during ion drift,17 an isotropic scattering expression for high field operation,19 terms to account for space-charge effects,20,21 and a semi-empirical correction for the primary sources of variance.12 All of these approaches except the latter assume a specific source of band broadening not accounted for in eqn (4). Despite extensive studies over the past 40 years concerning the theoretical nature of peak shape in IMS, there is no consensus as to the primary cause of the failings of eqn (4), and likely there is no single shortcoming, but rather an ensemble of variances which differ from one instrument platform to another. Thus, the semi-empirical peak width theory developed by Siems et al. is appropriate to apply to an IMS system where no prior hypothesis is made regarding the source of band broadening.12
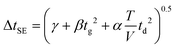 | (6) |
Here, three correction terms (α, β, and γ) are introduced and the value of these terms are found through linear regression analysis of empirical data. The α term replaces the diffusion term coefficient in eqn (4) 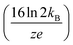 and is related to the ion drift time (residence time in the instrument). Deviations from the value of the diffusion term are attributed to broadening during ion drift, such as effects caused by field inhomogeneity, space-charge, and inelastic ion-neutral interactions. The β term accounts for dependencies on the initial ion gate pulse width, which include space-charge effects and distortions associated with the initial gating event. The γ term is a catch-all for additional sources of variance, such as peak broadening occurring outside of the ion mobility region, detector effects, and post-acquisition distortion of the arrival time distribution. For ideal correspondence to eqn (4), α = 0.957 × 103 V K−1, β = 1, and γ = 0 s2.
and is related to the ion drift time (residence time in the instrument). Deviations from the value of the diffusion term are attributed to broadening during ion drift, such as effects caused by field inhomogeneity, space-charge, and inelastic ion-neutral interactions. The β term accounts for dependencies on the initial ion gate pulse width, which include space-charge effects and distortions associated with the initial gating event. The γ term is a catch-all for additional sources of variance, such as peak broadening occurring outside of the ion mobility region, detector effects, and post-acquisition distortion of the arrival time distribution. For ideal correspondence to eqn (4), α = 0.957 × 103 V K−1, β = 1, and γ = 0 s2.
Combining eqn (3) and (6) with eqn (1) yields the following theoretical expression, termed the semi-empirical resolving power (RSE):
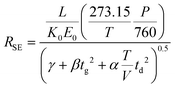 | (7) |
Once a semi-empirical linear regression analysis is conducted for a particular instrument platform, the correction terms can be included in eqn (7) to provide a theoretical means of predicting the resolving power for any analyte with a known gas-phase reduced mobility. The obvious caveat to this semi-empirical approach is that the solution to the correction terms in eqn (6) and (7) are instrument-specific and will not have predictive capabilities beyond that of the instrument configuration in which the initial evaluation data was obtained.
In this report, we investigate the extent of agreement between ion mobility resolving power theories and experimental results obtained on a commercially-available ion mobility-mass spectrometer (IM-MS). The IM-MS used in this work is a recently developed uniform field IMS coupled to a quadrupole time-of-flight MS.22 This instrument is based on the IM-MS designs by Smith and coworkers23–26 and incorporates a low-pressure (ca. 4 Torr) drift tube bracketed by electrodynamic ion funnels for efficient ion trap gating and transmission between spectrometer components. Because this instrument operates at uniform electric field and under conditions of constant temperature and pressure, it is expected that a semi-empirical treatment of resolving power theory should garner further insight into the separation performance of such instruments under constant conditions of controlled IMS parameters.
Experimental
Sample preparation
A commercially-available MS tuning solution consisting of a range of symmetrically-branched phosphazines (Agilent tuning mixture, ATM; Agilent Technologies, Santa Clara, CA) was used to generate the ion mobility data necessary for determining the semi-empirical terms. This ATM solution is predissolved in an acetonitrile/water solution (95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, % v
5, % v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) at a weight-to-volume (w/v) concentration of less than 0.01% for each constituent. The ATM solution was diluted by a factor of ten using a 59
v) at a weight-to-volume (w/v) concentration of less than 0.01% for each constituent. The ATM solution was diluted by a factor of ten using a 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v
1 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) acetonitrile
v) acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solution prior to use. For generalized comparisons, SDGRG peptide (Sigma-Aldrich), ten-carbon quaternary ammonium salt (TAA10, Sigma-Aldrich) and melittin peptide (Sigma-Aldrich) were obtained as dry powders and used at working concentrations of ca. 1 μg mL−1. SDGRG and melittin were reconstituted in a 1
water solution prior to use. For generalized comparisons, SDGRG peptide (Sigma-Aldrich), ten-carbon quaternary ammonium salt (TAA10, Sigma-Aldrich) and melittin peptide (Sigma-Aldrich) were obtained as dry powders and used at working concentrations of ca. 1 μg mL−1. SDGRG and melittin were reconstituted in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solution with ca. 1% trifluoroacetic acid to promote protonation. TAA10 was dissolved in a 1
water solution with ca. 1% trifluoroacetic acid to promote protonation. TAA10 was dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloroform solution.
chloroform solution.
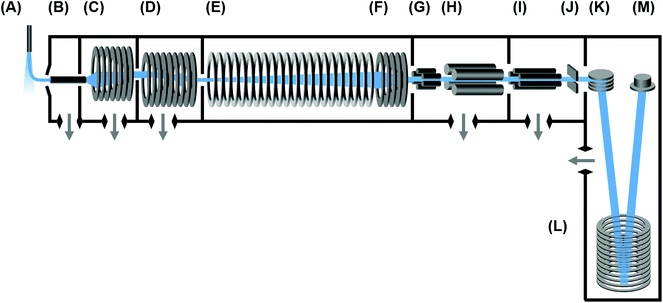
Uniform field IM-MS instrument
The instrumentation used in this study is a commercial IM-MS (6560 Ion Mobility-QTOF, Agilent) and has been described in detail previously.22 A conceptual schematic detailing the major components of the instrument is contained in Fig. 1. Briefly, ions are transferred to the ion mobility region through a heated capillary and a two-stage ion funnel. The first ion funnel stage operates at elevated pressures and serves to collect and focus ions exiting the capillary.24 The second ion funnel stage is configured as a dual-gate ion funnel trap,25 which operates in a trap-and-release scheme to introduce discretely-gated ion pulses into the IMS. An ion storage time of 2000 μs is used for these experiments. The ion release time (gate width) can be defined anywhere from 0 to upwards of several hundred ms, although for this study the gate widths were surveyed in the range of 100 to 500 μs. Following their release from the ion trap, ions are introduced directly into a uniform field drift tube operated at ambient temperature, which was slightly elevated for all days in which the data was obtained (305.4 ± 0.6 K). The drift tube is constructed from 0.6 mm thick guard rings of 5 cm inner diameter, has a length of 78.1 cm, and is capable of operating in a drift field range from 0.7 to 25 V cm−1 (E/N of 0.5 to 19.3 Td at 4 Torr). Nitrogen (UHP), helium (UHP), and carbon dioxide (Coleman Grade) maintained at ca. 4 Torr are used for ion mobility separations described in this work. All gases are passed through a gas purifier trap (nitrogen and helium; RMSN and RMSH, Agilent; for carbon dioxide, P600, VICI Metronics) and regulated into the IMS through a precision flow controller (640B 10 Torr range, MKS Instruments) monitoring the read-out from an absolute pressure capacitance gauge (CDG 500, Agilent) mounted directly on the drift tube chamber. In a single experiment, this flow controller setup is capable of maintaining a constant drift tube pressure to ±0.01 Torr, which enables high measurement reproducibility. To ensure purity, the IMS is operated at an elevated pressure with respect to the trapping ion funnel region. For nitrogen and carbon dioxide, this pressure difference is ca. 150 mTorr. For helium, it was found that a difference of ca. 230 mTorr or greater is necessary to ensure drift gas purity. Following IMS separation, radially-diffuse ions are recollected by a third ion funnel located at the exit end of the drift tube. This rear ion funnel is operated at the same pressure (4 Torr) as the drift tube with a DC field of ca. 18 V cm−1. Following the IMS, ions are transferred through a hexapole into the high vacuum Q-TOF stage of the instrument, where they are analyzed by their mass-to-charge. Optional mass selection and ion activation (collision-induced dissociation) can be conducted in this interfacing region between the IM and MS stages, though these schemes are not utilized in this present work. Although the time-of-flight mass spectrometer is capable of a resolving power greater than 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (m/Δm), for purposes of these experiments the instrument was operated with settings designed to improve sensitivity and mass transmission range (“extended dynamic range” mode), and this resulted in a mass resolving power of ca. 20
000 (m/Δm), for purposes of these experiments the instrument was operated with settings designed to improve sensitivity and mass transmission range (“extended dynamic range” mode), and this resulted in a mass resolving power of ca. 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
The ATM solution used to evaluate the semi-empirical fits was infused into one of two ion sources: a dual electrospray ionization source (dual “Jet Stream”, Agilent), or an orthogonally-configured nano-electrospray ionization source (G1992A Nanospray, Agilent). For the Jet Stream source, the ATM solution was infused from the “reference B” sample solution reservoir with the default injection backpressure. For nano-electrospray, the ATM solution was directly infused using a syringe pump (Cole-Parmer) at a flow rate of ca. 1 μL min−1.
Analytical precision
The instrumentation used in this work is considered a “high precision” ion mobility instrument in that it is capable of obtaining reproducible measurements of the mobility drift time to better than 0.1 ms. For conversion of drift time measurements to ion transport coefficients (K0 and collision cross section), this represents a relative error of better than 0.5%.22 Analytical precision affects the reproducibility of the ion mobility drift time, but does not directly affect the FWHM.Data acquisition and analysis
All ion mobility data was obtained using the MassHunter Data Acquisition software (Agilent). A software feature which allows individual experimental sequences to be defined was utilized to obtain consecutive ion mobility spectra at various drift potentials between 350 and 1750 V (4.5 to 22.4 V cm−1) in increments of 100 V. This corresponds to instrument settings from 600 V to 2000 V for the “drift tube entrance” potential and 250 V for the “drift tube exit” potential. For each sequence, data was signal averaged for 2 minutes. These drift voltage sequence experiments were acquired for initial ion gate widths ranging from 100 to 500 μs in 100 μs increments, which corresponds to the ion release time setting in the instrument control software. Following acquisition, each segmented data file was analysed using the MassHunter IMS Browser software (Agilent). Peaks of interest were isolated and their centroid drift time values and FWHM were extracted as tabulated data using capabilities within the software. In some cases, the FWHM was determined manually. K0 values necessary to conduct the resolving power analysis were obtained directly from the software, using procedures previously described.22 Briefly, this involves conducting drift time measurements for a sequence of fields in order to determine the time component associated with ion transit outside of the mobility region. K0 can then be solved viaeqn (3).Semi-empirical fitting procedure
The semi-empirical coefficients (α, β, and γ) for eqn (6) and (7) were determined for each ion system using procedures outlined by Siems et al.12 Details of the procedure as utilized in this study are included in the ESI.† Briefly, this involves a linear regression analysis of eqn (6). The α coefficient is the slope of the best-fit line to data projected as Ttd2/V (the diffusion parameter) versus Δt2 for a series of ions. The β coefficient is determined from a slope of the best-fit line to data plotted as tg2versus Δt2. The γ coefficient is obtained through orthogonal correlation of results from the linear regression analysis of α and β. Plots corresponding to this analysis are contained in Fig. S5 and S7.† A strong correlation was observed between the ion species and the β and γ coefficients, so these terms were replaced with an equation which includes K0 (Fig. S8†). These coefficients and coefficient equations are summarized at the bottom of Table 1.| Ion | K 0 (cm2 V−1 s−1) | α × 103 (V K−1) | β | γ (ms2) |
|---|---|---|---|---|
| a K 0 is calculated in nitrogen from 4 replicate measurements; variable gate width data for the β coefficient experiments was limited to m/z 322, 622, and 922. | ||||
| m/z 322 | 1.39 | 0.87 | 0.536 | 0.07 |
| m/z 622 | 1.01 | 0.84 | 0.298 | 0.06 |
| m/z 922 | 0.83 | 0.93 | 0.181 | 0.07 |
| m/z 1222 | 0.72 | 0.96 | — | 0.07 |
| m/z 1522 | 0.64 | 0.96 | — | 0.15 |
| m/z 1822 | 0.58 | 0.89 | — | 0.24 |
| m/z 2122 | 0.53 | 0.87 | — | 0.30 |
| m/z 2422 | 0.49 | 0.97 | — | 0.25 |
| m/z 2722 | 0.46 | 0.87 | — | 0.48 |
| α = 0.91 × 103 | ||||
| β = 0.3145 (K0)2 − 0.035 (K0) | ||||
| γ = 0.0434 (K0)(−2.811) | ||||
Results and discussion
Factors affecting semi-empirical coefficients
Because each of the semi-empirical coefficients are associated with a specific component of variance from eqn (6), their deviation from the “ideal” values (eqn (4)) can provide some insight into the physical source of band broadening within the instrument. For the α coefficient, previous work has demonstrated this value is consistently larger in stand-alone drift tube instruments than the ideal value of 0.957 × 10−3 V K−1, with experimental α values of ca. 1.2 × 10−3 V K−1 or greater.12 This observation has been previously attributed to inhomogeneity in the electric field. In this work, we obtain an average α value of 0.910 × 10−3 V K−1 (Table 1), which does not depend strongly on the ion species (Fig. S3†). The α value found in this study is close to the ideal value. A cursory explanation would be that the drift tube in this work operates with a high degree of homogeneity, yet ions also pass through an electrodynamic ion funnel prior to being measured (Fig. 1F). Because α is essentially the magnitude of the response of the peak width to the drift time, we can only say that for the current instrumentation, peaks broaden as expected from diffusion. This may be a general characteristic of drift tubes coupled to MS via a conductance-limiting aperture, as the previous work had been carried out on ambient pressure instrumentation using relatively large diameter Faraday plate detectors which would sample the entire radially-diffuse ion cloud. The explanation of β and γ is not so straightforward. Previous work had characterized these coefficients using measurements obtained from a single ion (Cl−, H3O+, or O2−), and thus the β and γ values were previously reported as a single value for each instrument geometry evaluated. In this present study, we evaluated these semi-empirical terms using a series of analytes possessing a wide range of mobility values. Thus, our results for β and γ are different for each ion investigated (Table 1). For β, we obtain a range of values from 0.181 to 0.536, which is significantly smaller than the ideal situation of β = 1. In the previous study by Siems et al., β was consistently greater than 1 (ca. 1.1 to 1.6). Since β is a multiplier for the gate width, this coefficient represents a correction for peak width variations which are caused during the ion gating event. Values greater than 1 were explained as originating from additional band broadening due to space-charge effects (Coulombic repulsion), which would become greater as the pulse width was increased, i.e., as more ions were introduced per pulse. In contrast, all of the β values measured in this work were well below 1, suggesting that the resulting ion pulse widths are narrower than would be expected from the time duration that the ions are admitted into the drift tube via the control software (i.e., the applied temporal gate width). We infer that this is a consequence of conducting the ion gating using an ion trap, rather than a more traditional electrostatic ion depletion gate (Tyndall or Bradbury-Nielsen gate). A similar ion compression effect has been observed when operating the ion gate region using multiple grid stages,27,28 and we suggest a field-focusing behaviour may also be occurring in the present instrumentation which utilizes a similar 2-grid structure in the region of ion confinement.25 We note that unlike what is observed for most ambient pressure IMS instruments, this instrument operates closer to the diffusion limit in terms of resolving power. For γ, the ideal value is 0 s2, that is, no additional sources of variance other than the initial gate width and normal diffusion.16 For previous drift tubes, the value for γ was found to vary anywhere from 0.47 × 10−8 s2 to as high as 2.1 × 10−8 s2,12 which corresponds to an added variance of between ca. 0.07 to 0.14 ms. In this work, the value of γ determined for the present instrumentation was found to be ion dependent, with upper values of 4.8 × 10−7 s2 (Table 1), which corresponds to a variance of ca. 0.69 ms. This value of γ is about 5-fold greater than what was determined in the previous study, where the source of band broadening was attributed to image current induction and detector response effects for the Faraday detector used. For the present IM-MS instrument, the IMS spectra are obtained through temporal correlation of ion signal from the electron multiplier in the MS stage. Microchannel plate electron multipliers exhibit peak broadening effects on the order of picoseconds,29 and so detector effects would not be an issue in this current work. We suggest that the primary source for γ is due to ion transit through the rear ion funnel, which is not accounted for in the length term used to determine the theoretical drift time from eqn (3). This claim is supported by the observation that γ is mobility-dependent (Table 1). The relatively large values for γ suggest that there is a significant contribution to band-broadening occurring in the rear funnel, yet the measured resolving power values and the analysis of the α coefficient both suggest that the instrument is operating near the diffusion limit. One explanation for this is that the band broadening which occurs in the rear funnel is counteracted by the additional mobility separation which occurs due the rear funnel operating as an extension of the drift tube. The additional contribution of the rear ion funnel as a mobility separator which operates with no significant loss in resolving power has been noted in a previous study.23 While the data in this current work also suggests that the funnel operates as an extension of the drift tube, no attempt was made to match the field between the drift tube and the rear funnel, which would be expected to further improve the quantitative agreement between experiment and theory.Finally, it is worth noting that drift time correction is not utilized in this study due to the difficulty in determining the peak width contribution of the non-mobility transit time of the ions. While not investigated further here, the temporal contribution of the rear ion funnel is well characterized and could be incorporated into the ion mobility peak width theory in the form of an added source of variance, as the ion funnel length (11.6 cm), pressure (4 Torr), and electric field (17.8 V cm−1) used in this present study are known.
Empirical correlation of theoretical resolving power
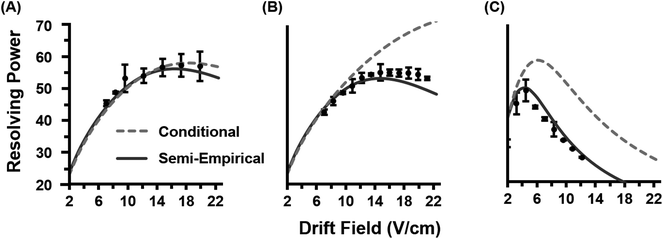
Once the semi-empirical coefficients are determined for a wide range of gate widths and ion systems, eqn (7) can be expanded in order to generate a generalized resolving power expression which describes the performance of the current instrumentation. These results are provided as eqn (S10) in the ESI.† An evaluation of both the conditional and semi-empirical theories is contained in Fig. 2 for the m/z 322, 622, and 922 ions. Experimental data is projected as points with error bars obtained from 4 replicate measurements. Of general note is that in many cases, the error associated with the measured resolving power for a single data point is in excess of 5%. This reflects the challenges associated with obtaining quantitatively-reproducible measurements of the peak width, as opposed to the drift time which exhibits close correlation to eqn (3) (Fig. S1†). In Fig. 2A, the conditional resolving power theory viaeqn (5) exhibits only qualitative agreement with experimental results, with significant deviation being observed at low and high gate widths. Conditional resolving power consistently predicts significantly better resolving power when using lower gate widths, but the data suggests that this is only significant when studying low-mass ions (i.e., ions possessing high K0 values above ca. 1 cm2 V−1 s−1). Experimental results indicate that higher mass ions do not benefit significantly in resolving power from smaller gate widths, and so for such studies, increasing the gate width would be advantageous to improve instrument sensitivity. This gate width dependence on the accuracy of eqn (5) is consistent with previous observations,13 and deviation has also been noted in experimental measurements at extreme pressures (up to 2280 Torr).30 Note that a gate width of 200 μs is commonly utilized in IMS studies, and under this condition, there is a coincidentally good correlation between conditional resolving power theory and experimental results (Fig. S2†), which suggests that deviations between theory and experiment are not obvious under routine investigations. To our knowledge this work represents the first study where the conditional resolving power was explicitly tested for ions spanning a wide range of reduced mobilities (Table 1), and in particular, for larger ions with K0 values below ca. 1 cm2 V−1 s−1 as what would be encountered for biomolecules. This work also represents the first comprehensive study of resolving power theory for reduced pressure IMS. Because the present instrumentation is configured in a manner that is far from the conditions assumed by conditional resolving power (i.e., ion trap gating, sub-ambient IMS pressures, and post-mobility focusing via the ion funnel), the observed deviations between conditional resolving power theory and empirical results is not surprising, particularly for larger ions which spend more time in the IMS stage of the instrument. Fig. 2B contains the results from the semi-empirical resolving power theory viaeqn (7) utilizing the methods described in the ESI.† A significant improvement in the correlation between experiment and theory is observed in this case across all initial ion gate widths investigated (100 to 500 μs, cf. Fig. S3†). Some deviation does occur for the lower mobility ion, m/z 922, where the semi-empirical treatment under-predicts the resolving power by about 15% on the high end, which is a fairly consistent deviation across all gate widths at this mobility (Fig. S3†). Similar results are also observed for the m/z 2722 ion (Fig. S4†). The m/z 922 ion was explicitly used in the initial evaluation of the semi-empirical theory, and so better correlation was anticipated, but this would appear to be a more realistic expectation of accuracy when working with a theory generalized against a wide range of parameters.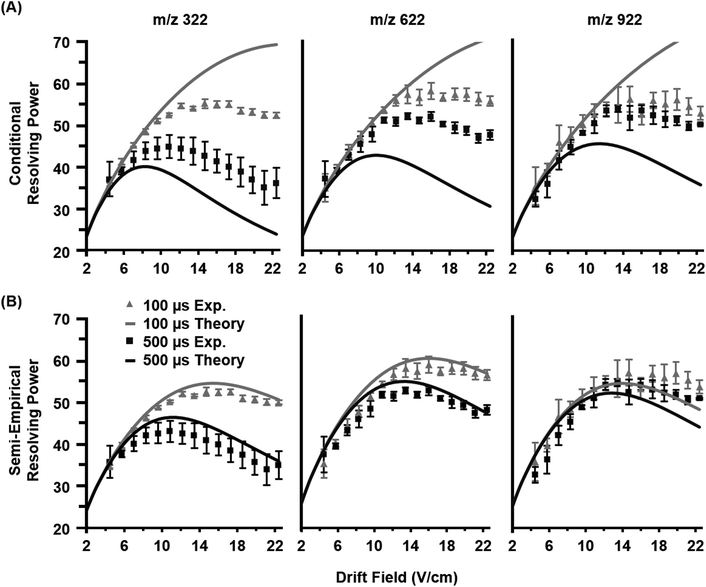 | ||
| Fig. 2 Empirical resolving power curves (data points) compared to theory (solid lines) as a function of the ion mobility separation field (drift field) for three molecular ions (nominal m/z 322, 622, and 922). Error bars for each point are obtained from four replicate measurements. (A) The conditional resolving power (Rc) from eqn (5) predicts the qualitative trends of the experimental observations, but quantitative correlation varies based on the ion system and gate width used. (B) The semi-empirical resolving power (RSE) from eqn (7) exhibits a more quantitative correlation than the conditional resolving power for all gate widths investigated in this study (100, 200, 300, 400, and 500 μs). For clarity, only the data for 100 and 500 μs gate widths are shown. | ||
Because both the conditional and semi-empirical resolving power expressions account for the ion's reduced mobility, a 3-dimensional resolving power curve can be obtained which is ion species dependent. Fig. 3 contains the resulting 3D analysis for both the conditional resolving power of eqn (5) (Fig. 3A), and the semi-empirical resolving power of eqn (7) (Fig. 3B). Both curves were generated using a drift gas pressure of 4.00 Torr and a temperature of 304.2 K and describe the performance of singly-charged ions only. A gate width of 200 μs was also chosen for comparison between the two theories, as the best correlation between conditional resolving power and experimental data was observed at this setting, meaning any differences observed between the two theories at this gate width is expected to be significant. Conditional resolving power predicts that higher resolving powers are accessible as the mobility of the ion decreases (i.e., large ions), and that accessing these higher resolving powers requires different drift fields.18 This observation suggests that conditional resolving power theory underestimates diffusional effects that increase with lower mobilities, which is accounted for in the semi-empirical treatment. Additionally, the semi-empirical treatment pertaining to observations from the current instrument indicates that the resolving power performance is relatively linear across a range of ion mobilities. This observation is better illustrated by extracting the resolving power maxima (highest values) for both 3D surfaces and plotting these as a function of K0 (Fig. 4A). This analysis indicates there is good correlation between conditional and semi-empirical resolving power theory at high mobilities (fast ions) where ions spend a limited amount of time in the mobility region, but deviation becomes significant in the low mobility (slow ions) regime. This deviation between the two theories occurs at a K0 of ca. 1 cm2 V−1 s−1, which for a peptide drifting in nitrogen represents an analyte mass of ca. 500 Da.22 Additional molecular-class specific mobility ranges for nitrogen drift gas are projected at the bottom of the plot to help frame these observations in the context of practical results. The implication of this observation is that for the current instrumentation, the accuracy of predictions made by the conditional resolving power theory are limited to small analyte systems (i.e., ions with high K0 values). A second observation which can be made from Fig. 3 is that the highest resolving power values predicted by the semi-empirical theory are fairly constant and experimentally-accessible across a relatively narrow range of drift fields (between 14 and 17 V cm−1). This can be better illustrated by plotting the drift field corresponding to the highest resolving power values as a function of the ion's reduced mobility (Fig. 4B). Thus, in practice, accessing high resolving power values should require only minor adjustments to the drift field. Taken collectively, these observations suggest that the present instrumentation performs at optimal resolving power for a wide dynamic range of ion species under similar operational conditions. This may be a general observation for all ion mobility instrumentation, as quantitative investigations of the conditional resolving power to date have focused only on small analytes with reduced mobility values greater than 1.2 cm2 V−1 s−1,13,18,31,32 although this study also represents the first test of conditional resolving power theory for reduced pressure IMS, so these results may also be specific to sub-ambient pressure operation around 4 Torr.
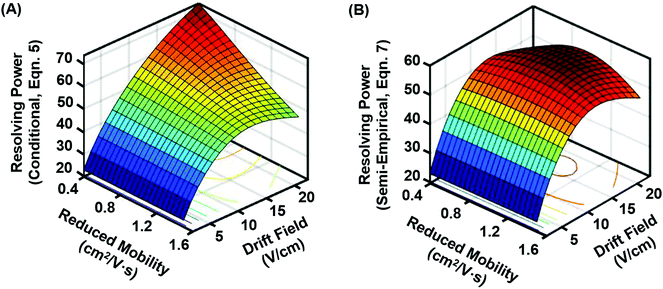 | ||
| Fig. 3 3D resolving power curves projecting the predicted resolving power for singly-charged ions across a range of drift fields and ion mobilities. (A) Conditional resolving power (eqn 5), and (B) semi-empirical resolving power viaeqn (7) using coefficient expressions obtained in this current work. Both expressions assume 4 Torr drift gas pressure with an initial gate width of 200 μs. As compared with the conditional resolving power, the semi-empirical resolving power predicts a relatively narrow drift field range for accessing the optimal resolving power, as well as a more uniform resolving power response for a wide range of ion species. | ||
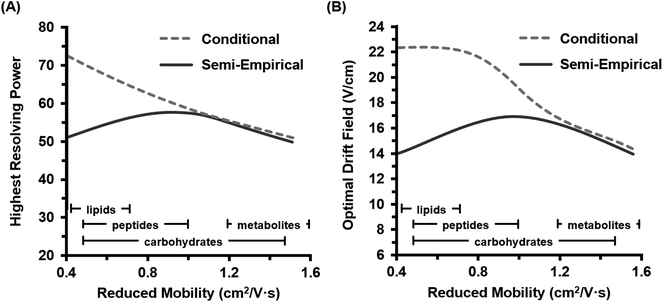 | ||
| Fig. 4 Plots of the highest achievable resolving power values predicted by both theories for singly-charged ions. Trends are extracted from the maxima in Fig. 3 (i.e., the “crest” of each surface plot). (A) The highest (optimal) resolving power accessible as a function of the reduced mobility. Corresponding molecular class-specific mobility ranges are also provided for ion mobility in nitrogen drift gas (lower bars). (B) The required drift field necessary to access the optimal resolving power as a function of the reduced mobility. Both projections indicate that the semi-empirical resolving power theory predicts a narrow range of both optimal resolving powers (50 to 60) and drift fields (14 to 17 V cm−1) across a fairly wide range of mobilities. | ||
Broad-scale validity of semi-empirical results
In order to further investigate the extent of correlation between experiment and theory, three ions systems exhibiting vastly different gas-phase transport properties were compared against the current theories. The ion systems used in this comparison are: (1) a small peptide in nitrogen with a K0 close to 1 (SDGRG, K0 = 1.02 cm2 V−1 s−1),22 (2) a quaternary ammonium cation in carbon dioxide, which exhibits very low mobility (TAA10, K0 = 0.50 cm2 V−1 s−1), and (3) a triply-charged peptide (melittin bee venom) in helium,33 which has a very high gas-phase mobility (K0 = 3.03 cm2 V−1 s−1). Typical operational conditions (200 μs gate width and 4 Torr drift gas) are used in these comparisons. Note that both theories are drift gas independent, since both theoretical expressions describe ion transport in terms of the gas-phase reduced mobility, which inherently accounts for differences in ion motion in various drift gases. Thus, the theories developed in this work are applicable to a variety of drift gases. Experimental results for the three ion systems are contained in Fig. 5. For ions with reduced mobility values around ca. 1 cm2 V−1 s−1, both theories correlate well with experimental results (Fig. 5A). This is consistent with the previous observation for m/z 622 (K0 = 1.01 cm2 V−1 s−1) at this gate width (Fig. S2 and S3†). At low mobilities, which represents large ions or ions drifting in more massive drift gases (such as carbon dioxide in this case), conditional resolving power theory significantly overestimates the magnitude of the resolving power, whereas the semi-empirical theory correlates closely to experimental results, albeit with slightly underestimated predictions (Fig. 5B). This is similar to the trends observed for the m/z 922 system (Fig. 2C, S2 and S3†). In the third case for very high mobility ions, both theories show qualitative agreement, with semi-empirical theory correlating better than conditional resolving power (Fig. 5B). Note that in this latter system, a multiply-charged ion is evaluated (z = 3), and thus requires that the integer charge state be introduced into the denominator of the diffusion term in the semi-empirical theory. Extension of the semi-empirical theory to higher charge-state systems was not an original intention of this work, but results are indeed favorable. We caution here, however, that preliminary work with a protein exhibiting even higher charge states (myoglobin, z = 9 to 24) has not resulted in the good correlation to semi-empirical theory as seen for the melittin system, so further refinement to the theory is necessary. While the systems in Fig. 5 represent extreme cases in terms of the reduced mobility, the good correlation observed indicates that the semi-empirical theory can be qualitatively extended beyond the range in which it was initially evaluated (cf., Table 1).Conclusions
A wide-scale evaluation of two current theories for ion mobility resolving power (conditional and semi-empirical) was applied to high precision results obtained on a recently developed IM-MS instrument. The predictive capabilities of conditional resolving power theory were found to be qualitatively good for high mobility ions (e.g., small molecules), but deviated significantly for low mobility ion systems and gate widths beyond 200 μs. Better correlation to experimental observations was found for a semi-empirical treatment of resolving power which was developed using empirical data on the current instrumentation, and initial evaluation of the semi-empirical theory demonstrated good correlation across a relatively wide range of ion mobilities (K0 between 0.50 and 3.03 cm2 V−1 s−1). The semi-empirical theory was used to generalize the performance of the current instrument and results suggest that the instrumentation is capable of accessing the optimal resolving power for a wide range of analytes within a relatively narrow range of drift fields, independent of the drift gas utilized. When taken collectively, these observations indicate that the linear response of the instrument in terms of ion mobility separation efficiency is high. The decreased dependency of the gate width on the accessible resolving power for lower mobility ions (K0 below ca. 1 cm2 V−1 s−1) indicates that for higher mass studies (greater than m/z of ca. 500), the gate width may be increased to improve sensitivity without a significant loss in resolving power. As with any semi-empirical treatment, the results are specific to the instrumentation and experimental conditions used in this study, namely operating the drift tube at ca. 4 Torr and ambient temperature, and investigating low charge-state ions. Conditional resolving power is thus recommended over the current semi-empirical theory for estimating the accessible resolving power for ion mobility instrumentation that differs significantly from the present study, such as ambient pressure drift tubes and stand-alone IMS instruments. Finally, it should be noted that obtaining quantitatively reproducible resolving power values on any drift tube platform is challenging without careful attention to maintaining drift gas purity and stability of all important ion mobility conditions, specifically drift fields, gas pressures, temperatures, and robust methods to extract the quantitative data (drift time centroids and temporal peak widths) from the raw measurements. The high precision capabilities of the present instrumentation greatly facilitates these types of quantitative studies.Acknowledgements
J.C.M, J.N.D, and J.A.M. thank M. Ray Keller for assistance in data analysis and Katrina L. Leaptrot for reviewing various drafts of the manuscript. Vanderbilt authors gratefully acknowledge a Thought Leader award from Agilent Technologies. Financial support for this research was provided by Agilent Technologies, the National Institutes of Health National Center for Advancing Translational Sciences (NIH-NCATS Grant 4UH3TR000491-3), the National Science Foundation (MRI CHE-1229341), the Vanderbilt Institute of Chemical Biology, the Vanderbilt Institute for Integrative Biosystems Research and Education, and Vanderbilt University.Notes and references
- H. Israel and L. Schulz, Terr. Magn. Atmos. Electr., 1933, 38, 285–300 CrossRef.
- N. E. Bradbury, Phys. Rev., 1932, 40, 508–523 CrossRef CAS.
- M. J. Cohen and F. W. Karasek, J. Chromatogr. Sci., 1970, 8, 330–337 CrossRef CAS.
- S. P. Cram and S. N. Chesler, J. Chromatogr. Sci., 1973, 11, 391–401 CrossRef CAS.
- F. W. Karasek, Anal. Chem., 1974, 46, 710A–720A CrossRef CAS.
- G. E. Spangler and C. I. Collins, Anal. Chem., 1975, 47, 403–407 CrossRef CAS.
- H. E. Revercomb and E. A. Mason, Anal. Chem., 1975, 47, 970–983 CrossRef CAS.
- F. W. Karasek, Study of Technology Relating to Plasma Chromatography Sensing Tubes, Final Report, Contract #8SU77-00227, University of Waterloo Research Institute, Waterloo, Ontario, Canada, 1980 Search PubMed.
- J. P. Carrico, D. W. Sickenberger, G. E. Spangler and K. N. Vora, J. Phys. E: Sci. Instrum., 1983, 16, 1058–1062 CrossRef CAS.
- S. Rokushika, H. Hatano, M. A. Baim and H. H. Hill, Anal. Chem., 1985, 57, 1902–1907 CrossRef CAS.
- P. Watts and A. Wilders, Int. J. Mass Spectrom. Ion Processes, 1992, 112, 179–190 CrossRef CAS.
- W. F. Siems, C. Wu, E. E. Tarver, H. H. Hill, P. R. Larsen and D. G. McMinn, Anal. Chem., 1994, 66, 4195–4201 CrossRef CAS.
- A. B. Kanu, M. M. Gribb and H. H. Hill, Anal. Chem., 2008, 80, 6610–6619 CrossRef CAS PubMed.
- J. C. May and J. A. McLean, Anal. Chem., 2015, 87, 1422–1436 CrossRef CAS PubMed.
- E. A. Mason and E. W. McDaniel, Transport Properties of Ions in Gasses, 1988 Search PubMed.
- G. E. Spangler, Int. J. Mass Spectrom., 2002, 220, 399–418 CrossRef CAS.
- M. L. Glasser, J. Appl. Phys., 1988, 63, 4823–4831 CrossRef.
- E. J. Davis, M. D. Williams, W. F. Siems and H. H. Hill, Anal. Chem., 2011, 83, 1260–1267 CrossRef CAS PubMed.
- G. F. Verbeck, B. T. Ruotolo, K. J. Gillig and D. H. Russell, J. Am. Soc. Mass Spectrom., 2004, 15, 1320–1324 CrossRef CAS PubMed.
- A. V. Mariano, W. Su and S. K. Guharay, Anal. Chem., 2009, 81, 3385–3391 CrossRef CAS PubMed.
- A. V. Tolmachev, B. H. Clowers, M. E. Belov and R. D. Smith, Anal. Chem., 2009, 81, 4778–4787 CrossRef CAS PubMed.
- J. C. May, C. R. Goodwin, N. M. Lareau, K. L. Leaptrot, C. B. Morris, R. T. Kurulugama, A. Mordehai, C. Klein, W. Barry, E. Darland, G. Overney, K. Imatani, G. C. Stafford, J. C. Fjeldsted and J. A. McLean, Anal. Chem., 2014, 86, 2107–2116 CrossRef CAS PubMed.
- K. Tang, A. A. Shvartsburg, H.-N. Lee, D. C. Prior, M. A. Buschbach, F. Li, A. V. Tolmachev, G. A. Anderson and R. D. Smith, Anal. Chem., 2005, 77, 3330–3339 CrossRef CAS PubMed.
- E. S. Baker, B. H. Clowers, F. Li, K. Tang, A. V. Tolmachev, D. C. Prior, M. E. Belov and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1176–1187 CrossRef CAS PubMed.
- B. H. Clowers, Y. Ibrahim, D. C. Prior, W. F. Danielson, M. Belov and R. D. Smith, Anal. Chem., 2008, 80, 612–623 CrossRef CAS PubMed.
- Y. M. Ibrahim, E. S. Baker, W. F. Danielson, R. V. Norheim, D. C. Prior, G. A. Anderson, M. E. Belov and R. D. Smith, Int. J. Mass Spectrom., 2014, 377, 655–662 CrossRef PubMed.
- Y. Du, W. Wang and H. Li, Anal. Chem., 2012, 84, 5700–5707 CrossRef CAS PubMed.
- Y. Du, W. Wang and H. Li, Anal. Chem., 2012, 84, 1725–1731 CrossRef CAS PubMed.
- J. L. Wiza, Nucl. Instrum. Methods, 1979, 162, 587–601 CrossRef CAS.
- E. J. Davis, P. Dwivedi, T. Maggie, W. F. Siems and H. H. Hill, Anal. Chem., 2009, 81, 3270–3275 CrossRef CAS PubMed.
- K. Kaplan, S. Graf, C. Tanner, M. Gonin, K. Fuhrer, R. Knochenmuss, P. Dwivedi and H. H. Hill, Anal. Chem., 2010, 82, 9336–9343 CrossRef CAS PubMed.
- K. M. Roscioli, E. Davis, W. F. Siems, A. Mariano, W. S. Su, S. K. Guharay and H. H. Hill, Anal. Chem., 2011, 83, 5965–5971 CrossRef CAS PubMed.
- J. C. May and J. A. McLean, Proteomics, 2015, article in press, DOI:10.1002/pmic.201400551.
Footnote |
| † Electronic supplementary information (ESI) available: Correlation plots of theoretical drift time, conditional, and semi-empirical resolving power theory to experimental data for all gate widths; details of semi-empirical fitting procedure; and resulting semi-empirical resolving power expression. See DOI: 10.1039/c5an00923e |
| This journal is © The Royal Society of Chemistry 2015 |