Label-free free-solution nanoaperture optical tweezers for single molecule protein studies
Ahmed A.
Al Balushi
,
Abhay
Kotnala
,
Skyler
Wheaton
,
Ryan M.
Gelfand
,
Yashaswini
Rajashekara
and
Reuven
Gordon
*
Department of Electrical and Computer Engineering, University of Victoria, Victoria, BC, Canada V8P5C2. E-mail: rgordon@uvic.ca
First published on 20th February 2015
Abstract
Nanoaperture optical tweezers are emerging as useful label-free, free-solution tools for the detection and identification of biological molecules and their interactions at the single molecule level. Nanoaperture optical tweezers provide a low-cost, scalable, straight-forward, high-speed and highly sensitive (SNR ∼ 33) platform to observe real-time dynamics and to quantify binding kinetics of protein–small molecule interactions without the need to use tethers or labeling. Such nanoaperture-based optical tweezers, which are 1000 times more efficient than conventional optical tweezers, have been used to trap and isolate single DNA molecules and to study proteins like p53, which has been claimed to be in mutant form for 75% of human cancers. More recently, nanoaperture optical tweezers have been used to probe the low-frequency (in the single digit wavenumber range) Raman active modes of single nanoparticles and proteins. Here we review recent developments in the field of nanoaperture optical tweezers and how they have been applied to protein–antibody interactions, protein–small molecule interactions including single molecule binding kinetics, and protein–DNA interactions. In addition, recent works on the integration of nanoaperture optical tweezers at the tip of optical fiber and in microfluidic environments are presented.
Introduction
Since the first demonstration of single beam optical trap,1 optical tweezers have been used to isolate and manipulate dielectric particles,2,3 carbon nanotubes,4–8 graphene flakes,9,10 nanodiamonds,11 semiconductor nanowires12–19 and metal nanoparticles.20–30 This has opened up new possibilities for studying nanometer-size biological particles and their interactions; for example, studying interactions including those of protein–protein, protein–small molecule, protein–DNA and protein–antibody.In order to achieve stable trapping of a single nanometer-sized molecule using conventional optical tweezers, two challenges have to be overcome. First, for trapping particles much smaller than the wavelength of light, the optical power required typically scales with the inverse third power of the particle size. Second, as the particle size decreases the viscous drag is decreased, making escape from the trap faster. Therefore, for trapping smaller particles high laser powers are needed – an option which is not always available, especially when working with temperature-sensitive biological molecules. One approach for trapping small biological particles with moderate laser powers is to use nanoapertures in metal films. Nanoaperture-based optical tweezers have emerged as a useful tool for single molecule studies.
In this paper, we review nanoaperture-based optical trapping schemes and discuss their unique features. We highlight the recent developments of aperture-based optical trapping for single protein studies and their interaction with small molecules and with DNA. We show how the high sensitivity of nanoaperture optical tweezers has enabled them to observe real-time binding dynamics and to quantify binding kinetics of protein–small molecule interactions by simply measuring the optical transmission of the same trapping laser beam through the aperture. We show how these nanoaperture traps can be used to probe the low-frequency Raman active modes of nanoparticles, including proteins and DNA molecules. Furthermore, we present some of the recent efforts towards integrating nanoaperture optical tweezers with microfluidic environment and at the tip of an optical fiber.
Nanopores and trapping
Conventional single beam optical traps are mathematically described using the perturbative gradient force formulation when trapping particles in the Rayleigh regime (diameter d ≪ wavelength λ).1 In this regime, two types of optical forces can be considered: the scattering force and the gradient force. The scattering force is the force exerted on an object in the propagation direction of the laser beam and can be expressed as1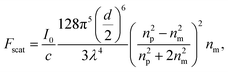 | (1) |
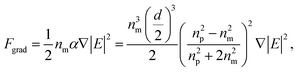 | (2) |
In order to overcome the limitations of conventional optical tweezers, a number of nanophotonic and plasmonic optical trapping techniques have been suggested,35–43 but these are usually perturbative and require high field intensities or highly polarizable particles to achieve stable trapping of particles less than 100 nm in size. Trapping using nanoapertures in metal films, when suitably configured, can be used to overcome the problem of required high beam intensities for <100 nm particles and they also allow for easy detection of trapping events by noting the abrupt increase in the transmission. Bethe's theory approximates the light transmission through a circular aperture (r ≪ λ) in an infinite perfect electric conductor (PEC) by the emission of a magnetic dipole, which can be expressed as
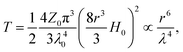 | (3) |
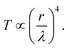 Simplistically, if a dielectric object with a refractive index np surrounds the aperture then the wavelength in the medium is scaled as
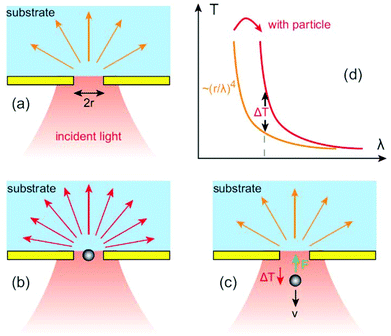
Simplistically, if a dielectric object with a refractive index np surrounds the aperture then the wavelength in the medium is scaled as 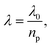 hence an increase in the transmission by a factor of np4 is obtained for the same aperture, as shown in Fig. 1b. The reference to Bethe's theory here is only an approximation, since that model considered infinitesimally thin films in perfect electric conductors. Here we consider films of finite thickness in real conductors that can have plasmonic effects. Nevertheless, it has been demonstrated that the transmission through the aperture in finite films drops off past the cut-off wavelength in a way that resembles the scaling of Bethe's theory.44
hence an increase in the transmission by a factor of np4 is obtained for the same aperture, as shown in Fig. 1b. The reference to Bethe's theory here is only an approximation, since that model considered infinitesimally thin films in perfect electric conductors. Here we consider films of finite thickness in real conductors that can have plasmonic effects. Nevertheless, it has been demonstrated that the transmission through the aperture in finite films drops off past the cut-off wavelength in a way that resembles the scaling of Bethe's theory.44
 | ||
| Fig. 1 Optical transmission through a single subwavelength circular aperture: (a) without dielectric particle. (b) Transmission is enhanced with a dielectric particle in the circular aperture. (c) Transmission is decreased by ΔT as the particle tries to escape from the aperture and as a result the total photon momentum traveling through the aperture decreases. This induces a force F in the opposite direction pulling the particle back to the hole. (d) The presence of the dielectric particle makes the aperture optically larger, red-shifting the transmission hence giving an increase in the transmission by ΔT. Reprinted from ref. 45, Copyright 2012, Y. Pang. | ||
This shows that nanoapertures in metal films can overcome the weak perturbative scattering by having the dielectric particle strongly influence the surrounding electromagnetic environment and consequently inducing an increase in the transmission; thereby allowing to work beyond the usual perturbative regime.
In addition to the scattering and gradient forces acting upon particles in the Raleigh regime, a number of studies have reported on the effect of thermally induced forces, on the trapped particle.46–51 Temperature increases of hundreds of Kelvin where reported when trapping gold nanoparticles near lipid vesicles exhibiting temperature-sensitive permeability.52 Such high increases in local heat intensities are generally undesirable especially when trapping dielectric particles as this might have some damaging effects.1 In addition, recent works on protein studies, like resonance-based plasmonic trapping53–55 and photonic crystal trapping56,57 systems are prone to heating issues and it might be needed to address them by applying a number of thermal management strategies; for example, by using adjacent metal films as a natural heat sink in nanopillar plasmonic trapping.58,59 Nanoaperture-based trapping, on the other hand, has the advantage of good thermal conductivity of the metal film which reduces significantly the heating effect. The temperature rise at the trapping site is expected to be on the order of 0.1 Kelvin.59 Indeed, nanoapertures in metal films have shown three orders of magnitude lower heating than in resonant nanorod antennas.60
Self-induced back action optical trapping
As predicted by Bethe's aperture theory, a small change in the electromagnetic environment surrounding a subwavelength aperture in a metal film, such as by the presence of a dielectric object with a refractive index higher than that of the surrounding medium, causes an increase in the transmission through it. Therefore, if the trapped particle tries to escape from the aperture transmission decreases, with a corresponding drop in the total photon momentum traveling through the aperture. Therefore, a restoring force in the opposite direction, according to Newton's Third Law, will act upon the particle to balance the momentum rate change; hence pulling it back to the equilibrium position towards the opening of the aperture, as shown in Fig. 1c. This so-called self-induced back-action (SIBA) trapping approach offers superior trapping ability at lower powers for Rayleigh particles and provide an automatic feedback control without the need for any external monitoring mechanisms.61–63Another way to view this effect is to consider the energy of the particle, which scales as E · p where p is the electric dipole moment of the particle, which is given by αE in the dipole approximation. With the particle in the aperture, not only is the energy increased, but also the E field is increased because of more light being transmitted through the aperture, so this further increases the trapping potential. Trapping using the SIBA effect with a simple circular aperture was used to achieve stable trapping of 50 nm polystyrene with only 1 mW of laser power64 opening the doors to trap <100 nm particles with low powers.
Unlike other trapping schemes that require advanced scattering schemes33,65,66 or fluorescence monitoring,40 the high sensitivity of the SIBA trapping approach allows for trapping detection by simply measuring the transmission through the aperture. Although the SIBA approach was first demonstrated with subwavelength circular apertures in metal films, the concept has been applied to a number of other aperture geometries as will be discussed in detail below. In addition, the generality of the SIBA approach can be optimized to accelerate efforts in the fields of nano-optics and metamaterials towards sensing applications.67–71
Although the perturbative optical force formulation (eqn (2)) gives a good approximation of the forces acting upon a particle in a homogeneous electromagnetic environment,3,72 it does not account for the strong change to the ambient electromagnetic environment caused by the trapped dielectric particle – as in the case for SIBA trapping. Therefore, working beyond the perturbative gradient force approximation necessitates the use of the comprehensive Maxwell stress tensor (MST) analysis. The force acting on a dielectric particle in this case is given by73
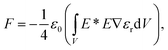 | (4) |
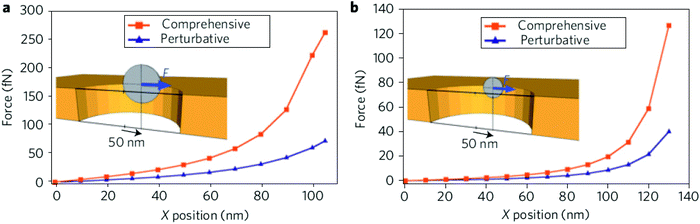 | ||
| Fig. 2 Numerical evaluation of optical forces acting upon a 50 nm (a) and 100 nm (b) polystyrene particles in a subwavelength nanohole optical trap using the rigorous MST analysis and the perturbative gradient force method. Reprinted from ref. 64, Copyright 2009, Nature Publishing Group. | ||
Extending optical trapping towards the nanometer regime with moderate optical powers requires a situation where the trapped particle plays an active role in the trapping mechanism. SIBA trapping exploits this concept whereby the target particle plays an active dynamic role in the trapping mechanism to create a larger change in the ambient electromagnetic field than that predicted by Rayleigh scattering and hence opening up the doors to work beyond the perturbative regime.
It should be noted here that nanoaperture SIBA-based optical tweezers do not require resonance from the trapped object, which makes them fundamentally different from trapping using resonances of atoms74,75 or quantum dots.76 In addition, while plasmonic based optical tweezers utilize localized surface plasmons to enhance the radiation force,77–81 SIBA-based optical tweezers rely on the strong influence the trapped particle has on the electric field to achieve a stable robust trapping; therefore, they do not need a plasmonic resonance either.
Furthermore, unlike microresonator trapping systems,82–88 which rely on high quality resonance, aperture-based SIBA tweezers are not as sensitive to wavelength and a straight forward measurement of the transmission of the same trapping laser beam through the aperture can be used to detect trapping events. This is due to the fact that nanoaperture are naturally background signal free. Therefore, nanoaperture tweezers can also be thought of as sensors, with reported signal-to-noise ratios (SNR) of up to 33.89 This has made them useful tools, not only for detecting single molecules, but also for observing their molecular interactions, as will be discussed in the subsequent sections.
Nanoaperture trapping geometries
Although circular apertures in metallic films, Fig. 3a, were used to stably trap 50 nm polystyrene particles with low powers,64 extending optical trapping towards even smaller particles requires looking for new nanoaperture designs. A number of nanoaperture shapes have been suggested for increased transmission,90–93 enhanced second harmonic generation,94,95 surface enhanced Raman scattering (SERS)96 and for local field enhancement.97–99 In addition, the cutoff wavelength of a certain aperture shape might be different than other apertures of the same area.100 Trapping 22 nm polystyrene particles was achieved using a rectangular plasmonic nanopore,101 as shown in Fig. 3b. Such a rectangular aperture has the advantage that the propagating gap plasmons can be tuned by adjusting its geometrical aspect ratio. In addition, it has a stronger resonant transmission than a circular aperture of the same area, yet both circular and rectangular apertures have the disadvantage of not having a sharply defined trapping site in the aperture. Double nanohole apertures, as shown in Fig. 3c, were used for trapping (and unfolding) a single protein,89 a 12 nm silica sphere102 and a single DNA molecule.103 Experimental results show that the double nanohole aperture trap can trap smaller particles more easily than larger particles, which is the opposite for other optical traps.102 This is due to the sensitivity to the gap size between the two nanoholes – it should be commensurate with the particle size. The bowtie nano-aperture geometry, Fig. 3d, combines high collection cross section and transmission with strong mode confinement, which also makes it a good candidate for SIBA trapping. Three-dimensional optical manipulation of 50 nm polystyrene particles was achieved using the bowtie nanoaperture on a tapered optical fiber, as will be described below.104 Typical trapping wavelengths for apertures in metal films are in the infra-red region, i.e. 750 nm to 1060 nm. | ||
| Fig. 3 Nanoaperture trapping geometries with corresponding near-field intensity maps: (a),(e) circular aperture, reprinted from ref. 64, Copyright 2009, Nature Publishing Group. (b),(f) Rectangular aperture, reprinted from ref. 101, Copyright 2011, American Chemical Society. (c),(g) Double nanohole aperture, reprinted from ref. 102, Copyright 2011, American Chemical Society, (d),(h) bowtie nanoaperture. Reprinted from ref. 104, Copyright 2013, Nature Publishing Group. | ||
Numerical simulation results of various aperture trapping geometries, Fig. 3(e)–(h), show that an enhancement in the local electric field intensity is obtained in the vicinity of the nanoapertures. This enhanced local field intensity is altered by the presence of the trapped particle. Therefore, as the particle tends to escape from the trap a SIBA force acts upon it pushing it back to the aperture, providing self-feedback on the particle's dynamics in the trap.
Nanoaperture trap stiffness
Trap stiffness is a measure of the strength of an optical trap; it is analogous to the spring constant defined in a mechanical spring system. It is a measure of the force, the optical trap exerts on the trapped particle when the particle is displaced from its equilibrium position due to external forces or Brownian motion imparted by the medium at a finite temperature. Thus, stiffness per laser power unit gives the efficiency of the optical trap, which can be used for calibration or performance evaluation and comparison. Nanoaperture trap stiffness has been calculated experimentally using two approaches: autocorrelation of Brownian induced intensity fluctuations and trapping transient analysis.105 The nanoaperture traps measures the transient change in transmission signal as the particle enters the trapping region and the intensity fluctuations of the transmission signal while the particle is trapped using a photodiode. These techniques are analogous to the power spectrum method and the step response method respectively,106,107 used for calculating the stiffness of a conventional laser tweezer. The only difference is that nanoaperture trap measure directly the transmission intensity signal as compared to the measurement of the position of the particle in the trap in the conventional laser tweezer. The latter approach is not suitable for nanoapertures as it is challenging to determine the precise position of very small particles (1–100 nm) in the nanoaperture using the quadrant photodiode or video microscope.108,109For nanoapertures, the transmission through the aperture is related to the position of the particle in the aperture, and so the Brownian motion induced intensity fluctuations of the transmission signal can be used to assess the trap stiffness. The autocorrelation of the signal is used to determine the characteristic time constant which is related to the trap stiffness. It should be noted that for an accurate measurement (10% precision) of the time constant from autocorrelation, the measurement time should be ∼1000τ.110
Another approach is the trapping transient technique, which is related to the drag force of the fluid as compared to the autocorrelation analysis which is based on thermal vibrations. The technique measures the time constant of the transition from the untrapped to trapped state due to trapping forces as opposed to viscous drag. The time constant obtained from the trapping transient and the autocorrelation analysis, are used to evaluate the stiffness of the nanoaperture trap. The motion of a particle in an optical trap under the influence of thermal fluctuation and drag force can be modelled by an over-damped Langevin equation as111
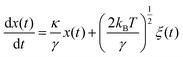 | (5) |
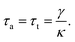 | (6) |
For the particles trapped at the nanoaperture site, additional drag force can arise due to the wall effects from the wall of the aperture. The effects are included in the calculation by using a modified Stokes drag coefficient, estimated using Faxén's law as113:
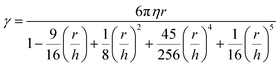 | (7) |
Fig. 4 shows an example of a trapping event of 20 nm polystyrene bead using a double nanohole aperture. The insets show the trapping transient and autocorrelation of Brownian induced intensity fluctuations used to find the respective time constant used for calculation of trap stiffness. These approaches were used to determine the trap stiffness of the double nanohole aperture traps.105
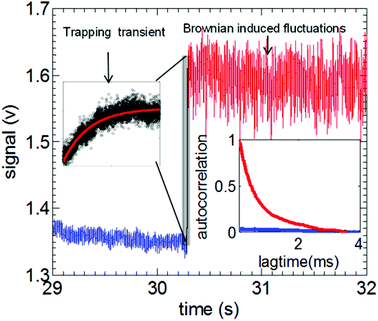 | ||
| Fig. 4 Illustration of the trapping transient and the autocorrelation of Brownian induced intensity fluctuations (inset) obtained from a typical trapping event of 20 nm polystyrene nanosphere using double nanohole nanoaperture tweezer (blue: untrapped state, red: trapped state). Insets shows expanded region of trapping transient with an exponential fit to calculate the time constant τt and autocorrelation of the trapped and untrapped transmission signal. Reprinted from ref. 105, Copyright 2014, American Chemical Society. | ||
Table 1 shows a comparison of the trap stiffness of different laser tweezers. The values have been scaled for 10 nm polystyrene particles. It is clear from this table that nanoapertures are 3–4 orders of magnitude more efficient than conventional tweezers. There are also other non-aperture type nanostructures for enhanced trapping; however, those require high local field intensities.
| Structure | Methoda | Stiffness (fN nm−1 mW−1) | Scaled stiffness (fN nm−1 mW−1) |
|---|---|---|---|
| a Exp.: experimental, sim.: simulation. b Scaled by Clausius–Mossotti factor to account for increased refractive index contrast used in calculations. | |||
| Nano pillar114 | Exp. | 0.013 | 0.013 × 10−3 |
| Slot waveguide40 | Sim. | 0.200 | 0.001 |
| Rectangular plasmonic aperture101 | Sim. | 0.018 | 0.018 |
| Plasmonic nano block pair115 | Exp. | 4.000 | 0.030 |
| Double nanohole aperture105 | Exp. | 0.100 | 0.100 |
| Slot waveguide72 | Sim. | 0.131 | 0.131 |
| Circular aperture64 | Sim. | 6.600 | 0.400 |
| Coaxial plasmonic aperture55 | Sim. | 0.190 | 1.56 (0.36b) |
| Conventional optical tweezer116 | Sim. | 0.030 | 0.3 × 10−4 |
Single particle trapping and analysis
Unlike conventional gradient force optical tweezers which require high laser intensities to trap Rayleigh particles, nanoaperture optical tweezers have been used to trap and manipulate nanometer-sized particles using moderate powers, typically between 1 and 10 mW.64,89,102 The trapped particle is held in a well defined region by the trapping laser beam. This brings up an issue that the trap will always apply a pulling force on the particle of interest. This may not be desired in some cases: for example, it may unfold the protein of interest, and this effect cannot be avoided while maintaining the trapping laser. The transmission of the trapping laser beam through the nanoaperture is monitored and a trapping event of dielectric particle is detected by the abrupt increase in the transmission (due to dielectric loading) through the aperture, as shown in Fig. 4. Associated with the abrupt increase in the transmission is an increase in the signal fluctuation which is attributed to the Brownian motion and the conformal changes of the trapped particle in the aperture. Valuable information regarding the trapped dielectric particle (like its dynamics and interactions, as well as the number of particles trapped, as will be shown in the subsequent sections) can be extracted from the transmission signal while the particle is in the trap.The nanoaperture trap has been used for sensing of nanoparticle size, concentration and the refractive index.117 The sensing technique is based on a simple diffusion theory of the nanoparticles in a simple microfluidic environment. The time-to-trap (τtrap) of the nanoparticle in the nanoaperture trap inside a microfluidic chip is directly proportional to the diffusion time (τ) of the particle. Time-to-trap is the time taken by the nanoaperture tweezer to trap the nanoparticle after the laser beam is turned on. A statistical analysis of time-to-trap can be used to quantify the concentration and size of the nanoparticles in the solution. Furthermore, it is possible to determine the refractive index of the particle by examining the percentage change in the transmission intensity at the trapping instant, which scales with the Clausius–Mossotti factor.
The dependence of time-to-trap on the nanoparticle size and concentration can be deduced from the theory of diffusion of particles in a solution where it was shown that the time to trap a particle in a nanoaperture tweezer under simple microfluidic consideration would show a linear dependence with the size of the nanoparticles and a −2/3 power-law dependence with the concentration of the nanoparticles.117 This has been shown using the double nanohole aperture optical trap where the time-to-trap was measured for 20 nm polystyrene spheres of different concentrations and sizes in the range of 20–60 nm.117Fig. 5a shows the mean time-to-trap for different particle sizes as a function of their diameter. The straight line fit shows good agreement with the theory where the time-to-trap is directly proportional to the diameter of the particles. Fig. 5b shows the average trapping time as a function of concentration of 20 nm polystyrene spheres. It showed a −0.655 power-law dependence, in reasonable agreement with the theoretical value.
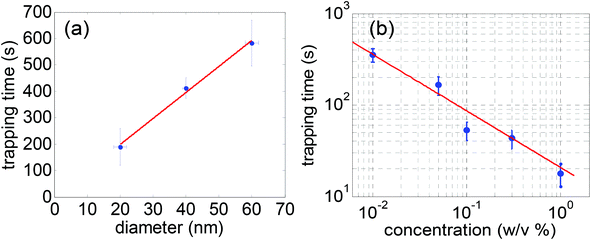 | ||
| Fig. 5 (a) Mean optical trapping time for varying polystyrene diameters. The horizontal and vertical error bars are standard deviation (manufacturer specified) and standard error of nanosphere size and trapping time respectively. The straight line is a linear fit to the data (b) average trapping time as a function of concentration of polystyrene spheres in aqueous solution. The dot represents the mean trapping time over multiple events (typically 10–20) for each concentration. The bar represents the standard error of the data. The straight line represents the power-law fit to the data. Reproduced from ref. 117. | ||
Nanoaperture tweezers can also be used to determine the refractive index of the trapped particle by observing the percentage change in the transmission signal when the particle is trapped. One of the factors which determine the amount of change in transmission level as the particle goes from the untrapped to the trapped state is the refractive index contrast of the particle (np − nm). This is attributed to trapping efficiency for particles which is expected to scale, at least to first order, as the Clausius–Mossotti factor K given by
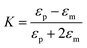 | (8) |
In a recent study, it was shown that it is possible to differentiate between DNA molecules of different lengths by measuring the scattered light through a circular aperture in a metallic film.118 Trapping events of a single 4.7 kbp plasmid DNA were compared with those of a 48 kbp lambda DNA, with the latter one showing stronger scattering signal through a 400 nm circular aperture in a gold film.
In an attempt to statistically analyze trapping dynamics of dielectric particles using nanoaperture optical tweezers, 22 nm polystyrene beads were trapped in a rectangular plasmonic nanopore.101 Experimental results which were supported by numerical calculations revealed that although this structure can trap a single polystyrene particle, double-bead polystyrene trapping showed higher stability in the trap, as shown in Fig. 6.
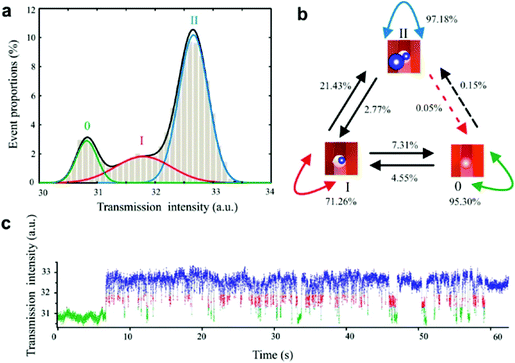 | ||
| Fig. 6 Statistic analysis of trapping 22 nm polystyrene beads. (a) Transmission intensity histogram of trapping events shown in Fig. 7(c), including Gaussian fits based on expectation minimization (EM) algorithm. The three peaks correspond to: nontrapping state (0), single-bead trapping state (I), and double-bead trapping state (II). (b) Markov diagram of the state transition of the trapping events shown in Fig. 2. (c) Discrimination of three states of trapping based on the hidden Markov model (HMM) method. Reprinted from ref. 101, Copyright 2011, American Chemical Society. | ||
In addition, Kramer's hopping, which refers to particles hopping between two energy minima separated by a barrier, was reported at the nanoscale using a double nanohole aperture for trapping a 20 nm polystyrene particle.119 For the double nanohole aperture, there are two stable trapping points at the two cusps of the aperture. Skewness analysis of the voltage distribution of the trapping events (showing negative values) were interpreted as the time the particle spends transitioning over the barrier between the two stable points. In addition, the low frequency roll-off in the power spectrum as well as the FDTD simulations all supported the Kramer's hopping hypothesis.
Nanoaperture optical tweezers as sensors are mainly limited by the acquisition time as they require a large sample space of the trapping events to accurately predict the time to trap value. This has been a major issue for low concentration sensors in general.120 This limitation can be overcome by parallelizing the process with multiple traps in a narrower channel.121 Some deviation from simple microfluidic theory may arise at higher concentrations or due to hydrodynamic effects. The potential applications are in size selectivity in heterogeneous samples, and isolation/analysis (e.g., spectroscopy) of particles once trapped. This could be useful in the study of virus populations in biological samples, where the population levels vary of many orders of magnitude and there is great heterogeneity in the population.122
Nanoaperture optical tweezer for protein studies
Protein–small molecule interaction (PSMI) studies typically use surface immobilization techniques combined with labeling. Surface immobilization uses some of the molecules’ binding sites and restricts its free motion; hence preventing it from being in its native state.123,124 Besides heating issues, labeling techniques suffer from photobleaching, blinking and low signal for single molecule applications.125,126 In addition, as is the case with surface immobilization, labeling disrupts the natural state of the molecule; hence affecting the accuracy of the data.127 Of course, this is not always an issue. For example, there are a number of studies showing that surface-based methods provide exactly the same results as solution-based techniques.128 However, in an attempt to overcome the problems associated with surface immobilization and labeling, a number of label-free, free-solution methods like calorimetry,129 enthalpic arrays130 and interferometry131 have been suggested. However, these alternative ensemble methods have disadvantages, like long preparation times, low sensitivity and poor detection limits. Nanoaperture optical tweezers, on the other hand, are emerging as an attractive method for protein studies for a number of reasons. First, they allow for working at the single molecule level without the need for tethers or labels and hence can provide information about single molecule interactions which are not accessible by ensemble methods.132,133 Second, protein–protein interactions are very temperature-sensitive and nanoaperture optical tweezers have been successfully used to trap 12 nm dielectric particles using around 3 mW of laser power.102 The good thermal conductivity of the metallic film of the nanoaperture plays an important role in dissipating any heat generated at the trapping site. Third, the high sensitivity of the transmitted light in nanoaperture tweezers to the shape, size and refractive index of the trapped particle makes them excellent candidates for detecting molecular interactions. Light transmitted through the double nanohole aperture was used to observe the real time dynamics and to distinguish between the bound and unbound forms of a protein.134 Fourth, unlike fluorescent-based methods, which due to blinking and bleaching are limited in terms of observation times to minutes, nanoaperture tweezers can extend observation times to hours and maybe days. In addition, the nanosecond resolution of nanoaperture tweezers (limited to detector) makes them superior to fluorescent-based techniques which are limited in terms of resolution to about 1 ms, due to photon counting. Fifth, cost and labour associated with tethering (for surface immobilization) and labeling and photon counting in fluorescent measurements makes them expensive as compared with current nanoaperture optical tweezers setups. It has been shown that it is possible to integrate nanoapertures at the end of optical fibers,104,135 hence bringing the cost even lower.Single protein binding detection
Single protein binding studies typically bind a protein to a surface and then look at protein interactions through additional binding events.136–138 A number of studies have shown single protein binding sensitivity using plasmonic nanoparticle by monitoring resonance shifts139–141 and by photo-thermal transduction to achieve increased sensitivity.142 Those works, however, have the disadvantage of using some of the binding sites of the molecule for surface immobilization and hence obscuring/blocking a specific side of the protein by the surface. They also restrict the motion of the protein, and so the binding event is not in its native state. The double nanohole aperture trap integrated with microfluidic channels, have been used to trap a single bovine serum albumin (BSA) molecule and then co-trap it with anti-BSA in a label-free free-solution microfluidic environment.119 When a single BSA molecule gets trapped between the cusps of the double nanohole aperture it dielectrically loads the region and causes an increase in the transmission. Once a stable trapping of a single BSA molecule was achieved, anti-BSA was flowed into the channel where it bound to the already trapped BSA molecule, causing further dielectric loading to the double nanohole aperture region and consequently a higher optical transmission was obtained. Single protein binding detection was further demonstrated using the streptavidin-biotin model with the same aperture trap configuration.143 In that work, as shown in Fig. 7, a double-syringe pump was used to deliver biotin-coated polystyrene particles to the double nanohole trapping site. Once stable trapping of biotin coated polystyrene particle was achieved, the double-syringe pump was used to flow in streptavidin solution to the trapping site. Protein binding was confirmed by performing two control experiments: (1) biotin-coated polystyrene particles were trapped and then streptavidin with the binding sites being blocked off by mixing it with excess biotin was flowed in, and (2) non-functionalized polystyrene particle trapping was achieved and then streptavidin was flowed in.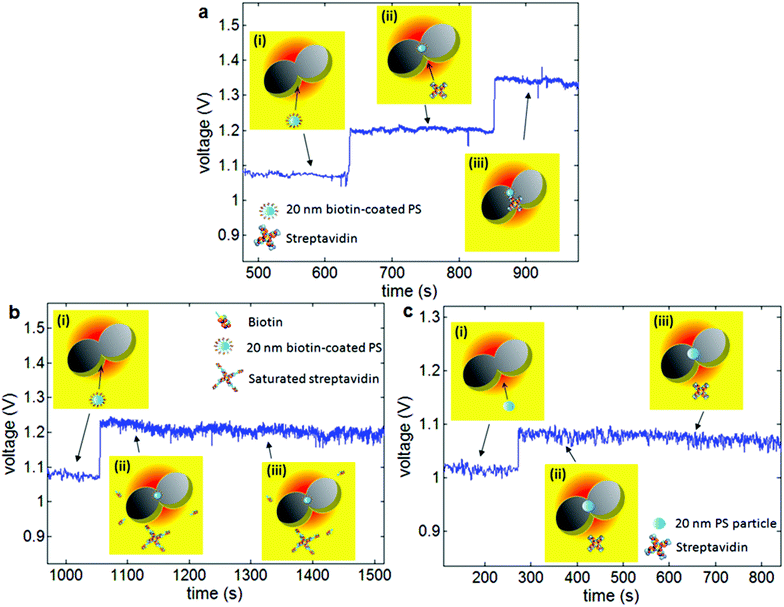 | ||
| Fig. 7 (a) Demonstration of single protein binding using the double nanohole aperture: (i) flowing 20 nm biotin-coated polystyrene particles, (ii) trapping event of 20 nm biotin-coated polystyrene particle in the double nanohole aperture and subsequently flowing streptavidin, (iii) binding of streptavidin with the trapped biotin-coated polystyrene particle. (b) First control experiment: (i) flowing 20 nm biotin-coated polystyrene, (ii) trapping event of 20 nm biotin-coated polystyrene particle and subsequently flowing saturated streptavidin, (iii) saturated streptavidin does not bind to the trapped 20 nm biotin-coated polystyrene particle. (c) Second control experiment: (i) flowing 20 nm non-functionalized polystyrene particles, (ii) trapping event of 20 nm polystyrene particle and then flowing streptavidin, (iii) streptavidin does not bind to the trapped 20 nm polystyrene particle. Reprinted from ref. 143, Copyright 2013, OSA. | ||
Single protein–small molecule interactions
The double nanohole optical tweezer has been used to observe the real-time dynamic variation in PSMI interactions with the primary focus on the effect of single and multiple binding events on the dynamics of the protein in the trap.134,144 In those studies, four forms of streptavidin were considered: bare streptavidin, bare monovalent streptavidin, biotinylated streptavidin and biotinylated monovalent streptavidin. Time traces of the trapping events of each one of the four forms were compared, with the bare form of the streptavidin showing slower timescale dynamics as compared to the biotinylated forms of the protein. The difference between the bare and bound form of the protein manifests itself clearly when plotting the autocorrelation functions of the trapping events for the four different forms, Fig. 8. The bare form of streptavidin and monovalent streptavidin show fluctuations on the time scale of 600 ms and 200 ms, while the biotinylated form of streptavidin and monovalent streptavidin molecules show faster timescale dynamics with respective fluctuations on the time scale of about 20 ms and 8 ms; which imply that the bound form of the protein is subject to less conformal changes in the double nanohole trap. This is consistent with numerical studies on streptavidin which suggest that the four binding loops are highly mobile in the absent of biotin;145 and is also consistent with other reports in the literature which suggest that a small molecule binding can substantially alter the molecular dynamics of the protein.146 These results demonstrate that the double nanohole optical trap is not only able to differentiate between the bound and unbound forms of the protein, but also distinguish multiple binding events from a single binding event.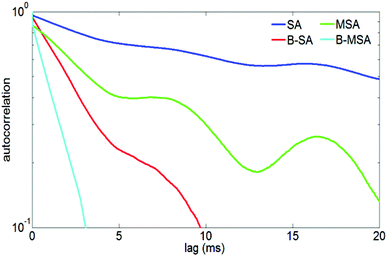 | ||
| Fig. 8 Autocorrelation of time traces of trapped streptavidin (SA), biotinylated streptavidin (B-SA), monovalent streptavidin (MSA) and biotinylated monovalent streptavidin (B-MSA). Reprinted from ref. 144, Copyright 2014, OSA. | ||
In addition, the double nanohole aperture trap can study the real-time binding kinetics of PSMIs and determine the disassociation constant.147 This can be done by using a statistical approach of measuring the resident time of the molecule in the bound and unbound states, as shown in Fig. 9. The nanoaperture tweezer system can detect the bound and unbound forms from the transmission signal as the protein in the bound state has a higher polarizability and hence higher transmission through the aperture, compared to the protein in the unbound state. From this, the affinities were determined and found to be in good agreement with past literature values.148–151 Furthermore, it was shown that the threshold for distinguishing the bound and unbound states could be varied by 20% with little sensitivity to the achieved results – therefore the approach is robust to small variations in the signal processing.
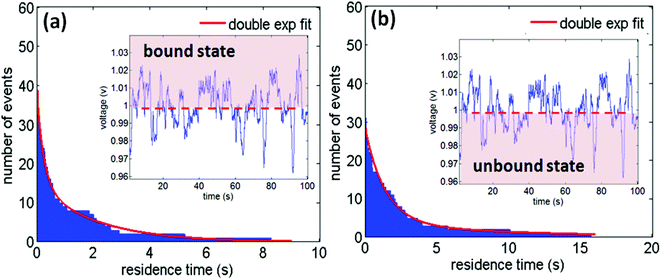 | ||
| Fig. 9 (a, b) Histograms of residence times of human serum albumin (HSA) molecule in the bound and unbound states respectively as obtained from the transmission signal (inset). The inset shows the interaction of HSA with tolbutamide during trapping in the double nanohole aperture. Reprinted from ref. 152, Copyright 2014, Society of Photo Optical Instrumentation Engineers. | ||
Single protein–DNA interactions
Using nanoaperture tweezers, it has been possible to extract valuable information regarding the dynamics and interaction of the biological molecules from the transmission signal obtained during the trapping of the given biological specimen. This has been illustrated using the double nanohole aperture trap which showed the unzipping of small hairpin DNA fragments (20 bases).103 A unique signature, showing an intermediate step in the transmission signal during the trapping instant is observed. The initial change in transmission is due to trapping with an intermediate step of time (Δt) and a second transition indicates the unzipping caused due to increase in polarizability as a result of elongation of DNA. The trapping event of single strand DNA with no hairpin structure showed no such intermediate step confirming the unzipping phenomenon of the hairpin DNA, Fig. 10.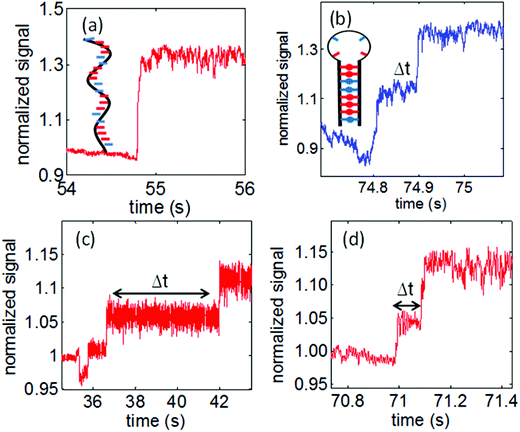 | ||
| Fig. 10 (a) Single strand DNA trapping event with no intermediate step. (b) A hairpin DNA trapping event showing the unzipping with an intermediate step of ∼0.1 s. (c) The wild type p53 suppresses the unzipping of the DNA hairpin for a delay of ∼5 seconds (d) the mutant p53 is incapable to suppress the unzipping of the DNA hairpin even though there is partial loss in binding activity. Reprinted with permission from ref. 103, Copyright 2014, OSA. | ||
The interaction of a transcription protein with DNA and its impact on the dynamics of the hairpin-DNA has also been shown by the double nanohole tweezers. The DNA binding protein can stabilize or destabilize the DNA structure and hence affect the unzipping behavior in the optical trap.153 The study was done for the sequence specific DNA binding protein p53. The mutations in p53 are implicated in approximately 75% of known cancers in humans,154 which makes the study of its interactions with DNA of critical importance. The wild-type p53 resulted in suppression of the unzipping phenomenon shown by increased unzipping time (Δt), as shown in Fig. 10a. This was attributed to strong binding strength of the p53 to the DNA molecule, critical for the biological activity of p53 as also shown by fluorescence anisotropy.155 The binding of the p53 to the DNA hairpin increases the energy barrier (ΔU) between the trapped and unzipped state. This results in longer unzipping time, which can then be used to quantify the unzipping suppression energy ΔU through the Arrhenius relation. The interaction of a mutant p53 with the hairpin DNA was also studied which showed a completely contrasting behaviour as compared to the wildtype p53. The mutation in p53 results in partial loss in the binding activity,156 but completely loses its ability to suppress the unzipping of the DNA hairpin shown by Fig. 10 with no appreciable change in the unzipping time (Δt). The double nanohole tweezer helps to understand and distinguish between the interactive behavior of the wild-type and mutant p53 with the DNA showing the specificity required by a single molecule sensor.
Nanoaperture optical traps can be used as a research tool for better understanding of various protein interactions in real time, at the single molecule level, in free-solution and in a label-free way. More specifically, the double nanohole optical trap can be used to understand the dynamics of protein–small molecule and protein–DNA interactions. This could provide aid to researchers in better understanding the biomolecular interactions which might be useful in many drug discovery applications. One potential limitation of this technique is the interaction of the trapped particles with the aperture surface. This include hydrodynamic interactions (such as governed by Faxén's law113), and potential charge interactions;157 both of which will modify the laser tweezer response as compared to usual laser tweezers operating in truly free solution. In a similar way, so far this approach has not been extended to membrane proteins, or intercellular media, which may be a fundamental limitation due to the physical presence of the aperture. Another limitation of this trapping approach is the requirement for nanofabrication. However, it has been shown recently that high-throughput approaches, such as template stripping, may be used to fabricate the apertures.158
Single particle spectroscopy of trapped particles
Raman spectroscopy
Raman is a tool that has been used for highly specific identification of particles and has seen wide spread use in the identification of ensembles, in some cases with single particle resolution.159–161 Although Raman works well for large ensembles and is a quick and effective tool, when working with smaller population ensembles the practicality begins to falter.162 In a solution with a low concentration of the target, optical trapping with nanoapertures can be used to increase the number of targets in the detection area. Additionally, these plasmonic structures have been shown to create enhancement in the Raman signal.163 The trapping achieved by the use of the plasmonic nanoaperture relies on the strong field confinement within them. 20 nm polystyrene spheres were successfully trapped and had their Raman signal detected using a plasmonic nanopore.164 As the particles accumulated in the nanopore, a shift in the Raman signal was observed that finally stabilized after the nanopore had become saturated. From this signal the polystyrene within the pore was identified.Acoustic Raman
While a particle is trapped in a nanoaperture it experiences the electrostriction force from the electric field between the two tips that create the trapping region. This electrostriction force pulls on the particle. It has been shown that this electrostriction force could be used to excite Raman active acoustic modes of an ensemble of particles.165 Recently, excitation of acoustic Raman modes of single polystyrene particles as well as single proteins and DNA molecules within the double nanohole aperture has been achieved by trapping the particle with two tunable trapping lasers166,167 as opposed to a single fixed laser source. In that work, once the protein was trapped in the double nanohole aperture, the lasers were detuned from each other, hence creating a tunable beat frequency between them. This beat frequency was used to modulate the electrostriction force on the trapped particle in the aperture. When the beat frequency matched the frequency of one of the particle's acoustic modes, the resonant motion of the particle increased the temperature of the system, hence increasing the root mean squared (RMS) variation of the transmission signal. This increase in the RMS is the signal that was recorded to detect a resonance and create a Raman spectrum by plotting the RMS of the signal against the beat frequency between the two laser sources. Spectra of two proteins carbonic anhydrase and conalbumin are shown in Fig. 11; however, 4 different proteins showed distinct spectra in that work.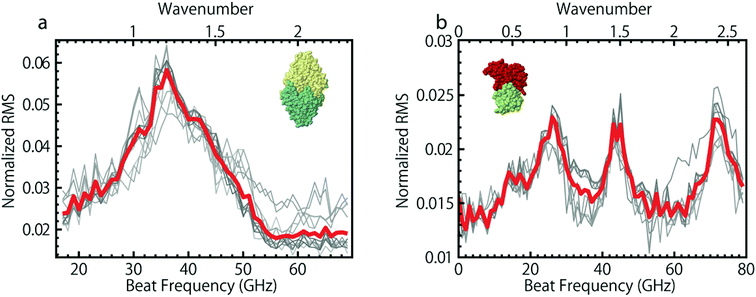 | ||
| Fig. 11 Raman spectra of two globular proteins. (a) 22 different sweeps across 11 trapping events of carbonic anhydrase showing a singular broad peak centered around 38 GHz. (b) 20 Different sweeps across 10 trapping events of conalbumin showing 2 distinct peaks and a single finely split peak. Red curves show the average of all sweeps. Reprinted from ref. 166, Copyright 2014, Nature Publishing Group. | ||
Integration
Microfluidic integration
The growth of molecular biology has stimulated the development of systems like microfluidic systems for analysis of biomolecules, DNA and proteins.168 Among the benefits resulting from the miniaturization of devices for use in these areas are: decreased cost in manufacture, use, and disposal; decreased time of analysis; reduced consumption of reagents and analytes; reduced production of potentially harmful by-products; and increased portability.168 Single-molecule studies of protein interactions require precise temporal and spatial control over the chemical environment of the observed biological molecules.169 Optofluidic microsystems are key components towards lab-on-a-chip devices for manipulation and analysis of biological specimens. In particular, the integration of optical tweezers in these devices allows stable sample trapping, while making available mechanical, chemical and spectroscopic analyses.Polydimethylsiloxane (PDMS) has been the most widely used material in the research and development of microfluidics.168 PDMS is an optically transparent elastomer that allows rapid prototyping of devices. PDMS microfluidic chambers have been used to trap nano particles in double nanohole apertures fabricated on gold samples.89,102 In those works, the gold sample was covered by a static fluidic chamber containing a diluted aqueous suspension of nanometre-sized polystyrene beads. Enabled by the integration of PDMS based flow channels with a double nanohole aperture trapping setup, the ability to trap nanoparticles against fluid flow for varying flow rates has been characterized.170 It was experimentally demonstrated in that work that the flow rate at which the trapped particle is released has an empirical linear dependence of 1 μL (min × mW)−1. The volumetric flow rate is relevant here since it determines how much solution can be delivered to the trapping site. At the same time, this is limited by the local flow rate. In that typical case, the flow velocity at the centre of the trapped polystyrene particle was estimated to be 5.9 mm s−1 which translated to 2 fN Stokes’ drag. It was shown that 10 mW of incident power in a double nanohole optical trap can hold on a particle for flow rates of up to 12 μL min−1. This gave promising results for the delivery of additional nanoparticles to interact with a trapped nanoparticle; for example, co-trapping of BSA with anti-BSA by sequential delivery of BSA and anti-BSA solutions to the trapping site using a microfluidic channel was achieved.119 More recently, single protein binding was detected using the double nanohole aperture integrated with PDMS based microfluidic channels.143
While easy to process and convenient, PDMS has some drawbacks like: (i) poor chemical compatibility with several organic solvents as it tends to swell upon contact, making it mainly suitable for aqueous applications; (ii) adsorbtion of hydrophobic molecules that can release contaminants into the liquid; (iii) nanoparticles of silica in commercial PDMS causes undesired scattering of light; (iv) channel walls fabricated in deformable material like PDMS may oscillate under pressure, creating lensing effects and variable focal length in the detection system.171 One way to overcome these issues is to translate PDMS-based microfluidic channels to glass. In order to achieve microfluidic chip fabrication without bonding process, UV curable epoxy was reported to produce a sealed microfluidic channel without using a bonding process.172 This new UV epoxy microfluidic channels were made by using very thin layer of UV epoxy as adhesive layer between glass substrate and the gold sample and connectors were glued with regular epoxy on either sides of the glass substrate to form inlet and outlet for this channel. These channels were tested for the ability to trap against flow and had similar results to that of PDMS based channels.
Fiber optic nanoaperture traps
Integrating apertures and other metallic nanostructures onto the facet of a fiber optic cable has the potential to open up new devices for chemical and biological sensing. Fiber optic is inexpensive, robust, compact, modular, operates at a wide variety of different wavelengths, and can survive harsh environments such as high temperature and humidity.173 Furthermore, most of the optical components for a device are also in fiber, therefore very little alignment is necessary. As a result these devices can be used to trap and isolate a particle of interest and then translocate it to a desirable location for further analysis. It can also be used to study its interaction in a different environment or with a different particle. A lot of research has been accomplished for developing fiber based sensors,174–176 only recently have aperture based approaches been integrated along with these existing technologies. The other major application for aperture based fiber probes is near scanning optical microscopy (NSOM), a technique developed since the 1980s and is primarily used to characterize the near optical field of nanostructures.177,178Nanoapertures have been integrated with fiber optic to be used is as hydrogen sensors.179 Furthermore fiber probe devices could be used as in situ biological sensors for detecting within cells. Tapered fibers with a nanoaperture in the metalized tip can be inserted into a cell and used to detect disease markers or track specific particles.180 In addition, fiber-based trapping was suggested to work as a nanopipet where a single nano scale particle could be trapped and then moved to the desired location.102
A bowtie nanoaperture milled into the facet end of a tapered fiber was used to trap and manipulate in all three dimensions a 50 nm polystyrene bead.104 This technique has the potential to trap and translocate a particle from one location to another and place that particle into an area of interest with great accuracy. A second demonstration181 performs the same experiment using an NSOM fiber probe and using a side mounted camera to observe the actual trapping even of a 500 nm latex bead. Both of these demonstrations used bowtie aperture geometry milled into a tapered fiber, as shown in Fig. 3c.
Tapering a fiber reduces its robustness and adds complicated fabrication steps. The latest demonstration shows the possibility of trapping on the end of regular flat facet without tapering using a double nanohole aperture to trap a single 20 nm polystyrene particle.135 The double nanohole aperture has already shown the ability to trap single protein molecules and study their real-time interactions. By integrating the latest aperture optical techniques with fiber optics, exciting new applications in biology, medicine, and chemistry may soon be explored. For example, it may be possible to use the aperture to isolate a single virus particle from solution and translate it to a new sample to infect a single cell, thereby enabling the study of virus infection at the single particle level.
Conclusions
Nanoaperture optical tweezers are emerging as an alternative to conventional optical tweezers for detecting single molecules and studying their interactions. They have all the advantages of other single molecule approaches, but also have the advantages of being label-free (no fluorescent markers), operating in free-solution (no tethering), being high speed, giving intrinsic information about the trapped particle (including recently acoustic Raman modes), having low cost and being scalable (using microfluidics and fiber-optics). They have been used successfully to study the interaction of proteins with small molecules and with DNA. Even without Raman, it is possible to determine concentration, size and composition of nanoparticles in solution- all using a single nanoaperture optical tweezer platform. Acoustic vibrational modes of single dielectric particles have been probed using nanoaperture optical tweezers making it possible to identify single biological molecules like proteins and hence opening the doors to possibly distinguish their mutant forms or identify interactions. With all these advances, it is possible to envision future technologies based on nanoaperture optical tweezers for drug discovery,182 precise nanoparticle analysis, and disease and pathogen detection,183,184 among other applications.References
- A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Observation of a single-beam gradient force optical trap for dielectric particles, Opt. Lett., 1986, 11, 288–290 CrossRef CAS.
- K. Dholakia, P. Reece and M. Gu, Optical micromanipulation, Chem. Soc. Rev., 2008, 37, 42–55 RSC.
- A. Rohrbach and E. H. K. Stelzer, Optical trapping of dielectric particles in arbitrary fields, J. Opt. Soc. Am. A, 2001, 18, 839–853 CrossRef CAS.
- S. Tan, H. A. Lopez, C. W. Cai and Y. Zhang, Optical trapping of single-walled carbon nanotubes, Nano Lett., 2004, 4, 1415–1419 CrossRef CAS.
- O. M. Maragò, P. H. Jones, F. Bonaccorso, V. Scardaci, P. G. Gucciardi, A. G. Rozhin and A. C. Ferrari, Femtonewton force sensing with optically trapped nanotubes, Nano Lett., 2008, 8, 3211–3216 CrossRef PubMed.
- O. M. Maragò, et al., Optical trapping of carbon nanotubes, Physica E, 2008, 40, 2347–2351 CrossRef PubMed.
- T. Rodgers, et al., Selective aggregation of single-walled carbon nanotubes using the large optical field gradient of a focused laser beam, Phys. Rev. Lett., 2008, 101, 127402 CrossRef.
- P. J. Pauzauskie, A. Jamshidi, J. K. Valley, J. H. Satcher and M. C. Wu, Parallel trapping of multiwalled carbon nanotubes with optoelectronic tweezers, Appl. Phys. Lett., 2009, 95, 113104 Search PubMed.
- O. M. Maragò, et al., Brownian motion of grapheme, ACS Nano, 2010, 4, 7515–7523 CrossRef PubMed.
- C. W. Twombly, J. S. Evans and I. I. Smalyukh, Optical manipulation of self-aligned graphene flakes in liquid crystals, Opt. Express, 2013, 21, 1324–1334 CrossRef CAS PubMed.
- M. Geiselmann, et al., Three-dimensional optical manipulation of a single electron spin, Nat. Nanotechnol., 2013, 8, 175–179 CrossRef CAS PubMed.
- P. J. Reece, W. J. Toe, F. Wang, S. Paiman, Q. Gao, H. H. Tan and C. Jagadish, Characterization of semiconductor nanowires using optical tweezers, Nano Lett., 2011, 11, 2375–2381 CrossRef CAS PubMed.
- R. Agarwal, et al., Manipulation and assembly of nanowires with holographic optical traps, Opt. Express, 2005, 13, 8906–8912 CrossRef.
- P. J. Pauzauskie, et al., Optical trapping and integration of semiconductor nanowire assemblies in water, Nat. Mater., 2006, 5, 97–101 CrossRef CAS PubMed.
- Y. Nakayama, et al., Tunable nanowire nonlinear optical probe, Nature, 2007, 447, 1098–1101 CrossRef CAS PubMed.
- P. J. Reece, et al., Combined optical trapping and microphotoluminescence of single InP nanowires, Appl. Phys. Lett., 2009, 95, 101109 Search PubMed.
- A. Irrera, et al., Size-scaling in optical trapping of silicon nanowires, Nano Lett., 2011, 11, 4879–4884 CrossRef CAS PubMed.
- F. Dutto, et al., Nonlinear optical response in single alkaline niobate nanowires, Nano Lett., 2011, 11, 2517–2521 CrossRef CAS PubMed.
- F. Wang, et al., Resolving stable axial trapping points of nanowires in an optical tweezers using photoluminescence mapping, Nano Lett., 2013, 13, 1185–1191 CrossRef CAS PubMed.
- K. Svoboda and S. M. Block, Optical trapping of metallic Rayleigh particles, Opt. Lett., 1994, 19, 930–932 CrossRef CAS.
- M. Pelton, M. Liu, H. Y. Kim, G. Smith, P. Guyot-Sionnest and N. F. Scherer, Optical trapping and alignment of single gold nanorods by using plasmon resonances, Opt. Lett., 2006, 31, 2075–2077 CrossRef CAS.
- K. C. Toussaint, et al., Plasmon resonance-based optical trapping of single and multiple Au nanoparticles, Opt. Express, 2007, 15, 12017–12029 CrossRef CAS.
- C. Selhuber-Unkel, I. Zins, O. Schubert, C. Sonnichsen and L. B. Oddershede, Quantitative optical trapping of single gold nanorods, Nano Lett., 2008, 8, 2998–3003 CrossRef CAS PubMed.
- M. Dienerowitz, M. Mazilu, P. Reece, T. Krauss and K. Dholakia, Optical vortex trap for resonant confinement of metal nanoparticles, Opt. Express, 2008, 16, 4991–4999 CrossRef.
- L. Bosanac, T. Aabo, P. M. Bendix and L. B. Oddershede, Efficient optical trapping and visualization of silver nanoparticles, Nano Lett., 2008, 8, 1486–1491 CrossRef CAS PubMed.
- P. H. Jones, et al., Rotation detection in light-driven nanorotors, ACS Nano, 2009, 3, 3077–3084 CrossRef CAS PubMed.
- L. Tong, V. D. Miljkovic and M. Käll, Alignment, rotation, and spinning of single plasmonic nanoparticles and nanowires using polarization dependent optical forces, Nano Lett., 2010, 10, 268–273 CrossRef CAS PubMed.
- L. Tong, et al., Plasmon hybridization reveals the interaction between individual colloidal gold nanoparticles confined in an optical potential well, Nano Lett., 2011, 11, 4505–4508 CrossRef CAS PubMed.
- E. Messina, et al., Plasmon-enhanced optical trapping of gold nanoaggregates with selected optical properties, ACS Nano, 2011, 5, 905–913 CrossRef CAS PubMed.
- M. Ploschner, T. Cizmar, M. Mazilu, A. Di Falco and K. Dholakia, Bidirectional optical sorting of gold nanoparticles, Nano Lett., 2012, 12, 1923–1927 CrossRef CAS PubMed.
- P. W. Smith, A. Ashkin and W. J. Tomlinson, Four-wave mixing in an artificial kerr medium, Opt. Lett., 1981, 6, 284–286 CrossRef CAS.
- A. Ashkin, J. M. Dziedzic and P. W. Smith, Continuous-wave self-focusing and self-trapping of light in artificial Kerr media, Opt. Lett., 1982, 7, 276–278 CrossRef CAS.
- F. Hajizadeh and S. N. S. Reihani, Optimized optical trapping of gold nanoparticles, Opt. Express, 2010, 18, 551–559 CrossRef CAS PubMed.
- A. Ashkin and J. M. Dziedzic, Optical trapping and manipulation of viruses and bacteria, Science, 1987, 235, 1517–1520 CAS.
- E. S. Kwak, et al., Optical trapping with integrated near-Field apertures, J. Phys. Chem. B, 2004, 108, 13607 CrossRef CAS.
- L. Huang and O. J. F. Martin, Reversal of the optical force in a plasmonic trap, Opt. Lett., 2008, 33, 3001–3003 CrossRef.
- M. Nieto-Vesperinas, P. C. Chaumet and A. Rahmani, Near-field photonic forces, Phil. Trans.: Math., Phys. Eng. Sci., 2004, 362, 719–737 CrossRef CAS PubMed.
- K. Okamoto and S. Kawata, Radiation force exerted on subwavelength particles near a nanoaperture, Phys. Rev. Lett., 1999, 83, 4534–4537 CrossRef CAS.
- L. Novotny, R. X. Bian and X. S. Xie, Theory of nanometric optical tweezers, Phys. Rev. Lett., 1997, 79, 645–648 CrossRef CAS.
- A. H. J. Yang, S. D. Moore, B. S. Schmidt, M. Klug, M. Lipson and D. Erickson, Optical manipulation of nanoparticles and biomolecules in sub-wavelength slot waveguides, Nature, 2009, 457, 71–75 CrossRef CAS PubMed.
- A. Ohlinger, S. Nedev, A. A. Lutich and J. Feldmann, Optothermal Escape of Plasmonically Coupled Silver Nanoparticles from a Three-Dimensional Optical Trap, Nano Lett., 2011, 11, 1770–1774 CrossRef CAS PubMed.
- M. Righini, A. S. Zelenina, C. Girard and R. Quidant, Parallel and selective trapping in a patterned plasmonic landscape, Nat. Phys., 2007, 3, 477–480 CrossRef CAS.
- M. Righini, G. Volpe, C. Girard, D. Petrov and R. Quidant, Surface Plasmon Optical Tweezers: Tunable Optical Manipulation in the Femtonewton Range, Phys. Rev. Lett., 2008, 100, 186804 CrossRef.
- Y. Pang and R. Gordon, Nanophotonics using a subwavelength aperture in a metal film, Nanotechnol. Rev., 2012, 1, 339–362 CAS.
- Y. Pang, Nanophotonics with subwavelength apertures: theories and applications, PhD diss., 2012 Search PubMed.
- V. Garces-Chavez, et al., Extended organization of colloidal microparticles by surface plasmon polariton excitation, Phys. Rev. B: Condens. Matter, 2006, 73, 085417 CrossRef.
- M. Ploschner, M. Mazilu, T. F. Krauss and K. Dholakia, Optical forces near a nanoantenna, J. Nanophotonics, 2010, 4, 041570 CrossRef PubMed.
- Y. Seol, A. E. Carpenter and T. T. Perkins, Gold nanoparticles: enhanced optical trapping and sensitivity coupled with significant heating, Opt. Lett., 2006, 31, 2429–2431 CrossRef CAS.
- P. M. Bendix, S. N. S. Reihani and L. B. Oddershede, Direct measurements of heating by electromagnetically trapped gold nanoparticles on supported lipid bilayers, ACS Nano, 2010, 4, 2256–2262 CrossRef CAS PubMed.
- S. Duhr and D. Braun, Why molecules move along a temperature gradient, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682 CrossRef CAS PubMed.
- C. Min, Z. Shen, J. Shen, Y. Zhang, H. Fang, G. Yuan, L. Du, S. Zhu, T. Lei and X. Yuan, Focused plasmonic trapping of metallic particles, Nat. Commun., 2013, 4, 2891 Search PubMed.
- A. Kyrsting, P. M. Bendix, D. G. Stamou and L. B. Oddershede, Heat profiling of three-dimensionally optically trapped gold nanoparticles using vesicle cargo release, Nano Lett., 2011, 11, 888–892 CrossRef CAS PubMed.
- J. S. Donner, G. Baffou, D. McCloskey and R. Quidant, Plasmon-Assisted Optofluidics, ACS Nano, 2011, 5, 5457–5462 CrossRef CAS PubMed.
- N. C. Lindquist, J. Jose, S. Cherukulappurath, X. Chen, T. W. Johnson and S. Oh, Tip-based plasmonics: squeezing light with metallic nanoprobes, Laser Photonics Rev., 2013, 7, 453–477 CrossRef CAS.
- A. A. E. Saleh and J. A. Dionne, Toward Efficient Optical Trapping of Sub-10 nm Particles with Coaxial Plasmonic Apertures, Nano Lett., 2012, 12, 5581–5586 CrossRef CAS PubMed.
- Y. F. Chen, X. Serey, R. Sarkar, P. Chen and D. Erickson, Controlled Photonic Manipulation of Proteins and Other Nanomaterials, Nano Lett., 2012, 12, 1633–1637 CrossRef CAS PubMed.
- S. Lin and K. B. Crozier, Trapping-Assisted Sensing of Particles and Proteins Using On-Chip Optical Microcavities, ACS Nano, 2013, 7, 1725–1730 CrossRef CAS PubMed.
- K. Wang and K. B. Crozier, Plasmonic Trapping with a Gold Nanopillar, ChemPhysChem, 2012, 13, 2639–2648 CrossRef CAS PubMed.
- K. Wang, E. Schonbrun, P. Steinvurzel and K. B. Crozier, Trapping and rotating nanoparticles using a plasmonic nano-tweezer with an integrated heat sink, Nat. Commun., 2011, 2, 469 CrossRef PubMed.
- P. Melentiev, A. Afanasiev, A. Kuzin, A. Baturin and V. Balykin, Giant optical nonlinearity of a single plasmonic nanostructure, Opt. Express, 2013, 21, 13896–13905 CrossRef PubMed.
- A. Ashkin and J. M. Dziedzic, Feedback stabilization of optically levitated particles, Appl. Phys. Lett., 1977, 30, 202–204 CrossRef PubMed.
- R. M. Simmons, J. T. Finer, S. Chu and J. A. Spudich, Quantitative measurements of force and displacement using an optical trap, Biophys. J., 1996, 70, 1813–1822 CrossRef CAS.
- A. E. Wallin, H. Ojala, E. Hæggström and R. Tuma, Stiffer optical tweezers through real-time feedback control, Appl. Phys. Lett., 2008, 92, 224104 CrossRef PubMed.
- M. L. Juan, R. Gordon, R. Pang, F. Eftekhari and R. Quidant, Self-induced back-action optical trapping of dielectric nanoparticles, Nat. Phys., 2009, 5, 915–919 CrossRef CAS.
- P. M. Hansen, V. K. L. Bhatia, N. Harrit and L. Oddershede, Expanding the optical trapping range of gold nanoparticles, Nano Lett., 2005, 5, 1937–1942 CrossRef CAS PubMed.
- L. Jauffred and L. B. Oddershede, Two-photon quantum dot excitation during optical trapping, Nano Lett., 2010, 10, 1927–1930 CrossRef CAS PubMed.
- S. Enoch, R. Quidant and G. Badenes, Optical sensing based on plasmon coupling in nanoparticle arrays, Opt. Express, 2004, 12, 3422–3427 CrossRef.
- P. K. Jain and M. A. El-Sayed, Noble metal nanoparticle pairs: effect of medium for enhanced nanosensing, Nano Lett., 2008, 8, 4347–4352 CrossRef CAS PubMed.
- N. Verellen, et al., Symmetry breaking in a plasmonic metamaterial at optical wavelength, Nano Lett., 2009, 9, 1663–1667 CrossRef CAS PubMed.
- N. Liu, et al., Planar metamaterial analogue of electromagnetically induced transparency for plasmonic sensing, Nano Lett., 2010, 10, 1103–1107 CrossRef CAS PubMed.
- A. B. Evlyukhin, et al., Detuned electrical dipoles for plasmonic sensing, Nano Lett., 2010, 10, 4571–4577 CrossRef CAS PubMed.
- A. H. J. Yang, T. Lerdsuchatawanich and D. Erickson, Forces and transport velocities for a particle in a slot waveguide, Nano Lett., 2009, 9, 1182–1188 CrossRef CAS PubMed.
- R. F. Marchington, M. Mazilu, S. Kuriakose, V. Garces-Chavez, P. J. Reece, T. F. Krauss, M. Gu and K. Dholakia, Optical deflection and sorting of microparticles in a near-field optical geometry, Opt. Express, 2008, 16, 3712–3726 CrossRef CAS.
- C. S. Adams and E. Riis, Laser cooling and trapping of neutral atoms, Prog. Quantum Electron., 1997, 21, 1–79 CrossRef CAS.
- P. W. H. Pinkse, T. Fisher, P. Maunz and G. Rempe, Trapping an atom with single photons, Nature, 2000, 404, 365–368 CrossRef CAS PubMed.
- T. Iida and H. Ishihara, Theoretical study of the optical manipulation of semiconductor nanoparticles under excitonic resonance condition, Phys. Rev. Lett., 2003, 90, 057403 CrossRef.
- M. Righini, et al., Nano-optical trapping of Rayleigh particles and Escherichia coli bacteria with resonant optical antennas, Nano Lett., 2009, 9, 3387–3391 CrossRef CAS PubMed.
- W. Zhang, L. Huang, C. Santschi and O. J. F. Martin, Trapping and sensing 10 nm metal nanoparticles using plasmonic dipole antennas, Nano Lett., 2010, 10, 1006–1011 CrossRef CAS PubMed.
- B. J. Roxworthy, K. D. Ko, A. Kumar, K. H. Fung, E. K. C. Chow, G. L. Liu, N. Fang and K. C. Toussaint, Application of Plasmonic Bowtie Nanoantenna Arrays for Optical Trapping, Stacking, and Sorting, Nano Lett., 2012, 12, 796–801 CrossRef CAS PubMed.
- Y. Tsuboi, T. Shoji, N. Kitamura, M. Takase, K. Murakoshi, Y. Mizumoto and H. Ishihara, Optical Trapping of Quantum Dots Based on Gap-Mode-Excitation of Localized Surface Plasmon, J. Phys. Chem. Lett., 2010, 1, 2327–2333 CrossRef CAS.
- T. Shoji and Y. Tsuboi, Plasmonic Optical Tweezers toward Molecular Manipulation: Tailoring Plasmonic Nanostructure, Light Source, and Resonant Trapping, J. Phys. Chem. Lett., 2014, 5, 2957–2967 CrossRef CAS.
- S. Arnold, D. Keng, S. I. Shopova, S. Holler, W. Zurawsky and F. Vollmer, Opt. Express, 2009, 17, 6230–6238 CrossRef CAS.
- J. Hu, S. Lin, L. C. Kimerling and K. Crozier, Phys. Rev. A, 2010, 82, 053819 CrossRef.
- M. Barth and O. Benson, Appl. Phys. Lett., 2006, 89, 253114 CrossRef PubMed.
- S. Lin, E. Schonbrun and K. Crozier, Optical manipulation with planar silicon microring resonators, Nano Lett., 2012, 10, 2408–2411 CrossRef PubMed.
- S. Mandal, X. Serey and D. Erickson, Nano manipulation using silicon photonic crystal resonators, Nano Lett., 2010, 10, 99–104 CrossRef CAS PubMed.
- F. Vollmer and S. Arnold, Whispering-gallery mode biosensing: label-free detection down to single molecules, Nat. Methods, 2008, 5, 591–596 CrossRef CAS PubMed.
- F. Vollmer, S. Arnold and D. Keng, Single virus detection from the reactive shift of a whispering-gallery mode, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20701–20704 CrossRef CAS PubMed.
- Y. Pang and R. Gordon, Optical trapping of a single protein, Nano Lett., 2011, 12, 402–406 CrossRef PubMed.
- E. X. Jin and X. Xu, Plasmonic effects in near-field optical transmission enhancement through a single bowtie-shaped aperture, Appl. Phys. B, 2006, 84, 3–9 CrossRef CAS PubMed.
- L. Wang, S. M. Uppuluri, E. X. Jin and X. F. Xu, Nanolithography using high transmission nanoscale bowtie apertures, Nano Lett., 2006, 6, 361–364 CrossRef CAS PubMed.
- B. Ai, Y. Yu, H. Möhwald and G. Zhang, Novel 3D Au nanohole arrays with outstanding optical properties, Nanotechnology, 2013, 24, 035303 CrossRef PubMed.
- B. Ai, Y. Yu, H. Möhwald, Y. Yu and G. Zhang, Asymmetric half-cone/nanohole array films with structural and directional reshaping of extraordinary optical transmission, Nanoscale, 2014, 6, 8997–9005 RSC.
- A. Lesuffleur, L. K. S. Kumar and R. Gordon, Enhanced second harmonic generation from nanoscale double-hole arrays in a gold film, Appl. Phys. Lett., 2006, 88, 261104 CrossRef PubMed.
- A. Lesuffleur, L. K. S. Kumar and R. Gordon, Apex-enhanced second-harmonic generation by using double-hole arrays in a gold film, Phys. Rev. B: Condens. Matter, 2007, 75, 045423 CrossRef.
- A. Lesuffleur, L. K. S. Kumar, A. G. Brolo, K. L. Kavanagh and R. Gordon, Apex-enhanced Raman spectroscopy using double-hole arrays in a gold film, J. Phys. Chem. C, 2007, 111, 2347–2350 CAS.
- L. K. S. Kumar and R. Gordon, Overlapping double-hole nanostructure in a metal film for localized field enhancement, IEEE J. Sel. Top. Quantum Electron., 2006, 12, 1228–1232 CrossRef CAS.
- T. Onuta, M. Waegele, C. C. DuFort, W. L. Schaich and B. Dragnea, Optical field enhancement at cusps between adjacent nanoapertures, Nano Lett., 2007, 7, 557–564 CrossRef CAS PubMed.
- D. E. Grupp, H. J. Lezec, T. W. Ebbesen, K. M. Pellerin and T. Thio, Crucial role of metal surface in enhanced transmission through subwavelength apertures, Appl. Phys. Lett., 2000, 77, 1569–1571 CrossRef CAS PubMed.
- R. Gordon and A. G. Brolo, Increased cut-off wavelength for a subwavelength hole in a real metal, Opt. Express, 2005, 13, 1933–1938 CrossRef.
- C. Chen, M. L. Juan, Y. Li, G. Maes, G. Borghs, P. Van Dorpe and R. Quidant, Enhanced optical trapping and arrangement of nano-objects in a plasmonic nanocavity, Nano Lett., 2011, 12, 125–132 CrossRef PubMed.
- P. Yuanjie and R. Gordon, Optical trapping of 12 nm dielectric spheres using double-nanoholes in a gold film, Nano Lett., 2011, 11, 3763–3767 CrossRef PubMed.
- A. Kotnala and R. Gordon, Double nanohole optical tweezers visualize protein p53 suppressing unzipping of single DNA-hairpins, Biomed. Opt. Express, 2014, 5, 1886–1894 CrossRef PubMed.
- J. Berthelot, S. S. Aćimović, M. L. Juan, M. P. Kreuzer, J. Renger and R. Quidant, Three-dimensional manipulation with scanning near-field optical nanotweezers, Nat. Nanotechnol., 2014, 9, 295–299 CrossRef CAS PubMed.
- A. Kotnala and R. Gordon, Quantification of high-efficiency trapping of nanoparticles in a double nanohole optical tweezer, Nano Lett., 2014, 14, 853–856 CrossRef CAS PubMed.
- K. C. Neuman and S. M. Block, Optical trapping, Rev. Sci. Instrum., 2004, 75, 2787–2809 CrossRef CAS PubMed.
- R. M. Simmons, J. T. Finer, S. Chu and J. A. Spudich, Quantitative measurements of force and displacement using an optical trap, Biophys. J., 1996, 70, 1813–1822 CrossRef CAS.
- S. F. Tolić-Nørrelykke, E. Schäffer, J. Howard, F. S. Pavone, F. Jülicher and H. Flyvbjerg, Calibration of optical tweezers with positional detection in the back focal plane, Rev. Sci. Instrum., 2006, 77, 103101 CrossRef PubMed.
- G. M. Gibson, J. Leach, S. Keen, A. J. Wright and M. J. Padgett, Measuring the accuracy of particle position and force in optical tweezers using high-speed video microscopy, Opt. Express, 2008, 16, 14561–14570 CrossRef.
- G. E. P. Box and G. M. Jenkins, Time Series Analysis: Forecasting and Control, Holden-Day, San Francisco, 1976 Search PubMed.
- F. Reif, Fundamentals of Statistical and Thermal Physics, McGraw-Hill, New York, 1965 Search PubMed.
- K. C. Neuman and A. Nagy, Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy, Nat. Methods, 2008, 5, 491–505 CrossRef CAS PubMed.
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics, Prentice-Hall, Inc., New Jersey, 1965 Search PubMed.
- A. N. Grigorenko, N. W. Roberts, M. R. Dickinson and Y. Zhang, Nanometric optical tweezers based on nanostructured substrates, Nat. Photonics, 2008, 2, 365–370 CrossRef CAS.
- Y. Tanaka, S. Kaneda and K. Sasaki, Nanostructured potential of optical trapping using a plasmonic nanoblock pair, Nano Lett., 2013, 13, 2146–2150 CrossRef CAS PubMed.
- A. Rohrbach, Stiffness of optical traps: quantitative agreement between experiment and electromagnetic theory, Phys. Rev. Lett., 2005, 95, 168102 CrossRef.
- A. Kotnala, D. DePaoli and R. Gordon, Sensing nanoparticles using a double nanohole optical trap, Lab Chip, 2013, 13, 4142–4146 RSC.
- J. Kim and Y. Lee, Trapping of a single DNA molecule using nanoplasmonic structures for biosensor applications, Opt. Express, 2014, 5, 2471–2480 CrossRef PubMed.
- A. Zehtabi-Oskuie, H. Jiang, B. R. Cyr, D. W. Rennehan, A. A. Al Balushi and R. Gordon, Double nanohole optical trapping: dynamics and protein–antibody co-trapping, Lab Chip, 2013, 13, 2563–2568 RSC.
- T. M. Squires, R. J. Messinger and S. R. Manalis, Making it stick: convection, reaction and diffusion in surface-based biosensors, Nat. Biotechnol., 2008, 26, 417–426 CrossRef CAS PubMed.
- E. Jaquay, L. J. Martínez, C. A. Mejia and M. L. Povinelli, Light-assisted, templated self-assembly using a photonic-crystal slab, Nano Lett., 2013, 13, 2290–2294 CrossRef CAS PubMed.
- S. Guha, L. F. Pease III, K. A. Brorson, M. J. Tarlov and M. R. Zachariah, Evaluation of electrospray differential mobility analysis for virus particle analysis: potential applications for biomanufacturing, J. Virol. Methods, 2011, 178, 201–208 CrossRef CAS PubMed.
- A. Cecconi, E. A. Shank, C. Bustamante and S. Marqusee, Direct Observation of the Three-State Folding of a Single Protein Molecule, Science, 2005, 309, 2057–2060 CrossRef PubMed.
- A. Borgia, P. M. Williams and J. Clarke, Single-Molecule Studies of Protein Folding, Annu. Rev. Biochem., 2008, 77, 101–125 CrossRef CAS PubMed.
- I. Heller, G. Sitters, O. D. Broekmans, G. Farge, C. Menges, W. Wende, S. W. Hell, E. J. G. Peterman and G. J. L. Wuite, STED nanoscopy combined with optical tweezers reveals protein dynamics on densely covered DNA, Nat. Methods, 2013, 10, 910–916 CrossRef CAS PubMed.
- M. A. Dijk, L. C. Kapitein, J. Mameren, C. F. Schmidt and E. J. Peterman, Combining optical trapping and single-molecule fluorescence spectroscopy: Enhanced photobleaching of fluorophores, J. Phys. Chem. B, 2004, 108, 6479–6484 CrossRef PubMed.
- C. B. Fox, J. R. Wayment, G. A. Myers, S. K. Endicott and J. M. Harris, Single-molecule fluorescence imaging of peptide binding to supported lipid bilayers, Anal. Chem., 2009, 81, 5130–5138 CrossRef CAS PubMed.
- Y. S. N. Day, C. L. Baird, R. L. Rich and D. G. Myszka, Direct comparison of binding equilibrium, thermodynamic, and rate constants determined by surface-and solution-based biophysical methods, Protein Sci., 2002, 11, 1017–1025 CrossRef CAS PubMed.
- A. Adessamad and J. E. Ladbury, Survey of the year 2005: literature on applications of isothermal titration calorimetry, J. Mol. Recognit., 2007, 20, 4–14 CrossRef PubMed.
- F. E. Torres, P. Kuhn, D. D. Bruyker, A. G. Bell, M. V. Wolkin, E. Peeters, J. R. Williamson, G. B. Anderson, G. P. Schmitz, M. I. Recht, S. Schweizer, L. G. Scott, J. H. Ho, S. A. Elrod, P. G. Schultz, R. A. Lerner and R. H. Bruce, Enthalpy arrays, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9517–9522 CrossRef CAS PubMed.
- D. J. Bornhop, J. C. Latham, A. Kussrow, D. A. Markov, R. D. Jones and H. S. Sørensen, Free-solution, label-free molecular interactions studied by back-scattering interferometry, Science, 2007, 317, 1732–1736 CrossRef CAS PubMed.
- W. E. Moerner, A dozen years of single-molecule spectroscopy in physics, chemistry, and biophysics, J. Phys. Chem. B, 2002, 106, 910–927 CrossRef CAS.
- G. A. T. Chansin, R. Mulero, J. Hong, M. J. Kim, A. J. DeMello and J. B. Edel, Single-molecule spectroscopy using nanoporous membranes, Nano Lett., 2007, 7, 2901–2906 CrossRef CAS PubMed.
- A. A. Al Balushi and R. Gordon, Label-Free Free-Solution Single-Molecule Protein–Small Molecule Interaction Observed by Double-Nanohole Plasmonic Trapping, ACS Photonics, 2014, 1, 389–393 CrossRef CAS.
- R. M. Gelfand, S. Wheaton and R. Gordon, Cleaved fiber optic double nanohole optical tweezers for trapping nanoparticles, Opt. Lett., 2014, 39, 6415–6417 CrossRef PubMed.
- J. H. Ahn, J. H. Kim, N. F. Reuel, P. W. Barone, A. A. Boghossian, J. Zhang, H. Yoon, A. C. Chang, A. J. Hilmer and M. S. Strano, Label-Free, Single Protein Detection on a Near-Infrared Fluorescent Single-Walled Carbon Nanotube/Protein Microarray Fabricated by Cell-Free Synthesis, Nano Lett., 2011, 11, 2743–2752 CrossRef CAS PubMed.
- A. Abbas, M. J. Linman and Q. A. Cheng, New trends in instrumental design for surface plasmon resonance-based biosensors, Biosens. Bioelectron., 2011, 26, 1815–1824 CrossRef CAS PubMed.
- A. Hoffmann, K. Neupane and M. T. Woodside, Single-molecule assays for investigating protein misfolding and aggregation, Phys. Chem. Chem. Phys., 2013, 15, 7934–7948 RSC.
- I. Ament, J. Prasad, A. Henkel, S. Schmachtel and C. Sönnichsen, Single Unlabeled Protein Detection on Individual Plasmonic Nanoparticles, Nano Lett., 2012, 12, 1092–1095 CrossRef CAS PubMed.
- Y. Zhuo, H. Hu, W. Chen, M. Lu, L. Tian, H. Yu, K. D. Long, E. Chow, W. P. King, S. Singamaneni and B. T. Cunningham, Single nanoparticle detection using photonic crystal enhanced microscopy, Analyst, 2014, 139, 1007–1015 RSC.
- S. S. Acimovic, M. A. Ortega, V. Sanz, J. Berthelot, J. L. Garcia-Cordero, J. Renger, S. J. Maerkl, M. P. Kreuzer and R. Quidant, LSPR Chip for Parallel, Rapid and Sensitive Detection of Cancer Markers in Serum, Nano Lett., 2014, 14, 2636–2641 CrossRef CAS PubMed.
- P. Zijlstra, P. M. R. Paulo and M. Orrit, “Optical detection of single non-absorbing molecules using the surface plasmon resonance of a gold nanorod, Nat. Nanotechnol., 2012, 7, 379–382 CrossRef CAS PubMed.
- A. A. Al Balushi, A. Zehtabi-Oskuie and R. Gordon, Observing single protein binding by optical transmission through a double nanohole aperture in a metal film, Biomed. Opt. Express, 2013, 4, 1504–1511 CrossRef PubMed.
- A. A. Al Balushi and R. Gordon, Real-Time Dynamics of Single Protein–Small Molecule Interactions with Label-Free, Free-Solution Double-Nanohole Optical Trapping, in Frontiers in Optics, Optical Society of America, 2014, pp. FTh1E-7 Search PubMed.
- S. Freitag, I. Le Trong, L. Klumb, P. S. Stayton and R. E. Stenkamp, Structural studies of the streptavidin binding loop, Protein Sci., 1997, 6, 1157–1166 CrossRef CAS PubMed.
- E. A. Meade, W. L. Smith and D. L. DeWitt, Differential inhibition of prostaglandin endoperoxide synthase cyclooxygenase) isozymes by aspirin and other non-steroidal anti-inflammatory drugs, J. Biol. Chem., 1993, 268, 6610–6614 CAS.
- A. A. Al Balushi and R. Gordon, A Label-Free Untethered Approach to Single-Molecule Protein Binding Kinetics, Nano Lett., 2014, 14, 5787–5791 CrossRef CAS PubMed.
- J. Chen and D. S. Hage, Quantitative analysis of allosteric drug-protein binding by biointeraction chromatography, Nat. Biotechnol., 2004, 22, 1445–1448 CrossRef CAS PubMed.
- P. Kurtzhals, S. Havelund, I. Joanassen and J. Markussen, Effect of fatty acids and selected drugs on the albumin binding of a long-acting acylated insulin analogue, J. Pharm. Sci., 1997, 86, 1365–1368 CrossRef CAS PubMed.
- B. E. Margarita Valero, R. Pelaez and L. J. Rodriguez, Naproxen: Hydroxypropyl-β-Cyclodextrin: Polyvinylpyrrolidone Ternary Complex Formation, J. Inclusion Phenom., 2004, 48, 157–163 CrossRef.
- J. Chen, C. Ohnmacht and D. S. Hage, Studies of phenytoin binding to human serum albumin by high-performance affinity chromatography, J. Chromatogr., B: Anal. Technol. Biomed. Life Sci., 2004, 809, 137–145 CrossRef CAS PubMed.
- A. Kotnala, A. A. Al Balushi and R. Gordon, Optical tweezers for free-solution label-free single bio-molecule studies, in SPIE NanoScience+Engineering, International Society for Optics and Photonics, 2014, pp. 916418–916418 Search PubMed.
- S. J. Koch, A. Shundrovsky, B. C. Jantzen and M. D. Wang, Probing protein–DNA interactions by unzipping a single DNA double helix, Biophys. J., 2002, 83, 1098–1105 CrossRef CAS.
- M. Hollstein, D. Sidransky, B. Vogelstein and C. C. Harris, p53 mutations in human cancers, Science, 1991, 253, 49–53 CAS.
- D. Veprintsev and A. Fersht, Algorithm for prediction of tumour suppressor p53 affinity for binding sites in DNA, Nucleic Acids Res., 2008, 36, 1589–1598 CrossRef CAS PubMed.
- J. Buzek, L. Latonen, S. Kurki, K. Peltonen and M. Laiho, Redox state of tumor suppressor p53 regulates its sequence-specific DNA binding in DNA-damaged cells by cysteine 277, Nucleic Acids Res., 2002, 11, 2340–2348 CrossRef PubMed.
- M. Krishnan, N. Mojarad, P. Kukura and V. Sandoghdar, Geometry-induced electrostatic trapping of nanometric objects in a fluid, Nature, 2010, 467, 692–695 CrossRef CAS PubMed.
- A. Zehtabi-Oskuie, A. A. Zinck, R. M. Gelfand and R. Gordon, Template stripped double nanohole in a gold film for nano-optical tweezers, Nanotechnology, 2014, 25, 495301 CrossRef PubMed.
- P. P. Patra, et al., Plasmofluidic single-molecule surface-enhanced Raman scattering from dynamic assembly of plasmonic nanoparticles, Nat. Commun., 2014, 5, 4357 CAS.
- K. Ajito and K. Torimitsu, Single nanoparticle trapping using a Raman tweezers microscope, Appl. Spectrosc., 2002, 56, 541–544 CrossRef CAS.
- S. Rao, et al., Single DNA molecule detection in an optical trap using surface-enhanced Raman scattering, Appl. Phys. Lett., 2010, 96, 213701 CrossRef PubMed.
- K. Kneipp, H. Kneipp, I. Itzkan, R. R. Dasari and M. S. Feld, Ultrasensitive Chemical Analysis by Raman Spectroscopy, Chem. Rev., 1999, 99, 2957–2975 CrossRef CAS PubMed.
- M. Moskovits, Surface-enhanced Raman spectroscopy: a brief retrospective, J. Raman Spectrosc., 2005, 36, 485–496 CrossRef CAS.
- S. Kerman, C. Chen, Y. Li, L. Lagae, T. Stakenborg and P. V. Dorpe, Raman spectroscopy and optical trapping of 20 nm polystyrene particles in plasmonic nanopores, Proc. SPIE 9126, Nanophotonics V, 2014, 912612 Search PubMed.
- Q. Zhong and J. Fourkas, J. Optical Kerr effect spectroscopy of simple liquids, J. Phys. Chem. B, 2008, 49, 15529–15539 CrossRef PubMed.
- S. Wheaton, R. M. Gelfand and R. Gordon, Probing the Raman-active acoustic vibrations of nanoparticles with extraordinary spectral resolution, Nat. Photonics, 2014, 9, 68–72 CrossRef.
- A. Kotnala, S. Wheaton and R. Gordon, Playing the notes of DNA with light: extremely high frequency nanomechanical oscillations, Nanoscale, 2015, 7, 2295–2300 RSC.
- G. M. Whitesides, The origins and the future of microfluidics, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- C. Liberale, G. Cojoc, F. Bragheri, P. Minzioni, G. Perozziello, R. La Rocca, L. Ferrara, V. Rajamanickam, E. Di Fabrizio and I. Cristiani, Integrated microfluidic device for single-cell trapping and spectroscopy, Sci. Rep., 2013, 3, 1258 CAS.
- A. Zehtabi-Oskuie, J. G. Bergeron and R. Gordon, Flow-dependent double-nanohole optical trapping of 20 nm polystyrene nanospheres, Sci. Rep., 2012, 2, 966 Search PubMed.
- S. Elodie, et al., Rapid prototyping polymers for microfluidic devices and high pressure injections, Lab Chip, 2011, 11, 3752–3765 RSC.
- C. Khoury, G. A. Mensing and D. J. Beebe, Ultra rapid prototyping of microfluidic systems using liquid phase photopolymerization, Lab Lhip, 2002, 2, 50–55 RSC.
- R. Chen, A. Yan, Q. Wang and K. P. Chen, Fiber-optic flow sensors for high-temperature environment operation up to 800 °C, Opt. Lett., 2014, 39, 3966–3969 CrossRef PubMed.
- P. Kundu, C. Ramakrishna and V. N. Saxena, Optical fiber sensors for smart structures: A review, Def. Sci. J., 2013, 46, 289–301 CrossRef.
- G. Y. Chen, M. Ding, T. P. Newson and G. Brambilla, A review of microfiber and nanofiber based optical sensors, Open Opt. J, 2013, 7, 21–57 CrossRef.
- K. Peters, Polymer optical fiber sensors—a review, Smart Mater. Struct., 2011, 20, 013002 CrossRef.
- H. Heinzelmann and D. W. Pohl, Scanning near-field optical microscopy, Appl. Phys. A, 1994, 59, 89–101 CrossRef.
- B. Hecht, B. Sick, U. P. Wild, V. Deckert, R. Zenobi, O. J. F. Martin and D. W. Pohl, Scanning near-field optical microscopy with aperture probes: Fundamentals and applications, J. Chem. Phys., 2000, 112, 7761–7774 CrossRef CAS PubMed.
- S. J. McKeown and L. L. Goddard, Hydrogen Detection Using a Single Palladium Nano-Aperture on a Fiber Tip, Lab-on-Fiber Technol., 2015, 181–208 Search PubMed.
- Y. Zhang, A. Dhawan and T. Vo-Dinh, Design and fabrication of fiber-optic nanoprobes for optical sensing, Nanoscale Res. Lett., 2011, 6, 18–23 Search PubMed.
- A. El Eter, N. M. Hameed, F. I. Baida, R. Salut, C. Filiatre, D. Nedeljkovic, E. Atie, S. Bole and T. Grosjean, Fiber-integrated optical nano-tweezer based on a bowtie-aperture nano-antenna at the apex of a SNOM tip, Opt. Express, 2014, 22, 10072–10080 CrossRef CAS PubMed.
- D. Yu, B. Blankert, J. Viré and J. Kauffmann, Biosensors in drug discovery and drug analysis, Anal. Lett., 2005, 38, 1687–1701 CrossRef CAS.
- P. B. Luppa, L. J. Sokoll and D. W. Chan, Immunosensors—principles and applications to clinical chemistry, Clin. Chim. Acta, 2001, 314, 1–26 CrossRef CAS.
- J. Mairhofer, K. Roppert and P. Ertl, Microfluidic systems for pathogen sensing: a review, Sensors, 2009, 9, 4804–4823 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |


