Photothermal deflectometry enhanced by total internal reflection enables non-invasive glucose monitoring in human epidermis

Abstract

We present TIR-PTD spectroscopy, an IR-pump/VIS-probe method for the measurement of IR absorption spectra by means of photothermal deflectometry (PTD) enhanced by total internal reflection (TIR). It overcomes the limitations of IR spectroscopy for the study of opaque samples and allows molecular fingerprinting of IR-active liquids or solids. Another important advantage of the presented approach over traditional IR spectroscopy methods is the ability to obtain IR information by means of VIS detection, which is generally much cheaper and easier to handle than IR detection. By application of mid-IR TIR-PTD spectroscopy on human skin in vivo, we are demonstrating the correlation between epidermal- and blood-glucose levels on a type 1 diabetic patient.

---

Introduction

After the absorption of IR light by a sample, the radiationless deexcitation of the vibrational–rotational states produces a temperature increase of the irradiated spot. If the produced heat diffuses to a material in contact with the sample, a temperature gradient resulting in a thermal lens is generated in the coupled material; as seen for instance in the ‘mirage-effect’ in the air layer next to a sun-exposed street. In the past, several authors have demonstrated that the deflection of a probe beam crossing the optically affected field can be used to study the thermal and optical properties of the sample.^1–5 An IR spectroscopic method based on this principle has unique characteristics unmatched by traditional IR spectroscopy approaches; like transmission or attenuated total reflectance IR spectroscopy. Perhaps the most remarkable characteristics are its ability to penetrate deep into opaque samples, the capability of performing spectral depth profiling,^3,6,7 its suitability for highly scattering media, and the fact that in this zero-offset technique the measured signal only depends on the amount of absorbed light; characteristics shared by most of the photothermal- and photoacoustic-based spectroscopic methods.^8–12 However, the realization of such a spectroscopic technique for the analysis of biological samples, especially in vivo, has been limited in part by the weak interaction of the probe beam with the thermal field in the coupling media, and by the complicated optical adjustment requirements between sample, excitation beam, and probe beam. Besides, another limiting factor has been the lack of strong and tunable laser sources in the mid-IR.

We addressed these limitations and were able to enhance the ‘mirage-effect’ by guiding the probe beam directly to the photothermally produced heat source by means of total internal reflection (TIR). This was done using an internal reflection element (IRE) as probe beam guidance also acting as the coupling material. As excitation source we used an external cavity quantum cascade laser (EC-QCL) emitting mid-IR radiation. We were able to demonstrate the potential of the proposed method for the analysis of biofluids or any other IR-active liquid or solid sample. As a promising biomedical application, we could demonstrate the correlation of blood glucose with glucose levels in the epidermis of a type 1 diabetic patient. This IR sensor principle could therefore be the basis for non-invasive glucose measurement for diabetes patients.

Results and discussions

Working principle of the TIR-PTD spectrometer

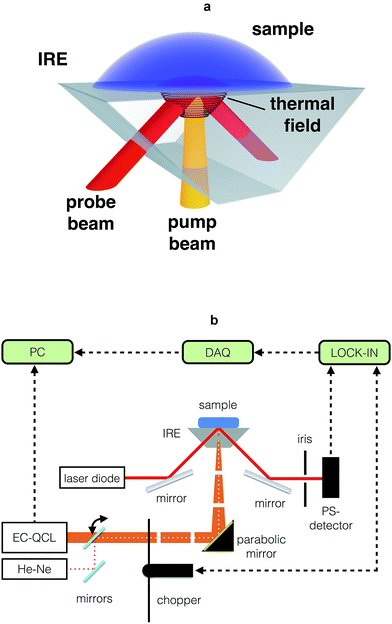
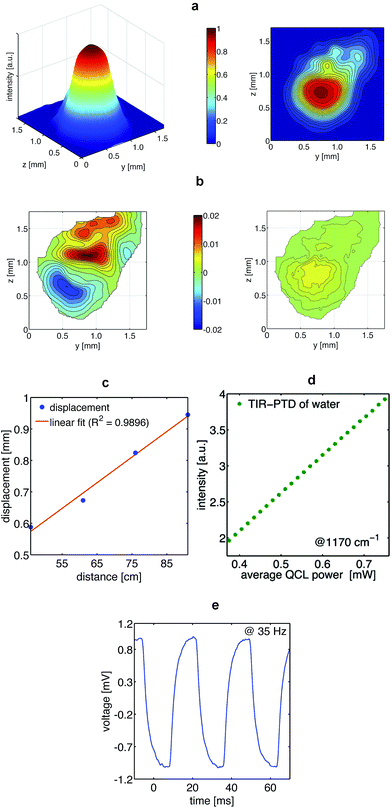
The key components of the TIR-PTD spectrometer are the pump laser, the probe laser, and the internal reflection element (Fig. 1a and b). As pump laser we used an EC-QCL tunable from 1000 cm⁻¹ to 1245 cm⁻¹. This light source has an average power output of 7.5 mW max. for a duty cycle of 5% and a pulse repetition rate ranging from 100 Hz to 100 kHz; for all experiments we used the maximum pulse width of 500 ns. The probe beam is emitted by a laser diode with 5 mW power output at 655 nm and a Gaussian beam intensity profile. The IRE is a truncated right-angle prism (Dove prism) made out of a ZnS crystal cut in such a way that the sloped edges form an angle of 45° with the base. The angle of incidence of the probe beam to the sloped edge of the IRE is adjusted in order to produce total internal reflection at the surface directly below the sample/IRE interface. The pump beam is normal to the truncated base of the prism and it is focused to the spot where the internal reflection of the probe beam is located. The IRE used here has a high transmittance, about 70%, for the pump and the probe beam and it is thus considered ‘transparent’ for both laser beams. With this configuration, the pump beam is adjusted to irradiate the sample at exactly the spot of total internal reflection of the probe beam. The absorption of IR light by the sample and its radiationless relaxation produces a local increase of temperature, which generates a thermal lens in the IRE that deflects the probe beam along the vertical and horizontal direction (Fig. 2a–c). Since the triggering effect is the photothermal deposition of energy in the sample, the intensity of the probe beam deflection, i.e. the deflection angle, depends directly on the output power of the pump laser and on the absorption coefficient of the sample (Fig. 2d and 3a–d); no significant variations in the intensity of the probe beam due to temperature-related changes of its penetration depth in the sample were observed. This photothermal beam deflection is at least 10⁶ higher than the deflection caused by the photoacoustic pressure wave and the Goos–Hänchen displacement and, therefore, both can be neglected.^13–15 By modulating the pump beam, the temperature at the sample/IRE interface and, consequently, the deflection of the probe beam oscillates with the same frequency of the thermal lens generated in the IRE by the sample's IR absorption (Fig. 2e). The latter is the very basic sensing signal for spectroscopy in the presented approach; the amplitude of the modulated deflection of the probe beam measured by a position sensitive quadrant diode detector. The absorption spectrum of a given sample is obtained by recording the output signal of a lock-in amplifier for different wavelengths along the emission range of the EC-QCL (Fig. 1b).

Fig. 1 (a) Principle of the TIR-PTD spectrometer as filed for patent under DE 10 2014 108 424.1 (b) the tunable pulsed QCL is modulated by the chopper and serves as pump laser to irradiate the sample and to produce a thermal field due to IR absorption. This thermal field couples into the IRE where the probe beam from the red laser diode is totally reflected. The irradiation spots of the pump and the probe beam spatially overlap. A refractive index change is induced due to the thermal field, resulting in the deflection of the probe beam. This deflection is measured by an intensity change on a position sensitive photodiode detector. An iris aperture is used to block stray light. The signal at the photodiode is amplified, filtered by a lock-in amplifier and stored on a computer for further processing.

Fig. 2 Characterization of the beam displacement: (a) 3D surface (left) and contour plot (right) of the intensity profile of the probe beam detected by a CMOS sensor (distance from IRE: 46 cm). (b) Beam displacement on the CMOS Sensor due to deflection in the IRE. The undeflected beam profile was subtracted from the deflected beam profile. Left: intensity differences for a water sample with and without IR-excitation. The laser wavelength was set to 1170 cm⁻¹ and the pulse repetition rate to 100 kHz. Right: control with IR-pump beam blocked. The same result is obtained if no sample is located atop of the IRE (data not shown) (c) linear dependence of the CMOS sensor signal with varying detecting distance. (d) TIR-PTD signal of water at 1170 cm⁻¹vs. QCL power, adjusted by the pulse repetition rate. (e) Detector signal transient representing the rise and decay of temperature indicated by deflection. The rise and decay time of the signal are specific for the heat capacity and conduction of the sample and the IRE.

Fig. 3 In vitro measurements on aqueous glucose solutions: (a) TIR-PTD spectra of glucose solutions in the range of 500 to 5000 mg dL⁻¹; glucose is identified by its characteristic peaks. (b) Integrated absorption vs. glucose concentration. The integrated absorbance between 1015 and 1245 cm⁻¹ correlates linearly with the glucose concentration with a regression coefficient of 0.9973. (c) Solid line: principle component 2 (PC2) of the spectra for physiological glucose concentrations (0 to 400 mg dL⁻¹). Dashed line: spectrum at high glucose concentration (5000 mg dL⁻¹) as shown in (a) demonstrating that glucose can be detected with chemometric tools at lower concentrations. (d) PLSR cross validation for spectra of the physiological glucose concentrations, the shaded area indicates the normal glucose concentration range on a healthy person (80–120 mg dL⁻¹).

In vitro and in vivo TIR-PTD spectroscopy of glucose

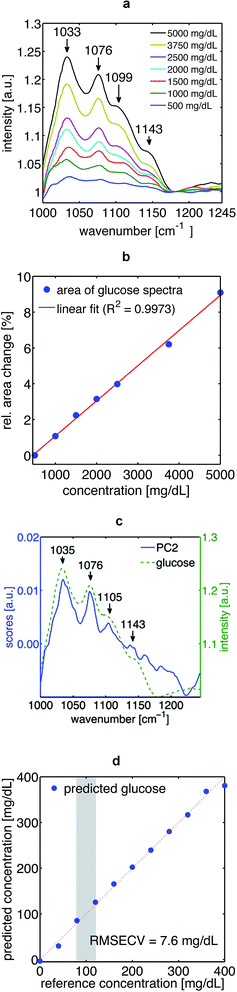
The absorption spectra of aqueous glucose solutions measured by TIR-PTD exhibit, as expected, the well-known spectral features of the glucose molecule in the fingerprint region¹⁶ (Fig. 3a and c). These spectra were obtained with a signal-to-noise ratio (SNR) between 140 and 300, defined as the inverse of the relative standard deviation; meaning that changes as small as 0.3% in the spectral features of a given sample can be detected. The TIR-PTD signal shows a broad linear response with the increase of glucose concentration in the whole range between 0 and 5000 mg dL⁻¹ (Fig. 3b and d). The glucose concentration range from 20 to 400 mg dL⁻¹ is of special interest for a future application in non-invasive glucose monitoring. In this concentration range for glucose in vitro, an error of prediction of 7.6 mg dL⁻¹ was found by partial least square regression.

Additional to the in vitro measurements, the TIR-PTD spectra of a post-prandial type 1 diabetic volunteer were measured for 1 hour (one laser-scan every 6 seconds) after insulin administration. During this time, the glucose concentration in blood, measured by a standard enzymatic device, dropped from 188 to 91 mg dL⁻¹. In general, the mid-IR spectrum of skin in the fingerprint region is dominated by the PO₂⁻ vibrations (symmetric stretch at 1080 cm⁻¹ and antisymmetric stretch at 1240 cm⁻¹), C–O, C–O–C and C=O vibrations (1047 cm⁻¹, 1120 cm⁻¹, 1159 cm⁻¹ respectively). These spectral features are mainly explained by the dominant content of lipids and proteins in skin, in particular, keratin from the Stratum corneum.^17,18 Since the mid-IR spectrum of glucose exhibits the specificity of a molecular fingerprint, it can be detected among the many other IR-active biomolecules in human skin by means of principal component analysis (PCA). Both, the scores of PC2 as well as its loadings fit to the spectral features of glucose in vitro and to the time course of the glucose concentration in blood, respectively (Fig. 4a and b). With this spectral information it was possible to establish a calibration system by means of PLS-regression. With a prediction error of 9 mg dL⁻¹, the leave-one-out cross-validation of this calibration system shows that the glucose concentration in human epidermis correlates well with the glucose concentration in blood (Fig. 4c and d).

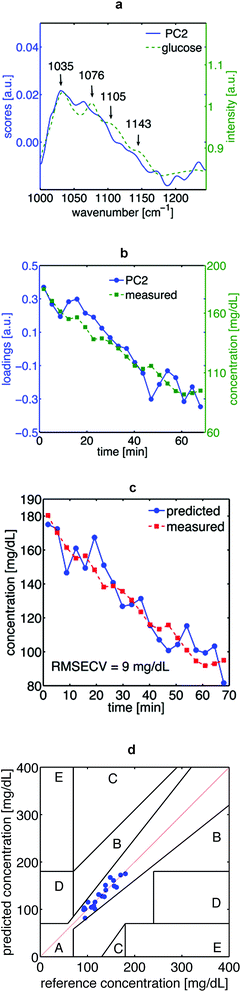Fig. 4 In vivo measurements on a volunteer: (a) solid line: principle component 2 (PC2) of the skin spectra. Dashed line: spectrum at high glucose concentration (5000 mg dL⁻¹) as shown in Fig. 3(a). In general, the scores of PC2 represent most of the spectral features of glucose. However, as seen for the absorption band at 1076 cm⁻¹, some mismatches are expected because of the comparison of glucose measured in different media; skin and water solutions. Besides, the scores of PC2 might show the linear combination of other components in the matrix. (b) Solid line: time course of loadings of PC2 dashed line: time course of invasively measured blood glucose concentration during the test. (c) Cross-validation of the partial least square regression. Dashed line: time course of blood glucose measured invasively. Solid line: non-invasively measured glucose level in the interstitial fluid, as calculated by PLSR, follows without delay the invasively measured blood glucose values. (d) Clarke error grid for the PLSR with 100% of predicted values in zone A (required for clinical applications).

Conclusions

In summary, TIR-PTD make it possible to measure IR absorption spectra of opaque samples at penetration depths for the pump beam only limited by the absorption coefficient and the thermal diffusion length of the sample. Applied to skin, it allows to reach the glucose-containing interstitial fluid in the Stratum spinosum in order to monitor the glucose levels non-invasively and in vivo. By means of TIR-PTD we can obtain spectral information from much deeper layers than what is possible with stablished IR methods like, for instance, attenuated total reflectance IR spectroscopy. The penetration depth for the latter is around 2–4 μm in skin, depending on the wavelength of the excitation beam and the refractive index of the IRE.

Since TIR-PTD is based on the photothermal effect, a depth profiling of the absorption and an analysis of the thermal properties of the samples is possible using different modulation frequencies. The latter opens the possibility of applying the presented setup in some previously reported photothermal-based imaging techniques^6,7 as well as in the analysis of skin properties or biofluids. An additional advantage of this technique is the ability of getting IR information by VIS detection; VIS optics and detectors are generally much cheaper and easier to handle than IR systems.

Material and methods

General description of the TIR-PTD spectrometer

The probe beam emitted by a laser diode (Edmund Optics Modell-no. 57-108) with an average power of 5 mW at 655 nm is focused into the IRE to form a spot with a diameter below 100 μm at the interface between the IRE and the sample. After leaving the IRE the probe beam passes an iris (17 cm behind) to block some stray light and to ensure a clear spot with a maximum size of 1.5 mm at the detector. The vertical deflection of the probe beam was measured using a position-sensitive quadrant photodiode detector (Thorlabs, PDQ80A) located at 18 cm from the irradiated spot. This sensor has a diameter of 7.8 mm, a rise time of 40 ns, and it is sensitive between 400–1050 nm. The modulated signal measured by this detector was filtered and amplified by a lock-in amplifier (SR810, Stanford Research Systems) using a time constant of 100 ms. The pulsed pump beam, focused to form a spot of about 300 μm at the IRE/sample interface, was further modulated by a mechanical chopper (ThorLabs MC 2000) at a frequency of 63 Hz. The thermal diffusion length of the thermal wave thus produced is approximately 30 μm in water.⁶ At this frequency, which served as reference for the lock-in amplifier, the measured spectra yielded the highest SNR and the most stable modulation. The output signal of the lock-in was digitized by a data acquisition card (NI 9239, National Instruments) and stored on a personal computer controlled by LabView (10.0f2, National Instruments) for further processing with MatLab (v. 7.1.0.246 (R14), Mathworks) and the PLS-toolbox (v. 4.01, Eigenvektor) (Fig. 1b).

System characterization

For the characterization and visualization of the photothermal effect and the resulting probe beam deflection, intensity profiles of the probe beam at on/off pump beam were recorded. For these experiments, four detection distances along the probe beam propagation were selected (46, 61, 76, and 91 cm) having the excitation spot as starting point. For detection, a C-mount microscope camera (ToupTek, UCMOS05100KPA-MT9P001) equipped with a 5.1 megapixel CMOS sensor (Aptina MT9P001) containing a pixel size of 2.2 × 2.2 μm was used. With this system, we generated an image stack of a 60 seconds recording window with a rate of nearly 60 fps and a resolution of 640 × 480 pixel. To avoid saturation of the sensor, the exposure time was adapted in the range between 5 and 10 ms and a 5% neutral density filter was placed in the light pathway. Using ImageJ 1.48q, the recorded image stack was transferred into an intensity map containing averaged and normalized intensity values for each pixel. Prior to analysis, a two-dimensional convolution kernel filter handling a 10 × 10 pixel area of the intensity map was used as a post-processing step to smooth out the raw data (MatLab 7.1.0.246 (R14), Mathworks).

Linearity between QCL output power and the probe beam deflection was verified by measuring the TIR-PTD signal of a water sample irradiated at 1170 cm⁻¹ with a fixed chopper frequency (63 Hz) and with different QCL pulse repetition rates; from 50 to 100 kHz in steps of 2 kHz.

For the spectroscopic measurements, the wavelength of the pump beam was scanned across the whole emission range of the EC-QCL; one scan takes about six seconds. In order to increase the SNR of the spectra, multiple scans were averaged: 20 scans for the sample and 50 scans for the reference; a 25 μL drop of water. The actual spectra were calculated by dividing the average of the sample scans by the average of the reference scans.

Spectroscopic measurement and chemometric methods

In order to estimate the sensitivity of TIR-PTD to detect changes in the concentration of an analyte in a simple matrix, i.e. water, two series of aqueous glucose concentrations were measured (sample volume 25 μL). The first series had a glucose concentration from 500 mg dL⁻¹ to 5000 mg dL⁻¹. The spectra measured for this series were normalized by dividing the TIR-PTD signal at each wavenumber by the signal at 1184 cm⁻¹. This wavenumber was selected for normalization because here glucose shows the lowest absorption in the considered spectral range. The second series of glucose spectra, with concentrations in the physiological range, was measured from 0 mg dL⁻¹ to 400 mg dL⁻¹ in steps of 40 mg dL⁻¹. These spectra were analyzed using two chemometric methods: principal component analysis (PCA) and partial least square regression (PLSR). PCA iteratively decomposes the spectral data into principal components (PC) each representing the maximum remaining variance. Every PC is composed of a scores and a loadings vector which represent the PC's spectra and concentration, respectively.¹⁹

For prediction of the glucose concentration from the TIR-PTD spectra, a PLSR was performed. This method is an extension of multiple linear regression that is capable of quantitatively analyzing data that are both noisy and collinear.²⁰ Instead of directly modeling the dependent data, PLSR calculates latent variables that are then used to estimate the dependent data. Similar to the principal components of PCA, these latent variables model the variance and are orthogonal to each other.²¹ However, they additionally have to correlate with the dependent variables. This third condition makes them different from the principal components of PCA and enables quantitative prediction.

Continuous TIR-PTD spectra were measured in vivo on the left hypothenar of a type 1 diabetic volunteer. A set of 400 scans (resulting in 20 spectra) were recorded over 70 minutes during the correction of postprandial glucose values with insulin. Parallel to TIR-PTD spectroscopy, every five minutes the blood glucose concentration was measured by a clinical blood glucometer (Hemocue B glucose analyzer, Hemocue) with a precision of ±4.3 mg dL⁻¹. The resulting spectra were processed by PLSR and PCA. In order to avoid over-fitting, in the PLSR model, the number of latent variables was determined by the minimum RMSECV.²⁰

Abbreviations

TIR	total internal reflection
PTD	photothermal deflection
QCL	quantum cascade laser
EC-QCL	external cavity quantum cascade laser
PA	photoacoustic
IRE	internal reflection element
PCA	principal components analysis
PLSR	partial least square regression
IR	infrared
mid-IR	mid infrared
CMOS	complementary metal-oxide-semiconductor
VIS	visible
SNR	signal-to-noise ratio
RMSECV	root mean square error of cross validation
fps	frames per second

Acknowledgements

The authors would like to thank Ernst Winter, Institut für Biophysik Goethe-Universität, for excellent mechanical engineering. Dr Andreas Roth and Dr Georg Wille are gratefully acknowledged for valuable discussions on electronics and biochemical aspects, respectively. Arne Küderle, a student in our group, is acknowledged for his help with the measurements.

References

1. N. A. George, Appl. Phys. B: Lasers Opt., 2003, 77, 77–80.
2. A. C. Boccara, D. Fournier and J. Badoz, Appl. Phys. Lett., 1980, 36, 130.
3. W. B. Jackson, N. M. Amer, A. C. Boccara and D. Fournier, Appl. Opt., 1981, 20, 1333–1344.
4. R. M. Banish, R.-F. Xiao and F. Rosenberger, J. Appl. Phys., 1988, 64, 2907.
5. M. Pfeifer, A. Ruf and P. Fischer, Opt. Express, 2013, 21, 25643.
6. J. Opsal, J. Appl. Phys., 1982, 53, 4240.
7. A. Rosencwaig, J. Appl. Phys., 1980, 51, 2210.
8. D. V. Bageshwar, A. S. Pawar, V. V. Khanvilkar and V. J. Kadam, Eurasian J. Anal. Chem., 2010, 5, 187–203.
9. C. Haisch, Meas. Sci. Technol., 2012, 23, 012001.
10. C. S. Sunandana, Phys. Status Solidi A, 1988, 105, 11–43.
11. A. Rosencwaig, Adv. Electron. Electron Phys., 1978, 46, 207–311.
12. J. M. Rey, J. Kottman and M. W. Sigrist, Appl. Phys. B, 2013, 112, 547–551.
13. J. C. Murphy and L. C. Aamodt, J. Appl. Phys., 1980, 51, 4580.
14. C.-F. Li, Phys. Rev. A, 2007, 76, 013811.
15. R. Yang, W. Zhu and J. Li, Opt. Express, 2014, 22, 2043.
16. L. P. Kuhn, Anal. Chem., 1950, 22, 276–283.
17. D. T. Downing, J. Lipid Res., 1992, 33, 301.
18. P. Garidel, Phys. Chem. Chem. Phys., 2002, 4, 5671–5677.
19. S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–52.
20. S. Wold and M. Sjostrom, Chemom. Intell. Lab. Syst., 2001, 58, 109–130.
21. W. G. Glen, W. J. D. Ih and D. R. Scott, Tetrahedron Comput. Methodol., 1989, 2, 349–376.

---