Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using solution state NMR spectroscopy to probe NMR invisible gelators†
Matthew
Wallace
*,
Jonathan A.
Iggo
and
Dave J.
Adams
*
Department of Chemistry, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK. E-mail: d.j.adams@liverpool.ac.uk
First published on 21st August 2015
Abstract
Supramolecular hydrogels are formed via the self-assembly of gelator molecules upon application of a suitable trigger. The exact nature of this self-assembly process has been widely investigated as a practical understanding is vital for the informed design of these materials. Solution-state NMR spectroscopy is an excellent non-invasive tool to follow the self-assembly of supramolecular hydrogels. However, in most cases the self-assembled aggregates are silent by conventional 1H NMR spectroscopy due to the low mobility of the constituent molecules, limiting NMR spectroscopy to following only the initial assembly step(s). Here, we present a new solution-state NMR spectroscopic method which allows the entire self-assembly process of a dipeptide gelator to be followed. This gelator forms transparent hydrogels by a multi-stage assembly process when the pH of an initially alkaline solution is lowered via the hydrolysis of glucono-δ-lactone (GdL). Changes in the charge, hydrophobicity and relative arrangement of the supramolecular aggregates can be followed throughout the assembly process by measuring the residual quadrupolar couplings (RQCs) of various molecular probes (here, 14NH4+ and isopropanol-d8), along with the NMR relaxation rates of 23Na+. The initially-formed aggregates comprise negatively charged fibrils which gradually lose their charge and become increasingly hydrophobic as the pH falls, eventually resulting in a macroscopic contraction of the hydrogel. We also demonstrate that the in situ measurement of pH by NMR spectroscopy is both convenient and accurate, representing a useful tool for the characterisation of self-assembly processes by NMR.
Introduction
Solution state NMR spectroscopy has been widely used to follow non-invasively the self-assembly of low molecular weight gelators (LMWGs) into supramolecular gel networks.1–3 However, most studies consider only the resonances of the gelators in solution as the self-assembled aggregates are usually not visible by solution-state NMR spectroscopy due to the very low mobility of the assembled molecules. By studying the resonances of the free gelator molecules, which generally decrease in intensity, broaden and shift in frequency as the molecules assemble,4,5 it is possible to obtain valuable information on the hydrogels, including the ratio of assembled to unassembled gelator,6,7 the kinetics of network formation,8 component selection,9 and the thermal stability of the gel networks.6,10,11 Nevertheless, by conventional solution-state 1H NMR spectroscopy it is not possible to probe the nature of the initially formed supramolecular aggregates or follow any subsequent rearrangement these may undergo en route to the final gel. Solid state NMR has been used in some cases,12,13 but the low concentration of the LMWG often precludes a detailed understanding, especially in the solvated state.We recently demonstrated that NMR-strength magnetic fields can induce significant anisotropy in the arrangement of the fibrillar aggregates formed by certain dipeptide gelators. This anisotropy manifests as splittings of the NMR resonances of deuterated probe molecules present in solution (D2O and/or water miscible deuterated organic solvents) that transiently interact with the gelator aggregates.14 We showed that the magnitude of the line splitting observed, the residual quadrupolar coupling (RQC), depends not only on the relative alignment of the gelator aggregates but also on the nature of the surface interaction between the aggregates and the deuterated solutes.
The nature of the fibre-solution interface is increasingly recognised as important for an understanding of both the final hydrogel and the process by which it forms; however, it is extremely difficult to study.15,16 Here, we show that a range of NMR probes including deuterated solvents and quadrupolar ions (23Na+, 14NH4+) can be used to follow the entire gelation process of a dipeptide gelator from a solution of mobile molecules at high pH to a hydrophobic gel network at low pH. This approach allows us to gain significant insight into the self-assembly process as well as providing a means of understanding key parameters such as the charge and hydrophobicity of the self-assembled fibres. Approaches similar to ours have been used to glean valuable information on surface-solute interactions in a variety of systems including clays and liquid crystals.17–20
Results and discussion
Functionalised dipeptides can be extremely effective gelators.21–23 We have previously shown that gels with highly reproducible rheological properties are formed on lowering the pH of solutions of a number of functionalised-dipeptide low molecular weight gelators.24,25 To form the gels, a solution of the dipeptide at high pH is first prepared. Hydrolysis of glucono-δ-lactone (GdL) to gluconic acid26 is then used to cause a slow and uniform lowering of the pH which triggers gelation.24 Since the hydrolysis occurs over hours, we are able to probe the assembly over time. We used NMR to monitor the disappearance of the gelator from solution;24,25 however, as the self-assembly proceeds, solid-like self-assembled fibres are formed which are NMR invisible. This is a common observation for many low molecular weight gelators triggered by different methods.Here, we focus on a single gelator (1, Scheme 1), the self-assembly process of which we have previously studied using a range of techniques including circular dichroism, fibre X-ray diffraction, fluorescence and electron microscopy.27,28 This has allowed us to compare and verify the new techniques outlined here against our previous data. This gelator begins to form gels at the apparent pKa of the terminal carboxylic acid (5.8) and the gel is formed by an entangled network of fibres.27
Solution pH is obviously an important parameter in studies of GdL triggered gelation. Previous studies have correlated NMR data with ex situ parallel pH measurements. For the present study, we have developed an in situ method to follow the pH of the system using NMR spectroscopy. The method is based on the pH dependence of the chemical shifts of groups of nuclei within molecules possessing acid/base behaviour in water and has previously been reviewed in detail.29–31 A full description of the specific methods used in the present work is provided in the Methods section below.
To probe the self-assembly process, NH4Cl and isopropanol-d8 (IPA) were added to the solution for 14N and 2H NMR studies respectively. Briefly, as stated above, when these probe molecules interact with anisotropic structures in solution, a residual quadrupolar coupling (RQC) is observed (Scheme 1c) which depends on both the anisotropy of the structures and the affinity of the probe for their surfaces. 14NH4+ can be expected to have a significant affinity for negatively charged carboxylate sites on the gel fibres while IPA, a molecule with surfactant-like behaviour,32 will have a higher affinity for more hydrophobic sites. Thus, by studying how the relative RQCs of 14NH4+ and IPA change during the assembly process we can infer how the charge and hydrophobicity of the self-assembled fibres are evolving. To further probe assembly, the T1 and T2 relaxation times of 23Na+ were also recorded. A decrease in the mobility of Na+ ions due to interaction with, for example, carboxylate sites on the gel fibres results in a decrease in both T1 and T2. The 23Na+T1 and T2 may thus reflect the 14NH4+ RQCs to some extent. A more complete discussion of the theory of RQCs and 23Na relaxation pertinent to the present study is provided in the Methods section below.
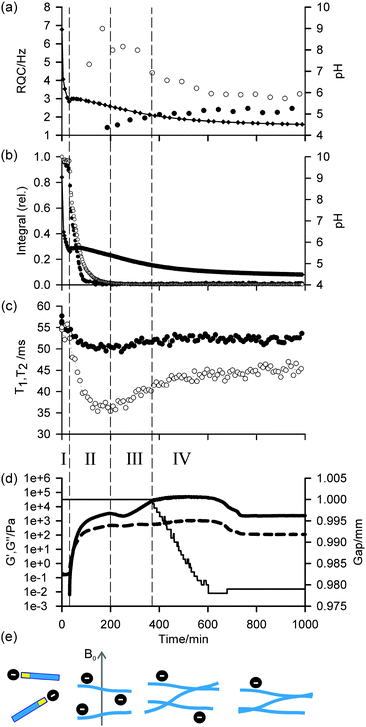
Profiles of the pH, 1H integrals of 1, RQCs of 14NH4+ and IPA, and rheological data (storage modulus (G′) and loss modulus (G′′)) versus time as the sample gelled are shown in Fig. 1. The data points at t = 0 were recorded on the sample prior to the addition of GdL. Due to time limitations during the experiment, the 23Na relaxation measurements and gelator integrals were recorded on a different sample to that on which the 14NH4+ and IPA RQCs were recorded. Nevertheless, the pH profiles in all experiments were very similar and so the data are directly comparable. Importantly, the rheological properties, pH, RQCs of IPA and NH4+, integrals from 1 and the 23Na+T1 and T2 values follow similar profiles in the presence/absence of NH4Cl and IPA and so we can be confident that the inclusion of these probe molecules does not significantly affect the gelation process (ESI,† Section 4). Gels prepared in the presence and absence of the strong magnetic field of the NMR instrument were found to have similar final mechanical properties (ESI,† Section 15).
In agreement with our previous rheological investigation of a similar system,33 four distinct phases can be identified. These phases can be summarised as follows: in phase I, the gelators are not assembled into large structures and behave as free molecules. During phase II, the gelators assemble into large fibrillar structures which possess a significant negative charge while the rheological properties of the sample develop into those of a cross-linked network. In phase III, the network loses some of its negative charge leading to stronger fibre–fibre interactions and a large increase in mechanical strength. During phase IV, the stronger fibre–fibre interactions lead to a significant macroscopic contraction of the entire gel network. These four phases, which are sketched in Fig. 1e, are now discussed in detail.
During phase I, the pH falls rapidly while the gelator remains mobile in solution with essentially all of the gelator detectable by NMR, as measured in the absence of GdL against an internal standard capillary. The aromatic resonances shift upfield while the valine methyl resonances remain at a relatively constant frequency (ESI,† Section 5), suggesting the gelators may be assembling into micellar structures with the naphthalene rings forming the hydrophobic core.4 The resonance of the α-proton of the valine residue does not shift significantly, indicating that the NMR-visible gelator remains deprotonated during this phase. The resonances of 14NH4+ and IPA remain as sharp single lines (Fig. 2a; ESI,† Section 6) and the 23Na+T1 and T2 are similar to those in a comparable solution in the absence of gelator which were measured as (56 ± 1) ms and (55 ± 2) ms respectively (ESI,† Section 7). In phase I, the rheological properties of a parallel sample are that of a liquid, with G′ and G′′ both being essentially zero. Solutions of 1 at high pH have comparatively low viscosity34 and the self-diffusion coefficient of 1 at pH 9 was measured as 4.1 × 10−10 m2 s−1 using pulsed field gradient NMR (PFG-NMR) which, from the Stokes–Einstein equation, corresponds to a hydrodynamic diameter of approximately 1.2 nm. We were unable to detect any structures using confocal microscopy. These observations indicate that, at this stage, the gelator behaves predominantly as free molecules and has not yet assembled into fibrillar structures such as the wormlike micelles formed by related gelators,34 although the transient existence of micellar aggregates cannot be ruled out.
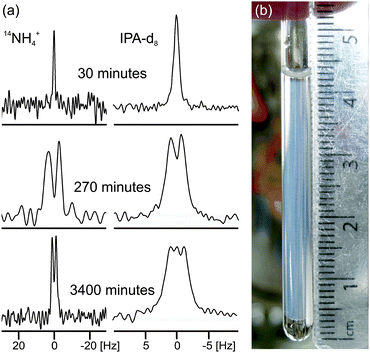 | ||
| Fig. 2 (a) Experimental 14N and 2H NMR spectra of sample from Fig. 1a at different times since addition of GdL to a solution of the gelator at high pH. The spectra have been scaled to account for the different number of transients recorded at different stages of gelation. (b) Photograph of the gel sample of Fig. 1a, 4000 minutes after GdL addition. The transparent exuded fluid is apparent above and below the slightly translucent gel. The NMR active region of the sample is centred at 18 mm from the base of the tube and stretches 8 mm either side. | ||
At the end of phase I, the pH rises followed by a gently falling plateau (phase II). This rise in pH is also observed using a conventional pH meter (Fig. 4) and is attributed to a sudden increase in the pKa of the gelators upon self-assembly.35–37 Self-assembly of the gelators is evidenced by a number of observations: there is a sudden increase in the mechanical properties of the parallel sample, G′ being initially approximately equal to G′′ but gradually increasing to dominate as gelation begins. There is a dramatic decrease in the amount of NMR-visible gelator while the aromatic resonances of the gelator display an abrupt downfield shift consistent with a phase separation between the mobile NMR-visible gelator in solution and the NMR-silent structures (ESI,† Section 5). The integral of the valine methyl groups decreases at a noticeably slower rate than that of the aromatic protons, pointing to a lower degree of mobility of the naphthalene ring as the gelator interacts/exchanges with the NMR silent aggregates. The 23Na+T1 and T2 both decrease sharply while a splitting of the 14NH4+ resonance becomes apparent, observations which strongly suggest these aggregates are anisotropically oriented fibrillar structures that possess a significant negative charge. We attribute these observations to the formation of worm-like micelles in which the naphthalene rings form the core of the micelles, stabilised by the charged carboxylates.34 The existence of such charge on the surface of fibres formed by related gelators has previously been suggested;36 however, this had been extremely difficult to prove experimentally. For example, previous investigations of the 1/GdL system by infra-red spectroscopy were inconclusive as to the protonation state of the carboxylates.27 We note here that the slight anisotropy that gives rise to the RQCs is due to the presence of the magnetic field during self-assembly since no RQCs are observed in samples prepared away from the field (ESI,† Section 8). Towards the end of phase II, the pH again begins to fall. The 14NH4+ RQC passes through a maximum before beginning to decrease while the 23Na+T1 and T2 pass through a minimum and a RQC for the IPA becomes apparent. At the end of phase II, all of the gelator has assembled into NMR invisible structures and G′ exceeds G′′ by approximately one order of magnitude, indicating a cross-linked network has been formed. The existence of thin fibrils at this stage has previously been demonstrated by TEM.27
During phase III, the pH continues to decrease as does the 14NH4+ RQC, while the 23Na+T1 and T2, and the IPA RQC all increase. These observations are consistent with the self-assembled structures becoming less charged and more hydrophobic. G′ and G′′ decrease before increasing again towards a second plateau, while the normal force experienced by the upper measurement plate of the rheometer decreases (ESI,† Section 14). These observations suggest that the sample may be undergoing syneresis and contracting slightly as the fibrils pack together, resulting in a weaker contact between the measurement plate and the sample. The monotonic decrease and singularity of the 14NH4+ RQC and increase in the IPA RQC suggest that charge is gradually and uniformly lost from the fibres rather than in ‘patches’, as previously proposed for a related system.33 This would instead lead to broad lineshapes with unresolvable splittings comprising superpositions of different RQCs. If any patches do form, they are smaller than the length scales, l, probed by the observed molecules given approximately by the expression:38
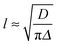 | (1) |
In the final phase, phase IV, the rate of pH decrease slows as does the rate at which the NMR parameters are changing. The gel continues to contract and the rheometer decreases the gap between the plates in order to maintain a constant normal force of 0 N. The apparent G′ has reached a plateau; however, the contraction of the gel eventually leads to a decrease in the apparent G′ and G′′ at long times. During this phase, the 14NH4+ and IPA RQCs and the 23Na+T1 and T2 approach a plateau and a singlet (isotropic) peak becomes visible in the 2H and 14N NMR spectra between the doublet peaks of IPA and 14NH4+ (ESI,† Section 6) suggesting that, from eqn (1), the contraction has produced regions of bulk fluid of almost macroscopic dimensions. Such regions are apparent in the final gel (Fig. 2b). The isotropic component of the IPA resonance in this gel is ca. 20% the area of the doublet which, assuming the isotropic resonance arises solely from bulk fluid exuded during the contraction of the gel and thus comprises ca. 20% of the sample volume, would require a concentric contraction of the gel by only 10% (0.2 mm). From Fig. 2b, the longitudinal contraction of the gel is of a similar extent. That such a concentric contraction takes place is supported by chemical shift imaging (CSI) analysis of the sample which demonstrated that the sample was homogeneous throughout the NMR-active region (ESI,† Section 9), and by the observation that the gels could fall down to the base of the tube if knocked. Time-lapse photography of a parallel sample during gelation revealed that the macroscopic contraction of the gel approximately coincides with the appearance of the resonance of the isotropic phase in the NMR spectra (ESI,† Section 10). The isotropic peak first becomes apparent on the 14NH4+ resonance after approximately 700 minutes and on the IPA resonance after 500 minutes (ESI,† Section 6). The isotropic component of the IPA resonance is noticeably larger than that of the 14NH4+, which becomes obscured as the RQC decreases. Such differences are readily explained by eqn (1), the more slowly diffusing IPA being more sensitive to the presence of the isotropic phase than the more rapidly diffusing NH4+. Analysis of gel samples by confocal microscopy was inconclusive as the self-assembled structures were below the resolution of our microscope and no structures could be discerned. Nevertheless, previous studies of the 1/GdL system by TEM demonstrated that the extent of lateral association of the gel fibres increases as the pH falls, in agreement with the results presented here.27
Increasing the GdL concentration to 10 mg mL−1 led to a significantly lower final pH (3.9 versus 4.3), faster gelation kinetics and, as has previously been reported,27 very similar final mechanical properties to the gel formed using 5 mg mL−1 GdL (ESI,† Section 11). For this gel, the 14NH4+ RQC was substantially smaller than that of IPA, 1.2 Hz versus 2.8 Hz (ESI†), which compares to 2.2 Hz and 2.4 Hz respectively at pH 4.3 with 5 mg mL−1 GdL. The 23Na+T1 and T2 values were (52 ± 1) ms and (49 ± 1) ms respectively, compared to (52 ± 1) ms and (48 ± 1) ms with 5 mg mL−1 GdL. These observations suggest the fibres at this lower pH are significantly less charged. Macroscopically, this sample had contracted to a similar extent as the sample prepared with 5 mg mL−1 GdL. As expected,24,27 decreasing the GdL concentration to 4 mg mL−1 resulted in a higher final pH of 4.8 and a 14NH4+ RQC substantially larger than that of IPA, 5.3 Hz versus 3.3 Hz (ESI,† Section 12), and 23Na+T1 and T2 values of (52 ± 1) and (44 ± 1) ms respectively. Both of these observations are consistent with the gel fibres at this higher pH possessing more negative charge.
Based on the theory described in the Methods section below, we can quantify the fraction of charged carboxylate sites, f−, on the fibres during the gelation process as follows: if we assume that the observable 14NH4+ and IPA RQCs arise mostly from charged and uncharged sites and are thus directly proportional to f− and (1 − f−) respectively, then assuming KSb(∂f−/∂t) ≫ Kf−(∂Sb/∂t), f−Sb(∂K/∂t) the following relation should hold:
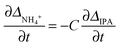 | (2) |
 | (3) |
ΔNH4+ (t) = ΔNH4+ (0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−k′(t − t0)β] + ΔNH4+(∞) exp[−k′(t − t0)β] + ΔNH4+(∞) | (4) |
| ΔIPA(t) = ΔIPA(∞)[1 − exp[−k′(t − t0)β]] + ΔIPA(0) | (5) |
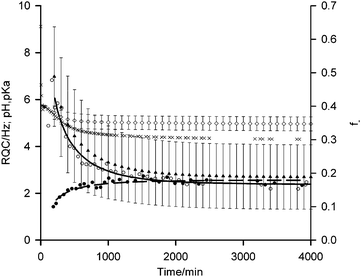 | ||
| Fig. 3 Plots of 14NH4+ (white circle) and IPA (black circle) RQCs from Fig. 1a, extended to 4000 minutes along with pH data (black cross). Fits of RQC data to eqn (4) and (5) are shown by solid and dashed lines respectively. f− (black triangle) and pKa (white diamond) values of carboxylate groups on the gel fibres, estimated using eqn (3)–(5), are shown with error bars calculated using the method described in the ESI,† Section 13. | ||
According to our fitting, at 200 minutes 50 ± 15% of the carboxylates are deprotonated at a pH of 5.4 corresponding to a pKa of 5.4 ± 0.3. This agrees well with the ‘apparent’ pKa of 5.8 determined via the titration of a solution of 1 with HCl.41 As time progresses, the pH falls to 4.3 after 4000 minutes with 20 ± 10% of the carboxylates remaining deprotonated corresponding to a pKa of 4.9 ± 0.3. These findings suggest that the significantly elevated apparent pKas of peptide-based gelators determined by conventional potentiometric titration with HCl, as reported in many studies,4,27,36,37,41–43 may be due to electrostatic rather than hydrophobic effects. It is known, for example, that the ionisation of one glutamic acid residue in a protein greatly elevates the pKa of a neighbouring un-ionised residue.44 If hydrophobic effects exerted the dominant influence, the pKa would be expected to increase with time while the fibres at pH 4.3 would be largely uncharged. The assertion that the fibres at such a low pH remain significantly charged is supported by the 23Na+T1 and T2 values which remain significantly below their values measured in the absence of gelator.45
Conclusions
We have shown that 1H, 2H, 14N and 23Na solution-state NMR can be used to follow the entire self-assembly process of a dipeptide gelator. In common with previous studies, we find assembly to be a multi-stage process driven by the gradual loss in charge from the gelator as the pH falls. However, for the first time, we are able to study changes to the relative hydrophobicity and charge of the self-assembled aggregates when the gelators themselves have become invisible by solution state 1H NMR. 2H, 14N and 23Na NMR reveal that the initially-formed fibrillar aggregates bear a very significant negative charge with perhaps as many as 50% of the carboxylates deprotonated. As this charge is lost, the fibres become more hydrophobic and show stronger inter-fibre interactions, the apparent mechanical properties of the gel network becoming substantially higher; however, these interactions eventually lead to the macroscopic contraction of the gel. Nevertheless, the final gel at pH 4.3 still possesses a significant negative charge. Our methods thus allow, in an essentially non-invasive way, the characterisation of the fibre-solution interface. These methods may thus provide further valuable insight into self-assembly processes of supramolecular hydrogels and allow the more informed design of controlled release systems based on guest-network interactions.Methods
In situ pH determination using NMR spectroscopy
The pH of the solution relates to the observed chemical shift and pKa of the indicator molecule via the modified Henderson–Hasselbalch equation:31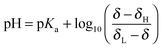 | (6) |
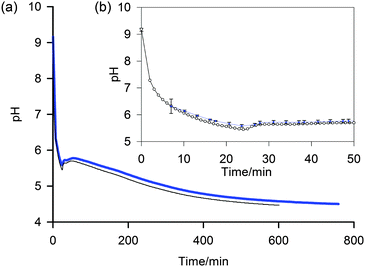 | ||
| Fig. 4 (a) Plot to compare the pH determined by the NMR method (blue, thick) with data from a conventional pH meter (black, thin) of a 5 mg mL−1 sample of 1 after the addition of GdL. (b) Expansion to show early stages of gelation and individual data points (NMR method – blue diamond, pH meter – white circle). Uncertainties in the pH determined via the NMR method, shown as error bars, were calculated using the method described in the ESI.† | ||
Residual quadrupolar couplings (RQCs)
Nuclei with a spin quantum number (I) greater than 1/2 (e.g.2H: I = 1, 14N: I = 1, 23Na: I = 3/2) possess an electric quadrupole moment which interacts with electric field gradients (EFGs) present at the nucleus. EFGs can arise intramolecularly, such as along the O–D bond in D2O,46 or intermolecularly as with sodium ions condensed on the surface of clay platelets.47 The effect of the EFG is to split the degeneracy of the 2I transitions of the nucleus. In isotropic solutions, the splitting is averaged to zero by rapid molecular tumbling; however, if the observed molecules in solution interact with anisotropically oriented structures, such as gel fibres, present in the sample then this averaging is incomplete and a small line splitting – a residual quadrupolar coupling (RQC, Δ) – is observed which is given by:17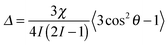 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 denoting a time average. In the simplest case of fast exchange of molecules between isotropic solution and a single type of binding site on an anisotropic structure, the RQC is described phenomenologically by:
〉 denoting a time average. In the simplest case of fast exchange of molecules between isotropic solution and a single type of binding site on an anisotropic structure, the RQC is described phenomenologically by:| Δ = fbΔb | (8) |
| Δ = fbSbK | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb − 1〉 and K = 3χ/4I(2I − 1).
θb − 1〉 and K = 3χ/4I(2I − 1).
If the relative RQCs of two probe molecules with different chemical characteristics, such as charge and hydrophobicity, change, then the nature of the surface of the gel fibres is also changing. This hypothesis is supported by our previous work in which a significant RQC was found for dioxane-d8 with hydrophobic self-assembled fibres, but a negligible RQC was found for D2O. Conversely, highly charged fibres gave a large RQC for D2O and only a small RQC for dioxane-d8.14 Here, we use 14NH4+ as a probe for negatively charged sites and the methanetriyl deuteron of IPA as a probe of uncharged hydrophobic sites. D2O, dioxane-d8, DMSO-d6 and CD3CN were tried as probe molecules but found not to give observable RQCs, possibly due to a lower degree of magnetic-field-induced anisotropy in 1/GdL gels than in the gels studied in our previous work.14 We attribute the sensitivity of IPA to its relatively high affinity for hydrophobic surfaces coupled with its restricted mobility when associated with such surfaces32 and the relatively large EFG present at the methanetriyl deuteron. Although some splitting of the 23Na+ resonance was apparent (ESI,† Section 2), this was insufficient for reliable RQCs to be extracted and the −1/2 ↔ 1/2 transition of this I = 3/2 nucleus would obscure the coexisting isotropic phase present in gels formed from 1.
23Na T1 and T2 relaxation
The relaxation of 23Na+ is dominated by the fluctuating quadrupolar coupling the ions experience as they diffuse in solution and transiently interact with any large immobile structures present. In the absence of such structures, or with a low volume fraction of relatively small structures such as spherical micelles, the ‘extreme narrowing’ condition is expected to apply within which T1 ≈ T2, with both time constants similar to those measured in the absence of gelator.50 Upon the formation of larger structures, the motion of 23Na+ will be reduced and both T1 and T2 will decrease, the latter to a significantly greater extent.51 The use of 23Na+ relaxation measurements to follow the formation of supramolecular hydrogels has previously been explored by Raue et al.52 These authors found that T2, and to a lesser extent T1, decreased significantly upon the thermally-induced gelation of a succinamic acid–based gelator in saturated NaHCO3 solution. This was attributed to a significant interaction between the Na+ ions and the carboxylate groups on the gel fibres. Although T2 is affected by the anisotropy of the structures present,47,53 in the present study the small size (<30 Hz) of the observed RQCs and the essentially monoexponential nature of the CPMG signal decays (ESI,† Section 3) suggest that, qualitatively, this effect can be ignored. The 2H T1 and T2 relaxation times of HDO and the methyl groups of IPA were found not to change significantly during the gelation process.Experimental
Materials
Gelator 1 was synthesised as described previously.27 All other chemicals were purchased from Sigma-Aldrich and used as received.Preparation of samples
A stock solution of NMR pH indicator compounds was prepared containing sodium formate (0.4 M), glycine (0.2 M), methyl phosphonic acid (0.2 M), sodium acetate (0.2 M), sodium methanesulfonate (0.1 M) and sodium hydroxide (0.6 M). Stock solutions of 1 at 5 mg mL−1 were prepared by dispersing an appropriate amount of the dipeptide in water before adding 1.2 ± 0.1 equivalents of standardised NaOH and stirring for at least six hours to form a transparent solution. After stirring, an appropriate volume of the NMR indicator solution was added to give the concentrations listed in the text. NH4Cl was added as an 0.5 M stock solution to give a final concentration of 10 mM for 14N NMR studies. The pH of the solutions was 9. Isopropanol-d8 (IPA, 0.05 vol%, 7 mM) was also added for 2H NMR studies.All gelled samples, unless otherwise stated, were prepared at a GdL concentration of 5 mg mL−1. Typically, 700 μL of a solution of 1, with additives, was transferred to a pre-weighed amount of GdL in a 14 mL glass vial. After dissolution of the GdL with gentle swirling, the solution was promptly transferred to a 5 mm NMR tube for analysis. The time quoted is the total time elapsed since the dipeptide solution was added to the GdL.
NMR
All NMR experiments were performed on a Bruker Avance II 400 MHz (1H) wide bore spectrometer operating at 400.20 MHz for 1H, 105.86 MHz for 23Na, 61.43 MHz for 2H and 28.91 MHz for 14N. All NMR experiments were performed off lock in H2O at 298 ± 0.5 K. 1H spectra were recorded in a single scan with presaturation applied to the H2O resonance for 5 s followed by a spoil gradient pulse (27 G cm−1, 1 ms) prior to a π/2 hard pulse and signal acquisition. 65536 data points were acquired with a sweep width of 15 ppm, giving a total acquisition time of 35 s with a 25 s delay at the start of the experiment prior to any pulses so that, as far as possible, the integrals obtained could be used quantitatively. Presaturation was found not to significantly suppress any resonances of 1. 2H spectra were recorded via the lock channel with 1964 data points, a 200 μs pulse (70°) and a sweep width of 8 ppm. At the start of the gelation experiment, 256 transients were acquired giving an acquisition time of 10 minutes. Once significant structure formation had occurred and the RQC of the methanetriyl resonance of IPA was appreciable, the number of transients was increased first to 512 and then to 1024, giving acquisition times of 20 and 40 minutes respectively, in order that spectra with acceptable signal to noise ratios could be obtained. Once the sample had stabilised at low pH, the number of transients was increased to 2048 giving an acquisition time of 90 minutes. 14N{1H} spectra were acquired with the aring sequence (π/2–τ–π/2–τ–π/2-acquire) in order to suppress acoustic ringing effects in our probe. A 46 μs π/2 pulse was used with a τ of 4 μs and a relaxation time of 0.1 s. CPD was applied (Waltz 16) during the pulses and signal acquisition in order to remove the effect of 14N–1H coupling. 578 data points with a sweep width of 10 ppm were acquired in 256 and 1024 transients prior to and after significant structure formation had occurred giving acquisition times of 5 and 20 minutes respectively. Once the sample had stabilised at low pH, the number of transients was increased to 2048 giving an acquisition time of 40 minutes. 23Na T1 and T2 were measured using the inversion-recovery and CPMG pulse sequences respectively. For T1, the inversion recovery time, t, was varied between 1 and 300 ms in 8 steps. For T2, the spacing between the π pulses was fixed at 1 ms and the number of pulses varied between 2 and 256 in 8 steps. 32 transients were collected in 6144 points with a 100 ppm sweep width and a relaxation delay of 0.1 s, giving an acquisition time of 2 minutes for both T1 and T2 measurements. For each sample, the 23Na π/2 pulse was calibrated at high pH prior to the addition of GdL using the Bruker optimisation procedure POPT, typical π/2 pulses being 34 μs in duration. PFG-NMR experiments to determine the diffusivity of 1 at high pH were performed using a double stimulated echo sequence (Bruker pulse program library dstegp3s) with presaturation applied to the H2O resonance during the relaxation delay (5 s) and diffusion delay periods. The gradient pulses, of 4 ms duration, were incremented in 32 steps with 48 transients from 2.7 G cm−1 to a maximum of 51 G cm−1, with the final value chosen so that the signal from 1 had completely decayed into the baseline. The signal decay curves could be fitted with one component to the modified Stejskal–Tanner equation54 with no slower component detectable. The diffusion coefficient thus obtained was found to be invariant of the diffusion delay time between 0.1 and 0.4 s. The diffusivity of IPA was measured at 0.05 vol% in H2O using non-deuterated IPA, following the same procedure used for 1. The diffusion coefficient was found to be invariant of the diffusion delay between 0.1 and 0.3 s.Data processing
All data was processed in Bruker Topspin 3.2 and Microsoft Excel 2010. No line broadening factor was applied to 2H or 14N spectra; however, prior to Fourier transformation the raw FIDs were trimmed to ensure a sufficient signal-noise ratio for analysis. For 14N spectra, the last data point containing signal was judged by eye, with a minimum of 300 experimental data points being used in the transformation. For 2H spectra, the first 1200 points were used where 512 transients had been recorded while 1400 points were used where 1024 or 2048 transients had been acquired. 2H RQCs of IPA were extracted by deconvolution of the spectra into overlapping Lorentzian lines; example fits are shown in the ESI,† Section 6. 14NH4+ RQCs were taken as the separation between the peak maxima of the doublet. Due to the poor signal to noise ratios and larger RQCs relative to IPA, Lorentzian deconvolution could not be expected to yield more accurate values. The time at which an RQC was recorded was taken as half way through the NMR acquisition. Uncertainties in f− calculated using eqn (3)–(5) were estimated using a Monte Carlo method based on that of Lambert et al.,55 discussed in the ESI,† Section 13. 23Na T1 and T2 values were extracted by fitting the data to eqn (10) and (11) respectively using a non-linear regression method developed for Microsoft Excel:56| I = I0[1 − P·exp(t/T1)] | (10) |
| I = I0exp(−t/T2) | (11) |
Rheology
All experiments were performed using an Anton Paar Physica MCR301 rheometer with parallel plate geometry. To run a time sweep, 2 mL of solution was mixed with GdL and transferred to the stationary (silicon rubber) lower plate whereupon the upper plate (50 mm, sandblasted) was lowered onto the sample to a gap of 1 mm. Low viscosity mineral oil was placed around the edge of the sample to prevent drying artefacts. G′ and G′′ were recorded at a frequency of 10 rad s−1 and 0.5% strain, a data point being recorded every 15 s for 15 hours. The gap between the measuring plates was adjusted automatically in order to maintain a constant normal force on the upper measuring plate. This adjustment was necessary as the sample was found to contract significantly during the experiment. The temperature of the sample was maintained at 25 °C.pH measurements
Unless otherwise stated, all pH measurements were obtained in situ using the NMR method. The ex situ measurements of Fig. 4 were obtained using a Hanna Instruments HI-2020 Edge pH logger equipped with an FC2020 probe. The stated accuracy of these measurements is ±0.01 units. Prior to use, the meter had been calibrated with fresh pH 4, 7 and 10 buffer solutions. The sample, of 2 mL volume in a glass container, was held at 25 °C in a thermostatic water bath. The same mixture of 1 and GdL was used for both in situ and ex situ data series on Fig. 4.Acknowledgements
We thank Andre Zamith Cardoso for collecting confocal microscopy images. We thank Unilever for a Case Award (MW) and the EPSRC for funding a DTA (MW). We thank the EPSRC for funding (EP/C005643/1 and EP/K039687/1). DA thanks the EPSRC for a Fellowship (EP/L021978/1).Notes and references
- Y. E. Shapiro, Prog. Polym. Sci., 2011, 36, 1184–1253 CrossRef CAS PubMed.
- G. Yu, X. Yan, C. Han and F. Huang, Chem. Soc. Rev., 2013, 42, 6697–6722 RSC.
- B. Escuder, M. Llusar and J. F. Miravet, J. Org. Chem., 2006, 71, 7747–7752 CrossRef CAS PubMed.
- A. Reddy, A. Sharma and A. Srivastava, Chem. – Eur. J., 2012, 18, 7575–7581 CrossRef CAS PubMed.
- Nonappa, D. Šaman and E. Kolehmainen, Magn. Reson. Chem., 2015, 53, 256–260 CrossRef CAS PubMed.
- A. R. Hirst, I. A. Coates, T. R. Boucheteau, J. F. Miravet, B. Escuder, V. Castelletto, I. W. Hamley and D. K. Smith, J. Am. Chem. Soc., 2008, 130, 9113–9121 CrossRef CAS PubMed.
- V. J. Nebot and D. K. Smith, Functional Molecular Gels, The Royal Society of Chemistry, 2014, pp. 30–66 Search PubMed.
- S. S. Rohner, J. Ruiz-Olles and D. K. Smith, RSC Adv., 2015, 5, 27190–27196 RSC.
- W. Edwards and D. K. Smith, J. Am. Chem. Soc., 2014, 136, 1116–1124 CrossRef CAS.
- M. M. Smith and D. K. Smith, Soft Matter, 2011, 7, 4856–4860 RSC.
- M. Tena-Solsona, B. Escuder, J. F. Miravet, V. Casttelleto, I. W. Hamley and A. Dehsorkhi, Chem. Mater., 2015, 27, 3358–3365 CrossRef CAS.
- S. Iqbal, F. Rodriguez-Llansola, B. Escuder, J. F. Miravet, I. Verbruggen and R. Willem, Soft Matter, 2010, 6, 1875–1878 RSC.
- Nonappa, M. Lahtinen, B. Behera, E. Kolehmainen and U. Maitra, Soft Matter, 2010, 6, 1748–1757 RSC.
- M. Wallace, A. Z. Cardoso, W. J. Frith, J. A. Iggo and D. J. Adams, Chem. – Eur. J., 2014, 20, 16484–16487 CrossRef CAS PubMed.
- J. Tritt-Goc, A. Rachocki and M. Bielejewski, Soft Matter, 2014, 10, 7810–7818 RSC.
- A. Caragheorgheopol, W. Edwards, J. G. Hardy, D. K. Smith and V. Chechik, Langmuir, 2014, 30, 9210–9218 CrossRef CAS PubMed.
- A. Delville, J. Grandjean and P. Laszlo, J. Phys. Chem., 1991, 95, 1383–1392 CrossRef CAS.
- D. Zhu, B. E. Herbert, M. A. Schlautman, E. R. Carraway and J. Hur, J. Environ. Qual., 2004, 33, 1322–1330 CrossRef CAS.
- V. E. Bahamonde-Padilla, J. J. López-Cascales, R. Araya-Maturana, M. Martínez-Cifuentes and B. E. Weiss López, ChemPhysChem, 2014, 15, 1422–1431 CrossRef CAS PubMed.
- G. Pellizer and F. Asaro, Magn. Reson. Chem., 2008, 46, S80–S85 CrossRef PubMed.
- S. Fleming and R. V. Ulijn, Chem. Soc. Rev., 2014, 43, 8150–8177 RSC.
- Y. Zhang, Y. Kuang, Y. Gao and B. Xu, Langmuir, 2011, 27, 529–537 CrossRef CAS PubMed.
- Z. Yang, G. Liang, M. Ma, A. S. Abbah, W. W. Lu and B. Xu, Chem. Commun., 2007, 843–845 RSC.
- D. J. Adams, M. F. Butler, W. J. Frith, M. Kirkland, L. Mullen and P. Sanderson, Soft Matter, 2009, 5, 1856–1862 RSC.
- K. L. Morris, L. Chen, J. Raeburn, O. R. Sellick, P. Cotanda, A. Paul, P. C. Griffiths, S. M. King, R. K. O’Reilly, L. C. Serpell and D. J. Adams, Nat. Commun., 2013, 4, 1480 CrossRef PubMed.
- Y. Pocker and E. Green, J. Am. Chem. Soc., 1973, 95, 113–119 CrossRef CAS.
- L. Chen, K. Morris, A. Laybourn, D. Elias, M. R. Hicks, A. Rodger, L. Serpell and D. J. Adams, Langmuir, 2010, 26, 5232–5242 CrossRef CAS PubMed.
- J. Raeburn, L. Chen, S. Awhida, R. C. Deller, M. Vatish, M. I. Gibson and D. J. Adams, Soft Matter, 2015, 11, 3706–3713 RSC.
- Z. Szakács, G. Hägele and R. Tyka, Anal. Chim. Acta, 2004, 522, 247–258 CrossRef PubMed.
- T. Tynkkynen, M. Tiainen, P. Soininen and R. Laatikainen, Anal. Chim. Acta, 2009, 648, 105–112 CrossRef CAS PubMed.
- J. J. H. Ackerman, G. E. Soto, W. M. Spees, Z. Zhu and J. L. Evelhoch, Magn. Reson. Med., 1996, 36, 674–683 CrossRef CAS PubMed.
- Z.-W. Dai, L.-S. Wan, X.-J. Huang, J. Ling and Z.-K. Xu, J. Phys. Chem. C, 2011, 115, 22415–22421 CAS.
- A. Z. Cardoso, A. E. Alvarez, B. N. Cattoz, P. C. Griffiths, S. M. King, W. J. Frith and D. J. Adams, Faraday Discuss., 2013, 166, 101–116 RSC.
- L. Chen, T. O. McDonald and D. J. Adams, RSC Adv., 2013, 3, 8714–8720 RSC.
- D. J. Adams, L. M. Mullen, M. Berta, L. Chen and W. J. Frith, Soft Matter, 2010, 6, 1971–1980 RSC.
- C. Tang, A. M. Smith, R. F. Collins, R. V. Ulijn and A. Saiani, Langmuir, 2009, 25, 9447–9453 CrossRef CAS PubMed.
- C. Tang, R. V. Ulijn and A. Saiani, Langmuir, 2011, 27, 14438–14449 CrossRef CAS PubMed.
- G. Lindblom, B. Lindman and G. J. T. Tiddy, J. Am. Chem. Soc., 1978, 100, 2299–2303 CrossRef CAS.
- K. Tanaka and T. Hashitani, Trans. Faraday Soc., 1971, 67, 2314–2317 RSC.
- O. Misran, B. A. Timimi, T. Heidelberg, A. Sugimura and R. Hashim, J. Phys. Chem. B, 2013, 117, 7335–7344 CrossRef CAS PubMed.
- L. Chen, S. Revel, K. Morris, L. C. Serpell and D. J. Adams, Langmuir, 2010, 26, 13466–13471 CrossRef CAS PubMed.
- K. A. Houton, K. L. Morris, L. Chen, M. Schmidtmann, J. T. A. Jones, L. C. Serpell, G. O. Lloyd and D. J. Adams, Langmuir, 2012, 28, 9797–9806 CrossRef CAS PubMed.
- S. Awhida, E. R. Draper, T. O. McDonald and D. J. Adams, J. Colloid Interface Sci., 2015, 455, 24–31 CrossRef CAS PubMed.
- T. K. Harris and G. J. Turner, IUBMB Life, 2002, 53, 85–98 CrossRef CAS PubMed.
- L. Piculell, B. Lindman and R. Einarsson, Biopolymers, 1984, 23, 1683–1699 CrossRef CAS PubMed.
- B. Halle and H. Wennerström, J. Chem. Phys., 1981, 75, 1928–1943 CrossRef CAS PubMed.
- P. Porion and A. Delville, Curr. Opin. Colloid Interface Sci., 2009, 14, 216–222 CrossRef CAS PubMed.
- J. P. Jacobsen and K. Schaumburg, J. Magn. Reson., 1977, 28, 191–201 CAS.
- H. J. Jakobsen, A. R. Hove, R. G. Hazell, H. Bildsøe and J. Skibsted, Magn. Reson. Chem., 2006, 44, 348–356 CrossRef CAS PubMed.
- H. Gustavsson and B. Lindman, J. Am. Chem. Soc., 1975, 97, 3923–3930 CrossRef CAS.
- D. E. Woessner, Concepts Magn. Reson., 2001, 13, 294–325 CrossRef CAS PubMed.
- M. Raue, A. Bernet, M. Küppers, S. Stapf, H. W. Schmidt, B. Blümich and T. Mang, in Intelligent Hydrogels, eds. G. Sadowski and W. Richtering, Springer International Publishing, 2013, vol. 140, ch. 4, pp. 45–51 Search PubMed.
- T. M. Barbara, R. R. Vold and R. L. Vold, J. Chem. Phys., 1983, 79, 6338–6340 CrossRef CAS PubMed.
- A. Jerschow and N. Müller, J. Magn. Reson., 1997, 125, 372–375 CrossRef CAS.
- R. J. W. Lambert, I. Mytilinaios, L. Maitland and A. M. Brown, Comput. Methods Programs Biomed., 2012, 107, 155–163 CrossRef.
- A. M. Brown, Comput. Methods Programs Biomed., 2001, 65, 191–200 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01760b |
| This journal is © The Royal Society of Chemistry 2015 |