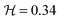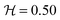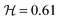Open Access Article
Open Access ArticlePurely elastic flow instabilities in microscale cross-slot devices†
P. C.
Sousa
a,
F. T.
Pinho
b,
M. S. N.
Oliveira
c and
M. A.
Alves
*a
aDepartamento de Engenharia Química, CEFT, Faculdade de Engenharia da Universidade do Porto, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal. E-mail: mmalves@fe.up.pt
bCEFT, Departamento de Engenharia Mecânica, Faculdade de Engenharia da Universidade do Porto, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal
cJames Weir Fluids Laboratory, Department of Mechanical and Aerospace Engineering, University of Strathclyde, Glasgow, G1 1XJ, UK
First published on 23rd September 2015
Abstract
We present an experimental investigation of viscoelastic fluid flow in a cross-slot microgeometry under low Reynolds number flow conditions. By using several viscoelastic fluids, we investigate the effects of the microchannel bounding walls and the polymer solution concentration on the flow patterns. We demonstrate that for concentrated polymer solutions, the flow undergoes a bifurcation above a critical Weissenberg number (Wi) at which the flow becomes asymmetric but remains steady. The appearance of this elastic instability depends on the channel aspect ratio, defined as the ratio between the depth and the width of the channels. At high aspect ratios, when bounding wall effects are reduced, two types of elastic instabilities were observed, one in which the flow becomes asymmetric and steady, followed by a second instability at higher Wi, in which the flow becomes time-dependent. When the aspect ratio decreases, the bounding walls have a stabilizing effect, preventing the occurrence of steady asymmetric flow and postponing the transition to unsteady flow to higher Wi. For less concentrated solutions, the first elastic instability to steady asymmetric flow is absent and only the time-dependent flow instability is observed.
Introduction
Complex fluids often exhibit unexpected flow phenomena, even in the absence of nonlinearities associated with inertia, as extensively documented by Boger and Walters.1 In particular, viscoelastic fluid flow can develop elastic instabilities,2–5 which in microfluidics are often purely elastic due to the typically low Reynolds number (Re) flows. The small length scales, together with the high deformation rates typically found in microfluidic systems, enable the generation of high Deborah (De) or Weissenberg (Wi) number flows, characterized by negligible inertial effects, hence leading to high elasticity number (El = Wi/Re) flows. These conditions induce strong viscoelastic flow effects even for dilute polymer solutions that would exhibit Newtonian-like behaviour at the macro-scale.The onset of purely elastic flow instabilities occurs above critical flow conditions and is due to the combination of streamline curvature and large normal stresses. McKinley and co-workers6,7 proposed a dimensionless criterion that can be used to estimate the critical conditions for the onset of purely elastic flow instabilities.
One geometrical configuration that has been extensively used in the investigation of nonlinear effects in complex fluids is the cross-slot arrangement.8–24 It consists of two perpendicular, bisecting channels with opposing inlets and opposing outlets, resulting in a flow field with a stagnation point at the centre of symmetry (cf.Fig. 1), where the flow velocity is zero and the velocity gradient is finite.13 A strong extensional flow is generated in the vicinity of the stagnation point and, for viscoelastic fluids, a nonlinear increase in the first normal stress difference (or similarly in the extensional viscosity) with the flow rate promotes the onset of elastic instabilities. In addition, near the stagnation point the residence time is sufficiently long for the polymer molecules to reach a steady-state elongation, allowing the estimation of the steady-state extensional viscosity, for example using birefringence measurements.10,11,13–18
Arratia et al.8 experimentally investigated the flow of a dilute polymeric solution in a cross-slot device and observed the existence of two types of purely elastic flow instabilities that occur as the flow rate increases. In the first instability, the flow patterns become asymmetric but remain steady with the fluid entering in each of the opposing inlet channels and exiting preferentially through one outlet. At higher flow rates, a second elastic instability sets in, in which the flow becomes time-dependent. Similar experimental observations were also reported in the same year by Pathak and Hudson10 using a micellar solution. In the following year, Poole et al.9 simulated numerically the two-dimensional cross-slot flow of an upper-convected Maxwell (UCM) fluid at low and negligible Re and predicted qualitatively the flow behaviour observed experimentally. In addition, the authors demonstrated that the transition to a steady asymmetry flow is purely elastic in nature and that inertial effects reduce the strength of the asymmetry and delay the onset of the elastic instability to higher De. Following these three pioneering studies, the viscoelastic fluid flow through a cross-slot geometry has received renewed attention in order to explore the rheological conditions that can affect the onset of purely elastic flow instabilities11,12,17,18,20,21 and was considered an important open mathematical problem for non-Newtonian fluids.22
Poole et al.23 investigated numerically the three-dimensional flow of an UCM fluid under creeping flow conditions by varying the depth of the geometry from conditions corresponding to the quasi-Hele Shaw flow (low aspect ratio) to quasi-two dimensional flow (high aspect ratio). Subsequently, Poole et al.24 predicted numerically the cross-slot flow using an Oldroyd-B model and a simplified Phan–Thien–Tanner model in order to assess the effects of the solvent viscosity and finite extensibility on the flow patterns, and they found that the steady asymmetric and unsteady flow regimes occur under different flow conditions, depending on the rheological parameters of the viscoelastic model. The effect of the type of solvent and viscosity on the viscoelastic fluid flow behaviour has been investigated experimentally in other applications, including rheometric flows25 or flows through microfluidic planar contractions.26,27 For instance, Rodd et al.27 used viscoelastic solutions with a constant concentration of polyethylene oxide (PEO) while varying the viscosity of the solvent, in order to vary El between 2.8 and 68. The same flow regimes (Newtonian-like flow, steady viscoelastic flow, diverging streamlines and vortex growth) were found for all solutions investigated, although at high elasticity numbers the transitions between the flow regimes occurred at higher Wi.
Motivated by the numerical studies of Poole et al.,23,24 here we investigate experimentally the effects of the aspect ratio of the channel, imposed by the bounding walls of the geometry, and the effects of the rheological characteristics of viscoelastic fluids on the onset of the purely elastic instabilities observed in a cross-slot device. We use several viscoelastic fluids with different rheological characteristics, in order to explore experimentally the conditions that lead to the onset of the purely elastic flow instabilities in microscale cross-slot devices.
Material and methods
Microchannel fabrication and experimental techniques
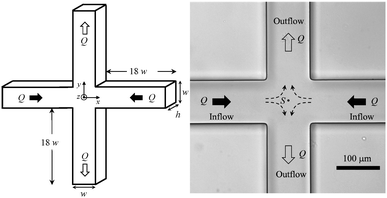
The microfluidic devices used in this work were fabricated from SU-8 photoresist moulds and are made of polydimethylsiloxane (PDMS; Sylgard 184, Dow Corning) using standard soft-lithography.28Fig. 1 shows a bright field image of a typical channel and relevant dimensions. We used three sets of cross-slots with microchannels that are 100 μm in width (w) and have depths (h) of 51 μm, 101 μm and 156 μm resulting in aspect ratios (AR = h/w) of 0.5, 1.0 and 1.6, respectively. The length of the inlet/outlet channels is large enough (at least 18w in length) to ensure that the flow is fully-developed far from the region of interest for all flow conditions investigated.Flow rates (Q) of equal magnitude are imposed in all four channels. For that purpose, a syringe pump with three independent modules (neMESYS, Cetoni GmbH) was used to inject with equal flow rates at the two inlets and remove the fluid from one outlet at the same flow rate. The remaining outlet is connected to a tube open to the atmosphere. For flow visualization, the fluids were seeded with 1 μm fluorescent tracer particles (Nile Red particles, Molecular Probes, Invitrogen, Ex/Em: 535/575 nm). Flow visualization was based on long exposure photography with the microchannels placed on an inverted epi-fluorescence microscope (DMI 5000M, Leica Microsystems GmbH) equipped with a 20× objective lens (numerical aperture, NA = 0.4) and a CCD camera (DFC350 FX, Leica Microsystems GmbH) or a sCMOS camera (Neo 5.5, Andor). Illumination was provided by a 100 W mercury lamp operating together with an adequate filter cube. Visualization of the flow patterns was performed at the centre plane of the microchannel, z = 0, at the mid-distance between the top and bottom bounding walls.
Test fluids
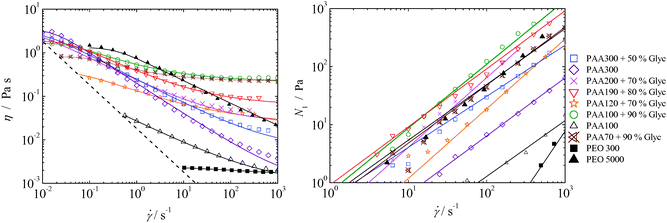
The viscoelastic solutions used were prepared by adding polyacrylamide (PAA, Mw = 18 × 106, Polysciences Inc.) or PEO (Mw = 8 × 106, Sigma Aldrich) to a Newtonian solvent, which was either water or a mixture of water and glycerol, as summarized in Table 1. A Newtonian fluid (distilled water) was also used as the reference. The fluids were characterized rheologically in shear flow at T = 20.0 °C using a stress-controlled rheometer (Physica MCR301, Anton Paar). For all fluids, the shear viscosity (η) and the first normal-stress difference (N1) measurements were fitted to a White–Metzner model:29,30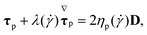 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the shear rate dependent relaxation time defined below and
) is the shear rate dependent relaxation time defined below and 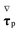 is the upper-convected derivative of the polymeric extra-stress tensor,
is the upper-convected derivative of the polymeric extra-stress tensor,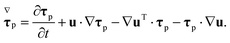 | (2) |
| Fluid | Polymer (ppm) | Glycerol (% w/w) | η 0 (Pa s) | η S (Pa s) | Λ (s) | n ( – ) | λ 0 (s) | β ( – ) | c* (ppm) | λ c (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| a Shear viscosity data fit. b Relaxation time function fit. | ||||||||||
| PAA300 + 50%Glyc | 300 | 50 | 2.8 | 0.0061 | 80 | 0.44 | 13 | 0.0022 | 95 | 0.178 |
| PAA300 | 300 | — | 3.50 | 0.001 | 60 | 0.30a | 0.55 | 0.00029 | 45 | 0.066 |
| 0.70b | ||||||||||
| PAA200 + 70%Glyc | 200 | 70 | 3.00 | 0.023 | 140a | 0.47a | 2.4 | 0.0077 | 130 | 0.658 |
| 200b | 0.73b | |||||||||
| PAA190 + 80%Glyc | 190 | 80 | 1.90 | 0.063 | 32 | 0.50 | 8.0 | 0.033 | 150 | 0.390 |
| PAA120 + 70%Glyc | 120 | 70 | 0.35 | 0.023 | 15 | 0.60 | 1.0 | 0.066 | 130 | 0.160 |
| PAA100 + 90%Glyc | 100 | 90 | 1.70 | 0.22 | 30 | 0.55 | 5.0 | 0.13 | 170 | 0.484 |
| PAA100 | 100 | — | 0.22 | 0.001 | 60 | 0.48 | 2.5 | 0.0045 | 45 | 0.012 |
| PAA70 + 90%Glyc | 70 | 90 | 0.82 | 0.22 | 10 | 0.50 | 4.0 | 0.27 | 170 | 0.351 |
| PEO300 | 300 | — | 0.0023 | 0.001 | 0.07a | 0.87a | 0.0045 | 0.43 | 350 | 0.040 |
| —b | 1.0b | |||||||||
| PEO5000 | 5000 | — | 1.33 | 0.001 | 3 | 0.48 | 0.7 | 0.00075 | 350 | 0.228 |
The total extra-stress tensor τ is defined as the sum of the solvent and polymeric contributions, τ = τp + τs, where the solvent contribution is given by τs = ηs(∇u + ∇uT). In the nonlinear White–Metzner model, both the shear viscosity and the first normal-stress difference depend on the shear rate, 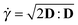 , where
, where 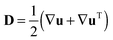 is the rate of deformation tensor. The shear viscosity function is given by a Carreau model,30ηp(
is the rate of deformation tensor. The shear viscosity function is given by a Carreau model,30ηp(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = (η0 − ηs)/[1 + (Λ
) = (η0 − ηs)/[1 + (Λ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )2](1−n)/2 and the first normal-stress difference is N1 = 2ηp(
)2](1−n)/2 and the first normal-stress difference is N1 = 2ηp(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )λ(
)λ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )
)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2, where ηs is the high shear rate viscosity, which approaches the solvent viscosity of dilute polymer solutions, η0 is the zero-shear rate viscosity, Λ is a time constant, n is the power-law like index and λ(
2, where ηs is the high shear rate viscosity, which approaches the solvent viscosity of dilute polymer solutions, η0 is the zero-shear rate viscosity, Λ is a time constant, n is the power-law like index and λ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is also given by a Carreau model, λ = λ0/[1 + (Λ
) is also given by a Carreau model, λ = λ0/[1 + (Λ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )2](1−n)/2. The shear viscosity and first normal-stress difference data measured in steady shear flow as well as the White–Metzner model fits are shown in Fig. 2. For most fluids, we use the same values of the parameters of the model to fit the data for both polymer shear viscosity and first normal-stress difference thus using an elastic modulus, G = ηp(
)2](1−n)/2. The shear viscosity and first normal-stress difference data measured in steady shear flow as well as the White–Metzner model fits are shown in Fig. 2. For most fluids, we use the same values of the parameters of the model to fit the data for both polymer shear viscosity and first normal-stress difference thus using an elastic modulus, G = ηp(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/λ(
)/λ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), which is independent of the shear rate. The exceptions are the PAA300, PAA200 + 70%Glyc and PEO300 fluids, for which the parameters n and Λ used to fit the polymer viscosity function were different from those used in the relaxation time to fit the first normal-stress difference data. The rheological parameters of the White–Metzner model are listed in Table 1 and are included to allow future comparisons of the experimental data with numerical simulations. The critical overlap concentration c* is also presented in Table 1 and was calculated according to Graessley31 as c* = 0.77/[η], where [η] is the intrinsic viscosity, which was measured for PAA solutions using a U-tube capillary viscometer using various solutions with the same solvent and different polymer concentrations. The intrinsic viscosity was determined using the Huggins equation.32 The critical overlap concentration was determined experimentally for PAA solutions composed of 90%, 60% and 0% glycerol and was estimated for the remaining PAA solutions. For aqueous PEO solutions the overlap concentration was calculated from the correlation obtained by Tirtaatmadja et al.33 for the intrinsic viscosity ([η] = 0.072Mw0.65, with [η] in units of cm3 g−1). We note that for dilute polymer solutions the zero-shear rate viscosity is expected to increase linearly with the polymer concentration (η0/ηs = 1/β ≈ 1 + c/c*) but a quadratic increase was found for the PAA solutions. The relaxation times measured in uniaxial extensional flow (λc) using a capillary break-up extensional rheometer (HAAKE CaBER™1, Thermo Scientific) are also presented in Table 1 together with the values of the solvent viscosity ratio, β, defined as β = ηs/η0.
), which is independent of the shear rate. The exceptions are the PAA300, PAA200 + 70%Glyc and PEO300 fluids, for which the parameters n and Λ used to fit the polymer viscosity function were different from those used in the relaxation time to fit the first normal-stress difference data. The rheological parameters of the White–Metzner model are listed in Table 1 and are included to allow future comparisons of the experimental data with numerical simulations. The critical overlap concentration c* is also presented in Table 1 and was calculated according to Graessley31 as c* = 0.77/[η], where [η] is the intrinsic viscosity, which was measured for PAA solutions using a U-tube capillary viscometer using various solutions with the same solvent and different polymer concentrations. The intrinsic viscosity was determined using the Huggins equation.32 The critical overlap concentration was determined experimentally for PAA solutions composed of 90%, 60% and 0% glycerol and was estimated for the remaining PAA solutions. For aqueous PEO solutions the overlap concentration was calculated from the correlation obtained by Tirtaatmadja et al.33 for the intrinsic viscosity ([η] = 0.072Mw0.65, with [η] in units of cm3 g−1). We note that for dilute polymer solutions the zero-shear rate viscosity is expected to increase linearly with the polymer concentration (η0/ηs = 1/β ≈ 1 + c/c*) but a quadratic increase was found for the PAA solutions. The relaxation times measured in uniaxial extensional flow (λc) using a capillary break-up extensional rheometer (HAAKE CaBER™1, Thermo Scientific) are also presented in Table 1 together with the values of the solvent viscosity ratio, β, defined as β = ηs/η0.
Results and discussion
For all aspect ratios and flow conditions investigated using the Newtonian fluid (maximum Remax = 27.0 for AR = 0.5, Remax = 13.6 for AR = 1.0, and Remax = 8.9 for AR = 1.6), the flow remains steady and symmetric as illustrated in Fig. 3a. We define the Reynolds number as Re = ρUw/η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), where ρ is the fluid density and U the average velocity in the channels. For the non-Newtonian fluids, we use the shear rate dependent viscosity evaluated at a characteristic shear rate,
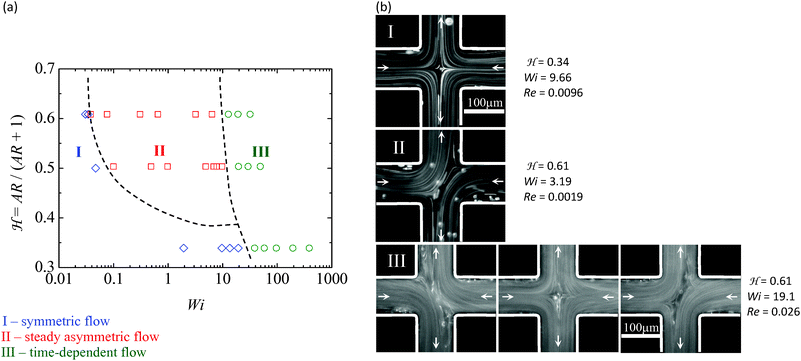
), where ρ is the fluid density and U the average velocity in the channels. For the non-Newtonian fluids, we use the shear rate dependent viscosity evaluated at a characteristic shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = U/(w/2). The results show that the micro-geometry is symmetric and that any slight geometric imperfections do not affect the fluid flow significantly, ensuring that any flow asymmetries observed for viscoelastic fluid flow (see the discussion below) are not due to imperfections in the channels. The flow behaviour observed for the viscoelastic fluids is far more complex than that found for the Newtonian fluid. For all viscoelastic fluids investigated, we observed that viscoelasticity can lead to the onset of different types of purely elastic instabilities, depending on the rheological properties of the fluids. For some viscoelastic fluids, such as PAA100 + 90%Glyc, only one type of elastic instability was observed at high flow rates, in which there is a direct transition from symmetric steady flow to unsteady flow above a critical Weissenberg number, here defined as Wi = λcU/(w/2). Note that due to the fact that the flow in the cross-slot device is strongly extensional, in the definition of Wi we use the relaxation time measured in extensional flow using the CaBER™1 extensional rheometer. For other fluids, such as PAA300 + 50%Glyc, two flow transitions are observed, the first one in which the flow becomes asymmetric, but remains steady (cf.Fig. 3b-ii) and a second one for higher Wi in which the flow becomes unsteady, as illustrated in Fig. 3b-iii. For viscoelastic fluids, the type of flow transition also depends on the aspect ratio of the cross-slot, and this was investigated using the PAA300 + 50%Glyc fluid. For the highest aspect ratios investigated (AR = 1 and 1.6), the flow is steady symmetric at low Weissenberg numbers (cf.Fig. 3b-i). When Wi is increased, the flow becomes steady asymmetric within an intermediate range of Wi as shown in Fig. 3b-ii. This phenomenon, also observed in the experimental and numerical studies of Arratia et al.8 and Poole et al.,23 respectively, is here described as the first purely elastic instability. The term purely elastic stems from the fact that the Reynolds numbers are small, hence inertial effects are negligible and the instabilities are a consequence of elastic effects alone. In agreement with the numerical results obtained by Poole et al.,9 the effect of inertia on the instability is negligible as found when comparing a creeping flow (Re = 0) with a low-Re flow (Re < 1 approximately). When the flow is steady asymmetric, a lip vortex is also observed in each inlet channel just upstream of the corners (Movie, ESI†). The formation of lip vortices close to re-entrant corners has also been extensively investigated in contraction flows34–36 and in flows in sharp 90 degree micro-bends.37 Upon further increasing the flow rate above a second critical Wi value, the flow exhibits a second purely elastic instability, becoming time-dependent (cf.Fig. 3b-iii and Movie, ESI†). For low AR (AR = 0.5), the viscoelastic fluid flow is steady and symmetric at low flow rates, with small lip vortices appearing upstream of the corners. When the flow rate (or Wi) is increased, the lip vortices grow and the flow patterns change directly from a steady symmetric condition to an unsteady state. To summarize, Fig. 4 shows a map of the flow patterns identified for the PAA300 + 50%Glyc fluid flowing in the cross-slot device and their location on the
= U/(w/2). The results show that the micro-geometry is symmetric and that any slight geometric imperfections do not affect the fluid flow significantly, ensuring that any flow asymmetries observed for viscoelastic fluid flow (see the discussion below) are not due to imperfections in the channels. The flow behaviour observed for the viscoelastic fluids is far more complex than that found for the Newtonian fluid. For all viscoelastic fluids investigated, we observed that viscoelasticity can lead to the onset of different types of purely elastic instabilities, depending on the rheological properties of the fluids. For some viscoelastic fluids, such as PAA100 + 90%Glyc, only one type of elastic instability was observed at high flow rates, in which there is a direct transition from symmetric steady flow to unsteady flow above a critical Weissenberg number, here defined as Wi = λcU/(w/2). Note that due to the fact that the flow in the cross-slot device is strongly extensional, in the definition of Wi we use the relaxation time measured in extensional flow using the CaBER™1 extensional rheometer. For other fluids, such as PAA300 + 50%Glyc, two flow transitions are observed, the first one in which the flow becomes asymmetric, but remains steady (cf.Fig. 3b-ii) and a second one for higher Wi in which the flow becomes unsteady, as illustrated in Fig. 3b-iii. For viscoelastic fluids, the type of flow transition also depends on the aspect ratio of the cross-slot, and this was investigated using the PAA300 + 50%Glyc fluid. For the highest aspect ratios investigated (AR = 1 and 1.6), the flow is steady symmetric at low Weissenberg numbers (cf.Fig. 3b-i). When Wi is increased, the flow becomes steady asymmetric within an intermediate range of Wi as shown in Fig. 3b-ii. This phenomenon, also observed in the experimental and numerical studies of Arratia et al.8 and Poole et al.,23 respectively, is here described as the first purely elastic instability. The term purely elastic stems from the fact that the Reynolds numbers are small, hence inertial effects are negligible and the instabilities are a consequence of elastic effects alone. In agreement with the numerical results obtained by Poole et al.,9 the effect of inertia on the instability is negligible as found when comparing a creeping flow (Re = 0) with a low-Re flow (Re < 1 approximately). When the flow is steady asymmetric, a lip vortex is also observed in each inlet channel just upstream of the corners (Movie, ESI†). The formation of lip vortices close to re-entrant corners has also been extensively investigated in contraction flows34–36 and in flows in sharp 90 degree micro-bends.37 Upon further increasing the flow rate above a second critical Wi value, the flow exhibits a second purely elastic instability, becoming time-dependent (cf.Fig. 3b-iii and Movie, ESI†). For low AR (AR = 0.5), the viscoelastic fluid flow is steady and symmetric at low flow rates, with small lip vortices appearing upstream of the corners. When the flow rate (or Wi) is increased, the lip vortices grow and the flow patterns change directly from a steady symmetric condition to an unsteady state. To summarize, Fig. 4 shows a map of the flow patterns identified for the PAA300 + 50%Glyc fluid flowing in the cross-slot device and their location on the 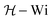 parameter space.
parameter space.
We use a normalized aspect ratio 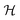 , defined as
, defined as 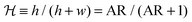 ,23 which varies in the range between
,23 which varies in the range between 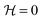 (for AR → 0 corresponding to the Hele-Shaw flow limit) and
(for AR → 0 corresponding to the Hele-Shaw flow limit) and 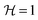 (for AR → ∞ corresponding to the two-dimensional flow limit). The range of Reynolds numbers attained for each aspect ratio investigated are also given in Fig. 4 to highlight the negligible effect of inertia on the viscoelastic fluid flow. The flow patterns reported in the map of Fig. 4 were identified in three different regions: (I) symmetric flow; (II) steady asymmetric flow (first purely elastic instability); and (III) time-dependent flow (second purely elastic flow instability). For the time-dependent regime, we show three images to illustrate the oscillatory nature of the flow. It should be noted that region III can be reached from region II or directly from region I by increasing Wi, through a purely elastic instability of the second type. The different flow behaviour depends on the channel aspect ratio. For
(for AR → ∞ corresponding to the two-dimensional flow limit). The range of Reynolds numbers attained for each aspect ratio investigated are also given in Fig. 4 to highlight the negligible effect of inertia on the viscoelastic fluid flow. The flow patterns reported in the map of Fig. 4 were identified in three different regions: (I) symmetric flow; (II) steady asymmetric flow (first purely elastic instability); and (III) time-dependent flow (second purely elastic flow instability). For the time-dependent regime, we show three images to illustrate the oscillatory nature of the flow. It should be noted that region III can be reached from region II or directly from region I by increasing Wi, through a purely elastic instability of the second type. The different flow behaviour depends on the channel aspect ratio. For 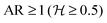 , the first elastic instability is observed, whereas for lower
, the first elastic instability is observed, whereas for lower 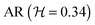 the steady asymmetric flow regime does not appear. The bounding walls (z = ±h/2) have a stabilizing effect, since the decrease in channel depth (or AR) increases the wall influence via enhanced shear stress thus reducing the influence of extensional effects. In addition, for the higher AR investigated, corresponding to
the steady asymmetric flow regime does not appear. The bounding walls (z = ±h/2) have a stabilizing effect, since the decrease in channel depth (or AR) increases the wall influence via enhanced shear stress thus reducing the influence of extensional effects. In addition, for the higher AR investigated, corresponding to 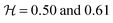 , the critical Wi at which the two flow transitions occur seems not to depend significantly on the channel aspect ratio. In contrast, the numerical predictions of Poole et al.23 showed that the second elastic instability appears at gradually smaller Wi as the AR is decreased and the Hele–Shaw flow is approached
, the critical Wi at which the two flow transitions occur seems not to depend significantly on the channel aspect ratio. In contrast, the numerical predictions of Poole et al.23 showed that the second elastic instability appears at gradually smaller Wi as the AR is decreased and the Hele–Shaw flow is approached 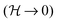 , but in their case a UCM model was used in the simulations. Such a model cannot predict the shear-thinning of the viscosity and the relaxation time observed with the fluids used in this work.
, but in their case a UCM model was used in the simulations. Such a model cannot predict the shear-thinning of the viscosity and the relaxation time observed with the fluids used in this work.
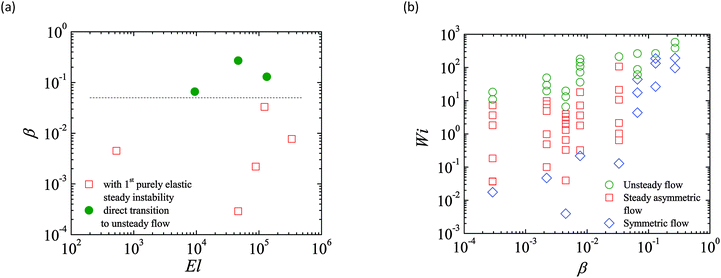
Another motivation of this work was to understand why the first elastic instability sets in only for some viscoelastic fluids, whereas for other viscoelastic fluids the transition occurs directly to time-dependent flow independently of the channel AR. For that purpose, we considered all the PAA solutions described in Table 1, which have significantly different solvent viscosity ratios and different elasticity levels. The plot in Fig. 5(a) indicates the presence or absence of the first instability in a map of viscosity ratio and elasticity number for all PAA solutions tested and AR = 1.0.
The elasticity number is defined as El = Wi/Re0 = 2λcη0/(ρw2) and is independent of the flow rate. As is shown, the rheological parameter that has a major influence on the onset of the first purely elastic instability is the solvent viscosity ratio. Viscoelastic fluids with β ≲ 0.05 (more concentrated polymer solutions) experience a first transition through a steady asymmetric flow, whereas for the fluids with larger β, the flow changes directly from Newtonian-like to time-dependent flow above a critical Wi. Experiments using the two PEO solutions were also carried out. The flow visualization results are not shown here for conciseness, but the corresponding Wi − β map is qualitatively similar to Fig. 5(b), with the more concentrated solution (lower β) showing the onset of the first and second instabilities at Wi ≈ 2 and Wi ≈ 100, respectively, whereas for the dilute solution (higher β), the flow changes directly from Newtonian-like to unsteady flow at Wi ≈ 50. The types of flow transitions are identical for both PAA and PEO polymer solutions, but occur at different values of Wi for each β.
It is important to note that the critical Wi values for the onset of the first elastic instability observed in the PAA solutions are lower than 1 [cf.Fig. 5(b)], especially for the more concentrated solutions, and it may be argued that elastic effects are unimportant because under these conditions the polymer molecules remain coiled. However, the CaBER relaxation times, used in the calculation of Wi, are probably underestimated. We also calculated the shear relaxation times estimated from the rheological oscillatory shear data 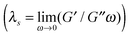 , where G′ and G′′ are the storage and loss moduli, and ω is the angular frequency of oscillation and we found that the extensional relaxation times are all significantly lower than these shear relaxation times, and also those that can be computed from the N1 data illustrated in Fig. 2. Similar results were obtained by Arnolds et al.38 for PEO solutions, with the authors reporting also that the ratio between the extensional and shear relaxation times decreases significantly with increasing concentration or molecular weight of the polymer. Nevertheless, instead of using a relaxation time determined from a shear flow, which leads to critical Wi values above 1, we opted to use the extensional relaxation times because the flow in the cross-slot device is strongly extensional.
, where G′ and G′′ are the storage and loss moduli, and ω is the angular frequency of oscillation and we found that the extensional relaxation times are all significantly lower than these shear relaxation times, and also those that can be computed from the N1 data illustrated in Fig. 2. Similar results were obtained by Arnolds et al.38 for PEO solutions, with the authors reporting also that the ratio between the extensional and shear relaxation times decreases significantly with increasing concentration or molecular weight of the polymer. Nevertheless, instead of using a relaxation time determined from a shear flow, which leads to critical Wi values above 1, we opted to use the extensional relaxation times because the flow in the cross-slot device is strongly extensional.
The onset of steady asymmetric flow seems to be related to the compressive flow near the cross-slot centre generated by the two inlet channels.9 The collision of the inlet streams generates opposite normal forces, the resulting momentum decreases near the stagnation point and, due to continuity, the fluid is pushed towards the corners triggering the onset of a flow asymmetry.9 According to McKinley and co-workers,6,7 the dimensionless criterion that must be exceeded for the onset of purely elastic flow instabilities can be expressed as 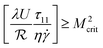 , where
, where 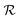 is the local radius of curvature, U the local streamwise velocity, τ11 the streamwise tensile stress and
is the local radius of curvature, U the local streamwise velocity, τ11 the streamwise tensile stress and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the local shear rate. Hence, an increase of the normal stress, combined with small streamline radii of curvature and high streamwise velocities meets the criterion for the appearance of the elastic instability. As the aspect ratio of the channel decreases, the critical region moves towards the corners of the geometry, where the streamwise velocity and shear rate increase,23 high tensile stress develops and the radius of curvature is small. In this case, the fluid experiences the onset of the second type of elastic instability whereas the asymmetric flow does not occur which is primarily driven by the strong extensional flow at the cross-slot centre.
the local shear rate. Hence, an increase of the normal stress, combined with small streamline radii of curvature and high streamwise velocities meets the criterion for the appearance of the elastic instability. As the aspect ratio of the channel decreases, the critical region moves towards the corners of the geometry, where the streamwise velocity and shear rate increase,23 high tensile stress develops and the radius of curvature is small. In this case, the fluid experiences the onset of the second type of elastic instability whereas the asymmetric flow does not occur which is primarily driven by the strong extensional flow at the cross-slot centre.
Conclusions
A range of viscoelastic fluids and a reference Newtonian fluid were used to study experimentally the extensional flow in a cross-slot micro-geometry, focusing on the onset of elastic instabilities under negligible inertial flow conditions. The experimental results suggest that the solvent viscosity ratio is a key parameter for the observation of the steady asymmetric flow instability. For β ≳ 0.05, only one type of purely elastic instability is observed, whereby the flow transitions from a steady symmetric regime to a time-dependent flow. In contrast, for more concentrated polymer solutions (β ≲ 0.05) another type of instability was identified, in which the flow becomes asymmetric, but remains steady. For these fluids, the microchannel aspect ratio was also shown to play an important role in determining the flow transitions. The experimental results show that the channel bounding walls have a stabilizing effect, and for small channel aspect ratios (AR ≤ 0.5) the steady flow asymmetry is suppressed and the flow changes directly from a steady and symmetric condition to an unsteady state at higher Wi. Increasing the aspect ratio of the channels reduces the shear effects and leads to a stronger extensional flow as Wi is increased, and the flow becomes steady and asymmetric (first purely elastic instability) within an intermediate range of Wi, while remaining symmetric and steady for low Wi as long as β is small. Upon further increasing the flow rate, above a second critical Wi, a second type of instability was observed in which the flow becomes unsteady.Acknowledgements
P. C. Sousa thanks Fundação para a Ciência e a Tecnologia (FCT) for the financial support through POPH/FSE and national funding from MEC (fellowship SFRH/BPD/75258/2010). M. S. N. Oliveira acknowledges the support from the U.K. Engineering and Physical Sciences Research Council (EPSRC) under the auspices of grant EP/L013118/1. M. A. Alves acknowledges funding from the European Research Council (ERC), under the European Commission “Ideas” specific programme of the 7th Framework Programme (Grant Agreement No. 307499).References
- D. V. Boger and K. Walters, Rheological phenomena in focus, Elsevier, Amsterdam, 1993 Search PubMed.
- J. Zilz, R. J. Poole, M. A. Alves, D. Bartolo, B. Levache and A. Lindner, J. Fluid Mech., 2012, 712, 203–218 CrossRef CAS.
- P. C. Sousa, F. T. Pinho, M. S. N. Oliveira and M. A. Alves, RSC Adv., 2012, 2, 920–929 RSC.
- S. J. Muller, E. S. G. Shaqfeh and R. G. Larson, J. Non-Newtonian Fluid Mech., 1993, 46, 315–330 CrossRef CAS.
- M. S. N. Oliveira, F. T. Pinho, R. J. Poole, P. J. Oliveira and M. A. Alves, J. Non-Newtonian Fluid Mech., 2009, 160, 31–39 CrossRef CAS PubMed.
- G. H. McKinley, P. Pakdel and A. Oztekin, J. Non-Newtonian Fluid Mech., 1996, 67, 19–47 CrossRef CAS.
- P. Pakdel and G. H. McKinley, Phys. Rev. Lett., 1996, 77, 2459–2462 CrossRef CAS.
- P. E. Arratia, C. C. Thomas, J. Diorio and J. P. Gollub, Phys. Rev. Lett., 2006, 96, 144502 CrossRef CAS.
- R. J. Poole, M. A. Alves and P. J. Oliveira, Phys. Rev. Lett., 2007, 99, 164503 CrossRef CAS.
- J. A. Pathak and S. D. Hudson, Macromolecules, 2006, 39, 8782–8792 CrossRef CAS.
- S. J. Haward, T. J. Ober, M. S. N. Oliveira, M. A. Alves and G. H. McKinley, Soft Matter, 2012, 8, 536–555 RSC.
- A. M. Afonso, M. A. Alves and F. T. Pinho, J. Non-Newtonian Fluid Mech., 2010, 165, 743–751 CrossRef CAS PubMed.
- S. J. Haward, M. S. N. Oliveira, M. A. Alves and G. H. McKinley, Phys. Rev. Lett., 2012, 109, 128301 CrossRef.
- J. Soulages, T. Schweizer, D. C. Venerus, J. Hostettler, F. Mettler, A. Kröger and H. C. Öttinger, J. Non-Newtonian Fluid Mech., 2008, 150, 43–55 CrossRef CAS PubMed.
- K. D. Coventry and M. R. Mackley, J. Rheol., 2008, 52, 401–415 CrossRef CAS.
- S. J. Haward, J. A. Odell, Z. Li and X.-F. Yuan, Rheol. Acta, 2010, 49, 633–645 CrossRef CAS.
- S. J. Haward and G. H. McKinley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031502 CrossRef.
- N. Dubash, P. Cheung and A. Q. Shen, Soft Matter, 2012, 8, 5847–5856 RSC.
- R. D. Spears, J. E. Townsend, L. J. Jacobson, L. L. Sohn and S. J. Muller, Lab Chip, 2010, 10, 1543–1549 RSC.
- G. N. Rocha, R. J. Poole, M. A. Alves and P. J. Oliveira, J. Non-Newtonian Fluid Mech., 2009, 156, 58–69 CrossRef CAS PubMed.
- F. A. Cruz, R. J. Poole, A. M. Afonso, F. T. Pinho, P. J. Oliveira and M. A. Alves, J. Non-Newtonian Fluid Mech., 2014, 214, 57–68 CrossRef CAS PubMed.
- H. J. Wilson, Nonlinearity, 2012, 25, R45–R51 CrossRef.
- R.J. Poole, M. A. Alves, A. M. Afonso, F. T. Pinho and P. J. Oliveira. Purely-elastic flow instabilities in a microfluidic cross-slot geometry, AIChE 2007 Annual Meeting. 2007:Paper 94827.
- R. J. Poole, M. A. Alves, A. M. Afonso, F. T. Pinho and P. J. Oliveira. Purely-elastic instabilities in a cross-slot flow, The Society of Rheology 79th Annual Meeting. 2007:Presentation FM9.
- P. E. Boukany and S.-Q. Wang, Soft Matter, 2009, 5, 780–789 RSC.
- O. L. Hemminger, P. E. Boukany, S.-Q. Wang and L. J. Lee, J. Non-Newtonian Fluid Mech., 2010, 165, 1613–1624 CrossRef CAS PubMed.
- L. E. Rodd, J. J. Cooper-White, D. V. Boger and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2007, 143, 170–191 CrossRef CAS PubMed.
- Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- J. L. White and A. B. Metzner, J. Appl. Polym. Sci., 1963, 7, 1867–1889 CrossRef PubMed.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids, John Wiley & Sons, 2nd edn, 1987, vol. 1 Search PubMed.
- W. W. Graessley, Polymer, 1980, 21, 258–262 CrossRef CAS.
- J. Brandrup, E. H. Immergut and E. A. Grulke, Polymer handbook, Wiley, New York, 1999 Search PubMed.
- V. Tirtaatmadja, G. H. McKinley and J. J. Cooper-White, Phys. Fluids, 2006, 18, 043101 CrossRef PubMed.
- R. E. Evans and K. Walters, J. Non-Newtonian Fluid Mech., 1989, 32, 95–105 CrossRef CAS.
- S. C. Xue, N. Phan-Thien and R. I. Tanner, J. Non-Newtonian Fluid Mech., 1998, 74, 195–245 CrossRef CAS.
- S. Nigen and K. Walters, J. Non-Newtonian Fluid Mech., 2002, 102, 343–359 CrossRef CAS.
- S. Gulati, C. S. Dutcher, D. Liepmann and S. J. Muller, J. Rheol., 2010, 54, 375–392 CrossRef CAS.
- O. Arnolds, H. Buggisch, D. Sachsenheimer and N. Willenbacher, Rheol. Acta, 2010, 49, 1207–1217 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Illustrative movies of the steady symmetric (Videos S1 and S2), steady asymmetric (Video S3) and time-dependent (Video S4) flows. See DOI: 10.1039/c5sm01298h |
| This journal is © The Royal Society of Chemistry 2015 |