The effect of hard block content on the orientation and mechanical properties of olefin block copolymer films as obtained via melt stretching†
Abstract
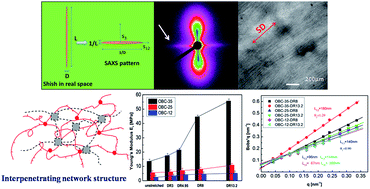
In this study, the orientation, structure and mechanical performance of a series of uniaxially oriented films based on olefin block copolymers (OBC) have been investigated in terms of the differences in hard block content and draw ratio (DR). Three OBCs with different hard block contents of 35 wt%, 25 wt% and 12 wt% were used. For un-stretched films, a change from close-packed spherulites into tiny crystallites is observed with decreasing hard block content, accompanied by an almost linear decrease in crystallinity. However, the change in mechanical properties does not follow the same path, with obviously higher tensile strength and modulus for OBC-35, but a lower and almost the same tensile strength and modulus for OBC-25 and OBC-12, in spite of the big difference in hard block content and crystallinity between them. For melt-stretched films, the degree of orientation of the amorphous phase is almost the same and slightly increases with the increase in the draw ratio for the three OBCs, disregarding their hard block contents. Crystalline orientation and shish content are much higher for OBC-35, and an obvious increase is seen as the draw ratio increases from 4.95 to 8, corresponding to the sharp increase in Young's modulus and stress. For OBC-25 and OBC-12, similar crystalline orientation and shish content are seen, which increase linearly with draw ratio and are consistent with the linear increase in modulus and stress as the draw ratio increases. Our study demonstrates the importance of the hard block content of OBC to determine the mechanical properties and the response to external stretching. A critical hard block content exists (in this case 35 wt%), above which a strong network is constructed by the hard block crystalline phase, resulting in a higher tensile strength and modulus. This strong network is destroyed as the draw ratio reaches a certain value (herein, 4.95 to 8), leading to an obvious increase in crystalline orientation, as well as a sharp increase in tensile strength and modulus. When the hard block is below the critical content (herein, 25 wt% and 12 wt%), the network constructed by the hard block is weak and less dependent on its content.

 Please wait while we load your content...
Please wait while we load your content...