Analysis of the conformational profiles of fenamates shows route towards novel, higher accuracy, force-fields for pharmaceuticals

Abstract

In traditional molecular mechanics force fields, intramolecular non-bonded interactions are modelled as intermolecular interactions, and the form of the torsion potential is based on the conformational profiles of small organic molecules. We investigate how a separate model for the intramolecular forces in pharmaceuticals could be more realistic by analysing the low barrier to rotation of the phenyl ring in the fenamates (substituted N-phenyl-aminobenzoic acids), that results in a wide range of observed angles in the numerous fenamate crystal structures. Although the conformational energy changes by significantly less than 10 kJ mol⁻¹ for a complete rotation of the phenyl ring for fenamic acid, the barrier is only small because of small correlated changes in the other bond and torsion angles. The maxima for conformations where the two aromatic rings approach coplanarity arise from steric repulsion, but the maxima when the two rings are approximately perpendicular arise from a combination of an electronic effect and intramolecular dispersion. Representing the ab initio conformational energy profiles as a cosine series alone is ineffective; however, combining a cos 2ξ term to represent the electronic barrier with an intramolecular atom–atom exp-6 term for all atom pairs separated by three or more bonds (1–4 interactions) provides a very effective representation. Thus we propose a new, physically motivated, generic analytical model of conformational energy, which could be combined with an intermolecular model to form more accurate force-fields for modelling the condensed phases of pharmaceutical-like organic molecules.

---

1. Introduction

Huge advances in our understanding of biomolecular behavior have been made using molecular mechanics force-fields such as AMBER,¹ GROMOS,² CHARMM³ and OPLS-AA,⁴ repaying the immense effort that has gone into parameterizing these force-fields. However, even for protein and nucleic acid polymers, which are well suited to assumptions of transferability of parameters for specific residues or bases, the search for increasing accuracy for more demanding energetic predictions continues,⁵ with more complex forms such as AMOEBA⁶ or the addition of numerical grids to model dihedral cross-terms more accurately.⁷ The traditional force-field includes explicit periodic torsional potentials, and applies the non-bonded terms to all intramolecular atom pairs separated by three or more covalent bonds (1–4 interactions and above). Thus, traditional force-fields are built on the reasonable assumption that, in biomolecules, the intramolecular non-bonded interactions are the same as intermolecular non-bonded interactions. The explicit torsional potential helps the force-field to model the low energy conformations of the peptide interacting with itself, ligands and solvents. The importance of an accurate balance of inter and intramolecular forces for challenging applications involving molecular recognition of pharmaceuticals, such as computer-aided drug design, cannot be overemphasized.⁸ However, it is clear that the traditional force-field model is limited in accuracy,^9,10 for example, the electrostatic models that are successfully used in modelling intermolecular forces are not valid at some 1–4 distances because of charge cloud overlap¹¹ leading to significant penetration effects.^12,13 The customary approximation in many force-fields of just halving the atom–atom non-bonded intermolecular functions for the 1–4 intramolecular energy terms cannot be very accurate.

Applying traditional force-fields to pharmaceutical-like molecules, with flexible bonds linking multiple functional groups, often relies on poorly justified transferability assumptions for lack of data for empirical fitting^14,15 and hence are often unsuccessful for simulating the properties of pharmaceuticals materials.¹⁶ For example, there have been no successes based on the use of force-fields for final lattice energy evaluations in the blind tests of organic crystal structure prediction (CSP).¹⁷ This can be due to the force-field giving a qualitatively wrong conformation even for the isolated molecule, as in the case of aspirin.¹⁸ Lattice energy minimizations with force-fields can change the molecular conformation within the crystal so much that the relative positions of the functional groups leads to a qualitatively different crystal structure.¹⁹ In other cases, the structures may be reproduced adequately but the failure to rank the energies properly has been traced to the use of the same charges and van der Waals interactions for the intermolecular and intramolecular forces.²⁰ Consequently, the most successful approaches to CSP rely on expensive electronic structure calculations of the molecular conformational energy. In one CSP approach, a specific tailor-made force-field is parameterized for the molecule from dispersion corrected density functional (DFT-D) calculations and used to generate crystal structures, but then the most promising crystal structures require refinement by periodic DFT-D lattice energy minimizations.²¹ In another CSP approach, ab initio calculations on a single molecule either in isolation^22,23 or in a polarizable continuum,²⁴ are used to evaluate the energy penalty for changes in conformation (ΔE_intra), and provide the distributed multipole representation of the molecular charge density^11,25,26 used for the electrostatic contribution to the intermolecular lattice energy. Thus, the crystal structure prediction methodologies that have advanced to aid solid form screening in pharmaceutical development^27–31 require a very large number of electronic structure calculations to define the conformational potential energy surface of the molecule. Hence, the approach needed to give the relative energies of different possible crystal structures is far too computationally demanding to be used in Molecular Dynamics simulations. Such simulations are highly desirable for calculating the relative free energies of organic polymorphs^32–34 as ambient conditions are rather too close to the melting temperatures of organic solids to rely on the harmonic approximation. Therefore, we need to model the molecular flexibility of typical pharmaceutical molecules by a force-field that accurately reproduces the relative energies of the known and thermodynamically competitive crystal structures and yet can be evaluated sufficiently quickly for realistic Molecular Dynamics simulations. Such a force-field would be used for assessing crystal stability at ambient temperatures, calculating the relative free energies of known and potential polymorphs, and for simulating nucleation and other molecular recognition processes of the molecules.³⁵

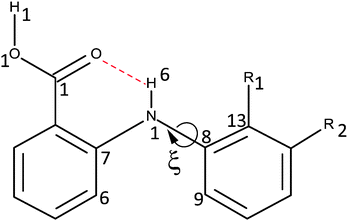
The success of CSP studies suggest that it is worth investigating decoupling the models for the intermolecular forces from those for the intramolecular forces (i.e. conformational profiles) as a route to more accurate force-fields for pharmaceutical molecules. The intermolecular forces could be modelled by anisotropic atom–atom potentials, as currently used in CSP studies, so the requirement is for an analytical form for the intramolecular energy changes (ΔE_intra). Hence, for a preliminary investigation into how we could model conformational energy differences of pharmaceuticals, we investigate a single torsion angle that both exemplifies the challenges of conformational flexibility in crystal structure prediction, and has long been seen as a key determinant in the pharmacological activity of a family of analgesics.³⁶ The fenamates (Fig. 1) are so prone to conformational polymorphism,³⁷ that the fenamate unit has been termed a polymorphophore.³⁸ The non-steroidal anti-inflammatory drug flufenamic acid (FFA) holds the current record for having crystal structures determined for nine polymorphs,³⁹ and another, tolfenamic acid (TA), has at least five polymorphs.³⁸ In the majority of fenamate crystal structures, the intramolecular and intermolecular (carboxylic acid dimer) hydrogen bonds are preserved, and it is the torsion angle (ξ) defining the orientation of the (substituted) phenyl “paddle wheels” that varies, leading to the marked differences in the crystal packing. Crystal structure prediction studies on fenamic (FA) and tolfenamic acid (TA)⁴⁰ show that it is the subtle compromise between the packing of the substituted phenyl rings and the small conformational energy penalty that leads to the polymorphism of TA and monomorphism of FA. Mefenamic acid (MA) differs from TA only by a chloro/methyl exchange at a position (R₂Fig. 1) that would not be expected to affect the torsional profile, and the chloro/methyl substitution can lead to isostructural crystal structures,^41–45 yet the crystal energy landscape of MA is distinct from that of TA.⁴⁶ Many studies have emphasized the difficulty in evaluating the relative energies of fenamate polymorphs,^47–49 or controlling the polymorphic outcome by varying the crystallization conditions.⁵⁰ A study of the distribution of the fenamate-like torsion angle ξ in the organic crystal structures within the Cambridge Structural Database⁵¹ shows that a wide range of angles can be adopted, but these correlate with very low conformational energies.⁴⁰

Fig. 1 The fenamate family, showing the low barrier torsion angle (ξ = C₇–N₁–C₈–C₉) and atomic numbering. ξ = 0 when the aromatic rings are coplanar as drawn. The fenamates mentioned in this paper are fenamic acid (FA) R₁ = R₂ = H, tolfenamic acid (TA) R₁ = CH₃, R₂ = Cl, mefenamic acid (MA) R₁ = R₂ = CH₃, flufenamic acid (FFA) R₁ = H, R₂ = CF₃ and clofenamic acid (ClFA) R₁ = H, R₂ = Cl. The dotted line represents an intramolecular hydrogen bond.

This study analyzes the one dimensional conformational profile for the fenamate torsion, ξ, contrasting FA, TA, ClFA, and MA (Fig. 1), which differ in substituents that would be expected to change the conformational profile (R₁) and those sufficiently distant (R₂) to be expected to have little effect.

To find an analytical model that can reproduce these low-energy conformational profiles accurately requires a physically justified functional form for effective parameterization. The cause of rotational barriers has long been controversial,⁵² with the ethane rotation barrier still generating discussion as to whether the origin is steric, hyperconjugation^53–55 or an electrostatic effect.⁵⁶ The quantitative distinction between electronic effects from changes in the molecular orbitals, as opposed to steric “non-bonded” effects, is dependent on the precise definition and type of charge density calculation. We investigate the qualitative issue for the fenamate molecules by constructing model molecules with minimal steric effects so that conformational profile is dominated by the change in the electronic effects, loosely termed conjugation. This type of effect would be expected to be represented by a few terms of the traditional explicit torsional term of the general form:

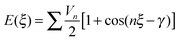where γ defines the phase shift, and n the periodicity. For FA, ξ defined in Fig. 1 requires that γ = 0 and symmetry dictates that n is an even integer. For substituted fenamates, odd values of n could contribute, though the conformational profile should be symmetric about ξ = 0.

If the origin of the conformational profile is predominantly steric, caused by the varying repulsion between the overlapping charge distributions of 1–4 atoms with ξ, then it should be well represented by non-bonded atom–atom interactions. An exp-6 atom–atom model would be expected to give a better representation than a Lennard-Jones (R⁻¹²) model of the variation of the repulsion with distance, given the success of the overlap model in parameterizing intermolecular repulsion potentials.^57,58 Thus a crude starting point for our investigation of the “non-bonded” contribution to the torsion potential is the exp-6 atom–atom model potential with a parameterization that has been developed for modelling the intermolecular forces between organic molecules in crystals:^59–62

where atoms i and k of atomic types ι and κ are separated by intramolecular distances R_ik, calculated from the molecular conformation with torsion angle ξ. Not including an explicit electrostatic term in the intramolecular potential considerably simplifies the implementation and extension to larger molecules. 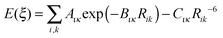The intermolecular electrostatic contributions are effectively implicitly modelled by fitting the parameters A_ικ, B_ικ and C_ικ without assuming any relationship between the like (ιι and κκ) and unlike (ικ) interactions.^59–62

The aim of this study is to establish the physical basis for the variation in conformational energy of the fenamates to determine what might be a reasonable analytical model. This tests whether the understanding of torsional potentials that has been developed for small molecules, such as ethane, need amending for larger organic systems. The work concentrates on fenamic acid (FA) and tolfenamic acid (TA) but the analysis is extended to related molecules to assess generality. If we can find an appropriate analytical functional form for the conformational energy of a family of molecules, then the combination of separate intermolecular and intramolecular potentials would provide more accurate analytical force-fields for pharmaceutical molecules.

2. Method

2.1. Ab initio conformational energy profiles

The conformational profiles used throughout this study, unless otherwise specified, were relaxed conformational energy scans at PBE0/6-31+G(d) level of theory, carried out using GAUSSIAN03.⁶³ We found that the results of TA were sensitive to the atoms used to define the torsion angle, (i.e. Fig. S1 of the ESI† shows that defining the torsion by H₆–N₁–C₈–C₉ or H₆–N₁–C₈–C₁₃ could double the height of the maximum at ξ = 0°, and even using C₇–N₁–C₈–C₁₃ could show differences at high energies as ξ approached 180°). This common observation that torsional scans depend on which 4-atom set is used to describe a torsion about a rotatable bond complicates the analysis of rotamer distributions.⁶⁴ The profiles were also dependent on the starting points. Hence, to determine the starting geometry, we performed a full optimization near each symmetry independent potential minimum. The grid consisted of the optimized structures and points ξ = 5n°, with the scans going from the potential minima. Highly repulsive points as ξ approached 180° for the substituted fenamates were omitted.

2.2. Investigation of electronic versus steric effects

To attempt to separate out the steric effects from electronic effects, a series of model molecules where the steric effects had been minimized were studied. When the benzoic acid group was replaced by a series of smaller molecular fragments, such as hydrogen atom, the three bonds to the nitrogen atoms were constrained to be coplanar by fixing an improper torsion angle relating the nitrogen to the three bonded atoms. This prevents the pyramidalization at the nitrogen in the torsional potential of phenylamine⁵⁶ and the major rearrangement of the second hydrogen that occurs in a relaxed scan of H₇–N₁–C₈–C₉.

2.3. Atom–atom modelling of torsion potentials

A starting point for considering intramolecular steric interactions is the exp-6 atom–atom intermolecular parameters derived by Gavezzotti by fitting to crystal structures and heats of sublimation of hydrocarbons, oxahydrocarbons, azahydrocarbons, chlorohydrocarbons and nitro compounds.⁵⁹ This provides the parameters for all intramolecular interactions involving C, N, O, Cl and H. The same parameters are used for all C and H atoms, whether aromatic or in the methyl or carboxylic acid groups, hence the atom typing is crude compared with current force-fields e.g. Sybyl typing.⁶⁵ There is a polar hydrogen type, HB, which we use for both polar hydrogens (H₁ and H₆ in Fig. 1) available from the extension of the exp-6 parameterization to hydrogen-bonded crystals.⁶⁰ The HB⋯O/N exp-6 potentials have particularly deep wells as they have absorbed the electrostatic effects in intermolecular hydrogen bonding.⁶⁰ Since the intermolecular parameter set does not have parameters for the H⋯HB and C⋯HB interactions, these were fitted in this study, using the parameters for H⋯H and C⋯H as a crude starting point. The intermolecular exp-6 parameters are given in Table S1 of the ESI,† with other types available from the scheme in Table S2 (ESI†).

The atom–atom interactions are summed over all 1–4 and higher bond-paths in the entire molecule (i.e. this explicit intramolecular force-field does not distinguish 1–4 from the other intramolecular interactions, as the 1–4 interactions are not always the shortest intramolecular atom–atom distances Tables S3 and S4, ESI†). The maximum bond-path is 1–11 for all three fenamates, and most pharmaceutical molecules are sufficiently small that there is no need to define a summation limit in terms of intramolecular distance or bond-path length. The use of 1–4 distances as the shortest intramolecular interactions included in the atom–atom summation is traditional, although we note that 1–3 interactions are used elsewhere, e.g. in the CSP code in GRACE where they have sometimes been found to be problematic, including in the case of a bulky side group attached to an aromatic ring which required specific scaling down.⁶⁶

The atom–atom formulation results in many virtually constant terms, such as the H⋯H, C⋯C and H⋯C contributions from within the aromatic rings. These terms contribute to the baseline energy, E_base, defined as the minimum energy found in the scan with a specific parameterized model.

2.4. Fitting analytical models to the conformational profiles

For this preliminary investigation of suitable functional forms, we have not applied any weighting to the conformational profile beyond restricting the points to conformational energies below 10 kJ mol⁻¹, i.e. not seeking to accurately represent the steric barrier above 145° for TA and MA. This gives N_p = 37 energy data points for the FA fit and N_p = 30 for TA and MA.

Since there is considerable correlation between the atom–atom coefficients, particularly the two repulsion parameters (A_ικ and B_ικ),^67,68 we seek to rescale selected repulsion and dispersion coefficients, giving a linear model that can be combined with an appropriate cosine term and an approximation to the baseline constant, c ∼ E_base, to give

A generalizable method of deriving analytical models for conformational profiles was developed during this work (Fig. S4, ESI†), which includes the FORTRAN code and NAG⁶⁹ library routines for systematically comparing the ability of various selections of the linear parameters (α, β_ικ, γ_ικ, c) to represent the ab initio data by least squares using a general linear regression model.⁷⁰

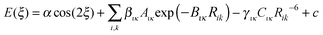3. Results

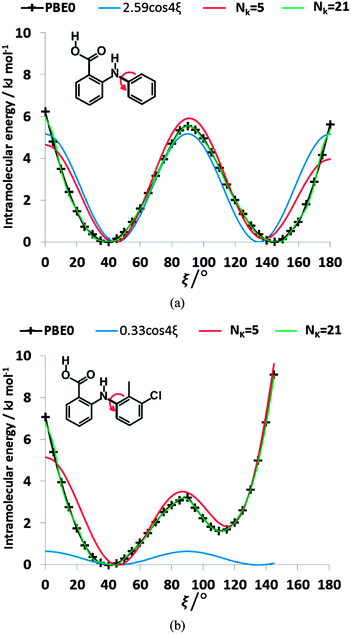
3.1. Conformational energy profile of the fenamates

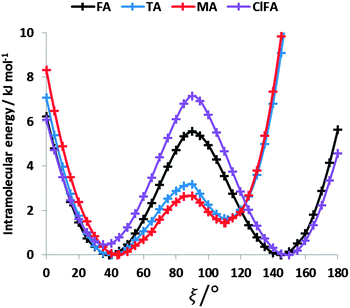
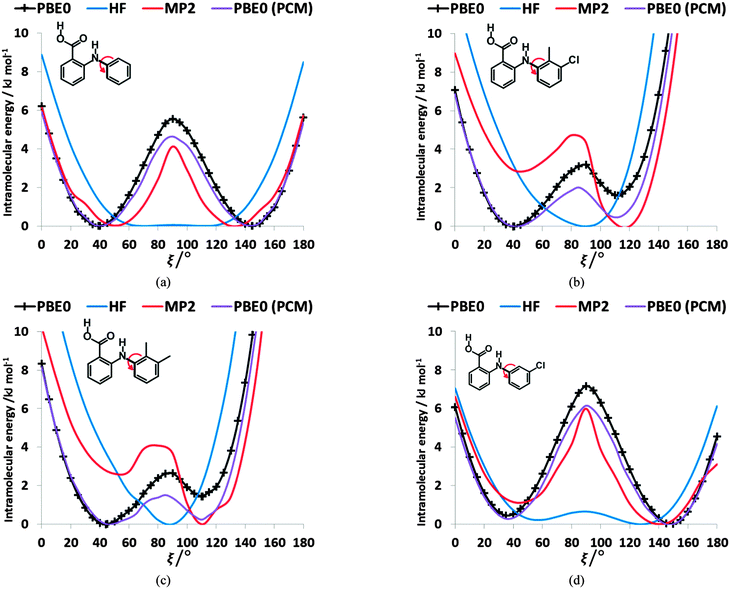
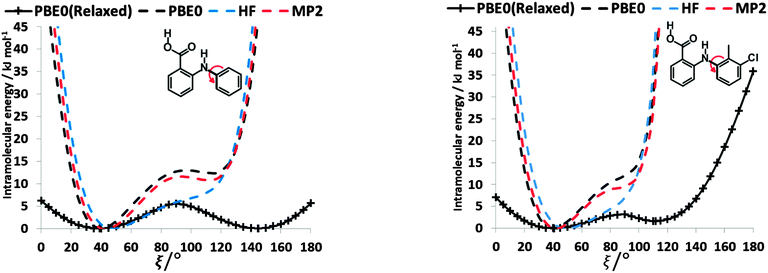
The conformational profiles for four of the fenamates (Fig. 2) show that there are two distinct minima, which are only close in energy for the symmetric FA and R₂-substituted ClFA. There is one potential maximum that varies a little between the molecules for the planar conformation (as drawn in Fig. 1), another maximum when the aromatic rings are approximately perpendicular, and a third where there is a significant steric clash for the R₁-substituted fenamates TA and MA as the other planar conformation is approached. An analysis of the observed values of this torsion angle in crystal structures containing the fenamate fragment (Fig. 2 of ref. 40) shows that the observed angles are clustered around the two minima, consistent with the expectation that most molecules adopt low energy conformations in crystal structures.³⁷ Hence, the two low energy barriers (around 5–9 kJ mol⁻¹) clearly have a major effect on the crystal packing and are large compared with most measured polymorphic energy differences, including those of TA which cover less than 2 kJ mol⁻¹.⁴⁰

Fig. 2 Relaxed conformational scans at PBE0/6-31+G(d) level of theory for the fenamates. The minima were at ξ = 38.94° and 144.71° for FA, 40.63° and 111.86° for TA, 44.08° and 110.48° for MA, and 35.86° and 148.38° for ClFA.

Testing the sensitivity of this conformational profile to the choice of ab initio method (Fig. 3) shows that even obtaining a conformational profile in qualitative agreement with that derived from experimental crystal structures is sensitive to method. The HF scan has only one minimum, at a conformation that is not observed in the crystal structures of fenamates; a CSP study based on this conformational profile would generate qualitatively incorrect crystal structures. Only the ab initio methods that include some description of electron correlation produce a maximum at around 90°. Nevertheless, there is fair agreement in the conformational barriers for these methods. However, it is notable that for TA and MA evaluating the energy using PBE0 geometries at the MP2 level swaps the relative energy of the two minima, with the PBE0 calculations being in better agreement with the analysis of the crystalline conformations of fenamate-like fragments with a substituent at C₁₃. Evaluating the conformational profile within a polarizable continuum model⁷¹ with ε = 3, a typical dielectric constant of organic crystals,⁷² showed a reduction in energy penalty around the energy maxima (ξ ∼ 90°) for all the fenamates (Fig. 3). The application of this polarizable continuum model (PCM) has been shown to improve the relative energy ranking of some conformational polymorphs.⁷² The results in Fig. 3 confirm that we cannot obtain definitive ab initio conformational energy scans, but the scans in Fig. 2 are adequate for the purposes of this study.

Fig. 3 Relaxed conformational scans of fenamates (a) FA, (b) TA, (c) MA and (d) ClFA at HF and PBE0 method with 6-31+G(d) basis set. These are contrasted with the single point energies at the MP2/6-31+G(d) level and within a polarizable continuum model (PCM) with ε = 3 for the PBE0/6-31+G(d) conformations.

To establish the importance of changes in the other torsion angles, bond angles and bond lengths during the relaxed scans in Fig. 2, the conformation scans were repeated, starting from the fully optimized structure at the PBE0/6-31+G(d) level of theory and only allowing the angle ξ to change. Thus each conformation is identical when a single point energy is evaluated for each ab initio method. The energy differences (Fig. 4) are very marked for all the fenamates, even in the lowest energy regions. The extent to which the positions of the other atoms relax to lower the conformational energy barrier is very marked around the energy maxima (Fig. 5), even though these maxima correspond to an energy of less than 7 kJ mol⁻¹ in the relaxed scans (Fig. 4). Even for FA, there is a significant change in the internal hydrogen bond with the reorientation of the benzoic acid around all maxima. Both methyl torsions play a role in reducing the energy around the 90° maximum for TA (Fig. 5). Indeed, even for FA, the changes in the other conformational variables produce the slight asymmetry between the two minima (Fig. S2 of the ESI†). Hence, the contrast between the relaxed and rigid (Fig. 4) scans and the corresponding conformations (Fig. 5) confirm that the changes in the other conformational variables play a major role in lowering the conformational barrier over a wide range of ξ angles, including those sampled within the crystal structures.⁴⁰

Fig. 4 Comparison of rigid (dotted line) scans of FA (left) and TA (right) at HF, MP2 and PBE0 methods with 6-31+G(d) basis set as a function of torsional angle ξ. The relaxed PBE0 scans from Fig. 3 are shown for comparison as a solid line.

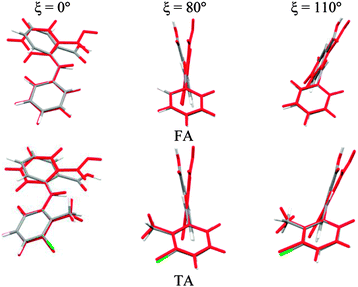Fig. 5 Overlay of relaxed (coloured by element, Fig. 2) and rigid (red, Fig. 4) conformations of FA and TA overlaying the atoms defining the torsion angle ξ = 0°, 80° and 110° at the PBE0/6-31+G(d) level of theory.

3.2. Splitting electronic from steric contributions to the barrier to rotation

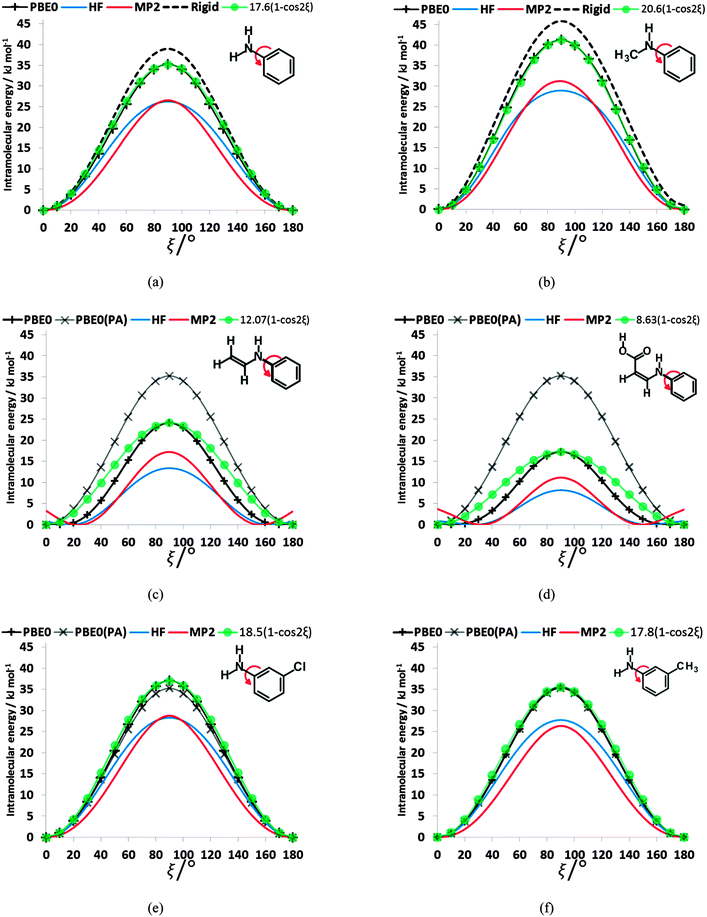
To establish the importance of the intramolecular steric clashes, the rigid and relaxed scans were repeated with model molecules in which the benzoic acid group was replaced with a smaller fragment and the bonds around the nitrogen constrained to be planar so as to avoid the pyramidalization of the amine (Fig. 6). The potential energy scan has a very large maximum at 90° for planar-N-constrained phenylamine (PA), approximately 6 times higher than the barrier in the fenamates. (Note that Fig. 6 has the same scale as the rigid scans in Fig. 4, covering a larger energy range than the relaxed scans in Fig. 2 and 3). Replacing one constrained hydrogen with a methyl (Fig. 6b) produces a slightly larger barrier but very little asymmetry, strongly suggesting that this is an electronic effect of conjugation between the lone pair on the nitrogen and the aromatic ring. Adding a double bond to PA reduces the barrier to rotation by 11.10 kJ mol⁻¹ (Fig. 6c), implying that the conjugation with the benzoic acid ring of the fenamates will have contributed significantly to reducing the electronic barrier. Adding a carboxylic acid that forms an intramolecular hydrogen bond to the N–H group further reduces this barrier by almost 7 kJ mol⁻¹ (Fig. 6d). The intramolecular hydrogen bond in this model molecule (Fig. 6d) varies in length from 1.94 to 1.92 Å as ξ changes from 0 to 180°, in comparison with the FA hydrogen bond varying from 1.87 to 1.84 Å, and so we may infer that the intramolecular hydrogen bonding in the fenamates will similarly reduce the electronic barrier. In contrast, substituting Cl and CH₃ at the meta position of PA (Fig. 6e and f) shows only a small change to the barrier height, h, with 3-chloroaniline (h = 37.0 kJ mol⁻¹) and 3-methylaniline (h = 35.6 kJ mol⁻¹) having only slightly larger barriers than PA (h = 35.2 kJ mol⁻¹).

Fig. 6 The relaxed (solid lines) torsional scan of planar-N-constrained models for the phenyl rotation, where the benzoic acid group of fenamic acid has been replaced by (a) hydrogen atom (PA), (b) methyl, (c) vinyl and (d) prop-2-enoic acid, and the hydrogen in the meta position of PA has been replaced by (e) chlorine, and (f) methyl using HF, PBE0 and MP2 methods with the 6-31+G(d) basis set. Plots of (h/2)(1 − cos(2ξ)) where h is the height of the barrier of relaxed PBE0/6-31+G(d) scans are shown in green. For (c)–(f) the PBE0/6-31+G(d) relaxed scans of PA from (a) are shown in grey for comparison. In (a) and (b) a rigid scan at the PBE0/6-31+G(d) level of theory is shown by a dotted line.

The scans in Fig. 6a, b, e and f clearly have no maxima at 0 or 180° confirming that the steric clash between the aromatic C₆–H and the C₉–H or C₁₃–R₁ groups of the phenyl ring are responsible for these maxima. These curves are very well reproduced by (h/2)(1 − cos(2ξ)) where h is the potential maximum. As the nitrogen substituents get larger (Fig. 6c and d), there are signs of additional steric effects at 0 and 180° and a larger difference in the barrier height at 90° between MP2 and HF calculations, suggesting there is more change in intramolecular dispersion. The difference between a rigid and relaxed scan is small (Fig. 6a and b), and the difference in the curves with type of calculation are relatively minor compared with the qualitative difference between the HF and correlated methods for the fenamates (Fig. 3). The overriding conclusion from contrasting the conformational scans of model molecules with minimal steric effects (Fig. 6) with those of the fenamates (Fig. 2) is that there is an electronic contribution to the torsional barrier at ξ = 90°, which can be represented by a (h/2)(1 − cos(2ξ)) term. This can be rationalised as resulting from the changing conjugation between the nitrogen lone pair and the phenyl ring. (The simple idea of conjugation, that a fenamate with ξ = 0 is stabilized by having a π orbital delocalized over both rings is inappropriate as this conformation is not planar (Fig. 5).) The changes in the phenyl molecular orbitals with conformation are similar for PA and the fenamates.⁷³

However, the electronic effects are not solely responsible for the maxima at ξ ∼ 90°. The intramolecular atom–atom dispersion contribution (−C_ικ/R_ik⁶) from eqn (2) using the intermolecular parameters produces a significant maximum in this region (ESI,† Section 1.3). The repulsion component (−B_ικR_ik) gives maxima at 0 and 180° and minima at 90°, consistent with the expectation that these two maxima occur because of steric clashes. Thus, the analysis of the torsional potentials of the fenamates reveals that there is an electronic effect from the change in the orbital interactions such as “conjugation” between the aromatic rings and the nitrogen lone pair destabilizing the non-planar conformations and steric effect from the variation in overlap of non-bonded atoms. For these larger molecules, in contrast to the well-studied small molecule torsional potentials (e.g. of ethane), intramolecular dispersion and small changes in the other conformational variables also make a very significant contribution to the torsional profile.

3.3. Representation of torsional potential by an analytical model

3.3.1. Cosine series model. The traditional cosine series expansion of the torsional potential,where N_k and N_p are the number of fitted coefficients and data points respectively, must include cos 4ξ to have the correct number of minima for the fenamates. This term alone gives a poor position of the minima for FA and is qualitatively wrong for TA (Fig. 7). A least squares fit including the lower cosines (N_k = 5, eqn (4)) gives a qualitatively reasonable representation (Fig. 7), but further improvement is slowly converging (Fig. S5 in the ESI†). This demonstrates that the cosine series is a fitting exercise, not reflecting the physics. It is effectively modelling the relaxed scans by a functional form that assumes the scan is rigid (i.e. only the torsion angle changes), whereas there are (Fig. 4) significant relaxation effects that reduce the conformational barrier. Poor convergence of the cosine model expansion has also been reported for a biphenyl torsion within a dye which required 7 terms,⁷⁴ while polynorbornene⁷⁵ required 6 and 15 terms for the meso and racemic dimer respectively.

Fig. 7 Comparison of the ab initio relaxed scan at PBE0/6-31+G(d) level of theory with linearly fitted least square cosine series model for (a) FA and (b) TA, with N_k = 5 (red lines), the optimal cos 4ξ terms (blue lines), and N_k = 21 (green lines, for which the quality of fit σ_intra = 0.17 kJ mol⁻¹ for FA and coincidentally for TA).

3.3.2. Rescaling the repulsion model. It is possible to get an excellent fit to the torsion potentials by summing the exp-6 potential (eqn (2)) over all 1–4 and higher intramolecular atom–atom distances (ESI,† Section 3.2), provided that a few of the intermolecular repulsion coefficients parameters A_ικ are rescaled by a factor β_ικ. Rescaling just two repulsion contributions for FA (C⋯H and H⋯H) and five for TA (C⋯H, C⋯HB, C⋯N, H⋯H and H⋯HB) produces a model that reproduces the torsional profile well (Fig. S6 in the ESI†). However, some of the fitted rescaling parameters were negative (β_ικ < 0), which implies that the exponential steric repulsion had become attractive. Thus, again, this appears to be an unphysical fitting exercise.

3.3.3. Combined physical model. If we assume a model that describes both the electronic effects and allows rescaling of the atom–atom interactions:then there are a huge number of ways of finding a satisfactory fitting of the data (ESI,† Tables S8 and S9). However, only when β and γ are positive do the contributions retain the repulsive and attractive (dispersion) nature respectively, and a negative value of α is required to give a maximum around ξ = 90° corresponding to “conjugation” (cf.Fig. 6). Fitting α and rescaling only a few atom–atom interactions gives a qualitatively accurate fit (Fig. 8). It is not surprising that the parameters involving H and HB require significant rescaling as the intermolecular values were not well defined.⁵⁹ Although virtually perfect fits can be obtained (Table S8 in ESI†), the variation in the fitted parameters is significant, which is not surprising given the exponential sensitivity of the repulsion to changes in atom–atom distances. These changes can be substantial, for example the two minima in the FA scan at ξ = 38.94° and 144.71° correspond to conformations that differ by 0.61 Å in the 1–4 distance between the amide proton and C₁₃ (or C₉) although the minima only differ in energy by 1.88 × 10⁻³ kJ mol⁻¹. Even the C₈–C₉ and C₈–C₁₃ aromatic bond lengths differ by ±0.0037 Å for ξ = 0 or 180°, but only by ±0.0004 Å for ξ = 80 or 100°, with larger changes in the bonded hydrogen positions. In contrast to FA, TA gives a qualitatively acceptable fit (Table S9 in ESI†) only when at least three types of atom–atom parameters are rescaled (N_k = 8), including C⋯N, as shown in Fig. 8. TA differs from FA in having many more intramolecular distances that change significantly with ξ including some within the same aromatic ring, such as methyl-chloro interactions (Table S5 in ESI†). Thus, we are able to obtain a variety of analytical models of the form of eqn (5) that can reproduce the torsional profiles of FA and TA with a high degree of accuracy, despite the significant variation in many atom–atom distances during the relaxed torsional scans. The ease with which this physically justified model could reproduce the conformational dependence of FA and TA shows that the approach is promising.

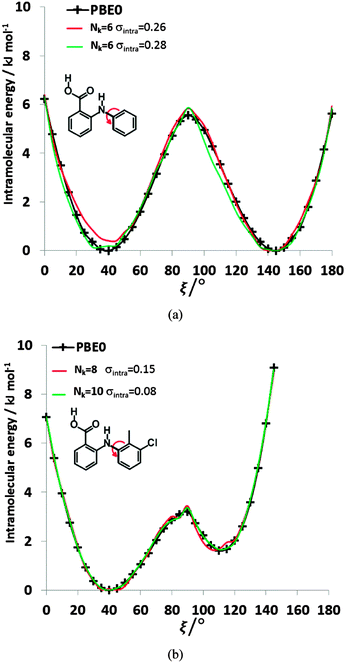Fig. 8 Comparison of the relative energies from ab initio calculations (solid black lines) of (a) FA and (b) TA with selected physical models. For FA, the selected N_k = 6, σ_intra = 0.26 kJ mol⁻¹ model has β_C–HB = 8.01, γ_C–HB = 16.54, β_H–H = 10.74, γ_H–H = 58, α = −3.39, and c = 123.69 kJ mol⁻¹, whilst the N_k = 6, σ_intra = 0.28 kJ mol⁻¹ model has β_C–H = 0.28, γ_C–H = 7.83, β_H–HB = 11.09, γ_H–HB = 34.79, α = −1.17, and c = 75.59 kJ mol⁻¹. For TA, the parameters of the selected fits N_k = 8, σ_intra = 0.15 kJ mol⁻¹ and N_k = 10, σ_intra = 0.08 kJ mol⁻¹ are highlighted in Table S8 of the ESI.†

3.4. Transferability

We can further investigate the physical applicability of the atom–atom plus electronic functional form (eqn (5)) by testing whether the models can describe the torsional potentials of related molecules. The difference between the energy scans when the substituents are far from the varying torsion angle, for example the change of H to Cl atom i.e. from FA to ClFA or between TA and MA (Fig. 2), should not change the main steric interactions, and will only have a small effect on the electronic term (Fig. 6e and f).

Transferring a set of parameters fitted to FA and adding Cl parameters, does indeed (Fig. 9) give some of the asymmetry in the well depths seen for ClFA, and with fitting the electronic term the higher central barrier (Fig. 2) is also reproduced. Similarly, a set of parameters fitted to TA can reproduce the lower barrier at ξ = 90° and higher barrier at ξ = 0° in MA (Fig. 9), despite the conformational relaxation of the methyl–methyl interaction being somewhat different from that of the methyl-chloro geometry (Fig. 5). Further examples of the transferability of the parameters are given in the ESI† Section 4.

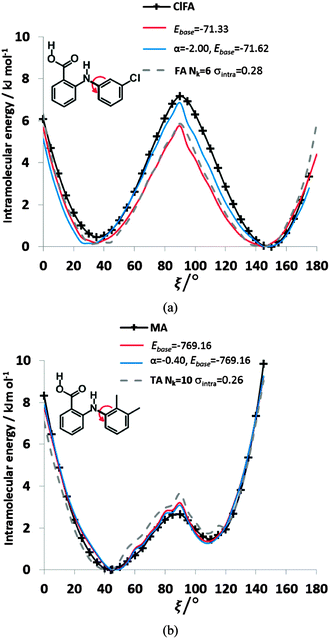Fig. 9 Comparison of the relative energies from ab initio calculations (solid black lines) with models using transferred β_ικ and γ_ικ parameters from FA and TA to (a) ClFA and (b) MA respectively. The red curve has only had the baseline adjusted, whereas the blue curve has the α parameter refitted to ClFA or MA respectively. The transferred FA parameters are those N_k = 6, σ_intra = 0.28 kJ mol⁻¹ in Fig. 8, while those of TA N_k = 10 σ_intra = 0.26 kJ mol⁻¹ are highlighted in Table S8 of the ESI.† The grey dotted lines give the conformational profiles for (a) FA and (b) TA from these parameters.

4. Discussion

4.1. Physical origins of torsional potentials

By analyzing the low energy torsional barrier in the fenamates (Fig. 2), it is clear that larger organic molecules retain the contributions identified for small model molecules, such as ethane, in that there is both an electronic and a steric component. However, as the molecules become larger, the effect of small correlated changes in the other bond angles and the dispersion contribution become very significant. The difference between the low energy torsional barrier and the one calculated holding other conformational variables constant is surprisingly large (Fig. 4). This means that attempts to represent the conformational barrier by a cosine series, ignoring the position of the other atoms beyond 1–4, degenerates into an ineffective fitting exercise (Fig. 7 and as shown in ref. 74 and 75). An atom–atom formulation can directly reflect the geometric changes in the relaxation.

We could not use a definitive ab initio torsional potential for each fenamate, so used a set of consistent, qualitatively realistic, potentials, because of the variation in the relative energies within the affordable methods (Fig. 3). As molecules increase in size, there is an increasing contribution to the conformational profile from the intramolecular equivalent of the intermolecular dispersion. Since dispersion is an electron correlation effect, this makes converging to an accurate ab initio torsional profile very demanding of the type and quality of electronic structure calculation^76,77 because of the importance of electron correlation and intramolecular basis set superposition error.⁷⁸ The Tyr-Gly peptide conformational minima,⁷⁹ alanine dipeptide ϕψ energy maps⁷ and the barriers to torsional rotation in π-conjugated polymers⁸⁰ have also been shown to vary significantly with choice of post-Hartree–Fock theoretical approach. Electron correlation plays a critical role in what we can qualitatively recognize as through space intramolecular dispersion effects and changing conjugation of the molecular orbitals. This is in addition to the variation in the repulsion and electrostatic interactions within the molecule that would be expected from the sensitivity of intermolecular interactions to the ab initio method.⁸¹ Separating the “through space” intramolecular dispersion from the other electron correlation effects that contribute to the (h/2)(1 − cos(2ξ)) electronic barrier from “conjugation” or delocalization between the two aromatic rings is probably not quantitatively meaningful when using a quantum mechanical method that approaches the quantitative accuracy needed. The challenge of extending the reliability and accuracy of electronic structure methods to larger molecules, which are more typical of pharmaceuticals and realistic biological molecules in isolation or condensed phases, is the subject of much active research.^76,82 This study emphasizes the risk in using affordable but approximate electronic structure methods to provide a large data set of conformational energies for fitting, as HF methods would provide qualitatively misleading results for the fenamates.

The most generalizable analytical models for torsion potentials will represent the physical origins of the contributions. For the fenamates, the electronic term is well represented by a cos(2ξ) contribution, and an atom–atom model is appropriate for representing the steric and dispersion contributions and automatically includes the effect of relaxation of the rest of the molecule. However, the simple exp-6 model used here is only a first approximation for the intermolecular forces^83,84 and could not be expected to translate accurately to the shorter intramolecular distances that vary with the torsion angle ξ. Pairs of atoms of atomic types that would rarely, if ever, be found in van der Waals intermolecular contact can be at very short and varying 1–4 distances within a molecule. Modelling conformational energies using a simple atom–atom exp-6 form is effective, but the interactions involving hydrogen atoms, and the methyl carbon nitrogen interaction for TA and MA, were described by significantly different parameters from those empirically fitted for modelling intermolecular forces. These atomic types are involved in some of the atom–atom distances that change most with ξ. The original intermolecular parameters appear to be able to capture the smaller changes from molecular relaxation adequately. The net result is that it is possible to obtain an analytical expression in the form of eqn (5) that can model the conformational curves of the individual fenamates extremely well (Fig. 8) and could be transferable (Fig. 9).

The range of the sets of atom–atom parameters that can reproduce the limited ab initio data on the torsional profiles of the fenamates shows that much more extensive sets of ab initio calculations with greater variations in the other degrees of freedom would be required for fitting eqn (5) to provide a robust analytical model. It would be helpful to have more stringent constraints on what would constitute a physically reasonable range of parameter values based on more careful characterization of intramolecular “steric” interactions. Nonetheless, the functional form appears promising for the ability to represent the complex interactions that lead to the low energy torsional potentials in fenamates.

4.2. Towards more accurate force-fields for pharmaceutical molecules

This approach to modelling conformational energies of the fenamates could be extended to many pharmaceuticals that comprise approximately rigid molecular fragments joined by flexible linkages that allow the molecule to adopt a wide range of conformations. We can envisage a general scheme for determining such potentials for a given molecule following a crystal structure prediction (CSP) study^22,85 which involves the calculation and storage of a large database of ab initio conformational energies and forces for the pharmaceutic al molecule.^27,28,30 This database will cover most of the range of conformations that are likely to be sampled in a Molecular Dynamics study of the molecules in condensed phases, with a strong bias towards the conformations that occur in low energy crystal structures, including known and possible polymorphs.⁸⁶ This database could be used to parameterize the analytical conformational energy model, adapting the fitting routines written for this study.

Using a physically motivated analytical functional form ensures that the extrapolation to other high energy conformations will be realistic. Building the analytical force-field in conjunction with a CSP study for a specific molecule would have the advantage that the analytical intramolecular force-field could be validated by ensuring that it reproduced the crystal energy landscape, i.e. that the energies of different packing, hydrogen bonding and stacking modes were correctly balanced with the accompanying conformational changes. The use of a physically based functional form is more conceptually pleasing in its generality than fitting the ab initio data by a molecule-specific force-field defined relative to the lowest energy conformation,⁸⁷ or constructing a neural network potential.⁸⁸

The application of separate analytical potentials for both intra- and intermolecular terms will require adaptation of molecular modelling codes; however, the coding for the energies, forces, and second derivatives of the proposed intramolecular force-field (eqn (5)) is already in most codes. The calculation of inter- and intramolecular terms would need to be separated in programs that use traditional force-fields such as DL_POLY^32,89 for Molecular Dynamics simulations. However, the greater accuracy of the intramolecular forces is most needed in combination with the more accurate anisotropic atom–atom intermolecular potentials for organic molecules. The analytical intramolecular potential models could be incorporated in the rigid-molecule codes DMACRYS²⁵ and DL_MULTI⁹⁰ which use distributed-multipole electrostatic models for static lattice and Molecular Dynamics modelling of organic crystals respectively. The conformation dependence of the distributed multipoles would need to be considered, but new methods of partitioning the charge density⁹¹ may reduce the conformation dependence, or it could be represented by an analytical model⁹² or interpolation scheme.⁹³

Although this change in approach to pharmaceutical force-fields is envisaging a specific model fitted for each molecule, the physical basis of the current model (eqn (5)) and the results in Fig. 9 and Fig. S7 (ESI†) suggest that a reasonably transferable set of atom–atom intramolecular exp-6 potentials could be fitted for families of molecules. Deriving a transferable model would require a very large dataset of ab initio conformational profiles of many molecules calculated at an appropriate accuracy. The transferability of the electronic term (α coefficients) would also need investigating. However, using separate atom–atom models for the forces within and between molecules could provide a significant improvement in accuracy on current force-fields, whilst maintaining the advantages of transferability for families of flexible pharmaceuticals.

5. Conclusions

The torsional potentials of organic molecules not only include short-range electronic “conjugation” effects and steric interactions, but also have a significant contribution from the intramolecular dispersion and small concerted changes in other conformational variables. This has two important consequences. Firstly the ab initio determination of organic molecule conformations is very sensitive to the treatment of electron correlation. Secondly, it is not possible to view a torsion as being simply transferable (i.e. the potential is defined by just the atomic types involved in 1–4 interactions) or expect it to be effectively modelled as a cosine series However, we have shown that an appropriate cosine term for the short-range electronic effects plus an isotropic atom–tom exp-6 intramolecular potential can model the conformational profiles of the fenamates well, provided that some of the coefficients are fitted to ab initio torsion potentials. It is clear that discarding the assumption that the same atom–atom models can be used for inter- and intramolecular forces is a route forward to more accurate force-fields.

Acknowledgements

We thank the Cambridge Crystallographic Data Centre and the M3S Centre for Doctoral Training (EPSRC GRANT EP/G036675/1) for financial and general support of Ogaga G. Uzoh.

Notes and references

1. J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
2. T. A. Soares, P. H. Hunenberger, M. A. Kastenholz, V. Krautler, T. Lenz, R. D. Lins, C. Oostenbrink and W. F. van Gunsteren, J. Comput. Chem., 2005, 26, 725–737.
3. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690.
4. W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
5. T. R. Stouch, J. Comput.-Aided Mol. Des., 2012, 26, 125–134.
6. J. W. Ponder, C. J. Wu, P. Y. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564.
7. A. D. Mackerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400–1415.
8. G. R. Marshall, J. Comput.-Aided Mol. Des., 2013, 27, 107–114.
9. G. Cisneros, M. Karttunen, P. Ren and C. Sagui, Chem. Rev., 2014, 114, 779–814.
10. S. K. Burger and G. Cisneros, J. Comput. Chem., 2013, 34, 2313–2319.
11. A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, 2nd edn, 2013.
12. D. M. Elking, G. Cisneros, J. P. Piquemal, T. A. Darden and L. G. Pedersen, J. Chem. Theory Comput., 2010, 6, 190–202.
13. R. J. Wheatley and J. B. O. Mitchell, J. Comput. Chem., 1994, 15, 1187–1198.
14. S. L. Price, Int. Rev. Phys. Chem., 2008, 27, 541–568.
15. S. L. Price, CrystEngComm, 2004, 6, 344–353.
16. Y. A. Abramov, Org. Process Res. Dev., 2013, 17, 472–485.
17. D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551.
18. R. S. Payne, R. C. Rowe, R. J. Roberts, M. H. Charlton and R. Docherty, J. Comput. Chem., 1999, 20, 262–273.
19. S. Brodersen, S. Wilke, F. J. J. Leusen and G. Engel, Phys. Chem. Chem. Phys., 2003, 5, 4923–4931.
20. M. D. Gourlay, J. Kendrick and F. J. J. Leusen, Cryst. Growth Des., 2007, 7, 56–63.
21. J. Kendrick, F. J. Leusen, M. A. Neumann and J. van de Streek, Chem. – Eur. J., 2011, 17, 10735–10743.
22. M. Vasileiadis, A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 677–685.
23. A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2011, 7, 1998–2016.
24. A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman, C. C. Pantelides, S. L. Price, P. T. Galek, G. M. Day and A. J. Cruz-Cabeza, Int. J. Pharm., 2011, 418, 168–178.
25. S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490.
26. A. J. Stone and A. J. Misquitta, Int. Rev. Phys. Chem., 2007, 26, 193–222.
27. S. Z. Ismail, C. L. Anderton, R. C. Copley, L. S. Price and S. L. Price, Cryst. Growth Des., 2013, 13, 2396–2406.
28. L. S. Price, J. A. McMahon, S. R. Lingireddy, S.-F. Lau, B. A. Diseroad, S. L. Price and S. M. Reutzel-Edens, J. Mol. Struct., 2014, 1078, 26–42.
29. J. Kendrick, G. A. Stephenson, M. A. Neumann and F. J. Leusen, Cryst. Growth Des., 2013, 13, 581–589.
30. D. E. Braun, J. A. McMahon, L. H. Koztecki, S. L. Price and S. M. Reutzel-Edens, Cryst. Growth Des., 2014, 14, 2056–2072.
31. M. Baias, C. M. Widdifield, J. N. Dumez, H. P. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Phys. Chem. Chem. Phys., 2013, 15, 8069–8080.
32. S. L. Price, S. Hamad, A. Torrisi, P. G. Karamertzanis, M. Leslie and C. R. A. Catlow, Mol. Simul., 2006, 32, 985–997.
33. Y. A. Abramov, J. Phys. Chem. A, 2011, 115, 12809–12817.
34. A. M. Campeta, B. P. Chekal, Y. A. Abramov, P. A. Meenan, M. J. Henson, B. Shi, R. A. Singer and K. R. Horspool, J. Pharm. Sci., 2010, 99, 3874–3886.
35. J. Anwar and D. Zahn, Angew. Chem., Int. Ed., 2011, 50, 1996–2013.
36. V. Dhanaraj and M. Vijayan, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 406–412.
37. A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2014, 114, 2170–2191.
38. V. Lopez-Mejias, J. W. Kampf and A. J. Matzger, J. Am. Chem. Soc., 2009, 131, 4554–4555.
39. V. Lopez-Mejias, J. W. Kampf and A. J. Matzger, J. Am. Chem. Soc., 2012, 134, 9872–9875.
40. O. G. Uzoh, A. J. Cruz-Cabeza and S. L. Price, Cryst. Growth Des., 2012, 12, 4230–4239.
41. M. R. Edwards, W. Jones, W. D. S. Motherwell and G. P. Shields, Mol. Cryst. Liq. Cryst., 2001, 356, 337–353.
42. M. Polito, E. D'Oria, L. Maini, P. G. Karamertzanis, F. Grepioni, D. Braga and S. L. Price, CrystEngComm, 2008, 10, 1848–1854.
43. N. K. Nath and A. Nangia, Cryst. Growth Des., 2012, 12, 5411–5425.
44. I. D. H. Oswald and W. A. Crichton, CrystEngComm, 2009, 11, 463–469.
45. J. van de Streek and S. Motherwell, J. Appl. Crystallogr., 2005, 38, 694–696.
46. R. E. Watson, 2014, Personal Communication.
47. A. O. Surov and G. L. Perlovich, J. Struct. Chem., 2010, 51, 308–315.
48. A. O. Surov, G. L. Perlovich, V. N. Emel'yanenko and S. P. Verevkin, J. Chem. Eng. Data, 2011, 56, 4325–4332.
49. A. Mattei and T. L. Li, Int. J. Pharm., 2011, 418, 179–186.
50. V. Lopez-Mejias, A. S. Myerson and B. L. Trout, Cryst. Growth Des., 2013, 13, 3835–3841.
51. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
52. T. K. Brunck and F. Weinhold, J. Am. Chem. Soc., 1979, 101, 1700–1709.
53. Y. Mo and J. Gao, Acc. Chem. Res., 2007, 40, 113–119.
54. V. Pophristic and L. Goodman, Nature, 2001, 411, 565–568.
55. S. Liu, J. Phys. Chem. A, 2013, 117, 962–965.
56. A. Pendas, M. Blanco and E. Francisco, J. Comput. Chem., 2009, 30, 98–109.
57. R. J. Wheatley and S. L. Price, Mol. Phys., 1990, 69, 507–533.
58. T. S. Totton, A. J. Misquitta and M. Kraft, J. Chem. Theory Comput., 2010, 6, 683–695.
59. G. Filippini and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 868–880.
60. A. Gavezzotti and G. Filippini, J. Phys. Chem., 1994, 98, 4831–4837.
61. A. Gavezzotti, Theoretical Aspects and Computer Modeling of the Molecular Solid State, John Wiley, Chichester, 1997.
62. A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen and M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian 03, Gaussian Inc., Wallingford, CT, 2004.
64. C. Schärfer, T. Schulz-Gasch, H. C. Ehrlich, W. Guba, M. Rarey and M. Stahl, J. Med. Chem., 2013, 56, 2016–2028.
65. M. Clark, R. D. Cramer and N. Van Opdenbosch, J. Comput. Chem., 1989, 10, 982–1012.
66. M. A. Neumann, J. Phys. Chem. B, 2008, 112, 9810–9829.
67. D. C. Sorescu, B. M. Rice and D. L. Thompson, J. Phys. Chem. B, 1997, 101, 798–808.
68. D. E. Williams and D. J. Houpt, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 286–295.
69. The Numerical Algorithms Group (NAG), The NAG Fortran Library, Oxford, United Kingdom, 2013, http://www.nag.com.
70. T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition, Springer, New York, 2nd edn, 2009, Corr. 7th printing 2013 edition, 2011, p. 745.
71. M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–45.
72. T. G. Cooper, K. E. Hejczyk, W. Jones and G. M. Day, J. Chem. Theory Comput., 2008, 4, 1795–1805.
73. O. G. Uzoh, Modelling molecular flexibility for crystal structure prediction, PhD thesis, University College London, 2015.
74. M. U. Schmidt, R. E. Dinnebier and H. Kalkhof, J. Phys. Chem. B, 2007, 111, 9722–9732.
75. S. Ahmed, S. A. Bidstrup, P. A. Kohl and P. J. Ludovice, J. Phys. Chem. B, 1998, 102, 9783–9790.
76. J. Klimes and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
77. C. Haettig, W. Klopper, A. Koehn and D. P. Tew, Chem. Rev., 2012, 112, 4–74.
78. T. van Mourik, P. G. Karamertzanis and S. L. Price, J. Phys. Chem. A, 2006, 110, 8–12.
79. T. van Mourik, J. Chem. Theory Comput., 2008, 4, 1610–1619.
80. C. Sutton, T. Koerzdoerfer, M. T. Gray, M. Brunsfeld, R. M. Parrish, C. Sherrill, J. S. Sears and J. L. Bredas, J. Chem. Phys., 2014, 140, 054310.
81. S. L. Price, J. S. Andrews, C. W. Murray and R. D. Amos, J. Am. Chem. Soc., 1992, 114, 8268–8276.
82. J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schutz and H. Chan, Science, 2014, 345, 640–643.
83. A. Gavezzotti, New J. Chem., 2011, 35, 1360–1368.
84. M. Vasileiadis, C. C. Pantelides and C. S. Adjiman, Chem. Eng. Sci., 2015, 121, 60–76.
85. P. G. Karamertzanis and C. C. Pantelides, Mol. Phys., 2007, 105, 273–291.
86. S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., 2013, 69, 313–328.
87. S. Grimme, J. Chem. Theory Comput., 2014, 10, 4497–4514.
88. J. Behler, J. Chem. Phys., 2011, 134, 074106.
89. W. Smith, I. T. Todorov and M. Leslie, Z. Kristallogr., 2005, 220, 563–566.
90. M. Leslie, Mol. Phys., 2008, 106, 1567–1578.
91. A. J. Misquitta, A. J. Stone and F. Fazeli, J. Chem. Theory Comput., 2014, 10, 5405–5418.
92. U. Koch, P. L. A. Popelier and A. J. Stone, Chem. Phys. Lett., 1995, 238, 253–260.
93. H. A. Le and R. P. A. Bettens, J. Chem. Theory Comput., 2011, 7, 921–930.

---

Footnote

† Electronic supplementary information (ESI) available: Preliminary analysis of the barrier to rotation in fenamates; the fitting algorithm and methodology; representation of torsional potential by various analytical models; and an additional transferability test. See DOI: 10.1039/c4cp05525j

---