Open Access Article
Open Access ArticleStatistical evaluation of toxicological bioassays – a review
Ludwig A.
Hothorn
Leibniz University, Institute of Biostatistics, Herrenhaeuserstr. 2, D-30419 Hannover, Germany. E-mail: hothorn@biostat.uni-hannover.de; Tel: +49 5117625566
First published on 8th August 2014
Abstract
The basic conclusions in almost all reports on new drug applications and in all publications in toxicology are based on statistical methods. However, serious contradictions exist in practice: designs with small samples sizes but use of asymptotic methods (i.e. constructed for larger sample sizes), statistically significant findings without biological relevance (and vice versa), proof of hazard vs. proof of safety, testing (e.g. no observed effect level) vs. estimation (e.g. benchmark dose), available statistical theory vs. related user-friendly software. In this review the biostatistical developments since about the year 2000 onwards are discussed, mainly structured for repeated-dose studies, mutagenicity, carcinogenicity, reproductive and ecotoxicological assays. A critical discussion is included on the unnecessarily conservative evaluation proposed in guidelines, the inadequate but almost always used proof of hazard approach, and the limitation of data-dependent decision-tree approaches.
1 Principles
Toxicology is a broad scientific field ranging from human exposure to toxicogenomics. This review article describes only the statistical evaluation of standardized in vitro and in vivo bioassays in both regulatory and environmental toxicology. Actually, these bioassays have the goal of proving the harmlessness of a test substance. Statistical significance tests are mainly used, but also estimation methods, such as the benchmark dose concept. Both techniques are discussed here with emphasis on the former. In bio-medical research, a distinction should be made between tests of effectiveness and tests on equivalence (two-sided alternative) or non-inferiority (one-sided alternative) in general. The former proof of hazard is mostly confined to common text books and statistical software, while the latter, the proof of safety, is rare in the literature. In this review, the first approach is discussed in regulatory toxicology, the second in environmental toxicology. This review takes into account publications from about 2000 onwards, only a few (selected) older ones.On the basis of a randomly selected recently-published example,1 the main statistical problems are illustrated by five questions. In their Fig. 4B the mean red fluorescence intensity of different doses of 2,4-D (a common herbicide) are compared with a negative and a positive control to demonstrate potential lung toxicity in A549 and WI38 cell lines. Data are presented as the means of at least three independent experiments (triplicated within independent samples) with standard error of the mean (SEM). Statistical analysis of data was done by one-way analysis of variance (ANOVA), followed by Student Newman Keuls (SNK) test using Sigma plot 11.0 software. A p value <0.05 was considered to be statistically significant and generate a star in their figure.
Five questions arise here: (1) are the stars as signs of significance appropriate?, (2) are the statistical tests (ANOVA, SNK-test) appropriate for these data (variances, sample sizes, distribution)?, (3) do these tests take the specific design into account (technical replicates within independent experiments, negative and positive control)?, (4) are the tests appropriately chosen for the experimental question?, and (5) is a proof of hazard or a proof of safety appropriate?
Unfortunately, the raw data are not available and therefore not all of these questions can be answered exhaustively.
(1) Although widely used, stars provide neither the magnitude of statistical significance nor any information concerning biological relevance of the findings, but confidence intervals do.2
(2) The SNK-test is a two-sided all-pairs multiple test assuming normally distributed errors with homogeneous variances. However, needed is a multiple test for decreasing trend against negative control, e.g. Williams trend test3 (see more details in section 3.2) and a non-inferiority test against the positive control,4 but no global ANOVA pre-test.5
(3) The idea of independent experiments is to demonstrate reproducibility and the randomized unit are the triplicated samples. Both bar-charts and statistical test seems to be incorrect from this perspective. Moreover, the sample size of ni = 3 was arbitrarily chosen.
(4) They want to know whether there is a trend, which concentrations have significantly lower intensities, which is the minimum effective concentration and whether this concentration lowered relevantly the effect with respect to the positive control.
(5) As with this experiment will be shown that these cell lines have a specific effect related to lung toxicity, the approach is correct and controlling the familywise error rate is appropriate. Even with this small example, several statistical pitfalls become apparent. Therefore, experimental design and evaluation of toxicological studies should be carefully carried out, since the aim is statistically significant and biologically relevant results on toxicity or harmlessness.
In the following, the statistical methods are discussed, structured for toxicological assays and methodological issues.
Following the evaluation of the most important books and guideline, the five important types of assay are discussed in detail, followed by some specific methods (kinetics, genomics, behavioral tests, benchmark dose, Bayesian analysis, software).
2 Guidelines and textbooks
The conduct and evaluation of studies in regulatory toxicology commonly follow specific recommendations of related guidelines. These guidelines contain lots of information, but only few precise statements for statistical analysis and for the definition of positive, negative and equivocal results. The following statements are common in the OECD, ICH, FDA-CDER guidelines: (i) When applicable, numerical results should be evaluated by an appropriate and generally acceptable statistical method,6 (ii) The application of statistical methods can aid in data interpretation; however, adequate biological interpretation is of critical importance,7 (iii) … criteria for a positive result, such as a dose-related increase …, or a clear increase in the mutant frequency in a single dose group compared to the solvent/vehicle control group,8 (iv) … use historical controls, e.g. for definition of statistical significant but biologically no meaningful results (effect … within the confidence intervals of the appropriate historical control values),7 (v) The statistical unit of measure should be the litter and not the pup,9 (vi) … nonparametric analysis should be justified by considering nature of the data (transformed or not) and their distribution,9 (vii) minimize false positive and false negative errors,9 (viii) repeated measures should be analyzed taking these dependencies into account,9 (ix) use survival adjustments, if needed,10 (x) relevance criteria e.g. The effect occurs only at the most toxic concentrations. In the MLA increases at 80% reduction in RTG For in vitro cytogenetics assays when growth is suppressed by 50%.7 Most details contains an OECD report on statistical analysis of ecotoxicity data11 and the guidance on statistical aspects of the design, analysis, and interpretation of chronic rodent carcinogenicity studies.12 However, several principles are not clear, e.g. contradiction between significance and relevance, how to test a trend, which tests are appropriate, test choice and data conditions.Only a few text books on statistics in toxicology were published in the last decade, e.g.ref. 13,14, where the latter is focusing on the decision tree approach. Furthermore, some chapter in toxicology textbooks on statistics are available15 (in ref. 16).
A few interesting discussion papers on the role of statistics in decision making from a toxicological perspective exist, e.g. for neurotoxicity and teratogenicity,17 long-term carcinogenicity studies,18,19 genotoxicity,20in vivo micronucleus assay,21 organ weights,22 repeated toxicity studies,23 and Comet assay.24
3 Repeated-dose toxicity studies
Several types of repeated-dose toxicity studies are used,25e.g. the OECD-408 90 days oral study on rodents. All share a common design (a negative control (NC) and 2–4 doses using both sexes), different-scaled multiple endpoints (continuous … hemoglobin; proportion … mortality rate, graded histopathological findings) and repeated measures (body weight). Guidance can be found for their evaluation in the US-NPT program,26 where the Dunnett and Williams procedure (and their non-parametric counterparts) as well as arcsine-transformation for proportions are recommended.3.1 Dunnett or multiple t-tests?
OECD407 recommends Comparisons of the effect along a dose range should avoid the use of multiple t-tests27 and the US-NTP26 recommends the Dunnett test. The difference between multiple t-tests against NC and Dunnett test is that the first controls a comparisonwise error rate (i.e. each test at level α) where the second controls a familywise error rate (FWER). Both approaches represent a proof of hazard, but the first reveals a smaller false negative rate, an important criterion in risk assessment. From this perspective, multiple t-tests can be recommended, however the guidelines recommend approaches with the control of the FWER with the consequence of tolerating higher false negative rates. Both allows the conclusion of a clear increase in any single dose group,8 but no conclusion on a dose-related trend. What is (simplified) a Dunnett-test? As effect size it uses the difference of mean values (hence a linear form), it focuses only on comparisons of treatments vs. a control, the test statistics (exactly k test statistics for k treatments) are similar to those of t-tests (i.e. it assumes normally distributed errors) – with the main distinctions: it uses a variance estimator over all groups (and hence assumes variance homogeneity), it uses also a degree of freedom from all groups (which is larger than for pairwise comparisons, i.e. less conservative particularly for rather small sample sizes e.g. ni = 3), it uses as critical value a quantile from a k-variate t-distribution (instead of the uni-variate), it allows either two-sided or one-sided tests (important for directed pathological endpoints, such as increase of MN), and it provides both multiplicity-adjusted p-values and simultaneous confidence limits.3.2 Trend tests
Several guidelines highlight as an important criterion for a positive result the demonstration of a dose-related trend. This seems obvious and a simple task. But, a linear regression model reveals reduced power for concave and convex curves; this is the case for the widely-used Cochran–Armitage28 and Jonckheere trend tests29 (e.g. recommended in ecotoxicology11). Therefore, trend tests are needed which are sensitive to any shapes of the dose–response relationships and take the comparison against NC into account. The one-sided Williams test30 fulfills these criteria. Moreover, in its generalized version as multiple contrast test3 it provides simultaneous confidence intervals (to claim biological relevance as an alternative to p-values) and is available for several relevant data conditions, namely variance heterogeneity,31 unbalanced designs,32 ratio-to-NC comparisons,33 proportions,34,35 poly-3 estimates,36 survival functions,37 a nonparametric version,38 and multiple endpoints.39 Therefore, the Williams trend test can be seen as the standard test in toxicology, accordingly recommended.11,26Nevertheless, the Williams test is not a silver bullet, and there are situations when it is suboptimal. First, the toxic effect of some variables, e.g. liver weight, can lead either to an increase or a decrease. Here a trend test is problematic and the two-sided Dunnett test should be used instead.40 Second, the Williams test allows statements about a global trend and its pattern, but not about the effect of each particular dose compared to NC.41 Again, the Dunnett's test is suitable here. Third, if downturn effects occur with high doses – and this is possible due to the overdosing tendency in toxicology – the Williams’ test may be problematic, i.e. it may not recognize a global trend. A downturn-protected modification42 or Dunnett's test can be used instead – however, without the statement of a trend.
What is a Williams-test (simplifying described)? Most arguments of the Dunnett-test (see above) hold true – but it assumes a monotone trend of arbitrary shape (i.e. it need not be a linear trend) by weighted pooling of selected doses (see the example in Table 1). Therefore it allows the claim for trend, and it is more powerful when a trend exists. Generally, power can be increased by restricting the alternative, e.g. one-sided instead of two-sided hypothesis or order restricted alternative instead of any-heterogeneity alternative hypothesis. The power of the trend test is increased in comparison to an heterogeneity test (F-test) by both restrictions one-sided and ordered alternative hypothesis. But this restriction has a price: a reduced robustness of the test if exactly these assumptions do not apply. A compromise approach is the use of Dunnett, Williams, and downturn-protected Williams tests simultaneously.5 At first glance, such a conservative approach seems to be misplaced in toxicology. But the conservativity is indeed bearable because of the high correlations between the individual comparisons. This approach allows all statements of interest: single comparisons with NC, global and local trends, as well as trends only up to a certain peak dose. The complex technique of multiple contrast tests is used, but easily available within the R-packages multcomp43 and mratios.44 This is illustrated by an example for the endpoint blood urea nitrogen (BUN) (in Table 1).
| Alternative | Test | Comparison | Adj. p-value |
|---|---|---|---|
| Dose vs. NC | Du1 | 1000-0 | 0.796 |
| Du2 | 500-0 | 1.310−06 | |
| Du3 | 250-0 | 0.110 | |
| Du4 | 125-0 | 0.020 | |
| Du5 | 62.5-0 | 0.051 | |
| Trend vs. NC | Wi1 = Du1 | 1000-0 | See Du1 |
| Wi2 | (1000 + 500)/2-0 | 0.003 | |
| Wi3 | (1000 + 500 + 250/3-0 | 0.006 | |
| Wi4 | (1000 + 500 + 250 + 125)/4-0 | 0.004 | |
| Wi5 | (1000 + 500 + 250 + 125 + 62.5)/5-0 | 0.004 | |
| Trend up to 500 | Dt1 = Du2 | 500-0 | See Du2 |
| Dt2 | (500 + 250)/2-0 | 1.110−04 | |
| Dt3 | (500 + 250 + 125)/3-0 | 3.010−04 | |
| Dt4 | (500 + 250 + 125 + 62.5)/4-0 | 6.510−04 | |
| Trend up to 250 | Dt5 = Du3 | 250-0 | See Du3 |
| Dt6 | (250 + 125)/2-0 | 0.023 | |
| Dt7 | (250 + 125 + 62.5)/3-0 | 0.015 | |
| Trend up to 125 | Dt8 = Du4 | 125-0 | See Du4 |
| Dt9 | (125 + 62.5)/2-0 | 0.012 | |
| Trend up to 62.5 | Dt10 = Du5 | 62.5-0 | See Du5 |
The smallest adjusted p-value is for the test Du2, indicating that the outcome for the 500 mg dose is most significantly increased over NC, but the next smallest p-value is for the test Dt2, indicating a trend up to 500 mg (excluding 1000 mg!), i.e. a monotone trend up to 500 mg occurs where the 250 and 125 mg dose contribute to this trend but to a lesser extent. Notice, the p-value for comparison Du2 within Dunnett test is marginally smaller only (7.3 × 10−07).
3.3 Decision tree approaches
In opposition to randomized clinical trials, where an a priori defined per-protocol evaluation is common, in toxicology a data-dependent analysis is used, commonly by decision trees. As an example, the method description for Comet and MN assay data analysis is used from a recently published study on the genotoxicity of Styrene Acrylonitrile Trimer in brain, liver, and blood cells of weanling F344 rats45: The Shapiro–Wilk test … was used to assess normality of the vehicle control group. Data that were normally distributed were analyzed using an independent sample's t-test to compare each dose level to the concurrent control … normally distributed data were also tested for homogeneity of variances using the F test; for data of unequal variances, the Welch's approximation … was used. Data that were not normally distributed were analyzed by the Mann–Whitney test …. In the case of equal variances, linear regression was used to test for a dose-related trend, and Williams’ test was used to test for pairwise differences between each treatment group and the vehicle control group. In the case of unequal variances, Jonckheere's test was used to test for a linear trend and pairwise differences with the Dunn test.Decision trees may contain: (i) pre-test on normal distribution and the use of either parametric or nonparametric tests, (ii) pre-test on variance homogeneity and the use of t-tests or Welch-tests or even strange parametric or nonparametric tests, (iii) ANOVA pre-test before Dunnett-test, i.e. no further testing when the ANOVA is not significant, (iv) outlier test with conditional removing of extreme values before tests. (Prior to statistical analysis, extreme values identified by the outlier test of Dixon and Massey (1951) are examined by NTP personnel, and implausible values are eliminated from the analysis.26) The counterarguments are: (i) for the common small sample sizes of ni = 3,…,10,…50 the power of Shapiro–Wilk-test is so small that a clear decision for (it is a lack-of-fit test) or against normal distribution is problematic,46 proposed the use of non-parametric tests a-priori, (ii) preliminary tests of equality of variances used before a test does not control level α,47,48 and common non-parametric tests (Wilcoxon-test, Kruskal–Wallis-test) are inappropriate for heterogeneous variances,49 see simulation results for Dunnett vs. Steel procedure,50 (iii) conditional ANOVA-test before Dunnett-test is unnecessary,51 (iv) to eliminate extreme values by statistical arguments is an inappropriate approach in safety risk assessment at all (this extreme value could be the signal) and robust tests should be used. In summary, the following can be recommended: use always and exclusively the parametric Dunnett/Williams or the non-parametric Steel/Shirley tests-modified for heterogeneous variances31,38 and report that approach with the smallest p-values (respective most distant confidence limits).
3.4 Repeated measures
Repeated measures occur commonly for body weights and food consumptions, but in some studies hematological parameters were measure repeatedly at the same animal.52 To model these dependencies within a subject correctly poses a statistical problem. The mixed effect linear model with random factor subject within repeated measures at the same subject is a recent and appropriate approach.53 Body weight growth data in repeated toxicity studies were analyzed accordingly using the Dunnett procedure for the fixed effect factor dose.54,553.5 Organ weights
Organ weights are used as a relevant biomarker56 and their analysis is recommended as an important part of the risk assessment.22,57 Common is the use of relative organ weights as a transformed endpoint, either as ratio-to-body weight, or conditionally as ratio-to-brain-weight, when a dose-dependent body weight change is observed.58 However, for an unbiased analysis of relative weights, the dependency between body and organ weight must be linear and the linear regression fit must go through the origin59 which is rarely the case and moreover a time-dependency exists.60,61 Because the distribution of a ratio-to-body endpoint is unknown, the (unadjusted) non-parametric confidence intervals for ratio-to-controls of relative weights for all organ weights (and its rank sum) are compared simultaneously.62 As an alternative the analysis of covariance is proposed.21 However, the treatment effect can be caused by the organ weight, the body weight or both. This violates the independence assumption in the analysis of covariance.63,64 A robust and easy-to-perform approach is still a challenge, i.e. be rather careful when analyzing organ weights by either relative weights or absolute weights or using the analysis of covariance. The pattern of a possible dose-related change of organ weight is of interest: either proportional to body weight or not. This can be identified by simultaneous evaluation of absolute and relative organ weights and a multivariate analysis.653.6 Pathological findings: proportions and severity-graded findings
In some studies a basic contradiction exists between variables which are measured precisely from a statistical perspective, such as hemoglobin but reveal a limited predictive toxic relevance, and proportions or graded histopathological findings, with a rather small data content but a substantial predictive value. The challenge exists to evaluate these proportions and ordinal variables as well. Examples for proportions can be found for mortality and tumor rates in section 5 and proportions with extra-binomial variability in section 4. The particularly interesting severity-graded histopathological findings can be analyzed by a non-parametric Williams-type procedure allowing for tied values,38 or a generalized estimating equations (GEE) approach for correlated ordinal multinomial responses.66 Up to now a related application in toxicology is missing, particularly nothing is known on the small sample behavior of these approaches.3.7 Using historical controls
Regulatory toxicology studies are performed routinely under similar conditions. Therefore the information of the historical controls can be compiled and used for statistical evaluation.67 Tumor incidence of long-term carcinogenicity studies are primarily used. Establishing such a database is not trivial, even tumor-specific heterogeneities must be considered.68 Related reference values are used to interpret rare tumors and unexpectedly high or low control group rates in a particular study.69 From a statistical perspective more interesting is the use of both historical and concurrent control rates jointly within a trend test, starting with a modification of the Cochran–Armitage28 trend test,70,71 using a Bayesian approach,72 for poly-3 estimates73,74 and to estimate simultaneous confidence intervals for Dunnett- and Williams-type tests.75 The impact of the historical control rate on the test decision is larger when the difference to the concurrent rate is large, the heterogeneity between the historical studies is small, their sample sizes are large and the number of historical studies is large.76 However, the number of available historical studies depends on various facts, not necessarily related to decision making. Therefore, a simplified Williams-type approach taking only the mean of historical controls into account was recently proposed.77 Moreover, the use of reference values for continuous endpoints would be helpful as well.783.8 Comparison against positive control
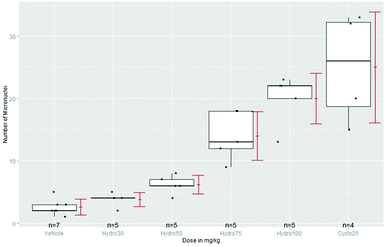
Some guidelines, e.g. for transgenic rodent somatic and germ cell gene mutation assays8 recommend the use of a positive control (PC): Concurrent positive control animals should normally be used…. The doses of the positive control chemicals should be selected so as to produce weak or moderate effects that critically assess the performance and sensitivity of the assay. Statistically assay sensitivity can be demonstrated by a superiority test of PC vs. NC. A more important use of PC is seldom addressed: the magnitude of a significant dose group can be identified by a k-fold non-inferiority or even superiority claim against PC. Just significant effects without any biological relevance occur sometimes in toxicological assays, e.g. because of variance underestimation or a negligible effect magnitude. As an example the number of micronuclei of four doses of hydroquinone, a NC and as PC 25 mg kg−1 cyclophosphamide,79 see the box-plots in Fig. 1. To keep the problem simple, we assume normally distributed errors and use unadjusted lower confidence limits for ratio-to-NC and ratio-to-PC (because an increase of MN is a potential toxic effect).In Table 2 the 95% confidence lower limits (ll) of k-fold changes vs. NC and PC are provided. In the last row assay sensitivity PC-to-NC is claimed (at least 592%). As long the ll > 1 the test against NC is significant. The question arises whether the increase of at least 67% is already biologically relevant (see also the box-plots in Fig. 1). Without an a-priori defined relevance threshold, e.g. 2-fold rule, it is difficult to answer. Because the 50 mg kg−1 dose reveals only at least 17% of the effect of PC, it might be characterized as statistically significant but biological not relevant. If a series of historical assays under comparable conditions is available, the historical NC and PC data can be used for a more robust estimate of the concurrent NC and PC.80
| Dose | ll k-fold change NC | k-fold change PC | Conclusion |
|---|---|---|---|
| 30 | 0.99 | 0.10 | Not significant, not relevant |
| 50 | 1.67 | 0.17 | Significant, not relevant |
| 75 | 3.68 | 0.37 | Significant and relevant |
| 100 | 5.48 | 0.55 | Significant and relevant |
| PC | 5.92 | — | Significant and relevant |
3.9 Power
In both clinical efficacy trials and toxicological assays hypothesis tests are used to claim treatment effects. However, a unfortunate situation exists: while in the ICH E9 guideline81 (in section 2.5), the a-priori choice of a sample size by a power approach with maximum false positive rate of 5% and false negative rate of 20% (i.e. a power of 80% to detect an effect of a given magnitude) is explicitly formulated, such clear requirements are missing in related toxicology guidelines. This is particularly curious since in the commonly used proof of hazard approach, some control of the false negative rate (f−) is possible only via a particular choice of sample size. Notice power is defined to π = 1 − f−. For most “regulatory” bioassays a minimal sample size is defined in the guidelines, e.g. at least triplicates in the Ames assay. To follow these recommended sample sizes guarantees some comparability of the false negative rates, even when they are too high. No recent publications were found where the choice of sample sizes is justified by a statistical power approach even though it has been stated: When confirming an effect of known size, it is considered best practice to estimate before conducting the experiments what sample size is needed to ensure statistical power of detection.82 On the other hand, the post-hoc power approach (i.e. power estimated from the experimental means, standard deviation and sample sizes) is used sometimes, e.g. for brain weights in pesticide neurotoxicity testing83 or cynomolgus monkey as a model in developmental toxicity.84 Particularly in studies with multiple endpoints and the same false positive rate of 5% rather different false negative rates for inherently equal sample sizes occur because of different variances, scales, distributions, spontaneous rates in tumor proportions, etc. A sample size of ni = 10 can cause a rather small false negative rate for body weight (continuous, normal distribution, small variance), but an unacceptably one for graded histopathological findings (ordered categorical data). It can be that body weight changes may be much less predictive than an increase in severity of a selected histopathological finding. Nowadays, the challenge is to increase predictivity of a multi-tiered approach while minimizing the number of animals within a particular bioassay.85 A specific aspect of power is the determination of randomized units (e.g. animals) and technical replicates (e.g. number of scored cells86).One insufficiently solved issue is the appropriate choice of the sample size with respect of the main goal of toxicology be confident in negative results, especially in non-regulatory toxicology. Notice, the commonly used p-value is not an appropriate measure of evidence in those studies with arbitrarily chosen ni. To put it straight: the smaller ni, the more likely the claim for “safety” (negative outcome) (when using the common proof of hazard approach).
3.10 Multivariate analysis
The large number of multiple endpoints in some studies, such as hematology in repeated-dose studies or tumors in carcinogenicity studies, suggests a multivariate analysis instead of the common separate per-endpoint analysis. However, multivariate approaches are used in toxicology mainly over several chemicals (e.g. their structural alerts) and over bioassays87 or in gene-expression analysis88,89 for prediction purposes. A commonly used approach is the principal component analysis (PCA) where the high dimensionality is reduced into a few components by linear combinations of the raw variables.90 Several conditions should be fulfilled, see a recent overview91 – difficult to verify on the basis of real data. Related robust solutions for designs with small sample sizes, e.g. using sparse PCA92,93 may be helpful. PCA analysis for multiple endpoints within a single bioassay was described for immunotoxicological endpoints,94 organ weights65 and a Dunnett-type approach.95 Multivariate trend tests are available as well, an extension of the Williams trend test (see section 3.2),39 or the nonparametric test on multivariate stochastic order,96 or for multivariate binary data (such as multiple tumors).97 Notice, these tests represent max-tests over the multiple endpoints and are consequently more conservative with higher dimensionality, which may be counterintuitive in safety assessment.98 To find appropriate multivariate tests for the small-sample size designs, the high dimension and the different scales (continuous, ordinal, binary) in more complex than one-way layouts are is still a challenging problem.4 In vivo and in vitro mutagenicity assays
Both in vivo and in vitro mutagenicity assays are used in regulatory toxicology, such as micronucleus,99 local lymphnode,100 Ames salmonella,101 and Comet assay.24 What is specific in the statistical evaluation of mutagenicity assays?First, in almost all assays a single endpoint is used, e.g. the number of micronuclei. Therefore, for specific assays relevance thresholds can be defined more easily, e.g. the 2-fold rule102 or 1.5-fold for cellularity in BALB/c mice local lymph node assay.103 The concept of a relevance threshold represents an alternative to the usual p-value criterion as a measure for a positive assay. The common use of p < 0.05 as a criterion leads to the contradiction between statistical significance and biological relevance. On the other hand, the use of a relevance threshold to classify single or mean values ignore their uncertainty. Therefore, the combination of both concepts, i.e. relevance threshold and statistical uncertainty is appropriate but missing as a criterion for a positive assay.100 To some extent, this concept is now available by the non-inferiority test with an 80% threshold in the significant toxicity approach104 for selected aquatic assays. Decision making in regulatory toxicology would be substantially improved if a consensus about assay- and endpoint-specific thresholds were published.
Second, proportions and counts are almost always used as endpoints. Based on the raw data a decision is needed whether to analyze proportions or counts. In case the number of polychromatic cells is constant (e.g. 1000 in ref. 105) the number of micronuclei should be analyzed as counts. If they vary (e.g. from 9776 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 154 in ref. 106), proportions should be used. Furthermore, a decision is needed whether to analyze the proportions summarized per treatment group, i.e. as 2 by k table by CA-trend test for % transformed colonies in the SHE cell transformation assay,107 or still individualized (i.e. proportion for each animal) as overdispersed proportions.99 Most endpoints represent a pathological process, such as the number of micronuclei, and therefore zero or near-to-zero counts or proportions in NC may occur.80 The choice between a generalized linear model,100 a generalized linear mixed model,108 and endpoint transformation methods77 depends also on the extremely small sample sizes used, e.g. triplicates in the Ames assay.
154 in ref. 106), proportions should be used. Furthermore, a decision is needed whether to analyze the proportions summarized per treatment group, i.e. as 2 by k table by CA-trend test for % transformed colonies in the SHE cell transformation assay,107 or still individualized (i.e. proportion for each animal) as overdispersed proportions.99 Most endpoints represent a pathological process, such as the number of micronuclei, and therefore zero or near-to-zero counts or proportions in NC may occur.80 The choice between a generalized linear model,100 a generalized linear mixed model,108 and endpoint transformation methods77 depends also on the extremely small sample sizes used, e.g. triplicates in the Ames assay.
Third, the concentrations used in in vitro assays are commonly arbitrary in relation to human exposure to some extent and therefore a tendency of overdosing with possible downturn effects at high doses may occur. When claiming an increasing trend this phenomenon should be considered, e.g. by a downturn-protected Williams trend test.42
Fourth, the use of positive and negative historical controls is quite common. Their analysis is described in sections 3.1 and 3.8.
Fifth, in some assays hierarchical designs are used with technical replicates. A particular example is the Comet assay, where the compound is administered in commonly three doses (plus a non-zero NC, plus a positive control) at commonly ni = 10 animals. From multiple organs, tissues are harvested into a cell suspension where commonly three samples are used for a gel which are investigated together in runs for electrophoresis, where several measurements (e.g. tail length of a Comet-shaped structure, or tail intensity) are available for commonly 50 cells per gel. This hierarchical design Dose ≻ Animal ≻ Organ ≻ Tissue ≻ Sample ≻ Run ≻ Gel ≻ Cells itself is complicated. A simple transformed endpoint (mean across replicate gels of the median of the log tail intensities) is proposed for evaluation in a pseudo one-way layout by the Williams procedure.24 Interesting is the shape of distribution (namely rather right skewed), and its dose-dependency (namely more higher values with higher doses), for all four endpoints (particularly for % – tail length) (in Fig. 1 of the original paper96), i.e. statistics using mean differences of means are not sensitive because of the large proportion of non-responders. Possible approaches are (i) non-parametric tests on stochastic order (whereas ref. 96 did not take the hierarchical design into account and propose a union-intersection test on the four multiple endpoints which is obviously counter-intuitive in safety assessment), (ii) using a characteristic of the responder values, such as 75% quantile109–111 or (iii) zero-inflated log-normal models.112 Suchlike evaluation is prototypical for toxicology: tests on differences of means assuming non-hierarchical designs (ignoring technical replicates) are inappropriate. The interesting question arises whether simplified methods, e.g. summarizing over sub-units and transformed endpoints are acceptable for designs with such small sample sizes. This should be subject of further research in applied biostatistics. The above complex design is sometimes even more complex by using repeated measures. Related joint modeling for longitudinal continuous and time-to-event outcomes can be used.113–115
5 Long-term carcinogenicity assays
What is specific in carcinogenicity assays? The complex relationship between tumor development and mortality. Firstly, an early mortality prevents the later expression of a tumor, secondly premature mortality can make the existence of tumors visible, thirdly longer living animals can develop tumors more likely than those dying earlier. Therefore three types of tumors were distinguished: fatal tumors (i.e. age-adjusted tumor lethality), incidental tumors (i.e. age-adjusted tumor prevalence) and mortality-independent tumors (e.g. skin tumors). Because direct observation of the tumor onset times is not possible for types (i) and (ii),116 the evaluation is possible only under some strong assumptions. Consequently, no optimal approach for a particular bioassay exists. In addition to the analysis of mortality,37 the tumors are analyzed with these cause-of-death information or without.12 Historically, the prevalence method, the death rate method, and the onset rate method were proposed for analyzing incidental, fatal, and mortality-independent tumors, respectively.117 These methods are complicated, hard to interpret in terms of biological relevance, the particular cause-of-death information may be difficult to achieve, no unique versions for trend and pairwise comparisons against NC36,118 are available. A simpler method without the need of cause-of-death information is the poly-k test assuming a Weibull survival function. A Cochran–Armitage trend test uses weighted proportions where animals dying without a tumor get weights w = (t/tmax)k (where t is the time when a non-tumor-bearing animal drops out of the experiment, tmax is the terminal sacrifice and k a particular chosen parameter (e.g. k = 3, or empirically chosen119) and animals dying with a tumor get the weight 1.120 Inherently no best test can exist121 but in most cases the poly-k-test can be used as a simple approach.122 The Cochran–Armitage trend test is mainly sensitive to linear shapes and therefore Williams-type modifications can be recommended instead.36,123,124 The mere comparison between the crude and mortality-adjusted tumor rate helps to interpret appropriately, e.g. for the methyleugenol bioassay example36 (Table 3).| Dose | 0 | 37 | 75 | 150 mg kg−1 |
|---|---|---|---|---|
| No. tumors/No. animal | 1/50 | 9/50 | 8/50 | 5/50 |
| Crude tumor rate | 0.020 | 0.180 | 0.160 | 0.100 |
| No. tumors/Poly-3 estimates | 1/41.4 | 9/40.3 | 8/38.7 | 5/32.7 |
| Poly-3 rate | 0.024 | 0.223 | 0.207 | 0.153 |
Commonly, the different tumor sites are analyzed independently. However, they are usually correlated and therefore a simultaneous analysis may be interesting, such as using a random effect logistic model with a matrix of coefficients representing log-odds ratios for tumors at different sites,125 copula-based multivariate distribution126 and Bayesian multivariate isotonic regression splines.127 Any test depends seriously on the spontaneous tumor rate. Even slight under- or overestimation of the tumor rate of the concurrent control may have a substantial impact. Commonly in a laboratory several long-term bioassays under similar conditions with the same animal strain are available and therefore historical control information can be used.67,68,74,75,128,129 To summarize, two concepts can be recommended, the poly-3 test per tumor site and the related use of historical control information. For the first approach software is available,130,131 for the second approach software is still not available.
6 Reproductive toxicity studies
What is specific in reproductive studies? The correlation between pups within a litter, i.e. not the pup is the randomized unit, but the pregnant female treated with the test compound. Therefore, five problems have to be solved: (i) modeling the sub-unit litter mates within the randomized experimental unit female, the so-called per-litter analysis, e.g. recommended by the ICH-guideline,132 (ii) modeling the multiple endpoints: number of pre-implantation, implantation, dead pups, malformations and their possible competition (e.g. between early loss and malformation), (iii) combined analysis of continuous and proportion endpoints (such as pup weight and malformation rate), (iv) taking possibly different litter sizes and possible group-specific over-dispersions into account, and (v) benchmark dose estimation for per-litter data.Three decades after the pioneering paper by Williams133 the contradiction between the available high-sophisticated statistical methods (see below) and the current practice of evaluation,134 the unspecific recommendations in the guidelines,132,135 the rather general description in recent text book16 and the lack of specific software is still evident. In the following an attempt is made, to discuss the problems and their solutions in a structured way.
First, the per-litter analysis differs for continuous endpoints (such as pup weight) and proportions (such as number of malformed pups to all pups) to some extent. Already the data structure of a pup weight example136 makes the first problems clear, see Table 4. Not only the endpoint weight and the factor treatment are in the data, but also a litter identifier, a pup identifier and the covariate litter size. A relationship between litter size and pup weight may exist, e.g. in groups with larger litter size smaller pup weights may occur. Therefore, an adjustment against the covariate litter size is highly recommended.137 Moreover, different litter sizes may be informative, i.e. treatment-dependent.138 The correlation between litter mates can be modeled by the random factor litter identifier within a mixed model. This is the common approach for correlated continuous data, such as repeated measures, technical replicates, or paired organs, see e.g.ref. 136,139. Using the estimates from such a mixed model, the adjusted p-values for Dunnett or Williams procedures can be calculated.140 Related Bayesian approaches are available for joint modeling of pup weight and the litter size using a shared latent variable model141 or its extension to correlated random effects.142,143 Notice, when inappropriately using the pup as randomized unit, the p-values are spuriously small (simply because of using too large pseudo sample sizes).
| Pup. id | Weight | Sex | Litter | Litsize | Treatment | |
|---|---|---|---|---|---|---|
| 1 | 1 | 6.60 | Male | 1 | 12 | Control |
| 2 | 2 | 7.40 | Male | 1 | 12 | Control |
| 3 | 3 | 7.15 | Male | 1 | 12 | Control |
| 4 | 4 | 7.24 | Male | 1 | 12 | Control |
| 5 | 5 | 7.10 | Male | 1 | 12 | Control |
| 6 | 6 | 6.04 | Male | 1 | 12 | Control |
| 7 | 7 | 6.98 | Male | 1 | 12 | Control |
| 8 | 8 | 7.05 | Male | 1 | 12 | Control |
| 9 | 9 | 6.95 | Female | 1 | 12 | Control |
| 10 | 10 | 6.29 | Female | 1 | 12 | Control |
| 11 | 11 | 6.77 | Female | 1 | 12 | Control |
| 12 | 12 | 6.57 | Female | 1 | 12 | Control |
| 13 | 13 | 6.37 | Male | 2 | 14 | Control |
| 14 | 14 | 6.37 | Male | 2 | 14 | Control |
Second, the other relevant endpoints are proportions, such as number of malformations, implantations or dead fetuses in relation to all. These proportions are estimated per litter, i.e. extra-binomial variation between litters within a treatment group may occur, and these overdispersions may be group-specific. Furthermore, litter sizes should be used as a covariate (see above). Several approaches for modeling extra-binomial variability are available, such as a quasi-binomial link-function in the generalized linear model (GLM). The common variance var() = pi(1 − pi) is extended by a dispersion parameter τ > 1 var() = τpi(1 − pi), called overdispersion. Therefore we can use the GLM with quasibinomial link function to estimate the dispersion parameter. The historical approaches using beta-binomial model,133 correlated-binomial model,144 and exchangeable binary data145 were extended for random cluster sizes,146,147 an EM algorithm,148 a GLM using a sequence of link functions149 or a cloglog link function,150 an exact unconditional procedure for exchangeable binary data with equal cluster sizes,151 a weighted sign test for unequal cluster sizes,152 a mixture of negative binomial distributions with truncation,153 a generalized linear mixed model154,155 and a trend with clustered binary data using the concept of stochastic order.156 Moreover, Bayesian parametric hierarchical,141 semiparametric157,158 or nonparametric mixture models159 were proposed. Today no fair comparison between these different approaches is available for real data scenarios, and therefore a recommendation is difficult. Notice, the naive analysis by summarized 2-by-k table data, i.e. just a single summarized proportion per group, ignores this between-litter variability, and can not be recommended.
Third, for the complex task of joint modeling of fetal death, fetal weight, and malformation regression models160 and weighted potential outcomes using principal strata161 are available.
Fourth, appropriate modeling of the complex dependencies between the multiple endpoints (pup weight, fetal death and malformation) and the factor dose, the covariate litter size and the possibly heterogeneous variances within and between the litters (i.e. group-specific overdispersion for the proportions162,163) is still a challenge – at least appropriate software is missing up to now, such as for modeling polychotomous ordinal fetal malformation outcomes by threshold models,164 and a bivariate random effects model.165
Fifth, benchmark dose models for per-litter data are available166 where threshold dose–response model with random litter effects167–169 can be used.
7 Environmental toxicology
What is specific in ecotoxicological assays? First, dose–response analysis focusing on potency measures, particularly NOEL and benchmark dose (BMD). Second, a feasible proof of safety approach proposed by an authority body (US-EPA). Moreover, a rather detailed guideline exists.11 The no or lowest observed effect concentration (NOEL (or LOEC)170 is commonly identified by testing methods. It is the lowest dose for which the mean response differs significantly from NC (and the consecutive doses have at least the same or increasing differences). This concept was criticized, e.g. because it depends on the design and the sample size,171 roughly speaking: the smaller the sample size, the larger the NOEL. Moreover, it doesn't allow inter- or even extrapolation to non-experimental concentrations. Some of the problems can be overcome by using a maximum safe dose172 or a model selection concept.173 As an alternative the benchmark dose (BMD) was proposed174 where methods for proportions and continuous endpoints are available.175,176A proof of safety approach, denoted as test of significant toxicity104,177 uses one-sided ratio-to-control tests for non-inferiority with a 75% tolerable threshold for inhibition endpoints in aquatic assays. Therefore, the more important false negative decision rate is directly controlled. This approach is important for statistics in toxicology in general, because a proof of safety178,179 is proposed by an authority body with the a-priori definition of a still tolerable inhibition. First time, the misguided distinction between statistical significance (of a point-zero null hypothesis) and biological relevance was overcome and the more important false negative rate is directly controlled: be confident in negative results.
7.1 Proof of safety vs. proof of hazard
The most convincing argument against widespread statistical tests in toxicology is: they control the less important error rate, namely the false positive rate, directly. While the more important error rate, the false negative rate, is ignored (e.g. in case studies whose sample sizes were neither planned nor defined by guidelines) or at best is secondary. Notice, the gold standard test, the Dunnett's test (after all, recommended by the U.S. NTP and one of the most cited statistical tests, mostly in toxicology180), controls the false positive rate so conservative (compared with local α control against the multiple group comparisons to the control), so that the false negative rate is particularly high. The way out of this dilemma is the proof-of-safety approach181 (see the recent significant toxicity approach in aquatic bioassay in section 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104).
104).
8 Toxicokinetics
The term toxicokinetics covers most diverse methods of time-dependence of absorption, distribution, metabolism, and excretion of substances.182,183 Therefore, several different statistical approaches are used. Here we focus on the estimation of a kinetic parameter, such as area under the curve (AUC) particularly using incomplete sampling in small animals and the comparison of such parameters between different conditions, such as species, doses. Several publications for AUC estimation for different incomplete designs are available,184–187 happily also a related R-package PK for noncompartmental kinetics.188 Confidence intervals for ratios between AUCs in the case of serial sampling can be used for testing group differences.1899 Toxicogenomics
Toxicogenomics is a relatively new field and far less standardized than e.g. mutagenicity assays. The aim is to select a few biomarkers (in in vivo studies) or to derive prediction models (in in vitro studies)190 from massively high-dimensional data. What is specific in toxicogenomics compared to the many recent genomics studies191,192? Especially, the use of a completely randomized design, continuous phenotypes and the focus on dose–response relationships88,89 (or even dose-by-time relationships) for high-dimensional endpoints. Related trend tests,193,194 particularly Williams-type tests195 and benchmark-dose approaches196 were used recently.10 Behavioral tests
A specific problem is the analysis of behavioral patterns presenting multiple endpoints with different scales (binary, counts, time-to-event, etc.). Data from Morris water maze experiments were analyzed according to rats spatial learning.197 The behavior of rats in Irwin's toxicity method, i.e. longitudinal measures of multiple endpoints (such as locomotor activity, or pupil size) of different scales (binary and continuous) were analyzed by means of generalized linear mixed model incorporating link functions and residual error structures for the various outcomes and their complex correlations.15411 The benchmark dose concept
When analyzing dose–response relationships by trend tests (such as the above-described Williams trend test) dose is assumed as factor, i.e. ordinal only. Alternatively dose can be assumed as a covariate, i.e. quantitative. Taking only the dose levels (zero (NC), low, medium, high) into account seems to be hopelessly inferior compared to full quantitative information on the dose-metameters. But trend tests are rather robust, e.g. assuming only monotonicity, particularly for designs with only few dose levels and small sample sizes. Estimation of relevant quantities such as LD50, relative potency or benchmark dose (BMD), based on the quantitative covariate dose, needs the a-priori choice of a particular non-linear model (remembering: all models are wrong, but some are useful).198In quantitative risk assessment compounds should be ranked by their potency. The trend-test-based no-observed-adverse effect level (NOAEL) concept was criticized.171 Notice in the meantime compromises between testing and modeling exist199 and a model selection approach using contrast tests is available.173 BMD is an estimated dose in low-dose interpolation that corresponds to an a priori defined still acceptable effect, a biologically motivated acceptable benchmark dose risk (BMR). For risk assessment its lower confidence limit is used reflecting most of uncertainty. It takes the complete dose–response relationship into account and is less dependent on the design. The BMR is the still acceptable probability of an abnormal response with respect to the effect at NC. Additive or extra risk definitions are used.200 For continuous endpoints the risk can be defined relative to the control mean.201 The lower confidence limit (BMDL) depends seriously on the underlying non-linear model. Either model selection methods or model averaging202,203 can reduced this dependency. Most models assume normally distributed errors with homogeneous variances, but transformations,204 non-parametric approaches205 and a mixed model extension for replicated microarrays176 are available. The BMD concept is now proposed by authority bodies206 and used routinely, e.g. in development toxicity studies,207,208 mutagenicity ring-studies209 or toxicogenomics.196 Different software is available.176,210,211
12 Bayesian analysis
The fact that some toxicological bioassays are highly standardized allows the use of historical control data for decision making. Their use as prior distribution with the Bayesian inference framework would be obvious. Diverse applications, especially for dose–response analysis have been proposed, e.g., the estimation of the no effect concentration (and its credibility interval) using several priors for the three parameters in a non-linear dose response model is used in aquatic assays.212 Bayesian model averaging is proposed for robust BMD estimation using logistic, probit and quantal-linear model as well integrating historical information.202,213 Using historical control data for count data to estimate relative inhibition concentrations in aquatic assays was proposed.214 Especially in reproductive studies Bayesian methods were used, e.g., a nonparametric mixture modeling framework for replicated count dose–response curves settings for categorical data (dead, normal, malformed),159 the particular adjustment against litter size by a Bayesian bootstrap approach215 and semiparametric Bayesian joint modeling of binary (malformation) and continuous (pup weights) outcomes.21613 Software: related R packages
Nowadays, biostatistics in toxicology is inconceivable without accessible software. The following two sections focus on the public-domain project R (http://www.r-project.org), itemizing add-on packages that are useful to evaluate bioassays as well as examples of raw data, rather important to understand the complex approaches by non-statisticians.13.1 Software to evaluate bioassays
• drfit: fitting dose–response curves (incl. hormesis)• ETC: equivalence to control (proof of safety)98,179
• drc: analysis of dose–response curve data217
• CorrBin: nonparametrics with clustered binary and multinomial data156
• coin: conditional inference procedures in a permutation test framework218,219
• mratios: inferences for ratios of coefficients in the general linear model33,220
• multcomp: inferences for differences in the general linear model43
• nparcomp: perform multiple comparisons for nonparametric relative contrast effects38,221
• PK: basic non-compartmental pharmacokinetics188
• bmd: benchmark dose analysis for dose–response data176
• medrc: mixed effect dose–response curves?
• goric: approaches using generalized order-restricted information criterion173
• IsoGene dose–response studies in microarray experiments195
• EnvStat EnvStats, an R Package for Environmental Statistics
13.2 Toxicological data sets
• data(antifoul): IM1xIPC81 Dose–Response data for 1-methyl-3-alkylimidazolium tetrafluoroborates in IPC-81 cells – in package drfit• data(ASAT): ASAT values of the serum of female Wistar rats six months after application – in package mratios (and data(asat) – in package coin)
• data(beetles): mortality of confused flour beetles – in package binomTools
• data(BW): body weights measured in a toxicological study – in package mratios
• data(bronch): rodent bronchial carcinoma data – in package MCPAN
• data(cleft.palate): dose–response data on cleft palate – in package bmd
• data(cta): cell transformation assay – in package mcprofile
• data(daphnids): Daphnia assay – in package drc
• data(dehp): developmental toxicology study of DEHP in mice – in package CorrBin
• data(earthworms): earthworm toxicity test – in package drc
• data(egde): developmental toxicity experiment on the effect of ethylene glycol diethyl ether on fetal development of New Zealand white rabbits – in package CorrBin
• data(ethylene): developmental toxicity study of ethylene glycol in mice – in package rmp
• data(ex2116): aflatoxicol and liver tumors in trout – in package Sleuth2
• data(fishtoxin): toxicity effect on fish – in package gpk
• data(hydroquinone): Hydroquinone mutagenicity assay in package gMCP
• data(impla): numbers of implantations – in package nparcomp
• data(lirat): low-iron rat teratology data – in package VGAM
• data(liver): relative liver weight – in package nparcomp
• data(methyl): NTP bioassay data of methyleugenol on skin fibroma – in package MCPAN
• data(mice): pregnant female mice experiment144 – in package aods3
• data(Mutagenicity): mutagenicity assay for 4 doses of hydroquinone – in package mratios
• data(NoP): Ames test data of 4NoP – in package CAMAN
• data(nitrofen): toxicity of nitrofen in aquatic systems – in package boot
• data(photocar): multiple dosing photococarcinogenicity experiment – in package coin
• data(pyrithione): cytotoxicity data for different pyrithionates and related species – in package drfit
• data(rats): litter-matched time-to-response data – in package TSHRC
• data(ratpub): birth weight of the rat pup – in package WWGbook
• data(rat.weight): body weight of rats in a toxicity study – in package mratios
• data(reaction): reaction times of mice – in package nparcomp
• data(salmonellaTA98): Salmonella reverse mutagenicity assay – in package dispmod
• data(shelltox): developmental toxicology data set of pregnant Dutch rabbits – in package CorrBin
14 Conclusions
Still today remarkable contradictions for statistics in toxicology exist: (i) between missing details in most guidelines and the need of appropriate statistical approaches to evaluate the commonly complex designs in various toxicological bioassays, (ii) between those complex statistical approaches (e.g. per-litter analysis for multiple endpoints) and the availability of related software, (iii) between statistical significance and biological relevance (mainly caused by the inappropriate use of point-zero-null hypothesis tests and the dominance of p < 0.05 significance criteria), (iv) between the commonly used proof-of-hazard and the often more appropriate proof-of-safety (particularly the needed a-priori defined tolerable thresholds, such as 2-fold rule or 70% rule in aquatic bioassays), (v) between the oversimplifications (or even errors) in statistical methods sections in various toxicological papers and the actual requirements from a statistical view, and (vi) between testing and modeling approaches for dose–response relationships. and (vii) between the unwillingness of editors of toxicological papers to accept statistical publications and the high-sophisticated publications in statistical journals – however hardly read by toxicologists.Statistics in toxicology is not at the end – it is in the middle.
References
- D. Ganguli, A. Choudhuri and G. Chakrabarti, Toxicol. Res., 2014 10.1039/C3TX50082A.
- D. P. Lovell, J. Agric. Food Chem., 2013, 61, 8340–8348 CrossRef CAS PubMed.
- F. Bretz, Comput. Stat. Data Anal., 2006, 50, 1735–1748 CrossRef PubMed.
- P. Bauer, J. Rohmel, W. Maurer and L. Hothorn, Stat. Med., 1998, 17, 2133–2146 CrossRef CAS.
- T. Jaki and L. A. Hothorn, Arch. Toxicol., 2013, 87, 1901–1910 CrossRef CAS PubMed.
- OECD408, Repeated Dose 90-Day Oral Toxicity Study in Rodents, Updated Guideline, adopted 21st September 1998, OECD Paris technical report, 1998 Search PubMed.
- ICH-S2, Guidance on genotoxicity testing and data interpretation for pharmaceuticals intended for human use, ICH technical report, 2008 Search PubMed.
- OECD488, Transgenic Rodent Somatic and Germ Cell Gene Mutation Assays, Oecd technical report, 2013 Search PubMed.
- OECD-426, Guideline for the testing of chemicals, Developmental Neurotoxicity Study, 2007 Search PubMed.
- OECD451, OECD Guideline for the Testing of Chemicals. Carcinogenicity Studies, OECD technical report, 2009 Search PubMed.
- OECD, Current Approaches in the Statistical Analysis of Ecotoxicity Data: A Guidance to Application, OECD, Paris, France, pp. 62–102 technical report, 2006 Search PubMed.
- Center for Drug Evaluation and Research, Guidance for Industry: Statistical Aspects of the Design, Analysis, and Interpretation of Chronic Rodent Carcinogenicity Studies of Pharmaceuticals, US Food and Drug Administration technical report, 2001 Search PubMed.
- S. Gad, Statistics and Experimental Design for Toxicologists and Pharmacologists, CRC Press, 2005 Search PubMed.
- K. Kobayashi, Applied Statistics in Toxicology and Pharmacology, Sci. Publisher, 2004 Search PubMed.
- T. Vidmar, L. Freshwater and R. Collins, Chapter 30: Biostatistics for Toxicologists, Academic Press, 2013 Search PubMed.
- A Comprehensive Guide to Toxicology in Preclinical Drug Development, ed. A. Faqi, Academic Press, 2013 Search PubMed.
- F. L. Bookstein and P. D. Sampson, Neurotoxicol. Teratol., 2005, 27, 407–415 CrossRef CAS PubMed.
- M. Elwell, W. Fairweather, X. Fouillet, K. Keenan, K. Lin, G. Long, L. Mixson, D. Morton, T. Peters, C. Rousseaux and D. Tuomari, Toxicol. Pathol., 2002, 30, 415–418 CrossRef.
- D. Morton, Toxicol. Pathol., 2001, 29, 670–672 CrossRef CAS.
- D. P. Lovell, I. Yoshimura, L. A. Hothorn, B. H. Margolin and K. Soper, Environ. Mol. Mutagen., 2000, 35, 260–263 CrossRef CAS.
- P. Jarvis, J. Saul, M. Aylott, S. Bate, H. Geys and J. Sherington, Pharm. Stat., 2011, 10, 477–484 CrossRef PubMed.
- R. S. Sellers, D. Morton, B. Michael, N. Roome, J. K. Johnson, B. L. Yano, R. Perry and K. Schafer, Toxicol. Pathol., 2007, 35, 751–755 CrossRef PubMed.
- K. Kobayashi, K. S. Pillai, S. Guhatakurta, K. M. Cherian and M. Ohnishi, J. Environ. Biol., 2011, 32, 11–16 Search PubMed.
- J. Bright, M. Aylott, S. Bate, H. Geys, P. Jarvis, J. Saul and R. Vonk, Pharm. Stat., 2011, 10, 485–493 CrossRef PubMed.
- W. S. Redfern, L. C. Ewart, P. Lainee, M. Pinches, S. Robinson and J. P. Valentin, Toxicol. Res., 2013, 2, 209–234 RSC.
- National Toxicology Program. Statistical Procedures. Expanded Overview (2013) http://ntp-server.niehs.nih.gov/?objectid=72015E2C-BDB7-CEBA-F17F9ACA7AE5346D .
- OECD407, Repeated Dose 28-Day Oral Toxicity Study in Rodents, Updated Guideline, adopted 3rd October 2008, OECD Paris technical report, 2008 Search PubMed.
- P. Armitage, Biometrics, 1955, 11, 375–386 CrossRef.
- A. R. Jonckheere, Biometrika, 1954, 41, 133–145 CrossRef.
- D. A. Williams, Biometrics, 1971, 27, 103–117 CrossRef CAS.
- M. Hasler and L. A. Hothorn, Biom. J., 2008, 50, 793–800 CrossRef PubMed.
- K. Kobayashi, Y. Sakuratani, T. Abe, S. Nishikawa, J. Yamada, A. Hirose, E. Kamata and M. Hayashi, J. Toxicol. Sci., 2010, 35, 79–85 CrossRef CAS.
- G. Dilba, E. Bretz, V. Guiard and L. A. Hothorn, Methods Inf. Med., 2004, 43, 465–469 CAS.
- F. Schaarschmidt, M. Sill and L. A. Hothorn, Biom. J., 2008, 50, 782–792 CrossRef PubMed.
- L. A. Hothorn, M. Sill and F. Schaarschmidt, Int. J. Biostat., 2010, 6, 15 Search PubMed.
- F. Schaarschmidt, M. Sill and L. A. Hothorn, J. Biopharm. Stat., 2008, 18, 934–948 CrossRef PubMed.
- E. Herberich and L. A. Hothorn, Regul. Toxicol. Pharmacol., 2012, 64, 26–34 CrossRef PubMed.
- F. Konietschke and L. A. Hothorn, Stat. Biopharm. Res., 2012, 4, 14–27 CrossRef.
- M. Hasler and L. A. Hothorn, Stat. Biopharm. Res., 2012, 4, 57–65 CrossRef.
- M.-L. Delignette-Muller, C. Forfait, E. Billoir and S. Charles, Environ. Toxicol. Chem., 2011, 30, 2888–2891 CrossRef CAS PubMed.
- K. Kobayashi, K. S. Pillai, M. Michael, K. M. Cherian, A. Araki and A. Hirose, J. Toxicol. Sci., 2012, 37, 255–260 CrossRef CAS.
- F. Bretz and L. Hothorn, ATLA, Altern. Lab. Anim., 2003, 31, 81–96 CAS.
- T. Hothorn, F. Bretz and P. Westfall, Biom. J., 2008, 50, 346–363 CrossRef PubMed.
- G. Dilba, M. Hasler, D. Gerhard and F. Schaarschmidt, mratios: Inferences for ratios of coefficients in the general linear model, 2008 Search PubMed.
- C. A. Hobbs, R. S. Chhabra, L. Recio, M. Streicker and K. L. Witt, Environ. Mol. Mutagen., 2012, 53, 227–238 CrossRef CAS PubMed.
- M. Wang and M. Riffel, Ecotoxicol. Environ. Saf., 2011, 74, 684–692 CrossRef CAS PubMed.
- D. W. Zimmerman, Br. J. Math. Stat. Psychol., 2004, 57, 173–181 CrossRef PubMed.
- A. F. Hayes and L. Cai, Br. J. Math. Stat. Psychol., 2007, 60, 217–244 CrossRef PubMed.
- D. W. Zimmerman, Percept. Motor Skills, 1999, 88, 556–558 CrossRef.
- U. Munzel and L. A. Hothorn, Biom. J., 2001, 43, 553–569 CrossRef.
- L. A. Hothorn, Commun. Stat., 2014 Search PubMed , accepted.
- D. Ghosh, T. A. Deisher and J. L. Ellsworth, J. Pharmacol. Toxicol. Methods, 1999, 42, 157–162 CrossRef CAS.
- C. Y. Liu, T. P. Cripe and M. O. Kim, Mol. Ther., 2010, 18, 1724–1730 CrossRef CAS PubMed.
- W. P. Hoffman, D. K. Ness and R. B. L. van Lier, Toxicol. Sci., 2002, 66, 313–319 CrossRef CAS PubMed.
- W. P. Hoffman, J. Recknor and C. Lee, J. Biopharm. Stat., 2008, 18, 883–900 CrossRef PubMed.
- E. Wahlstrom, A. Ollerstam, L. Sundius and H. Zhang, Toxicol. Pathol., 2013, 41, 902–912 CrossRef PubMed.
- B. Michael, B. Yano, R. S. Sellers, R. Perry, D. Morton, N. Roome, J. K. Johnson and K. Schafer, Toxicol. Pathol., 2007, 35, 742–750 CrossRef PubMed.
- S. A. Bailey, R. H. Zidell and R. W. Perry, Toxicol. Pathol., 2004, 32, 448–466 CrossRef PubMed.
- D. Curran-Everett, Adv. Physiol. Educ., 2013, 37, 213–219 CrossRef PubMed.
- Y. Piao, Y. N. Liu and X. D. Xie, J. Toxicol. Pathol., 2013, 26, 29–34 CrossRef PubMed.
- D. J. Marino, J. Toxicol. Environ. Health, Part A, 2012, 75, 148–169 CrossRef CAS PubMed.
- M. J. Wolfsegger, T. Jaki, B. Dietrich, J. A. Kunzler and K. Barker, Toxicol. Appl. Pharmacol., 2009, 240, 117–122 CrossRef CAS PubMed.
- Y. K. Tu, G. R. Law, G. T. H. Ellison and M. S. Gilthorpe, Pharm. Stat., 2010, 9, 77–83 CrossRef PubMed.
- E. A. C. Shirley and P. Newnham, Stat. Med., 1984, 3, 85–91 CrossRef CAS PubMed.
- H. Andersen, S. Larsen, H. Spliid and N. D. Christensen, Toxicology, 1999, 136, 67–77 CrossRef CAS.
- A. Touloumis, A. Agresti and M. Kateri, Biometrics, 2013, 69, 633–640 CrossRef PubMed.
- S. A. Elmore and S. D. Peddada, Toxicol. Pathol., 2009, 37, 672–676 CrossRef PubMed.
- G. E. Dinse, S. D. Peddada, S. F. Harris and S. A. Elmore, Toxicol. Pathol., 2010, 38, 765–775 CrossRef PubMed.
- C. Keenan, S. Elmore, S. Francke-Carroll, R. Kemp, R. Kerlin, S. Peddada, J. Pletcher, M. Rinke, S. P. Schmidt, I. Taylor and D. C. Wolf, Toxicol. Pathol., 2009, 37, 679–693 CrossRef PubMed.
- R. E. Tarone, Biometrics, 1982, 38, 215–220 CrossRef.
- Y. P. Ma, J. H. Guo, N. Z. Shi and M. L. Tang, Biometrics, 2002, 58, 917–927 CrossRef PubMed.
- D. G. Chen, Comput. Stat. Data Anal., 2010, 54, 1646–1656 CrossRef PubMed.
- S. D. Peddada, G. E. Dinse and G. E. Kissling, J. Am. Stat. Assoc., 2007, 102, 1212–1220 CrossRef CAS.
- G. E. Dinse and S. D. Peddada, Stat. Biopharm. Res., 2011, 3, 97–105 CrossRef PubMed.
- A. Kitsche, L. A. Hothorn and F. Schaarschmidt, Comput. Stat. Data Anal., 2012, 56, 3865–3875 CrossRef PubMed.
- J. T. Marringwa, C. Faes, M. Aerts, H. Geys, G. Teuns, B. Van Den Poel and L. Bijnens, J. Biopharm. Stat., 2007, 17, 493–509 CrossRef CAS PubMed.
- L. A. Hothorn, K. Reisinger, T. Wolf, A. Poth, D. Fieblingere, M. Liebsch and R. Pirow, Mutat. Res., Genet. Toxicol. Environ. Mutagen., 2013, 757, 68–78 CrossRef CAS PubMed.
- L. E. Lillie, N. J. Temple and L. Z. Florence, Hum. Exp. Toxicol., 1996, 15, 612–616 CAS.
- D. Hauschke and L. A. Hothorn, ATLA, Altern. Lab. Anim., 2003, 31, 77–80 CAS.
- T. Jaki, A. Kitsche and L. A. Hothorn, JP J Biostat, 2014 Search PubMed , accepted.
- Statistical Principles for Clinical Trials, EU: Adopted by CPMP, March 1998, issued as CPMP/ICH/363/96 technical report, 1998.
- Reporting Life Sciences Research. Nature Publishing Group .
- S. Weichenthal, S. Hancock and K. Raffaele, Regul. Toxicol. Pharmacol., 2010, 57, 235–240 CrossRef CAS PubMed.
- P. Jarvis, S. Srivastav, E. Vogelwedde, J. Stewart, T. Mitchard and G. F. Weinbauer, Birth Defects Res., Part B, 2010, 89, 175–187 CAS.
- K. L. Chapman, H. Holzgrefe, L. E. Black, M. Brown, G. Chellman, C. Copeman, J. Couch, S. Creton, S. Gehen, A. Hoberman, L. B. Kinter, S. Madden, C. Mattis, H. A. Stemple and S. Wilson, Regul. Toxicol. Pharmacol., 2013, 66, 88–103 CrossRef CAS PubMed.
- J. Hayes, A. T. Doherty, D. J. Adkins, K. Oldman and M. R. O'Donovan, Mutagenesis, 2009, 24, 419–424 CrossRef CAS PubMed.
- Y. Kuroda and M. Saito, Toxicol. in Vitro, 2010, 24, 661–668 CrossRef CAS PubMed.
- T. Waldmann, E. Rempel, N. V. Balmer, A. Konig, R. Kolde, J. A. Gaspar, M. Henry, J. Hescheler, A. Sachinidis, J. Rahnenfuhrer, J. G. Hengstler and M. Leist, Chem. Res. Toxicol., 2014, 27, 408–420 CrossRef CAS PubMed.
- C. Parfett, A. Williams, J. L. Zheng and G. Zhou, Regul. Toxicol. Pharmacol., 2013, 67, 63–74 CrossRef CAS PubMed.
- B. Everitt and T. Hothorn, An Introduction to Applied Multivariate Analysis with R, Springer, Heidelberg, 2011 Search PubMed.
- J. Shlens, arXiv: 1404.1100, 2014.
- D. Shen, H. P. Shen and J. S. Marron, J. Multivar. Anal., 2013, 115, 317–333 CrossRef PubMed.
- PMA: Penalized Multivariate Analysis by Witten, D. and Tibshirani, R. and Nasimhan, B., 2013.
- D. Keil, R. W. Luebke, M. Ensley, P. D. Gerard and S. B. Pruett, Toxicol. Sci., 1999, 51, 245–258 CrossRef CAS PubMed.
- S. Kropf, L. Hothorn and J. Laeuter, Drug Inf. J., 1997, 30, 433–447 Search PubMed.
- O. Davidov and S. Peddada, Biometrics, 2013, 69, 982–990 CrossRef PubMed.
- O. Davidov and S. Peddada, J. Am. Stat. Assoc., 2011, 106, 1394–1404 CrossRef CAS PubMed.
- M. Hasler and L. A. Hothorn, Stat. Med., 2013, 32, 1720–1729 CrossRef CAS PubMed.
- L. A. Hothorn and D. Gerhard, Arch. Toxicol., 2009, 83, 625–634 CrossRef CAS PubMed.
- L. A. Hothorn and H. W. Vohr, Regul. Toxicol. Pharmacol., 2010, 56, 352–356 CrossRef PubMed.
- B. S. Kim and B. H. Margolin, Mutat. Res., Rev. Mutat. Res., 1999, 436, 113–122 CrossRef CAS.
- N. Cariello and W. Piegorsch, Mutat. Res., Genet. Toxicol., 1996, 369, 23–31 CrossRef CAS.
- G. Ehling, M. Hecht, A. Heusener, J. Huesler, A. O. Gamer, H. van Loveren, T. Maurer, K. Riecke, L. Ullmann, P. Ulrich, R. Vandebriel and H. W. Vohr, Toxicology, 2005, 212, 69–79 CrossRef CAS PubMed.
- D. L. Denton, J. Diamond and L. Zheng, Environ. Toxicol. Chem., 2011, 30, 1117–1126 CrossRef CAS PubMed.
- J. Oliver, J. R. Meunier, T. Awogi, A. Elhajouji, M. C. Ouldelhkim, N. Bichet, V. Thybaud, G. Lorenzon, D. Marzin and E. Lorge, Mutat. Res., Genet. Toxicol. Environ. Mutagen., 2006, 607, 125–152 CrossRef CAS PubMed.
- Technical Report on 5-(4-Nitrophenyl)-2,4-pentadien (NPPD) Micronucleus Assay in Mice US-NTP.
- K. Pant, S. W. Bruce, J. E. Sly, T. Kunkelmann, S. Kunz-Bohnenberger, A. Poth, G. Engelhardt, M. Schulz and K. R. Schwind, Mutat. Res., Genet. Toxicol. Environ. Mutagen., 2012, 744, 54–63 CrossRef CAS PubMed.
- S. Sauco, J. Gomez, F. R. Barboza, D. Lercari and O. Defeo, PLoS One, 2013, 8 Search PubMed.
- P. Duez, G. Dehon, A. Kumps and J. Dubois, Mutagenesis, 2003, 18, 159–166 CrossRef CAS.
- S. J. Wiklund and E. Agurell, Mutagenesis, 2003, 18, 167–175 CrossRef CAS.
- D. P. Lovell and T. Omori, Mutagenesis, 2008, 23, 171–182 CrossRef CAS PubMed.
- N. Li, D. A. Elashoff, W. A. Robbins and L. Xun, Stat. Methods Med. Res., 2011, 20, 175–189 CrossRef PubMed.
- A. Efendi, G. Molenberghs, E. N. Njagi and P. Dendale, Biom. J., 2013, 55, 572–588 CrossRef PubMed.
- A. H. Ghebretinsae, C. Faes, G. Molenberghs, M. De Boeck and H. Geys, J. Biopharm. Stat., 2013, 23, 618–636 CrossRef PubMed.
- D. Rizopoulos, Joint Models for Longitudinal and Time-to-Event Data: With Applications in R, CRC Press, 2012 Search PubMed.
- H. Ahn, H. Moon and R. L. Kodell, J. Biopharm. Stat., 2008, 18, 901–914 CrossRef PubMed.
- R. Peto, M. Pike, N. Day, R. Gray, P. Lee, S. Parish, J. Peto, S. Richards and J. Wahrendorf, Guidelines for Simple, Sensitive Significance Tests for Carcinogenic Effects in Long term Animal Experiments, in Long-term and Short-term Screening Assays for Carcinogens: An Critical Appraisal, World Health Organization, 1980 Search PubMed.
- R. C. T. Mohammad and A. Rahman, Health, 2012, 4, 910–918 CrossRef.
- H. Moon, H. Ahn, R. L. Kodell and J. J. Lee, Stat. Med., 2003, 22, 2619–2636 CrossRef PubMed.
- C. J. Portier and A. J. Bailer, Fundam. Appl. Toxicol., 1989, 12, 731–737 CrossRef CAS.
- M. Gebregziabher and D. Hoel, Hum. Ecol. Risk Assess., 2009, 15, 858–875 CrossRef CAS PubMed.
- R. L. Kodell, Stat. Biopharm. Res., 2012, 4, 118–124 CrossRef.
- S. D. Peddada, G. E. Dinse and J. K. Haseman, Journal of the Royal Statistical Society Series C-Applied Statistics, 2005, 54, 51–61 CrossRef PubMed.
- S. D. Peddada and G. E. Kissling, Environ. Health Perspect., 2006, 114, 537–541 CrossRef CAS.
- L. Wang and D. B. Dunson, Biometrics, 2010, 66, 493–501 CrossRef PubMed.
- W. H. A. Chiu and K. S. Crump, J. Agric. Biol. Environ. Stat., 2012, 17, 107–127 CrossRef PubMed.
- B. Cai and D. B. Dunson, J. Am. Stat. Assoc., 2007, 102, 1158–1171 CrossRef CAS.
- D. B. Dunson and G. E. Dinse, Journal of the Royal Statistical Society Series C-Applied Statistics, 2001, 50, 125–141 Search PubMed.
- D. G. Chen, Comput. Stat. Data Anal., 2010, 54, 1646–1656 CrossRef PubMed.
- H. Moon, H. Ahn and R. L. Kodell, J. Stat. Software, 2006, 16, 7 Search PubMed.
- MCPAN: Multiple comparisons using normal approximation, Frank Schaarschmidt and Daniel Gerhard and Martin Sill, 2013 url http://CRAN.R-project.org/package=MCPAN.
- ICH-S5A, Reproductive toxicology: Detection of toxicity to reproduction for medicinal products including toxicity to male fertility, CPMP/ICH/386/95 technical report, 1994 Search PubMed.
- D. A. Williams, Biometrics, 1975, 31, 949–952 CrossRef CAS.
- M. S. Marty, B. H. Neal, C. L. Zablotny, B. L. Yano, A. K. Andrus, M. R. Woolhiser, D. R. Boverhof, S. A. Saghir, A. W. Perala, J. K. Passage, M. A. Lawson, J. S. Bus, J. C. Lamb and L. Hammond, Toxicol. Sci., 2013, 136, 527–547 CrossRef CAS PubMed.
- OECD GUIDELINE FOR TESTING OF CHEMICALS Adopted by the Council on 27th July 1995 Reproduction/Developmental Toxicity Screening Test No. 421, 1995.
- B. West and K. Welch, Linear Mixed Models: A Practical Guide Using Statistical Software, Chapman Hall CRC Press, 2006 Search PubMed.
- P. J. Catalano and L. M. Ryan, J. Am. Stat. Assoc., 1992, 87, 651–658 CrossRef.
- Z. Chen, B. Zhang and P. S. Albert, Stat. Med., 2011, 30, 1825–1836 CrossRef PubMed.
- H. P. Piepho, A. Buchse and K. Emrich, J. Agron. Crop Sci., 2003, 189, 310–322 CrossRef.
- L. A. Hothorn, Statistics in Toxicology using R, Leibniz University, Institute of Biostatistics Technical Report, 2014 Search PubMed.
- D. B. Dunson, Z. Chen and J. Harry, Biometrics, 2003, 59, 521–530 CrossRef.
- R. V. Gueorguieva, Biometrics, 2005, 61, 862–866 CrossRef PubMed.
- R. V. Gueorguieva and G. Sanacora, Stat. Med., 2006, 25, 1307–1322 CrossRef CAS PubMed.
- L. L. Kupper and J. K. Haseman, Biometrics, 1978, 34, 69–76 CrossRef CAS.
- E. O. George and R. L. Kodell, J. Am. Stat. Assoc., 1996, 91, 1602–1610 Search PubMed.
- J. L. Xu and P. C. Prorok, Stat. Med., 2003, 22, 2401–2416 CrossRef PubMed.
- C. Yu and D. Zelterman, Comput. Stat. Data Anal., 2008, 52, 1636–1649 CrossRef PubMed.
- C. Stefanescu and B. W. Turnbull, Biometrics, 2003, 59, 18–24 CrossRef.
- X. Dang, S. L. Keeton and H. X. Peng, Stat. Med., 2009, 28, 2580–2604 CrossRef PubMed.
- A. Y. C. Kuk, Journal of the Royal Statistical Society Series C-Applied Statistics, 2004, 53, 369–386 CrossRef.
- G. G. Shan, Stat. Probab. Lett., 2013, 83, 644–649 CrossRef PubMed.
- H. Ahn, H. Moon, S. Kim and R. L. Kodell, Comput. Stat. Data Anal., 2002, 38, 263–283 CrossRef.
- F. Tan, G. J. Rayner, X. Wang and H. Peng, J. Stat. Plann. Inference, 2010, 140, 2849–2859 CrossRef PubMed.
- C. Faes, N. Aerts, G. Molenberghs, H. Geys, G. Teuns and L. Bijnens, Stat. Med., 2008, 27, 4408–4427 CrossRef PubMed.
- C. Faes, G. Molenberghs, M. Aerts, G. Verbeke and M. G. Kenward, Am. Stat., 2009, 63, 389–399 CrossRef.
- A. Szabo and E. O. George, Biometrika, 2010, 97, 95–108 CrossRef PubMed.
- F. Dominici and G. Parmigiani, Biometrics, 2001, 57, 150–157 CrossRef CAS PubMed.
- D. J. Nott and A. Y. C. Kuk, J. Agric. Biol. Environ. Stat., 2010, 15, 101–118 CrossRef PubMed.
- K. Fronczyk and F. Kottas, J. Am. Stat. Assoc., 2014 Search PubMed , accepted.
- P. J. Catalano, D. O. Scharfstein and L. Ryan, Teratology, 1993, 47, 281–290 CrossRef CAS PubMed.
- M. R. Elliott, M. M. Joffe and Z. Chen, Biometrics, 2006, 62, 352–360 CrossRef PubMed.
- K. K. Saha, Biom. J., 2014 DOI:10.1002/bimj.201300105.
- K. K. Saha, R. Bilisoly and D. M. Dziuda, J. Appl. Stat., 2014, 41, 439–453 CrossRef.
- C. Faes, M. Aerts, H. Geys, G. Molenberghs and L. Declerck, Environ. Ecol. Stat., 2004, 11, 305–322 CrossRef.
- L. J. Lin, D. Bandyopadhyay, S. R. Lipsitz and D. Sinha, Biometrics, 2010, 66, 287–293 CrossRef PubMed.
- B. Allen, R. J. Kavlock, C. A. Kimmel and E. M. Faustman, Fundam. Appl. Toxicol., 1994, 23, 496–509 CrossRef CAS.
- D. L. Hunt and S. N. Rai, J. Appl. Toxicol., 2005, 25, 435–439 CrossRef CAS PubMed.
- D. L. Hunt and C. S. Li, Toxicol. Sci., 2006, 92, 329–334 CrossRef CAS PubMed.
- D. L. Hunt, S. N. Rai and C. S. Li, Dose-Response, 2008, 6, 352–368 CrossRef PubMed.
- M. A. Murado and M. A. Prieto, Sci. Total Environ., 2013, 461, 576–586 CrossRef PubMed.
- W. Leisenring and L. Ryan, Regul. Toxicol. Pharmacol., 1992, 15, 161–171 CrossRef CAS.
- L. Hothorn and D. Hauschke, J. Biopharm. Stat., 2000, 10, 15–30 CrossRef CAS PubMed.
- R. M. Kuiper, D. Gerhard and L. A. Hothorn, Stat. Biopharm. Res., 2014, 6, 55–66 CrossRef.
- R. L. Kodell, Environ. Ecol. Stat., 2009, 16, 3–12 CrossRef CAS PubMed.
- W. Slob, M. Moerbeek, E. Rauniomaa and A. H. Piersma, Toxicol. Sci., 2005, 84, 167–185 CrossRef CAS PubMed.
- C. Ritz, D. Gerhard and L. A. Hothorn, Stat. Biopharm. Res., 2013, 5, 79–90 CrossRef.
- J. M. Diamond, D. L. Denton, J. W. Roberts and L. Zheng, Environ. Toxicol. Chem., 2013, 32, 1101–1108 CrossRef CAS PubMed.
- D. Hauschke, M. Kieser and L. A. Hothorn, Biom. J., 1999, 41, 295–304 CrossRef.
- L. A. Hothorn and M. Hasler, J. Biopharm. Stat., 2008, 18, 915–933 CrossRef PubMed.
- T. P. Ryan and W. H. Woodall, J. Appl. Stat., 2005, 32, 461–474 CrossRef.
- I. D. Bross, Biometrics, 1985, 41, 785–793 CrossRef CAS.
- OECD417: Guideline for the Testing of Chemicals – Toxicokinetics.
- ICH Topic S 3 A Toxicokinetics: A Guidance for Assessing Systemic Exposure in Toxicology Studies, 1995.
- M. J. Wolfsegger and T. Jaki, J. Pharmacokinet. Pharmacodyn., 2005, 32, 757–766 Search PubMed.
- M. J. Wolfsegger and T. Jaki, J. Pharmacokinet. Pharmacodyn., 2009, 36, 479–494 Search PubMed.
- M. J. Wolfsegger and T. Jaki, Biom. J., 2009, 51, 1017–1029 Search PubMed.
- T. Jaki and M. J. Wolfsegger, Stat. Med., 2012, 31, 1059–1073 CrossRef PubMed.
- T. Jaki and M. J. Wolfsegger, Pharm. Stat., 2011, 10, 284–288 CrossRef PubMed.
- T. Jaki, M. J. Wolfsegger and M. Ploner, Pharm. Stat., 2009, 8, 12–24 CrossRef PubMed.
- A. K. Krug, R. Kolde, J. A. Gaspar, E. Rempel, N. V. Balmer, K. Meganathan, K. Vojnits, M. Baquie, T. Waldmann, R. Ensenat-Waser, S. Jagtap, R. M. Evans, S. Julien, H. Peterson, D. Zagoura, S. Kadereit, D. Gerhard, I. Sotiriadou, M. Heke, K. Natarajan, M. Henry, J. Winkler, R. Marchan, L. Stoppini, S. Bosgra, J. Westerhout, M. Verwei, J. Vilo, A. Kortenkamp, J. R. Hescheler, L. Hothorn, S. Bremer, C. van Thriel, K. H. Krause, J. G. Hengstler, J. Rahnenfuhrer, M. Leist and A. Sachinidis, Arch. Toxicol., 2013, 87, 123–143 CrossRef CAS PubMed.
- A. K. Goetz, B. P. Singh, M. Battalora, J. M. Breier, J. P. Bailey, A. C. Chukwudebe and E. R. Janus, Regul. Toxicol. Pharmacol., 2011, 61, 141–153 CrossRef CAS PubMed.
- D. P. Lovell, Toxicology, 2007, 240, 160–161 CrossRef PubMed.
- S. Pramana, D. Lin, P. Haldermans, Z. Shkedy, T. Verbeke, H. Gohlmann, A. De Bondt, W. Talloen and L. Bijnens, R J., 2010, 2, 5–12 Search PubMed.
- D. Lin, Z. Shkedy, D. Yekutieli, T. Burzykowski, H. W. H. Gohlmann, A. De Bondt, T. Perera, T. Geerts and L. Bijnens, Stat. Appl. Genet. Mol. Biol., 2007, 6, 26 Search PubMed.
- D. Lin, L. Hothorn and G. Djira, Chapter 15: Multiple Contrast Tests for Testing Dose-response Relationships Under Order Restricted Alternatives, in Modeling Dose-response Microarray Data in Early Drug Development Experiments With R, Springer, 2012 Search PubMed.
- M. B. Black, B. B. Parks, L. Pluta, T. M. Chu, B. C. Allen, R. D. Wolfinger and R. S. Thomas, Toxicol. Sci., 2014, 137, 385–403 CrossRef CAS PubMed.
- C. Faes, M. Aerts, H. Geys and L. De Schaepdrijver, Pharm. Stat., 2010, 9, 10–20 CrossRef PubMed.
- Citation in: G. E. P. Box and N. R. Draper, Empirical Model Building and Response Surfaces, John Wiley & Sons, New York, NY., 1987, p. 424 Search PubMed.
- J. Pinheiro, B. Bornkamp and F. Bretz, J. Biopharm. Stat., 2006, 16, 639–656 CrossRef PubMed.
- W. W. Piegorsch, H. Xiong, R. N. Bhattacharya and L. Z. Lin, Environmetrics, 2012, 23, 717–728 CrossRef CAS PubMed.
- S. Sand, D. von Rosen, P. Eriksson, A. Fredriksson, H. Viberg, K. Victorin and A. F. Filipsson, Toxicol. Sci., 2004, 81, 491–501 CrossRef CAS PubMed.
- K. Shao and J. S. Gift, Risk Anal., 2014, 34, 101–120 CrossRef PubMed.
- M. W. Wheeler and A. J. Bailer, Regul. Toxicol. Pharmacol., 2013, 67, 75–82 CrossRef CAS PubMed.
- K. Shao, J. S. Gift and R. W. Setzer, Toxicol. Appl. Pharmacol., 2013, 272, 767–779 CrossRef CAS PubMed.
- W. W. Piegorsch, H. Xiong, R. N. Bhattacharya and L. Z. Lin, Risk Anal., 2014, 34, 135–151 CrossRef PubMed.
- E. F. A. Brandon, A. S. Bulder, J. G. M. van Engelen, C. M. Mahieu, W. C. Mennes, M. E. J. Pronk, A. G. Rietveld, B. M. van de Ven, S. E. C. G. ten Voorde, G. Wolterink, W. Slob, M. J. Zeilmaker and J. G. M. Bessems, Regul. Toxicol. Pharmacol., 2013, 67, 182–188 CrossRef CAS PubMed.
- B. L. Wu and A. R. de Leon, J. Agric. Biol. Environ. Stat., 2014, 19, 39–56 CrossRef.
- J. S. Najita and P. J. Catalano, Risk Anal., 2013, 33, 1500–1509 CrossRef PubMed.
- L. L. Tang, M. Guerard and A. Zeller, Environ. Mol. Mutagen., 2014, 55, 15–23 CrossRef CAS PubMed.
- J. A. Davis, J. S. Gift and Q. J. Zhao, Toxicol. Appl. Pharmacol., 2011, 254, 181–191 CrossRef CAS PubMed.
- Package bmd Benchmark dose analysis in R by Christian Ritz .
- D. R. Fox, Ecotoxicol. Environ. Saf., 2010, 73, 123–131 CrossRef CAS PubMed.
- K. Shao and M. J. Small, Hum. Ecol. Risk Assess., 2012, 18, 1096–1119 CrossRef CAS.
- J. Zhang, A. J. Bailer and J. T. Oris, Environmetrics, 2012, 23, 696–705 CrossRef CAS PubMed.
- G. Aldridge and D. Bowman, J. Stat. Comput. Simul., 2005, 75, 81–91 CrossRef.
- B. S. Hwang and M. L. Pennell, Stat. Med., 2014, 33, 1162–1175 CrossRef PubMed.
- C. Ritz and L. Van der Vliet, Environ. Toxicol. Chem., 2009, 28, 2009–2017 CrossRef CAS PubMed.
- T. Hothorn, K. Hornik, M. A. Van de Wiel and A. Zeileis, Am. Stat., 2006, 60, 257–263 CrossRef.
- T. Hothorn, K. Hornik, M. A. V. van de Wiel and A. Zeileis, J. Stat. Software, 2008, 28, 8 Search PubMed.
- G. Dilba, F. Schaarschmidt and L. Hothorn, R News, 2007, 7, 20–23 Search PubMed.
- F. Konietschke, M. Placzek and F. Schaarschmidt, H. L. nparcomp: An R Software Package for Nonparametric Multiple Comparisons and S. C. Intervals, J. Stat. Software, 2014 Search PubMed.
- Data and R-Code of BUN and MN example available via http://www.biostat.uni-hannover.de/software.html.
| This journal is © The Royal Society of Chemistry 2014 |