Determination of the n-director direction of low bend-angle banana-shaped molecules by solid-state ¹³C NMR

Abstract

The structural behavior of 2,3-naphthylene bis[2-fluoro-4-(4-(dodecyloxybenzoyloxy)benzoate], an acute-shaped banana liquid crystal (LC) molecule, in the smectic and nematic phases was investigated using solid-state nuclear magnetic resonance (NMR) spectroscopy in an 11.7 T magnetic field. Analysis of the alignment-induced shifts in both the LC phases indicated that the LC directors were aligned with the external magnetic field direction, and the “bow-string” direction in the present bent-core LC molecule was parallel to the layer direction in the smectic phase. In addition, systematic quantum chemical calculations were performed to determine the three-dimensional structure, and it was found that two arms of the LC molecule are close to one another and overlap via π-stacking interactions, such that the overall shape is a U-shape.

---

Introduction

It has been shown by Watanabe and co-workers¹ that liquid crystal (LC) molecules in the 1,3-benzene bis[4-(4-n-alkoxyphenyliminomethyl)benzoate] homologous series, known as classic banana LC molecules, exhibit spontaneous polarization and chirality despite the fact that these molecules themselves are achiral. More recently, a variety of new LC phases classified and designated as B-phases have been discovered and reported.^2–4 A classic banana LC molecule commonly contains a 1,3-phenylene central core and a bending angle of approximately 120° due to the structure of the central core moiety. The overall shape of such an LC molecule looks like a bow and a boomerang, with the direction of the director in the mesophases thought to lie parallel to the bow-string direction, i.e., the molecular long axis, particularly when banana phases are formed.

The relationship between the molecular bend angle and banana LC mesomorphism has been intensively investigated by adopting different central core moieties that provide a wide range of molecular bend angles. The introduction of lateral substituents and heterocyclic five-membered ring systems, such as oxadiazole and thiadiazole moieties, into the central core revealed that the ideal bend angle for obtaining banana phases falls in the range of 110° to 140°.^5,6 Acute-shaped molecules with smaller bend angles of approximately 60° have also been widely investigated. Matsuzaki et al. and Kuboshita et al. prepared molecules based on 1,2-phenylene and 2,3-naphthalene central cores with bend angles of approximately 60° and reported that only conventional nematic and smectic phases were formed.^7,8 However, by synthesizing six types of bent-shaped molecules with typical Schiff base side wings substituted at various positions around the central naphthalene core, Watanabe et al. discovered that molecules composed of 1,7-naphthalene derivatives form typical banana phases, such as B₄ and antiferroelectric smectic A (SmAP_A) phases, despite their small bend angles.^9–12 Furthermore, Kang et al. reported the formation of novel switchable hexagonal columnar (Col_h) and cubic (Cub) phases constructed of enclosed smectic layers with similar homologues based on a small bend angle 1,7-naphthalene core.^13,14 Very recently, Kang et al. also described the formation of typical polar B₂ and B₇ banana phases for low-angle bent-core LC molecules based on a 1,2-bis(phenylethynyl)benzene central core that possesses an acute V-shape with a 60° bend angle.¹⁵ It is thus believed that suitable central cores with small bend angles can promote not only molecular packing along the bend direction, which gives rise to the formation of polar banana phases, but also the formation of a diverse array of deformed structures, such as Col_h and Cub phases.

However, two possible molecular arrangements can arise in the smectic layers of these V-shaped LC molecules, i.e., with the bow-string direction parallel or perpendicular to the layers. Consequently, it remains controversial whether the molecular arrangements in the mesophases of these compounds are banana-like or calamitic, as discussed by Choi et al.^16,17 and Ros et al.^18,19 with different interpretations. Both prepared homologous series based on 2,3-naphthalene central cores; Choi et al. claimed a polar SmA phase whereas Ros et al. reported a non-polar SmA. Although X-ray diffraction analysis is one of the most powerful tools for investigating the structural properties of LC phases, we believe that it is unreliable or nearly impossible to directly determine molecular conformations and arrangements in LC phases only based on d-spacing values, particularly when two possible molecular accommodation states provide a similar spatial distance. Therefore, the structural properties of LC layers, which is very important information needed for the further developments of acute-shaped banana LC molecules, remain uncertain.

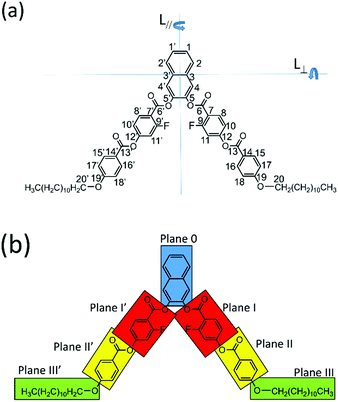
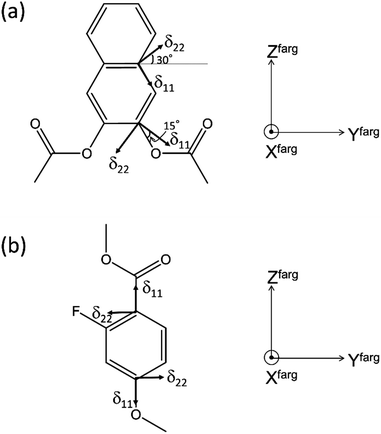
Recently, solid-state nuclear magnetic resonance (NMR) spectroscopy has attracted the attention of researchers in the LC field because it can be used to unambiguously determine the molecular structures, orientation orders, and molecular dynamics of compounds.^20–26 In particular, it is an ideal technique for elucidating the direction of the directors in LCs in the nematic phase for which n-directors are aligned parallel to the direction of an external magnetic field. In addition, the director in the smectic phase can be discussed by considering the phase transition from the nematic to the smectic phases. In this paper, we describe the experimental determination of the director directions in low bend-angle banana-shaped LC molecules using solid-state ¹³C NMR. The newly synthesized banana LC compound 2,3-naphthylene bis[2-fluoro-4-(4-dodecyloxybenzoyloxy)benzoate], denoted as N(2,3)–F–O12 (Fig. 1(a)), for which the two directors, L_∥ and L_⊥, are possible, has a novel bent-core that enabled the measurement of the solid-state NMR spectrum within the LC phase because of lowering of the nematic–isotropic transition temperature through the introduction of a lateral fluorine substituent. Although N(2,3)–F–O12 is classified as a V-shaped LC molecule, we discuss three-dimensional molecular structures in its LC phases because there is a flexible ester linkage to the 2,3-naphthalene central core and flexible sections in the lateral wings. To the best of our knowledge, the present investigation is the first report of the determination of the director of a bent-core V-shaped LC molecule in the smectic layer and the nematic phase, which we believe is a key element for achieving enhanced molecular designs in the near future.

Fig. 1 (a) Molecular structure of 2,3-naphthylene bis[2-fluoro-4-(4-dodecyloxybenzoyloxy)benzoate] (N(2,3)–F–O12) with the atomic labeling as used in this study. Two possible directors, namely, L_∥ and L_^, are given in the figure. (b) View showing the flexible planes in N(2,3)–F–O12. The molecule was conveniently divided into seven parts, and each plane was assumed to be rigid.

Experimental

Sample preparation

The compound N(2,3)–F–O12 was synthesized, as shown in Scheme 1. A mixture of 4-dodecyloxybenzoic acid (1.41 g, 4.59 mmol), N,N′-dicyclohexylcarbodiimide (0.95 g, 4.59 mmol), a catalytic amount of 4-(N,N-dimethylamino)pyridine (0.06 g, 0.46 mmol), 2,3-naphthylene bis(2-fluoro-4-hydroxybenzoate) (0.95 g, 4.59 mmol), and dichloromethane (30 mL) was stirred for approximately 24 h at room temperature. The precipitated N,N′-dicyclohexylurea was removed by filtration, and the filtrate was washed with 5% aqueous acetic acid and water. The solvent was then removed from the organic layer under reduced pressure. The obtained material was purified using silica-gel chromatography with chloroform/ethyl acetate (20 : 1) as the eluent. Removal of the solvent afforded a white material, which was recrystallized from chloroform/ethanol (2 : 3). Yield: 34%; FT-IR (KBr pellet, cm⁻¹): 3079 (aromatic C–H stretch), 2919, 2851 (aliphatic C–H stretch), 1746 (conj. C=O stretch), 1616 (aromatic C=C stretch), 1148 (C–F stretch), 1246, 1168 (C–O stretch); ¹H NMR (CDCl₃, δ in ppm): 8.16 (d, 4H, Ar-H), 8.11 (t, 2H, Ar-H), 7.90 (s, 4H, Ar-H), 7.55–7.51 (m, 2H, Ar-H), 7.15 (d, 4H, Ar-H), 6.99 (d, 4H, Ar-H), 4.06 (t, 4H, OCH₂CH₂(CH₂)₉CH₃), 1.86–1.79 (m, 4H, OCH₂CH₂(CH₂)₉CH₃), 1.30 (s, 36H, OCH₂CH₂(CH₂)₉CH₃), 0.91 (t, 6H, OCH₂(CH₂)₁₀CH₃); anal. calcd. for C₆₂H₇₀F₂O₁₀: C 73.50, H 6.96; found: C 72.76, H 7.06.

Scheme 1 Synthetic route to N(2,3)–F–O12.

DSC measurements

Transition temperatures and corresponding enthalpies were determined via differential scanning calorimetry (DSC) using a Perkin-Elmer Pyris-1 calorimeter in an N₂ gas atmosphere at a scanning rate of 10 °C min⁻¹. The DSC measurements were carried out from 273 to 493 K, and no differences were found in the phase-transition temperatures at the heating/cooling rates of between 2 K min⁻¹ and 10 K min⁻¹.

Polarization microscopy (POM) observations and electro-optical measurements

The optical textures of the mesophases were observed using an Olympus BX50 polarizing microscope equipped with a Mettler FP 82 HT hot stage and a Mettler FP 90 automatic controller. The electro-optical switching behaviour was observed using a high-speed voltage amplifier (FLC Electronics, F20A) connected to a function generator (NF Electronic Instruments, WF 1945A). The sample was injected between ITO coated glass-plates covered with thin layers of polyimide. The polarization reversal current was measured by applying a triangular wave voltage.

WAXD measurements

Wide-angle X-ray diffraction (WAXD) measurements were performed using a Bruker D8 DISCOVER equipped with a Vantec-500 detector using Cu-Kα radiation. Powder X-ray diffraction (XRD) investigations were performed in a glass capillary tube for the sample with homeotropic alignment, which was prepared by slow cooling from the corresponding isotropic liquid in a magnetic field.

NMR measurements

¹H and ¹³C NMR experiments were performed at 500.194 and 125.774 MHz, respectively, on an 11.7 T JEOL ECA 500 spectrometer (JEOL, Tokyo, Japan) using a 4 mm magic-angle spinning (MAS) probe between 290 and 480 K. Whenever the temperature changed, the system was held for more than 10 min to allow it to reach thermal equilibrium. Potassium bromide and adamantane were used to adjust the magic-angle and as a reference, respectively. A standard ramped cross-polarization (CP) sequence was used with a mixing time of 5 ms and high-power irradiation to achieve heteronuclear decoupling during each detection period. Accumulations of 1000–3000 scans were required to provide most of the stationary NMR spectra presented here. The MAS frequencies were 10–15 kHz for the CPMAS experiments. Dipole-dephasing experiments were performed using a gradually increased dipole-dephasing time, up to 2.2 ms such that only peaks from quaternary carbons remained. In addition, 2D total sideband suppression (TOSS) reverse-TOSS experiments²⁷ were performed using MAS frequencies of 3.00 and 3.40 kHz and an offset frequency of 130 ppm. A total of 188–256 t₁ increments were collected. Spectral simulations for Herzfeld–Berger plots²⁸ were performed using the Herzfeld–Berger analysis (HBA) program tool developed by Eichele.²⁹ The error bar for each component was estimated to be ±5 ppm. All the NMR spectra were processed using DELTA (JEOL USA, Inc.) software. All spectral simulations and chemical shift calculations were performed by employing a program developed by us using MATLAB (Math Works, Inc., Natick, MA, USA).

Quantum chemical calculations

All the quantum chemical calculations of the ¹³C CS tensors and structural optimizations were performed using the Gaussian09 program package³⁰ on TSUBAME2.5 at the Global Scientific Information and Computing Center at the Tokyo Institute of Technology and/or the Research Center for Computational Science at the National Institutes of Natural Sciences, Okazaki Research Facility. The gauge-induced atomic orbital approach^31,32 was used for the CS calculations at the B3LYP^33–35/6-311G(2df,2p) level. The geometry optimization calculations were performed at the ωB97X-D³⁶/6-311G(d,p) level, using the initial geometries described in the following section, and the optimized structures were verified to have an equilibrium geometry using the Hessian index calculated on the basis of the results of a vibrational analysis. Terminal alkyl chains were replaced with –O(CH₂)₄CH₃ to reduce the calculation costs.

Results and discussion

The phase-transition temperatures of N(2,3)–F–O12 as determined by DSC analysis are summarized in Table 1. Each phase was assigned using both WAXD and POM analyses. No further peaks were observed below the smectic phases in either the cooling or 2nd heating directions, except for a vitrification confirmed at 298 K by both WAXD and POM, although a crystal phase was obtained for the as-synthesized sample at 298 K prior to the 1st heating step. Apparently, N(2,3)–F–O12 formed its crystal phase just after recrystallization at 298 K, but became vitrified after melting once, thus exhibiting thermal history. In the rest of this paper, the crystal phase of N(2,3)–F–O12 implies the former.

Table 1 Phase-transition temperatures of N(2,3)–F–O12, determined by differential scanning calorimetry

Smectic–nematic phase		Nematic–isotropic phase
Cooling	416 K	453 K
2^nd heating	417 K	454 K

---

It should be noted that polar switching behavior was not observed in either of the LC phases (nematic and smectic) on the basis of the electro-optical and second harmonic generation (SHG) analyses, which is a distinct characteristic of banana LC phases.

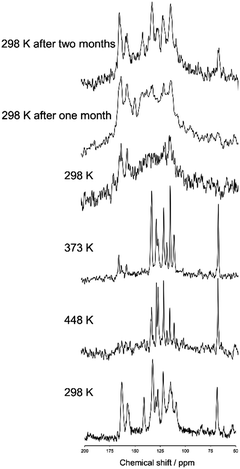
Fig. 2 shows a magnified view of the ¹³C CPMAS NMR spectra of N(2,3)–F–O12 acquired at various temperatures and a MAS frequency of 10 kHz. For clarity, the aliphatic region is omitted. The NMR spectrum was initially observed at 298 K in the crystal phase (lowest) after which the sample was heated to 468 K in the isotropic phase. The ¹³C CPMAS NMR spectra were then obtained at 448, 373, and 298 K with decreasing temperature. The same NMR measurements were also carried out at 298 K after one and two months each. Melting of N(2,3)–F–O12 was confirmed by the lack of peaks in the ¹³C CPMAS and the presence of sharp peaks in the ¹H NMR spectra. Fig. 2 shows that the chemical shifts for the spectrum of the nematic phase were nearly the same as those in the spectrum of the smectic phase, indicating that no dynamic change in the molecular environment occurred during the phase transitions, i.e., the director directions did not change. It can also be seen that the line shapes broadened significantly at 298 K after the sample was melted once, reflecting vitrification of the sample. Interestingly, those line shapes gradually changed and sharp peaks appeared after one month possibly because of a spontaneous crystallization. On the basis of these results, the remaining NMR experiments except for the 2D TOSS-reverse TOSS experiments were performed with decreasing temperature after melting.

Fig. 2 Magnified views of the ¹³C CPMAS NMR spectra of N(2,3)–F–O12 acquired at various temperatures. The spectrum at 298 K (lowest) was obtained, after which the sample was heated to 468 K in the isotropic phase. The NMR spectra were then observed at 448, 373, and 298 K with decreasing temperature.

Liquid crystals in their nematic phase can be readily aligned by an external magnetic field.^26,37,38 Assuming that a liquid crystal is a uniaxial molecule, the chemical shift in the field-aligned molecule, δ_exp, is expressed as²⁶

δ_exp = δ_iso + {(δ₃₃ − δ_iso)P₂(cos β_F) + (1/2)(δ₁₁ − δ₂₂) × cos 2α_F sin² β_F}P₂(cos β_M)S₀₀P₂(cos β_L) (1)

where

P₂(cos β_M) = (1/2)(3 cos² β_M − 1) (2)

P₂(cos β_L) = (1/2)(3 cos² β_L − 1) (3)

It should be noted that there was a typographical error in eqn (18) of ref. 26 in which the last term of the left-hand side should be P₂(cos β_L) rather than P₂(cos β_F). In the above equations, δ₁₁, δ₂₂, and δ₃₃ are the principal components of the chemical shielding (CS) tensor, α_F and β_F are the Euler angles describing the Wigner rotation from the principal axis system (PAS) to the system for the moment of inertia of a fragment (FRAG), and β_M and β_L are the angles between the z axis in the FRAG and the long axis of the system for the moment of inertia of the molecule (MOL), and between the liquid crystal molecule director and the external magnetic field direction, respectively. Thus, the observed chemical shift depends on the magnitudes and directions of the CS tensor, the relative orientation between FRAG and MOL, the order parameter, and the direction of the director in an external magnetic field.

Recently, Pelzl et al.³⁹ successfully demonstrated that solid-state ¹³C NMR provided useful information on the molecular conformation of a chlorine-substituted classic banana LC molecule in the B₂ phase using the above relationship. It was necessary to obtain unambiguous spectral assignments for the ¹³C NMR spectrum for this purpose, even though numerous lines overlapped in narrow regions. In their work, a small dependence of the intensity and line width on the experimental NMR conditions, including the ¹H decoupling and/or Hartmann–Hahn match conditions for ¹H–¹³C CP, was deftly used for the spectral assignment. However, in the present case, the presence of a large number of peaks with relatively poor spectral resolution made it nearly impossible to assign all of the peaks in the stationary ¹³C NMR spectrum for the nematic and smectic phases (shown below). Thus, assuming the two possible directors L_∥ and L_⊥ (more specifically, two angles for β_M), the theoretical chemical shifts for several of the quaternary carbons in the backbone of the field-aligned molecule were calculated and compared to the corresponding experimental chemical shifts, leading to the conclusion which direction an n-director was aligned to. The calculation procedure was as follows. First, the peaks for the quaternary carbon sites in N(2,3)–F–O12 were assigned and the magnitudes of the ¹³C CS tensors were determined for the crystal phase. Second, stationary ¹³C CP NMR spectra were obtained for the nematic and smectic phases, and the range of chemical shifts was experimentally determined for the quaternary carbon sites. Third, the orientation of the ¹³C CS tensors with respect to the molecular frame was determined using quantum chemical calculations. Finally, the theoretical chemical shifts of the main quaternary carbons in the naphthalene and benzene rings were calculated on the basis of the above results using order parameters obtained via XRD analysis, and these results were compared to the corresponding experimental values, enabling the determination of the direction of the directors and the molecular structures of the N(2,3)–F–O12 in LC phases.

Fig. 3 shows a magnified view of the ¹³C CPMAS NMR spectrum (lower) and dipole-dephasing NMR spectrum (upper) of N(2,3)–F–O12 at 298 K in the crystal phase with the spectral assignment. The atomic labeling is given in Fig. 1(a). At an adequate dephasing time, τ, only the quaternary carbon sites appear in the dipole dephasing NMR spectrum. For example, the aromatic carbon peaks (1/1′, 2/2′, 4/4′, 8/8′, 9/9′, 10/10′, 11/11′, 15/15′, 16/16′, 17/17′, and 18/18′) and a peak for the 20/20′ carbon site were fully eliminated at τ = 2.0 ms. Assignment of the ¹³C peaks was successfully achieved using quantum chemical calculations and extrapolation of the solution ¹³C NMR (data not shown). Two doublet peaks were found for the 5/5′ and 12/12′ carbon sites, indicating that the molecule may contain an asymmetric structure in the crystal phase. However, because of the low spectral resolution, the average ¹³C chemical shielding tensors for these doublet peaks were used in the following discussion. Note that no doublet peaks were observed in the LC phases, suggesting that the structures for N(2,3)–F–O12 in the LC phases are symmetrical. Unfortunately, the 6/6′, 13/13′, and 19/19′ carbon sites completely overlapped in the range of 160–166 ppm; thus these sites could not be used for the present analysis.

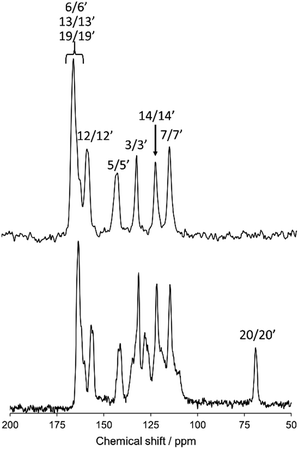Fig. 3 The ¹³C CPMAS NMR spectrum (lower) and dipole-dephasing NMR spectrum (upper) of N(2,3)–F–O12 at 298 K with spectral assignments. The atomic labeling is given in Fig. 1(a).

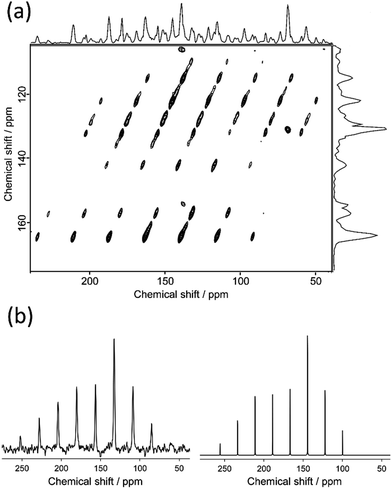
Fig. 4 shows the 2D ¹³C TOSS reverse-TOSS spectrum of N(2,3)–F–O12 in the crystal phase, acquired at a MAS frequency of 3.00 kHz. Both the f₁ and f₂ projections are also given on the side and top, respectively. For clarity, the aliphatic carbon region is omitted. In the f₁ dimension, only the isotropic chemical shifts were observed, whereas in the f₂ dimension, both the isotropic and spinning sidebands were observed. A Herzfeld–Berger plot analysis²⁸ was then applied to each cross-section of the spectrum along the f₂ dimension, giving the three principal components of the ¹³C CS tensors. Fig. 4(b) shows the f₂ projections at 156 ppm for the above two-dimensional spectrum (left) and the best-fitted calculated spectra (right). The results for the ¹³C CS tensors for the selected quaternary carbon peaks in N(2,3)–F–O12 are summarized in Table 2.

Fig. 4 2D ¹³C TOSS reverse-TOSS spectrum of N(2,3)–F–O12 in the crystal phase acquired at the MAS frequency of 3.00 kHz and (b) f₂ projections at 156 ppm of the two-dimensional spectrum (left) and the corresponding calculated spectra (right).

Table 2 Experimental ¹³C CS Tensors in ppm for N(2,3)–F–O12 obtained by 2D TOSS Reverse-TOSS at 298 K. Each isotropic chemical shift was determined by the ¹³C CPMAS NMR spectra at 298 K

Site	δ iso	δ 11	δ 22	δ 33
3/3′	131.4	216	178	2
5/5′	141.2/142.2	218	133	75
7/7′	114.7	178	135	33
12/12′	155.9/156.9	251	141	79
14/14′	121.9	201	133	32

---

Fig. 5 shows a magnified view of the ¹³C CP stationary NMR spectra of N(2,3)–F–O12 in the nematic phase as a function of temperature. The sample tube was fixed using Kapton adhesive tape and was not rotated in the MAS probe. An airflow was used to control the temperature. The sharp signals and drastic changes in the chemical shifts up to approximately 225 ppm clearly indicated that the LC molecules were aligned with the magnetic field. It can also be seen that the chemical shifts for nearly all of the carbon sites shifted to lower frequencies with increasing temperature. This behavior is due to the fact that, according to eqn (1), chemical shifts of aligned LC molecules in a magnetic field depend on their order parameters, which are temperature dependent in the nematic phase.

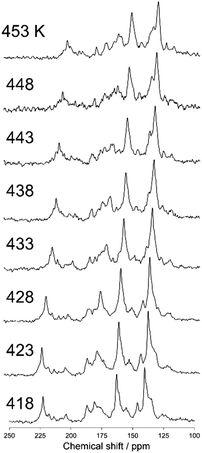Fig. 5 The ¹³C CP stationary NMR spectra of N(2,3)–F–O12 in the nematic phase as a function of temperature. The sample was not rotated in the MAS probe.

Fig. 6 shows a magnified view of the ¹³C CP stationary NMR spectra of N(2,3)–F–O12 in the smectic phase as a function of temperature. Again, the sample was not rotated during the NMR measurements. Whereas sharper peaks were observed in the NMR spectra of the smectic phase at higher temperatures, unlike for the nematic phase, no temperature-dependence was observed for the chemical shifts because the order parameters in the smectic phase are not acutely influenced by changes in temperature. Broader peaks were observed at lower temperatures because of vitrification, which is consistent with the results obtained for the ¹³C CPMAS experiments shown in Fig. 2.

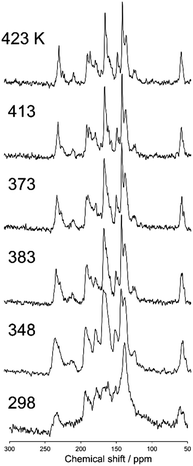Fig. 6 The ¹³C CP stationary NMR spectra of N(2,3)–F–O12 in the smectic phase as a function of temperature. The sample was not rotated in the MAS probe.

The order parameter for N(2,3)–F–O12 in the smectic phase was determined from the oriented wide angle X-ray diffraction patterns to be 0.6 (see Fig. S1 in the ESI†). Here, the order parameter, S₀₀, is a function of the distribution of the azimuthal angle (β) and the corresponding intensity, I(β), based on the conventional equation:^40,41

S₀₀ = (1/2)(3〈cos² β〉 − 1) (4)

where the average cosine square, 〈cos² β〉, was obtained from the following equation:

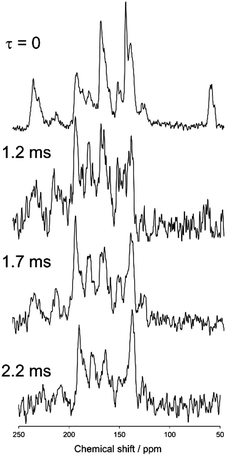
Fig. 7 and 8 show magnified views of the dipole-dephasing ¹³C stationary NMR spectra of N(2,3)–F–O12 at 358 K in the smectic phase and at 421 K in the nematic phase, respectively, at several dephasing times, τ. It can be observed in the smectic phase that the carbon peak at approximately 62 ppm gradually decreased at longer τ. The carbon peaks remaining in the range of 130–220 ppm at τ = 2.2 ms were assigned as quaternary carbons. Unfortunately, it was very difficult to assign each peak because of the lack of information. Hence, two models with the directors L_∥ and L_⊥ were constructed, and each theoretical chemical shift was calculated using eqn (1)–(3) and then compared to the above experimental data.

Fig. 7 The dipole-dephasing NMR spectra of N(2,3)–F–O12 at 358 K with several dephasing times, τ.

Fig. 8 The dipole-dephasing NMR spectra of N(2,3)–F–O12 at 421 K with several mixing times.

First, the quaternary carbon sites in the naphthalene rings (3/3′ and 5/5′) were considered. As mentioned previously, the orientation of the ¹³C CS tensor with respect to the molecular frame is required for the present calculations. The ideal technique for obtaining information about the orientations of NMR tensors is a single-crystal NMR experiment. However, large single crystals suitable for NMR analysis are often difficult to obtain. Recently, ab initio calculations have been used to obtain reliable information on ¹³C CS tensors; thus, it was assumed that the calculated orientations of the ¹³C CS tensors were correct in the following discussion. The calculated orientations for the quaternary carbon sites (3/3′ and 5/5′) are plotted in Fig. 9(a) with the FRAG coordinate used for the present discussion (right). For the carbon site (3/3′), for example, the δ₂₂ component lies in the molecular plane approximately 30° off the extension of the directions of the carbon sites (3 and 3′), and the δ₃₃ component is perpendicular to the plane. These orientations are in reasonable agreement with the data of previous literature.^42,43 The relative orientation between the PAS and the FRAG was then expressed as (α_F, β_F, γ_F) = (−30°, −90°, 0°) and (α_F, β_F, γ_F) = (−45°, −90°, 0°) for the quaternary carbon sites (3/3′) and (5/5′), respectively. Using the present definition of β_M (the angle between the z axes of the FRAG and the MOL), L_∥ and L_⊥ correspond to β_M = 0° and β_M = 90°, respectively. Fig. 10 shows the calculated isotropic chemical shifts for the 3/3′ (○) and 5/5′ (□) carbon sites as a function of the order parameters for the two models (a) L_∥ and (b) L_⊥. These values were calculated using eqn (1)–(3) from S₀₀ = 0.00 to S₀₀ = 1.00 and ΔS₀₀ = 0.20. From this figure, it can be deduced that the range of the chemical shifts for the carbon sites (3/3′ and 5/5′) in the smectic phase (S = 0.60) should be 162–176 and 109–132 ppm for the L_∥ and L_⊥ models, respectively. In addition, the chemical shifts for these quaternary carbon sites are expected to shift to low frequencies as the order parameter decreases, i.e., with increasing temperature. Therefore, it can be concluded that the direction of the director for N(2,3)–F–O12 in both LC phases is L_∥.

Fig. 9 Selected ¹³C CS tensor directions in (a) naphthalene and (b) benzene rings of N(2,3)–F–O12 with respect to the local molecular structure and principal axis moment of inertia system for the fragment (FRAG). All the δ₃₃ components are perpendicular to the molecular planes.

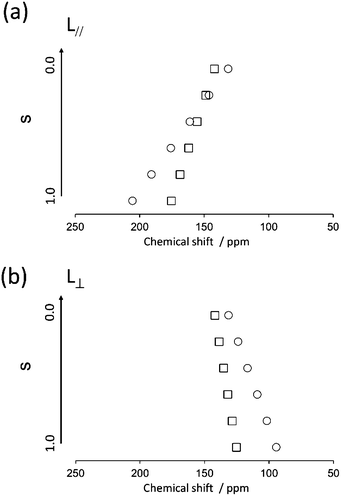Fig. 10 Calculated isotropic chemical shifts for carbon sites of 3 (○) and 5 (□) as a function of the order parameter in two possible directors; (a) L_∥ and (b) L_⊥.

Next, the quaternary carbon sites in the benzene rings of the lateral wing (7/7′, 12/12′, and 14/14′) were considered. The calculated orientations for the ¹³C CS tensors for the carbon sites (7/7′ and 12/12′) are schematically depicted in Fig. 9(b) with the corresponding FRAG used for the calculations. For both carbon sites, the δ₁₁ components lie in the molecular plane and are parallel to the C–O bond directions, and the δ₃₃ components are perpendicular to the plane. The orientation of the carbon site (14/14′) was nearly the same as that of the carbon site (7/7′). Again, β_M was required to calculate the theoretical chemical shifts using eqn (1)–(3). Clearly, β_M depends on the conformation of the lateral wing of N(2,3)–F–O12; however, to the best of our knowledge, three-dimensional molecular structures of this type in the LC phase have not yet been reported. At first glance, the bent-core V-shaped molecule takes a molecular conformation in which the lateral wing expands to be as far apart from each other as possible in order to minimize the total energy while maintaining a bending angle of 60°, i.e., a V-shape. However, a molecular conformation in which the lateral wings come close together and overlap each other may be possible because the ester-linkage to the 2,3-naphthalene central core is flexible, as are several parts of the lateral benzene cores. In this case, the overall shape would be that of a rod-like LC molecule, i.e., a U-shape. Thus, we systematically performed ab initio calculations to optimize the structure for N(2,3)–F–O12 and estimate the value of β_M. It is important to point out that the results for optimized structures of this type of an LC molecule depend completely on the initial geometries used for the calculations.^25,44 In other words, it is necessary to consider all the possible initial geometries to determine the most stable structure. It has been shown^25,44,45 that for banana LC molecules containing ester-linkages such as the C5–O–C6(O)–C7 and C12–O–C13(O)–C14 linkage shown in Fig. 1(a), the flexible torsion angles are constrained by π-conjugation and steric hindrance. Therefore, as shown in Fig. 1(b), the present molecule was conveniently divided into seven parts, and each plane was assumed to be rigid. In addition, the following torsion angles were used to construct the initial geometries: Λ = ∠C4–C5–O–C6, M = ∠C4′–C5′–O–C6′, P = ∠F–C9–C7–C6–O(car), Σ = ∠F–C9′–C7′–C6′–O(car), N = ∠C10–C12–O–C13, O = ∠C10′–C12′–O–C13′, Π = ∠C17–C19–O–C20, and Θ = ∠C17′–C19′–O–C20′. Previously, it was found^25,44 that it is important to consider the initial geometries using a combination of the following angles: Λ = 60°, M = ±60°, N = O = ±60° or ±120°. For Π and Θ, the resultant angles were found to be either 0° or 180° for all initial geometries; thus for convenience, Π = Θ = 180° and Π = Θ = 0° were defined as the cis and trans isomers, respectively. Although the P and Σ angles are temporarily fixed at 180° in Fig. 1(a), there may have been free rotations around C6–C7 or C6′–C7′ when N(2,3)–F–O12 was synthesized; thus, a combination of P = Σ = 0° or 180° was also considered. Overall, a total of 110 conformations were used in the present calculations as initial geometries (see Table S1 in the ESI† for details). Table 3 summarizes the activation energies of the lowest nine structures, with the corresponding initial geometries used for the calculations. The lowest energy was set to zero; thus, the energies in Table 3 are expressed as differences from the lowest values. A U-shape was found for all the calculated structures, and the most stable structure for N(2,3)–F–O12 is shown in Fig. 11. Each benzene ring in the lateral wing overlaps with the fluorine, carbonyl and alkoxy oxygen atoms of the opposite wing via π-stacking interactions. The other eight structures also exhibited nearly the same structure as that shown in Fig. 11, except for the directions of the carbonyl and alkoxy oxygen atoms. It should be noted that there is little difference in the energy gaps in Table 3, indicating that the U-shape is maintained in the LC phases, but each plane may undergo flipping. Fig. 12(a) shows the calculated chemical shifts for the 7/7′ (△), 12/12′ (☓), and 14/14′ (◇) carbon sites as a function of the order parameters. For reference, the case for L_⊥ is given in Fig. 12(b). For the 7/7′ carbon sites, for example, the values for β_M for L_∥ and L_⊥ were determined to be 7° and 96°, respectively, from the molecular structure in Fig. 11. It can be clearly seen that the calculated chemical shifts for the L_∥ model are in remarkable agreement with the experimental observations, both with respect to the range of chemical shift values and their temperature-dependence, demonstrating that N(2,3)–F–O12 in the LC phases adopts a U-shape structure, and the long-axis of the molecule is aligned to L_∥. Overall, the bow-string direction of N(2,3)–F–O12, which is a short-distance, in the smectic layers is aligned perpendicular to the layer normal, in contrast to the cases of classic banana LC molecules.

Table 3 Initial conformations used for optimization calculations of N(2,3)–F–O12, the resultant molecular shape, and the corresponding activation energies. The definitions used in this table are given in the text

Initial conformation (Λ, M) (P, Σ) (N, O) (Π, Θ)	Molecular shape (V-shape or U-shape)	ΔE/kJ mol^−1
(60°, 60°) (180°, 180°) (60°, 60°) (cis, cis)	U	0
(60°, 60°) (0°, 180°) (60°, 60°) (cis, cis)	U	1.30
(60°, −60°) (180°, 180°) (120°, −60°) (cis, cis)	U	1.35
(60°, −60°) (180°, 180°) (120°, −60°) (trans, trans)	U	1.52
(60°, −60°) (180°, 0°) (−60°, 120°) (cis, cis)	U	1.53
(60°, −60°) (0°, 180°) (−60°, 120°) (cis, cis)	U	1.53
(60°, −60°) (0°, 180°) (120°, 120°) (cis, cis)	U	1.54
(60°, −60°) (180°, 180°) (120°, −60°) (cis, trans)	U	1.62
(60°, −60°) (0°, 180°) (120°, −60°) (trans, trans)	U	1.70

---

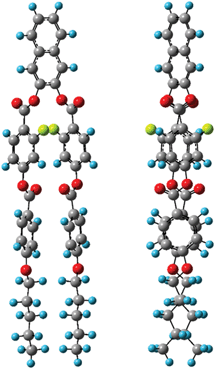Fig. 11 The most stable structures of N(2,3)–F–O12 calculated at the ωB97X-D/6-311G(d,p) level with the viewpoint shifted by 90 degrees.

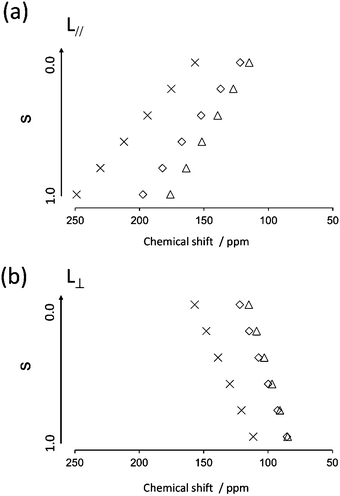Fig. 12 Calculated isotropic chemical shifts for carbon sites of 7/7′ (△), 12/12′ (☓) and 14/14′ (◇) as a function of order parameters in two possible directors; (a) L_∥ and (b) L_⊥.

Conclusions

We investigated the structural behaviours of N(2,3)–F–O12 in a strong magnetic field via solid-state ¹³C NMR analysis. Sharp signals were observed in the ¹³C CP stationary NMR spectra of the nematic and smectic LC phases, indicating that the directors were parallel to the magnetic field. Nearly all of the chemical shifts in the nematic phase gradually shifted to low frequencies as the temperature increased, whereas no shifts were observed for the peaks in the NMR spectrum of the smectic phase. In addition, 2D TOSS reverse-TOSS experiments in the crystal phase enabled derivation of the ¹³C CS tensors for several quaternary carbon sites, and quantum chemical calculations provide the tensor orientations with respect to the molecular frames. The order parameters for the smectic phase were determined to be 0.6 via XRD observations. Furthermore, analysis of the alignment-induced shifts combined with the above information indicated that the “bow-string” direction in the present bent-core LC molecule was aligned parallel to the layer direction in the smectic phase. Finally, systematic quantum chemical calculations were performed for structural optimization, and a final molecular structure with the lowest energy in which the two arms of the bent-core structure were found to overlap one other was obtained. The overall shape of N(2,3)–F–O12 is thus a U-shape. This study therefore successfully demonstrated that solid-state ¹³C NMR is a very useful tool for the structural investigation of LCs.

Acknowledgements

This work was supported by JSPS KAKENHI Grant numbers 2641007 and 26410086. The numerical calculations were carried out on the TSUBAME2.5 supercomputer at the Tokyo Institute of Technology, Tokyo, Japan, and on the supercomputer at the Research Center for Computational Science, Okazaki, Japan.

Notes and references

1. T. Niori, T. Sekine, J. Watanabe, T. Furukawa and H. Takezoe, J. Mater. Chem., 1996, 6, 1231.
2. G. Pelzl, S. Diele and W. Weissflog, Adv. Mater., 1999, 11, 707.
3. H. Takezoe and Y. Takanishi, Jpn. J. Appl. Phys., 2006, 45, 597.
4. R. A. Reddy and C. Tschierske, J. Mater. Chem., 2006, 16, 907.
5. I. Wirth, S. Diele, A. Eremin, G. Pelzl, S. Grande, L. Kovalenko, N. Pancenko and W. Weissflog, J. Mater. Chem., 2001, 11, 1642.
6. S. Kang, Y. Saito, N. Watanabe, M. Tokita, Y. Takanishi, H. Takezoe and J. Watanabe, J. Phys. Chem. B, 2006, 110, 5205.
7. H. Matsuzaki and Y. Matsunaga, Liq. Cryst., 1993, 14, 105.
8. M. Kuboshita, Y. Matsunaga and H. Matsuzaki, Mol. Cryst. Liq. Cryst., 1991, 199, 319.
9. S. K. Lee, Y. Naito, L. Shi, M. Tokita, H. Takezoe and J. Watanabe, Liq. Cryst., 2007, 34, 935.
10. S. K. Lee, M. Tokita, H. Takezoe and J. Watanabe, Ferroelectrics, 2008, 365, 1.
11. S. K. Lee, L. Shi, R. Ishige, S. Kang, M. Tokita and J. Watanabe, Chem. Lett., 2008, 37, 1230.
12. S. K. Lee, X. Li, S. Kang, M. Tokita and J. Watanabe, J. Mater. Chem., 2009, 19, 4517.
13. X. Li, S. Kang, S. K. Lee, M. Tokitaa and J. Watanabe, Jpn. J. Appl. Phys., 2010, 49, 121701.
14. S. Kang, M. Harada, X. Li, M. Tokita and J. Watanabe, Soft Matter, 2012, 8, 1916.
15. E. W. Lee, K. Takimoto, M. Tokita, J. Watanabe and S. Kang, Angew. Chem., Int. Ed., 2014, 53, 8216.
16. E.-J. Choi, X. Cui, C.-W. Ohk, W.-C. Zin, J.-H. Lee and T.-K. Kim, J. Mater. Chem., 2010, 20, 3743.
17. E.-J. Choi, E.-C. Kim, S.-B. Park, W.-C. Zin, Y.-J. Lee and J.-H. Kim, J. Mater. Chem., 2012, 22, 24930.
18. N. Gimeno, M. J. Clemente, P. Forcén, J. L. Serrano and M. B. Ros, New J. Chem., 2009, 33, 2007.
19. I. Alonso, J. Martinez-Perdiguero, J. Ortega, C. L. Folcia, J. Etxebarria, N. Gimeno and M. B. Ros, Liq. Cryst., 2010, 37, 1465.
20. NMR of Liquid Crystals, ed. J. W. Emsley, Reidel, Dordrecht, The Netherlands, 1985.
21. R. Y. Dong, Nuclear Magnetic Resonance of Liquid Crystals, Springer, New York, 1994.
22. J. W. Emsley, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, John Wiley & Sons, Chichester, U.K., 1996, vol. 4, p. 2788.
23. R. Y. Dong, Annu. Rep. NMR Spectrosc., 2004, 53, 67.
24. J. W. Emsley, M. Lelli, A. Lesage and G. R. A. Luckhurst, J. Phys. Chem. B, 2013, 117, 6547.
25. K. Yamada, S. Kang, K. Takimoto, M. Hattori, K. Shirata, S. Kawauchi, K. Deguchi, T. Shimizu and J. Watanabe, J. Phys. Chem. B, 2013, 117, 6830.
26. K. Yamada, K. Marumo, S. Kang, K. Deguchi, T. Nakai, T. Shimizu and J. Watanabe, J. Phys. Chem. B, 2013, 117, 16325.
27. H. Geen and G. Bodenhausen, J. Chem. Phys., 1992, 97, 2928.
28. J. Herzfeld and A. E. Berger, J. Chem. Phys., 1980, 73, 6021.
29. K. Eichele and R. E. Wasylishen, HBA ver. 1.4, Dalhousie University, 2001.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
31. R. Ditchfield, Mol. Phys., 1974, 27, 789.
32. K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251.
33. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
34. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
36. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
37. T. Nakai, S. Miyajima, Y. Takanishi, S. Yoshida and A. Fukuda, J. Phys. Chem. B, 1999, 103, 406.
38. T. Nakai, H. Fujimori, D. Kuwahara and S. Miyajima, J. Phys. Chem. B, 1999, 103, 417.
39. G. Pelzl, S. Diele, S. Iele, S. Grande, A. Jaekli, C. H. Lischka, H. Kresse, H. Schmalfuss, I. Wirth and W. Weissflog, Liq. Cryst., 1999, 26, 401.
40. L. E. Alexander, X-ray Diffraction Methods in Polymer Science, John Wiley & Sons, Inc., New York, 1969.
41. S. Kang, S. Nakajima, Y. Arakawa, M. Tokita, J. Watanabe and G. Konishi, Polym. Chem., 2014, 5, 2253.
42. P. D. Murphy, T. Taki and B. C. Gerstein, J. Magn. Reson., 1982, 49, 99.
43. M. H. Sherwood, J. C. Facelli, D. W. Alderman and D. M. Grant, J. Am. Chem. Soc., 1991, 113, 750.
44. T. Imase, S. Kawauchi and J. Watanabe, J. Mol. Struct., 2001, 560, 275.
45. V. Domenici, L. A. Madsen, E.-J. Choi, E. T. Samulski and C. A. Veracini, Chem. Phys. Lett., 2005, 402, 318.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4tc01687d

---