Role of vacancies to p-type semiconducting properties of SiGe nanowires

Abstract

Many experiments have shown that both composition-randomly-distributed Si_1−xGe_x nanowires (NW) and the Ge/Si core/shell NW possess excellent p-type semiconducting properties without relying on any doping strategy. Vacancies in both NW are believed to play a key role in the p-type semiconducting properties. To gain deeper insights into the role of vacancies, we performed first-principle calculations to systematically study the effects of single Si or Ge vacancies in four distinct SiGe NW, namely, randomly-distributed triangular-prism (RTP) NW, fused triangular-prism (FTP) NW, the Ge_coreSi_shell NW and Si_coreGe_shell NW. We find that the tendency for vacancy formation depends strongly on the structures of the NW. The defective RTP, FTP and Ge_coreSi_shell NW show promising p-type semiconducting properties while the defective Si_coreGe_shell NW does not. The Si vacancies in the inner region are attributed to the p-type properties of the RTP NW, and both the Si and Ge vacancies at the core/shell interfaces are attributed to the p-type properties of the FTP and the Ge_coreSi_shell NW. Our results show how the vacancies affect the electronic structures and the semiconducting properties of different SiGe NW, and offer an explanation of why the synthesized Si_1−xGe_x and Ge_coreSi_shell NW possess excellent p-type semiconducting properties without relying on any doping strategy.

---

Introduction

Semiconductor nanowires (NW) are one of the most important one-dimensional (1-D) nanostructures because of their unique properties¹ and good potentials for applications in many fields such as field-effect transistors (FET),^2,3 solar cells,⁴ integrated circuits,⁵ and biological or chemical sensors.^6–11 Among the 1-D nanostructures, Si NW are regarded as the most promising one for nanoelectronic devices because of the existing and mature Si-based semiconductor technology. However, previous experimental and theoretical studies have found that the semiconducting performance of Si NW is not as good as bulk Si because it is more difficult to realize efficient electron- or hole-doping in Si NW than in the bulk Si, implying that Si NW may not be the best candidate nanostructures for nanoelectronic devices. Among others, one reason for the relatively low semiconducting performance of doped Si NW is that ionization of the dopants in the Si NW is usually much harder than that in Si bulk because of the quantum confinement in the Si NW. To date, reducing the ionization energies of dopants in Si NW is still an active area of research.

Furthermore, the search for other types of semiconductor nanostructures to use as alternatives to the Si NW has also been an active area of research in recent years. SiGe NW have aroused extensive attention because of their novel electronic properties.^12–25 In fact, composition-randomly-distributed SiGe NW (referred to as Si_1−xGe_x) have been successfully fabricated in the laboratory.^16–21 Importantly, the band gaps of Si_1−xGe_x NW can be modulated over a wide range by tuning the composition of x and the area of the NW cross-sections. Furthermore, Si_1−xGe_x NW possess p-type semiconducting properties without relying on any doping strategy, possibly because of the oxidation at the Si/Ge interfaces as explained in the literature. The Ge_coreSi_shell NW have attracted even more attention because of their high-density free hole gas revealed in the experiments (without implementation of any doping strategy), as well as recently established high-performance FET based on Ge_coreSi_shell NW.^22–25

Inspired by these previous experimental findings on the SiGe core/shell NW, much of the recent research efforts have been devoted to the origin of the high-density free hole gas in the Ge_coreSi_shell NW, and how to realize efficient electron and hole doping in the NW. The band offset at the radial heterojunction between the Ge core and the Si shell, the Si dangling bonds at the surface, as well as metal impurities (transition metal particles are usually used as catalyst for the growth of SiGe NW) were thought to be possible sources for contributing to the high-density hole gas in the Ge_coreSi_shell NW.^26–28 Amato et al. studied structure stabilities, electronic properties, and quantum confinement effects of the different types of SiGe NW based on first-principle calculations.^29–33 They predicted that the Ge_coreSi_shell NW are very stable energetically, and that efficient electron and hole doping can be easily realized because of the band offset in the type-II heterojunction of the Ge_coreSi_shell NW.^34,35 Following Amato's work, we have systematically studied substitution doping in various compositionally abrupt Si/Ge NW using the first-principle method because of the presence of type-II band offsets in other types of compositionally abrupt Si/Ge NW in addition to the Ge_coreSi_shell NW.³⁶ In our previous study, the core/shell Ge_core/Si_shell and Si_core/Ge_shell NW, as well as the fused triangular-prism SiGe NW with much larger diameters, were considered. The effects of dopants Al, B, N, O or P, were explored. Based on the first-principle calculations, substitution of Ge by the pentavalent P at the interfacial region of Ge/Si NW results in an easy injection of high-density free-electron-like carriers, whereas substitution of Si by trivalent Al or B at the interfacial region results in an easy injection of high-density free-hole-like carriers. However, introduction of the pentavalent N has little effect on the conductivity of the three types of SiGe NW. For the divalent O dopant, only substitution of Si by O in the fused triangular-prism SiGe NW can result in high-density free-hole-like carriers at low temperatures. The efficient doping suggested from the calculation was later realized by experiments in Ge_core/Si_shell³⁷ and Ge/Si_xGe_1−x core/shell NW.³⁸

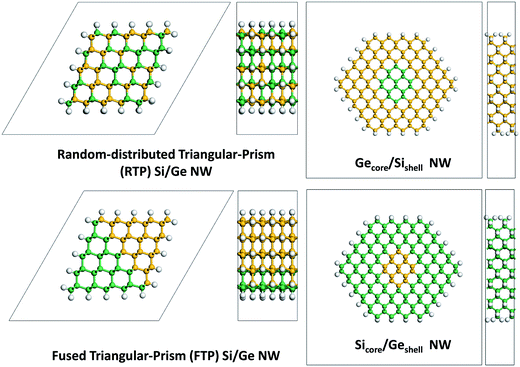
Note that in the fabricated Si_1−xGe_x NW and the Ge_core/Si_shell NW, the p-type semiconducting characteristics are achieved without relying on any doping strategy. Although the oxidation at the interfaces and Au impurities are thought to be possible reasons, vacancies at the interfaces may play an even more important role as vacancies are unavoidable in the growth of SiGe NW. However, few studies have been reported on how different types of vacancies in different types of SiGe NW can influence the electronic properties of SiGe NW. To this end, we have studied the effects of vacancies on the electronic properties of the following four types of SiGe NW: (1) randomly-distributed triangular-prism (RTP) NW, (2) the fused triangular-prism (FTP) NW, (3) the Ge_coreSi_shell NW, and (4) Si_coreGe_shell NW (see Fig. 1).

Fig. 1 Model structures of randomly distributed triangular-prism (RTP) Si/Ge NW, Ge_core/Si_shell NW, fused triangular-prism (FTP) Si/Ge NW, random-distributed, and Si_core/Ge_shell NW, respectively. Color code: Si (gold), Ge (green), H (white).

Computational details and models of SiGe nanowires

Our first-principle calculations were performed within the framework of density functional theory (DFT) as implemented in the Siesta 3.1 code.³⁹ We used a norm-conserving pseudopotential for the core electrons and expanded the one-electron wavefunction of the valence electrons with a double-zeta basis set plus polarization functions. The Perdew–Burke–Ernzerhof (PBE)⁴⁰ exchange-correlation functional within the generalized gradient approximation (GGA) was employed. A real-space grid with an equivalent cutoff of 180 Ry was adopted to expand the electron density for numerical integration. The periodic boundary condition was applied in all spatial directions, with the vacuum region among NW >15 Å, to neglect the interaction among the periodic images. For the randomly distributed and FTP NW, three unit cells along the axial direction (lattice constants c are about 12.0 Å) were included in the supercell, which ensures that the interaction among the periodic images of the impurity could be neglected.⁴¹ For the core/shell NW, supercells containing two unit cells along the axial direction (c ∼ 8.0 Å with which the interaction between periodic images is weak) are selected to reduce computational cost. For structural relaxation, 1 × 1 × 8 and 1 × 1 × 6 meshes within the Monkhorst–Pack special k-point scheme⁴² in the Brillioun zone were considered for the core/shell and triangular-prism NW, respectively. Denser k grids of 1 × 1 × 16 and 1 × 1 × 12 were used for the core/shell and triangular-prism NW, respectively, in the calculation of electronic structures. Both mesh cutoff and the k points were tested carefully to make sure no significant changes in the total energy when their values are increased.

All the SiGe NW are oriented along the 〈110〉 direction (see Fig. 1), i.e., the most common growth orientation for Si and Ge NW.⁴³ The diameter of the core/shell and lateral length scale of the triangular-prism SiGe NW are about 30 Å and 15 Å, respectively. For the core/shell NW, the diameter of the core is about 10 Å. In the triangular-prism NW, all the side surfaces are the {111} crystal planes which ensure high stability of the NW structures. For the core/shell NW, a hexagon-like interface is selected to lower the computational cost. The dangling bonds on the surface are saturated with hydrogen atoms for all the NW, which is an effective way to remove surface states within the band gap of the materials. The lattice constant along the growth orientation and the atomic positions of all the NW are fully relaxed without symmetry constraints, using the conjugate-gradient algorithm. The geometric optimization is completed when the maximum component of the stress tensors and the maximum force on each atom are less than 0.5 GPa and 0.02 eV Å⁻¹, respectively.

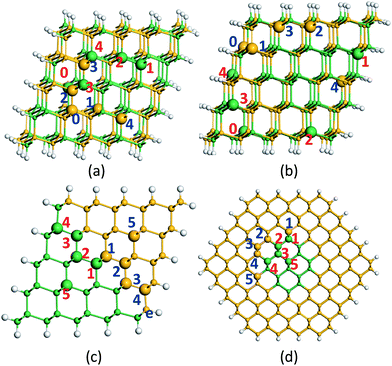
Single atomic vacancies of Si and Ge at different sites in the Ge_core/Si_shell, Si_core/Ge_shell, FTP and RTP Si/Ge NW are considered. Positions of the vacancies are as shown in Fig. 2. For the segregated Si/Ge NW, i.e., Ge_core/Si_shell, Si_core/Ge_shell, and FTP Si/Ge NW, the vacancies near the interface between the Si and Ge parts are mainly considered, while for the RTP Si/Ge NW, the Si (Ge) vacancies with different coordination surroundings are considered, e.g., the vacancies of Si which are coordinated with four Ge atoms, three Ge and one Si, two Ge and two Si, one Ge and three Si, or four Si. For the Ge_core/Si_shell and Si_core/Ge_shell NW, five different Si (Ge) vacancies, denoted as V_Si1 to V_Si5 (V_Ge1 to V_Ge5), are studied. For the FTP Si/Ge NW, five Si (Ge) vacancies from the center to the surface of the NW, denoted as V_Si1 to V_Si5 (V_Ge1 to V_Ge5), are investigated. The notations of the vacancies are different for the RTP Si/Ge NW, where V_Si0, V_Si1, …, V_Si4 represents the Si vacancies coordinated with zero, one, …, or four Ge atoms, while V_Ge0, V_Ge1, …, V_Ge4 represents Ge vacancies coordinated with zero, one, …, or four Si atoms. According to our notation scheme, V_Ge0 and V_Si4 in the RTP NW have the same surrounding conditions, i.e., both are surrounded by four Ge atoms. The same conditions are true for V_Ge1 and V_Si3, V_Ge2 and V_Si2, V_Ge3 and V_Si1, V_Ge4 and V_Si0.

Fig. 2 Positions of the vacancies in (a) within the RTP Si/Ge NW (b) surface of the RTP Si/Ge NW (c) the FTP Si/Ge NW, and (d) the Ge_core/Si_shell NW. Positions of the vacancies of Ge are marked with red numbers, while those of Si are marked with blue numbers. Distribution of the vacancies in the Si_core/Ge_shell NW is similar to that in the Ge_core/Si_shell NW.

Results and discussion

1. Relative stabilities of Ge and Si vacancies at different sites

First, we evaluated the relative possibilities of Ge and Si vacancy formation at different sites in the Si/Ge NW by calculating the formation energies of vacancies based on the following formula:

E_f = E_tot − E_perfect + μ_Si (or μ_Ge)

where: E_f is the energy of formation, E_tot is the total energy of a Si/Ge NW containing one Si or Ge vacancy per supercell, E_perfect is the total energy of the perfect Si/Ge NW, and μ_Si, μ_Ge are the chemical potentials of Si and Ge, respectively. The calculated formation energies of Si and Ge vacancies at various sites considered in different Si/Ge NW are listed in Table 1.

Table 1 The formation energies of a single vacancy in different Si/Ge NWs. Lowest Si and Ge formation energies are highlighted in bold

Vacancy site	Formation energy (eV)
Body of RTP NW	VGe0	VGe1	VGe2	VGe3	VGe4	VSi0	VSi1	VSi2	VSi3	VSi4
	2.524	2.792	2.834	3.313	2.971	3.029	2.497	2.773	2.584	2.355
Surface of RTP NW	VGe0	VGe1	VGe2	VGe3	VGe4	VSi0	VSi1	VSi2	VSi3	VSi4
	1.965	2.158	2.439	2.484	2.951	2.555	2.592	2.691	2.180	2.451
FTP NW	VGe1	VGe2	VGe3	VGe4	VGe5	VSi1	VSi2	VSi3	VSi4	VSi5
	3.137	2.205	2.206	1.814	2.594	3.061	3.385	2.580	2.169	3.784
Gecore/Sishell	VGe1	VGe2	VGe3	VGe4	VGe5	VSi1	VSi2	VSi3	VSi4	VSi5
	2.482	2.089	1.899	2.100	1.726	2.372	1.919	1.948	0.532	3.051
Sicore/Geshell	VGe1	VGe2	VGe3	VGe4	VGe5	VSi1	VSi2	VSi3	VSi4	VSi5
	2.467	2.605	2.483	2.588	2.593	2.412	2.440	2.728	3.238	2.754

---

For all the Si/Ge NW considered, the formation energies of Si or Ge vacancies are all positive (or endothermic). Thus, the higher the formation energy is, the harder it is for it to form. The formation energies exhibit different trends for different types of NW. For the RTP NW, the formation energies of Si vacancies tend to be a bit lower than those of Ge vacancies under the same surrounding conditions within the body of the NW, namely, V_Si1vs. V_Ge3, V_Si2vs. V_Ge2, V_Si3vs. V_Ge1, V_Si4vs. V_Ge0, except for V_Si0vs. V_Ge4. However, the trend is reversed when the vacancies are on the surface. It is surprising that the formation of the Si vacancy costs less energy than that of Ge under the same surrounding conditions in the body of the RTF NW, even though the bonding strength of Si is usually stronger than that of Ge. A possible reason is that local structural relaxation around the Si vacancy is more substantial and thereby results in more energy gain than that around the Ge vacancy when both are in the body. On the other hand, on the surface, local structural relaxation around either the Si or Ge vacancy is comparable in energy gain, so the effect of the bond strength because of losing an atom is more substantial. Obviously, the formation energies of Ge vacancies have an upward trend with increasing number of surrounding Si atoms, while the trend of the formation energies of Si vacancies is downward with increasing number of surrounding Ge atoms. These trend changes are entirely due to the stronger bonding of Si over Ge. The formation of vacancies on the surfaces is usually easier than that in the body because of higher freedom for the surrounding atoms of the vacancies on the surface than in the body.

For the FTP NW, the formation energies of Si vacancies tend to be a bit higher than those of Ge vacancies at similar sites, again because of the stronger bonding of Si over Ge. When the vacancies are located on the surface, the formation energies tend to decrease. As shown in Table 1, the formation energies of Ge and Si vacancies in the FTP NW are slightly lower than those at similar places (see Fig. 2) in the RTP NW. So, vacancies are easier to generate near the flat interface.

For the core/shell NW, it seems more difficult to generate a vacancy in the core than in the shell, as shown in Table 1, contrary to the trend for the substituted dopants for which the substitution in the core is slightly preferred over the shell.³⁶ Among the four types of Si/Ge NW, formation of vacancies in the Ge_core/Si_shell NW seems the easiest. The lowest formation energies of Ge and Si vacancies near the interface of the Ge_core/Si_shell NW are 1.726 and 0.532 eV, respectively (see Table 1). It should be noted that the Ge_core/Si_shell NW is also the most stable type of Si/Ge NW according to previous calculations.^31–33 Thus, it is expected that in the realistic Ge_core/Si_shell NW more vacancies would be formed at the core/shell interfaces. This is possibly the main reason for the high-density of the hole gas detected in the Ge_core/Si_shell NW.^22–25

2. Electronic structures

(a) Vacancies in the RTP Si/Ge NW. First, we consider the vacancies in the body of the RTP Si/Ge NW. Although the surroundings of the vacancies are different, the computed electronic structures are quite similar. We selected two Ge vacancies and two Si vacancies for discussion. Computed band structures along with those of the perfect RTP Si/Ge NW, are shown in Fig. 3. The band structures for other vacancy systems are shown in the ESI Fig. S1.† For the V_Ge0-body system, two flat bands (B2 and B3) originating from the vacancies are located within the band gap. The two flat bands cannot lead to carrier conduction, as indicated by the wavefunction iso-surface (see Fig. 3 (b)). The wavefunctions corresponding to B2 and B3 bands are apparently localized at the vacancy area, and they do not extend to the whole supercell along the axial direction. Besides the two non-conducting bands (B2 and B3), there is a conducting band below the Fermi level, originating mainly from the states of the defect (B1 band). It lies above the top of the valence bands and tilts downwards. So it can lead to hole conduction. From the band structures, we know that the V_Ge0-body in the RTP Si/Ge NW acts as both defective center and acceptor. The roles of V_Ge1-body, V_Ge2-body and V_Ge3-body are similar to V_Ge0-body, and their corresponding band structures (see ESI Fig. S1†) are close to those of the V_Ge0-body system too. For the V_Ge4-body system, the band structures are much different from those of the V_Ge0-body to V_Ge3-body systems. The three defect bands all exhibit curvatures. B1 tilts downwards similar to that of the V_Ge0-body, while B2 and B3 tilt upward. So, B1 is a valence band whereas B2 and B3 are conduction bands. Compared to the band structures of the V_Ge0-body system, the bands B2 and B3 of the V_Ge4-body system depart from one another so that B2 moves below the top of the B1 band and crosses it. Because of the repulsion between the B1 and B2 bands, a very small gap opens at the crossing point of the B1 and B2 bands. The Fermi level is just located in this small gap. Thus, holes can be easily generated. It is expected that in this case high-density hole gas may exist at finite temperatures.

Fig. 3 (a) Computed band structures of the RTP Si/Ge NW with a Ge and Si single vacancy in the body. Wavefunction iso-surface of the defect bands near the Fermi level for (b) the V_Ge0-body, and (c) the V_Ge4-body. The iso-surface value is 0.05. In (a), Down and Up refer to the spin-up and spin-down channel, respectively. In (b) and (c), the left panel in each pair of panels is axial view while the right panel is side view of the NW.

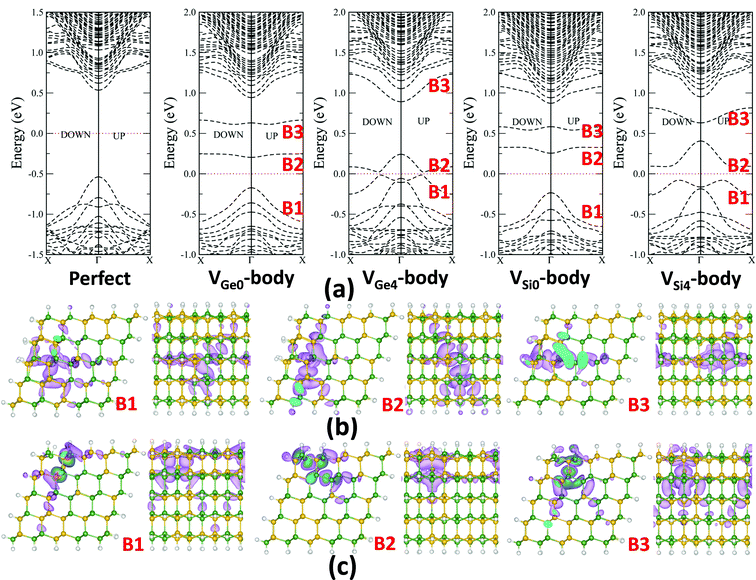
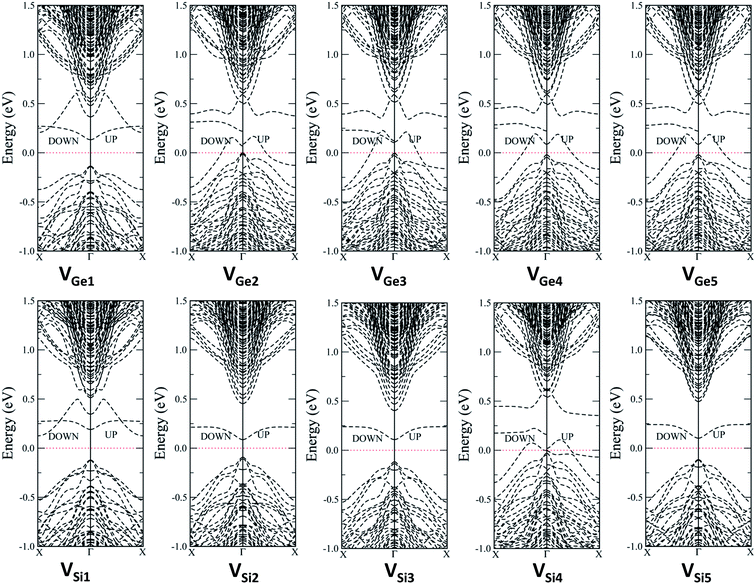
For the Si vacancy, the band structures of the V_Si0-body system are very similar to those of the V_Ge0-body system. Near the energy gap, there are two localized bands (B2, B3) and one delocalized band (B1) originated from the Si vacancy. The band structures of the V_Si4-body system are similar to those of the V_Ge4-body system. An obvious difference between the band structures of the V_Si4-body and the V_Ge4-body is that the gap between B1 and B2 for the V_Si4-body system is a bit larger than that of the V_Ge4-body system. So, generation of carriers would be a bit harder with the Si vacancies. The band structures of the V_Si1-body to the V_Si3-body systems are all similar to those of the V_Si4-body system (see ESI Fig. S1†).

Interestingly, the band structures of V_Ge0 and V_Si4, and those of V_Ge4 and V_Si0 are quite different while the vacancy surroundings in these systems are the same (four Ge atoms for V_Ge0 and V_Si4, four Si atoms for V_Si0 and V_Ge4, respectively). The local structure relaxation at the vacancy sites may be the main reason for this difference. So the electronic properties of the compositionally-random-distribution SiGe NW can be hard to predict. Relative formation abilities of different vacancies may give some guidance about their electronic properties. Referring to Table 1, because the formation energy of the V_Ge0-body is the lowest while that of the V_Ge4-body is the highest, there is a greater possibility that V_Ge0-body vacancies will be generated. Moreover, for the Si vacancies, the generation of V_Si4-body vacancies has the greatest possibility while that of the V_Si0-body vacancies is hardest. So, in the RTF NW, if the vacancies are mainly Ge vacancies, the NW should be insulating, while if the vacancies are mainly Si vacancies, the NW would be semiconducting. Generation of the V_Si4-body vacancies is slightly easier than the V_Ge0-body vacancies, so that the defective RTF NW is more likely to be semiconducting if the vacancies are located in the body of the NW.

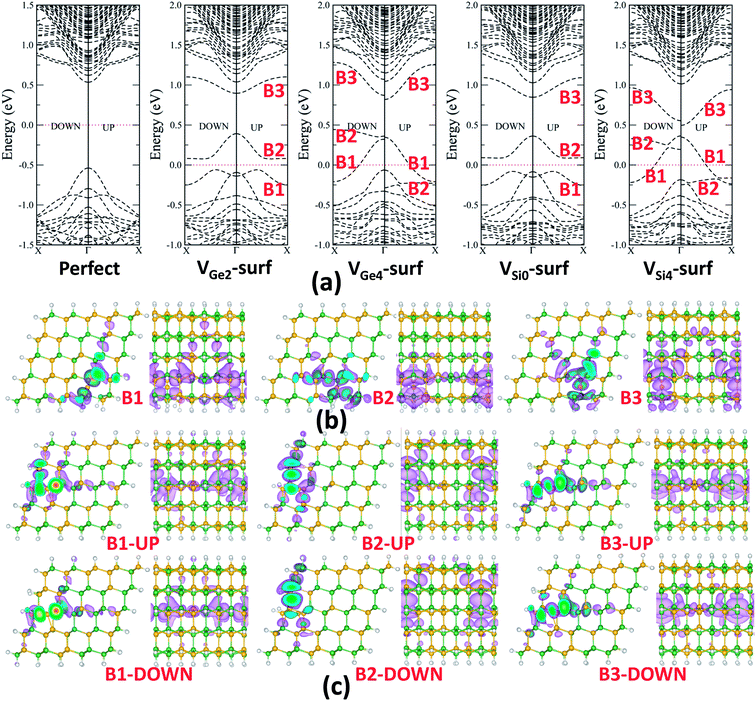
Next, we studied how the vacancies on the surfaces of the RTP NW influence their electronic structures. The band structures of V_Ge2-surf and V_Ge4-surf systems, as well as V_Si0-surf and V_Si4-surf systems, are shown in Fig. 4. The band structures of other systems are shown in ESI Fig. S2.† From the band structures, one can see that V_Ge0-surf, V_Ge1-surf, V_Ge3-surf and V_Si3-surf systems cannot conduct current at low temperatures because the defective bands are strongly localized as in the V_Ge0-body system. The band structures of V_Ge2-surf, V_Si0-surf, V_Si1-surf and V_Si2-surf systems are similar to each other and to the band structure of V_Ge4-body system. The B1 and B2 bands cross one another and also repel each other, resulting in a small band gap (about 0.2 eV in this case). The Fermi level is just located within the small band gap, implying that holes can be generated at finite temperatures. In summary, all these vacancy systems show p-type semiconducting properties.

Fig. 4 (a) Computed band structures of the RTP Si/Ge NW with a Ge and Si single vacancy on the surface. Wavefunction iso-surface of the defect bands near the Fermi level for (b) the V_Ge2-surf, and (c) the V_Ge4-surf systems. The iso-surface value is 0.05. In (a), Down and Up refer to the spin-up and spin-down channel, respectively. In (b) and (c), the left panel in each pair of panels is axial view while the right panel is side view of the NW.

A very different and interesting behavior was also noticed in the band structures of the V_Ge4-surf and V_Si4-surf systems. As shown in Fig. 4, the Fermi level crosses the B1 band for both systems. Because the B1 band suggests that there will be good conductivity because of the extensively delocalized distribution of the wavefunctions along the axial direction, V_Ge4-surf and V_Si4-surf NW are predicted to be conductors. Moreover, the spin polarized B2 band splits and the spin-down band moves up relatively. In contrast to the V_Ge2-surf and V_Si0-surf systems, there is no gap opening between bands B1 and B2 for the V_Ge4-surf and V_Si4-surf systems. The reason for the spin splitting may be the strong repulsion between the conduction band B1 and the non-conduction band B2. Interestingly, the spin splitting only occurs in the V_Ge4-surf and V_Si4-surf systems, in which the vacancy sites are surrounded by four Si atoms or four Ge atoms, and this only occurs for the highly localized B2 bands.

Note also that the formation energies of V_Ge0-surf and V_Ge1-surf vacancies are obviously lower than those of other Ge vacancies, and the formation energy of V_Si3-surf is obviously lower than those of other Si vacancies. For V_Ge0-surf, V_Ge1-surf, and V_Si3-surf systems, computed band structures show that they are all insulators. Thus, the vacancies on the surface of a RTF NW are of no help to the conductivity of the NW.

Seong et al. reported that the synthesized Si_xGe_1−x NW exhibit a p-type feature and they attributed this feature to the oxidation of Ge at the interfaces between Si_xGe_1−x and SiO_x oxidation surfaces.²¹ According to our calculations, the point vacancy defect may be another reason for their p-type semiconducting properties. The contribution of the vacancies to the p-type semiconducting properties was not considered in ref. 21 because the density of vacancies is much lower compared to that which is seen in oxidation. For an oxidation-free Si_xGe_1−x NW, the vacancies can lead to p-type semiconducting properties.

(b) Vacancies in the fused-triangular-prism (FTP) Si/Ge NW. For the FTP Si/Ge NW, there is an abrupt interface between the Si and Ge sections. We consider four different Si vacancies (V_Si1 to V_Si4) and four Ge vacancies (V_Ge1 to V_Ge4) at the interface, respectively. For comparison, the Si vacancy and the Ge vacancy at the center of the Si portion and the Ge portion (V_Si5 and V_Ge5) are also considered. Computed band structures of all systems as well as those of the perfect FTP Si/Ge NW are shown in Fig. 5. The computed band structures of the V_Ge3 system are very similar to those of the V_Ge2 system.

Fig. 5 Computed band structures of the FTP Si/Ge NW with a Ge and a Si single vacancy at various sites.

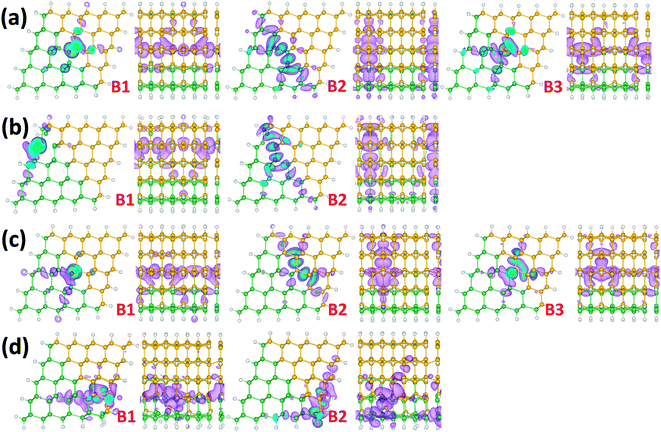
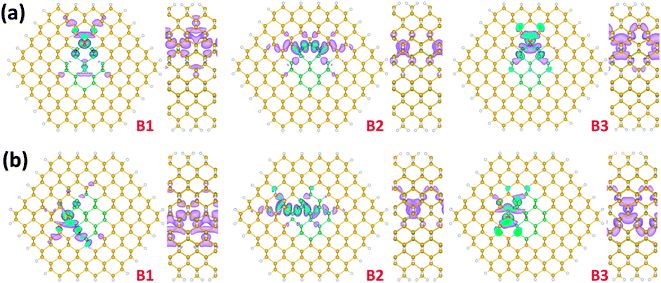
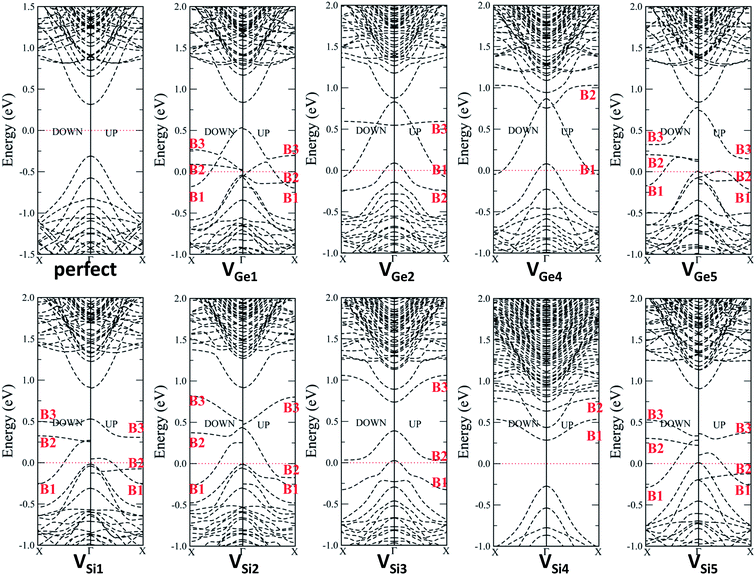
As seen in Fig. 5, in most systems, the vacancies in the FTP Si/Ge NW introduce three defect bands within the band gap of the perfect FTP/SiGe NW. The electronic properties of each defect band can be understood from their wavefunction distributions. In Fig. 6, the wavefunction iso-surfaces corresponding to the defect bands of V_Ge1, V_Ge4, V_Si1 and V_Si4 systems are shown. Apparently, in all systems, B1 bands correspond to the conducting bands as the band lines disperse over extensive energy ranges and the associated wave functions are delocalized along the axial direction. Furthermore, for most systems the B1 band should lead to hole conduction because their band lines tilt downwards from the center of the first Brillouin zone to the surface (Γ to X), except for those of the V_Si4 system. The B2 bands for all systems are normally very flat and localized. As shown in Fig. 6, the wavefunctions of the B2 band are distributed dispersedly along the interface, but are localized along the axial direction. So, the B2 bands for all systems cannot lead to carrier conduction. The wavefunctions of the B3 bands are also mainly localized around the vacancy sites, and exhibit little delocalization along the axial direction in some systems. So, the B3 bands may give minor conduction of holes or electrons.

Fig. 6 Computed wavefunction iso-surface corresponding to the defect bands for the (a)V_Ge1, (b) V_Ge4, (c) V_Si1 and (d) V_Si4 vacancy in the FTP Si/Ge NW. The iso-surface value is 0.05. The left panel in each pair of panels is axial view while the right panel is side view of the NW.

In addition, spin splitting is seen for the V_Ge1, V_Ge5, V_Si1, V_Si2 and V_Si5 systems but not others. Again, the spin splitting mainly occurs in the highly delocalized B2 bands. For some systems, the B3 bands exhibit spin splitting too. The Fermi levels for these five systems all cross the corresponding conduction B1 bands. For the V_Ge2, V_Ge3 and V_Ge4 systems, Fig. 5 clearly shows that the Fermi levels cross both the top valence band and the B1 defect band, resulting in carrier conduction. The B2 and B3 bands for the V_Ge4 system are very high compared to those for other Ge vacancy systems. The B3 band (not marked in Fig. 5) even merges with the conduction bands for the V_Ge4 system. For the V_Si3 system, the maximum of the valence band and the minimum of the B2 band are almost the same. The Fermi level is just located above the maximum of the valence band. So, the V_Si3 system may also have good conductivity.

Again, V_Si4 system is quite different. As shown in Fig. 5, the B1 band for the V_Si4 system is close to the conduction bands and tilts upwards, suggesting that there is good conductivity of the electrons but not the holes. Both B1 and B2 bands are located very high, far from the top valence band. A relatively big band gap (∼0.5 eV) is seen between the top valence band and the B1 band, and the Fermi level is located at the center of the gap. Contrary to other systems, the V_Si4 system is an insulator at low temperatures. As shown in Fig. 6(d), the wavefunctions of the B2 band for the V_Si4 system are mainly contributed by the vacancy states and the surface states, but not the interface states.

In summary, with vacancies in the FTP Si/Ge NW, except in the V_Si4 system, all the systems are semiconducting. Because the formation of Ge vacancies is easier than that of Si vacancies in the FTP Si/Ge NW, the defective FTP Si/Ge NW is likely to have a high possibility of exhibiting p-type semiconducting properties.

(c) Vacancies in the Ge_core/Si_shell NW and Si_core/Ge_shell NW. The Ge_core/Si_shell NW are important because of their high hole conductivities as demonstrated experimentally. The vacancies, especially those at the interface areas, may be attributed to the high conductivities for the undoped Ge_core/Si_shell NW. Here, we consider various Si or Ge vacancies near the interfaces of the Ge_core/Si_shell NW. Computed band structures for the V_Ge1 to V_Ge5 and the V_Si1 to V_Si4 systems, as well as those of the perfect Ge_core/Si_shell NW, are shown in Fig. 7. The band structures of the V_Si5 system are almost the same as those of V_Si4 system although their stabilities are much different.

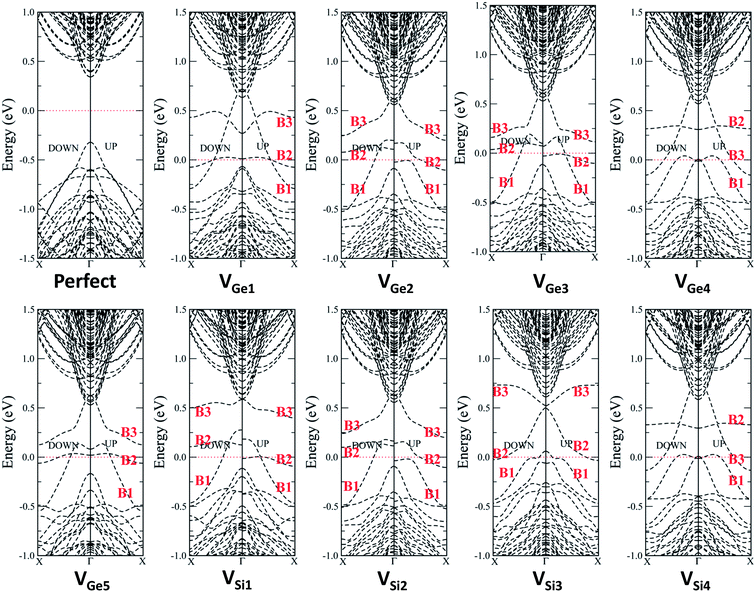Fig. 7 Computed band structures of the Ge_core/Si_shell NW with a Ge and Si single vacancy at various sites in the intersection area.

Compared to the band structures of the perfect Ge_core/Si_shell NW, one can easily see that the defects result in three bands in the gap region, called B1, B2, and B3 bands according to their wavefunction distributions (Fig. 8). The B1 band is highly delocalized. It disperses over the band gap for the Ge_core/Si_shell NW. So, it is a conducting band. Because it tilts downwards along the direction Γ → X, the conducting carriers should be holes. The B2 band is the flattest among the three defect bands. It is also localized and cannot lead to carrier conduction. The wavefunctions of the B2 band are localized along the axial direction and slightly delocalized along the radial direction. The wavefunction distribution of the B3 band is between those of the B1 and B2 bands. In some cases, it is quite flat while in other cases it is not. Normally, the B3 band tilts upwards firstly and then turns downwards, along the direction Γ → X in the Brillouin zone. Because of the high localization, in some systems, the spin polarized B2 and B3 bands are split.

Fig. 8 Computed wavefunction iso-surface of the defect bands for (a) V_Ge1, and (b) the V_Ge4 vacancy in the Ge_core/Si_shell NW. The iso-surface value is 0.05. The left panel in each pair of panels is axial view while the right panel is side view of the NW.

For all systems, the Fermi levels cross at least the B1 band. Because the B1 band suggests high conductivity for holes, all the systems should have good conductivities. In experiments, a high density of hole carriers are found in the core of the Ge_core/Si_shell NW.^22–25 Park et al.²⁸ studied the Si dangling bond on the surface and the Au impurity within the Si shell of the Ge_core/Si_shell NW to explain why a high density of holes is present in the Ge_core/Si_shell NW. However, the dangling bonds at the interfaces were not considered. Vacancies are expected to be formed more easily at the interfaces than in the inner part of core or shell during the growth, because of the mismatch of the lattice constants and the constraint stresses. The hole carriers generated due to the ionization of the vacancies at the interfaces are easier to transfer to the core region, compared to those generated on the surfaces. Therefore, the vacancies at the interfacial region of the Ge_core/Si_shell NW are more likely to give rise to a high-density hole gas as demonstrated experimentally.

For the Si_core/Ge_shell NW, the difference in stress at the interface region makes the band structures of Si_core/Ge_shell NW much different from those of the Ge_core/Si_shell NW (see Fig. 9). Apparently, with the Ge vacancies, most systems are still conducting, except for the V_Ge1 system which is not. However, with the Si vacancies, all the systems are not conducting because of the lack of band crossing through the Fermi level. By comparing the band structures of the Si_core/Ge_shell NW and the Ge_core/Si_shell NW, one can see that for the non-conducting systems, the B1 band is either shifted upwards, leaving a big gap from the Fermi level, or downwards into the valence bands. For the conducting systems, V_Ge2 to V_Ge5 and V_Si4, the formation energies of the vacancies are all much higher than those for the Ge_core/Si_shell NW. So vacancies in the Si_core/Ge_shell NW are not as important a contribution as those in the Ge_core/Si_shell NW to the conductivity.

Fig. 9 Computed band structures of the Si_core/Ge_shell NW with a Ge and Si single vacancy at various sites in the intersection area.

Conclusion

We have studied the effects of single vacancies on semiconducting properties of four different types of SiGe NW, i.e., RTP NW, the FTP NW, the Ge_coreSi_shell and the Si_coreGe_shell NW. Si and Ge vacancies at different sites are investigated. The calculated formation energies indicate that the formation tendency of single Si or Ge vacancies is strongly dependent on the structures of the NW. The formation of vacancies at the interface of the Ge_coreSi_shell NW entails least energy among all the NW considered. The computed band structures suggest that the defective RTP, FPT and Ge_coreSi_shell NW exhibit p-type semiconducting properties, whereas the semiconducting properties of the defective Si_coreGe_shell NW are much less apparent. For the RTP NW, the hole-carriers are likely originated from the Si vacancies located in the inner area, while in the FPT and Ge_coreSi_shell NW both the Si and Ge vacancies at the interfaces can generate high-density hole carriers. The hole injection in the Ge_coreSi_shell NW is likely to be the easiest among all the NW considered. Our theoretical results are consistent with experimental observations, thereby providing a compelling explanation on why the experimentally synthesized Si_1−xGe_x and Ge_coreSi_shell NW can exhibit remarkable p-type semiconducting properties without relying on any doping strategy.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant no. 11104056), the Natural Science Foundation of Anhui Province (Grant no. 11040606Q33). XCZ is supported by ARL (Grant no. W911NF1020099) and a grant from USTC for (1000 Talents Program) Qianren-B summer research.

References

1. D. D. D. Ma, C. C. Lee, F. C. K. Au, S. Y. Tong and S. T. Lee, Science, 2003, 299, 1874–1877.
2. Y. Cui and C. M. Lieber, Science, 2001, 291, 851–853.
3. J. Xiang, W. Lu, Y. J. Hu, Y. Wu, H. Yan and C. M. Lieber, Nature, 2006, 441, 489–493.
4. T. J. Kempa, B. Z. Tian, D. R. Kim, J. S. Hu, X. L. Zeng and C. M. Lieber, Nano Lett., 2008, 8, 3456–3460.
5. S. W. Nam, X. C. Jiang, Q. H. Xiong, D. Ham and C. M. Lieber, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21035–21038.
6. Y. Cui, Q. Q. Wei, H. K. Park and C. M. Lieber, Science, 2001, 293, 1289–1292.
7. P. Alivisatos, Nat. Biotechnol., 2004, 22, 47–52.
8. G. F. Zheng, F. Patolsky, Y. Cui, W. U. Wang and C. M. Lieber, Nat. Biotechnol., 2005, 23, 1294–1301.
9. J. Hahm and C. M. Lieber, Nano Lett., 2004, 4, 51–54.
10. F. Patolsky, G. F. Zheng, O. Hayden, M. Lakadamyali, X. W. Zhuang and C. M. Lieber, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14017–14022.
11. W. U. Wang, C. Chen, K.-H. Lin, Y. Fang and C. M. Lieber, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3208–3212.
12. M. Amato, M. Palummo, R. Rurali and S. Ossicini, Chem. Rev., 2014, 114, 1371–1412.
13. M. Amato, S. Ossicini and R. Rurali, Nano Lett., 2012, 12, 2717–2721.
14. L. Zhang, M. d'Avezac, J.-W. Luo and A. Zunger, Nano Lett., 2012, 12, 984–991.
15. T. Markussen, Nano Lett., 2012, 12, 4698–4704.
16. J. E. Yang, C. B. Jin, C. J. Kim and M. H. Jo, Nano Lett., 2006, 6, 2679–2684.
17. X. Zhang, K.-K. Lew, P. Nimmatoori, J. M. Redwing and E. C. Dickey, Nano Lett., 2007, 7, 3241–3245.
18. C. Qi, G. Goncher, R. Solanki and J. Jordan, Nanotechnology, 2007, 18, 075302.
19. U. Givan and F. Patolsky, Nano Lett., 2009, 9, 1775–1779.
20. T. Shimizu, Z. Zhang, S. Shingubara, S. Senz and U. Gösele, Nano Lett., 2009, 9, 1523–1526.
21. H. K. Seong, E. K. Jeon, M. H. Kim, H. Oh, J. O. Lee, J. J. Kim and H. J. Choi, Nano Lett., 2008, 8, 3656–3661.
22. J. Xiang, W. Lu, Y. J. Hu, Y. Wu, H. Yan and C. M. Lieber, Nature, 2006, 441, 489–493.
23. W. Lu, J. Xiang, B. P. Timko, Y. Wu and C. M. Lieber, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10046–10051.
24. S. X. Zhang, F. J. Lopez, J. K. Hyun and L. J. Lauhon, Nano Lett., 2010, 10, 4483–4487.
25. L. Y. Li, D. J. Smith, E. Dailey, P. Madras, J. Drucker and M. R. McCartney, Nano Lett., 2011, 11, 493–497.
26. L. Yang, R. N. Musin, X. Q. Wang and M. Y. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195325.
27. A. Nduwimana, R. N. Musin, A. M. Smith and X. Q. Wang, Nano Lett., 2008, 8, 3341–3344.
28. J. S. Park, B. Ryu, C. Y. Moon and K. J. Chang, Nano Lett., 2010, 10, 116–121.
29. M. Amato, M. Palummo and S. Ossicini, Mater. Sci. Eng., B, 2012, 177, 705–711.
30. M. Palummo, M. Amato and S. Ossicini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 073305.
31. M. Amato, M. Palummo and S. Ossicini, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235333.
32. M. Amato, M. Palummo and S. Ossicini, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 201302.
33. M. Amato, M. Palummo and S. Ossicini, Phys. Status Solidi B, 2010, 247, 2096–2101.
34. M. Amato, S. Ossicini and R. Rurali, Nano Lett., 2011, 11, 594–598.
35. M. Amato, M. Palummo and S. Ossicini, J. Comput. Electron., 2012, 11, 272–279.
36. P. Li, R. Zhou and X. C. Zeng, Nanoscale, 2013, 5, 3880–3888.
37. N. Fukata, M. Mitome, T. Sekiguchi, Y. Bando, M. Kirkham, J. Hong, Z. L. Wang and R. L. Snyder, ACS Nano, 2012, 6, 8877–8895.
38. D. C. Dillen, K. Kim, E.-S. Liu and E. Tutuc, Nat. Nanotechnol., 2014, 19, 116–120.
39. D. S. Portal, P. Ordejon, E. Artacho and J. M. Soler, Int. J. Quantum Chem., 1997, 65, 453–461.
40. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
41. E. Durgun, N. Akman, C. Ataca and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245323.
42. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
43. Y. Wu, Y. Cui, L. Huynh, C. J. Barrelet, D. C. Bell and C. M. Lieber, Nano Lett., 2004, 4, 433–436.

---

Footnote

† Electronic supplementary information (ESI) available: Computed band structures of the random-distributed triangular-prism (RTP) Si/Ge NW with Ge and Si single vacancy in the body and on the surface. See DOI: 10.1039/c4tc00958d

---