Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Local lattice distortions in oxygen deficient Mn-doped ZnO thin films, probed by electron paramagnetic resonance
Michael
Lorenz
*,
Rolf
Böttcher
,
Stefan
Friedländer
,
Andreas
Pöppl
,
Daniel
Spemann†
and
Marius
Grundmann
Institut für Experimentelle Physik II, Universität Leipzig, Linnéstr. 5, 04103 Leipzig, Germany. E-mail: mlorenz@physik.uni-leipzig.de
First published on 4th April 2014
Abstract
The structure and functional properties of metal oxide films for device applications are largely affected by oxygen vacancies. While the macroscopic relationship between functionality and oxygen supply during growth is easy to access, the local influence of changing oxygen content on the incorporated metal atoms has been rarely investigated. As a model system, we use Mn as a local probe in hetero- and homoepitaxial ZnO thin films for electron paramagnetic resonance (EPR). Mn is expected to be incorporated as Mn2+ in the Zn-lattice site of ZnO films grown in a wide range of oxygen partial pressures. The zero field splitting (ZFS) parameter D depends on the crystallographic c/a ratio of ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn lattice constants as it measures the trigonal distortion of oxygen tetrahedra at the Zn2+ site with respect to the Mn2+ site. The ZFS parameter D correlates linearly with displacement of Mn2+ ions along the c-axis in the MnO4 tetrahedra and the corresponding bond lengths between the Mn2+ ions and the axial oxygen ion.
Mn lattice constants as it measures the trigonal distortion of oxygen tetrahedra at the Zn2+ site with respect to the Mn2+ site. The ZFS parameter D correlates linearly with displacement of Mn2+ ions along the c-axis in the MnO4 tetrahedra and the corresponding bond lengths between the Mn2+ ions and the axial oxygen ion.
1. Introduction
Oxide materials, in particular oxide thin films, gain more and more attention from both basic and applied points of view, due to interesting phenomena such as strong electron correlations and transparent oxide electronics. The functional properties of metal oxide thin films may be controlled by tuning the preparation conditions. However, in the interplay of structure, morphology and the functional properties such as conductivity or the ferroic properties, often an oxygen deficient growth environment is chosen because of the requirements of a smooth surface and an interface.1 In pulsed laser deposition (PLD), one of the most flexible growth methods of oxide thin films,2 the oxygen partial pressure during growth controls the distribution of oxygen vacancies.3 Thus, oxygen vacancies are a common phenomenon in functional oxides, due to the often used oxygen deficient growth conditions. The effect of oxygen vacancies on structures and macroscopic functional properties is a highly interesting and current topic of interest, as the following examples show.In the high-Tc superconductor Y1Ba2Cu3O7-δ, under-doped surfaces with ordered oxygen vacancies result in an ortho-II band folding of the Fermi surface.4 Detailed point defect analysis using both computational modeling and PLD growth of SrTiO3 shows that precise growth control allows tuning of the concentration of anion and cation vacancies and tailoring the performance of doped perovskite films.5 Borisevich et al. report on the increasing consideration of “oxygen vacancies… to play a role in phenomena observed at transition-metal oxide interfaces”.6 There, cation displacements are observed at SrRuO3/La0.7Sr0.3MnO3 (LSMO) interfaces, indicating interface dipoles between the two metallic oxides. Magnetic exchange bias and coercive fields in LSMO/SrTiO3 were found to increase with decreasing oxygen growth pressure in PLD and sputtering, thus opening a route for tuning exchange bias by the oxygen vacancy concentrations.7 Detailed structural and X-ray photoelectron spectroscopy on LSMO revealed clear correlations of structural, electronic and transport properties with oxygen vacancy concentration from 0 to about 7%.8 Other recent experimental examples are the effect of oxygen vacancies on resistive switching in TiO2−x films9 and on the two-dimensional electron gas at the SrTiO3 surface.10 In addition, first principle and density functional theory investigations have been performed on native point defects in LaAlO3,11 on magnetic properties of Mg doped BiFeO3 with and without oxygen vacancies,12 and on energetics of intrinsic defects and their complexes in ZnO.13 Lany and Zunger calculated the donor level energy of the oxygen vacancy in ZnO to be at or below the midgap, using GW approximation calculations.14
The above examples show that the macroscopic correlation between functionality and oxygen supply during growth seems to evoke a lot of interesting phenomena. However, much less is known about the local atomic structure of the functional oxides on the availability of oxygen. To contribute to this question, we use as a model system, Mn2+ ions as paramagnetic probes in heteroepitaxial ZnO. The ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn thin films are grown by PLD on a-plane sapphire substrates in a wide range of oxygen partial pressures. Electron paramagnetic resonance (EPR) spectroscopy of the Mn2+ ions allows monitoring the influence of the oxygen growth pressure on the structural properties of the films on a local scale by precise measurements of the zero field splitting (ZFS) of the divalent manganese ions. The Mn2+ ZFS parameters are then correlated with (volume-averaged) in-plane and out-of-plane lattice constants a and c of the thin films, respectively, as obtained by high-resolution X-ray diffraction (HR-XRD).
Mn thin films are grown by PLD on a-plane sapphire substrates in a wide range of oxygen partial pressures. Electron paramagnetic resonance (EPR) spectroscopy of the Mn2+ ions allows monitoring the influence of the oxygen growth pressure on the structural properties of the films on a local scale by precise measurements of the zero field splitting (ZFS) of the divalent manganese ions. The Mn2+ ZFS parameters are then correlated with (volume-averaged) in-plane and out-of-plane lattice constants a and c of the thin films, respectively, as obtained by high-resolution X-ray diffraction (HR-XRD).
2. Electron paramagnetic resonance of Mn2+ in ZnO thin films
The incorporation site and the electronic state of paramagnetic transition metal ions in ZnO bulk materials have extensively been studied by EPR spectroscopy.15,16 Divalent ions such as Mn2+ are incorporated in the trigonally distorted tetrahedral Zn lattice sites (C3v symmetry). Therefore, the Mn2+ EPR spectrum in ZnO displays a characteristic ZFS with an axial ZFS parameter D = −707 MHz as observed for weakly Mn-doped ZnO single crystals.17,18 The D parameter is considered as a measure of the trigonal distortion of the oxygen tetrahedra by the Mn2+ ions substituting Zn2+ at the metal ion sites in the ZnO wurtzite structure. Indeed, a linear correlation D ∝ εV between D and the volume compression ratio of the unit cell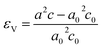 | (1) |
Therefore, in the present work we choose only low manganese concentrations of either 0.2 or 0.02 at% to avoid dipolar line broadening and to access the full spectral information of the Mn2+ EPR spectra. Moreover, the low doping levels prevent a significant increase in the c-axis lattice parameter of the films that might already be caused by the direct Mn2+ incorporation in the Zn sites of ZnO films.19,20 In that way, we are now able to measure precisely both c-plane and a-plane lattice parameters of the ZnO thin films and the Mn2+ ZFS parameters and their distribution widths that are dependent on the oxygen partial pressure during their PLD growth process without the interference of other crucial parameters. The ZFS parameters are correlated with the c- and a-lattice constants of the films and the displacement of the Mn2+ in the oxygen tetrahedra along the c-axis using the superposition model.
3. Results
3.1. Structural characterization
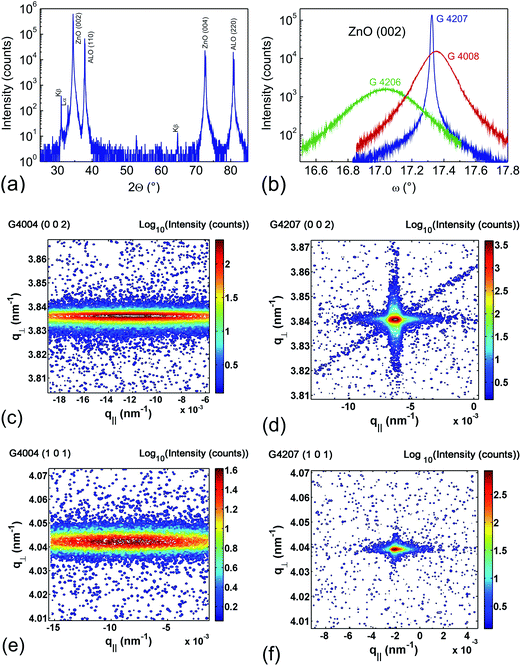
Fig. 1 shows typical results of the structural investigations by XRD and HR-XRD. All ZnO films grow with perfect c-axis orientation on a-plane sapphire (Fig. 1a) and c-plane ZnO, in agreement with previous investigations.21 The HR-XRD rocking curves and reciprocal space maps (RSMs) show remarkable differences for hetero- and homoepitaxial samples, for numerical values of the FWHM of the ZnO(002) rocking curves see Table 1. Fig. 1b shows three typical ZnO(002) rocking curves with FWHM from 0.0129° to 0.320°, indicating huge differences in tilt mosaicity of the sample types. The different structural quality of hetero- and homoepitaxial ZnO is further explained by the RSMs in Fig. 1c–f. Here, in addition to the tilt mosaicity expressed by the horizontal broadening of (002) reflections, the broadening of skew-symmetric (101) reciprocal lattice points demonstrates the twist mosaicity, because these peaks are measured with a high chi-tilt angle of 61.61° in HR-XRD. In contradiction to the clearly higher tilt and twist mosaicity of the heteroepitaxial films, the uncertainty of d-spacing as expressed by the vertical broadening of the reciprocal lattice points, is much lower. The extrapolated out-of plane and in-plane lattice constants of all samples are listed in Table 1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn thin films on a-plane sapphire. Sample G4207 was homoepitaxially grown on c-plane ZnO (O-face)
Mn thin films on a-plane sapphire. Sample G4207 was homoepitaxially grown on c-plane ZnO (O-face)
| Sample | p O2 (mbar) | c MnO (%) | c (Å) | a (Å) | FWHM (°) | D (MHz) | ΔD (MHz) | ΔE (MHz) |
|---|---|---|---|---|---|---|---|---|
| a For Mn2+ in the ZnO single crystalline substrate, which, however, also contains Fe, Co, Ni. Assuming a homogeneous Fe distribution in the film and the substrate, cFe(III) is 2.3 × 1015 ions per sample. | ||||||||
| G4438 | 6 × 10−5 | 2 × 10−2 | 5.2305 | 3.242 | 0.452 | — | — | — |
| G4437 | 3 × 10−4 | 2 × 10−2 | 5.2267 | 3.246 | 0.357 | −584 | 140 | 40 |
| G4009 | 2 × 10−3 | 2 × 10−2 | 5.2233 | 3.249 | 0.195 | −611 | 110 | 40 |
| G4005 | 2 × 10−3 | 2 × 10−1 | 5.228 | 3.245 | 0.225 | −611 | 100 | 40 |
| G4592 | 5 × 10−3 | 2 × 10−2 | 5.2263 | 3.246 | 0.160 | −606 | 95 | 20 |
| G4207a ZnO substrate | 1.6 × 10−2 | 2 × 10−2 | 5.2063 | 3.2497 | 0.0129 | −707 | 10 | 0 |
| G4008 | 1.6 × 10−2 | 2 × 10−2 | 5.2131 | 3.247 | 0.148 | −650 | 35 | 15 |
| G4004 | 1.6 × 10−2 | 2 × 10−1 | 5.2130 | 3.246 | 0.130 | −653 | 40 | 20 |
| G4591 | 5 × 10−2 | 2 × 10−2 | 5.2085 | 3.249 | 0.134 | −674 | 35 | 15 |
| G4436 | 8 × 10−2 | 2 × 10−2 | 5.2065 | 3.249 | 0.568 | −703 | 180 | 40 |
| G4206 | 1.6 × 10−1 | 2 × 10−2 | 5.2061 | 3.250 | 0.320 | −707 | 120 | 40 |
| G4590 | 5 × 10−1 | 2 × 10−2 | 5.2084 | 3.2475 | 0.194 | −671 | 90 | 20 |
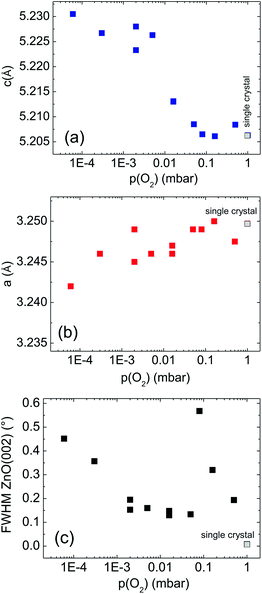
Fig. 2 shows the oxygen partial pressure dependence of the c- and a-axis lattice parameters and the FWHM of the ZnO(002) rocking curves. The lattice parameters of all samples show an almost smooth variation with the oxygen partial pressure, indicating c-axis expansion and a-axis compression of ZnO with decreasing oxygen pressure, i.e. increasing concentration of oxygen vacancies (Fig. 2a and b).22 This in-plane contraction and out-of-plane expansion of the c-axis oriented ZnO unit cells are in qualitative agreement with calculated local atomic relaxations around the neutral oxygen vacancy V0O, see Fig. 4 in ref. 23, as obtained from first-principle local density approximations.
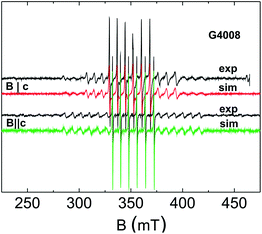 | ||
Fig. 3 Experimental and simulated EPR spectra at 297 K of the ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02% Mn (pO2 = 1.6 × 10−2 mbar) thin film sample G4008 for 0.02% Mn (pO2 = 1.6 × 10−2 mbar) thin film sample G4008 for ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0042_20d1.gif) ||c and ||c and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0042_20d1.gif) ⊥ c. ⊥ c. | ||
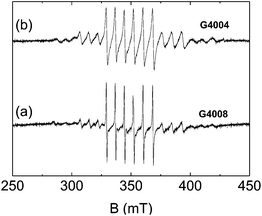 | ||
Fig. 4 Experimental EPR spectra at 297 K of (a) ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02% Mn (G4008) and (b) ZnO 0.02% Mn (G4008) and (b) ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2% Mn (G4004) thin films both grown at pO2 = 1.6 × 10−2 mbar 0.2% Mn (G4004) thin films both grown at pO2 = 1.6 × 10−2 mbar ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0042_20d1.gif) ⊥ c. ⊥ c. | ||
For the FWHM (002), three samples were intentionally included which do not follow the general behavior of the majority of films, probably because of substrate issues (top right in Fig. 2c). However, all samples from Fig. 2c fit well the results discussed further below, demonstrating the general validity of our work.
3.2. EPR spectroscopy
The EPR spectra of the heteroepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn thin films (Fig. 3 and 4) and of the homoepitaxial ZnO
Mn thin films (Fig. 3 and 4) and of the homoepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn films (Fig. 5a) display the typical thirty line spectrum of Mn2+ ions with their 3d5 electronic configuration having a 6S5/2 electronic ground state for the two orientations of the external magnetic field, parallel or perpendicular to the crystallographic c-axis. Here the total electron spin S = 5/2 gives rise to a zero field splitting into five fine structure (fs) transitions, each split into six hyperfine (HF) interaction lines due to the HF interaction with the nuclear spins I = 5/2 of the 55Mn nuclei. If we assume isotropic electron Zeeman and 55Mn HF interactions the EPR spectra of the Mn2+ ions can be described by the following spin Hamiltonian,17,18,24
Mn films (Fig. 5a) display the typical thirty line spectrum of Mn2+ ions with their 3d5 electronic configuration having a 6S5/2 electronic ground state for the two orientations of the external magnetic field, parallel or perpendicular to the crystallographic c-axis. Here the total electron spin S = 5/2 gives rise to a zero field splitting into five fine structure (fs) transitions, each split into six hyperfine (HF) interaction lines due to the HF interaction with the nuclear spins I = 5/2 of the 55Mn nuclei. If we assume isotropic electron Zeeman and 55Mn HF interactions the EPR spectra of the Mn2+ ions can be described by the following spin Hamiltonian,17,18,24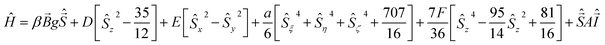 | (2) |
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ‖ c and
‖ c and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ⊥ c that have been analyzed here. D refers to the axial ZFS and a and F are the cubic ZFS parameters. The (x, y, z) and (ξ, η, ζ) coordinates refer to the trigonal and cubic axes of the crystal field, respectively. Although the Mn2+ ions are incorporated in nominally axially symmetric Zn2+ lattice sites (C3v symmetry) a rhombic contribution to ZFS measured by the parameter E has been included in the spin Hamiltonian. It may allow for possible rhombic distortions of the crystal field in the heteroepitaxial ZnO
⊥ c that have been analyzed here. D refers to the axial ZFS and a and F are the cubic ZFS parameters. The (x, y, z) and (ξ, η, ζ) coordinates refer to the trigonal and cubic axes of the crystal field, respectively. Although the Mn2+ ions are incorporated in nominally axially symmetric Zn2+ lattice sites (C3v symmetry) a rhombic contribution to ZFS measured by the parameter E has been included in the spin Hamiltonian. It may allow for possible rhombic distortions of the crystal field in the heteroepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn films acting on the manganese ions due to strains caused by the sapphire substrate.
Mn films acting on the manganese ions due to strains caused by the sapphire substrate.
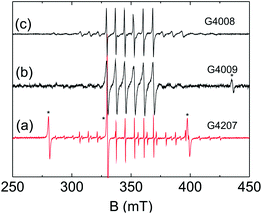
As a typical example for a heteroepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn film Fig. 3 illustrates the experimental Mn2+ EPR spectra of the ZnO:0.02% Mn (pO2 = 1.6 × 10−2 mbar) thin film sample G4008 for
Mn film Fig. 3 illustrates the experimental Mn2+ EPR spectra of the ZnO:0.02% Mn (pO2 = 1.6 × 10−2 mbar) thin film sample G4008 for ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ‖ c and
‖ c and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ⊥ c together with simulated spectra based on the spin Hamiltonian in (2). The line widths of the five fs transitions centered at 265 mT (mS = 5/2 ↔ 3/2), 306 mT (mS = 3/2 ↔ 1/2), 351 mT (mS = 1/2 ↔ −1/2), 396 mT (mS = −1/2 ↔ −3/2), and 441 mT (mS = −3/2 ↔ −5/2) for
⊥ c together with simulated spectra based on the spin Hamiltonian in (2). The line widths of the five fs transitions centered at 265 mT (mS = 5/2 ↔ 3/2), 306 mT (mS = 3/2 ↔ 1/2), 351 mT (mS = 1/2 ↔ −1/2), 396 mT (mS = −1/2 ↔ −3/2), and 441 mT (mS = −3/2 ↔ −5/2) for ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ‖ c differ significantly and increase with increase in the magnetic spin quantum number mS. Such a behavior is indicative of a distribution in the ZFS parameters and has been taken into account by Gaussian distributions of the ZFS parameters D and E with the corresponding distribution widths ΔD and ΔE in our spectral simulations. We have to note that the spectra for
‖ c differ significantly and increase with increase in the magnetic spin quantum number mS. Such a behavior is indicative of a distribution in the ZFS parameters and has been taken into account by Gaussian distributions of the ZFS parameters D and E with the corresponding distribution widths ΔD and ΔE in our spectral simulations. We have to note that the spectra for ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ‖ c are only influenced by the axial ZFS parameter D in the case of isotropic g-tensors whereas the spectra are sensitive to both, D and E, for
‖ c are only influenced by the axial ZFS parameter D in the case of isotropic g-tensors whereas the spectra are sensitive to both, D and E, for ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ⊥ c. Therefore, the distributions ΔD and ΔE can be separated from each other by simulations of spectra recorded for the two different orientations.
⊥ c. Therefore, the distributions ΔD and ΔE can be separated from each other by simulations of spectra recorded for the two different orientations.
The simulations revealed an axial ZFS parameter D = −650 MHz with distribution width ΔD = 35 MHz and a small distribution ΔE = 15 MHz of the rhombic ZFS parameter about E = 0 (Table 1). The D parameter is in the typical range reported for Mn2+ incorporated in Zn2+ lattice sites in ZnO.17–19 The overall axial symmetry of the ZFS interaction (E = 0) was confirmed by a rotation of the magnetic field perpendicular to the c-axis of the film where no significant changes of the positions or line widths of the four outer fs transitions (mS = ±3/2 ↔ ±1/2, mS = ±5/2 ↔ ±3/2) have been observed for sample G4008. In the simulations an isotropic g-value g = 2.001 and an isotropic 55Mn HF interaction parameter A = −222 MHz was assumed. The negative sign of the D parameter can be deduced from the spectral simulations. In particular the field positions of the mS = ±3/2 ↔ ±1/2 transitions depend on the sign of the parameter ratio A/D. The cubic ZFS parameters a = 18 MHz and F = 12 MHz were taken from a single crystal study of Mn2+ ions in ZnO.
The influence of the Mn2+ concentration on the ZFS parameters has been examined at two distinct oxygen partial pressures, pO2 = 1.6 × 10−2 mbar (samples G4008 and G4004) and pO2 = 2 × 10−3 mbar (samples G4009 and G4005), during the PLD process. Although the Mn2+ concentrations differ in each case by one order of magnitude the ZFS parameters D and E as well as their distribution widths ΔD and ΔE as determined by spectral simulations do not vary significantly (Table 1). However, the higher Mn2+ doping results in a substantial increase in the homogeneous EPR line widths ΔBhompp as seen in Fig. 4 for the samples G4008 and G4004 due to enhanced dipolar interactions between the paramagnetic ions in the higher doped films. Here ΔBhompp increases from 9 MHz to 18 MHz with increasing Mn concentration whereas for samples G4009 and G4005 ΔBhompp increases even by a factor of 3 (12 MHz versus 36 MHz).
In contrast to the concentration of the dopants the oxygen partial pressure pO2 during the PLD process affects crucially the axial ZFS parameters D and ΔD. Fig. 5 illustrates the influence of pO2 on the Mn2+ EPR spectra at ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ⊥ c for two selected samples. Obviously, the line widths caused by the distribution in the ZFS parameters increase strongly for the film prepared at lower oxygen partial pressures (Fig. 4b) leading to less resolved outer fs transitions. The spectral simulation for both film orientations
⊥ c for two selected samples. Obviously, the line widths caused by the distribution in the ZFS parameters increase strongly for the film prepared at lower oxygen partial pressures (Fig. 4b) leading to less resolved outer fs transitions. The spectral simulation for both film orientations ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ⊥ c and
⊥ c and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ‖ c (spectra not shown) indicates clearly that this increase in line broadening is mainly caused by the distribution ΔD in the axial ZFS parameter D. There is also an effect of the oxygen partial pressures on the distribution ΔE of the rhombic fs parameter E but it appears to be less pronounced. In addition to the ΔD values, the absolute value of the axial ZFS parameter D depends likewise in a characteristic manner on pO2. Overall it decreases with lower oxygen partial pressures. All ZFS parameters of the studied films as obtained from the spectral simulations are summarized in Table 1. In addition the ZFS parameters of Mn2+ impurities present in the homoepitaxial ZnO
‖ c (spectra not shown) indicates clearly that this increase in line broadening is mainly caused by the distribution ΔD in the axial ZFS parameter D. There is also an effect of the oxygen partial pressures on the distribution ΔE of the rhombic fs parameter E but it appears to be less pronounced. In addition to the ΔD values, the absolute value of the axial ZFS parameter D depends likewise in a characteristic manner on pO2. Overall it decreases with lower oxygen partial pressures. All ZFS parameters of the studied films as obtained from the spectral simulations are summarized in Table 1. In addition the ZFS parameters of Mn2+ impurities present in the homoepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn film sample (G4207) are presented in the table as well. For comparison its EPR spectrum is also displayed in Fig. 5a. It is worth noting that the ΔD parameter in the homoepitaxial ZnO
Mn film sample (G4207) are presented in the table as well. For comparison its EPR spectrum is also displayed in Fig. 5a. It is worth noting that the ΔD parameter in the homoepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn film sample is substantially smaller (by a factor of four or more) than those of the heteroepitaxial film samples. In the case of the homoepitaxial sample we have to take into account that Mn2+ and Fe3+ ions are also present in the ZnO single crystal substrate as impurities for EPR spectroscopy appreciable concentrations, compare ref. 25. In contrast the sapphire substrates did not exhibit EPR signals from Mn2+ impurities. Only some minor Fe3+ signals were detected in the measured magnetic field range that did not interfere with the Mn2+ spectrum of the ZnO
Mn film sample is substantially smaller (by a factor of four or more) than those of the heteroepitaxial film samples. In the case of the homoepitaxial sample we have to take into account that Mn2+ and Fe3+ ions are also present in the ZnO single crystal substrate as impurities for EPR spectroscopy appreciable concentrations, compare ref. 25. In contrast the sapphire substrates did not exhibit EPR signals from Mn2+ impurities. Only some minor Fe3+ signals were detected in the measured magnetic field range that did not interfere with the Mn2+ spectrum of the ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn films. But the EPR spectra of the homoepitaxial sample do not allow us to distinguish between manganese ions incorporated in the thin film and the Mn2+ impurities of the ZnO substrate since only a single Mn2+ species is observed. Moreover, as the Mn2+ signal intensity for the sample G4207 is substantially higher than those for the heteroepitaxial ZnO
Mn films. But the EPR spectra of the homoepitaxial sample do not allow us to distinguish between manganese ions incorporated in the thin film and the Mn2+ impurities of the ZnO substrate since only a single Mn2+ species is observed. Moreover, as the Mn2+ signal intensity for the sample G4207 is substantially higher than those for the heteroepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn films we assume that the Mn2+ EPR signal of the homoepitaxial ZnO
Mn films we assume that the Mn2+ EPR signal of the homoepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn film is mainly caused by manganese impurity ions in the ZnO single crystal substrate. Indeed the obtained spin Hamiltonian parameters of its Mn2+ ions (Table 1) are in agreement with those reported for Mn2+ impurities in low concentrations in ZnO single crystals.17,18 Therefore we may refer to this sample as a ZnO single crystal in the following and consider it as a reference sample for Mn2+ substitution in undisturbed ZnO single crystals.
Mn film is mainly caused by manganese impurity ions in the ZnO single crystal substrate. Indeed the obtained spin Hamiltonian parameters of its Mn2+ ions (Table 1) are in agreement with those reported for Mn2+ impurities in low concentrations in ZnO single crystals.17,18 Therefore we may refer to this sample as a ZnO single crystal in the following and consider it as a reference sample for Mn2+ substitution in undisturbed ZnO single crystals.
4. Discussion
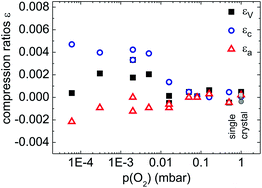
The XRD data reveal an obvious relationship between the lattice axes parameters c and a and the oxygen partial pressure during the growth process. We suppose that the major reason for the observed dependence of this biaxial strain on pO2 is the formation of oxygen vacancies at low pO2 values. Pseudomorphic, i.e. in-plane lattice matched growth can be excluded for the heteroepitaxial ZnO films on sapphire. For films grown at pO2 > 5 × 10−2 mbar both lattice constants appear to be comparable to the single crystal values. However, the c-axis parameter increases strongly with decreasing pressure for pressures pO2 < 5 × 10−2 mbar, whereas the parameter a declines slightly. These opposing trends for c and a indicate that the volume of the unit cell of the ZnO films does not significantly change with oxygen partial pressure and stays comparable with that of the single crystal. This fact is illustrated by a comparison of the volume compression ratios εV for the various films with the single crystal value as displayed in Fig. 6.The figure also includes the compression ratios for the c- and a-axes lattice parameters εc = c/c0 − 1 and εa = a/a0 − 1. The data suggest that the unit cell of the ZnO films shrink perpendicular to the crystallographic c-axis with increasing formation of oxygen vacancies at lower oxygen partial pressures and consequently the bond length between the Zn2+ ion and the three non-axial oxygen atoms in the ZnO4 tetrahedra are becoming shorter. This, however, is related to an increase in the axial Zn–O bond length R1(0) along the c-axis as the overall unit cell volume is conserved. For lower oxygen partial pressures and enhanced oxygen vacancy formation the strain in the films seems to increase as well as indicated by the widths of the diffraction peaks (Fig. 1c).
Supplementary to the XRD data the manganese ZFS parameters as determined from EPR spectroscopy provide a microscopic perspective at the changes of the ZnO4 or more precisely the MnO4 tetrahedra upon the enhanced formation of oxygen vacancies with decreasing oxygen partial pressures in the ZnO films. Indeed, we observe within the experimental accuracy almost linear correlations between the axial ZFS parameter D and the axis lattice parameter ratio c/a of the films and between distribution widths ΔD of the axial ZFS parameter and the widths of the diffraction peaks (Fig. 7). In that way a correlation can be established between the c/a ratio and the distortions of the metal ion–oxygen tetrahedra. The results confirm that the MnO4 tetrahedra experience the same structural modification as the ZnO4 units and the paramagnetic Mn2+ ions can be considered to be suitable probes to monitor the structural variations of the films on a local microscopic scale. However, the D parameter of the Mn2+ ions would not become zero even for an assumed case of an ideal wurtzite structure22 (c/a = (8/3)1/2), see Fig. 7a. The reason is a small displacement δ of the Mn2+ ions with respect to the Zn2+ site along the c-axis in the metal–oxygen tetrahedron presumably due to minor differences in the ionic radii.24,26 We have to note that the axial ZFS parameter D monitors the increase of the axial metal ion–oxygen bond length R1 along the c-axis, which is related to an axial elongation of the unit cell and an increase in the lattice parameter c as observed in the XRD experiments. In addition, the determined distribution widths ΔD of the axial ZFS parameter point at some variance in the bond lengths R1 and consequently at some structural distortions of the MnO4 tetrahedra depending on oxygen growth pressure and the formation of oxygen vacancies in the films. Moreover, a small distribution ΔE of the rhombic ZFS parameter about E = 0 was likewise observed for all studied ZnO thin films (Table 1) indicating some deviation from the perfect C3v symmetry of the tetrahedra. This might be caused either by slightly different non-axial metal ion–oxygen bond lengths or bond angles. Otherwise for the ZnO single crystal the EPR spectra reveal ΔE = 0 within the experimental accuracy. Therefore we suppose that the distortions of the C3v symmetry of the tetrahedra indicate the presence of small strains in the films due to a misfit between the ZnO films and the a-sapphire substrates.
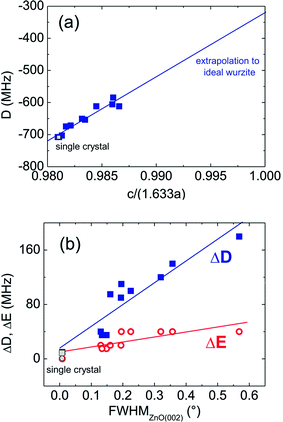 | ||
| Fig. 7 Experimentally determined (a) ZFS parameter D depending on the ratio of the lattice parameters c and a and (b) ZFS distribution widths (filled squares) ΔD and (open circles) ΔE depending on FWHM of the ZnO(002) peak for ZnO thin film samples and the ZnO single crystal (gray filled symbols). The scaling 1.633 = (8/3)1/2 in the c by a ratio takes into account the lattice parameter ratio c/a = (8/3)1/2 of the ideal wurtzite structure.22 The solid lines are linear fits to the data points. | ||
In the final step we want to rationalize why the absolute value of the ZFS parameter D decreases with increasing axial elongation of the metal ion–oxygen tetrahedra as indicated by the increase of the axis parameter c with decreasing pO2 (Fig. 7a). Our analysis will further provide an interpretation of the experimentally obtained D parameters of the Mn2+ ions in terms of displacements of the metal ion in the oxygen tetrahedra depending on the axes lattice parameters c and a of the ZnO films.
Recently, Zi-Yuan26 derived a local structure model of the MnO4 tetrahedra from the D parameter of Mn2+ ions measured for lightly doped ZnO single crystals (D = −707 MHz) using the superposition model.27 In the proposed model the structures of the MnO4 tetrahedra differ slightly from those of the ZnO4 tetrahedra in the parent ZnO material. The Mn2+ ion is displaced by δ = 0.03 Å with respect to the Zn2+ site along the c-axis towards the basal of the oxygen tetrahedra. Here, the displacement δ = 0.03 Å was taken from the average ionic radii of Mn2+ (0.8 Å) and Zn2+ (0.74 Å). Then, the D value was assumed to be related to a small deviation Δθ = 1° of the angle θ between c-axis and the bond directions of the three non-axial basal oxygen ions in the MnO4 tetrahedra in comparison with the parent ZnO4 tetrahedra. However, as only a single experimental D value with a single set of structural data, those from the single crystal, was used the validity of the structure model could not be tested.
By exploring the Mn doped ZnO thin films grown under different oxygen partial pressures we have a whole set of ZnO materials with different structural parameters and corresponding Mn2+D ZFS parameters available to identify the structure of the MnO4 tetrahedra. In order to interpret the axial ZFS parameters we use high-order perturbation theory based on the spin–orbit coupling mechanism for S-state ions in a weak-field scheme28,29 for the computation of the dependence of D on the structural parameters of the ZnO thin films. We postulate likewise that the Mn2+ ions are incorporated in the Zn2+ lattice sites but may be displaced by δ with respect to the zinc site along the c-axis towards the basal of the oxygen tetrahedra (Fig. 8) due to the slightly larger ionic radii of Mn2+versus Zn2+. However, we do not assume a fixed displacement but rather consider δ as a function of the lattice parameters c and a that depend on the oxygen partial pressure during the growth process.
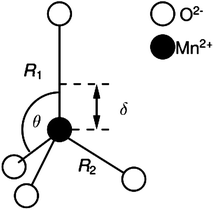 | ||
Fig. 8 Schematic drawing of the structure of the MnO4 tetrahedra in the ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn films with the structural parameters θ, R1, R2, and δ. Mn films with the structural parameters θ, R1, R2, and δ. | ||
The axial ZFS parameter D that depend on the crystal field parameters B20, B40, and B43 in the case of trigonal symmetry has been calculated in the weak field scheme, where the total crystal field and the spin–orbit coupling are taken as perturbations, by Ju et al.28 and Zheng et al.29
| D ≈ −P1(B,C)−1(3ξd2B202 + 63ξd2B20) − P2(B,C)−1(10ξd2B402 − 7ξd2B432). | (3) |
The parameters
| P1(B,C) = 70(7B + 7C)2(17B + 5C) | (4) |
| P2(B,C) = 126(7B + 7C)2(10B + 5C) | (5) |
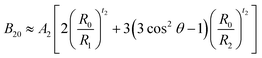 | (6) |
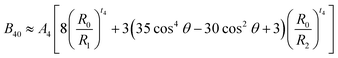 | (7) |
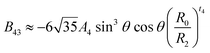 | (8) |
| R1(δ) = uc − δ | (9) |
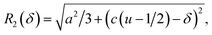 | (10) |
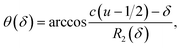 | (11) |
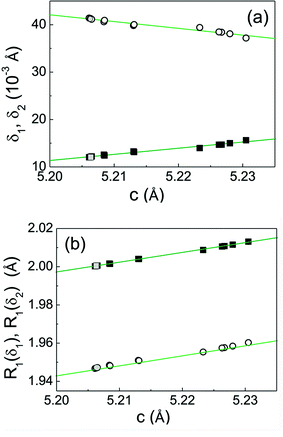
The displacement δ of the Mn2+ ion along the c-axis with respect to the positions of the Zn2+ site can then be determined numerically for each set of film parameters c, a, and D by solving eqn (3)–(11). Two solutions δ1 < 0 and δ2 > 0 for the displacements are obtained for each parameter set and their absolute values are displayed to be dependent on the c-axis lattice parameter in Fig. 9a. The corresponding bond angles for the two solutions θ1 = 107.7° and θ1 = 109.5° vary by only ±0.1° within the obtained range of δ1,2 values. Using eqn (9) two choices for the bond length between the Mn2+ ion and the axial oxygen ion, R1(δ1) and R1(δ2), can be calculated for the two solutions δ1 and δ2 (Fig. 9b).
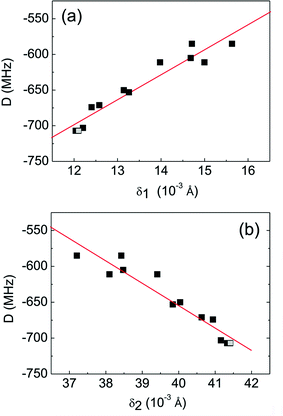
In the case of R1(δ1) the Mn2+ ion is displaced towards the axial oxygen ion along the c-axis with respect to the Zn2+ site whereas for R1(δ2) it is shifted towards the basal oxygen ions of the tetrahedron. In each situation the Mn–O bond distances increase with the increasing lattice axis parameter c and enhanced formation of oxygen vacancies with decreasing pO2 during the growth of the ZnO films. The crystal field at the manganese ion becomes weaker with the increasing c-axis parameter. This explains why the absolute value of the axial ZFS parameter D decreases with increasing lattice axis parameter c although the axial distortion of the tetrahedron becomes larger. Fig. 10 illustrates the linear dependence of D on the absolute values of the computed displacement solutions δ1 and δ2.
On the basis of our analysis of the D parameter we cannot safely rule out one of the two possible Mn2+ positions described by R1(δ1) and R1(δ2). We may only speculate that a displacement R1(δ1) towards the axial oxygen ion with respect to the Zn2+ position seems to be more likely as that such a shift has been observed for divalent manganese ions incorporated in the likewise axially distorted tetrahedral metal sites in GaN and AlN.17,18,24 However, we can firmly rule out the above discussed model suggested by Zi-Yuan et al. where the axial ZFS splitting was assumed to be caused only by a variation in the angle θ between the MnO4 and the host ZnO4 tetrahedra.26 Varying exclusively the angle θ in eqn (6)–(8) but keeping R1 and R2 constant, we have not been able to reproduce our experimental D parameters.
5. Experimental
ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn thin films were grown by PLD using a KrF excimer laser from polycrystalline source targets mixed, pressed and sintered from ZnO and MnO powders (Alpha Aesar, 5N purity). As a substrate we used a-plane sapphire, or a c-plane O-face ZnO single crystal, both supplied by CrysTec GmbH. The growth temperature of the films was about 650 °C and 45
Mn thin films were grown by PLD using a KrF excimer laser from polycrystalline source targets mixed, pressed and sintered from ZnO and MnO powders (Alpha Aesar, 5N purity). As a substrate we used a-plane sapphire, or a c-plane O-face ZnO single crystal, both supplied by CrysTec GmbH. The growth temperature of the films was about 650 °C and 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser pulses were applied. The oxygen partial pressure was controlled in between 10−1 and 6 × 10−5 mbar. Table 1 gives an overview of the samples (for identification of consecutively grown samples we maintain the original sample ID no.). For more details of our ZnO thin film growth activities see ref. 21 and references therein.
000 laser pulses were applied. The oxygen partial pressure was controlled in between 10−1 and 6 × 10−5 mbar. Table 1 gives an overview of the samples (for identification of consecutively grown samples we maintain the original sample ID no.). For more details of our ZnO thin film growth activities see ref. 21 and references therein.
XRD rocking curves and reciprocal space maps were measured with a Philips X'pert diffractometer with Cu Kα1 point focus, a 4× Ge (220) Bartels primary monochromator, a 4-axis goniometer (Eulerian craddle), and either an open detector or a secondary monochromator (triple axis), respectively. XRD wide-angle 2θ − ω scans were measured with Cu Kα1/2 radiation and the focussing Bragg Brentano goniometer (Philips X'pert) with a graphite secondary monochromator for suppression of bremsstrahlung. For highly precise determination of out-of-plane (c) and in-plane (a) lattice constants of the heteroepitaxial films we used a PANalytical X'pert PRO MRD with a parabolic mirror and a Bartels monochromator as primary optics with Cu Kα1 line focus and the PIXcel3D detector in 1D scanning mode with 255 channels. In order to precisely correct the goniometer height errors, we measured (002), (004), and if possible also (006) symmetric and (101) and (202) asymmetric peaks, and extrapolated the lattice constants from plots over cos2(θ). This method was recently proved to yield highly precise (5 × 10−4 and 5 × 10−5) lattice constants for heteroepitaxial ZnO films and single crystals, respectively, in agreement with independently determined values from X-ray multiple reflections.31
Proton induced X-ray emission (PIXE) and Rutherford backscattering spectrometry (RBS) were used for determination of Mn concentration, layer thickness, and for trace element analysis. A 1.2 MeV H+ beam of the Leipzig ion probe LIPSION with a beam diameter of 0.4 mm and a collected charge of 10 μC per measurement was used. PIXE and RBS spectra were fitted with the GeoPIXE II32 and RUMP33 software, respectively.
The obtained Mn concentrations confirmed within the experimental uncertainty that the PLD target compositions were transferred almost unchanged into the ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn thin films. The metal to oxygen ratio was 1.00 ± 0.02 for the samples grown at intermediate oxygen partial pressure. The ZnO
Mn thin films. The metal to oxygen ratio was 1.00 ± 0.02 for the samples grown at intermediate oxygen partial pressure. The ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn film thickness of the heteroepitaxial samples was determined to be between 1.08 and 1.46 μm, depending on the growth conditions and using a mass density of 5.62 g cm−2. These thickness values are in good agreement with the HR-XRD result of the homoepitaxial sample G4207, where around ZnO(002) Pendellösung oscillations could be observed (see Fig. 1d). The mean fringe period of 0.00653° yields a mean ZnO
Mn film thickness of the heteroepitaxial samples was determined to be between 1.08 and 1.46 μm, depending on the growth conditions and using a mass density of 5.62 g cm−2. These thickness values are in good agreement with the HR-XRD result of the homoepitaxial sample G4207, where around ZnO(002) Pendellösung oscillations could be observed (see Fig. 1d). The mean fringe period of 0.00653° yields a mean ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn thickness of 1.41 ± 0.10 μm for this particular sample.
Mn thickness of 1.41 ± 0.10 μm for this particular sample.
EPR experiments have been performed on an X-band Bruker ELEXSYS E580 spectrometer at room temperature using a cylindrical ER4119 HS cavity. The ZnO thin film samples (area size 2 mm × 4 mm) and the ZnO single crystal (with homoepitaxial ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn film) were mounted on a quartz rod sample holder. The angle between the c-axis of the ZnO crystal and the direction of the applied magnetic field was controlled by a goniometer. Spectral simulations of the Mn2+ EPR spectra were done using the EasySpin EPR simulation package34 which employs full matrix diagonalization of the complete Mn2+ spin Hamiltonian operator.
Mn film) were mounted on a quartz rod sample holder. The angle between the c-axis of the ZnO crystal and the direction of the applied magnetic field was controlled by a goniometer. Spectral simulations of the Mn2+ EPR spectra were done using the EasySpin EPR simulation package34 which employs full matrix diagonalization of the complete Mn2+ spin Hamiltonian operator.
6. Summary and conclusions
The influence of the oxygen partial pressure during the PLD growth process on the structural properties was explored for manganese doped heteroepitaxial ZnO thin films by HR-XRD and EPR spectroscopy of Mn2+ ions substituting Zn2+ in the ZnO lattice. This combined approach allowed us to correlate the induced changes of the overall film structure with the local properties at the tetrahedral incorporation site of the divalent manganese ions. Our work reveals a significant expansion of the ZnO film structure along the c-axis combined with the a-axis compression with decreasing oxygen partial pressure that we ascribe to the enhanced formation of oxygen vacancies under oxygen deficient growth conditions. This increase of the c-axis lattice parameter translates into an increase of the bond distances between the metal ions and the axial oxygen ions along the c-axis in the metal ion–oxygen tetrahedra of the ZnO films. In the case of Mn2+ substituting Zn2+ this enlargement of the Mn–O bond distance is monitored by the axial Mn2+ ZFS parameter D. Using the superposition theory of crystal fields, the Mn–O bond distances could be calculated from the D parameter for the distinct oxygen partial pressures and related to the c-axis lattice parameters. In that way, linear relations have been obtained between the c-axis expansion and the ZFS parameter D as well as the axial Mn–O bond distance R1. Although the D parameter decreases by about 120 MHz for the films grown under the lowest oxygen partial pressure (pO2 = 3 × 10−4 mbar) used here in comparison with films grown at pO2 = 1.6 × 10−1 mbar or the ZnO single crystal, the corresponding increase in the axial Mn–O bond distance R1 is only 0.013 Å that indicates the high sensitivity of the Mn2+ ZFS parameter with respect to small local structural distortions. We assume that the Mn2+ ion is slightly shifted towards the axial oxygen ion with respect to the Zn2+ site. In this case, the bond distance between the Mn2+ ion and the axial oxygen ion will increase with the increasing c-axis lattice parameter in comparison with the corresponding axial Zn–O bond length and the displacement of the Mn2+ ion from the Zn2+ site becomes smaller with an enhanced expansion of the ZnO lattice.We would like to emphasize that the enhanced formation of oxygen vacancies at lower oxygen partial pressures also results in higher structural distortions of the films as indicated by the increase of the width of the HR-XRD rocking curves and, locally measured by the EPR of the Mn2+ ions, the larger distribution widths of the ZFS parameter D. The latter could again be interpreted in terms of increasing variation in the axial Mn–O bond distance R1 at higher oxygen vacancy concentrations. The presented investigations may be extended to doped oxide thin films with low Mn2+ concentration as local probes for lattice distortions and bond lengths.
Acknowledgements
We thank Gabriele Ramm for PLD target preparation, Holger Hochmuth for PLD growth, Sascha Bader for technical support in the HR-XRD lattice constant determination. We gratefully acknowledge the financial support by the DFG within SFB 762 “Functionality of Oxide Interfaces” and the SPP 1601 “New Frontiers in Sensitivity for EPR Spectroscopy: From Biological Cells to Nano Materials”.References
- S. X. Zhang, S. Dhar, W. Yu, H. Xu, S. B. Ogale and T. Venkatesan, Appl. Phys. Lett., 2007, 91, 112113 CrossRef PubMed.
- M. Lorenz and R. Rao, J. Phys. D: Appl. Phys., 2014, 47, 030301 CrossRef.
- G. L. Yuan, L. W. Martin, R. Ramesh and A. Uedono, Appl. Phys. Lett., 2009, 95, 012904 CrossRef PubMed.
- Y. Sassa, M. Radovic, M. Mansson, E. Razzoli, X. Y. Cui, S. Pailhes, S. Guerrero, M. Shi, P. R. Willmott, F. Miletto Granozio, J. Mesot, M. R. Norman and L. Patthey, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 140511 CrossRef.
- E. Ertekin, V. Srinivasan, J. Ravichandran, P. B. Rossen, W. Siemons, A. Majumdar, R. Ramesh and J. C. Grossman, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195460 CrossRef.
- A. Y. Borisevich, A. R. Lupini, J. He, E. A. Eliseev, A. N. Morozovska, G. S. Svechnikov, P. Yu, Y.-H. Chu, R. Ramesh, S. T. Pantelides, S. V. Kalinin and S. J. Pennycook, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 140102 CrossRef.
- D. Schumacher, A. Steffen, J. Voigt, J. Schubert, Th. Brückel, H. Ambaye and V. Lauter, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144427 CrossRef.
- J. Rubio-Zuazo, L. Onandia, P. Ferrer and G. R. Castro, Appl. Phys. Lett., 2014, 104, 021604 CrossRef PubMed.
- P. Bousoulas, I. Michelakaki and D. Tsoukalas, J. Appl. Phys., 2014, 115, 034516 CrossRef PubMed.
- A. R. Silva and G. M. Dalpian, J. Appl. Phys., 2014, 115, 033710 CrossRef PubMed.
- M. Choi, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214117 CrossRef.
- R. Yang, S. Lin, X. Fang, X. Gao, M. Zeng and J. Liu, J. Appl. Phys., 2013, 114, 233912 CrossRef PubMed.
- R. Vidya, P. Ravindran, H. Fjellvag, B. G. Svensson, E. Monakhov, M. Ganchenkova and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045206 CrossRef.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 113201 CrossRef.
- N. C. Giles, N. Y. Garces, L. Wang and L. E. Halliburton in Quantum Sensing and Nanophotonic Devices: Proc. of SPIE, SPIE, ed. M. Razeghi and G. J. Brown, Bellingham, WA, 2004, pp 267−278 Search PubMed.
- M. D. McCluskey and S. J. Jokela, J. Appl. Phys., 2009, 106, 071101 CrossRef PubMed.
- J. Schneider and S. R. Sircar, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1962, 17, 570 Search PubMed.
- A. Hausmann and H. Huppertz, J. Phys. Chem. Solids, 1968, 29, 1369 CrossRef CAS.
- M. Diaconu, H. Schmidt, A. Pöppl, R. Böttcher, J. Hoentsch, A. Klunker, D. Spemann, H. Hochmuth, M. Lorenz and M. Grundmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085214 CrossRef.
- S. S. Kim, J. H. Moon, B.-T. Lee, O. S. Sung and J. H. Je, J. Appl. Phys., 2004, 95, 454 CrossRef CAS PubMed.
- M. Lorenz, Pulsed laser deposition of ZnO-based thin films, in Transparent Conductive Zinc Oxide. Basics and Applications in Thin Film Solar Cells (Springer Series in Materials Science vol. 104), ed K. Ellmer et al, Berlin, Springer, 2008, ch. 7, pp. 303–58 Search PubMed.
- H. Morkoc and Ü. Özgür, Zinc Oxide: Fundamentals, Materials and Device Technology, Wiley-VCG Verlag GmbH, 2009 Search PubMed.
- A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165202 CrossRef.
- T. Graf, M. Gjukic, M. Hermann, M. S. Brandt, M. Stutzmann and O. Ambacher, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165215 CrossRef.
- M. Lorenz, C. Schmidt, G. Benndorf, T. Böntgen, H. Hochmuth, R. Böttcher, A. Pöppl, D. Spemann and M. Grundmann, J. Phys. D: Appl. Phys., 2013, 46, 065311 CrossRef.
- Y. Zi-Yuan, Chin. Phys. B, 2009, 18, 1253 CrossRef.
- D. J. Newman and B. Ng, Rep. Prog. Phys., 1988, 52, 699 CrossRef.
- W. L. Ju and M. G. Zhano, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 9254 CrossRef.
- W.-C. Zheng, S.-Y. Wu and J. Zi, Z. Naturforsch., A: Phys. Sci., 2001, 56a, 473 Search PubMed.
- V. A. Coleman and C. Jagadish, in Zinc Oxide Bulk, Thin Films and Nanostructures, ed. C. Jagadish and S. Pearton, Elsevier Ltd., 2006, pp. 1–20 Search PubMed.
- M. Grundmann, M. Scheibe, M. Lorenz, J. Bläsing and A. Krost, Phys. Status Solidi B, 2014, 251, 850–863 CrossRef CAS.
- C. G. Ryan, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 181, 170 CrossRef CAS.
- L. Doolittle, Nucl. Instrum. Methods Phys. Res., Sect. B, 1985, 9, 344 CrossRef.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42 CrossRef CAS PubMed.
Footnote |
| † Present address: Steinstr. 23, D-04275 Leipzig, Germany. |
| This journal is © The Royal Society of Chemistry 2014 |