Synthesis of highly luminescent wurtzite CdSe/CdS giant-shell nanocrystals using a fast continuous injection route

Abstract

We synthesized CdSe/CdS giant-shell nanocrystals, with a CdSe core diameter between 2.8 nm and 5.5 nm, and a CdS shell thickness of up to 7–8 nm (equivalent to about 20 monolayers of CdS). Both the core and shell have a wurtzite crystal structure, yielding epitaxial growth of the shell and nearly defect-free crystals. As a result, the photoluminescence (PL) quantum efficiency (QE) is as high as 90%. Quantitative PL measurements at various excitation wavelengths allow us to separate the nonradiative decay into contributions from interface and surface trapping, giving us pathways for future optimization of the structure. In addition, the NCs do not blink, and the giant shell and concurring strong electron delocalization efficiently suppress Auger recombination, yielding a biexciton lifetime of about 15 ns. The corresponding biexciton PL QE equals 11% in 5.5/18.1 nm CdSe/CdS. Variable-temperature time-resolved PL and PL under magnetic fields further reveal that the emission at cryogenic temperature originates from a negative trion-state, in agreement with other CdSe/CdS giant-shell systems reported in the literature.

---

Introduction

Colloidal nanocrystals (NCs), in particular CdSe/CdS core/shell heterostructures, have proven to be a versatile class of nanomaterials with potential applications in light-emitting diodes,^1,2 lasers,^3–6 bio-labels^7,8 and single photon sources.^9,10 Control over the synthesis parameters currently permits embedment of nanocrystalline CdSe cores into a variety of shell structures. In the case of a spherical CdS coating, the shell thickness can be tuned from only a few CdS monolayers to up to 9 nm yielding so-called giant-shell nanocrystals (g-NCs).^11,12 Both wurtzite (WZ) and zincblende (ZB) CdSe quantum dots have been used as seed materials, although it has been proven to be challenging to preserve the ZB crystal phase throughout the coating procedure.¹³ This may also be used beneficially, by growing a polytypic CdS shell with a ZB lattice epitaxially grown on the ZB CdSe core, followed by a thicker WZ phase. This is the case of recently introduced dot-in-bulk heterostructures that, as a result of the thin ZB CdS interlayer separating the CdSe core from the thick WZ CdS shell, are capable of emitting from both core and shell states under continuous wave optical excitation or even electrical pumping.^14,15 Anisotropic structures can also be synthesized, consisting of a CdSe seed inside a disk-like shell,¹⁶ or inside one (rod),^17,18 four (tetrapod)¹⁸ or even eight (octapod) CdS arms.¹⁹ The symmetry of the latter two implies that ZB CdSe NCs are used as seeds, while for quantum rods one typically starts from WZ CdSe NCs.

In CdSe/CdS NCs, the CdS shell both enhances the photoluminescence (PL) quantum efficiency (QE) by passivating CdSe surface states and provides a unique level of control over the exciton energy and recombination dynamics.^17,20,21 Specifically, because of the large energy offset between the valence band of CdSe and CdS, photogenerated holes are rapidly captured in the core region. On the other hand, the small conduction band offset allows for partial delocalization of the electron wave function from the core into the shell.^22,23 As a result, excitons in CdSe/CdS heterostructures assume a peculiar donor-like character, with the electron orbiting in the Coulomb potential of the core-localized hole, similar to charges bound to localized donor/acceptor states in bulk semiconductors.^24,25

Several applications requiring a high degree of control over the excitonic structure, such as two-photon absorbers,^6,26 gain materials,^3–6 and quantum emitters,^9,10 have already been explored. They benefit from the strongly increased absorption cross-section and large ‘global’ Stokes shift due to the large CdS volume, as well as a suppressed rate of Auger recombination by the reduced electron–hole overlap and the smoothened confinement potential in interfacially alloyed g-NCs.^27,28 The controlled selective localization of wave functions further reduces the electron–hole exchange interaction, leading to smaller energy splitting of the band-edge states^20,21,29 and overall longer exciton lifetime^20,22 and smaller exciton dephasing rate.³⁰

Clearly, given their distinct advantages over conventional NCs, fast and reliable synthesis protocols are required. CdSe/CdS dot-in-rods are synthesized in a time frame of minutes and the high growth temperatures of 350–380 °C lead to NCs with a high PL quantum efficiency.¹⁷ Nevertheless, they still display PL intermittency (blinking) unless the rod diameter strongly exceeds the core diameter.^31,32 Giant-shell NCs with spherical symmetry circumvent this issue by placing the CdSe in the centre of a thick shell, which separates the exciton from surface trapped charges resulting in blinking-free PL.^11,12 Furthermore, the thick CdS shell acts as a spacer in close packed NC solids, increasing the core-to-core distance above the Förster energy transfer radius, thus suppressing exciton diffusion and boosting the efficiency of NC-LEDs.¹⁵ However, these particles are mostly grown via the sequential ion layer addition and reaction (SILAR) method, a labour-intensive process that can take hours to days.

Only recently Galland et al. described a method to fabricate CdSe/CdS NCs with shell thickness as large as 9 nm by continuous injection of precursors, here starting from a ZB core and coating it with a WZ shell.¹⁴ Considering the reported injection rate of 1 mmol per hour, a 25 ML shell would be obtained after about 20 hours of growth. Earlier work by Mahler et al. also described a procedure to fabricate ZB/ZB core/shell NCs by continuous injection, yet the final diameter was limited to about 10 nm.¹³ Another approach was taken by Cirillo et al., where the synthesis of WZ/WZ NCs with a final diameter of up to 17 nm was achieved in merely 3 minutes, however final samples yielded a PL QE of only 10–15%.³³

Here we apply a procedure similar to the one proposed by Galland et al.¹⁴ to synthesize g-NCs starting from WZ CdSe seeds and growing a WZ CdS shell. With respect to reported literature protocols, we were able to reduce the growth time to as short as 30 minutes without significantly affecting the NC structure. Defect-free epitaxial growth of the shell at the relatively high reaction temperatures used leads to an excellent PL QE of up to 90%. According to progressive delocalization of electrons in thicker-shell CdSe/CdS NCs, the exciton lifetimes are in the range of 400–700 ns, depending on the core diameter. The Auger recombination rate and exciton blinking are strongly suppressed. Time-resolved PL measurements show the progressive acceleration of the decay rate with decreasing temperature, accompanied by the increase of the PL intensity at zero delay from the excitation pulse. These are typical signatures of the emission by charged states.³⁴ The formation of negative trions at low temperature is confirmed by polarization-dependent PL measurements under high magnetic fields (up to 5 T), revealing that our NCs emit circularly polarized light arising from the Zeeman splitting of negative trion states.

Experimental

Materials

CdO (>99%), Se (>99%) and S powder (99%), trioctylphosphine (90%) and trioctylphosphine oxide (99%) were purchased from STREM Chemicals, octadecylphosphonic acid (>99%) from PCI Synthesis, and oleic acid (90%), octadecene (90%) and chloroform (>99%) from Sigma-Aldrich. Methanol, isopropanol and toluene were all of analytical grade (>99%) and obtained from Carlo Erba Reagents.

Synthesis

CdSe seeds were synthesized at 380 °C, according to the procedure described by Carbone et al.¹⁷ After synthesis, the NC suspensions were purified by precipitating them with methanol, followed by centrifugation and resuspension in toluene (procedure repeated 3 times). The final size (diameter) and concentration of the NCs were determined from the absorption spectrum of the NCs dispersed in chloroform, using a known sizing curve and the molar extinction coefficient at 350 nm.³⁵

For the shell growth, Cd and S-precursors were prepared separately as a 0.5 M solution of TOPS, and Cd-oleate dissolved in ODE, respectively. Next, 2 × 10⁻⁷ mol of CdSe NCs were added to 10 ml of ODE and heated up to 300 °C. Depending on the desired shell thickness, an appropriate amount of the precursor solutions was mixed, loaded in a syringe, and added dropwise over the course of 0.5–4 hours. After synthesis, the samples were purified by precipitation with isopropanol, followed by centrifugation and resuspension in toluene. A second purification step was performed with methanol as nonsolvent and samples were finally suspended in toluene.

Structural characterization

X-ray diffraction patterns were measured with a Rigaku SmartLab 9 kW diffractometer. A Bragg–Brentano geometry was used and the X-ray source was operated at 40 kV and 150 mA. The samples were prepared by drop casting concentrated NC solutions onto a miscut silicon substrate.

For conventional TEM measurements and analysis of the size distribution, the samples were prepared by drop casting concentrated NC solutions on carbon-coated 200 mesh copper grids, and the images were collected with a JEOL JEM 1011 microscope equipped with a tungsten thermo-ionic source operating at 100 kV. High Resolution TEM (HRTEM), Scanning TEM (STEM), High Angle Annular Dark Field (HAADF) imaging and Energy Dispersive X-ray Spectroscopy (EDS) analyses were performed with a JEOL JEM-2200FS microscope equipped with a field emission gun working at 200 kV, a CEOS spherical aberration corrector of the objective lens allowing for a spatial resolution of 0.9 Å, and an in-column Omega energy filter. The chemical composition of the NCs was determined by EDS, performed in STEM-HAADF mode, using a Bruker Quantax 400 system with a 60 mm² XFlash 6T silicon drift detector (SDD). For HRTEM characterization and STEM-EDS chemical analysis, the NC solutions were drop cast onto copper grids covered with an ultrathin amorphous carbon film and the measurements were carried out using an analytical holder equipped with a low background beryllium tip.

Photoluminescence measurements

Room-temperature, nanosecond time-resolved spectra were recorded using an Edinburgh Instruments FLS920 spectrofluorometer. The NCs were dispersed in chloroform and excited at 400 nm with a xenon lamp for the steady-state measurements, and at 400 nm with a pulsed laser (50 ps pulse duration) for the time-resolved traces. Typically, a region of 10 nm around the peak maximum was selected for the decay measurements. The time-resolved traces are fitted with a multi-exponential function; here we always report the resulting area-weighted average lifetime τ_avg. Absolute quantum efficiencies were determined with an integrating sphere, exciting the samples at 450 nm and 550 nm. The optical density of these samples was tuned to 0.1 at the excitation wavelength for each measurement. A calibration of the system using rhodamine 101 in ethanol yielded 92% ± 7% in agreement with literature values of 91.5% (ref. 36) to 96%.³⁷ The corresponding uncertainty also applies to the QE values reported here.

The biexciton room temperature PL was measured with a Hamamatsu streak camera. Samples were drop cast as close-packed thin films and excited at 400 nm, with a repetition rate of 1 kHz (using an 800 nm, 80 MHz femtosecond Ti:Sa laser coupled to a regenerative amplifier and frequency-doubled using a BBO crystal). The optical intensity was tuned between 8 μW cm⁻² and 2.3 mW cm⁻² to ensure that we measure the single exciton recombination dynamics at low power and a clear biexciton dynamics at the higher power.

Low temperature magneto-PL measurements were performed on drop cast films on silica substrates, inserted in the variable temperature insert of a split-coil 5 T magnet with direct optical access. The PL was excited at 405 nm using a picosecond pulsed diode laser, and collected with an optical fibre coupled to a spectrometer with a nitrogen-cooled charged coupled device (CCD) camera. For circularly polarized PL experiments, the emitted light was collected with a lens doublet and sent through a quarter wave plate coupled to a Glan–Thompson linear polarizer. Angularly resolved PL measurements were then conducted by rotating the quarter wave plate with an automated servo-motor that allowed for precise control of the angular position. Depolarization of the emerging linearly polarized light was provided by a 6 m long optical fibre. Time-resolved PL measurements were performed using the same excitation source and revealing the signal with a photomultiplier tube coupled to a time-resolved single photon counting unit.

For the single-dot PL measurements, a home-built scanning confocal microscope was used. The samples were prepared by drop casting highly diluted toluene solutions of NCs on 0.17 mm cover slips. After a brief drying period the cover slips were mounted on a glass microscope slide using Mowiol (Sigma) mounting medium. The Mowiol helps to minimize the light reflecting from the coverslip/sample interface. The final NC density was <1 NC per μm². The excitation source was a home-built super continuum laser³⁸ producing ∼50 ps pulses at a repetition rate of 80 MHz. The excitation beam used for the experiments was obtained by spectrally filtering (Bright Line HC 488/6 nm, AHF analysentechnik), yielding a 488 nm excitation wavelength. The beam was reflected by a dichroic mirror (zt-488-RDC, AHF analysentechnik) and focused by an oil-immersion objective with a numerical aperture of 1.4 (HCX PL APO 100×/1.40–0.70 Oil, Leica Microsystems) onto the NCs. The average optical intensity used to excite the samples equalled 3 mW cm⁻². The photoluminescence was collected by the same objective, transmitted by the dichroic mirror, filtered by a band-pass filter (Bright Line HC 629/56 nm, AHF analysentechnik) and focused into a fiber pigtailed single photon avalanche diode (SPAD) (PDF Series, MicroPhotonDevice). The graded index multimode fiber with a 62.5 μm core of the SPAD acted as a confocal pinhole. Photon counting measurements were accomplished by a time-correlated single photon card (TCSPC) (SPC-830, Becker & Hickl).

Results and discussion

Synthesis of CdSe/CdS nanocrystals

The core diameter of the CdSe seeds used for the CdS shell growth is tuned from 2.8 nm to 5.5 nm by adjusting the growth time. A typical synthesis of g-NCs starts from these seeds to grow a 15–20 monolayer (ML) shell in 4 hours. Transmission electron microscopy (TEM) images of aliquots taken during synthesis yield a direct view on the NC growth, here starting from 5.5 nm CdSe seeds and aiming for a CdS shell of 20 ML (Fig. 1). The CdSe core is converted into a CdSe/CdS core/shell NC with a total diameter of 11.6 nm (after 1 hour), 15.6 nm (2 hours) and finally 18.1 nm (4 hours). Calculating the expected diameter at these intervals from the mmol of Cd-oleate and TOPS added and a CdS atomic volume of 22.48 ų, we find values of 12.1 nm, 15.1 nm and 18.9 nm, respectively, agreeing well with the experimental data. CdS is thus deposited quantitatively on the CdSe seed NCs, without additional homogeneous nucleation of small CdS clusters.

Fig. 1 TEM images of the 5.5 nm CdSe seeds (a), and a series of CdSe/CdS aliquots taken after 1 hour (b, 11.6 nm ± 1.1 nm, average diameter and standard deviation of the size distribution), 2 hours (c, 15.6 nm ± 1.3 nm) and 4 hours (d, 18.1 nm ± 3.8 nm). The scale bar represents 20 nm.

X-ray diffraction (XRD) patterns obtained on the core and core/shell NCs (Fig. 2) were indexed according to CdS (JCPDS card no. 01-074-9663) and CdSe (JCPDS card no. 01-071-4772) hexagonal phases, confirming that they have a WZ crystal structure both before and after shell growth. These patterns clearly distinguish our NCs from others obtained through different continuous injection routes, which typically lead to ZB/WZ or ZB/ZB NCs, and hold promise for a detailed comparison of crystal-structure dependent opto-electronic properties in these materials.

Fig. 2 (a and b) XRD pattern of 4.0 nm CdSe NCs (a) and 4.0/14.2 nm CdSe/CdS (b) core/shell NCs. Vertical lines correspond to the bulk WZ pattern of CdSe (a) and CdS (b), respectively. The multi-peak structure between 20° and 30°, and the peak around 35° 2θ confirm that our NCs have a WZ crystal phase. (c) HRTEM image of two representative NCs of the 5.5/18.1 nm sample. (d) Details of a selected nanocrystal (white square) exhibiting (01̄1), (110) and (11̄2) lattice sets compatible with the [11̄1̄] zone axis projection of the WZ CdS phase, with lattice plane distances of 3.15 Å, 2.1 Å and 1.75 Å, respectively. (e) Lattice parameters are confirmed by the vector and angular relationship in the corresponding Fourier transform (FT) of the projected crystal potential.

Further crystal structure characterization of representative core/shell NCs (CdSe/CdS sample with 5.5/18.1 nm diameter) was carried out via HRTEM imaging (Fig. 2c–e). These observations confirmed the absence of defects and twinned structures, nor did we observe any multi-domain textures. The NCs exhibited a single crystalline nature throughout. Starting from the HRTEM data, a lattice parameter assessment, performed considering both vector and angular relationships between lattice sets in direct and reciprocal space, revealed lattice constants consistent with a CdS WZ crystal structure (JCPDS card no. 80-0006). STEM-EDX analysis of the same NCs yielded a chemical composition consisting mostly of CdS, with merely (0.6 ± 0.3) at% of Se present. This amount is compatible with a 5.5 nm CdSe core in an overall 18.1 nm NC, which is expected to yield 1.16 at%, and explains why the lattice parameters are dominated by the CdS crystal.

Growth times can be reduced to about 30 minutes without significantly affecting the material quality. Fig. 3a–c show that, starting from ca. 4 nm CdSe seeds and adding the required amount of CdS to grow 15 ML in 2 hours, 1 hour and 30 minutes, the final NC diameter is always close to the targeted value of 14.1 nm. For an even faster synthesis, i.e. when growing the 15 ML shell in only 10 minutes, we observed a significant fraction of homogeneously nucleated CdS NCs, as evidenced by a secondary PL peak around 500 nm. This also resulted in a smaller average CdSe/CdS diameter of 7.3 nm. Hence, one should limit the synthesis time to 30 minutes, or equivalently maintain a maximum Cd and S injection rate of ca. 10 mmol per hour. Note that for growth times of 30–60 minutes, PL spectra still revealed a minor secondary peak around 500 nm, however, as already discussed, the final CdSe/CdS diameter is not affected here, suggesting that the amount of homogeneously nucleated CdS constitutes a negligible fraction. Furthermore, they can be easily removed by size-selective precipitation.

Fig. 3 Synthesis of CdSe/CdS with a 4 nm core and a 15 ML CdS shell with a growth time of 2 hours (a), 1 hour (b), 30 min (c) and 10 min (d). The respective average diameters and standard deviations are 13.3 nm ± 1.3 nm, 14.5 nm ± 0.9 nm, 15.0 nm ± 1.0 nm, and 7.3 nm ± 2.8 nm, all in agreement with the expected diameter of 14.1 nm except for the last sample, grown in 10 min. The scale bar equals 20 nm.

CdSe/CdS giant-shell luminescence properties

Typical absorbance and PL spectra of the WZ/WZ giant-shell heterostructures, here 4.0/14.2 nm CdSe/CdS NCs, are shown in Fig. 4a. Due to the large volume of the CdS shell, the CdSe band-edge absorption is only about 1% of the CdS band-edge absorption, leading to a system that is nearly transparent in the emission region and has an effective global Stokes shift of 170 nm. The sample was synthesized using a growth time of 1 hour; PL spectra from the different aliquots are shown in Fig. 4b. The progressive red shift of the band-edge PL confirms the growth of a thick CdS shell, leading to strong electron delocalization in the shell region. Due to the attractive Coulomb potential of the core-localized hole that limits the spread of the exciton size, the PL red shift gradually reduces with increasing shell thickness. The corresponding time-resolved decay traces (Fig. 4c) show a progressively longer lifetime as the electron–hole overlap is reduced. Interestingly, the major increase is observed when the CdS shell thickness exceeds 3 nm (ca. 9 ML), with a final lifetime reaching 417 ns for 4.0/14.2 nm CdSe/CdS. Long PL lifetimes are also obtained for other core sizes: we find values of 647 ns (2.8/18.9 nm CdSe/CdS) and 464 ns (5.5/18.1 nm CdSe/CdS), respectively, for NCs with a shell of about 20 ML. This exceptionally long recombination lifetime requires dedicated attention. While extended lifetimes compared to core-only CdSe NCs are commonly observed in dot-in-rods, with values up to 35 ns,^22,39,40 and other spherical g-NCs, with longer lifetimes of 200–300 ns,²⁰ our decay times still systematically exceed the latter by a factor of 2 to 3. Time-resolved PL spectroscopy thus suggests that the electron–hole wave function overlap in our structures is further reduced with respect to other CdSe/CdS nanostructures, possibly by slight yet significant differences in the conduction band offset in WZ/WZ systems, although the exact nature remains to be investigated. The slightly non-exponential PL decay observed in Fig. 4c is at first unexpected considering the high PL QE values for these samples. Yet, with respect to type I core/shell NCs, the dynamics in quasi-type II NCs depends strongly on the electron–hole overlap,²⁰ which can still vary within the ensemble due to the distribution of interface features. Since this affects the PL dynamics much more than the PL emission energy, multi-exponential decays can be observed without significant broadening of the PL spectrum.

Fig. 4 (a) Absorbance (dashed line) and PL (full line) spectrum of 4.0/14.2 nm g-NCs. (b) PL spectra of a series of aliquots, with a red shift of 58 nm between the 4.0 nm core CdSe NCs and the final 4.0/14.2 nm core/shell NCs. (c) Time-resolved decay traces of the corresponding samples. (d) The lifetime increases strongly once the shell thickness surpasses 3 nm.

Another important aspect of our WZ/WZ giant-shell quantum dots is to have optical properties that are comparable with other materials in terms of PL QE, intermittency (blinking), and Auger recombination dynamics. First, when evaluating the (relative) PL QE as a function of the shell thickness, we observed that it steeply rises for thin shells, then decreases again slowly when the thickness surpasses 2–3 nm (Fig. 5a). As samples are excited at 400 nm, well into the CdS absorption band, the initial rise indicates that the shell passivates the CdSe core efficiently, yet beyond a given CdS volume, trapping of carriers on the CdS surface is able to compete with relaxation into the CdSe core. To quantify this behavior, we performed absolute PL QE measurements on the final aliquots using an integrating sphere. Exciting the samples at 450 nm, i.e. slightly above the CdS absorption edge, we found values of QE_sh = 38, 60, and 79% for giant-shell CdSe/CdS NCs with seed diameters of 2.8 nm, 4.0 mn and 5.5 nm, respectively. The QE further increased to QE_co = 72, 87 and even 90% when exciting the core directly at 550 nm. Note that the absolute QE is not to be compared with the relative QE values of Fig. 5a, due to the higher excitation wavelength of 400 nm compared to 450 nm, which might give rise to additional nonradiative hot exciton relaxation in the first case.⁴¹

Fig. 5 (a) Relative PL efficiency as a function of CdS shell thickness for 2.8 nm (blue circles), 5.5 nm (red triangles) and 4.0 nm (open green triangles: 2 hour synthesis, filled green triangles: 1 hour) CdSe seeds. The PL peaks around a CdS thickness of 2–3 nm, followed by a slow decrease. (b) Carrier relaxation scheme.

The PL QE data already confirm that a thick shell can lead to relaxation into surface traps and subsequent nonradiative recombination, especially when the core diameter is small. Using the QE values and a carrier relaxation schematic as depicted in Fig. 5b, we can derive the emission and trapping efficiencies after high energy excitation. Following assumptions are made: the high QE_co implies that the electron and hole interface trapping rates k_int,e and k_int,h are slow (on a nanosecond time scale), as they must be comparable to the radiative decay rate. The surface trapping rate k_sur on the other hand competes with the much faster (picosecond) carrier relaxation k_rel from the shell into the core. A recent field-assisted PL study on LEDs embedding dot-in-bulk NCs¹⁵ showed that, because of the rapid localization of holes from the shell to the core (20 ps for DiB NCs), surface hole trapping plays a minor role in the recombination of core excitons. On the other hand, photogenerated shell electrons (upon UV excitation) reside in the shell conduction band for longer times as they require prior hole localization in the core for being pulled away from the NC surfaces by its Coulomb potential. As a result, electrons are more significantly affected by surface defects than holes. Based on these observations and the fact that hole localization in our g-NCs is faster than in dot-in-bulk systems – confirmed by the absence of shell emission from g-NCs under low excitation fluence – we can reasonably assume that electron trapping in surface defects is the dominant non-radiative relaxation channel for shell electrons also in our NCs. As a result, we can consider k_int ≪ k_sur for both electrons and holes, while k_sur,h ≪ k_rel,h and k_sur,e ≤ k_rel,e which causes the lower PLQE under shell excitation.

The surface trapping efficiency can then be expressed as E_sur = 1 − QE_sh/QE_co. The interface trapping efficiency then equals E_int = 1 − QE_sh − E_sur. Table 1 summarizes the results for the 3 samples investigated. Clearly, both surface and interface trapping rates decrease as the core diameter increases. The first can be rationalized from a faster shell-to-core relaxation rate, simply because the core volume is larger. The second is likely related to the reduced overlap of the electron wave function with the CdSe/CdS interface in large CdSe core systems, reducing the possibility for interface trapping.

Table 1 PL efficiency QE_co when exciting the NC core (at 550 nm), QE_sh when exciting the CdS shell (at 450 nm), and resulting interface E_int and surface E_sur trap efficiencies

CdSe/CdS	QEco	QEsh	E int	E sur
2.8/18.9 nm	72	38	15	47
4.0/14.2 nm	87	60	9	31
5.5/18.1 nm	90	79	9	12

---

Carrier dynamics

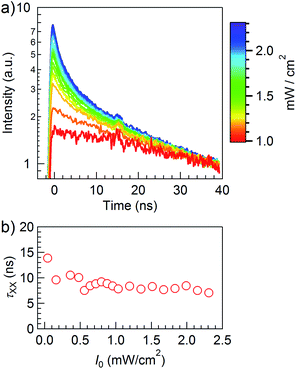
In line with the high PL QE, the PL intermittency measured on different single dots shows that large-core g-NCs do not blink. A typical PL intensity trace of a 5.5/18.1 nm CdSe/CdS NC, measured over the course of 10 minutes, is shown in Fig. 6. After some time the PL intensity changes somewhat due to drift, and the sample was realigned every 200 seconds, yet overall the PL remains high and the histogram shows a single peak. The standard deviation of the histogram equals 129 counts per 10 ms, which is about twice as large as the width of a Poisson distribution that has the same average rate (57 counts per 10 ms), indicating that the PL trace still contains small fluctuations, possibly induced by small changes in the local NC environment.⁴² When the core diameter is reduced to 2.8 nm, the predominant fraction in the ensemble remains optically stable, yet some NCs show fluctuations between a bright and a dark state.

Fig. 6 (a) 5 × 5 μm overview image of a distribution of single NCs (5.5/18.1 nm). The central NC (inset: 500 × 500 nm zoom of the NC) is used for measuring the time-dependent PL trace. (b) A typical NC does not show blinking. Due to drift, we needed to realign the system, at times indicated by the vertical lines. A count rate distribution is calculated for the period of 400–520 seconds. (c) The resulting histogram (red area) has a line width of 129 counts per 10 ms, about twice as large as the width of a Poisson distribution (black curve). (d) Similar measurements on 2.8/18.9 nm NCs reveal that most NCs are again stable, with a typical trace shown in the bottom panel. A small fraction however displays PL fluctuations, or even cease to emit after a prolonged exposure to the excitation beam (top trace).

The PL intermittence already suggests that the NCs are stable in time with no occurrence of dark states in the case of charging events. To further support this, we measured the biexciton recombination dynamics, from which the Auger recombination rate can be derived. At increasing excitation intensities, the time-resolved PL decay traces show an additional fast multi-exponential component on top of the slow decay due to single exciton recombination (Fig. 7a, 5.5/18.1 nm sample). From the effective lifetime of 14 ns at low power (Fig. 7b), and taking the PL QE and resulting radiative single exciton lifetime of 516 ns derived from the low-fluence PL dynamics, we obtain an expected biexciton radiative lifetime of 129 ns, yielding a biexciton emission efficiency of 11%. Measurements on CdSe/CdS with a 2.8 nm core diameter reveal a similar behaviour, yet with a biexciton decay time of 15 ns at low power and the corresponding efficiency of 6.7%, slightly lower than the first sample due to the longer single-exciton radiative lifetime of 899 ns. The reduced value compared to 5.5/18.1 nm NCs is in line with the increased PL intermittence observed for this sample, yet more importantly, the biexciton PL QE of our CdSe/CdS NCs is comparable to other CdSe/CdS giant-shell systems⁴³ and even CdSe/CdS NCs with an alloyed interface,⁴⁴ again confirming the high quality of our material.

Fig. 7 (a) Time-resolved PL decay traces normalized at 40 ns to the single-exciton decay. The superposed signal is due to multi-exciton recombination. (b) The resulting effective multi-exciton lifetime varies between 14 ns and 7 ns, corresponding to a PL QE of 5.4% (high input power, multi-exciton recombination) to 11% (low input power, biexciton recombination).

Cooling to cryogenic temperatures allows us to further understand the photophysics of the g-NCs. In Fig. 8a we report the temperature controlled PL decay traces of 5.5/18.1 nm CdSe/CdS NCs together with their respective PL spectra. Upon lowering the temperature, the emission energy progressively increases according to the gradual widening of the energy gap of both CdSe and CdS. Concomitantly, the PL lifetime decreases and the PL intensity at zero delay after the excitation pulse increases by a factor of two. The red shift of the emission spectrum together with the extension of the relaxation dynamics at higher temperatures could suggest progressive delocalization of the electron wave function due to equalization of the conduction band energies of the core and shell.²² However, the simultaneous enhancement of the PL intensity at zero delay and the weak, yet measurable drop of the PL QE at decreasing T (not shown) point to the formation of charged excitons that have twice the radiative recombination rate of neutral excitons and lower emission efficiency due to the activation of Auger recombination (cfr. the 11% biexciton emission efficiency, compared to the 90% single exciton efficiency).^34,45

Fig. 8 (a) Photoluminescence decay traces as a function of temperature of 5.2/18.1 nm CdSe/CdS g-NCs excited at 3.1 eV. The respective PL spectra are shown as the inset. (b) Polarization-resolved PL spectra of the same NCs at a magnetic field of B = 5 T and T = 1.5 K. The solid and dashed lines are σ⁻ and σ⁺ polarized PL, respectively. Inset: schematic representation of the energy levels of a negative trion with a heavy hole. (c) PL peak intensity dependence on the polarization angle at an increasing magnetic field (T = 1.5 K). Fit to a sine squared function for each field is shown in solid lines. (d) Polar plot of the polarized PL intensity as a function of the magnetic field (B = 1–5 T).

To unambiguously resolve what applies here, we performed polarization resolved PL measurements in the presence of high magnetic fields. Fig. 8b shows the circular polarization resolved PL spectra of the same NCs of Fig. 8a measured at 1.5 K in the presence of a 5 T magnetic field. In agreement with a recent study by Javaux et al.⁴⁶ that showed that the low temperature emission from giant-shell CdSe/CdS NCs is dominated by negative trion recombination, the PL is circularly polarized with a stronger emission from the σ⁻ component. The energy level scheme of the negative trion is shown in the inset of Fig. 8b.²⁴ The PL intensity dependence on the polarization angle was fitted with a squared sine function (Fig. 8c) and the polar diagram is shown in Fig. 8d for an increasing magnetic field. At B = 0 T, the almost null polarization evidences a balance between the co-circular and the counter-circular contributions which indicates an equal population of the +3/2 and −3/2 trion states. Increasing magnetic fields lift the degeneracy between the trion states, leading to circularly polarized emission dominated by the σ⁻ component that, as expected, reaches its maximum intensity at 45° between the quarter wave plate and the linear polarizer. By comparing the PL intensities in perpendicular polarization conditions corresponding to the maximum contribution of either the σ⁻ or the σ⁺ component, we obtain a polarization degree P_circ = (σ⁺ − σ⁻)/(σ⁻ + σ⁺) = −0.2, in good agreement with ref. 47. Considering both the temperature controlled PL dynamics and the magneto-PL data, the WZ/WZ g-NCs obtained through our modified fast route have a similar tendency to charge with excess electrons at low temperature as systems produced with other reported protocols and crystal structures.

Conclusions

Both the CdSe core and the CdSe/CdS core/shell NCs are synthesized at high temperatures, 380 °C and 300 °C, respectively. This yields monocrystalline NCs, with an epitaxial growth of a nearly defect-free CdS shell. As a result, the PL QE reaches values of up to 90% when exciting the core directly in 5.5/18.1 nm CdSe/CdS NCs. Even NCs with a smaller core, and thus stronger electron delocalization and increased overlap with the CdSe/CdS interface maintain a QE of 72%. The PL lifetime falls in the range of 450–700 ns, which is among the longest values reported for CdSe/CdS giant-shell NCs. Measurements of the PL intermittency show that the g-NCs with a 5.5 nm core continuously emit from their bright state, with no evidence of Auger induced quenching. Reducing the core size somewhat increased PL fluctuations, yet overall the sample shows a comparable behavior. Time-resolved PL decay spectroscopy confirms the suppressed Auger recombination, and when cooling down the samples to cryogenic evidence, we have found clear evidence of emission from a negative trion state. Overall, the WZ/WZ g-NCs presented here are compared with the state-of-the-art g-NCs described in the literature, while the different (WZ) crystal structures for the CdSe core hold promise for further engineering of opto-electronic properties.

Acknowledgements

The authors acknowledge financial support from the European Community's Seventh Framework Program (FP7/2007-2013) under grant agreement no. 324603 (EDONHIST, S.B.) and 298022 (NIRPLANA, I.M.). S.B. acknowledges support from the Cariplo Foundation (2012-0844).

Notes and references

1. J. Zhao, J. A. Bardecker, A. M. Munro, M. S. Liu, Y. Niu, I.-K. Ding, J. Luo, B. Chen, A. K.-Y. Jen and D. S. Ginger, Nano Lett., 2006, 6, 463–467.
2. W. K. Bae, S. Brovelli and V. I. Klimov, MRS Bull., 2013, 38, 721–730.
3. F. Garcia-Santamaria, Y. Chen, J. Vela, R. D. Schaller, J. A. Hollingsworth and V. I. Klimov, Nano Lett., 2009, 9, 3482–3488.
4. M. Zavelani-Rossi, M. G. Lupo, R. Krahne, L. Manna and G. Lanzani, Nanoscale, 2010, 2, 931.
5. I. Moreels, G. Rainò, R. Gomes, Z. Hens, T. Stöferle and R. F. Mahrt, Adv. Mater., 2012, 24, OP231–OP235.
6. G. Xing, Y. Liao, X. Wu, S. Chakrabortty, X. Liu, E. K. L. Yeow, Y. Chan and T. C. Sum, ACS Nano, 2012, 6, 10835–10844.
7. R. C. Somers, M. G. Bawendi and D. G. Nocera, Chem. Soc. Rev., 2007, 36, 579–591.
8. A. P. Alivisatos, W. Gu and C. Larabell, Annu. Rev. Biomed. Eng., 2005, 7, 55–76.
9. X. Brokmann, G. Messin, P. Desbiolles, E. Giacobino, M. Dahan and J. P. Hermier, New J. Phys., 2004, 6, 99.
10. F. Pisanello, L. Martiradonna, G. Lemenager, P. Spinicelli, A. Fiore, L. Manna, J.-P. Hermier, R. Cingolani, E. Giacobino, M. De Vittorio and A. Bramati, Appl. Phys. Lett., 2010, 96, 033101.
11. B. Mahler, P. Spinicelli, S. Buil, X. Quelin, J.-P. Hermier and B. Dubertret, Nat. Mater., 2008, 7, 659–664.
12. Y. Chen, J. Vela, H. Htoon, J. L. Casson, D. J. Werder, D. A. Bussian, V. I. Klimov and J. A. Hollingsworth, J. Am. Chem. Soc., 2008, 130, 5026–5027.
13. B. Mahler, N. Lequeux and B. Dubertret, J. Am. Chem. Soc., 2010, 132, 953–959.
14. C. Galland, S. Brovelli, W. K. Bae, L. A. Padilha, F. Meinardi and V. I. Klimov, Nano Lett., 2013, 13, 321–328.
15. S. Brovelli, W. K. Bae, C. Galland, U. Giovanella, F. Meinardi and V. I. Klimov, Nano Lett., 2014, 14, 486–494.
16. E. Cassette, B. Mahler, J.-M. Guigner, G. Patriarche, B. Dubertret and T. Pons, ACS Nano, 2012, 6, 6741–6750.
17. L. Carbone, C. Nobile, M. De Giorgi, F. Della Sala, G. Morello, P. Pompa, M. Hytch, E. Snoeck, A. Fiore, I. R. Franchini, M. Nadasan, A. F. Silvestre, L. Chiodo, S. Kudera, R. Cingolani, R. Krahne and L. Manna, Nano Lett., 2007, 7, 2942–2950.
18. D. V. Talapin, J. H. Nelson, E. V. Shevchenko, S. Aloni, B. Sadtler and A. P. Alivisatos, Nano Lett., 2007, 7, 2951–2959.
19. S. Deka, K. Miszta, D. Dorfs, A. Genovese, G. Bertoni and L. Manna, Nano Lett., 2010, 10, 3770–3776.
20. S. Brovelli, R. D. Schaller, S. A. Crooker, F. García-Santamaría, Y. Chen, R. Viswanatha, J. A. Hollingsworth, H. Htoon and V. I. Klimov, Nat. Commun., 2011, 2, 280.
21. G. Rainò, I. Moreels, A. Hassinen, T. Stöferle, Z. Hens and R. F. Mahrt, Nano Lett., 2012, 12, 5224–5229.
22. G. Rainò, T. Stöferle, I. Moreels, R. Gomes, J. S. Kamal, Z. Hens and R. F. Mahrt, ACS Nano, 2011, 5, 4031–4036.
23. M. Zavelani-Rossi, M. G. Lupo, F. Tassone, L. Manna and G. Lanzani, Nano Lett., 2010, 10, 3142–3150.
24. A. Shabaev, A. V. Rodina and A. L. Efros, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205311.
25. H. Eshet, M. Grünwald and E. Rabani, Nano Lett., 2013, 13, 5880–5885.
26. M. Allione, A. Ballester, H. Li, A. Comin, J. L. Movilla, J. I. Climente, L. Manna and I. Moreels, ACS Nano, 2013, 7, 2443–2452.
27. F. García-Santamaría, S. Brovelli, R. Viswanatha, J. A. Hollingsworth, H. Htoon, S. A. Crooker and V. I. Klimov, Nano Lett., 2011, 11, 687–693.
28. J. I. Climente, J. L. Movilla and J. Planelles, Small, 2012, 8, 754–759.
29. G. Rainò, T. Stöferle, I. Moreels, R. Gomes, Z. Hens and R. F. Mahrt, ACS Nano, 2012, 6, 1979–1987.
30. N. Accanto, F. Masia, I. Moreels, Z. Hens, W. Langbein and P. Borri, ACS Nano, 2012, 6, 5227–5233.
31. F. T. Rabouw, P. Lunnemann, R. J. A. van Dijk-Moes, M. Frimmer, F. Pietra, A. F. Koenderink and D. Vanmaekelbergh, Nano Lett., 2013, 13, 4884–4892.
32. F. Pisanello, G. Leménager, L. Martiradonna, L. Carbone, S. Vezzoli, P. Desfonds, P. D. Cozzoli, J.-P. Hermier, E. Giacobino, R. Cingolani, M. De Vittorio and A. Bramati, Adv. Mater., 2013, 25, 1974–1980.
33. M. Cirillo, T. Aubert, R. Gomes, R. Van Deun, P. Emplit, A. Biermann, H. Lange, C. Thomsen, E. Brainis and Z. Hens, Chem. Mater., 2014, 26, 1154–1160.
34. P. P. Jha and P. Guyot-Sionnest, ACS Nano, 2009, 3, 1011–1015.
35. J. Jasieniak, L. Smith, J. van Embden, P. Mulvaney and M. Califano, J. Phys. Chem. C, 2009, 113, 19468–19474.
36. C. Würth, J. Pauli, C. Lochmann, M. Spieles and U. Resch-Genger, Anal. Chem., 2012, 84, 1345–1352.
37. R. F. Kubin and A. N. Fletcher, J. Lumin., 1982, 27, 455–462.
38. G. Vicidomini, I. Coto Hernández, M. d' Amora, F. Cella Zanacchi, P. Bianchini and A. Diaspro, Methods DOI:10.1016/j.ymeth.2013.06.029.
39. G. Xing, S. Chakrabortty, S. W. Ngiam, Y. Chan and T. C. Sum, J. Phys. Chem. C, 2011, 115, 17711–17716.
40. C. She, A. Demortière, E. V. Shevchenko and M. Pelton, J. Phys. Chem. Lett., 2011, 2, 1469–1475.
41. P. Kambhampati, J. Phys. Chem. C, 2011, 115, 22089–22109.
42. G. Schlegel, J. Bohnenberger, I. Potapova and A. Mews, Phys. Rev. Lett., 2002, 88, 137401.
43. Y.-S. Park, A. V. Malko, J. Vela, Y. Chen, Y. Ghosh, F. García-Santamaría, J. A. Hollingsworth, V. I. Klimov and H. Htoon, Phys. Rev. Lett., 2011, 106, 187401.
44. Y.-S. Park, W. K. Bae, L. A. Padilha, J. M. Pietryga and V. I. Klimov, Nano Lett., 2014, 14, 396–402.
45. C. Galland, Y. Ghosh, A. Steinbrück, M. Sykora, J. A. Hollingsworth, V. I. Klimov and H. Htoon, Nature, 2011, 479, 203–207.
46. C. Javaux, B. Mahler, B. Dubertret, A. Shabaev, A. V. Rodina, A. L. Efros, D. R. Yakovlev, F. Liu, M. Bayer, G. Camps, L. Biadala, S. Buil, X. Quelin and J.-P. Hermier, Nat. Nanotechnol., 2013, 8, 206–212.
47. F. Liu, L. Biadala, A. V. Rodina, D. R. Yakovlev, D. Dunker, C. Javaux, J.-P. Hermier, A. L. Efros, B. Dubertret and M. Bayer, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035302.

---