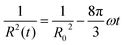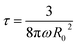Highly ordered and tunable polyHIPEs by using microfluidics

Abstract

We demonstrate how to generate highly ordered porous matrices from dextran-methacrylate (DEX-MA) using microfluidics. We use a flow focusing device to inject an aqueous solution of DEX-MA and surfactant to break the flow of an organic solvent (cyclohexane) into monodisperse droplets at a high volume fraction (above 74% v/v) to form an ordered high internal phase emulsion (HIPE). We collect the crystalline HIPE structure and freeze it by gelling. The resulting polyHIPEs are characterized by an interconnected and ordered morphology. The size of pores and interconnects ranges between hundreds and tens of micrometers, respectively. The technique that we describe allows for precise tuning of all the structural parameters of the matrices, including their porosity, the size of the pores and the lumen of interconnects between the pores. The resulting ordered and precisely tailored HIPE gels represent a new class of scaffolds for applications in tissue engineering.

---

1. Introduction

PolyHIPEs are a class of porous and permeable materials obtained by curing the external phase of a high internal phase emulsion (HIPE), i.e. an emulsion in which the internal volume fraction, Φ_d, is larger than the critical value of the most compact arrangement of spheres (Φ_d = 0.74). These porous polymeric matrices are useful materials for a wide range of advanced applications, such as catalyst supports, ion-exchange modules, separation media, electrochemical sensing, etc. Last but not least, these materials are perfectly suited to serve as scaffolds in tissue engineering, where the trabecular and fully interconnected morphology is essential for their function.¹ An interconnected network of pores of appropriate dimension permits proper exchange of liquids, migration of cells and vascularization. These features prompted the development of various polyHIPE materials, based on both synthetic and natural polymers, and their application in tissue engineering.^2–8 The use of polyHIPEs in tissue engineering presents two outstanding challenges. First, pores in materials templated on sheared emulsions typically have too small diameters, well below 100 μm. Small diameters of pores hamper colonization of scaffolds by cells. The seeded cells are often unable to penetrate into the material and, as a result, proliferate only at its outer surface.⁹ Few attempts have been made to adapt the morphological parameters of polyHIPEs to the needs of tissue engineering via a controlled destabilization of the precursor HIPE. This destabilization leads to the production of scaffolds with slightly larger pores. As a consequence, this approach has met only limited success.^10,11 Second, both pores and interconnects are typically highly polydisperse with standard deviations of the order of tens of percent of the mean sizes. This has numerous negative implications. Cells grown within such an inhomogeneous scaffold experience a highly varied chemical and geometrical environment which may lead to an unwanted phenotypic diversity within a 3D colony. Moreover, scaffolds are often modified with bioactive molecules such as growth factors, drugs or adhesion peptides. A non-uniform spatial structure prohibits homogeneous distribution of the chemical stimuli. From a structural point of view, the local properties of scaffolds fabricated with conventional polyHIPEs are highly and randomly varied. For instance, a distribution of the wall thickness of adjacent pores influences the local mechanical properties and the degradation rate of the scaffold when exposed to a biological environment. All these factors may lead to failures in the use of polyHIPE scaffolds in vivo. Also in this respect attempts to narrow polyHIPE pore size distribution have been pursued, such as the addition of pre-formed droplets of the same dimension through an HPLC pump. This approach has reduced to some extent the width of pore size distribution and increased the degree of cell colonization but nevertheless improvements were still limited.^12,13

The problems outlined above are directly related to the technology of production of polyHIPEs that use conventionally prepared emulsions. Shear based methods for generation of emulsions allow neither for control nor for tuning of the final morphology of the scaffold.

Recognition of the importance of structural homogeneity in tissue engineering inspired the use of rapid prototyping (RP) for a greater degree of control over the morphology of the scaffolds.^14–17 Controlled and precise layer-by-layer deposition of the scaffold according to a predetermined design allows for a programmed fabrication of scaffolds that addresses the needs of a range of cell types. In spite of the benefits of the top-down approach, the scaffolds manufactured via RP still present inhomogeneities in their structure. Usually, pores that are perpendicular to the deposition plane are considerably narrower than those in the plane.¹⁸

Recently microfluidics has been used in conjunction with the HIPE technique in the synthesis of monodisperse polymer particles and rods exhibiting the typical polyHIPE morphology.¹⁹ Here we show that with the use of microfluidics it is possible to obtain structures that possess the desired trabecular morphology, are highly ordered and uniformly spaced in all dimensions. We illustrate via detailed structural analysis the benefit of using microfluidics in generating highly porous, ordered and customizable matrices from O/W emulsions. Below, we demonstrate the possibility of tuning the morphology (in terms of porosity, pores size and the lumen of the interconnects between the pores) of the scaffolds by adjusting the flow rates of the two phases, by scaling the dimensions of channels of the microfluidic device, as well as by changing the surfactant content in the aqueous matrix liquid.

2. Materials and methods

2.1 Materials

All chemicals were purchased from Sigma Aldrich and used without further purification. The average molecular weight of dextran (T70), M_w, was 70.000 g mol⁻¹.

2.2 Synthesis of dextran-methacrylate (DEX-MA)

DEX-MA was synthesized following the procedure described previously.^20,21 Briefly, 5 g of dextran were dissolved in 45 ml of anhydrous DMSO in a round bottom flask under an Argon atmosphere. Then 1 g of 4-(N,N-dimethylamino)pyridine (DMAP) and a calculated amount of glycidyl methacrylate (GMA) for a theoretical degree of substitution (DS, the percentage number of methacrylate groups per 100 dextran glucopyranose residues) of 50% were added to the solution. The reaction was stirred in the dark at room temperature for 48 h and then an equimolar amount of HCl was added to neutralize the DMAP and to stop the reaction. Finally, DEX-MA was purified in dialysis tubing (MWCO = 2 kDa) at 4 °C against distilled water until reaching its nominal conductivity (0.5 μS cm⁻¹).

Quantitative determination of the degree of vinyl substitution (DS) was obtained by measuring the ratio between the average value of the integrals of the double-bond protons (δ ≈ 5.8 and 6.2 ppm) and the integral of the anomeric proton signals (δ ≈ 5.0 ppm) in the ¹H-NMR spectrum (Fig. S1†). The DS was 35% with respect to moles of repeating units.

2.3 Production of polycarbonate (PC) chips

The microfluidic chips were realized with a CNC milling machine (MSG402, ErgWind, Poland) on a polycarbonate (PC) sheet 5 mm in thickness. The chips were sonicated in isopropanol for 30 minutes and then sealed with a hot press at 130 °C for about 30 min and let to cool down slowly to room temperature. After sealing, the PC surfaces where modified to render them resistant to the organic inner phase following a procedure describe in the literature.²²

The reaction mixture used to modify the surface of PC consists of an ethanolic solution of SnCl₂ (20% w/w), which was injected through the microchannels for 2 h (Q_l = 2 ml h⁻¹). During this time, the temperature is kept constant at 60 °C. At the end of this step, the chip is cleaned with deionized water for 20 minutes and soon after it is ready to use.

2.4 Study of the accessible ranges for Φ_d and D_drop within microfluidic chips

Before starting with the production of scaffolds, we extensively studied the accessible ranges for the volume fraction of the oily phase (Φ_d) and the diameter of droplets (D_drop) within the designed chips on varying the flow rates of both phases. A typical experiment consists of setting Q_c and then slowly increasing the flow rate of the dispersed phase Q_d. After each increase of Q_d, the system needs generally less than one minute to reach the equilibrium. During this operation, the diameter of droplets increases until reaching an upper limit. Once this limit is overcome, the system becomes unstable and the formation of a continuous thread of the dispersed phase is observed in the outlet channel. In this way, we scanned for each Q_c the complete range of Q_d for which droplets are formed in a stable manner.

2.5 Scaffold production

Microfluidic samples. 200 mg of DEX-MA were dissolved in 1 ml of deionized water. Then, 0.5% w/v of Irgacure 2959, 1% w/v of ammonium persulfate (APS), and 20% w/v of Pluronic F-68 were added to the aqueous solution. As the dispersed phase cyclohexane was used. Since room light can catalyze radical dissociation of the photo-initiator and then trigger the polymerization of DEX-MA, during the production of emulsions, syringes were covered with an aluminum foil to keep the DEX-MA solution in the dark. A typical experiment consists of regulating the flow rates of the phases until a dense steady-state packing of the droplets (with Φ_d always greater than 74% v/v) is reached in the outlet channel. The production of HIPEs was monitored continuously with a Photron Fastcam 1024 PCI at 500 fps, and the recorded videos were used for image analysis. The two phases were supplied with syringe pumps (Harvard Apparatus PhD 2000). At the exit of the outlet channel, the HIPE is collected for few minutes in glass cylinders of 8 mm in diameter until reaching a thickness of about 1 cm and then cross-linked under a UV-lamp (1.2 W, λ = 365 nm) for 20 min. During cross-linking, HIPEs were isolated from the atmosphere with a thin layer of cyclohexane. No coalescence phenomena were observed during exposure to UV radiation. Then the semi-cross-linked HIPEs were put in an oven at 50 °C for 24 h to activate the APS and complete the cross-linking reaction. After cross-linking of the outer aqueous phase, the organic inner phase was removed from the matrix with multiple extractions with DMSO and this in turn was removed by washing several times with distilled water for 3 days until reaching its nominal conductibility. The scaffolds were frozen at −75 °C and then freeze-dried.

Conventional polyHIPEs. The synthesis and purification of conventional DEX-MA based polyHIPEs has been described in detail in a previous work.²³ In conformity with microfluidic polyHIPEs, the chemical compositions of the continuous and dispersed phases are identical in both cases. The only differences regarded dextran molecular weight (40.000 g mol⁻¹) and Pluronic F-68 concentration (5% w/v).

2.6 SEM analysis

The structures of the scaffolds were investigated using scanning electron microscopy (SEM) (Nova NanoSEM) operating at 5 kV. Prior to observation, fractured samples were mounted on aluminum stubs using adhesive carbon tape to increase the conductivity. All samples were observed without any sputtering.

2.7 Micro-computed tomography (μCT) analysis

Micro-computed tomography is a non-destructive technique that generates a stack of 2D cross-sectional images of a sample using an X-ray source. Through the manipulation of these 2D images, it is possible to create a 3D reconstruction of the sample and, as a consequence, to perform 3D analyses. Acquisition was performed on freeze-dried scaffolds using an Xradia MicroXCT-400 with the following parameters: 40 kV voltage, 10 W power, no filter material, and 0.18° rotation step in an angle interval of 184°. The voxel size was the same for all microfluidic samples (2 × 2 × 2 μm), while for the conventional HIPEs was smaller (1 × 1 × 1 μm). Scanning was performed at atmospheric pressure and room temperature (25 °C). Image analysis of data obtained from μCT was carried out following the same procedure described in a precedent work.²⁴

2.8 Numerical calculations

Numerical calculations of the shape of a single droplet compressed by the surrounding droplets, all forming a periodic hcp or fcc crystal lattice, were performed with an open-source software Surface Evolver.²⁵ The software triangulates the numerically implemented liquid interface and moves its vertices, under predefined constraints, towards the final equilibrium shape by the steepest descent of energy. In the present case, the interface was constrained to evolve inside a Voronoi cell (implemented as rigid walls) of the chosen crystal lattice preserving the volume of the liquid. Due to symmetry considerations only a twelfth portion of the droplet needed to be calculated and its shape turned out to be the same regardless of the hcp or fcc lattice. While the Voronoi cell in an hcp lattice is characterized by mirror symmetry in the direction perpendicular to the plane defined by the hexagonal arrangement of the surrounding cells, the cell in an fcc lattice lacked this symmetry. However, the latter could be obtained from the former by twisting its half, as cut by the plane of symmetry, by the angle π/3 with respect to the other half (compare Fig. 8e and 9d, which show the views perpendicular to the plane). We assumed that the surface tension of the droplet–droplet interface in general differed from the surface tension of the free droplet. As such this effectively set the contact angle with the walls of the Voronoi cell, which in turn influenced the final equilibrium surface area of the droplet–droplet interfaces (interconnections). If the contact angle θ is set to π, this corresponded to non-adhesive droplets, which did not develop interconnections (Fig. 8d). If the contact angle was less than we observed formation of interconnections: circular, rhombic (fcc and hcp) or trapezoidal (hcp) depending on both θ and the volume fraction Φ_d (in principle decreasing θ leads to rounding off of edges while increasing Φ_d leads to an opposite trend). Note that Φ_d was calculated as the volume of the droplet divided by the total volume of the Voronoi cell.

3. Results

Microfluidic systems manipulate small volumes of fluids offering precise and reproducible control of flow. In 2002, Anna et al. reported the first example of a planar flow focusing (FF) circuit integrated into a microfluidic chip.²⁶Fig. 1 illustrates this geometry.

Fig. 1 Optical micrograph of the flow focusing chip FF1 showing production of monodisperse droplets. Scale bar is 100 μm.

In order to produce a monodisperse oil-in-water (O/W) emulsion, the continuous aqueous phase must preferentially wet the walls of the channels. This phase flows from the side channels to enclose and focus a stream of the dispersed oily phase delivered via the central one.

Immediately downstream of the channels that deliver the two immiscible liquids, there is an orifice – a constriction that focuses the flow. The oily droplet phase periodically enters the orifice, inflates a droplet in the outlet channel and then is squeezed by the continuous phase, releasing a droplet.^27,28

FF chips allow for a very precise control over the parameters of the emulsion that they form.²⁹ By changing the flow rates of the two phases (Q_c, flow of the continuous phase, and Q_d, flow of the dispersed phase), it is possible to tune in a wide range (i) the frequency of generation of droplets, (ii) their diameter (D_drop), and (iii) the nominal volume fraction of the dispersed phase (Φ_d ≈ Q_d/(Q_d + Q_c)) of the emulsion.^27–30 These features, i.e. well controlled monodisperse size, and well-controlled volume fraction represent a perfect basis for the design of tailored scaffolds of desired porosity (fixed by Φ_d) and a very sharp pore size distribution (PSD, fixed by D_drop).

In order to highlight the benefits of using microfluidics, we decided to produce and compare HIPE templated scaffolds of the same chemical composition fabricated via a conventional approach based on a sheared emulsion and by using templates generated with microfluidic FF systems. In all cases we imposed a constant volume fraction of the dispersed phase to Φ_d ≈ 0.8 – i.e. we set the value of porosity of the scaffolds to about 80%. This value of Φ_d, from our experience, represents a good compromise between large porosity and good mechanical robustness of the resulting 3D matrices. Higher porosity results in weak and fragile scaffolds while lower volume fraction decreases the number and the diameter of interconnects, which might hamper the colonization and proliferation of cells within the matrices.

We used dextran-methacrylate as the material for the scaffolds. Dextran is a biocompatible polysaccharide comprising glucose units connected by α-(1 → 6)-glucosidic linkages with occasional branches in C(3), and is widely used in biomedicine. Dextran is highly soluble in water (up to 50% w/v). Due to the highly flexible structure of dextran, its aqueous solutions, even at high concentrations present moderate viscosity that allows for processing in microfluidic systems. Dextran can be readily functionalised with methacrylic groups. The resulting derivatives can then be cross-linked via radical polymerization.

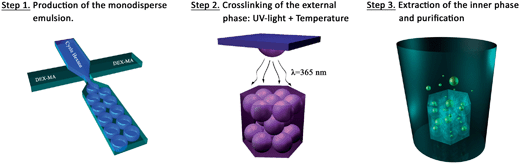
The experimental process of fabrication of scaffolds prepared either with the conventional approach or within microfluidic FF systems involves 3 steps: (i) production of the O/W emulsion, (ii) cross-linking of the external aqueous phase, and (iii) extraction of the inner oily phase and purification. The conventional polyHIPE scaffold (we will refer to it as SC_conv) was synthesized following a procedure previously described while the synthesis of microfluidic based scaffolds is sketched in Fig. 2.²³

Fig. 2 Schematic representation of the production process of 3D scaffolds through microfluidic HIPEs. The entire process consists of three steps. In the first one, we structured the templating of an aqueous solution of DEX-MA within the FF chip through the production of monodisperse droplets of cyclohexane (C-HEX). The resultant O/W emulsion is collected at the end of the outlet channel inside glass cylinders. In the second step, the emulsion is cross-linked firstly under UV-light (λ = 365 nm) and then at 50 °C for 24 h. The last step consists of extracting the inner oily phase with an organic polar solvent. The obtained 3D porous hydrogel is then purified through several washing steps with ultrapure water until it reaches its nominal conductivity.

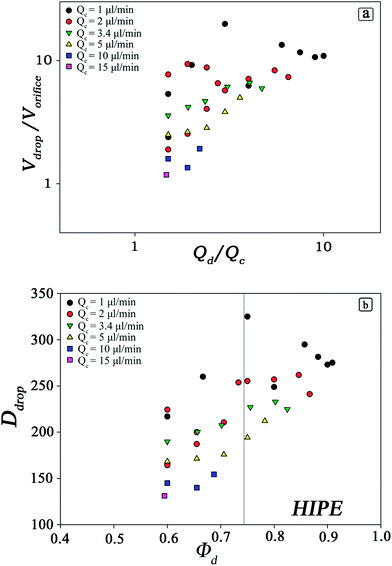
As the volumes of the droplets depend strongly on the geometry of the microfluidic device, on the flow rates and to a certain extent on the material parameters of the liquids, the first important step in preparation of templates is to determine the range of values accessible by the processing parameters.^{27–29,31,32} These are constituted by independent physical variables such as Q_c and Q_d and the dependent parameters Φ_d and D_drop (Fig. 3). We analysed accurately the relationship between these parameters via experiments within the chip FF1.

Fig. 3 (a) A log–log variation in the dimensionless droplet volume, V_drop/V_orifice, of the dispersed phase plotted as a function of flow rate ratios of the two immiscible phases and (b) available diameters of droplets (D_drop) plotted as a function of Φ_d within chip FF1.

The data shown in Fig. 3 imply large degree of freedom in tailoring the morphology of microfluidic polyHIPEs. As we are interested in scaffolds with Φ_d > 0.74, we studied the production of droplets for Φ_d > 0.6 and for values of Q_c in the range 1 ÷ 15 μl min⁻¹. The volume of droplets depends strongly on the flow rates of both phases. For a constant value of Q_d/Q_c, the volume of droplets decreases with increasing flow rate of the continuous phase. At the same time Φ_d decreases with increasing Q_c. Moreover, analysing the portion of the curves with Φ_d ≥ 0.74, only values of Q_c up to 5 μl min⁻¹ give rise to HIPEs.

In our experiments, the continuous polymeric phase (DEX-MA) had a constant dynamic viscosity μ_c = 21.7 mPas and the dispersed phase (cyclohexane) μ_d = 0.82 mPas.

The use of liquids of different viscosities requires inspection of the ranges of flow that produce monodisperse droplets. It is known that high viscosities of the droplet phase allow for the generation of monodisperse droplets, although within narrowed range of flow rates.²⁹

The effect of high viscosities of the continuous phase was much less investigated, although it has been shown that even viscoelastic continuous liquids may produce monodisperse droplets.³³

We also checked that the range of D_drop can be expanded by tuning the dimensions of the channels of the flow-focusing chip. Thus, we designed two additional microfluidic devices to produce larger droplets with a two-fold volume (FF2) and five-fold volume (FF5) compared to those produced within FF1 (Table 1). We will refer to the scaffolds fabricated within microfluidic devices as SC_FF1, SC_FF2 and SC_FF5. Both these two new microfluidic circuits were subjected to the same kind of investigation carried out for FF1. The range of Φ_d explored was limited to 60–90% which is of interest for our purposes. The ranges of Q_c and Q_d explored were for FF2 Q_c = 1 ÷ 15 μl min⁻¹, Q_d = 2 ÷ 35 μl min⁻¹, and for FF5 Q_c = 5 ÷ 20 μl min⁻¹ and Q_d = 7 ÷ 40 μl min⁻¹. Within these ranges of Q_c and Q_d, we were able to produce monodisperse droplets with a diameter D_drop = 150 ÷ 400 μm inside the FF2 chip and D_drop = 250 ÷ 600 μm inside the FF5 chip.

Table 1 W _or = orifice width; W_out = outlet channel width; h = channel depth. The scale factors are relative to FF1. Flow rates of the continuous phase Q_c and the dispersed phase Q_d used for the production of HIPE templates. D_drop is the diameter of droplets inside microfluidic chips measured from the recorded high-speed video. f is the frequency of droplet production

	W or (μm)	W out (μm)	h (μm)	Scale factor	Q c (μl min^−1)	Q d (μl min^−1)	D drop ± 5% (μm)	f (Hz)
FF1	100	400	100	1	3.4	13.8	220	50
FF2	140	560	140	1.4	7.0	28.0	280	63
FF5	230	920	230	2.3	8.0	33.0	400	71

---

The last important parameter of the process of generation of a template for the scaffold is the frequency (f) of generation of droplets in the FF junction. Low frequencies result in long production cycles and introduce the risk of coalescence and of Ostwald ripening of droplets – processes that both broaden the distribution of volumes of the drops. We thus chose to work with possibly high rates of flow and high frequencies of generation of droplets that yield the desired diameter and volume fraction of droplets. The flow rates of Q_c and Q_d used for the production of O/W emulsions are listed in Table 1.

We used the HIPEs as templates for 3D scaffolds and characterized the scaffolds by means of Scanning Electron Microscopy (SEM), optical microscopy and high-resolution computed micro-tomography (μCT). The SEM micrographs (Fig. 4) clearly show that microfluidic templated scaffolds (Fig. 4b–d) present a superior degree of order and uniformity of the porous texture in terms of pores and interconnects when compared with SC_conv (Fig. 4a). The considerable increase in pore size experienced by the three scaffolds generated by the three microfluidic devices reported in Table 1 is evident. It is interesting to observe the morphological differences exhibited by microfluidic scaffolds between the surface (Fig. 4b and c), which represents the ‘boundary’ of the scaffolds, and the bulk material: more external pores possess a different morphology with a large interconnect interfacing with the external world and a smaller number of the regularly sized interconnects, while pores in the bulk material (Fig. 4d) generally have 12 similar interconnects oriented regularly in the space.

Fig. 4 SEM micrographs of scaffolds fabricated through (a) conventional HIPE formation (SC_conv) and (b–d) microfluidic flow-focusing devices (b) SC_FF1, (c) SC_FF2 and (d) SC_FF5. The scale bars measure respectively (a) 30 μm and (b), (c), and (d) 100 μm. Panels (b) and (c) show the surface of the microfluidic scaffolds while panels (a) and (d) show random fractured sections.

The top views of SC_FF1 in the swollen state (Fig. 5), observed by optical microscopy, clearly show large crystalline domains. Most often we observed closely packed structures – i.e. face-centered cubic (fcc, also called cubic close packed) and hexagonal close packed (hcp). The water filled pores behave as divergent lenses and reflect the pattern of the layers below. This creates the fractal-like pattern shown in Fig. 5. Upon close analysis we were able to identify few different facets of the crystalline arrangement of the pores, including hcp, fcc [111] and fcc [100] (Fig. 5a–c).

Fig. 5 Optical micrographs of SC_FF1 scaffolds in the swollen state. Large domains of crystal lattices of closely packed pores are clearly visible. By examining the shadows inside each pore, it is possible to distinguish between (a) the hexagonal close packing (hcp) and (b) the face-centered cubic (fcc) in the [111] direction. In (c) the fcc in the [100] direction is reported while in (d) the transition between fcc arrangements in the [111] and [100] directions is shown. The insets show the numerical simulations for a single pore assuming respectively an (a) hcp, (b) fcc [111] and (c) fcc [100] crystal domains. The scale bars in (a), (b) and (c) measure 200 μm while in (d) 1 mm.

In order to estimate quantitatively and accurately the morphological parameters, i.e. the percentage porosity, the mean pore diameter size 〈D〉 and the mean diameter of interconnects 〈d〉, we performed high-resolution computer micro-tomographic scans (μCT) on all four types of scaffolds. In Fig. 6, the pore sizes distributions (PSDs) of the four samples in the dry state are shown and the results are summarized in Table 2.

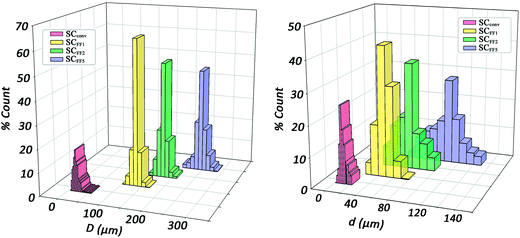Fig. 6 (Left) pore size distributions (PSDs) and (right) interconnect size distributions of the scaffolds in the dry state produced through microfluidic O/W HIPE and conventional HIPE methods.

Table 2 〈D〉 = mean pore diameter size; 〈d〉 = mean diameter of interconnects; σ = standard deviation; I (%) = percentage interconnectivity among pores; P (%) = percentage porosity; SSA = specific surface area estimated from μCT data of the scaffolds produced either via microfluidic or conventional HIPE

	〈D〉 (μm)	σ 〈D〉 (μm)	σ %	〈d〉 (μm)	σ 〈d〉 (μm)	σ %	I (%)	P (%)	SSA (mm^2 mm^−3)
SCFF1	136	8	6	46	9	20	100	82	35
SCFF2	171	14	8	62	15	25	100	85	28
SCFF5	241	22	9	106	32	30	100	84	19
SCconv	25	7	28	12	6	50	100	82	240

---

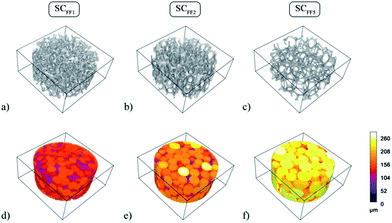
All three microfluidic HIPE-based matrices presented very narrow distributions of pore diameters, with standard deviations always below 10% of the mean value. A visual appreciation of such monodispersity can be gained from the 3D coloured-calibrated maps of pores (Fig. 7d–f). Such images together with the 3D reconstructions (Fig. 7a–c) illustrate that the scaling of the microfluidic flow-focusing junction can be effectively used to tune the mean diameter of the pores. Both average pore diameters and relative standard deviations are reported in Table 2. As it can be noted σ_%〈D〉 tends to increase to some extent from SC_FF1 to SC_FF2. This may be due to the occurrence of few coalescence phenomena. The probability of droplet coalescence is proportional to droplet dimension. This is well illustrated by the following formula describing quantitatively the kinetics of coalescence in a concentrated emulsion:

where R(t) is the droplet size at time t, R₀ is the initial droplet radius, ω is the frequency of rupture per unit surface of the continuous phase film and τ is the time to complete coalescence (R = ∞). Such a description predicts a divergence of R(t) at a time τ, hence predicting a finite time for total de-emulsification. The divergence, or equally the dramatic acceleration of the droplet growth with time, is the direct consequence of coalescence. Indeed, the larger the droplets, the more rapid is the process of coalescence of droplets that results in a non-uniform distribution of the volumes and hence less ordered 3D assemblies of the droplets.³⁴

Fig. 7 3D reconstruction of microfluidic scaffolds obtained from μCT data: (a) SC_FF1, (b) SC_FF2, and (c) SC_FF5. Below, the corresponding color-calibrated maps of pores of (d) SC_FF1, (e) SC_FF2, (f) SC_FF5. ROI: 1.5 mm width, 0.5 mm height.

The highly resolved μCT scans (the voxel dimension was 2 × 2 × 2 μm for microfluidic samples and 1 × 1 × 1 μm for SC_conv), permitted us to accurately estimate the distributions of interconnect diameters (Table 2). As expected, SC_conv has a very small mean interconnect size, comparable or even smaller than many human cells. In tissue engineering applications, the size of interconnects is extremely important not only during cell seeding but also during colonization and in growth of cells within the scaffold.

The supply of nutrients and oxygen and the disposal of metabolic wastes throughout the whole scaffold are strictly related to the dimension of interconnects. The insufficient mean size of interconnects exhibited by scaffolds manufactured with conventional approaches, limits the performance of these materials in cell culture experiments. Conversely, microfluidic samples exhibit about a one order of magnitude larger mean interconnect diameter (from 40 μm to 100 μm) opening new applications of polyHIPE-based materials in tissue engineering.

We note that although narrow, the distribution of the diameters of interconnects is slightly wider than the corresponding PSDs (Table 2). This is likely caused by the defects in the crystalline arrangement of pores and possibly also by defects introduced by the freeze-drying process.

Comparison of the mean diameter of the droplets D_drop (Table 1) with the mean pore diameter 〈D〉 (as obtained from the μCT analysis in the dry state, Table 2) indicates that the latter underwent ca. 40% shrinkage of size during cross-linking and freeze-drying processes. A comparison between the dimension of the droplets inside the exit channel of the three scaled microfluidic chips and of average pore size in the corresponding materials is reported in Fig. S2 of the ESI.†

The data and analysis shown above demonstrate that the use of highly monodisperse emulsions as a template for polyHIPEs produce highly ordered and uniform scaffolds. This approach can be used to increase the mean diameter of pores and interconnects of microfluidic polyHIPEs in comparison to the conventionally prepared materials and to tune these to sizes appreciably bigger than the dimensions of all kinds of human cells.

Another remarkable advantage of this method is the ability to vary independently the dimension of interconnects while keeping pores size constant. Few studies in the past investigated the process of formation of interconnects between pores.^35,36 Surprisingly, it was found that the concentration of surfactant – or in other words the O/W interfacial tension – was more important than the volume fraction of the internal phase in determining the final morphology (open-cellular or closed) of polyHIPEs. Here we show that this effect, in conjunction with the highly ordered character of the microfluidic polyHIPEs, can be used to tune the size of the interconnects very precisely – a feature that was not available with conventional techniques. We prepared three HIPEs using the FF1 device, setting a constant Φ_d and using three different concentrations of Pluronic F68, C_s: 1%, 7% and 25% w/v. Fig. 8 reports the SEM micrographs of the resulting polyHIPEs.

Fig. 8 Comparison among SEM micrographs of DEX-MA PolyHIPEs fabricated within FF1 with constant Φ_d = 0.8 but different concentrations of Pluronic F68: (a) 1% w/v, (b) 7% w/v and (c) 25% w/v. Scale bars are 100 μm. Below: visualizations of individual pores (assuming the hcp crystal lattice) obtained numerically by surface energy minimization for various effective surface tensions γ₀ of the double layer of surfactant between neighboring droplets (appearing as the interconnections) as compared to the surface tension γ of the droplets, and for a fixed volume fraction Φ_d = 0.91: (d) γ₀/γ > 2 (no interconnects) and (e) γ₀/γ = 1.99, (f) γ₀/γ = 1.81.

The micrographs displayed in Fig. 8a–c illustrate opening and progressive increase in the size of interconnects upon increasing the concentration of surfactant in the host phase.

The interpretation of this behaviour is that for a given geometry of the microfluidic circuit and imposed flow rates of the two phases, the diameters of the droplets produced remain constant irrespective of C_s. The dimension of droplets is dictated primarily by the width of neck upstream of the point of intersection between the horizontal and vertical channels. This implies that the interfacial W/O area remains constant as well. The increase in C_s brings about an increase in the surfactant excess at the interface and a concomitant lowering of the interfacial tension. This causes a thinning of the layer of the continuous phase surrounding the droplets of the dispersed phase because such a film becomes more easily deformable and at the point of maximum approach, adjacent droplets tend to flatten forming facets from which the interconnects later originate. These facets can be interpreted as films of surfactant molecules which prevent the neighbouring droplets from coalescing.

From our experiment we cannot judge about the molecular structure of those films, but we explain the increase in their size with decrease in the associated effective surface tension γ₀ as compared to the surface tension γ of the surfactant-covered oil-water interface. We calculate the shape of the pores as a function of γ₀/γ by numerically minimizing the total surface energy (by using Surface Evolver), including the contributions both from the oil–water interface and from the facets with the neighbouring droplets, assuming either the hcp or fcc lattice structure.

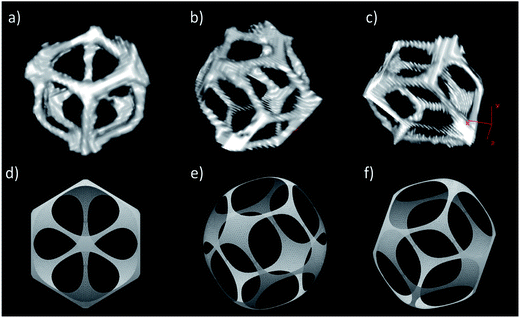
Besides the observed increase in the surface area of the interconnects, our calculations reveal a change in their shape from rounded rhombic (nearly elliptical) to circular (Fig. 8e–f) with decreasing γ₀/γ (increasing C_s), though this change is not clearly evident from SEM micrographs (Fig. 8b and c). On the other hand our model predicts the opposite trend in the case of the increasing volume fraction. Indeed, the rhombic shape of interconnects can be appreciated on μCT scans of a single chosen pore (Fig. 9) taken at a higher volume fraction Φ_d = 0.90 (as compared to Φ_d = 0.81 in Fig. 8). We also note the larger size of interconnects in this case. Moreover, the number, distribution and shape of interconnects allows us to identify and distinguish between the hcp and fcc order (Fig. 5). In the case of the fcc lattice all 12 interconnections are rhombic while in the case of the hcp lattice only 6 of them are rhombic and the remaining 6 are trapezoidal.

In this context, we want to underline the necessity of taking a larger input porosity (Φ_d) in the numerical model than the experimental one in order to obtain similar structures (Fig. 8 and 9). This allows us to hypothesize that besides the interfacial tension there are additional mechanisms responsible for opening of the pores, possibly occurring during the process of cross-linking or freeze-drying of the sample.

4. Discussion

The use of 3D scaffolds in tissue engineering requires tight control over the size of pores and of the size of interconnects between them. The morphology of the material influences the void percentage for cell seeding, bulk mechanical properties, and concentrations of nutrients and waste throughout the scaffold. Recent advances in computer-aided microfabrication techniques such as photolithographic patterning and layering, direct writing and two-photon stereo-lithography allow for fabrication of scaffolds with desired pore size and controlled 3D interconnectivity.^37–39 However, these methods are usually cost prohibitive.

Emulsions, and particularly high internal phase emulsions (HIPEs), can be used as templates to create porous materials. Monomers and a cross-linker are polymerized around emulsion droplets, resulting in a porous monolithic material, known as polyHIPE, with a pore diameter determined by the structure of the emulsion.^40–43 Although practical and inexpensive, the method has not so far been optimum because the materials were characterized by their highly heterogeneous structures. This results from the highly polydisperse character of sheared emulsions, and from coarsening of the emulsion in flow.⁴⁴ According to the Krieger–Dougherty equation, the viscosity increases exponentially as the maximum drop density is approached.⁴⁵ For Φ_d < 0.74, the droplets of the dispersed phase are spherical in shape, and when subjected to an external stress, they can flow past one another without being deformed. When the droplets are concentrated above the random close-packing limit (0.74), they cannot move freely and are trapped by their neighbours and are forced to deform. Thus, during the process of addition of the dispersed phase as Φ_d increases the constant shear stress supplied will encounter increasing difficulties in incorporating the dispersed phase and homogenizing it into a collection of droplets characterized by narrow size distribution. All these effects cause considerable polydispersity of the size of droplets, and give rise to a porous matrix characterized by polydisperse pores and interconnects. Such prepared porous matrices do not promote truly three-dimensional, homogeneous, cell cultures.^11,46

Here we demonstrated that all the morphological limitations of the conventional HIPE templating approach can be overcome by generating the HIPE with a microfluidic device. In such a system, droplets are generated one at a time under controlled and reproducible conditions. This circumvents the problems experienced in preparation and handling of conventional HIPEs. Microfluidics allows to produce trains of droplets of equal dimension arranged in a highly ordered fashion within the confined space of the outlet channel (Fig. 1).

An additional benefit is that the method of generation of the template is physical, so that it does not depend crucially on any specific chemistry. The condition of immiscibility of the two phases, and a reasonably large interfacial tension can be met by a very large set of pairs of liquids. This imposes very little constraints on the materials that can be processed. Ideally, a solution (either aqueous or oily) of any monomer or polymer can be used as the continuous phase. For this reason, it is possible to synthesize both hydrophilic and hydrophobic 3D porous matrices. The only critical condition is that the dispersed phase does not wet the walls of the chip. The wettability of the polymer and glass surfaces can be well controlled with a wide range of methods for modification of surface chemistry.^47–51

The high degree of monodispersity of the droplets promotes the crystalline order of the scaffolds. Through the analysis of light micrographs of the scaffolds in the swollen state, it was possible to evidence the presence of two different lattice structures: hcp, and fcc in the directions [111] and [100] (Fig. 5). We further characterized these crystalline regions by analyzing the structure of a single pore obtained from the μCT scan. We compared this reconstruction with a numerically calculated pore shape assuming a fcc crystal lattice. Interestingly, the interconnect windows have a rhombic shape in both cases and appear exactly at the location predicted by simulations (Fig. 9).

Fig. 9 Comparison of μCT scan of a single pore ([pluronic F68] = 20% w/v, Φ_d = 0.90) viewed at various angles with the numerically calculated shapes of the pore, obtained assuming an FCC crystal lattice for γ₀/γ = 1.81 and Φ_d = 0.97. Note the agreement in topology as well as the rhombic shape of individual interconnections. This shape becomes evident only for large enough porosity as a consequence of the fact that the neighboring droplets of the template emulsion, for a large enough volume fraction of the dispersed phase, strongly press against each other. This forces pores to adopt a shape very close to the shape of the Voronoi cell for the FCC lattice, being rhombic dodecahedra.

Another great advantage of synthesizing a porous matrix through microfluidics is the possibility to vary independently the morphological elements which make up the polyHIPE texture: pores and interconnects. In conventional synthesis of polyHIPE all the strategies adopted to change one morphological feature independently from the other failed. For instance, increasing the pore volume lead to a parallel increase of both pores and interconnects.¹⁰ Here we demonstrated that pores could be tuned over wide ranges independently of the interconnect size. One way to achieve this control is to tune the size of the microfluidic flow focusing junction. Another vista is to vary the water/oil interfacial tension through variation of the surfactant concentration. The size and number of interconnects as well as the average wall thickness changed accordingly as shown by morphological characterization and numerical calculations (Fig. 8). These aspects, together with well-defined ranges of parameters that promote generation of stable HIPEs demonstrate the ability to rationally engineering the morphology of scaffolds. This, in turn, allows to tune the scaffolds to the culturing needs of specific cell lines, similar to what is possible with more sophisticated (and expensive) techniques such as rapid prototyping.

The use of microfluidics brings in also another attractive feature. The absence of mutual shearing forces among droplets, which causes droplet deformation (as it happens with the conventional way of producing HIPEs) allows for the use of significantly higher polymeric concentration in the matrix liquid. With the devices reported here we were able to process as high as 50% w/v total polymer concentration solution (DEX-MA + Pluronic F68) without any difficulty.

Present limitations of scaffold fabrication through microfluidics are represented by the production rate of the emulsion (of the order of tens of μl min⁻¹). This problem can be addressed either by parallelizing chips or by parallelizing the junctions on a single chip.^52,53 We note that HIPEs exhibit considerable kinetic stability (from hours to months). This allows to produce the emulsion over extended intervals, while limiting the freeze drying and cross-linking processes to short procedures. We also wish to note that drop-on-demand (DOD) methods expand the advantages of microfluidics to the independent control of the droplet diameter and the volume fraction of the dispersed phase. In other words, the production of highly customizable emulsions by using a single chip and, in turn, the production of scaffolds with completely tailored properties could be possible.⁵⁴

5. Conclusion

We demonstrated the use of microfluidics to produce highly 3D organized dextran-methacrylate matrices with uniform size of pores and interconnects. This technique can be used to generate scaffolds with extremely monodisperse and ordered structures with the ability to tune the sizes of pores and interconnects independently of each other. This method is compatible with many monomers and polymers. Novel scaffolds produced with this methodology should provide ideal culture models presenting highly controlled and uniform microenvironments. We believe that this work opens new vistas to generate a range of foam-like structures of different pore sizes and densities and to explore in detail the physical properties of the obtained scaffolds as well as their performances in the culture of various cell lines.

Acknowledgements

The authors thank “Sapienza” University of Rome (Ateneo funds) and MIUR (PRIN-2008) for financial support. J.G. acknowledges the Foundation for Polish Science Homing Plus and Polish Ministry of Science Iuventus Plus (IP 016971) grants. This work was supported by the European Regional Development Fund within the Innovative Economy Operational Programme in the frame of project BIO-IMPLANT (Grant no. POIG.01.01.02-00-022/09) and by the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement no. 279647.

Notes and references

1. S. D. Kimmimns and N. R. Cameron, Adv. Funct. Mater., 2011, 21, 211–225.
2. M. A. Bokharia, G. Akaya, S. Zhang and M. A. Birch, Biomaterials, 2005, 26, 5198–5208.
3. A. Barbetta, M. Massimi, L. Conti Devirgiliis and M. Dentini, Biomacromolecules, 2006, 7, 3059–3068.
4. G. Akaya, M. A. Birch and M. A. Bokhari, Biomaterials, 2004, 25, 3991–4000.
5. R. S. Moglia, J. L. Holm, N. A. Sears, C. J. Wilson, D. M. Harrison and E.C. Hernandez, Biomacromolecules, 2011, 12, 3621–3628.
6. M. W. Hayman, K. H. Smith, N. R. Cameron and S. A. Przyborski, Biochem. Biophys. Res. Commun., 2004, 314, 483–488.
7. J. L. Robinson, R. S. Moglia, M. C. Stuebben, M. A. P. McEnery and E. Cosgriff-Hernandez, Tissue Eng., Part A, 2014, 20, 1103–1112.
8. S. Zhou, A. Bismarck and J. H. G. Steinke, J. Mater. Chem. B, 2013, 1, 4736–4745.
9. S. Caldwell, D. W. Johnson, M. P. Didsbury, B. A. Murray, J. J. Wu, S. A. Przyborskibde and N. R. Cameron, Soft Matter, 2012, 8, 10344–10351.
10. A. Barbetta, M. Dentini, E. M. Zannoni and M. E. De Stefano, Langmuir, 2005, 21, 12333–12341.
11. A. Barbetta, M. Massimi, B. Di Rosario, S. Nardecchia, M. De Colli, L. Conti Devirgiliis and M. Dentini, Biomacromolecules, 2008, 9, 2844–2856.
12. M. Bokhari, R. J. Carnachan, S. A. Przyborski and N. R. Cameron, J. Mater. Chem., 2007, 17, 4088–4094.
13. M. De Colli, M. Massimi, A. Barbetta, B. Di Rosario, S. Nardecchia, L. Conti Devirgiliis and M. Dentini, Biomed. Mater., 2012, 7, 1–13.
14. B. Derby, Science, 2012, 338, 921–926.
15. T. Billiet, M. Vandenhaute, J. Schelfhout, S. Van Vlierberghe and P. Dubruel, Biomaterials, 2012, 33, 6020–6041.
16. W. Y. Yeong, C. K. Chua, K. F. Leong and M. Chandrasekaran, Trends Biotechnol., 2004, 22, 643–652.
17. A. D. Lantada and P. L. Morgado, Annu. Rev. Biomed. Eng., 2012, 14, 73–96.
18. H. J. Lee and G. H. Kim, RSC Adv., 2012, 2, 7578–7587.
19. M. T. Gokmen, W. Van Camp, P. J. Colver, St. A. F. Bon and F. E. Du Prez, Macromolecules, 2009, 42, 9289–9294.
20. W. N. E. van Dijk-Wolthuis, O. Franssen, H. Talsma, M. J. van Steenbergen, J. J. Kettenes-van den Bosch and W. E. Hennink, Macromolecules, 1995, 28, 6317–6322.
21. W. N. E. van Dijk-Wolthuis, J. J. Kettenes-van den Bosch, A. van der Kerk-van Hoof and W. E. Hennink, Macromolecules, 1997, 30, 3411–3413.
22. P. Jankowski, D. Ogonczyk, L. Derzsi, W. Lisowski and P. Garstecki, Microfluid. Nanofluid., 2013, 14, 597–604.
23. A. Barbetta, M. Dentini, M. S. De Vecchis, P. Filippini, G. Formisano and S. Caiazza, Adv. Funct. Mater., 2005, 15, 118–124.
24. C. Colosi, M. Costantini, A. Barbetta, R. Pecci, R. Bedini and M. Dentini, Langmuir, 2013, 29, 82–91.
25. K. Brakke, Exp. Math., 1992, 1, 141–165.
26. S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366.
27. P. Garstecki, H. A. Stone and G. M. Whitesides, Phys. Rev. Lett., 2005, 94, 164501.
28. W. Lee, L. M. Walker and S. L. Anna, Phys. Fluids, 2009, 21, 032103.
29. P. Garstecki, I. Gitlin, W. DiLuzio, G. M. Whitesides, E. Kumacheva and H. A. Stone, Appl. Phys. Lett., 2004, 85, 2649–2651.
30. Z. Nie, M. S. Seo, S. Xu, P. C. Lewis, M. Mok, E. Kumacheva, G. M. Whitesides, P. Garstecki and H. A. Stone, Microfluid. Nanofluid., 2008, 5, 585–594.
31. B. Dollet, W. van Hoeve, J. P. Raven, P. Marmottant and M. Versluis, Phys. Rev. Lett., 2008, 100, 034504.
32. J. D. Tice, A. D. Lyon and R. F. Ismagilov, Anal. Chim. Acta, 2004, 507, 73–77.
33. L. Derzsi, M. Kasprzyk, J. P. Plog and P. Garstecki, Flow focusing with viscoelastic liquids, Phys. Fluids, 2013, 25, 092001/1.
34. B. Deminiere, A. Colin, F. L. Calderon and J. Bibette, Lifetime and destruction of concentrated emulsion undergoing coalescence, in Modern Aspects of Emulsion Science, edn. B. P. Binks, The Royal Society of Chemistry, 1998.
35. N. R. Cameron, D. C. Sherrington, L. Albiston and D. P. Gregory, Colloid Polym. Sci., 1996, 274, 592–595.
36. J. M. Williams and D. A. Wrobleski, Langmuir, 1988, 4, 656–662.
37. D. Gallego, N. Ferrell, Y. Sun and D. J. Hansford, Mater. Sci. Eng. C, 2008, 28, 353–358.
38. J. L. Simon, S. Michna, J. A. Lewis, E. D. Rekow, V. P. Thompson, J. E. Smay, A. Yampolsky, J. R. Parsons and J. L. Ricci, J. Biomed. Mater. Res., Part A, 2007, 83, 747–758.
39. P. Tayalia, C. R. Mendonca, T. Baldacchini, D. J. Mooney and E. Mazur, Adv. Mater, 2008, 20, 4494–4498.
40. H. Zhang and A. I. Cooper, Soft Matter, 2005, 1, 107–113.
41. A. Barbetta, R. J. Carnachan, K. H. Smith, C. T. Zhao, N. R. Cameron, R. Kataky, M. Hayman, S. A. Przyborski and M. Swan, Macromol. Symp., 2005, 226, 203–211.
42. I. Pulko and P. Krajnc, Macromol. Rapid Commun., 2012, 33, 1731–1746.
43. S. D. Kimmins and N. R. Cameron, Adv. Funct. Mater., 2011, 21, 211–225.
44. P. Walstra and P. E. A. Smulders, Emulsion formation, in Modern Aspect of Emulsion Science, edn. B.P. Binks, The Royal Society of Chemistry, 1998, ch. 2.
45. T. F. Tadros, in Emulsion-A Fundamental and Practical Approach, edn. J. Sjöblom, Kluwer, Dordrecht, 1992, p. 173.
46. S. Caldwell, D. W. Johnson, M. P. Didsbury, B. A. Murray, J. J. Wu, S. A. Przyborskibde and N. R. Cameron, Soft Matter, 2012, 8, 10344–10351.
47. I. Wong and C. M. Ho, Microfluid. Nanofluid., 2009, 7, 291–306.
48. A. R. Abate, D. Lee, T. Do, C. Holtze and D. A. Weitz, Lab Chip, 2008, 8, 516–518.
49. P. Jankowski, D. Ogonczyk, A. Kosinski, W. Lisowski and P. Garstecki, Lab Chip, 2011, 11, 748–752.
50. R. Lin and M. A. Burns, J. Micromech. Microeng., 2005, 15, 2156–2162.
51. S. Roy and C. H. Yue, Plasma Processes Polym., 2011, 8, 432–443.
52. W. Li, J. Greener, D. Voicu and E. Kumacheva, Lab Chip, 2009, 9, 2715–2721.
53. T. Nisisako and T. Torii, Lab Chip, 2008, 8, 287–293.
54. J. Guzowski, P. M. Korczyk, S. Jakiela and P. Garstecki, Lab Chip, 2011, 11, 3593–3595.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3tb21227k

---