 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assessment of polyanion (BF4− and PF6−) substitutions in hybrid halide perovskites
Christopher H.
Hendon
,
Ruo Xi
Yang
,
Lee A.
Burton
and
Aron
Walsh
*
Centre for Sustainable Chemical Technologies and Department of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: a.walsh@bath.ac.uk
First published on 22nd October 2014
Abstract
Halide perovskites have attracted attention for light-to-electricity conversion in solar cells due to their favorable optoelectronic properties. In particular, the replacement of the A cation by an isovalent molecule has proven highly successful. We explore the substitution of the X anion, producing polyanion perovskites based on hexafluorophosphate and tetrafluoroborate. Starting from CsPbI3, the effect of partial and complete substitution is investigated using relativistic electronic structure calculations. BF4− results in a larger perturbation to the electronic structure than PF6−; however, both localise the band edge states, and the end member compounds are predicted to be wide band gap dielectrics.
The characteristic structural motif of the perovskite (ABX3) crystal structure is a corner-sharing array of BX6 octahedra. The three-dimensional arrangement of these octahedra gives rise to a range of polymorphs (i.e. the four tilt systems dictated by Glazer1). The 12-coordinate hole formed at the centre of each octahedral cage is occupied by a cation at the A site (see Fig. 1).
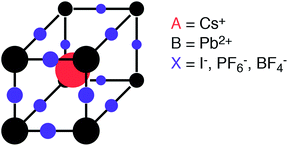 | ||
| Fig. 1 Schematic of the perovskite crystal structure composed of two cations (A and B) and an anion (X). Here we consider both elemental and molecular anions. | ||
For charge neutrality of the material, the simple rule is that the formal oxidation states of the cations (A + B) balance those of the anions (3X). While oxide perovskites are the most widely studied (i.e. A + B = VI), there are many examples of halide perovskites (i.e. A + B = III). There are fewer allowed metal combinations for the halides, with the typical case being A = I and B = II, e.g. NaFeF3. In addition to charge balance, geometric constraints restrict the range of possible compositions. These are summarised by the radius ratio rules as defined by the Goldschmidt tolerance factor:2
In addition to inorganic perovskite solid-solutions and ordered-defect structures, a diverse family of hybrid perovskites are also known to exist.4 In the simplest case, the A metal is replaced by an isovalent molecule and the BX3 connectivity is maintained. A popular example is CH3NH3PbI3, where α = 0.91.5 There are many examples of where 2D and 1D networks are formed due to steric factors.6 More exotic ‘perovskite like’ metal–organic frameworks also exist, e.g. the bimetallic azido systems (e.g. (N(CH3)4)2[Cr,Na(N3)6]).7
One recent driving force for the study of halide perovskites has been in photovoltaics, where both inorganic (e.g. CsSnI3) and hybrid (e.g. CH3NH3PbI3) perovskites have demonstrated high power conversion efficiencies for low-temperature solution-processed materials.8–10 The remarkable performance can be attributed to the combination of strong optical absorption, light carrier effective masses, large dielectric constants and, currently less well understood, ferroelectricity.11,12
In this Communication, we consider hybrid halide perovskites from a different perspective: the hybrid solid formed by substituting the anion, rather than the cation. Specifically, we investigate CsPbX3 (X = I, PF6 and BF4) including partial and complete substitutions. The crystal structures and electronic properties are predicted by a first-principles method. The successful synthesis of BF4 incorporated CH3NH3PbI3 was recently reported,13 which highlights that even more complex “double hybrid” compounds are possible to synthesise.
Calculations were performed using density functional theory in the code VASP.14,15 A two-step procedure was adopted, with structure optimisation at the level of PBEsol16 and electronic structure analysis with the non-local HSE06 exchange-correlation functional including 25% screened Hartree–Fock exchange.17,18 The basis set (500 eV cutoff), k-points (6 × 6 × 6) and internal forces (1 meV Å−3) were converged for the properties of interest. Particular care was given to relativistic effects, which are known to be large for Pb-containing compounds: scalar relativistic corrections were included in the projector-augmented wave core potentials and spin–orbit interactions were treated for the valence electrons. The optimised crystal structures are available in an on-line repository.19 The effective masses were determined using the package Boltztrapp20via Pymatgen.21
It should be noted that the computed band gap values reported here (see Table 1) are qualitative for two reasons: (i) many body effects are particularly large in these systems, which can renormalize both the band gap and band dispersion;22 (ii) the cubic perovskite lattice may represent an average structure that is subject to effects from dynamic disorder (local symmetry breaking).23 The general trends are expected to be reliable.
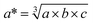 from DFT/PBEsol), the electronic band gap (Eg), and the average of the effective mass tensor (m*h in units of free electron mass) of the valence band are each listed. See the note in text regarding the qualitative nature of the band gap values reported here
from DFT/PBEsol), the electronic band gap (Eg), and the average of the effective mass tensor (m*h in units of free electron mass) of the valence band are each listed. See the note in text regarding the qualitative nature of the band gap values reported here
| Material | α | a* (Å) | E g (eV) | m *h (me) |
|---|---|---|---|---|
| CH3NH3PbI3 | 0.91 | 6.29 | 0.81 | 0.20 |
| CsPbI3 | 0.85 | 6.26 | 0.51 | 0.16 |
| CsPb[I2][PF6] | 0.85 | 6.83 | 1.07 | 0.41 |
| CsPb[I2][BF4] | 0.85 | 6.22 | 2.37 | 0.48 |
| CsPb[PF6]3 | 0.84 | 8.11 | 7.47 | 4.62 |
| CsPb[BF4]3 | 0.85 | 6.75 | 6.83 | 4.41 |
The cubic perovskite structure of CsPbI3 has octahedral symmetry (space group Pm-3m) and the iodide sites have linear coordination with respect to Pb. The tolerance factor of 0.85 is insensitive to the polyanion substitutions considered here (Table 1). For the octahedral PF6 anion, the linear coordination is maintained through the axial termini, which maintains cubic perovskite symmetry for CsPb[PF6]3. For the tetrahedral BF4 anion, the linear coordination is symmetric through two edges of the tetrahedron and is thus not inline with any B–F bond (Cs symmetry, space group C1m1).
The lattice parameter of CsPbI3 is increased by 8% and 30% for BF4 and PF6, respectively, due to their larger effective ionic radii (see Table 1). Two partially substituted structures were also considered with one (001) layer of iodine replaced by the respective polyanion. The equilibrium crystal structures exhibit a tetragonal distortion (a/c) of 0.91 (BF4) and 0.74 (PF6). For BF4, the Pb–I chains are also perturbed, with the bond angle decreasing from 180 to 149°.
The electronic structure of CsPbI3 follows the oxidation states of the elements: Cs(I) is electronically inert; Pb(II) has a filled 6s band and an empty 6p band; iodide has a complete 5p shell. Therefore, the upper valence and lower conduction bands – key for hole and electron transport – are formed by the overlap of Pb 6s/I 5p and Pb 6p atomic orbitals, respectively. The corresponding charge density profiles are drawn in Fig. 2, and the electronic density of states provided in Fig. 3.
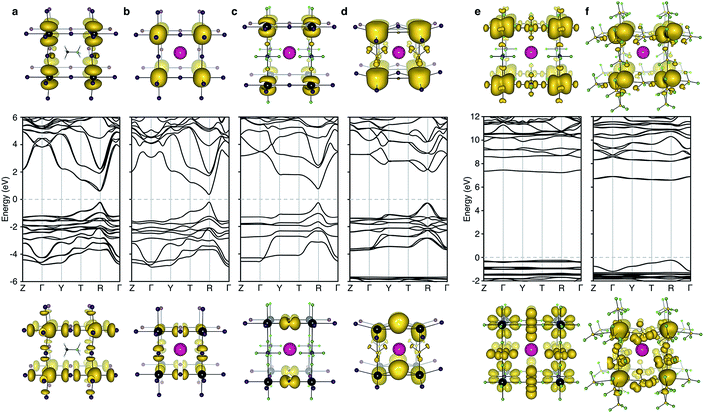 | ||
| Fig. 2 Electronic band structure (DFT/HSE06 including spin–orbit coupling) of (a) CH3NH3PbI3 (b) CsPbI3, (c) CsPb[I2][PF6], (d) CsPb[I2][BF4], (e) CsPb[PF6]3 and (f) CsPb[BF4]3. The structure for (a) is taken from ref. 28 and corresponds to the 〈100〉 pseudo-cubic orientation of methylammonium. Shown below and above the bandstructures are the charge density isosurfaces of the valence band maximum and conduction band minimum, respectively. Visualization is performed in the code VESTA.29 Note that for the partial polyanion substitutions (c–d), the band gap remains at the R point (1/2, 1/2, 1/2) of the Brillouin zone. Strong relativistic Dresselhaus splitting is predicted for the lower conduction band of (d) due to the breaking of inversion symmetry associated with the BF4 anion. | ||
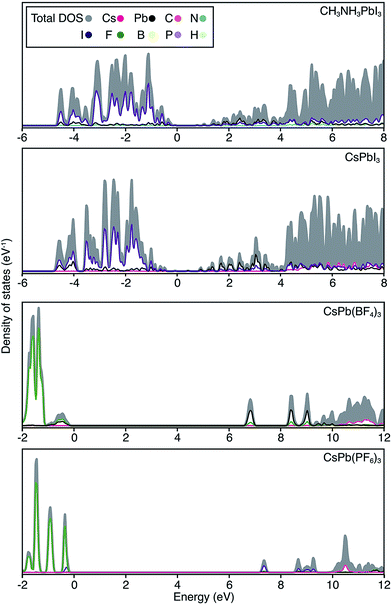 | ||
| Fig. 3 Electronic density of states are shown for CH3NH3PbI3, CsPbI3, CsPb[BF4]3 and CsPb[PF6]3. The top of the valence band is set to 0 eV in each case, and the partial ion contributions are determined from a spherical integration around each lattice site. The similarity between the electronic structure for Cs and CH3NH3 compounds has previously been noted.30 For the polyanion compounds, the band gaps are widened and the band edges become more localized, in accordance with the band structures shown in Fig. 2. | ||
In these structures, the occupied Pb 6s electrons are stereochemically “inactive”, but the formation of a direct lone pair can occur and is associated with the ferroelectric activity of Pb(II) containing materials.24 CsPbI3 exhibits significant band dispersion in reciprocal space, corresponding to light hole effective masses (0.16 me), which are comparable to the solar cell absorber CH3NH3PbI3 (0.20 me; further decreased to 0.12 me with many body corrections).22 A direct band gap is predicted at the boundary of the first Brillouin zone (R point) in agreement with other studies.25,26
For the layered compounds, the first notable change in electronic structure is the anisotropy in the chemical bonding. Band dispersion is significantly reduced along the stacking direction (Γ to Z in Fig. 2). It is clear that the molecular orbitals of the polyanion groups hybridise less strongly with the atomic orbitals of Pb. The magnitudes of the band gaps are therefore increased (with decreased band widths). The upper valence band is still dominated by I 5p, but the bonding is in 2D sheets rather than a 3D network. The conduction band remains formed by Pb 6p orbitals, while again the connectivity is modified.
For the complete polyanion substitutions, the band structures show almost no dispersion in reciprocal space, and the density of states becomes more localised. Due to reduced bandwidths, the band gaps are further blue-shifted to the deep UV region (>6 eV). Here the contributions to the upper valence band are solely from the molecular orbitals of the polyanions. Correspondingly, the hole effective masses are heavier than the free electron mass. These materials will be electrically inert and insulating or poorly conducting in the polaronic “hopping” limit. The suggestion that the substitution of I− by BF4− leads to hole doping is erroneous.13
Considering the limited range of possible halide perovskite materials, the use of polyanions presents a simple route to further extending their optoelectronic properties. Replacement of chemically reactive halides by more robust polyanions also provides a mechanism to enhance stability. This approach has led to great success in the development of electrodes for lithium batteries.27 For the two cases studied here, band gaps are increased to shorter wavelengths. Anion engineering could be useful for spectral tuning of multi-junction absorber materials for solar cells, in the dilute regime, or for producing selective electron or hole blocking layers. For the end member compounds, the increased transparency may be exploited as luminescent host materials, e.g. for phosphors, or as dielectric layers in electrical devices.
Conclusions
A computational exploration, combined with the recent synthesis of BF4 incorporated CH3NH3PbI3, has highlighted the chemical versatility of multi-component perovskites. These materials are most commonly solution processed at low temperatures in a kinetic regime that can allow for thermodynamically metastable structures to be synthesized. While ab initio screening of the global stability of a material is challenging in this case, it does vastly increase the range of potential hybrid structures. The recent application of the Goldschmidt tolerance factor analysis to hybrid perovskites has suggested a range of plausible compositions.5 Extension of this analysis to polyanion systems predicts that larger organic cations such as imidazolium and dimethylammonium are optimal for maintaining a perovskite network (α ∼ 1) with BF4 and PF6 anions. The combination of molecular cations and polyanions in a single framework opens up an array of possibilities that can be exploited for functional materials design and optimization.Acknowledgements
The authors thank A. T. Murray for insightful remarks. We acknowledge membership of the U.K.'s HPC Materials Chemistry Consortium, which is funded by EPSRC Grant EP/L000202. Additional support has been received from EPSRC Grants EP/K016288/1 and EP/J017361/1, the Royal Society and the ERC (Grant 277757).Notes and references
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem, 1972, 28, 3384–3392 CrossRef CAS.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12 RSC.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014 10.1039/C4SC02211D.
- D. B. Mitzi, S. Wang, C. A. Feild, C. A. Chess and A. M. Guloy, Science, 1995, 267, 1473–1476 CrossRef CAS PubMed.
- Z.-Y. Du, Y.-P. Zhao, C.-T. He, B.-Y. Wang, W. Xue, H.-L. Zhou, J. Bai, B. Huang, W.-X. Zhang and X.-M. Chen, Cryst. Growth Des., 2014, 14, 3903–3909 CAS.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 643 CrossRef PubMed.
- J. M. Ball, M. M. Lee, A. Hey and H. J. Snaith, Energy Environ. Sci., 2013, 1739–1743 CAS.
- G. Eperon and S. Stranks, Energy Environ. Sci., 2014, 7, 982 CAS.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- Y. Kutes, L. Ye, Y. Zhou, S. Pang, B. D. Huey and N. P. Padture, J. Phys. Chem. Lett., 2014, 5, 3335–3339 CrossRef CAS.
- S. Nagane, U. Bansode, O. Game, S. Y. Chhatre and S. Ogale, Chem. Commun., 2014, 50, 9741 RSC.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Angyan, J. Chem. Phys., 2006, 124, 154709–154713 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef PubMed.
- https://github.com/WMD-Bath/Hybrid-perovskites, accessed 1st April 2014.
- G. Madsen and D. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef PubMed.
- F. Brivio, K. T. Butler, A. Walsh and M. van Schilfgaarde, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155204 CrossRef.
- M. Dove, Am. Mineral., 1997, 82, 213–244 CAS.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- L. Lang, J.-H. Yang, H.-R. Liu, H. J. Xiang and X. G. Gong, Phys. Lett. A, 2014, 378, 290–293 CrossRef CAS PubMed.
- Y. Chang, C. Park and K. Matsuishi, J. Korean Phys. Soc., 2004, 44, 889–893 CAS.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185–204 RSC.
- F. Brivio, A. B. Walker and A. Walsh, APL Mater., 2013, 1, 042111 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. Even and L. Pedesseau, J. Phys. Chem. Lett., 2013, 4, 2999 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |

