Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum-chemical study of stable, meta-stable and high-pressure alumina polymorphs and aluminum hydroxides†
Michael F.
Peintinger
*a,
Michael J.
Kratz
b and
Thomas
Bredow
b
aMax Planck Institute for Chemical Energy Conversion, Stiftstrasse 34 - 36, 45470 Mülheim an der Ruhr, Germany. E-mail: michael.peintinger@gmail.com
bMulliken Center for Theoretical Chemistry, Institut für Physikalische und Theoretische Chemie, University of Bonn, Beringstr. 4-6, D-53115 Bonn, Germany
First published on 24th June 2014
Abstract
The structure, electronic properties and relative stability of seven thermodynamically stable, meta-stable and high-pressure alumina polymorphs as well as the structure and relative stability of four aluminum hydroxides were calculated with periodic hybrid density functional theory calculations and compared with available experimental data. For a number of polymorphs several structure models that are discussed in the literature were compared in terms of their agreement with structural data and stability. In order to compare oxides and hydroxides the energies and heats of atomization of the latter were corrected by the reaction energy with water. The following overall energetic order was obtained: gibbsite < bayerite < boehmite < akdalaite < α-Al2O3 < κ-Al2O3 < θ-Al2O3 < δ-Al2O3 < γ-Al2O3 < η-Al2O3 < ι-Al2O3.
1. Introduction
Alumina (Al2O3) is one of the most important ceramic materials for technological applications. Corundum (α-Al2O3) is used in spark plugs due to its high electrical resistance, in parts of acid and brine pumps due to its corrosion resistance, in melting pots and thermocouple tubes due to its high temperature resistance and in prostheses because of its bio-compatibility. Also under high pressure conditions there are numerous technological applications for aluminum oxide. For example ruby (Al2O3 doted with Cr3+) is used as a pressure calibrator in “diamond-anvil-cells”1 and sapphire (Al2O3 doted with various cations) as a window material in shock wave experiments.2 Besides the thermodynamically stable corundum there is a variety of metastable alumina phases of technological importance.The κ-modification is used for surface coating of cutting tools because of its extreme hardness.3,4 Since the γ-phase provides a large surface due to its porous structure5 it is used in as support and structural promoter in catalysts in synthesis,6 for the reduction of automotive pollutants, oil refining and in absorbents.7,8
But alumina is also of high interest in recent fundamental material chemistry research. The properties of iron and titanium defects and aggregates in sapphire were theoretically investigated by Walsh and coworkers.9 Bai and others have observed an improvement in the growth and dielectric properties of carbon nanotubes by hybridization with ceramic microparticles.10 Carreon et al. have reported the synthesis of continuous cobalt–adeninate metal–organic framework (MOF) membranes supported on porous alumina tubes.11 Very recently the synthesis and detailed structural studies of mesoporous alumina as thin films and as powders12 were reported by Rønning et al. In energy research it was used as coating material for high voltage cathodes for enhanced electrochemical performance.13 Alumina was even used in photochemistry to create and stabilize aqueous solutions of electrons14 and the fabrication of free-standing Al2O3 nanosheets promise high mobility flexible graphene field effect transistors.15
Despite its technological importance, there was no comprehensive experimental or theoretical work that covered all known alumina phases. With this manuscript we now present the first extensive quantum-chemical investigation of the geometric and electronic structure and the relative stability for all known Al2O3 modifications.
Aluminium hydroxides, a family of the seven compounds akdalaite (tohdite),16 bayerite,17 boehmite,18 diaspore,19 doyleite,20 gibbsite17 and nordstrandite20 were extensively studied by Demichelis et al. They recently published a complete, systematic, and homogeneous review investigating the physico-chemical properties at hybrid density functional theory level21 employing the B3LYP functional. To investigate the role of electron correlation in the stability of the hydroxides, Casassa and Demichelis reinvestigated their findings with periodic local Møller–Plesset second-order perturbative approach, aiming at providing a reliable trend of stability on the basis of a proper description of both the long-range Coulomb interactions and the short-range correlation effects.22
For comparison purposes we also include the four aluminum hydroxides boehmite (γ-AlO(OH)), gibbsite (γ-Al(OH)3), bayerite (α-Al(OH)3) and akdalaite (Al10O15·H2O) in our study. The latter represent precursors of alumina phases which are formed during the calcination process.
Some phases are produced from other precursors, for example δ-Al2O3, which is also formed during thermal oxidation of aluminum.23 The most common processing routes are shown in Fig. 1.
 | ||
| Fig. 1 Common calcination routes of aluminum hydroxides and phase transitions of metastable aluminum polymorphs towards the formation of corundum.23 | ||
Boehmite represents the main component of many bauxite minerals and can be synthesized by precipitation of certain aluminum salts in aqueous solution or by hydrothermal synthesis just as gibbsite and bayerite.24 Gibbsite is also a part of bauxite minerals25 whereas the structurally related bayerite is rarely found in nature.23 In addition to the above-mentioned ways it can be produced with the Bayer process.23 Akdalaite is most commonly processed from gibbsite by hydrothermal synthesis.26
In the metastable polymorphs, the oxygen anions form either face-centered cubic (fcc) or hexagonal close-packed (hcp) lattices.23 The distribution of cations within these lattices results in a large number of different polymorphs. The structures based on the fcc packing of the oxygen atoms include γ, η (cubic), θ (monoclinic), δ (either tetragonal or orthorhombic) and γ′ (tetragonal). The structures based on the hcp packing include α (trigonal), κ (orthorhombic), κ′ (hexagonal) and ι (orthorhombic). Additional phases named θ′, θ′′, λ (all monoclinic), U (orthorhombic) and χ (cubic27 or hexagonal28) have been mentioned in the literature but were discarded in the present study because the reported structure data are incomplete. U–Al2O3 was discovered in nanocomposite Al2O3–SiC coatings using XRD.29 θ′−, θ′′−, λ-Al2O3 were found by Levin et al. via electron diffractometry and high-resolution electron microscopy in plasma-sprayed Al2O3 layers and in amorphous, anodic Al2O3 films.30–32 χ-Al2O3 is formed during calcination of gibbsite and represents the structural transition from gibbsite to κ-Al2O3.23 It is assumed that the χ phase has a complex layer structure with a random stacking order where the oxygen atoms are similarly packed as in gibbsite.28
Moreover, we investigate several existing structural models of high-pressure alumina phases. It is known that corundum is transformed into the so-called Rh2O3 phase at about 80–100 GPa which turns into the CaIrO3 phase at about 130 GPa. In order to overcome the kinetic barriers between these modifications, temperatures above 1000 °C are needed.33,34 As there are to our knowledge no recent extensive studies of the structure and properties of these high-pressure phases, the results of the present theoretical study may be useful for future studies, e.g. on phase transformations, surface and adsorption studies as well as reaction paths.
Details of our computational approach can be found in the section Computational details.
2. Results and discussion
2.1 Aluminum hydroxides
The calculated lattice constants are given in Tables 1–4. They show good agreement with experimental values with relative errors of less than 0.9% for boehmite, 2.8% for gibbsite, 0.8% for bayerite, and 0.6% for akdalaite, respectively.It should be mentioned that the layer structures may be slightly improved with an additional dispersion correction to DFT.35 In this study no dispersion correction was applied because the effects are expected to be small.
In order to include the hydroxides to the comparison of the relative stability of the alumina phases where the atomization enthalpy ΔAH0 was taken as measure, the atomization enthalpy Δ*AH0 of Al2O3 was recalculated from the reaction enthalpy ΔRH0 of the hydroxides and H2O and normalized to one formula unit Al2O3.
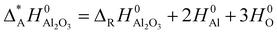 | (1) |
The enthalpies H0 have been calculated including zero point energies and vibration contributions at 298 K. The atomic energies were corrected from basis set superposition error with the counterpoise method (ATOMBSSE).
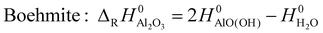 | (2) |
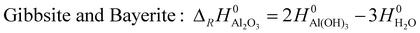 | (3) |
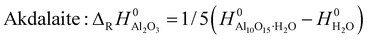 | (4) |
2.2 Alumina phases
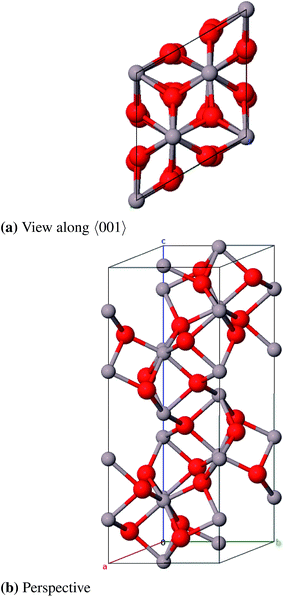
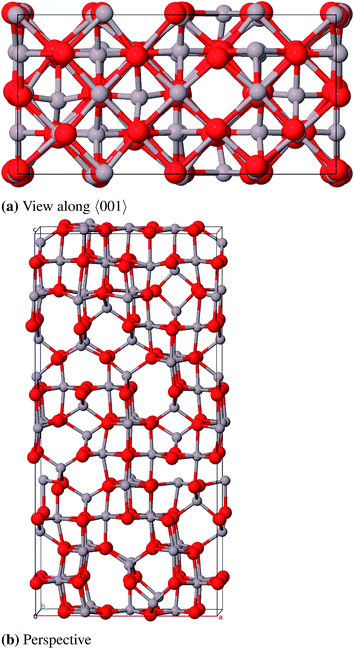
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, no. 167) and can be described with either a rhombohedral or a hexagonal lattice system. The oxygen atoms form an hcp packing of spheres where 2/3 of the octahedral vacancies are occupied by aluminum atoms. The conventional unit cell (hexagonal axes, see Fig. 6) contains 30 atoms (Al12O18, primitive cell: Al4O6) where the oxygen atoms occupy position 18e (x, 0, 0.25) and the aluminum atoms occupy position 12c (0, 0, z).23 Different from the ideal hcp cell the values of the x- and z-coordinate (x = 0.307 and z = 0.352)42 differ from the value 1/3 because the aluminum atoms move towards the unoccupied octahedral interstices and hereby induce a repositioning of the oxygen atoms as well.23
c, no. 167) and can be described with either a rhombohedral or a hexagonal lattice system. The oxygen atoms form an hcp packing of spheres where 2/3 of the octahedral vacancies are occupied by aluminum atoms. The conventional unit cell (hexagonal axes, see Fig. 6) contains 30 atoms (Al12O18, primitive cell: Al4O6) where the oxygen atoms occupy position 18e (x, 0, 0.25) and the aluminum atoms occupy position 12c (0, 0, z).23 Different from the ideal hcp cell the values of the x- and z-coordinate (x = 0.307 and z = 0.352)42 differ from the value 1/3 because the aluminum atoms move towards the unoccupied octahedral interstices and hereby induce a repositioning of the oxygen atoms as well.23
The calculated bulk properties are shown in Table 5. After relaxation the atomic positions are almost identical to the experimental data and the results for the lattice constants are very satisfying as well with a relative error of 0.8%. The calculated heat of atomization ΔAH0 of 3005 kJ mol−1 (corrected by the basis set superposition error (BSSE)) is 78 kJ mol−1 below the experimental value and thus shows an acceptable error of 2.5%. A study with electron energy loss spectroscopy (EELS)44 yielded a fundamental band gap of 8.5 eV that is very close to the calculated 8.6 eV. The band structure yields a HOCO–LUCO-transition at the Γ-point (HOCO, highest occupied crystalline orbital; LUCO, lowest unoccupied crystalline orbital) which is consistent with a previous theoretical study.45 From the projected density of states (PDOS) it can be concluded that the valence band consists mainly of oxygen orbitals and the conduction band mainly of aluminum orbitals as it is expected for an ionic compound in the form of Al23+O32−. Band structures, atomic positions and density of states for all investigated modifications are listed in the ESI.†
With a relative error of less than 1% pob-DZVP/PW1PW provides good results for the lattice constants (Table 6). For the band gap a vertical transition of 7.4 eV was calculated in this work whereas a theoretical study on the electronic structure of four Al2O3 modifications by Lee et al.51 predicted a band gap of 5.49 eV. In the same study the band gap of corundum was underestimated by 2 eV which can be addressed to the use of the LDA functional and the well-known self-interaction error.
The calculated lattice constants are listed in Table 7 and agree well with experimental data presenting a relative error of 1.4%. An indirect band gap of 6.9 eV was calculated and may be compared to the value of 5.04 eV from Lee et al.51 with an assumed underestimation of about 2 eV as discussed above.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, no. 227) that is composed of a close-packed oxygen lattice (position 32e) whose tetrahedral (position 8a) and octahedral interstices (position 16d) are occupied by aluminum atoms. As the anion–cation ratio is 4
m, no. 227) that is composed of a close-packed oxygen lattice (position 32e) whose tetrahedral (position 8a) and octahedral interstices (position 16d) are occupied by aluminum atoms. As the anion–cation ratio is 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in an ideal spinel, cation vacancies have to occur to ensure the correct stoichiometry of aluminum oxide (2
3 in an ideal spinel, cation vacancies have to occur to ensure the correct stoichiometry of aluminum oxide (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
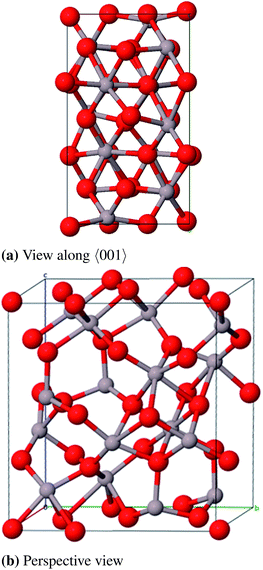
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3).55 Moreover a slight tetragonal distortion was reported in 1964 based on XRD results (0.983 < a/c < 0.987).56 There have been a large number of experimental and theoretical studies to determine the octahedral–tetrahedral ratio in which the vacancies appear and to illuminate whether hydrogen is a part of the structure. It was concluded that hydrogen is only a part of the surface structure and thus does not appear within the bulk.57,58 The vacancy ratio is a controversial issue as investigations with XRD, neutron powder diffraction and electron microscopy reveal that vacancies are located only in octahedral positions,59,60 or only in tetrahedral positions61,62 or in both octahedral and tetrahedral positions.63 The latter result is also backed up by NMR and theoretical studies by Lee et al.64 However, a variety of theoretical studies result in solely octahedral vacancies.58,65–67 It has also been reported that several ”non-spinel” positions are occupied in γ-Al2O368,69 and that the unit cell was tetragonal with
3).55 Moreover a slight tetragonal distortion was reported in 1964 based on XRD results (0.983 < a/c < 0.987).56 There have been a large number of experimental and theoretical studies to determine the octahedral–tetrahedral ratio in which the vacancies appear and to illuminate whether hydrogen is a part of the structure. It was concluded that hydrogen is only a part of the surface structure and thus does not appear within the bulk.57,58 The vacancy ratio is a controversial issue as investigations with XRD, neutron powder diffraction and electron microscopy reveal that vacancies are located only in octahedral positions,59,60 or only in tetrahedral positions61,62 or in both octahedral and tetrahedral positions.63 The latter result is also backed up by NMR and theoretical studies by Lee et al.64 However, a variety of theoretical studies result in solely octahedral vacancies.58,65–67 It has also been reported that several ”non-spinel” positions are occupied in γ-Al2O368,69 and that the unit cell was tetragonal with 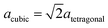 .69 This tetragonal structure can be regarded as a contraction of the cubic lattice along one direction with the space group I41/amd (no. 141) which is a maximum subgroup of Fd
.69 This tetragonal structure can be regarded as a contraction of the cubic lattice along one direction with the space group I41/amd (no. 141) which is a maximum subgroup of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.
Calculated diffraction patterns of cubic and tetragonal models where ”non-spinel” positions are occupied have agreed very well with experimental data unlike diffraction patterns of defective spinel structure models.53,70 Paglia et al. have created supercells (160 atoms) with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m as well as I41/amd where aluminum atoms occupy ”non-spinel” positions. This approach led to structures with the general space group P1 whose total energies were a little bit higher than the one of a defective spinel structure, but whose diffraction patterns correspond very well with experimental findings. Due to the poor crystallinity such a supercell can only be an approximation to the real structure of γ-Al2O3, but at the same time it contains all the representative characteristics of this phase. In general a random vacancy distribution is found in defective structures which is reflected only by a statistical mean value of many different defective cell models. As a consequence it is reasonable to choose the cell size as large as possible but as a consequence also the number of possible configurations and the computational costs increase along with the cell size.
m as well as I41/amd where aluminum atoms occupy ”non-spinel” positions. This approach led to structures with the general space group P1 whose total energies were a little bit higher than the one of a defective spinel structure, but whose diffraction patterns correspond very well with experimental findings. Due to the poor crystallinity such a supercell can only be an approximation to the real structure of γ-Al2O3, but at the same time it contains all the representative characteristics of this phase. In general a random vacancy distribution is found in defective structures which is reflected only by a statistical mean value of many different defective cell models. As a consequence it is reasonable to choose the cell size as large as possible but as a consequence also the number of possible configurations and the computational costs increase along with the cell size.
Based on comparison of the diffraction patterns, Paglia et al.69 concluded that γ-Al2O3 produced from boehmite can be better described with space group I41/amd than with Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. It was noted that the experimental diffraction patterns can vary if different precursors are used. For example γ-Al2O3 produced from amorphous precursors via CVD could be better described by Fd
m. It was noted that the experimental diffraction patterns can vary if different precursors are used. For example γ-Al2O3 produced from amorphous precursors via CVD could be better described by Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.
In this study we compare the structure model of Paglia et al. (space group I41/amd, no. 141) and the defective spinel model. A recent model for γ-Al2O3 by Menendez-Proupin and Gutierrez53 was not included as it was developed by relaxing a defective spinel model without preserving the crystallographic system which we want to maintain for all structures.
But we want to mention that Ferreira et al. have compared this spinel-like structure proposed by Menendez-Proupin and Gutierrez53,71 to a triclinic structure proposed by Pinto et al.72 regarding their thermodynamic stability, lattice vibrational modes, and bulk electronic properties using DFT calculations.73 They found the spinel-like model to be thermodynamically more stable by 4.55 kcal mol−1 per formula unit on average from 0 to 1000 K. Also the simulated infrared spectra of the spinel-like model showed better agreement with experimental data.
For the defective spinel model (γ-spinel) we started with a tripled primitive unit cell (Al6O8 → Al18O24) and removed two cations in octahedral positions in a way that the resulting vacancies are as far away from each other as possible. This stoichiometric cell contains 40 atoms (Al16O24) and is relaxed under the restriction that the cubic crystal system is maintained at all times (Fig. 9). All defective structures in this work were relaxed while maintaining the specific crystal system. For model (γ-P) of Paglia et al. we chose the most stable structure that they obtained by optimizing a 2 × 1 × 3-I41/amd supercell with frozen lattice parameters (Fig. 10).
Regarding the large number of atoms in the primitive cell (160) and the symmetry lowering due to the removal of individual atoms, the calculation of the γ-P-model is very expensive. Therefore no frequency calculation could be performed in this case. The lattice constants (Table 8 and 9) agree very well to the experimental data with relative errors of 0.2% (γ-spinel) and 0.9% (γ-Paglia). The calculated band gaps differ by about 1 eV from the experimental reference, but in contrast to the spinel-model a direct transition was calculated for the Paglia-model. Energetically the spinel-model lies 12 kJ mol−1 (per formula unit) below the Paglia-model and is closer to the experimentally found heat of atomization. This is in agreement with the findings of Ferreira et al. mentioned above.
However, in conclusion we favor the Paglia-model as representative bulk structure for γ-Al2O3 because (a) Paglia et al. showed that the diffraction patterns agree very well with experimentally found patterns and (b) the periodic defective spinel model would lead to a structure with a highly ordered distribution of vacancies. This feature is rather known for the thermodynamically more stable δ phase and would not fit the picture of a structure with a minor long-range order. Moreover, due to the enormous number of possible modifications Paglia et al. could not investigate all potential cells that can be derived from their approach, so it is likely that there exist energetically more favorable structures than the model we used.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, no. 227) where several aluminum atoms occupy the 48f-position.
m, no. 227) where several aluminum atoms occupy the 48f-position.
Shirasuka et al.74 concluded from an XRPD study that 5/8 of the aluminum atoms are situated on the octahedral 16c- and 16d-position and the remaining 3/8 are distributed over the tetrahedral 8a- and 48f-positions. The results of a high-resolution transmission electron microscopy (HRTEM) study by Ernst et al.75 differ from those of Shirasuka et al. only in the distribution of the cations over the 8a- (5.35%) and 48f-position (32.15%) while the 16c- and 16d-positions are occupied to the same amount.
Based on a Rietveld refinement Zhou and Snyder68 suggested that the 8a- and 16c-positions are unoccupied and furthermore that about 10% of the aluminum atoms are situated on the ”non-spinel” position 32e. But it is not yet clarified whether the latter model is only restricted to the surface region or not.
It was reported by Lippens and De Boer56 that there is a slight tetragonal distortion (0.985 < a/c < 0.993) and that the oxide lattice is less ordered than in γ-Al2O3.
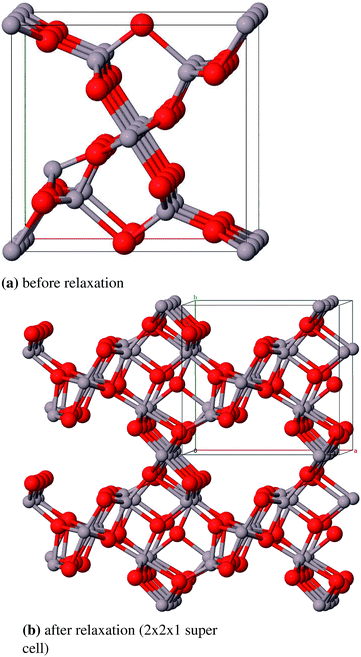
In this study we employ Zhou and Snyders model (η-ZS) and the one proposed by Ernst (η-E). For both models we constructed two 1 × 1 × 3-supercells leading to a composition of Al72O24 for η-ZS and Al66O24 for η-E assuming that all positions are fully occupied. Hence 56 and 50 atoms, respectively, had to be removed to achieve the correct stoichiometry. We removed the atoms in such a way that all the remaining interatomic distances are as large as possible. This procedure led to several structures for both models. The energetically most favorable version was selected as representative for the specific model.
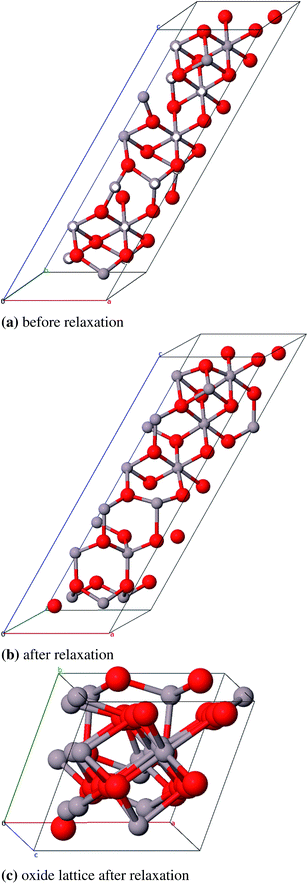
We could not find a model of η-E where less than three atomic pairs exhibit a distance of 1.8 Å (Fig. 11a). After geometry optimization however those atoms lie at least 2.8 Å apart (Fig. 11b). For the η-ZS models we could only reduce the amount of 1.8 Å bonds to six (Fig. 12a) but in the relaxed structure the bonds are all ≥2.8 Å (Fig. 12b).
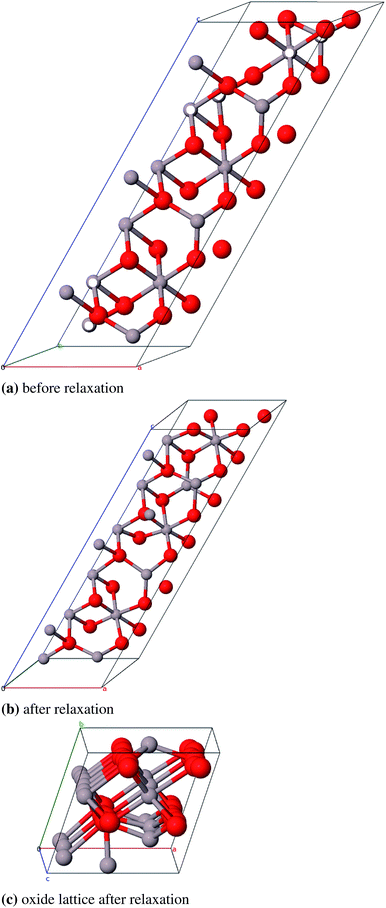 | ||
| Fig. 11 Primitive unit cell of η-E-Al2O3 (α = β = γ = 60°), atom pairs with d = 1.8 Å are marked white, with dgeq 2.8 Å grey. | ||
 | ||
| Fig. 12 Primitive unit cell of η-ZS-Al2O3 (α = β = γ = 60°), atom pairs with d = 1.8 Å are marked white, with dgeq 2.8 Å grey. | ||
Fig. 12c and 11c show the distortion of the oxide lattice of η-ZS-Al2O3 compared to η-E-Al2O3. Regarding the relative errors of the calculated lattice constants (0.6% vs. 2.6%) and the heat of atomization (2930 kJ mol−1vs. 2890 kJ mol−1) we conclude that η-E-Al2O3 is the preferable model (Table 10). Moreover, as mentioned above, the Zhou and Snyder model may be restricted to the surface region. Both structures have indirect band gaps (4.4 eV and 5.5 eV) that are rather small compared to the other modifications.
Tsybulya and Kryukova79 have obtained refined lattice constants through XRPD and electron microscopy and suggested the space group P41212 (no. 92). The cation vacancies are distributed over octahedral positions.76,78,80
Coincidently γ-Fe2O3 is also composed of a tripled (spinel) cell with cation vacancies exclusively on octahedral positions and has the same space group P41212,81 therefore this model has already been used for calculations of δ-Al2O3.82 Repelin and Husson78 made a “least-squares fitting” of X-ray diffraction patterns of δ-Al2O3 which resulted in different lattice constants ( and cδ = 23.657 Å) that match well with a tripled cell of tetragonal γ-Al2O3.69 In this work we have used the γ-Fe2O3-(δ-FE) as well as the Repelin–Husson-model (δ-RH, space group P
and cδ = 23.657 Å) that match well with a tripled cell of tetragonal γ-Al2O3.69 In this work we have used the γ-Fe2O3-(δ-FE) as well as the Repelin–Husson-model (δ-RH, space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2, no. 115) as starting structures. It should be mentioned that Pecharroman et al.83 concluded that the IR- and NMR spectra of δ-Al2O3 would rather fit to a mix of θ- and γ-Al2O3 than to a tripled spinel cell based on a spectra comparison of γ-Fe2O3 and δ-Al2O3.
m2, no. 115) as starting structures. It should be mentioned that Pecharroman et al.83 concluded that the IR- and NMR spectra of δ-Al2O3 would rather fit to a mix of θ- and γ-Al2O3 than to a tripled spinel cell based on a spectra comparison of γ-Fe2O3 and δ-Al2O3.
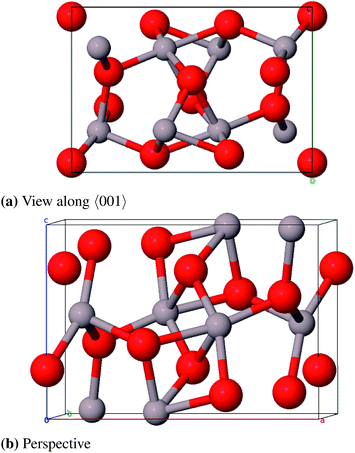
We simplified the δ-RH model (80 atoms) concerning the actual occupancy of the six 4j (x, 0, z) and 4k (x, 1/2, z) positions of the aluminum atoms (each 83.3%) to be able to build a cell with less than 240 atoms: One 4j and 4k position is fully occupied while three of the remaining four positions are occupied. Consequently there are four cation vacancies in this model which were positioned as far away from each other as possible (Fig. 13a). The crystallographic data for the δ-FE model already include the vacancy positions, thus no atoms had to be removed in that case (Fig. 13b).
As for the γ-P-model we could not perform frequency calculations for δ-FE due to the large size of the unit cell (160 atoms). δ-RH provides better results for the calculated lattice parameters (Table 11 and 12) with a relative error of 1.0% compared to δ-FE-Al2O3 (1.9%). The calculated band gaps of 6.6 eV and 7.2 eV, respectively, are direct transitions at the Γ-point. Regarding the energies per formula unit, δ-FE-Al2O3 is 9 kJ mol−1 more stable than δ-RH-Al2O3. However, this result must be taken with some care, since we used a simplified model for δ-RH and only analyzed one of a variety of possible vacancy arrangements. Moreover, the δ-RH-model is – unlike the δ-FE-model – based on crystallographic data of δ-Al2O3 and is considered as the more appropriate model in the end.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
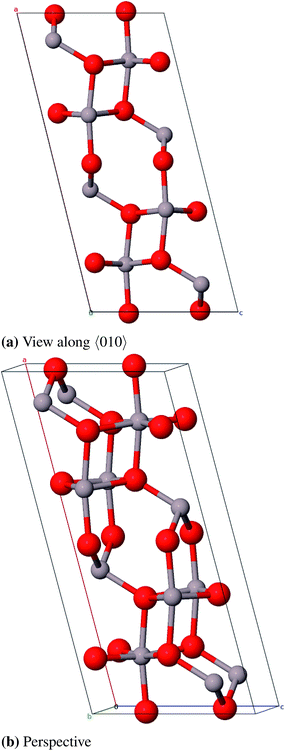
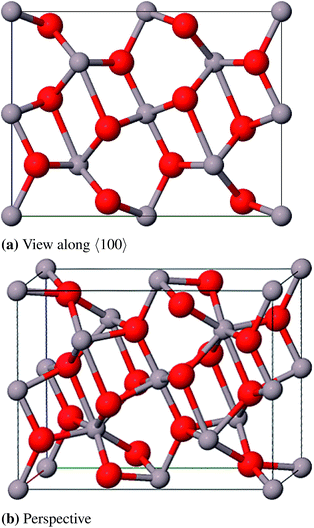
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio (Al2.826Si0.174O4.588). Starting from this compound the remaining silicon atoms were substituted by aluminum atoms and some oxygen atoms were removed to achieve the correct stoichiometry. One 2a position (0, 0, 0) is fully occupied and two 4h positions (x, y, 1/2) are partially occupied by aluminum atoms (58.7% and 41.3%). The oxygen atoms occupy a 4g Wyckoff position (x, y, 0) and a 4h position (x, y, 1/2) and a second 4h position by 25%. The unit cell suggested by Aryal et al. contains 240 atoms and is not used in this study because of the large computational costs. Instead we constructed a smaller cell (45 atoms) from a 1 × 1 × 3-supercell of Al-substituted mullite (Al31O36) and removed 13 aluminum and 9 oxygen atoms (Al18O27). First priority was to remove the aluminum atoms in a fashion that all Al–Al-distances are ≥3.0 Å. Afterwards selected oxygen atoms were removed with the aim that the remaining oxygen atoms stay in the vicinity of as many aluminum atoms as possible. We created three such models and chose the energetically lowest as the starting structure for geometry optimizations (Fig. 14).
Si ratio (Al2.826Si0.174O4.588). Starting from this compound the remaining silicon atoms were substituted by aluminum atoms and some oxygen atoms were removed to achieve the correct stoichiometry. One 2a position (0, 0, 0) is fully occupied and two 4h positions (x, y, 1/2) are partially occupied by aluminum atoms (58.7% and 41.3%). The oxygen atoms occupy a 4g Wyckoff position (x, y, 0) and a 4h position (x, y, 1/2) and a second 4h position by 25%. The unit cell suggested by Aryal et al. contains 240 atoms and is not used in this study because of the large computational costs. Instead we constructed a smaller cell (45 atoms) from a 1 × 1 × 3-supercell of Al-substituted mullite (Al31O36) and removed 13 aluminum and 9 oxygen atoms (Al18O27). First priority was to remove the aluminum atoms in a fashion that all Al–Al-distances are ≥3.0 Å. Afterwards selected oxygen atoms were removed with the aim that the remaining oxygen atoms stay in the vicinity of as many aluminum atoms as possible. We created three such models and chose the energetically lowest as the starting structure for geometry optimizations (Fig. 14).
As there are no experimental structure data available for ι-Al2O3, the theoretical model by Aryal et al. is used as a reference. With a relative deviation of the lattice constants of 9.3% our Al18O27 model significantly differs from the Aryal-model (Table 13). Schneider et al.87 found that the lattice constant a of a mullite compound increases with increasing aluminum content. The parameter a of the starting compound Al2.826Si0.174O4.588 is 7.739 Å, thus the observation Schneider et al. made applies to the Aryal-model with a = 7.837 Å, in contrast to our model with a = 7.613 Å. Taking this into account the Aryal-model is more appropriate for describing bulk properties of ι-Al2O3.
Aryal et al. calculated a direct band gap of 3 eV with an LDA functional. With the PW1PW hybrid functional we received an indirect band gap of 7.1 eV. Taking into account the well-known self-interaction error of LDA which is reduced with hybrids, the PW1PW result is considered as more accurate. For a final clarification of the electronic structure it would be necessary to run a calculation of the Aryal-model with the PW1PW functional, which is, however, computationally demanding.
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 (no. 115), similar to Repelin and Husson’s78 structural description of δ-Al2O3. Nevertheless the structure of γ′-Al2O3 is way more complex as there appear octahedral as well as tetrahedral interstices and several positions are only partially occupied by aluminum atoms. Further increasing the calcination temperature resulted in a more ordered cation distribution so that the structure approaches that of δ-Al2O3 but still contains a few partially occupied positions.
m2 (no. 115), similar to Repelin and Husson’s78 structural description of δ-Al2O3. Nevertheless the structure of γ′-Al2O3 is way more complex as there appear octahedral as well as tetrahedral interstices and several positions are only partially occupied by aluminum atoms. Further increasing the calcination temperature resulted in a more ordered cation distribution so that the structure approaches that of δ-Al2O3 but still contains a few partially occupied positions.
In order to construct a supercell model with correct stoichiometry, 16 aluminum atoms had to be removed from the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2-cell with fully occupied positions (Al48O48), resulting in a cell with 80 atoms (Al32O48). Unfortunately, all geometry optimizations of this model led to extreme convergence problems with CRYSTAL-PW1PW. Therefore this structure was excluded from the energetic comparison.
m2-cell with fully occupied positions (Al48O48), resulting in a cell with 80 atoms (Al32O48). Unfortunately, all geometry optimizations of this model led to extreme convergence problems with CRYSTAL-PW1PW. Therefore this structure was excluded from the energetic comparison.
2.3 High-pressure Al2O3 polymorphs
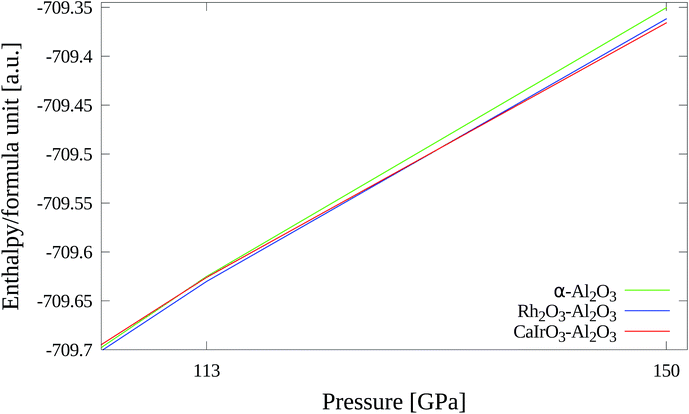
For comparison with the Al2O3 polymorphs found at normal pressure we also studied metastable phases that can only be obtained under high pressure. With CRYSTAL it is possible to optimize the structure parameters of bulk unit cells with external hydrostatic pressure (EXTPRESS). This feature has been used in the following to calculate the structure and stability of high-pressure phases.The calculated lattice parameters (see Table 14) agree rather well with the experimental reference values. The deviations are less than 1.1%. The calculated direct band gap of 11.7 eV is very high compared to the other polymorphs.
Geometry optimization was performed taking atomic positions of CaIrO6 from Sugahara et al.90 and lattice constants for CaIrO3–Al2O3 at room temperature and 150 GPa (XRPD) from Ono and Oganov34 as starting points. The optimized structure is shown in Fig. 16.
In Table 15 the calculated and measured lattice parameters are compared. There is good agreement between theory and experiment with deviations of the cell parameters being smaller than 1.2%. In this case the calculated band gap is indirect and has a value of 10.8 eV.
| 1013 hPa | 113 GPa | 150 GPa | |
|---|---|---|---|
| α-Al2O3 | 0 | +13 | +41 |
| Rh2O3–Al2O3 | +44 | 0 | +11 |
| CaIrO3–Al2O3 | +131 | +11 | 0 |
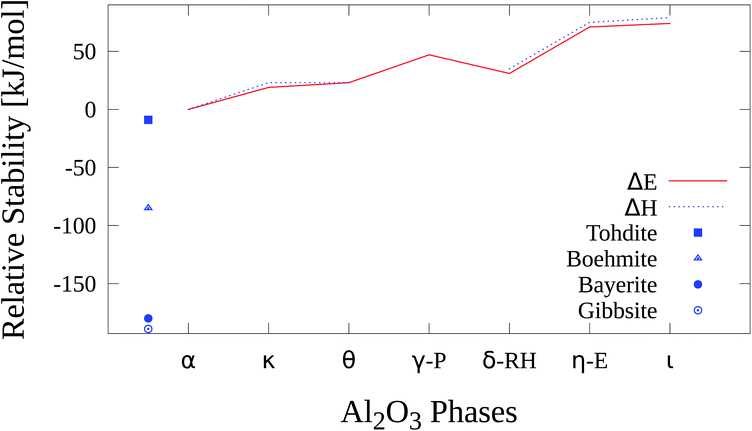
2.4 Relative stability
The relative stability of the Al2O3 phases and hydroxides is shown in Fig. 18 and Table 17. The hydroxides are thermodynamically more stable than all Al2O3 phases. Within the oxides gibbsite represents the most stable with an adjusted relative enthalpy of −189 kJ mol−1 followed by bayerite (−180 kJ mol−1), boehmite (−85 kJ mol−1) and akdalaite (−9 kJ mol−1).| Gibbsite | Bayerite | Boehmite | Akdalaite | α-Al2O3 | κ-Al2O3 | |
|---|---|---|---|---|---|---|
| ΔE0 | — | — | — | — | 0 | +19 |
| ΔH0 | −189 | −180 | −85 | −9 | 0 | +23 |
| θ-Al2O3 | γ-P-Al2O3 | δ-RH-Al2O3 | η-E-Al2O3 | ι-Al2O3 | |
|---|---|---|---|---|---|
| ΔE0 | +23 | +47 | +31 | +71 | +74 |
| ΔH0 | +23 | — | +35 | +75 | +79 |
These findings are in agreement with previous studies21,22 where gibbsite was found to be more stable by 7.7 kJ mol−1 than bayerite and boehmite is less stable than bayerite by 20.8 kJ mol−1 at B3LYP level.
κ-Al2O3 has a relative enthalpy ΔH(α − κ) of 23 kJ mol−1, close to the experimental value of 15 kJ mol−1 which was found in a calorimetric study by Yokokawa et al.50 where also ΔH(α − γ) and ΔH(α − δ) were determined.
Theoretical studies by Lee et al.51 (plane-wave LDA) and Conesa et al.82 (plane-wave GGA) obtained values of 20 kJ mol−1 and 11.5 kJ mol−1, respectively, for ΔE(α − κ). The latter work examined the impact of a dispersion correction (DFT-D) on the relative stability of several alumina phases. The uncorrected DFT calculations yielded 8.2 kJ mol−1 for ΔE(α − κ) which means that the dispersion correcture led to a small change of 3.3 kJ mol−1 in this case. Thus we conclude that the neglect of dispersion corrections in the present study will not affect the main results.
With PW1PW the θ modification is less stable than κ-Al2O3 with a relative energy ΔE(α − θ) of 23 kJ mol−1 which agrees well with the LDA results of Lee et al. where the difference is 4 kJ mol−1. At variance Conesa et al. determined the θ phase to be about 1 kJ mol−1 more stable than κ-Al2O3. There is no experimental reference value for ΔE(α − θ), but one can conclude from the calcination sequence of boehmite (Fig. 1) that the θ phase is probably even slightly more stable than δ-Al2O3 and thus more stable than κ-Al2O3.
The experimental values of E(α − γ), 22 kJ mol−1, and ΔE(α − δ), 11 kJ mol−1, are overestimated by 25 kJ mol−1 and 20 kJ mol−1. From a solution calorimetry study of MgAl2O4·Al8/3O4 by Navrotsky et al.91 a value for ΔH(α − γ) of about 23 kJ mol−1 was derived which almost matches the value from Yokokawa et al. As already mentioned energetically more favorable γ-cells may be derived from the Paglia-model if more defect configurations are considered. A possible explanation for the deviation of our results for δ-Al2O3 from experiment is the usage of a simplified model. According to our PW1PW calculations the η and ι phases are the least stable polymorphs with ΔE(α − η) = 71 kJ mol−1 and ΔE(α − ι) = 74 kJ mol−1. There are no direct experimental or theoretical reference values for the relative stability of these two modifications. If the calcination process of bayerite (Fig. 1) is considered, η-Al2O3 is less stable than θ-Al2O3. Due to the similarity of η-Al2O3 and γ-Al2O3 it is plausible that there is no significant energetical difference between these two phases. As well as for the other self constructed models for the defective structures it can be assumed that energetically more favourable atomic configurations exist for that model.
3. Computational details
All quantum-chemical calculations were performed with a development version of the crystalline orbital program CRYSTAL.92,93 Structure optimizations were performed employing the hybrid DFT functional PW1PW94 which has been shown to provide good structural and thermochemical results for oxides and other compounds.94–96 The correlation functional is PW91 (ref. 97) while the exchange functional is a mixture of 20% Hartree–Fock (HF) and 80% PW91 exchange.The performance of twelve DFT functionals in the study of crystal systems with the focus on aluminum hydroxides was investigated by Demichelis et al.98 They found that recent GGA functionals reproduce the structure of orthosilicates quite well, but fail for the H-bonded layered Al hydroxides, where the inclusion of HF exchange in the hybrid functionals leads to a significant improvement.
The pob-DZVP basis sets recently developed by Peintinger et al.99 were employed that have been parameterized for solid state systems. These basis sets were optimized in the same way as described here recently100 and are available in the ESI.† The Monkhorst-Pack k-point-lattices have been converged for each system. The values of the shrinking factors are given in the ESI.†
4. Summary and conclusion
In this work we have investigated the structure, electronic structure and relative stability of alumina polymorphs. The PW1PW functional and the small pob-DZVP basis sets have delivered satisfactory results and have proven to be suitable for calculations of Al2O3 bulk properties for those modifications where sufficient experimental information about the atomic positions was available. To our knowledge this was the first time that models for the defective structures η- and δ-Al2O3 were constructed and quantum-chemically investigated. Exceptions are γ′-Al2O3 and κ′-Al2O3. Both represent defective structures with large unit cells and several partially occupied positions which makes the construction of a convergent cell very complex and time consuming. Besides the alumina phases four aluminum hydroxides were successfully investigated and added to the relative stability comparison. We received reasonable results for the lattice constants. A dispersion correction101 is expected to further improve the agreement with experiment for the layer structures. Due to the computational expense frequency calculations for the thermodynamic functions were not feasible for all systems, but it was concluded that the relative energies only slightly deviate from the relative enthalpies because of cancellation effects. The following energetic order was obtained: gibbsite < bayerite < boehmite < akdalaite < α-Al2O3 < κ-Al2O3 < θ-Al2O3 < δ-Al2O3 < γ-Al2O3 < η-Al2O3 < ι-Al2O3. This agrees with earlier studies except for δ-Al2O3 which was found to be more stable than κ-Al2O3. A possible cause for this discrepancy is the simplified model for δ-Al2O3 besides inaccuracies of the functional and basis set. For a further improvement of the accuracy a gcp-correction102 is desirable which takes basis set errors into account in structure optimizations. The implementation of these corrections into CRYSTAL is currently in progress. Both high-pressure phases were part of this study as well. The calculated results agree with the experiments that the Rh2O3 modification is the most stable phase at 113 GPa and the CaIrO3 modification is the ground state at 150 GPa. Moreover the transition pressures is well reproduced by the calculations. So α-Al2O3 transforms to the Rh2O3 phase at about 88 GPa (exp. 80–100 GPa) which is transformed to the CaIrO3 phase at about 132 GPa (exp. 130 GPa).Acknowledgements
This work was supported by the German Research Foundation ”Deutsche Forschungsgemeinschaft” (DFG) within the Collaborative Research Area SFB 813 ′′Chemistry at Spin Centers - Concepts, Mechanisms, Functions” in the Project C5 ′′Spin centers in molecular solids - from paramagnetic salts to organic conductors”. All structural images were generated with Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org.References
- J. H. Eggert, K. A. Goettel and I. F. Silvera, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 5724 CrossRef CAS.
- R. G. McQueen and D. G. Isaak, JGR, J. Geophys. Res., 1990, 95, 21753–21765 CrossRef.
- S. Vuorinen and J. Skogsmo, Thin Solid Films, 1990, 193, 536–546 CrossRef.
- C. G. Chatfield, J. N. Lindstrom, M. E. K. Sjostrand and I. K. M. Collin, CVD of Al2O3 layers on cutting inserts, 1996, US Patent 5,543,176 Search PubMed.
- G. Paglia, C. E. Buckley, A. L. Rohl, R. D. Hart, K. Winter, A. J. Studer, B. A. Hunter and J. V. Hanna, Chem. Mater., 2004, 16, 220–236 CrossRef CAS.
- M. Minnermann, B. Neumann, V. Zielasek and M. Baumer, Catal. Sci. Technol., 2013, 3, 3256–3267 CAS.
- S.-H. Cai, S. N. Rashkeev, S. T. Pantelides and K. Sohlberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 224104 CrossRef.
- R. McPherson, J. Mater. Sci., 1980, 15, 3141–3149 CrossRef CAS.
- J. K. Bristow, D. Tiana, S. C. Parker and A. Walsh, J. Mater. Chem. A, 2014, 2, 6198–6208 CAS.
- A. B. Dichiara, J. Yuan, S. Yao, A. Sylvestre, L. Zimmer and J. Bai, J. Mater. Chem. A, 2014, 2, 7980–7987 CAS.
- Z. Xie, T. Li, N. L. Rosi and M. A. Carreon, J. Mater. Chem. A, 2014, 2, 1239–1241 CAS.
- G. J. B. Voss, E. A. Chavez Panduro, A. Midttveit, J. B. Floystad, K. Hoydalsvik, A. Gibaud, D. W. Breiby and M. Ronning, J. Mater. Chem. A, 2014, 2, 9727–9735 CAS.
- Y.-S. Lee, A. S. K. Kaliyappan, G. Kim and K. S. Nahm, RSC Adv., 2014, 4, 23107–23115 RSC.
- R. Musat, G. Vigneron, D. Garzella, S. LeCaer, J. F. Hergott, J. P. Renault and S. Pommeret, Chem. Commun., 2010, 46, 2394–2396 RSC.
- M. W. Jung, W. Song, W. J. Choi, D. S. Jung, Y. J. Chung, S. Myung, S. S. Lee, J. Lim, C.-Y. Park, J.-O. Lee and K.-S. An, J. Mater. Chem. C, 2014, 2, 4759–4763 RSC.
- R. Demichelis, Y. Noel, C. Zicovich-Wilson, C. Roetti, L. Valenzano and R. Dovesi, J. Phys.: Conf. Ser., 2008, 012013 CrossRef.
- R. Demichelis, B. Civalleri, Y. Noel, A. Meyer and R. Dovesi, Chem. Phys. Lett., 2008, 465, 220–225 CrossRef CAS.
- Y. Noel, R. Demichelis, F. Pascale, P. Ugliengo, R. Orlando and R. Dovesi, Phys. Chem. Miner., 2009, 36, 47–59 CrossRef CAS.
- R. Demichelis, Y. Noel, B. Civalleri, C. Roetti, M. Ferrero and R. Dovesi, J. Phys. Chem. B, 2007, 111, 9337–9346 CrossRef CAS PubMed.
- R. Demichelis, M. Catti and R. Dovesi, J. Phys. Chem. C, 2009, 113, 6785–6791 CAS.
- R. Demichelis, Y. Noöl, P. Ugliengo, C. M. Zicovich-Wilson and R. Dovesi, J. Phys. Chem. C, 2011, 115, 13107–13134 CAS.
- S. Casassa and R. Demichelis, J. Phys. Chem. C, 2012, 116, 13313–13321 CAS.
- I. Levin and D. Brandon, J. Am. Ceram. Soc., 1998, 81, 1995–2012 CrossRef CAS.
- R. Poisson, J. P. Brunelle, P. Nortier and A. B. Stiles, Catalyst Supports and Supported Catalysts. Theoretical and Applied Concepts, ed. A.B. Stiles, Butterworths, Boston, 1987 Search PubMed.
- D. Ksenofontov and Y. K. Kabalov, Inorg. Mater., 2012, 48, 142–144 CrossRef CAS.
- T. Ishigaki, Y. Bando, Y. Moriyoshi and M. Boulos, J. Mater. Sci., 1993, 28, 4223–4228 CrossRef CAS.
- H. C. Stumpf, A. S. Russell, J. W. Newsome and C. M. Tucker, Ind. Eng. Chem., 1950, 42, 1398–1403 CrossRef CAS.
- G. W. Brindley and J. O. Choe, Am. Mineral., 1961, 46, 771–785 Search PubMed.
- M. U. Devi, Ceram. Int., 2004, 30, 555–565 CrossRef CAS.
- I. Levin, L. A. Bendersky, D. G. Brandon and M. Rühle, Acta Mater., 1997, 45, 3659–3669 CrossRef CAS.
- I. Levin, T. Gemming and D. G. Brandon, Phys. Status Solidi A, 1998, 166, 197–218 CrossRef CAS.
- I. Levin and D. G. Brandon, Philos. Mag. Lett., 1998, 77, 117–124 CrossRef CAS.
- A. R. Oganov and S. Ono, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10828–10831 CrossRef CAS PubMed.
- S. Ono, A. R. Oganov, T. Koyama and H. Shimizu, Earth Planet. Sci. Lett., 2006, 246, 326–335 CrossRef CAS.
- J. Moellmann, S. Ehrlich, R. Tonner and S. Grimme, J. Phys.: Condens. Matter, 2012, 24, 424206 CrossRef PubMed.
- A. N. Christensen, M. S. Lehmann and P. Convert, Acta Chem. Scand., 1982, 36, 303–308 CrossRef.
- H. Saalfeld and M. Wedde, Z. Kristallogr., 1974, 139, 129–135 CrossRef CAS.
- F. Zigan, W. Joswig and N. Burger, Z. Kristallogr., 1978, 148, 255–273 CrossRef CAS.
- G. Yamaguchi, M. Okumiya and S. Ono, Bull. Chem. Soc. Jpn., 1969, 42, 2247–2249 CrossRef CAS.
- M. Digne, P. Sautet, P. Raybaud, H. Toulhoat and E. Artacho, J. Phys. Chem. B, 2002, 106, 5155–5162 CrossRef CAS.
- D. W. Bennett, Understanding Single-Crystal X-Ray Crystallography, Wiley-VCH, Weinheim, 2010, pp. 12–34 Search PubMed.
- L. Lutterotti and P. Scardi, J. Appl. Crystallogr., 1990, 23, 246–252 CrossRef CAS.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. Linstrom and W. Mallard, National Institute of Standards and Technology, 2009 Search PubMed.
- J. Olivier and R. Poirier, Surf. Sci., 1981, 105, 347–356 CrossRef CAS.
- W. Y. Ching and Y.-N. Xu, J. Am. Ceram. Soc., 1994, 77, 404–411 CrossRef CAS.
- J. Skogsmo, P. Liu, C. Chatfield and H. Norden, 12 th International Plansee Seminar 89, 1989, pp. 129–142 Search PubMed.
- P. Liu and J. Skogsmo, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 425–433 CrossRef.
- H.-L. Gross and W. Mader, Chem. Commun., 1997, 55–56 RSC.
- B. Ollivier, R. Retoux, P. Lacorre, D. Massiot and G. Férey, J. Mater. Chem., 1997, 7, 1049–1056 RSC.
- T. Yokokawa and O. Kleppa, J. Phys. Chem., 1964, 68, 3246–3249 CrossRef CAS.
- C.-K. Lee, E. Cho, H.-S. Lee, K. S. Seol and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245110 CrossRef.
- E. Husson and Y. Repelin, Eur. J. Solid State Inorg. Chem., 1996, 33, 1223–1231 CAS.
- E. Menendez-Proupin and G. Gutierrez, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035116 CrossRef.
- W.-Y. Ching, L. Ouyang, P. Rulis and H. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014106 CrossRef.
- T. Hahn, International tables for crystallography. Volume A, Space-group symmetry, Kluwer Academic Publishers, 1995 Search PubMed.
- B. C. Lippens and J. H. De Boer, Acta Crystallogr., 1964, 17, 1312–1321 CrossRef CAS.
- G. Paglia, C. E. Buckley, T. J. Udovic, A. L. Rohl, F. Jones, C. F. Maitland and J. Connolly, Chem. Mater., 2004, 16, 1914–1923 CrossRef CAS.
- C. Wolverton and K. Hass, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024102 CrossRef.
- G. N. Kryukova, D. O. Klenov, A. S. Ivanova and S. V. Tsybulya, J. Eur. Ceram. Soc., 2000, 20, 1187–1189 CrossRef CAS.
- D. Y. Li, B. H. O'Conner, G. I. D. Roach and J. B. Cornell, XVth Congress of the International Union of Crystallography (Bordeaux), 1990 Search PubMed.
- V. Jayaram and C. G. Levi, Acta Metall. Mater., 1989, 37, 569–578 CrossRef CAS.
- H. Saalfeld and B. Mehrotra, Ber. Dtsch. Keram. Ges, 1965, 42, 161–166 CAS.
- J. Wang, X. Bokhimi, A. Morales, O. Novaro, T. Lopez and R. Gomez, J. Phys. Chem. B, 1999, 103, 299–303 CrossRef CAS.
- M.-H. Lee, C.-F. Cheng, V. Heine and J. Klinowski, Chem. Phys. Lett., 1997, 265, 673–676 CrossRef CAS.
- S.-D. Mo, Y.-N. Xu and W.-Y. Ching, J. Am. Ceram. Soc., 1997, 80, 1193–1197 CrossRef CAS.
- F. H. Streitz and J. W. Mintmire, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 773 CrossRef CAS.
- G. Gutiérrez, A. Taga and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 012101 CrossRef.
- R.-S. Zhou and R. L. Snyder, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 617–630 CrossRef.
- G. Paglia, C. E. Buckley, A. L. Rohl, B. A. Hunter, R. D. Hart, J. V. Hanna and L. T. Byrne, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144110 CrossRef.
- G. Paglia, A. L. Rohl, C. E. Buckley and J. D. Gale, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224115 CrossRef.
- E. Menéndez-Proupin and G. Gutiérrez, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035116 CrossRef.
- H. P. Pinto, R. Nieminen and S. D. Elliott, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125402 CrossRef.
- A. R. Ferreira, M. J. Martins, E. Konstantinova, R. B. Capaz, W. F. Souza, S. S. X. Chiaro and A. A. Leitão, J. Solid State Chem., 2011, 184, 1105–1111 CrossRef CAS.
- K. Shirasuka, H. Yanagida and G. Yamaguchi, J. Ceram. Assoc., 1976, 84, 610–613 CrossRef CAS.
- F. Ernst, P. Pirouz and A. Heuer, Philos. Mag. A, 1991, 63, 259–277 CrossRef CAS.
- S. J. Wilson, Mineral. Mag., 1979, 43, 301–306 CAS.
- S. J. Wilson, J. Solid State Chem., 1979, 30, 247–255 CrossRef CAS.
- Y. Repelin and E. Husson, Mater. Res. Bull., 1990, 25, 611–621 CrossRef CAS.
- S. V. Tsybulya and G. N. Kryukova, Powder Diffr., 2003, 18, 309–311 CrossRef CAS.
- Y. G. Wang, P. M. Bronsveld, J. T. M. DeHosson, B. Djuričić, D. McGarry and S. Pickering, J. Am. Ceram. Soc., 1998, 81, 1655–1660 CrossRef CAS.
- J.-E. Jørgensen, L. Mosegaard, L. E. Thomsen, T. R. Jensen and J. C. Hanson, J. Solid State Chem., 2007, 180, 180–185 CrossRef.
- J. C. Conesa, J. Phys. Chem. B, 2010, 114, 22718–22726 CAS.
- C. Pecharroman, I. Sobrados, J. E. Iglesias, T. Gonzalez-Carreno and J. Sanz, J. Phys. Chem. B, 1999, 103, 6160–6170 CrossRef CAS.
- P. A. Foster, J. Electrochem. Soc., 1959, 106, 971–975 CrossRef CAS.
- M. Korenko, M. Kucharík and D. Janičkovi&ccaron, Chem. Pap., 2008, 62, 219–222 CAS.
- S. Aryal, P. Rulis, L. Ouyang and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 174123 CrossRef.
- H. Schneider, J. Schreuer and B. Hildmann, J. Eur. Ceram. Soc., 2008, 28, 329–344 CrossRef CAS.
- M. Okumiya and G. Yamaguchi, Bull. Chem. Soc. Jpn., 1971, 44, 1567–1570 CrossRef CAS.
- J.-F. Lin, O. Degtyareva, C. T. Prewitt, P. Dera, N. Sata, E. Gregoryanz, H.-k. Mao and R. J. Hemley, Nat. Mater., 2004, 3, 389–393 CrossRef CAS PubMed.
- M. Sugahara, A. Yoshiasa, A. Yoneda, T. Hashimoto, S. Sakai, M. Okube, A. Nakatsuka and O. Ohtaka, Am. Mineral., 2008, 93, 1148–1152 CrossRef CAS.
- A. Navrotsky, B. A. Wechsler, K. Geisinger and F. Seifert, J. Am. Ceram. Soc., 1986, 69, 418–422 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09 User's Manual, University of Torino, Torino, 2009 Search PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà and Y. Noël, CRYSTAL14 User’s Manual, University of Torino, Torino, 2014.
- T. Bredow and A. R. Gerson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 5194 CrossRef CAS.
- T. Bredow, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 144102 CrossRef.
- M. M. Islam, T. Bredow and C. Minot, J. Phys. Chem. B, 2006, 110, 9413–9420 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef.
- R. Demichelis, B. Civalleri, P. D'Arco and R. Dovesi, Int. J. Quantum Chem., 2010, 110, 2260–2273 CrossRef CAS.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, 2014, unpublished.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2012, 34, 451–459 CrossRef PubMed.
- W. Reckien, F. Janetzko, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2012, 33, 2023–2031 CrossRef CAS PubMed.
- J. G. Brandenburg, M. Alessio, B. Civalleri, M. F. Peintinger, T. Bredow and S. Grimme, J. Phys. Chem. A, 2013, 117, 9282–9292 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ta02663b |
| This journal is © The Royal Society of Chemistry 2014 |