Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of the La/W ratio and doping on the structure, defect structure, stability and functional properties of proton-conducting lanthanum tungstate La28−xW4+xO54+δ. A review
Anna
Magrasó
* and
Reidar
Haugsrud
Department of Chemistry, University of Oslo, Centre for Materials Science and Nanotechnology (SMN), FERMiO, Gaustadalléen 21, NO-0349, Oslo, Norway. E-mail: a.m.sola@smn.uio.no; annamagraso@gmail.com; Fax: +47-22840651; Tel: +47-22840660
First published on 4th April 2014
Abstract
The present review focuses on characteristics of lanthanum tungstate in the compositional region 25–30 mol% La2O3 in the La2O3–WO3 phase diagram. These tungstates represent an interesting family of materials for technological applications being proton or mixed proton–electron conductors depending on conditions. The material family was traditionally identified as La6WO12. However, recent efforts have shown that lanthanum tungstate can more correctly be represented by the formula La28−xW4+xO54+δ, where nearly one tungsten (x ∼ 1) dissolves in lanthanum sites to form a stable composition. In the present contribution, the importance of the crystal structure and the effect of the La/W ratio on stability, defect chemistry and, accordingly, transport properties of this material are reviewed. A revisited phase diagram in this compositional region is presented. Reported doping strategies on both the A- and B-sites are discussed in view of the applicability of these materials as dense ceramic H2 separation membranes.
1. Stoichiometry, chemical formula, and phase diagram
Early works on rare-earth tungstates (“Ln6WO12”) were carried out in the 60s and 70s by various researchers,1–9 where the chemical formula originated from an older nomenclature expressing the proportion of the parent oxides, i.e. Ln2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) WO3 = 3
WO3 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This nomenclature has also been widely used for isostructural materials, such as rhenates, uranates and molybdates, generally written as Ln6MO12, where Ln is a rare earth element or Y, and M = Mo, U or Re.1,10–12 This has led to confusion regarding the actual chemical formula of lanthanum tungstate (and likely for other tungstates with large rare-earth cations), and to an incorrect range of the La/W ratio with single phase compositions, as argued in the following. Some researchers initially claimed that “La6WO12” was a single phase material after annealing powders prepared by traditional solid state reaction at ∼1400 °C.8 However, when Chang and Phillips7 indexed the XRD patterns of “La6WO12” according to a fluorite-related structure, two additional reflections were present, more recently identified as La2O3.13 Yoshimura and Rouanet9 studied the phase diagram of the La2O3–WO3 system in more detail based on rapid quenching of oxide melts (see Fig. 1a, re-drawn by Chambrier et al.14). They observed that La6WO12 is not thermodynamically stable below 1740 °C,9,15 but rather that a more tungsten rich phase, La10W2O21 (also written as La2O3
1. This nomenclature has also been widely used for isostructural materials, such as rhenates, uranates and molybdates, generally written as Ln6MO12, where Ln is a rare earth element or Y, and M = Mo, U or Re.1,10–12 This has led to confusion regarding the actual chemical formula of lanthanum tungstate (and likely for other tungstates with large rare-earth cations), and to an incorrect range of the La/W ratio with single phase compositions, as argued in the following. Some researchers initially claimed that “La6WO12” was a single phase material after annealing powders prepared by traditional solid state reaction at ∼1400 °C.8 However, when Chang and Phillips7 indexed the XRD patterns of “La6WO12” according to a fluorite-related structure, two additional reflections were present, more recently identified as La2O3.13 Yoshimura and Rouanet9 studied the phase diagram of the La2O3–WO3 system in more detail based on rapid quenching of oxide melts (see Fig. 1a, re-drawn by Chambrier et al.14). They observed that La6WO12 is not thermodynamically stable below 1740 °C,9,15 but rather that a more tungsten rich phase, La10W2O21 (also written as La2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) WO3 = 5
WO3 = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), forms below this temperature. Due to the numerous ways of reporting the chemical formula of lanthanum tungstate (summarized in Table 1) it is convenient to use the La/W ratio to avoid misperception, as they all refer to the same material with small variations in the cation ratio. The compositions will be labeled as LWOx, where x represents the nominal La/W ratio multiplied by 10.
2), forms below this temperature. Due to the numerous ways of reporting the chemical formula of lanthanum tungstate (summarized in Table 1) it is convenient to use the La/W ratio to avoid misperception, as they all refer to the same material with small variations in the cation ratio. The compositions will be labeled as LWOx, where x represents the nominal La/W ratio multiplied by 10.
 | ||
| Fig. 1 (a) Phase diagram by Yoshimura and Rouanet,9 re-drawn by Chambrier et al.14 (b) Revised La2O3–WO3 phase diagram based on the data extracted from ref. 13. The dotted lines have been hypothetically extrapolated. | ||
Recently, Magrasó et al.13 have shown that neither LWO60 (“La6WO12”) nor LWO50 (“La10W2O21”) are single phase materials after firing freeze dried powders at temperatures in the range of 1300–1500 °C. In addition to the fluorite-related material forming for both compositions, La/W = 6 yields La2O3 segregation while for La/W = 5, a W-rich phase identified as La6W2O15 was formed. Later, other laboratories have independently confirmed that LWO60 and LWO50 are not single phase materials also when using conventional solid state synthesis methods16,17 at temperatures below 1500–1600 °C. Recently,18 it was stated that the previous chemical formulae considered as two different compositions (“La6WO12” or “La10W2O21”) refer to the same material (both containing segregations), and may be seen as a simplification of a more complex formula: La28−xW4+xO54+3x/2 (LWO).19 Indeed, the powder data files available for “La6WO12” (pdf: 30-0687, a = 11.179 Å) and “La10W2O21” (pdf: 30-0686, a = 11.167 Å) reveal that the number of reflections and their intensities are essentially equal, with only a small difference in the lattice parameters.
From the data available in ref. 13, a new phase diagram was constructed in the region 6 ≥ La/W ≥ 4.8 (Fig. 1b) at temperatures of 1000–1600 °C. Important to note from this diagram is firstly that there is a solid solution where the cubic fluorite-related phase (La28−xW4+xO54+3x/2, x ∼ 1) is identified. This can be concluded since there are no apparent differences in the number of peaks (from XRD) or their relative intensity, meanwhile the lattice parameter changes continuously as a function of La/W ratio (Fig. 2). Secondly, the composition range where LWO is a single phase material, depends on the temperature. This reflects that the solubility of tungsten in La2 sites (x in La28−xW4+xO54+3x/2) varies with temperature. Thirdly, if the solid solubility range is extrapolated to temperatures above 1600 °C (dotted lines in Fig. 1b) the composition written by Yoshimura and Rouanet9 as “La6WO12” reported to be stable above 1740 °C, indeed falls inside the single phase region. It is interesting to note from the phase diagram reported by Yoshimura and Rouanet (cf., Fig. 1a)9 that the two undefined high temperature regions present around La10W2O21 and La6WO12 correspond to one single solid solution region, as shown in Fig. 1b.
 | ||
| Fig. 2 Variation of the lattice parameter obtained by XRD as a function of the nominal La/W ratio after firing at 1300, 1400 or 1500 °C. | ||
Fig. 2 shows the variation of the lattice parameter as a function of the nominal La/W ratio derived from XRD after firing the different compositions at 1300, 1400 or 1500 °C. As reported previously,13 there are three distinguishable regions. In region I (low La/W ratio) and region III (high La/W ratio) the lattice parameter is virtually independent of the La/W ratio (though dependent on the firing temperature), and XRD patterns show segregation of La6W2O15 or La2O3 phases, respectively. In region II the patterns show only the single phase and the lattice parameters increase with increasing lanthanum content, following a linear behavior. The La/W-composition range of region II depends on the firing temperature, well in accordance with the phase diagram shown in Fig. 1b. At lower firing temperatures, the lattice parameters level off at lower values, which indicates that the LWO phase contains a lower La/W ratio compared to higher temperatures. At 1500 °C, LWO is a single phase material for 5.7 ≥ La/W ≥ 5.3, and the interval narrows down with decreasing final temperature (e.g. 5.4 ≥ La/W ≥ 5.2 at 1300 °C).
2. The crystal structure of lanthanum tungstate
Reports indexing X-ray diffraction patterns of the tungstates with larger lanthanide cations have existed since the 60s and 70s6,7,20–23 but these studies did not present complete structural details (e.g. atomic positions). One of the inconsistencies with the traditionally written formula La6WO12 realized recently13 was the density of the material. The density of single-phased powders was measured by He-pycnometry to be essentially independent of the composition and equal to ∼6.3–6.4 g cm−3 (see Table 2).13 With the stoichiometry “La6WO12” (Z = 4, i.e. La24W4O48) and the cell parameter (a ∼ 11.19 Å), the density can be calculated to be 5.75 g cm−3. This is significantly lower than the experimental density, and unequivocally implies that the unit cell contains more ions than 24 lanthanum, 4 tungsten and 48 oxygen. Taking the cation content of a cell into account, a structural model for lanthanum tungstate was put forward using the space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m13 where lanthanum occupies 2 different Wyckoff positions, La1 and La2. La1 resides in 4a (0, 0, 0) sites, with full occupancy, while La2 sits on 24f (1/4, 1/4, 1/4) positions, close to full occupancy. Tungsten is in position 4b (1/2, 1/2, 1/2). All the oxygen is placed in 16e sites (x, x, x) with x ∼ 0.13 and x ∼ 0.87. A follow up study suggested that X-ray and neutron powder diffraction data can be indexed using either F
3m13 where lanthanum occupies 2 different Wyckoff positions, La1 and La2. La1 resides in 4a (0, 0, 0) sites, with full occupancy, while La2 sits on 24f (1/4, 1/4, 1/4) positions, close to full occupancy. Tungsten is in position 4b (1/2, 1/2, 1/2). All the oxygen is placed in 16e sites (x, x, x) with x ∼ 0.13 and x ∼ 0.87. A follow up study suggested that X-ray and neutron powder diffraction data can be indexed using either F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m or Fm
3m or Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic cells, with only minor differences between the two.18 It is important to emphasize that the thermal factors for La2 and O2 were quite high using both these models, which indicated disorder in the respective sublattices.
m cubic cells, with only minor differences between the two.18 It is important to emphasize that the thermal factors for La2 and O2 were quite high using both these models, which indicated disorder in the respective sublattices.
| Acronym | LWO53 | LWO54 | LWO56 | LWO57 | LWO60 |
|---|---|---|---|---|---|
| La/W nominal | 5.3 | 5.4 | 5.6 | 5.7 | 6.0 |
| La/W EPMA | 5.30 | 5.45 | 5.68 | 5.75 | 6.01 |
| 2σst (95%) | 0.10 | 0.07 | 0.08 | 0.07 | 0.17 |
| Density (g cm−3) | 6.38 | 6.34 | — | 6.43 | — |
Later high resolution X-ray synchrotron studies19 revealed a very small distortion from the cubic cell, below the detection limit of a conventional laboratory X-ray diffractometer. Anyhow, the synchrotron data confirmed the atomic positions of the structural model (La1 in 4a, La2 in 24f, W1 in 4b, and O1–O2 in 16e sites) reported in ref. 13. The stoichiometry in this case (and also when using F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m or Fm
3m or Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m s.g.) would render La28W4O54 (La/W = 7), which leads to a La/W ratio higher than the one measured experimentally (La/W ∼ 5.3–5.7). Consequently, other tungsten positions must exist in the structure. Density Functional Theory (DFT) predicted that W dissolves in La2 sites,19 locating the “additional” tungsten. The atomic arrangements of two “ideal” compositions from DFT calculations, La28−xW4+xO54+δv2−δ for x = 0 and 1, are shown in Fig. 3. These correspond to La28W4O54v2 (La/W = 7, LWO70, x = 0) and La27W5O55.5v0.5 (La/W = 5.4, LWO54, x = 1). From the models shown in Fig. 3, it is clear that the structure of lanthanum tungstate on the local scale is complex. There is disorder on the oxygen sublattice18 and static disorder on the La2 site.24 The disorder rationalizes the high and anisotropic thermal factors of the O2 and La2 sites mentioned previously.
m s.g.) would render La28W4O54 (La/W = 7), which leads to a La/W ratio higher than the one measured experimentally (La/W ∼ 5.3–5.7). Consequently, other tungsten positions must exist in the structure. Density Functional Theory (DFT) predicted that W dissolves in La2 sites,19 locating the “additional” tungsten. The atomic arrangements of two “ideal” compositions from DFT calculations, La28−xW4+xO54+δv2−δ for x = 0 and 1, are shown in Fig. 3. These correspond to La28W4O54v2 (La/W = 7, LWO70, x = 0) and La27W5O55.5v0.5 (La/W = 5.4, LWO54, x = 1). From the models shown in Fig. 3, it is clear that the structure of lanthanum tungstate on the local scale is complex. There is disorder on the oxygen sublattice18 and static disorder on the La2 site.24 The disorder rationalizes the high and anisotropic thermal factors of the O2 and La2 sites mentioned previously.
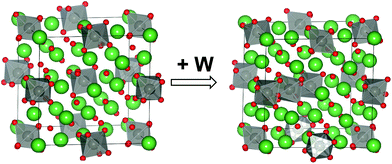 | ||
| Fig. 3 Schematic representation of the local crystal structure of lanthanum tungstate. Left: La28W4O54v2 (“stoichiometric” composition, not stable). Right: La27W5O55.5v0.5 (one tungsten dissolves in La2(24g) sites to form a stable composition). Reproduced from ref. 19 with permission from the Royal Society of Chemistry. | ||
Further insight of the local atomic arrangements in lanthanum tungstate (LWO54) has been obtained from the combination of atomic pair distribution function analysis (PDF) of time-of-flight neutron and synchrotron X-ray data with the models from DFT.25 These experimental data verified the presence of W on the La2 site as suggested from DFT (Fig. 3)19 and revealed that these calculations led to a plausible model to describe the experimental data of this complex oxide. Another work elucidated a local model combining synchrotron X-ray PDF analysis and EXAFS.24 They reported that the structure of LWO54 can be described by an average model (cubic fluorite supercell; space group Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) with disorder in the oxygen and La2 sublattice. To describe the static disorder of the La2 site, the authors in ref. 24 use the space group Pa
) with disorder in the oxygen and La2 sublattice. To describe the static disorder of the La2 site, the authors in ref. 24 use the space group Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (instead of F
(instead of F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m or Fm
3m or Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Nevertheless, these two final models from ref. 24 and 25 are in good agreement with each other. It is important to highlight that the latter24 detected experimentally ∼4.4% of anti-site disorder on the La2 site, thus confirming the dissolution of W on La2 sites predicted previously from DFT calculations (1/24: 4.2%).19,25
m). Nevertheless, these two final models from ref. 24 and 25 are in good agreement with each other. It is important to highlight that the latter24 detected experimentally ∼4.4% of anti-site disorder on the La2 site, thus confirming the dissolution of W on La2 sites predicted previously from DFT calculations (1/24: 4.2%).19,25
One important outcome of the structural model presented in Fig. 3 is the overall stoichiometry: La28−xW4+xO54+δv2−δ (δ = 3x/2). From this formula, it is straightforward to deduce the variation in the number of oxygen vacancies with the lanthanum-to-tungsten ratio and some examples are given in Table 3. There are 2 vacancies per formula unit in the “stoichiometric” composition (LWO70). However, to reduce the number of vacancies to about 1/2 per unit cell and stabilize the structure, approximately one W is accommodated in La2 sites per formula unit as a donor dopant,  . LWO54 is accordingly a stable composition.19 In other words, lanthanum tungstate is a nominally undoped material with an inherently deficient oxygen sublattice where the concentration of vacancies depends directly on the La/W ratio (and the final sintering temperature) (see Table 3). This can be related to the phase diagram shown in Fig. 1b: the temperature dependence of the LWO phase likely reflects the temperature dependence of the solubility of W in the La2 site.
. LWO54 is accordingly a stable composition.19 In other words, lanthanum tungstate is a nominally undoped material with an inherently deficient oxygen sublattice where the concentration of vacancies depends directly on the La/W ratio (and the final sintering temperature) (see Table 3). This can be related to the phase diagram shown in Fig. 1b: the temperature dependence of the LWO phase likely reflects the temperature dependence of the solubility of W in the La2 site.
There is one example in the literature that reports a stable composition with a cation ratio of 7-to-1 that is comparable to the lanthanum tungstate: Y7ReO14−δ (with δ∼0; Y28Re4O56v∼0).26 The main difference between La28W4O54v2 and Y28Re4O56v∼0 is the vacancy concentration, related to the oxidation state of W(VI) and Re(VII). Rhenium will most probably not dissolve in yttrium sites because there are no more vacancies which can compensate a possible donor in the lattice, while tungsten dissolves in La2 sites to reduce the vacancy concentration from 2 to ∼1/2 per unit cell.
3. The compositional stability of LWO
Fig. 4 shows the variation of the electrical conductivity for different lanthanum tungstates with time at 1100 °C in wet H2; for LWO53 and LWO54 the conductivity remains essentially constant and stable, while it degrades rapidly for LWO56 and LWO57. This behavior may be rationalized by the thermodynamic stability of the phase (Fig. 1b). At 1100 °C, the diagram shows that LWO54 and LWO53 are single phase materials, while LWO56 and LWO57 are not. Although LWO56 and LWO57 are single phase after sintering (1500 °C), the cations will reorganize at lower temperatures toward the stable composition with a lower La/W ratio and therefore La2O3 is segregated at 1100 °C. One could, in principle, expect that the conductivity of LWO57/LWO56 levels off at the same value as LWO54, but it continues to decrease. This may be associated with the formation of La2O3, possibly segregating to the grain boundaries, decreasing the total conductivity.To further elucidate the origin of this degradation in electrical conductivity, the dependence of the conductivity on pO2 at 1000 °C for LWO53 and LWO57 was determined before and after long term annealing at 1100 °C (Fig. 5); the LWO53 data is unaltered, while for LWO57 the heat treatment induces a significant decrease in the ionic, pO2 independent plateau in conductivity at intermediate oxygen pressures. XRD confirmed that La2O3 segregations can be found after the conductivity measurements shown in Fig. 4 for LWO57/LWO56, while these are absent for LWO54/LWO53 (Fig. 6). The lattice parameter of the nominal LWO56 decreases from 11.187 Å to 11.175 Å (in accordance with the latter being richer in tungsten cf., Fig. 2), whereas the lattice parameter of LWO54 remains essentially constant before and after the treatment (11.176 Å and 11.178 Å, respectively). These gradual changes encountered for the LWO56 and LWO57 with time altogether reflect the relative increase in the number of W donors at the La2 site followed by a decrease in the oxygen vacancy concentration. This behavior is attributed to the higher stability of the crystal structure with low concentration of vacancies at lower temperatures. There is, therefore, a trade-off between high ionic conductivity and stability where LWO54 probably is the best compromise.
 | ||
| Fig. 5 Variation of the total conductivity as a function of oxygen partial pressure at 1000 °C before and after a thermal treatment in wet H2 at 1100 °C during 60 hours. | ||
 | ||
| Fig. 6 X-ray diffractograms of various LWO compositions before and after long term annealing under reducing conditions at 1100 °C. | ||
It is worth to mention that there is no visible effect of the La/W ratio on the microstructure of the materials.13 The average grain size of powders prepared from freeze-dried precursors increases from 1–3 μm (1400 °C), 3–10 μm (1500 °C) to 10–30 μm (1600 °C) independent of the composition. The densification properties and variation of the particle size of the different LWO compositions do not differ significantly, even for those containing segregations of either La- or W-rich phases.13
4. Defect structure in LWO and hydration thermodynamics
The effect of oxygen partial pressure on the electrical conductivity of LWO for various La/W ratios is shown in Fig. 7. The flat regime at intermediate oxygen partial pressures represents ionic conductivity, while the contributions at either side represent n- and p-type electronic conductivities, in accordance with previous studies.27,28 The overall conductivity behavior of LWO56, LWO57 and LWO60 is rather similar. This reflects that the level of lanthanum in the structure is saturated and therefore the maximum number of vacancies has been reached. It is evident that below La/W = 5.6, the ionic conductivity decreases monotonically with decreasing La/W ratios (see the pO2 independent plateau in Fig. 7), and is roughly proportional to the concentration of vacancies according to La28−xW4+xO54+δv2−δ. This is further illustrated in Fig. 8 displaying the ionic conductivity at 800 °C. The difference in ionic conductivity between LWO56 and LWO52 is approximately one order of magnitude, as shown by the temperature dependence in wet Ar (Fig. 9). Overall, this behavior supports the hypothesis that W on the La site (x) acts as a donor, , and is mainly compensated by oxide ions filling up the oxygen vacancies (v). Consequently, tungsten reduces the ionic conductivity due to a decrease in the concentration of oxygen vacancies, as reported by Erdal et al.29 The positive donors also increase the concentration of electrons, which rationalizes the somewhat higher relative contribution of n-type conductivity in LWO53 than in LWO57. Electrons remain in minority concentration-wise, but with higher mobility they still have a tangible effect on the total conductivity. The ionic conductivity in LWO has been calculated based on the defect model described in ref. 30, using the concentration of vacancies from Table 3 for each LWO composition within the single phase region. The calculated conductivities at 800 °C are in accordance with the experimental ones (cf., Fig. 8), supporting the present defect model.
, and is mainly compensated by oxide ions filling up the oxygen vacancies (v). Consequently, tungsten reduces the ionic conductivity due to a decrease in the concentration of oxygen vacancies, as reported by Erdal et al.29 The positive donors also increase the concentration of electrons, which rationalizes the somewhat higher relative contribution of n-type conductivity in LWO53 than in LWO57. Electrons remain in minority concentration-wise, but with higher mobility they still have a tangible effect on the total conductivity. The ionic conductivity in LWO has been calculated based on the defect model described in ref. 30, using the concentration of vacancies from Table 3 for each LWO composition within the single phase region. The calculated conductivities at 800 °C are in accordance with the experimental ones (cf., Fig. 8), supporting the present defect model.
 | ||
| Fig. 7 Variation of the total conductivity as a function of oxygen partial pressure at different temperatures from wet H2 to wet O2 for decreasing lanthanum content (from left to right) in LWO. All specimens were prepared using the freeze-drying method,13 except LWO60, prepared by solid state chemistry, taken from ref. 28. Conductivity data is taken from ref. 28 (LWO60) and ref. 29 (for LWO57, LWO54 and LWO53). Additional compositions were measured in parallel experiments. | ||
 | ||
| Fig. 8 Variation of the experimental ionic conductivity at 800 °C (from Fig. 7) as a function of nominal amount of vacancies in La28−xW4+xO54+δv2−δ (Table 3), compared to calculated ionic conductivity from the model described in ref. 30. | ||
 | ||
| Fig. 9 Temperature dependency of the conductivity from 1100 to ∼200 °C in wet Ar for LWO56 and LWO52. It mainly reflects ionic conductivity (oxide ion + protonic). Data recorded in parallel with experiments from ref. 29. | ||
The effect of water vapour partial pressure (pH2O) at constant pO2 on the conductivity of LWO57 and LWO53 is shown in Fig. 10. The conductivity increases with increasing pH2O, and the functional dependence increases with decreasing temperature. This reflects that the concentration of protons and, accordingly, their contribution to the total conductivity, increases with decreasing temperature and increasing water vapor pressure, in accordance with the exothermic hydration reaction:
 | (1) |
 | ||
| Fig. 10 Variation of the total conductivity as a function of water vapour partial pressure in O2 at different temperatures from 500 to 800 °C for LWO57 (ref. 41) and LWO53. | ||
This reaction is, however, only strictly correct for materials with doubly charged oxygen vacancies, which is typically the result of acceptor doping. LWO, on the other hand, has inherent vacancies with partial occupancy. Norby31 has derived a Kröger–Vink compatible notation for defects in inherently defective sublattices, and Erdal et al.29 applied this approach to LWO. Hydration of La28−xW4+xO54+δv2−δ can accordingly be written as follows:
 | (2) |
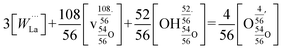 | (3) |
The reader is referred to ref. 29 and 31 for details on the derivation. From this model, the hydration and the ionic conduction can be rationalized. The effective charges of the vacancies (∼1.93) and the protons (∼0.93) are very close to those of a standard acceptor-doped system (2 and 1, respectively), so lanthanum tungstate behaves, in practice, as if it was effectively acceptor doped. As outlined above, electrons and electron holes are not significant concentration-wise in the present experimental window and contribute to the conductivity of lanthanum tungstate as minority defects (at relatively high temperatures) only. The simplified electroneutrality condition (eqn (3)) accordingly takes only ionic defects into account.
Now comparing the behaviour of the different tungstates shown in Fig. 10, we observe that there is essentially no difference in the water vapor dependency of the conductivity of LWO57 and LWO53, which confirms that the defect chemical model is the same for both materials. The conductivity of LWO57 is higher than LWO53, as expected from the higher vacancy concentration in the dry state and the higher concentration of protons upon hydration at intermediate and low temperatures. The conductivity is close to being proportional to pH2O1/3 at the lowest temperature, which was initially speculated to be related to the hydration of oxygen interstitials in LWO.28,32 Later investigations of the hydration of lanthanum tungstate by means of thermogravimetry33 revealed that the dependency of the proton concentration is essentially proportional to pH2O1/2 at relatively high temperature, in accordance with the defect chemical model from eqn (3). This behavior is typical for the exothermic hydration of oxygen vacancies generally encountered in acceptor doped systems and shows that LWO indeed behaves as though it was nominally acceptor doped. From the TG data, one finds that LWO53 hydrates up to a level corresponding to the oxygen vacancy content from Table 3, in line with the crystal structure derived by Magrasó et al.19 LWO56, however, hydrates only 66% of the nominal vacancies. There are several possible reasons for this discrepancy: as demonstrated previously in this contribution, compositions with high lanthanum contents are thermodynamically unstable at lower temperatures (typically below 1200 °C), forming LWO54 and a La2O3 secondary phase. As part of this process, the number of oxygen vacancies potentially available for hydration decreases. Consequently, the maximum level of hydration for LWO56 will be sensitive to thermal history and treatments like the drying procedure at 1000–1100 °C performed in ref. 33 before the actual hydration experiment. In this respect, it is interesting to note that the maximum level of hydration reached for LWO56 corresponds essentially to a fully hydrated LWO54 composition.33 An alternative interpretation to the low hydration level in the LWO56 composition that cannot be entirely ruled out is that vacancy ordering in the compositions with higher vacancy concentration shown by TEM19 may inhibit hydration in LWO56.
5. Effects of A-site doping in LWO
Iso-valent substitution
Haugsrud28 reported that the protonic conductivity of a series of tungstates “Ln6WO12” decreases in the order La > Nd > Gd > Er, likely related to a decrease in crystal symmetry towards the smaller rare-earth elements.5 The conductivity of all these materials is dominated by protons under wet atmospheres below 900 °C. The maximum in proton conductivity is observed for nominally undoped “La6WO12” on the order of 3–5 × 10−3 S cm−1. “Nd6WO12” exhibits higher p-type conductivity and lower protonic conductivity compared to the lanthanum counterpart. Escolástico et al.34 reported later that the protonic conductivity of La-substituted “Nd6WO12” is higher for the composition with more La, in line with the studies by Haugsrud.28 Partial substitution of Y by La16 lowered the overall electrical conductivity. The effect of Y is likely related to a decrease in crystal symmetry and to an ordering of the vacancies in the lattice as reported by Diot et al.,35 reducing the mobility of protons and oxygen vacancies.Donor-doping
Shimura et al.27 showed that partial substitution of Zr for La decreases the conductivity. Zr is probably substituting lanthanum, acting as a donor dopant , reducing the concentration of vacancies, and therefore, the ionic conductivity. Similarly, another study36 showed that when Ce was replaced by La, the ionic conductivity decreased with increasing cerium content, accompanied by a slight increase in the electronic conductivity under reducing conditions, both demonstrating the donor effect.
, reducing the concentration of vacancies, and therefore, the ionic conductivity. Similarly, another study36 showed that when Ce was replaced by La, the ionic conductivity decreased with increasing cerium content, accompanied by a slight increase in the electronic conductivity under reducing conditions, both demonstrating the donor effect.
Acceptor-doping
Haugsrud28,32 also reported that acceptor doping decreased the ionic conductivity for LWO60 when lanthanum was substituted by calcium (0.5 and 5%). This was unexpected, and initially speculated to reflect that acceptor substitution decreased the number of protons incorporated, or slowed down their mobility. It was suggested that the acceptor (Ca2+) traps protons based on the observation that the apparent enthalpy of proton mobility increased upon acceptor doping. The effect of Ba doping also proved to decrease the overall conductivity.37 In this case, impedance spectroscopy showed that the grain boundaries were orders of magnitude more resistive than the bulk.Later studies report that there is no detectable difference, neither in conductivity nor in the crystal structure between LWO56 and 2% Ca-doped LWO56.18 In the present contribution, we report that the conductivity actually depends on the thermal history, illustrated here in Fig. 11, showing the effects of annealing at different temperatures for 2% Ca-doped LWO56. As evident, the conductivity remains essentially stable at 800 °C (1) in wet Ar (representing the ionic conductivity), but decreases over time at 1000 °C (2), and even more rapidly at 1200 °C (3). The level of the conductivity at 800 °C also decreases gradually as the annealing time at the higher temperature increases. Interestingly, however, opposite effects are encountered after annealing at temperatures as high as 1400 °C; the conductivity increases during the annealing and also the level at 800 °C is higher than the original as-sintered one. This behavior either indicates that LWO phases with different La/W ratios are stabilized (as the phase diagram shown in Fig 1b suggests) at high temperatures, or that Ca-doping is meta-stable and tends to be released at intermediate temperatures between ex-solution and (re)dissolution temperatures. It is important to emphasize that LWO has low solubility of acceptor dopants (e.g. Ca2+ and Sr2+), around 1 mol%, or less. In comparison with other systems, there are a number of ternary or higher oxides in which two cations of different valences are site disordered, and where doping has none or unexpected effects.38 In those cases, doping results only in shifting the ratio of the two disordered cations, as this may have a much lower energy cost. This is accompanied by the precipitation of a phase or domains rich in the released cation, as probably occurs in our case.
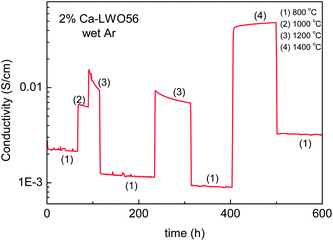 | ||
| Fig. 11 Variation of the conductivity of 2% Ca–LWO56 in wet Ar over time upon changes in temperature. Measurement recorded after the experiments from ref. 18. | ||
Overall, A-site doping in LWO has, so far, been unsuccessful to enhance the conducting properties of the material.
6. Effects of B-site doping in LWO
Nb substitution in LWO was reported to increase the ionic conductivity by acceptor doping on the W-site.39 The highest conductivity was measured for La27NbW4O55 to be 0.01 S cm−1 at 800 °C in wet N2. This is slightly higher than 7 × 10−3 S cm−1 (for LWO56) and 4 × 10−3 S cm−1 (for LWO54) in wet Ar, at 800 °C. The authors mentioned that these materials are nearly pure ionic conductors at low temperatures, with transport numbers close to 1 (∼0.98) below 800 °C. Replacement of W by Re has also been reported.40 The conductivity of undoped LWO55 is ∼3 × 10−3 S cm−1, and it increases to ∼4 × 10−3 S cm−1 at 800 °C in wet H2 when 20% Re substitutes W. The authors report that the conductivity is independent of pO2 under reducing conditions. This indicates that ionic conductivity dominates under these conditions and that rhenium probably acts as an acceptor dopant. Although both studies39,40 report effects of water vapour that indicate contribution of protons under wet conditions at intermediate temperatures, the ratio between oxide ion and protonic conductivity has not been determined for any of these substitutions. This should be studied further to evaluate the potential use of these materials in hydrogen technology applications.Amsif et al.41 have recently shown that the replacement of tungsten by molybdenum in lanthanum tungstate [La28−y(W1−xMox)4+yO54+δ] is efficient to improve the electronic conductivity substantially without altering the protonic conductivity significantly, at least up to x = 0.4. This affirmation is based on the following experimental results: (i) the ionic conductivity is relatively independent of the Mo content up to 40% substitution, see pO2 dependencies in Fig. 12, taken from ref. 30 and 41; (ii) the ratio between proton and oxide ion conductivity does not seem to be affected by Mo up to 40% substitution, see pH2O dependencies in ref. 30 and 41 and the comparison between Mo-free and Mo-containing compositions, shown in Fig. 13; and (iii) the partial protonic conductivities measured using the EMF method render similar values for LWO54 and 30% Mo-substituted LWO54.30 This implies that Mo substitution in LWO results in an overall increase of the ambipolar proton–electron conductivity and thereby enhance the H2 permeation in dense ceramic membranes, as also shown by others.40,42 This is addressed in more detail in Section 7.
 | ||
| Fig. 12 Variation of the total conductivity as a function of oxygen partial pressure at different temperatures for increasing molybdenum content (from left to right), La28−y(W1−xMox)4+yO54+δ (x = 0–0.4), taken from ref. 29, 30 and 41. | ||
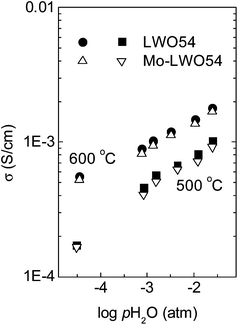 | ||
| Fig. 13 Variation of the total conductivity as a function of water vapour partial pressure in O2 at 500 and 600 °C for LWO54 and 30% Mo-substituted LWO54, taken from ref. 30. | ||
All in all, B-site doping of LWO has proven to be more successful than A-site doping to enhance the conductivity of the materials. Either the ionic or electronic/ambipolar conductivity can be increased depending on the dopant.
7. Discussion: applicability of the materials
Lanthanum tungstate and related compositions have during the last years attracted considerable attention as electrolyte materials for proton conducting solid oxide fuel cells (PC-SOFCs) and dense hydrogen gas separation membranes.43 LWO has the potential of being a suitable proton conducting electrolyte material in the range of 600–700 °C, with proton conductivities in the order of 1 mS cm−1. At high temperatures, LWO dehydrates, oxygen vacancies start to form at the expense of protons according to eqn (1) and (2), and oxide ion conductivity dominates over proton conductivity above ∼750 °C.28,30 Therefore, LWO-based PC-SOFCs should operate up to temperatures of about 600 °C, where the electrolyte membrane behaves as a pure proton conductor. Fuel cell testing with ∼1 mm thick electrolyte and Pt electrodes has confirmed that LWO is predominantly an ionic conductor. The mediocre power output achieved,30 however, shows that thin electrolytes (∼1 μm) with tailor-made electrodes are required to make LWO-based PC-SOFCs competitive. NiO is not chemically compatible with LWO44 so Ni-cermet-supports with in situ reduction of sintered NiO–LWO composites are not viable. Serra and co-workers44,45 tested LaCrO3-based materials as anodes. The best performance was achieved when La0.75Ce0.1Sr0.15CrO3−δ was infiltrated with nickel nanoparticles. The overall ASR for this system was 0.3 Ω cm2 at 750 °C in wet H2. LWO is chemically and mechanically stable with LSM (La0.7Sr0.3MnO3−δ) and LSCM (La0.75Sr0.25Cr0.5Mn0.5O3−δ),46 but relatively high ASRs were measured 3–4 Ω cm2 in wet air at 750 °C for LSM-based cathodes.46,47 Optimized 50% Pr2NiO4–50% LWO composites show ASR values of only 0.5 Ω cm2 at 700 °C, as such being a promising cathode candidate for use in PC-SOFCs.48Focus onwards will be on the regime where LWO is a mixed proton–electron conductor. There is an increasing number of reports on the hydrogen flux in membranes of LWO-based materials, and the potential as a hydrogen permeable membrane has thus been demonstrated. For unsubstituted LWO, the electronic conductivity is relatively low at T < 800 °C, and the H2 permeation via ambipolar transport of protons and electrons is low at these temperatures. Even up to ∼950 to 1000 °C, the hydrogen flux is limited by n-type electronic conductivity, whereas protons are the limiting species above this temperature due to the dehydration of the material. At 1000 °C, the ambipolar proton–electron conductivity in lanthanum tungstate (LWO56) is approximately 10−3 S cm−1,49 which renders hydrogen fluxes comparable to the best mixed proton–electron conducting perovskites. The hydrogen flux of LWO56 is 0.041 ml min−1 cm−2 (wet H2 on the feed side),49 0.046 ml min−1 cm−2 for Nd-substituted LWO55 (wet 50% H2)34 or ∼0.08 ml min−1 cm−2 for LWO55 (wet 50% H2),40 all at 1000 °C and with wet Ar on the permeate side. These membranes were 1–2 mm thick, and the flux can be further increased by decreasing the membrane thickness. Gil et al.50 reported that a 25–30 μm LWO56 supported on a porous matrix of the same composition led to an increased hydrogen flux (0.14 ml min−1 cm−2 in wet 10% H2–Ar). This value was, however, lower than expected based on measurements for thicker membranes. The deviation may indicate that surface kinetics is limiting the flux across the thinner membrane, as also suggested by the sluggish transport kinetics in LWO56 reported by Hancke et al.,51 and suggested to reflect slow surface kinetics, in line with the flux data.
It is important to highlight when discussing the application of these materials as hydrogen membranes that the level of H2 in the permeate increases dramatically when the carrier gas on the permeate side is wetted. This could, in principle, be related to a higher degree of hydration of the membrane, but it has been shown that water splitting is the main cause.42 Water splits as a consequence of the oxygen gradient from the sweep side to the feed side and the oxide ions migrate through the membrane towards the feed, leaving H2 behind at permeate side. This H2 does consequently not originate from ambipolar transport of protons and electrons from the feed side to the permeate side. This effect becomes more important at the higher temperatures, as the oxide ion conductivity increases with increasing temperature. Although for H2 separation purposes water splitting does not pose a problem, it is in many cases important to realize how much of the detected H2 that comes from permeation (representing actual gas separation) and how much that stems from water splitting at the permeate side (hydrogen production, not separation). It has been shown that the hydrogen flux detected when the permeate side is dry is in accordance with the value estimated from ambipolar transport of protons and electrons,42 and can be taken as a reference to differentiate H2 separation and H2 production.
The chemical stability of LWO against CO2 has been confirmed for LWO55.40 This represents one of the main advantages of this family of materials over the previous state-of-the-art, SrCeO3, which readily forms carbonates even in atmospheres containing small amounts of CO2. It is also interesting to highlight that LWO is more stable towards cation diffusion-related degradation than many of the most promising oxygen transport membrane materials, since bulk diffusivities of W and La are very similar and relatively slow.52 The thermal expansion coefficient (TEC) for lanthanum tungstate was determined by different laboratories to be ∼11–12 × 10−6 K−1 [ref. 18 and 53], and the expansion is isotropic since the crystal symmetry is cubic. It is important from a technological point of view that a material with a practical application exhibits a linear isotropic thermal expansion coefficient, to make thermal compatibility with the surrounding materials easier. In addition, the TEC is essentially independent of pO2 (LWO does not reduce or oxidize significantly) and only slightly dependent on pH2O, due to hydration.
As mentioned previously, B-site doping strategies have been the most successful approach to increase the conductivity in LWO. The replacement of tungsten by molybdenum in lanthanum tungstate is particularly interesting, since the electronic conductivity is enhanced substantially without altering the protonic conductivity significantly.30,41 Other authors have claimed that Mo substitution decreases protonic conductivity.40 However, the statement was based on results from measurement of the pH2O dependency on the electrical conductivity under reducing conditions. Under these conditions electronic conductivity prevails and the relative contribution of protonic conductivity is smaller for the Mo-substituted LWO, but it does not necessarily mean that the σH+ is smaller. The influence of electronic defects on the water vapour dependence of the conductivity can be minimized if the measurements are done under inert or oxidizing conditions, as performed in ref. 30 and 41 and shown here in Fig. 12 (all in O2). We should remind the reader that p-type conductivity is relatively independent of the Mo-content,41 and quite low at the temperatures measured (500–800 °C).
The ambipolar proton–electron conductivity
 | (4) |
 | ||
| Fig. 14 Estimated ambipolar conductivities in wet H2 of undoped and Mo-substituted LWO. The partial proton conductivities are taken from those obtained using the EMF method (see ref. 30), which are assumed constant as a function of Mo doping up to 40% (the author is referred to the text to support this statement). The partial electronic conductivities are extracted from the dependency of the conductivity vs. pO2 at each indicated temperature (from ref. 30 and 41). Lines are guides to the eye, only. | ||
When compared to the other state-of-the-art materials for hydrogen permeation, systems based on acceptor-doped SrCeO3 are the most studied so far, see e.g.ref. 54–58. These materials are predominantly protonic conductors below 600–700 °C,54 so that high ambipolar conductivity can only be obtained via suitable doping and/or by increasing temperature. Oh et al.58 reported that the ambipolar conductivity of SrCe0.85Eu0.15O3−δ was close to 10−3 S cm−1 at 900 °C, which is comparable to that of 40% Mo–LWO at 600 °C. The hydrogen flux measured for 1 mm thick SrCe0.95Yb0.05O3−δ at 677 °C is ∼0.007 ml cm−2 min−1,59 or ∼0.05 ml cm−2 min−1 for 0.8 mm thick SrCe0.95Tm0.05O3−δ at 950 °C.60 The flux can increase substantially with decreasing membrane thickness, as reported for 33 μm thick SrCe0.7Zr0.2Eu0.1O3−δ (0.23 ml cm−2 min−1 at 900 °C),61 and for 2 μm thick SrCe0.95Yb0.05O3−δ (∼15 ml cm−2 min−1 at 677 °C).59 The main drawback for a widespread application of SrCeO3-based materials is the low chemical stability, and the tungstates can offer a feasible alternative with substantially increased chemical stability. The H2 permeation of 5 μm-thick 40% Mo-substituted LWO is predicted to be ∼2 ml cm−2 min−1 at 600 °C, using a gradient of pH2 of one order of magnitude, an ambipolar conductivity of ∼1.6 × 10−3 S cm−1, and assuming that bulk diffusion is limiting. We should emphasize, however, that surface limitations have been encountered for LWO and Mo-substituted LWO,42 and that surface treatment to increase kinetics must be taken into account in the optimization process.
All in all, Mo-substituted LWO embraces a family of truly competitive materials for H2 permeation and further development on the optimization of the cation ratio, microstructure of the membrane and surface treatment will be dealt with in the future.
Acknowledgements
The data reported and the discussion thereof summarizes work financed by Research Council of Norway (grant nos 187160, 193816, 190901, 171157, 191346, nn4604k). All the insight gained through these projects and the collaboration with all the project partners is gratefully acknowledged. In addition, thanks to Prof. Truls Norby, PhD fellows, and Post Docs, for sharing thoughts, results, and discussions.References
- S. F. Bartram, Inorg. Chem., 1966, 5(5), 749–754 CrossRef CAS.
- S. F. Bartram, E. F. Juenke and E. A. Aitken, J. Am. Ceram. Soc., 1964, 47, 171–175 CrossRef CAS PubMed.
- E. A. Aitken, S. F. Bartram and E. F. Juenke, Inorg. Chem., 1964, 3(7), 949–953 CrossRef CAS.
- H. J. Borchardt, Inorg. Chem., 1963, 2(1), 170–173 CrossRef CAS.
- G. J. McCarthy, R. D. Fisher, G. G. Johnson and C. E. Gooden, National Bureau of Standards Special Publication, Solid State Chemistry in Proceedings of the 5th Materials Research Symposium, 1972, p. 397 Search PubMed.
- L. L. Y. Chang, M. G. Scroger and B. Phillips, J. Inorg. Nucl. Chem., 1966, 28(5), 1179–1184 CrossRef CAS.
- L. L. Y. Chang and B. Phillips, Inorg. Chem., 1964, 3(12), 1792–1794 CrossRef CAS.
- M. M. Ivanova and E. M. Reznik, Izvestiya Akademii Nauk SSSR, Neorg. Mater., 1972, 8(5), 981–983 CAS.
- M. Yoshimura and A. Rouanet, Mater. Res. Bull., 1976, 11, 151–158 CrossRef CAS.
- T. Hartmann, H. Ehrenberg, G. Miehe, G. Wltschek and H. Fuess, J. Solid State Chem., 1999, 148, 220–223 CrossRef CAS.
- D. Michel and A. Kahn, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1437–1441 CrossRef.
- A. P. Richard and D. D. Edwards, J. Solid State Chem., 2004, 177, 2740–2748 CrossRef CAS PubMed.
- A. Magrasó, C. Frontera, D. Marrero-López and P. Núñez, Dalton Trans., 2009, 10273–10283 RSC.
- M. H. Chambrier and F. Goutenoire, JEEP, EDP Sciences, 2009, p. 00022 Search PubMed.
- M. Yoshimura and J. F. Baumard, Mater. Res. Bull., 1975, 10(9), 983–988 CrossRef CAS.
- A. Lashtabeg, J. Bradley, A. Dicks, G. Auchterlonie and J. Drennan, J. Solid State Chem., 2010, 183(5), 1095–1101 CrossRef CAS PubMed.
- C. Solis, S. Escolastico, R. Haugsrud and J. M. Serra, J. Phys. Chem. C, 2011, 115, 11124–11131 CAS.
- A. Magrasó, C. H. Hervoches, I. Ahmed, S. Hull, J. Nordström, A. W. B. Skilbred and R. Haugsrud, J. Mater. Chem. A, 2013, 1, 3774 Search PubMed.
- A. Magrasó, J. M. Polfus, C. Frontera, J. Canales-Vazquez, L.-E. Kalland, C. H. Hervoches, S. Erdal, R. Hancke, M. S. Islam, T. Norby and R. Haugsrud, J. Mater. Chem., 2012, 22(5), 1762–1764 RSC.
- M. Yoshimura, F. Sibieude, A. Rouanet and M. Foex, J. Solid State Chem., 1976, 16(3–4), 219–232 CrossRef CAS.
- V. K. Trunov, G. I. Tyushevskaya and N. S. Afonskii, Zh. Neorg. Khim., 1968, 13(4), 936–939 CAS.
- G. J. McCarthy, Mater. Res. Bull., 1971, 6(1), 31–39 CrossRef CAS.
- E. Summerville, J. Drennan and D. J. M. Bevan, J. Phys. Colloq., 1977, 38(C7), 73–79 CrossRef.
- T. Scherb, S. A. J. Kimber, C. Stephan, P. F. Henry, G. Schumacher, J. Just, S. Escolastico, J. M. Serra, J. Seeger, A. H. Hill and J. Banhart, arXiv:1305.3385v1, 2013.
- L.-E. Kalland, A. Magrasó, A. Mancini, C. Tealdi and L. Malavasi, Chem. Mater., 2013, 25(11), 2378–2384 CrossRef CAS.
- H. Ehrenberg, T. Hartmann, K. G. Bramnik, G. Miehe and H. Fuess, Solid State Sci., 2004, 6, 247–250 CrossRef CAS PubMed.
- T. Shimura, S. Fujimoto and H. Iwahara, Solid State Ionics, 2001, 143, 117–123 CrossRef CAS.
- R. Haugsrud, Solid State Ionics, 2007, 178(7), 555–560 CrossRef CAS PubMed.
- S. Erdal, L.-E. Kalland, R. Hancke, J. Polfus, R. Haugsrud, T. Norby and A. Magrasó, Int. J. Hydrogen Energy, 2012, 37(9), 8051–8055 CrossRef CAS PubMed.
- A. Magrasó, J. Power Sources, 2013, 240, 583–588 CrossRef PubMed.
- T. Norby, J. Korean Ceram. Soc., 2010, 47, 19–25 CrossRef CAS.
- R. Haugsrud and C. Kjølseth, J. Phys. Chem. Solids, 2008, 69(7), 1758–1765 CrossRef CAS PubMed.
- R. Hancke, A. Magrasó, T. Norby and R. Haugsrud, Solid State Ionics, 2013, 231, 25–29 CrossRef CAS PubMed.
- S. Escolástico, C. Solís and J. M. Serra, Solid State Ionics, 2012, 216, 31–35 CrossRef PubMed.
- N. Diot, P. Benard-Rocherulle and R. Marchand, Powder Diffr., 2000, 15(04), 220–226 CrossRef CAS.
- N. Alyeshkina, Defects and Transport in Ce-doped La27W5O55.5, M.Sc. thesis, University of Oslo, 2013.
- X. Cui, Defects and Transport in Ba-doped La27W5O55.5, M.Sc. thesis, University of Oslo, 2013.
- W. Xing, K. Toyoura and T. Norby, Int. J. Hydrogen Energy, 2012, 37(9), 8062–8065 CrossRef CAS PubMed.
- M. J. Zayas-Rey, L. dos Santos-Gomez, D. Marrero-Lopez, L. Leon-Reina, J. Canales-Vazquez, M. A. G. Aranda and E. R. Losilla, Chem. Mater., 2013, 25(3), 448–456 CrossRef CAS.
- S. Escolastico, J. Seeger, S. Roitsch, M. Ivanova, W. A. Meulenberg and J. Serra, ChemSusChem, 2013, 6(8), 1523–1532 CrossRef CAS PubMed.
- M. Amsif, A. Magrasó, D. Marrero-López, J. C. Ruiz-Morales, J. Canales-Vázquez and P. Núñez, Chem. Mater., 2012, 24(20), 3868–3877 CrossRef CAS.
- E. Vøllestad, C. K. Vigen, A. Magrasó and R. Haugsrud, J. Membr. Sci., 2014, 461, 81–88 CrossRef PubMed.
- R. Haugsrud, New high-temperature proton conductors for fuel cells and gas separation membranes, Handbook of Fuel Cells, 2010 Search PubMed.
- C. Solis, V. B. Vert, M. Balaguer, S. Escolastico, S. Roitsch and J. M. Serra, ChemSusChem, 2012, 5, 2155 CrossRef CAS PubMed.
- M. Balaguer, C. Solis, F. Bozza, N. Bonanos and J. M. Serra, J. Mater. Chem. A, 2013, 1(9), 3004–3007 CAS.
- E. Quarez, K. V. Kravchyk and O. Joubert, Solid State Ionics, 2012, 216, 19–24 CrossRef CAS PubMed.
- C. Solís, L. Navarrete, S. Roitsch and J. M. Serra, J. Mater. Chem., 2012, 22, 16051 RSC.
- E. Quarez, Y. Oumellal and O. Joubert, Fuel Cells, 2013, 13(1), 34–41 CrossRef CAS.
- S. Erdal, Hydrogen in Oxides: incorporation, transport and effects on electrical properties, Ph.D. thesis, University of Oslo, 2011.
- V. Gil, J. Gurauskis, C. Kjølseth, K. Wiik and M.-A. Einarsrud, Int. J. Hydrogen Energy, 2013, 38(7), 3087–3091 CrossRef CAS PubMed.
- R. Hancke, S. Fearn, J. A. Kilner and R. Haugsrud, Phys. Chem. Chem. Phys., 2012, 14(40), 13971–13978 RSC.
- E. Vøllestad, T. Norby and R. Haugsrud, Solid State Ionics, 2013, 244, 57–62 CrossRef PubMed.
- E. Quarez, K. V. Kravchyk and O. Joubert, Solid State Ionics, 2012, 216, 19–24 CrossRef CAS PubMed.
- T. Norby and R. Haugsrud, Dense Ceramic Membranes for Hydrogen Separation. I: Nonporous Inorganic Membranes for Chemical Processing, Wiley-VCH Verlagsgesellschaft, 2006, pp. 1–48, ISBN 3-527-31342-7 Search PubMed.
- S.-J. Song, E. D. Wachsman, J. Rhodes, S. E. Dorris and U. Balachandran, Solid State Ionics, 2003, 164, 107–116 CrossRef CAS PubMed.
- X. Qi and Y. S. Lin, Solid State Ionics, 2000, 130, 149–156 CrossRef CAS.
- G. C. Mather and M. S. Islam, Chem. Mater., 2005, 17, 1736–1744 CrossRef CAS.
- T. Oh, H. Yoon and E. D. Wachsman, Solid State Ionics, 2009, 180, 1233–1239 CrossRef CAS PubMed.
- S. Hamakawa, L. Li, A. Li and E. Iglesia, Solid State Ionics, 2002, 148, 71–81 CrossRef CAS.
- S. Cheng, V. K. Gupta and J. Y. S. Lin, Solid State Ionics, 2005, 176, 2653–2662 CrossRef CAS PubMed.
- J. Li, H. Yoon and E. D. Wachsman, J. Membr. Sci., 2011, 381, 126–131 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |