First exploration of Na-ion migration pathways in the NASICON structure Na₃V₂(PO₄)₃

Abstract

Ion occupation and migration pathways are investigated to explore the ion-migration mechanism of Na₃V₂(PO₄)₃ with the help of first principles calculations. Na₃V₂(PO₄)₃ with a NASICON framework generates high performances as a cathode material in sodium-ion batteries.

---

Since the significant development of lithium-ion battery (LIB) technologies, they have been widely used in various applications ranging from electronic devices to increasing numbers of electric vehicles (EVs) and large-scale energy storage equipment.^1–4 The cost and safety concerns are of vital importance, which are under current investigation for the long-term success of large-scale rechargeable battery systems.^1,5,6 In particular, the limited lithium resources which make up about 0.0065% of the earth's crust may be mainly responsible for the increasingly high cost of LIBs. Recently, intense attention has been focused on sodium-ion batteries (SIBs) due to the abundant resources, low material cost and easy accessibility of new reserves widely existing in the sea.^4,7,8 Furthermore, the established theories for LIBs would be helpful to make sodium as an element of electrochemical equivalence and suitable potential to substitute lithium to meet the demands of rechargeable batteries. SIBs are promising alternatives to LIBs and more suitable as stationary batteries for smart grid and renewable storage applications, for which the requirement of energy densities does not have such serious implications.⁹ Consequently tremendous interest has been paid to the search for potential electrode materials and considerable effort has been dedicated to the design and fabrication of novel but high-performance electrodes.^10–12 Materials such as Na_xCoO₂,¹³ NaCrO₂,¹⁴ Na_xVO₂,¹⁵ Na₄Mn₉O₁₈,¹⁶ Na₃M₂(PO4)₃ (M = Ti, Fe, and V),^5,12,17,18 and Na₃V₂(PO₄)₂F₃^19,20 have been explored for hosting Na⁺ ions while the framework materials based on phosphate polyanions are considered to be favourable compared with the corresponding metal oxides due to the remarkable structural and thermal stability^5,21,22 originating from anion group substitution. When strong covalent (PO₄)³⁻ units are substituted instead of the smaller O²⁻ ions in phosphate-based Na-insertion hosts, the exhibited voltage can be altered to a high value as a result of the changes in the metal ion energy levels and the ion concentration could be shifted at which a given redox reaction takes place. Na₃V₂(PO4)₃, with a NASICON (Na Super Ionic Conductor)-type framework reported to be a fast ionic conductor, recently has been investigated as a prospective cathode material for SIBs.²³ Na₃V₂(PO₄)₃ has been shown to exhibit two potential plateaus at 3.4 V and 1.6 V vs. Na⁺/Na, corresponding to the V³⁺/V⁴⁺ and V²⁺/V³⁺ redox couples with related specific capacities of 117 and 50 mA h g⁻¹ for the high and low voltage zones, respectively. Moreover, the relatively higher voltage plateau located at 3.4 V would render it applicable as a potential cathode material in sodium-ion batteries,^24–29 and the lower potential at 1.6 V could also allow it to be an anode.^12,30 Thus, Na₃V₂(PO₄)₃ can be viewed as a multifunctional electrode material for use in batteries, for which the applied voltage range would determine the utilized assignment of Na₃V₂(PO₄)₃ with correlated energies around the two potential plateaus associated with different Na distributions.⁷

Notably, the number of migrated Na ions from the Na sites of Na₃V₂(PO₄)₃ should directly influence the capacity performances,^8,20 though there are multiple possibilities for the occupation of the interstitial sites in this compound referred to the reported literature. Consequently it is of significant importance to the field to explore the ion migrated mechanism and the probable ion pathways, which would be of great importance to understand electrochemical behaviours of Na₃V₂(PO₄)₃.

In this work, Na₃V₂(PO₄)₃ has been synthesized by a novel solution-based carbothermal reduction (S-CTR) method and used as a cathode material to construct Na₃V₂(PO₄)₃/NaClO₄/Na sodium-ion batteries for investigation. Additionally, Density Functional Theory (DFT) calculations on Na₃V₂(PO₄)₃ have been performed to obtain insight into the structural characteristics and formation energy along the three-dimensional (3D) migration paths in conjunction with the crystal structure (for Experimental sections, see the ESI†); this is the first report on a dual experimental and mechanistic approach. This work is of great significance and of guidance to those working in and constructing such batteries (both industry and academia) to understand the 3D character for ion transport by exploration of the internal diffusion ways of Na₃V₂(PO₄)₃ combined the experiments with first principles calculations.

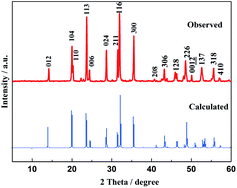
Fig. 1 displays the powder X-ray diffraction pattern (XRD) of the as-prepared Na₃V₂(PO₄)₃ as well as the XRD calculated by DFT. All the diffraction peaks of the observed XRD can be indexed to the rhombohedral NASICON structure with the R3̄c space group (2 Na in the 18e position; 1 Na in the 6b position), which are in good agreement with previous literature^12,18,31 and JCPDS card no. 53-0018. The lattice parameters are a = b = 8.72 Å and c = 21.764 Å, and these sharp peaks of the experimental results match the DFT calculations very well including the peak positions and intensities, for which they could indicate the good crystallinity of the as-prepared Na₃V₂(PO₄)₃ when the simulated models were optimized based on the first principles calculations.¹⁸

Fig. 1 XRD pattern of Na₃V₂(PO₄)₃.

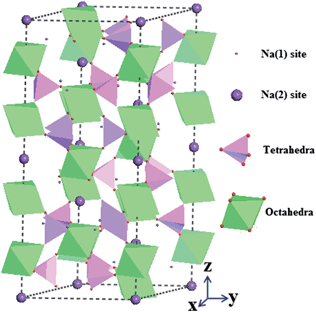
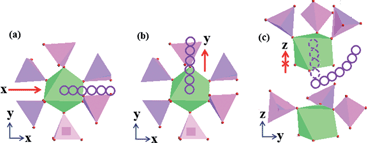
Fig. 2 shows the Na₃V₂(PO₄)₃ crystal structure with a NASICON framework. The octahedral VO₆ interlinks via corners with tetrahedral PO₄ to establish a three-dimensional (3D) V₂(PO₄)₃ framework which is interconnected through PO₄ with the neighboring units. These created lantern units could feature a highly covalent open structure that generates large interstitial spaces through which Na ions can diffuse. Two different oxygen-environment interstitial sites, Na(1) (one position per formula unit) and Na(2) (three positions per formula unit), in this rhombohedral form are usually filled (fully or partially) by mobile Na ions of which the Na(1) site has six fold coordination situated between two adjacent V₂(PO₄)₃ units along the z axis and the Na(2) site has eight fold coordination located at the same z value as the phosphorus atoms between two PO₄ tetrahedra. Houria¹⁷ and Soo et al.⁷ have reported that if all of the Na(1) and Na(2) sites were occupied by Na ions, four cations could be totally hosted in the voids/channels per formula unit of Na₄V₂(PO₄)₃, one for the Na(1) site and three for Na(2) sites. However to the best of our knowledge, very few literature reports have published the theoretical investigation towards the ion occupations in the Na sites of Na₃V₂(PO₄)₃. According to the sparse literature, a high theoretical capacity of 236 mA h g⁻¹ is reported to be capable to be delivered with a corresponding extraction of 4 Na ions per formula unit which depends on the applied potential range and the variation between V^3+/4+ and V^3+/2+ redox states.⁵ However, as a consequence of the unstable state of V²⁺ in Na₄V₂(PO₄)₃, Na₃V₂(PO₄)₃ is more favourable to be synthesized with the relatively stable state of V³⁺, while it is possible to generate V²⁺ from Na₃V₂(PO₄)₃ by electrochemical reduction methods.⁸ Accompanied by the redox reactions of Na₃V₂(PO₄)₃, the ion migration would take place where the ion number could play an important role in the capacity performances. By comparison with the bond populations between Na and O atoms (Table S1–S6†), it was found that the Na ions at Na(2) sites can be extracted more easily than those at Na(1) sites due to the smaller bond populations of Na(2) sites which are associated with the relatively weak limited environments, and thus the transported behaviours of ions at Na(2) sites should be responsible for the exhibited electrochemical properties.

Fig. 2 Schematic representation of the Na₃V₂(PO₄)₃ structure.

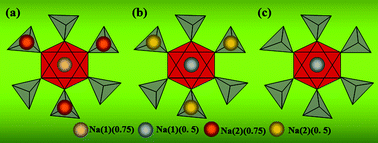
In order to explore the ion-migrated mechanism of Na₃V₂(PO₄)₃, studies on ion occupations are of significance though only Soo et al.⁷ have defined the ion occupations that one Na ion occupies the Na(1) site (1 occupancy) and two Na ions occupy the Na(2) site (0.67 occupancy) in the crystal structure of Na₃V₂(PO₄)₃. According to their conclusions, this could be used to demonstrate the extracted ion number of nearly two from Na(2) sites, but correspond to a primary unit cell of Na_3.01V₂(PO₄)₃ when six Na(1)-site and two Na(2)-site ions exist in the DFT model, the same as those used in this work. However, the calculated results based on the atom coordinates of Na₃V₂(PO₄)₃ and NaV₂(PO₄)₃ originating from Landolt–Börnstein Database in Springer Materials (Table S7 and S8†) seem successful to explain the ion-migration mechanism for Na₃V₂(PO₄)₃ with the scheme of possible ion migration shown in Fig. 3. The ion occupations with 0.75 in Fig. 3a are capable of contributing to the primary cell of Na₃V₂(PO₄)₃ which involves eight ions in the DFT model, two ions for Na(1) sites and six for Na(2) sites. This arrangement would change to one-Na-extracted Na₂V₂(PO₄)₃ with 0.5 occupation for all Na ions as shown in Fig. 3b after a structural reorganization and for the further extraction, the six Na ions at Na(2) sites would be migrated to produce a configuration leaving two Na(1)-site ions with 0.5 occupation as shown in Fig. 3c. In this way, it is reasonable to explain the theoretical capacity of 117 mA h g⁻¹ (ref. 5 and 7) corresponding to the extraction of two ions which are generated by a two-phase reaction from Na₃V₂(PO₄)₃ to NaV₂(PO₄)₃.

Fig. 3 Scheme representing ion occupations based on the calculated [Na₃V₂(PO₄)₃]₂ unit model, (a) the primary state with 0.75 occupation for all Na sites, (b) one Na ion extracted configuration with 0.5 occupation for the sites and (c) two Na ions extracted configuration with 0.5 occupation for the left Na(1) sites.

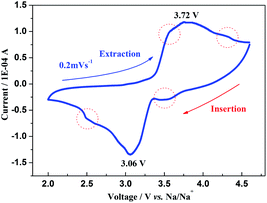
Fig. 4 shows a typical cyclic voltammogram (CV) of a Na₃V₂(PO₄)₃ sodium-ion battery at a scan rate of 0.2 mV s⁻¹, from which the obvious redox peaks are due to the extraction/insertion of two Na ions during the phase transformation by the V^3+/4+ reaction. These small peaks circled in red could be attributed to the structural reorganization related to the change of ion occupations. Moreover, the hysteretic voltage (ΔV) between the two redox peaks is 0.66 V of which the minimal value could show good reversibility of Na₃V₂(PO₄)₃ due to its open 3D framework. It is interesting to explore the ion migrated pathways in this NASICON structure since it is helpful to understand the ion-transport characteristics.

Fig. 4 CV curve of the Na₃V₂(PO₄)₃ sodium-ion battery at a scan rate of 0.2 mV s⁻¹.

The simulation methods based on the first principles calculations can be used to enhance the comprehension of migration pathways by evaluating the activation energies for various possible mechanisms at the atomic level. Three main migrated mechanisms are considered within this 3D NASICON structure involving conventional vacancy hopping between neighbouring Na positions similar to the previous discussion.³²Fig. 5a shows mechanism A where a Na ion would migrate through the channel between two PO₄ tetrahedra along the x direction and Fig. 5b displays mechanism B where a Na ion could pass through the voids between a PO₄ tetrahedron and a VO₆ octahedron along the y direction. Migration energies (E) for these mechanisms can be calculated along the diffusion path, and it is found that the values of E for mechanisms A and B are similar to 0.0904 and 0.11774 eV, respectively. While for mechanism C where the ions migrate across the channels between adjacent octahedra along the z direction, the corresponding high migration energy (>200 eV) shows that this method is not an appropriate diffusion path. However, when the ions are transported in a curved pathway to bypass the octahedron and go into the voids/channels between the adjacent PO₄ tetrahedron and VO₆ octahedron, the calculated E with ca. 2.438 eV would demonstrate that this curved course in Fig. 5c may be also feasible for ion migration. Examination of the calculated results has revealed two favoured pathways along the x and y directions and one possible curved route for ion migration in this NASICON structure, which could be utilized to confirm the 3D transport characteristic of Na₃V₂(PO₄)₃. Here, this conclusion is consistent with the literature, but in this work it has been expounded with the combination of DFT calculations with experimental results. Reasonably, this open framework with 3D dimensions for ion transport would contribute to a fast chemical diffusion and probably be able to achieve a high rate capability.

Fig. 5 Possible Na ion migration paths in Na₃V₂(PO₄)₃ along (a) x, (b) y and (c) curved z directions.

Fig. 6a depicts the CV curves of the sodium-ion battery with Na₃V₂(PO₄)₃ at different scan rates of 0.1, 0.2, 0.5, 0.8 and 1 mV s⁻¹ in a voltage range of 2–4.6 V vs. Na⁺/Na, respectively. One couple of redox CV peaks still exists, even at a high scan rate, but the peak differences seem to augment with the increment of scan rate which indicates an enlarged irreversibility at high current densities. Furthermore, the linear relationship between the peak current i_p and the square root of the scan rate v^1/2 as presented in Fig. 6b illustrates that the whole electrode reaction would be favoured to be a diffusion-controllable process, while the chemical diffusion of Na ions D_Na+ could be determined using the Randles–Sevcik equation (eqn (1)).

i_p/m = 0.4463(F³/RT)^1/2n^3/2AD^1/2Cv^1/2 (1)

where m is the mass of active cathode material, F is the Faraday constant, R is the gas constant, T is the absolute temperature, n is the number of electrons in the reaction (n = 2), A is the effective contact area between the electrode and electrolyte (here the geometric area of the electrode, 0.79 cm², is used for simplicity as commonly employed in the literature^33–36), D is the diffusion constant and C is the concentration of Na ions in the Na₃V₂(PO₄)₃ cathode calculated based on the crystallographic parameters. Thus, the anodic and cathodic D_Na+ in Na₃V₂(PO₄)₃ could be calculated to be 1.06 × 10⁻¹¹ cm² s⁻¹ and 1.02 × 10⁻¹¹ cm² s⁻¹, respectively, of which the diffused values could be viewed considerably largely for the Na ions in a sodium-ion battery. This could be naturally attributed to the special 3D pathways for ion transport which have greatly enhanced the ion mobility among the interstitial sites. However, these obtained D_Na+ values are smaller than those of other NASICON-type compounds with metallic lithium anodes and lithium-based electrolytes,^8,20 for which the heavier mass and larger volume of sodium ions during transport should be responsible for the results.

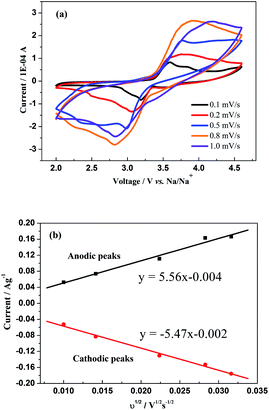Fig. 6 (a) CV curves at different scan rates of Na₃V₂(PO₄)₃ in a voltage range of 2–4.6 V vs. Na⁺/Na and (b) the relationship between the square root of the scan rate v^1/2 and peak current i_p.

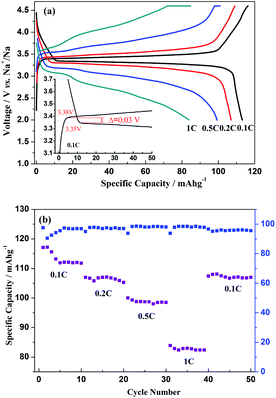
The first charge/discharge profiles of Na₃V₂(PO₄)₃ sodium-ion batteries at different current densities of 0.1C, 0.2C, 0.5C and 1C (note that 1C refers to two Na extraction from the crystal structure per formula unit in 1 h) are displayed in Fig. 7a, with corresponding specific capacities of 113, 107, 99 and 84 mA h g⁻¹, respectively, in a voltage range of 2–4.6 V vs. Na⁺/Na. It could be found that the corresponding Coulombic efficiencies are as high as 97.4%, 98.1%, 98.4% and 99.5%, respectively, of which the efficiencies would also be ascribed to the characteristic of the NASICON framework. Additionally, an electrode polarization could reach 0.03 V for this Na₃V₂(PO₄)₃ sodium-ion battery under a current density of 0.1C, and this lower value when compared with the result of Jian's work (0.07 V) could be a result of the good electronic and ionic conduction.^7,9Fig. 7b exhibits the C-rate and cycling performances of the Na₃V₂(PO₄)₃ sodium-ion battery. For the 50th cycle, the specific capacity is 107 mA h g⁻¹ with a capacity retention of 95% related to the initial capacity at 0.1C, and the corresponding Coulombic efficiency is also as high as 95.6% when the battery was cycled for 50 times in a sequence of C-rates. All these electrochemical properties demonstrate that Na₃V₂(PO₄)₃ could be a promising cathode material for utilisation in sodium-ion batteries.

Fig. 7 (a) First charge/discharge profiles of Na₃V₂(PO₄)₃ sodium-ion batteries at 0.1C, 0.2C, 0.5C and 1C, respectively, in a voltage range of 2–4.6 V vs. Na⁺/Na and the inset shows the polarization of the battery tested at 0.1C. (b) The cycling performances of the Na₃V₂(PO₄)₃ sodium-ion battery.

Conclusions

In conclusion, NASICON framework favoured Na₃V₂(PO₄)₃ has been used as a cathode in sodium-ion based batteries. The ion-occupation change was investigated for the first time to explain the ion-migrated mechanism of Na₃V₂(PO₄)₃. A cell configuration of Na₃V₂(PO₄)₃ with an ion occupation of 0.75 would change to Na₂V₂(PO₄)₃ and then to NaV₂(PO₄)₃ with 0.5 occupation accompanied by structural reorganization. First principles calculations have been firstly employed to explore the migration pathways by evaluating the activation energies for possible mechanisms towards Na₃V₂(PO₄)₃. It is proved that two pathways along the x and y directions and one possible curved route for ion migration are favoured with a 3D transport characteristic, from which a diffusion constant of 10⁻¹¹ cm² s⁻¹ is estimated.

Acknowledgements

Financial support from the NNSF of China (no. 51134007, 21003161, and 21250110060), Program for the New Century Excellent Talents in University (no. NCET-11-0513), Funds for Distinguished Young Scientists of Hunan Province, China (no. 13JJ1004), Fundamental Research Funds for Central South University (no. 2013zzts159 and no. 2012zzts059) and Innovation and Entrepreneurship Training Program of China for University Students are greatly appreciated.

Notes and references

1. M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657.
2. C.-X. Zu and H. Li, Energy Environ. Sci., 2011, 4, 2614–2624.
3. H. Li and H. Zhou, Chem. Commun., 2012, 48, 1201–1217.
4. Z. Jian, W. Han, X. Lu, H. Yang, Y.-S. Hu, J. Zhou, Z. Zhou, J. Li, W. Chen, D. Chen and L. Chen, Adv. Energy Mater., 2013, 3, 156–160.
5. J. Kang, S. Baek, V. Mathew, J. Gim, J. Song, H. Park, E. Chae, A. K. Rai and J. Kim, J. Mater. Chem., 2012, 22, 20857–20860.
6. J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
7. S. Y. Lim, H. Kim, R. A. Shakoor, Y. Jung and J. W. Choi, J. Electrochem. Soc., 2012, 159, A1393–A1397.
8. W. Song, X. Ji, C. Pan, Y. Zhu, Q. Chen and C. E. Banks, Phys. Chem. Chem. Phys., 2013, 15, 14357–14363.
9. Z. Jian, L. Zhao, H. Pan, Y.-S. Hu, H. Li, W. Chen and L. Chen, Electrochem. Commun., 2012, 14, 86–89.
10. S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710–721.
11. V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5, 5884–5901.
12. K. Saravanan, C. W. Mason, A. Rudola, K. H. Wong and P. Balaya, Adv. Energy Mater., 2013, 3, 444–450.
13. R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80.
14. S. Komaba, T. Nakayama, A. Ogata, T. Shimizu, C. Takei, S. Takada, A. Hokura and I. Nakai, ECS Trans., 2009, 16, 43–55.
15. D. Hamani, M. Ati, J.-M. Tarascon and P. Rozier, Electrochem. Commun., 2011, 13, 938–941.
16. Y. Cao, L. Xiao, W. Wang, D. Choi, Z. Nie, J. Yu, L. V. Saraf, Z. Yang and J. Liu, Adv. Mater., 2011, 23, 3155–3160.
17. H. Kabbour, D. Coillot, M. Colmont, C. Masquelier and O. Mentre, J. Am. Chem. Soc., 2011, 133, 11900–11903.
18. Z. Jian, W. Han, X. Lu, H. Yang, Y.-S. Hu, J. Zhou, Z. Zhou, J. Li, W. Chen, D. Chen and L. Chen, Adv. Energy Mater., 2013, 3, 156–160.
19. R. A. Shakoor, D.-H. Seo, H. Kim, Y.-U. Park, J. Kim, S.-W. Kim, H. Gwon, S. Lee and K. Kang, J. Mater. Chem., 2012, 22, 20535–20541.
20. W. Song and S. Liu, Solid State Sci., 2013, 15, 1–6.
21. F. Cheng, J. Liang, Z. Tao and J. Chen, Adv. Mater., 2011, 23, 1695–1715.
22. H.-K. Song, K. T. Lee, M. G. Kim, L. F. Nazar and J. Cho, Adv. Funct. Mater., 2010, 20, 3818–3834.
23. M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–985.
24. Y. Liao, K.-S. Park, P. Xiao, G. Henkelman, W. Li and J. B. Goodenough, Chem. Mater., 2013, 25, 1699–1705.
25. K. T. Lee, T. N. Ramesh, F. Nan, G. Botton and L. F. Nazar, Chem. Mater., 2011, 23, 3593–3600.
26. S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12, 355–358.
27. S. Komaba, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Adv. Funct. Mater., 2011, 21, 3859–3867.
28. D. Kim, S.-H. Kang, M. Slater, S. Rood, J. T. Vaughey, N. Karan, M. Balasubramanian and C. S. Johnson, Adv. Energy Mater., 2011, 1, 333–336.
29. S. Tepavcevic, H. Xiong, V. R. Stamenkovic, X. Zuo, M. Balasubramanian, V. B. Prakapenka, C. S. Johnson and T. Rajh, ACS Nano, 2011, 6, 530–538.
30. V. Palomares, M. Casas-Cabanas, E. Castillo-Martinez, M. H. Han and T. Rojo, Energy Environ. Sci., 2013, 6, 2312–2337.
31. J. Gopalakrishnan and K. K. Rangan, Chem. Mater., 1992, 4, 745–747.
32. D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30–A32.
33. X. H. Rui, N. Ding, J. Liu, C. Li and C. H. Chen, Electrochim. Acta, 2010, 55, 2384–2390.
34. W. Song, X. Ji, Z. Wu, Y. Zhu, Y. Y. Yao, K. H. Huangfu, Q. Chen and C. E. Banks, J. Mater. Chem. A, 2014, 2, 2571–2577.
35. W. Song, X. Ji, Y. Yao, H. Zhu, Q. Chen, Q. Sun and C. E. Banks, Phys. Chem. Chem. Phys., 2014, 16, 3055–3061.
36. T. Jiang, Y. J. Wei, W. C. Pan, Z. Li, X. Ming, G. Chen and C. Z. Wang, J. Alloys Compd., 2009, 488, L26–L29.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental sections and the calculated results. See DOI: 10.1039/c4ta00230j

---