Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect chemistry of Ti and Fe impurities and aggregates in Al2O3
Jessica K.
Bristow
,
Davide
Tiana
,
Stephen C.
Parker
and
Aron
Walsh
*
Centre for Sustainable Chemical Technologies and Department of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: a.walsh@bath.ac.uk; Tel: +44 (0)1225 385432
First published on 5th February 2014
Abstract
We report a theoretical evaluation of the properties of iron and titanium impurities in sapphire (corundum structured α-Al2O3). Calculations using analytical force fields have been performed on the defect structure with the metals present in isolated, co-doped and tri-cluster configurations. Crystal field parameters have been calculated with good agreement to available experimental data. When titanium and iron are present in neighbouring face and edge-sharing orientations, the overlap of the d-orbitals facilitates an intervalence charge transfer (FeIII/TiIII → FeII/TiIV) with an associated optical excitation energy of 1.85 eV and 1.76 eV in the respective configurations. Electronic structure calculations based on density functional theory confirm that FeIII/TiIII is the ground-state configuration for the nearest-neighbour pairs, in contrast to the often considered FeII/TiIV pair. Homonuclear intervalence charge transfer energies between both FeIII/FeII and TiIV/TiIII species have also been calculated, with the energy lying in the infra-red region. Investigation of multiple tri-clusters of iron and titanium identified one stable configuration, TiIII–(TiIV/FeII), with the energy of electron transfer remaining unchanged.
1 Introduction
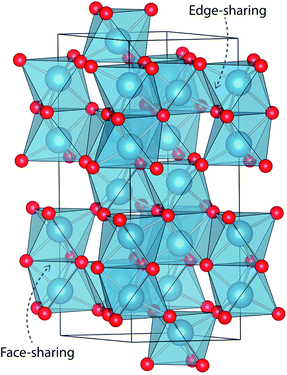
The mineral corundum (α-Al2O3) is a transparent and mechanically tough material, widely used for industrial applications such as catalyst supports, substrate layers in photovoltaic devices and solid-state lasers.1–3 The presence of metal impurities in α-Al2O3, predominantly iron and titanium, dramatically alters its optical properties. Previous studies concerning the defect structure of sapphire and other polymorphs of Al2O3 have been essential in understanding its optical properties and methods to optimise its functionality.4–9 These studies, however, have not connected the multiple optical processes that occur within and between these cation impurities in a complete analysis.Al2O3 formally consists of Al3+ and O2− ions and adopts a trigonal lattice symmetry in its ground-state corundum structure.10 The Al centres are surrounded by six oxide ligands in a distorted octahedral geometry filling 2/3 of all available octahedral holes. These octahedral units are linked in both face-sharing and edge-sharing orientations as parallel and perpendicular to the c-axis, respectively.11 The relative orientation of the metal centres causes a pseudo Peierls distortion, resulting in neighbouring metal centres that are rotated at an angle of 64.3° away from each other. Elongation in pairs of the surrounding oxide ligands (Fig. 1) results in a pentagonal bi-pyramidal geometry belonging to the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c.12 The tetrahedrally coordinated oxide ligands form a close-packed sub-lattice. The material is largely ionic in nature with a wide band gap of 9.25 eV.
c.12 The tetrahedrally coordinated oxide ligands form a close-packed sub-lattice. The material is largely ionic in nature with a wide band gap of 9.25 eV.
To induce the colours characteristic of minerals formed from Al2O3 (e.g. blue sapphire and red ruby), the presence of impurities is required. As a consequence to doping, electronic energy levels are inserted into the band gap of the material. Lower energy transitions within the visible and/or thermal range can occur, giving rise to colour and conducting behaviour in the insulating and transparent host material.13,14
We have focused on two of the most common and researched impurities that increase the absorption of visible light. These impurities can be found in naturally occurring minerals or can be incorporated synthetically during synthesis or post-annealing. Titanium and iron, for electrostatic reasons, are primarily found in the trivalent state (FeIII/TiIII) at approximate concentrations ranging between 280 and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm.15–17
000 ppm.15–17
Titanium-doped sapphire is used in solid-state lasers.18–20 The recognition that TiIII, a d1 cation, gives a tunable laser was reported in 1982.21 It is the intra-valence d–d transitions occurring within the metal and the vibrational interactions with the sapphire lattice, which initiate the electronic transitions as a consequence of photon absorption. The interactions between the oxide host and titanium impurity are therefore crucial with regard to determining the optical properties of the doped material.1,18 In addition to efficient emission of near IR (infra-red) light, the ceramic material with a significant thermal conductivity also has a high damage threshold.18,22
Once present in the α-Al2O3 structure, Ti will substitute Al and remain on the same lattice site (eqn (1)). In addition to the isovalent TiIII impurity, titanium has also been reported as TiIV. This tetravalent cation will cause a larger lattice distortion and therefore is found at lower concentrations in natural sapphire. Compensation mechanisms, such as those shown in eqn (2) and (3), are required for the aliovalent substitution in order to maintain overall charge neutrality. The binding energies between the isolated point defects and more complex charge compensating clusters have previously been calculated.5,23
The standard Kröger–Vink notation has been used to describe the charge compensation mechanisms, following the standard notation AYB, where A represents the dopant, B the host lattice site and Y the charge relative to the host lattice site; × indicates no net charge. B can also be i, representing an interstitial defect and A can also be V, representing a vacancy defect.24Eqn (1)–(3) refer to reactions involving TiIII, TiIV and TiIV respectively, with the atomic chemical potentials determined by the respective binary oxides.
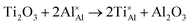 | (1) |
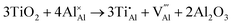 | (2) |
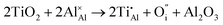 | (3) |
Iron-doped sapphire has not been as intensely studied as the TiIII–Al2O3 system, but is still known to produce interesting optical properties. The increase in conductivity when doped with iron has applications including thin-film stress sensors and planar optical waveguides.25 Sapphire doped only with iron has been shown to result in yellow crystals, demonstrating visible light absorption.26 With homonuclear intervalence charge transfer and interactions with other dopants in the structure, iron-doped sapphire has the potential to display more complex optical properties. Again, two oxidation states can be incorporated, FeII (from FeO) and FeIII (from Fe2O3):
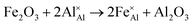 | (4) |
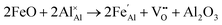 | (5) |
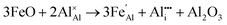 | (6) |
Iron is present as FeII (eqn (5) and (6)) at a much lower concentration than FeIII (eqn (4)); however, the concentration of divalent iron can be increased by the application of heat.27 Lehmann and Harder (1970) gave an extensive review of the effect of the concentration of FeIII and FeII on the colour of corundum crystals, also confirming in natural samples the isovalent FeIII to be the dominant oxidation state.28 The transfer of an electron between the two valence states of iron can also be initiated by light (eqn (7)). The energy required for the described homonuclear charge transfer between neighbouring FeIII and FeII will be calculated and compared to the experimentally determined values ranging from 1.40–1.55 eV (800–886 nm).26,29
 | (7) |
The substitution of both iron and titanium in Al2O3 results in the vibrant blue colour of sapphire crystals. The energy and intensity of light absorbed by the material has been shown to be dramatically affected by the concentration of either cation.30,31 With multiple charge transfer and intra-valence excitations occurring between and within these cations, spectroscopic analysis of natural sapphire samples is often disputed and inconclusive.
An optical charge transfer process between iron and titanium is understood to be the origin of colour in blue sapphire. The overlap of metal d-orbitals of the neighbouring metals facilitates the transfer of an electron between species.32 The transfer is initiated by visible light absorption, resulting in the alternate valence states of the metals.
 | (8) |
Multiple studies have demonstrated the ease of incorporating Fe and Ti into sapphire and its epitaxial growth for functional applications and analysis.33–36 As a consequence of heating, the blue colour of a sapphire crystal intensifies, making this a standard industrial process to increase their market value.27
In this paper, following our initial communication,37 we report the calculated optical transition energies of Fe and Ti in the Al2O3 lattice and offer suggestions as to the assigning of the absorption spectra of natural sapphires. Our predictions are compared to available experimental evidence. The investigation includes isolated titanium and iron substitutions, the co-doped systems with both metals present in differing valence states, and metal tri-clusters that may form in the lattice.
2 Methodology
We employ Mott-Littleton defect calculations, based on analytical pairwise potentials, to probe the potential energy landscape associated with inter-atomic charge transfer and intra-atomic crystal field excitations. Further electronic structure calculations are performed using a range of density functionals in order to confirm the ground-state magnetic structures.2.1 Interatomic potentials
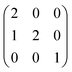
Calculations within the Born model of ionic solids were performed using the GULP (General Utility Lattice Programme) code.38 The interatomic interactions are represented in the form of the pairwise Buckingham potential, inclusive of a long-range Coulombic term (eqn (9)) evaluated via an Ewald summation and a short-range potential active within 15 Å.39–41 The potential parameters (A, ρ and C) have been taken from Catlow and Lewis to model the pure and doped systems (Table 1).40,41 The shell model of Dick and Overhauser has been employed to model the electronic polarisation of the system,42 with the harmonic spring constant (k) fitted to reproduce the experimental high-frequency (ε∞) and static (ε0) dielectric tensors. It should be noted that the relatively large error in the calculated elastic constants is common in pair potential methods and does not influence the properties of interest (Table 2).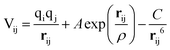 | (9) |
| Parameter | α – Al2O3 |
|---|---|
| A (+ −) (eV) | 1474.4 |
| ρ (+ −) (Å) | 0.00 |
| C 6 (+ −) (eV Å6) | 0.300 |
| A (− −) (eV) | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764.3 764.3 |
| ρ (− −) (Å) | 20.37 |
| C 6 (− −) (eV Å6) | 0.149 |
| Y + (|e−|) | 1.458 |
| k + (eV Å−2) | 588.71 |
| Y − (|e−|) | −3.000 |
| k − (eV Å−2) | 69.28 |
| Property | Experiment | Calculated |
|---|---|---|
| Lattice energy (eV) | — | −158.94 |
| a, b, c (Å) | 4.76 | 4.83 |
| α, β, γ (°) | 55.17 | 56.79 |
| ε 0 11 | 9.34 | 9.24 |
| ε 0 33 | 11.54 | 13.94 |
| ε ∞ 11 | 3.10 | 3.11 |
| ε ∞ 33 | 3.10 | 3.13 |
| C11 (GPa) | 497.4 | 611.28 |
| C12 (GPa) | 164.00 | 297.90 |
| C44 (GPa) | 147.40 | 134.99 |
2.2 Embedded crystal defect calculations
The defect formation energies were calculated within the Mott-Littleton approach.44 The simulated lattice surrounding the central defect is divided into multiple regions, the details of which have been reviewed extensively elsewhere.5 Sizes were set at 10 Å (950 ions) and 25 Å (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278 ions) for regions 1 and 2, respectively. The interatomic potentials used to model the extrinsic transition metals are listed in Table 3.
278 ions) for regions 1 and 2, respectively. The interatomic potentials used to model the extrinsic transition metals are listed in Table 3.
| Parameter | TiIII | TiIV | FeII | FeIII |
|---|---|---|---|---|
| A (+ −) (eV) | 1715.7 | 754.2 | 694.1 | 1102.4 |
| ρ (+ −) (Å) | 0.0 | 0.0 | 0.0 | 0.0 |
| C 6 (+ −) (eV Å6) | 0.3069 | 0.3879 | 0.3399 | 0.3299 |
| Y + (|e−|) | 1.23 | 2.89 | 2.00 | 4.97 |
| k + (eV Å−2) | 43.97 | 37.30 | 10.92 | 304.70 |
Two local minimisation approaches were required for the calculation of the energies associated with intervalence charge transfer. The first, full optimisation, results in the lowest energy local configuration of the ions and shells in region 1, calculated via a Newton–Raphson procedure. The second minimisation technique is ‘shell only’. During this optimisation, the cores of the ions are fixed in location and only the shells are allowed to relax, representing the polarisation of the electrons due to the charge transfer process. As a consequence, a vertical optical transition as defined by the Franck–Condon principle can be modelled, in addition to the adiabatic (thermal) excitation energy. The pairs of ions involved in the intervalence charge transfer (FeII/TiIV and FeIII/TiIII), which are charge compensating when substituted into corundum, were modelled separately.
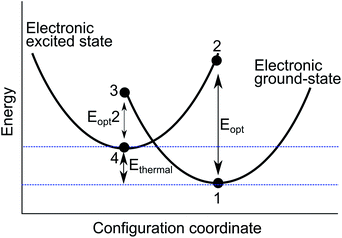
A configurational coordinate diagram can be constructed using the results of the two energy minimisation techniques, as illustrated in Fig. 2. The diagram is a representation of the relative potential energy of different ionic configurations as a function of the defect geometry; the structure of the system is described by a collective configuration coordinate. Each parabola represents the pair of cations involved in the intervalence charge transfer. The defect energies are labelled 1–4, which have been calculated using the techniques described above. The local minima (1 and 4) are calculated by full geometry optimisation of each charge state. The adiabatic energy Ethermal is the difference between these minima. The alternate valence pair is then substituted into the previously optimised positions to model vertical optical excitations (2 and 3).
The calculation of the absolute charge transfer energy between iron and titanium requires an additional term to align their ionisation potentials (Ediff), as determined from the lattice energies (ΔELE) of the respective binary oxides:
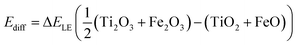 | (10) |
An alignment term is not required for homonuclear intervalence charge transfer as the ionisation potentials and electron affinity of the two valence states cancel out.
2.3 Ligand field splitting
The AOLM (angular overlap model) developed and implemented by Woodley was employed to obtain the crystal field parameters of the transition metal cations.46 The inclusion of angular functions into the purely radial Buckingham and Coulomb potentials allows non-spherical cations to be modelled and additional electronic properties to be calculated. The model has been successfully applied to metal oxide structures such as LaMnO3 and Mn2O3 which contain non-spherical ions.47–49 The augmented short-range potentials have been applied to 3d impurities to calculate the energies of the d-orbitals in the distorted environments of the sapphire lattice.The distortion of the cation environments in sapphire from perfect octahedra, as shown in Fig. 1, reflects their anti-prismatic geometry. In this geometry the octahedral units rotate from the c-axis. The pairwise elongation of the oxide ligands results in a pinching and consequent destabilisation of the dxy orbitals. In this configuration the dz2 and dx2−y2 orbitals are degenerate (Fig. 3).
The crystal field parameters were fitted through the calculations of hexa–aqua complexes in order to obtain the absolute energy splittings for each cation. The interatomic potentials (Table 1 and 3) were used to model these complexes, with the splittings compared to available reference values.50 Spin–orbit coupling and Jahn–Teller distortions are not considered in this study; however, their effects should be minor. In particular, Jahn-Teller effects will not change the vertical excitation energies.
2.4 Electronic structure calculations
To compare with and validate the results obtained using the analytical potentials, first-principles electronic structure calculations were performed on Al2O3 using VASP (Vienna ab initio Simulation Package).51–54 Calculations were initially performed by treating the exchange and correlation effects within Density Functional Theory (DFT)55–57 using the PBEsol generalised gradient functional and a 2 × 2 × 2 k-point grid for the supercell. A quasi-Newton relaxation was performed for local structure optimisation, which was converged the forces to 0.005 eV Å−1 or lower. The wave functions were constructed via a plane wave basis set, with a cut off of 500 eV. The projector augmented wave method was employed to represent the interactions between the core and valence electrons of the ions.53It should be noted that even within an excited-state approach such as time-dependent DFT, the description of charge-transfer excitations remains a significant challenge. Therefore, the focus of the electronic structure studies here is to probe the ground-state electron and spin distributions. To determine the dependence of the results on the exchange-correlation functional, in particular for the correct magnetic ground state, additional calculations were performed at the DFT + U (5 eV for Ti and Fe d bands), meta-GGA (TPSS and MBJ), hybrid DFT (HSE06) with 25% non-local Fock exchange, and Hartree–Fock (HF) levels of theory.58–60 Images of chemical structures and electron densities were made using the VESTA software.61
We employ the standard supercell approach to investigate Ti and Fe incorporation into Al2O3. The conversion from the hexagonal unit cell to an orthorhombic supercell expansion reduces the interactions between defect species in neighbouring supercells.62 The resulting cuboid was of dimensions 8.27 × 9.55 × 13.01 Å and contained 120 atoms. This was formed by via an anisotropic expansion of the form:63
For these calculations we have maintained the equilibrium lattice parameters of Al2O3, relaxing only the internal coordinates during the defect calculations, which is appropriate for perturbations in the dilute limit. Effective doping concentrations for the singularly and co-doped systems were 0.83% and 1.67%, respectively.
3 Results and discussion
3.1 Ti-doped sapphire
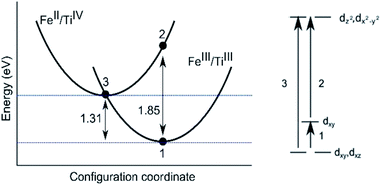
Sapphires doped only with Ti in the trivalent state are pale pink in colour representing the absorption of energy between 2.21 and 2.53 eV, as confirmed by optical spectroscopy. More specifically, absorption maxima are given as 2.25 eV and 2.56 eV by Johnson et al.64 As shown in Table 4 our calculated crystal field parameter of 2.47 eV is in good agreement.65 The three underlying optical processes are labelled in Fig. 3.| Optical transition | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| Ti | 0.28 | 2.19 | 2.47 |
| Fe | 0.90 (SF) | 2.14 (SF) | 2.94 (SF) |
With a 13% increase in ionic radius, TiIII incorporation causes a distortion to the local structure. Bond lengths for the face and edge-sharing configurations are 2.81 Å and 2.90 Å, respectively. We have calculated the solutional substitutional enthalpy of each metal dopant in the sapphire lattice, representing the incorporated isolated defect at infinite dilution (see eqn (1)–(6)). This enthalpy was calculated by the subtraction of the total energy of the defective system (with the dopant present) from that of the pure system (with no defects present), which was balanced thermodynamically using the lattice energies of the binary oxides of the 3d metal dopants (eqn (1)).
In addition to a substitution energy of 3.41 eV, we have found that isovalent titanium disrupts the local environment around the lattice site. However, the cations remain in a trigonal anti-prismatic geometry (Fig. 1). Typical intensities of d–d transitions range between 1–103 M−1 cm−1 (Table 5), but due to the distortion of the 3d cations the intensities of these transitions should be greater. The solutional substitution energy for the optically inactive TiIV is calculated to be 2.78 eV and 3.05 eV from eqn (2) and (3), respectively.
| Governing condition | Range of absorption intensities (ε) (M−1 cm−1) |
|---|---|
| Spin and symmetry forbidden | 10−5−100 |
| Spin-allowed, symmetry-forbidden | 100−103 |
| Spin and symmetry allowed | 103−105 |
3.2 Fe-doped sapphire
Fe is found in sapphires in both its divalent and trivalent oxidation states.36,67 Sapphires doped only with Fe, predominately in the trivalent state, are yellow in colour. It is still under debate if this is due to intravalence d–d transitions within a single impurity, or to an intervalence charge transfer between the divalent and trivalent valences of iron.26,31,68 This colour arises from visible light absorption in the energy region of between 2.88 eV and 3.26 eV.The energy calculated for the intra-valence transition in trivalent Fe is 2.94 eV (Table 4), which is within the measured energy range.26 The results suggest, in support of Ferguson and Fielding, that visible light absorption in Fe-doped sapphire is due to intra-valence d–d transitions in the dopant cation even though all electronic transitions in these dopants are formally spin forbidden. Typical intensities for such transitions are given in Table 5. As shown they range between 10−5–100 M−1 cm−1. The electron transfer energy between divalent and trivalent Fe has also been calculated to further support this conclusion (see Section 3.3).
The calculated enthalpy of solution for FeIII (eqn (4)) is 0.40 eV, while for FeII the two compensation mechanisms (eqn (5) and (6)) were calculated to be 1.12 eV and 1.53 eV, respectively. The larger ionic radii of FeII and FeIII in comparison to AlIII is 7% and 1%, respectively, which contributes to the smaller solution energy of the latter. The isovalent FeIII substitution also avoids the formation of charge compensating point defects. When considering the difference in enthalpy of solution for isolvalent Ti and Fe, the increased energy calculated for Ti is purely due to the steric affect of the size of either cation. As Ti is larger than Fe the distortion of the lattice with its substitution is greater, which has an associated energetic penalty.
3.3 Co-doping sapphire
When neighbouring, FeIII and TiIII are at a distance ranging from 2.88 to 2.99 Å. An electron can be transferred between the species, initiated by the absorption of light, resulting in the FeII/TiIV configurations being formed (eqn (8)). This intervalence charge transfer is not limited by symmetry or spin selection rules, resulting in optically allowed transitions.
The energy absorbed during the intervalence optical transfer has been speculated to be responsible for the intense blue colour of sapphire, with this initial suggestion dating back to 1967.31 Alternative mechanisms are still debated, e.g. that Ti is a charge compensating cation and Fe is the colour centre.28 However, it is more popularly considered that the FeII/TiIV configuration represents the ground state and FeIII/TiIII the excited state.26,29,69,70 We confirm that intervalence charge transfer is responsible for colour, but this instead occurs for the FeIII/TiIII pairs.37 For this to be a viable mechanism, an energy between 1.99 and 2.14 eV must be absorbed.
We have calculated the energy required for the transfer of an electron between FeIII and TiIII (the principal absorption) in both edge and face-sharing configurations. There is a third possible environment where the cations could be substituted parallel to the c-axis, resulting in a separation of 3.37 Å. The transfer of an electron would be less probable, due to smaller d-orbital overlap and substitution at this site has therefore not been investigated. As shown in Fig. 3, the absorption occurs with the transfer of an electron from the more stable FeIII/TiIII to FeII/TiIV. The FeII/TiIV configuration represents a metastable excited state; thermal relaxation (1.31 eV) to the FeIII/TiIII configuration is favoured; however, we cannot comment on the timescale for this process.37
We have also investigated the energy associated with defect clustering. For the FeII/TiIV configuration there is a binding energy of 0.64 eV owing to the strong Coulomb attraction of oppositely charge defects, which may stabilise neighbouring impurities during synthesis or annealing:
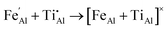 | (11) |
Absorption spectroscopy shows a strong, broad band with maximum between 2.14 and 2.17 eV.29,70 We can assign this peak as the intervalence charge transfer for the co-doped systems between TiIII and FeIII (eqn (8)). The measured signal is broadened by the changes in environment that are characteristic of an intervalence charge transfer.
Firstly the corundum structure was optimised (PBEsol functional), with good agreement with both experiment and the pair potentials.51–54 The dopants were then incorporated in adjacent sites for the substitution of Al in both orientations, as had previously been modelled with the ionic potentials. The relative energies were assessed based on the self-consistent total energies.
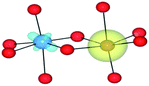
Different magnetic and charge-state configurations can be stabilised accordingly to the initialisation of the calculation in terms of total and local magnetic moments. Spin density profiles (ρ↑ − ρ↓) were plotted to confirm the location and topology of the magnetisation. These results were compared to the configurational coordinate diagram (Fig. 2). The d occupations associated with each of the metals in their formal oxidation states are d0(TiIV), d1(TiIII), d5(FeIII) and d6(FeII). For Ti, the local spin moment is well defined; however, Fe may access both low (LS) and high (HS) spin configurations. In the binary oxide FeO, FeII adopts a high spin configuration (with anti-ferromagnetic alignment), while in haematite, corundum structured Fe2O3, FeIII is also high spin (with anti-ferromagnetic alignment).71–73
As shown by the spin-density profiles, independent of the magnetic initialisation, when the metals were in high spin, the FeII/TiIII configuration was always observed (Table 7). This phenomenon confirms the instability of the FeII/TiIV configuration and supports the configurational coordinate diagram. This spontaneous electron transfer demonstrates that the FeII/TiIV configuration is less stable, in agreement with the pair potential results. Calculations based upon hybrid and meta-DFT, as well as HF, confirm the absence of electron transfer (Table 7).
| Bi-particle | Configuration | Process | Energy (eV) |
|---|---|---|---|
| FeIII/TiIII | Face-sharing | E opt | 1.85 |
| FeII/TiIV | Face-sharing | E opt2 | 0.00 |
| FeIII/TiIII | Edge-sharing | E opt | 1.76 |
| FeII/TiIV | Edge-sharing | E opt2 | UNS |
| FeII/FeIII | Face-sharing | E opt | 1.43 |
| FeII/FeIII | Edge-sharing | E opt | 1.30 |
| TiIII/TiIV | Face-sharing | E opt | 1.44 |
| TiIII/TiIV | Edge-sharing | E opt | UNS |
| Bi-particle | Binding energy (eV) |
|---|---|
| FeIII–TiIII | −0.02 |
| FeII–TiIV | −0.64 |
| FeII–FeIII | 0.00 |
| TiIII–TiIV | −0.02 |
The energies of all configurations relative to the calculated ground-state high spin FeIII/TiIII are presented in Table 7. In low spin, when the FeII/TiIV pair is stabilised, the resultant configuration is 1.18 eV higher than the ground-state. The energy difference between the two optimised configurations (1.18 eV) also closely correlates to the adiabatic electron transfer reported in the previous section (1.31 eV). We note that in order to fully probe the optical excitations from electronic structure theory, an explicit time dependent approach should be applied.
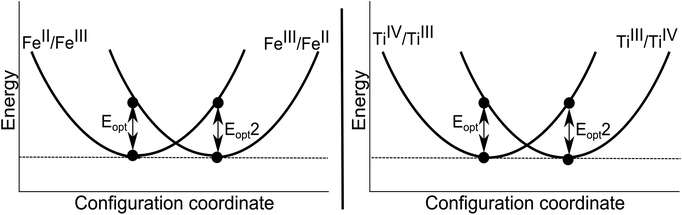
Both FeIII/FeII and TiIII/TiIV pairs were considered. The calculated charge transfer energies are given in Table 6. The energy of homonuclear intervalence charge transfer has been calculated to occur in the thermal range. These have no direct contribution to the colour of the crystal, but will influence the thermoelastic properties.
The mirror symmetry of the transitions (Eopt and Eopt2) are typical of a homonuclear system, with each configuration representing the same valence states of cations but occupying the opposite sites in the lattice. From these calculated results of 1.2–1.4 eV, we can further conclude the origin of the colour of yellow sapphires to be due to the intra-valence transitions in the FeIII cations (Table 4) and not due to homonuclear intervalence charge transfer (Table 6).
Binding energies of 0.00 eV and −0.02 eV were calculated for FeII/FeIII and TiIII/TiIV pairs with bond lengths of 2.92 Å and 3.05 Å, respectively. Results suggest that there is no strong driving force for impurity aggregation and hence a low probability of homonuclear charge transfer.
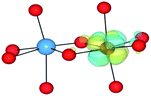
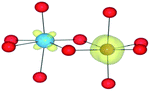
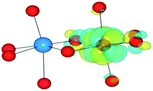
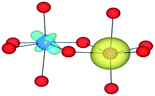
We have also performed electronic structure analysis of the homonuclear systems for neighbouring aliovalent pairs. Spin density profiles have been plotted to illustrate the magnetic structure and are presented in Table 9. The limitations of the underlying DFT and HF techniques should be noted, which are based on a single determinant when calculating the self-consistent field, which means that the electronic minimisation procedure is unable to distinguish between symmetric homonuclear cations. As a consequence, the models may be biased towards electron delocalisation between the two metal centres.
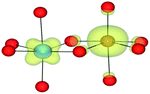
For the homonuclear Fe system, the spin density is similar – and almost spherical – on each ion. Results are shown for the most stable high-spin configuration, which suggests a preference for two FeIII(d5) ions with the occupation of the minority spin t2g orbital split between them. An equivalent electron count is found around each metal. The same results were observed at the GGA, hybrid DFT and HF levels of theory; the latter two results are shown in Table 9. Results including explicit breaking of the homonuclear symmetry are also presented. A model isoelectronic heteronuclear system was constructed: CoIII/FeIII, i.e. d6/d5. As shown, the topology of the Co/Fe spin density is similar, but analysis of electronic charge and magnetisation for each ions confirms the occupation of the minority spin t2g state on Co. Therefore, neighbouring d6/d5 centres are possible.
Analysis of the spin density for the homonuclear Ti system displays a similar delocalisation when modelled at all levels of theory (Table 9). Instead of a d1/d0 configuration, a single d band on each Ti centre is partially occupied by one electron. Within HF theory, which fully describes the electron-exchange term, the density is also depicted as delocalised (positive spin density on both Ti cations), suggesting this effect is not due to the electron self-interaction, which was further confirmed using the electron localisation function.74,75 A model calculation was again conducted to remove the mirror symmetry, via the substitution of one Ti for Y: TiIII/YIII, i.e. d1/d0. Here, the single d electron is forced to localise on Ti, resulting in the asymmetric spin density shown in Table 9. These results confirm that neighbouring d1/d0 centres are also possible, but appear not to be accessible for the homonuclear system, at least not within a single-determinant framework.
3.4 Tri-clusters in sapphire
In addition to isolated defects and bi-particles, larger defect clusters are also possible, especially at high impurity concentrations. The attraction and consequent binding of charge compensating defects, with the substitution of Al for an aliovalent cation has previously been reported.23,76We have modelled possible metal tri-clusters to assess their optical properties and to see if they can further stabilise FeII/TiIV pairs (Table 10). All tri-clusters have been modelled as L-shaped, with each cluster containing edge and face-sharing metals (Fig. 5). The co-doped edge-sharing FeII/TiIV configurations were unstable, this is also true when incorporated into a tri-cluster configuration. We therefore modelled the tri-clusters involving FeII/TiIV as face-sharing, with the third metal in an edge-sharing configuration.
| Cluster | Binding | E opt Fe−Ti |
|---|---|---|
| FeIII–(TiIII–FeIII) | −0.13 | 1.84 |
| FeIII–(FeIII–TiIII) | −0.15 | 1.91 |
| FeIII–(TiIV–FeII) | −0.33 | −0.05 |
| FeIII–(FeII–TiIV) | −0.44 | 0.17 |
| TiIII–(TiIV–FeII) | −0.89 | −0.09 |
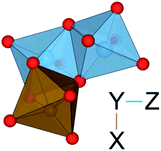 | ||
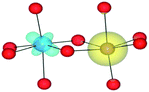
| Fig. 5 Illustration of a TiIII–(TiIV–FeII) tri-cluster. The L-shaped geometry of metal tri-clusters is shown, where X–Y are edge-sharing and Y–Z are face-sharing. The notation X–(Y–Z) is used in Table 10. | ||
The calculations demonstrate that the intervalence charge transfer energy between trivalent Fe and Ti remains within the visible range when present in a tri-cluster. Absorption energies remain almost unchanged compared to the isolated pairs. There is only one cluster, [TiIII–(TiIV–FeII)], which gains stability by forming this aggregate (Table 8). It is unlikely that the remaining clusters would form to any significant concentration.
The [TiIII–(TiIV–FeII)] cluster would offer a greater stability to the FeII/TiIV pairs and may extend their lifetime in the crystal. However, even if formed, the optical process would remain largely unchanged by the third neighbouring cation. We propose that experimental detection of these aliovalent cations can be due either to the isolated TiIV–FeII pairs, or their presence within the tri-cluster as described. Homonuclear intervalence charge transfer was also modelled in these tri-clusters and the energies were found to remain unaffected (Table 10).
Preliminary attempts to model more complex clusters consisting of these metal dopants with charge compensating intrinsic point defects such as vacancies and interstitials have been made. However, these larger clusters have large positive binding energies and therefore will not form under conditions of thermodynamic equilibrium in sapphire.
4 Conclusions
We have investigated the structural, energetic and optical properties of Ti and Fe in the corundum Al2O3 lattice using two materials modelling techniques. Our insights can be summarised as follows:1. Crystal field parameters have been calculated for the trivalent cations showing their intra-valence optical transitions to occur within the visible light region.
2. The dominant intervalence charge transfer resulting in the absorption of visible light occurs between FeIII/TiIII to produce the metastable FeII/TiIV configuration.
3. Electronic structure calculations have confirmed the instability of the FeII/TiIV pairs in sapphire, with total energies more than 1 eV higher than the FeIII/TiIII configuration.
4. Homonuclear iron and titanium charge transfer has been shown to occur within the IR range and will have no contribution to visible light absorption of the material.
5. Electronic structure calculations, based on DFT and HF, have been unable to stabilise nearest neighbour FeII/FeIII and TiIII/TiIV pairs. Delocalisation of the excess electron occurs between the two metal centres, which would prohibit nearest-neighbour intra-valence charge transfer.
6. Possible Ti and Fe tri-clusters in differing nearest neighbour configurations were modelled. The calculated binding energies between these species identified one configuration to be thermodynamically accessible. [TiIII–(TiIV–FeII)] is the most stable combination, which may be formed in doped sapphire samples.
Moving beyond low concentrations of defects, ternary and quaternary compounds formed of these elements should display a similar behaviour. Ilmenite (FeTiO3) also adopts the corundum structure, consisting of edge and face-sharing iron and titanium cations throughout the crystal structure.77,78 A description of charge transfer processes in these systems, within a first-principles framework, would represent a major development to their materials chemistry.
Acknowledgements
J.K.B is funded by the EPSRC (Grant no. EP/G03768X/1). We would like to thank C.R.A. Catlow and S.M. Woodley for useful discussions and use of the AOLM. A.W. acknowledges support from the Royal Society University Research Fellowship scheme. D.T. was funded under ERC Starting Grant 277757. The work benefits from the high performance computing facility at the University of Bath. Access to the HECToR supercomputer was facilitated through membership of the HPC Materials Chemistry Consortium (EP/F067496).References
- K. Wall and A. Sanchez, Linc. Lab. J., 1990, 3, 447–462 Search PubMed.
- A. K. Datye, J. Catal., 2003, 216, 144–154 CrossRef CAS.
- D. Redfield, Appl. Phys. Lett., 1974, 25, 647–648 CrossRef CAS PubMed.
- P. W. M. Jacobs and E. A. Kotomin, Philos. Mag., 1993, 68, 695–709 CrossRef CAS.
- C. R. A. Catlow, R. James, W. C. Mackrodt and R. F. Stewart, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 1006–1026 CrossRef CAS.
- D. McClure, J. Chem. Phys., 1962, 36, 2757 CrossRef CAS PubMed.
- Y. Kitaoka, K. Nakamura, T. Akiyama, T. Ito, M. Weinert and A. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205113 CrossRef.
- M. Choi, A. Janotti and C. G. Van de Walle, J. Appl. Phys., 2013, 113, 044501–044505 CrossRef PubMed.
- N. Hine, P. Haynes, A. Mostofi and M. Payne, J. Chem. Phys., 2010, 133, 114111–114123 CrossRef CAS PubMed.
- W. H. Bragg, J. Am. Chem. Soc., 1922, 121, 2766–2787 RSC.
- S. Mitra, Fundamentals of Optical, Spectroscopic and X-ray Mineralogy, New Age International, 1996 Search PubMed.
- K. S. Jheeta and D. C. Jain, Afr. Phys. Rev., 2008, 1, 56–66 Search PubMed.
- L. Cuadra, A. Martí and A. Luque, IEEE Trans. Electron Devices, 2004, 51, 1002–1007 CrossRef CAS.
- S. Licht, J. Phys. Chem. B, 2001, 105, 6281–6294 CrossRef CAS.
- J. Baltrusaitis, C. D. Hatch and R. Orlando, J. Phys. Chem. C, 2012, 116, 18847–18856 CAS.
- Y. Ikuma and R. S. Gordon, J. Am. Ceram. Soc., 1983, 66, 139–147 CrossRef CAS.
- A. R. Moon and M. R. Phillips, J. Am. Ceram. Soc., 1994, 77, 356–367 CrossRef CAS.
- J. Zhang, J. Ding and Y. Zhang, Solid State Commun., 2009, 149, 1188–1192 CrossRef CAS PubMed.
- P. Lacovara, L. Esterowitz and M. Kokta, IEEE J. Quantum Electron., 1985, 21, 1614–1618 CrossRef.
- F. Seifert, V. Petrov and M. Woerner, Opt. Lett., 1994, 19, 2009–2011 CrossRef CAS.
- P. F. Moulton, et al. , Opt. News, 1982, 8, 9 CrossRef.
- J. M. Eggleston, L. G. Deshazer and K. W. Kangas, IEEE J. Quantum Electron., 1988, 24, 1009–1015 CrossRef CAS PubMed.
- K. J. W. Atkinson, R. W. Grimes, M. R. Levy, Z. L. Coull and T. English, J. Eur. Ceram. Soc., 2003, 23, 3059–3070 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 Search PubMed.
- N. Yu, Q. Wen, D. R. Clarke, P. C. McIntyre, H. Kung, M. Nastasi, T. Simpson, I. Mitchell and D. Li, J. Appl. Phys., 1995, 78, 5412–5421 CrossRef CAS PubMed.
- J. Ferguson and P. E. Fielding, Aust. J. Chem., 1972, 25, 1371–1385 CrossRef CAS.
- T. Kittiauchawal and P. Limsuwan, Kasetsart J., 2007, 41, 262–266 Search PubMed.
- G. Lehmann and H. Harder, Am. Mineral., 1970, 55, 98–105 CAS.
- L. V. Nikolskaya, V. M. Terekhova and M. I. Samoilovich, Phys. Chem. Miner., 1978, 3, 213–224 CrossRef CAS.
- M. N. Taran and M. Koch-Müller, Phys. Chem. Miner., 2011, 38, 215–222 CrossRef CAS.
- M. G. Townsend, Solid State Commun., 1968, 6, 81–83 CrossRef CAS.
- R. G. Burns, Mineralogical Applications of Crystal Field Theory, Cambridge University Press, 1993, vol. 5 Search PubMed.
- G. W. Hollenberg and R. S. Gordon, J. Am. Ceram. Soc., 1973, 56, 140–147 CrossRef CAS.
- E. Traversa, M. Baroncini, E. Di Bartolomeo, G. Gusmano, P. Innocenzi, A. Martucci and A. Bearzotti, J. Eur. Ceram. Soc., 1999, 19, 753–758 CrossRef CAS.
- J. Tartaj and G. L. Messing, J. Eur. Ceram. Soc., 1997, 17, 719–725 CrossRef CAS.
- N. Yu and M. Nastasi, Appl. Phys. Lett., 1994, 65, 180–182 CrossRef CAS PubMed.
- J. K. Bristow, S. C. Parker, C. R. A. Catlow, S. M. Woodley and A. Walsh, Chem. Commun., 2013, 49, 5259–5261 RSC.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- P. P. Ewald, Ann. Phys., 1921, 64, 253 CrossRef.
- C. R. A. Catlow, Proc. R. Soc. A, 1977, 353, 533–561 CrossRef CAS.
- G. V. Lewis, Physica B + C, 1985, 131, 114–118 CrossRef CAS.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90 CrossRef.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC press, 2012 Search PubMed.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485–499 RSC.
- G. V. Lewis and C. R. A. Catlow, J. Phys.: Condens. Matter, 1985, 18, 1149–1161 CAS.
- S. M. Woodley, P. D. Battle, C. R. A. Catlow and J. D. Gale, J. Phys. Chem. B, 2001, 105, 6824–6830 CrossRef CAS.
- S. M. Woodley, P. D. Battle, J. D. Gale and C. R. A. Catlow, Phys. Chem. Chem. Phys., 1999, 1, 2535–2542 RSC.
- S. M. Woodley, C. R. A. Catlow, J. D. Gale and P. D. Battle, Chem. Commun., 2000, 1879–1880 RSC.
- S. M. Woodley, P. D. Battle, J. D. Gale and C. R. A. Catlow, Chem. Mater., 2003, 15, 1669–1675 CrossRef CAS.
- J. E. Huheey, E. A. Keiter, R. L. Keiter and O. K. Medhi, Inorganic chemistry: principles of structure and reactivity, Harper & Row, New York, 1983, p. 412 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- L. Sham and W. Kohn, Phys. Rev., 1966, 145, 561 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett., 1999, 82, 2544–2547 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 653–658 CrossRef.
- A. Walsh, J. L. F. Da Silva, Y. Yan, M. M. Al-Jassim and S. H. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 073105 CrossRef.
- A. A. Sokol, A. Walsh and C. R. A. Catlow, Chem. Phys. Lett., 2010, 492, 44–48 CrossRef CAS PubMed.
- M. L. Johnson, M. E. Mercer, E. Fritsch, P. Maddison and J. E. Shigley, Gems Gemol., 1995, 31, 188–195 CrossRef.
- P. Lacovara, L. Esterowitz and M. Kokta, IEEE J. Quantum Electron., 1985, 21, 1614–1618 CrossRef.
- D. C. Harris and M. D. Bertolucci, Symmetry and Spectroscopy: an Introduction to Vibrational and Electronic Spectroscopy, Dover Publications, 1989 Search PubMed.
- N. Udomkan, P. Limsuwan, P. Winotai and S. Meejoo, Int. J. Mod. Phys. B, 2005, 19, 3273–3284 CrossRef CAS.
- V. Palanza, A. Galli, R. Lorenzi, F. Moretti, M. C. Mozzati, A. Paleari and G. Spinolo, Luminescence study of transition metal ions in natural magmatic and metamorphic yellow sapphires, 2010, vol. 15, p. 12086 Search PubMed.
- K. Eigenmann and H. H. Günthard, Chem. Phys. Lett., 1972, 13, 58–61 CrossRef CAS.
- I. Fontana, A. Le Donne, V. Palanza, S. Binetti and G. Spinolo, J. Phys.: Condens. Matter, 2008, 20, 125228 CrossRef.
- I. Dzyaloshinsky, J. Phys. Chem. Solids, 1958, 4, 241–255 CrossRef CAS.
- J. Badro, V. V. Struzhkin, J. Shu, R. J. Hemley, H.-k. Mao, C.-c. Kao, J.-P. Rueff and G. Shen, Phys. Rev. Lett., 1999, 83, 4101–4104 CrossRef CAS.
- I. Solovyev, A. Liechtenstein and K. Terakura, J. Magn. Magn. Mater., 1998, 185, 118–120 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS PubMed.
- A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187–188 CrossRef.
- K. P. D. Lagerlöf and R. W. Grimes, Acta Mater., 1998, 46, 5689–5700 CrossRef.
- N. C. Wilson, J. Muscat, D. Mkhonto, P. E. Ngoepe and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 075202 CrossRef.
- G. R. Seda and T. Hearne, J. Phys.: Condens. Matter, 2004, 16, 2707 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |