Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Softening and yielding of soft glassy materials
Simon
Dagois-Bohy
ab,
Ellák
Somfai
 c,
Brian P.
Tighe
c,
Brian P.
Tighe
 *d and
Martin
van Hecke
*d and
Martin
van Hecke
 ae
ae
aHuygens-Kamerlingh Onnes Lab, Leiden University, P.O. Box 9504, 2300 RA Leiden, The Netherlands
bLaboratoire de Mécanique des Fluides et d'Acoustique, UMR CNRS 5509 Université de Lyon, INSA de Lyon 36, Avenue Guy de Collongue, 69134 Écully cedex, France
cInstitute for Solid State Physics and Optics, Wigner Research Center for Physics, Hungarian Academy of Sciences, P.O. Box 49, H-1525 Budapest, Hungary
dDelft University of Technology, Process & Energy Laboratory, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands. E-mail: b.p.tighe@tudelft.nl
eAMOLF, Science Park 104, 1098 XG Amsterdam, The Netherlands
First published on 20th November 2017
Abstract
Solids deform and fluids flow, but soft glassy materials, such as emulsions, foams, suspensions, and pastes, exhibit an intricate mix of solid- and liquid-like behavior. While much progress has been made to understand their elastic (small strain) and flow (infinite strain) properties, such understanding is lacking for the softening and yielding phenomena that connect these asymptotic regimes. Here we present a comprehensive framework for softening and yielding of soft glassy materials, based on extensive numerical simulations of oscillatory rheological tests, and show that two distinct scenarios unfold depending on the material's packing density. For dense systems, there is a single, pressure-independent strain where the elastic modulus drops and the particle motion becomes diffusive. In contrast, for weakly jammed systems, a two-step process arises: at an intermediate softening strain, the elastic and loss moduli both drop down and then reach a new plateau value, whereas the particle motion becomes diffusive at the distinctly larger yield strain. We show that softening is associated with an extensive number of microscopic contact changes leading to a non-analytic rheological signature. Moreover, the scaling of the softening strain with pressure suggest the existence of a novel pressure scale above which softening and yielding coincide, and we verify the existence of this crossover scale numerically. Our findings thus evidence the existence of two distinct classes of soft glassy materials – jamming dominated and dense – and show how these can be distinguished by their rheological fingerprint.
The rheology of soft glassy materials is an intricate mixture of elastic, viscous and plastic behaviors. Oscillatory rheology is an ideal tool to characterize these materials, as variation of the driving frequency and driving amplitude allows one to quantify the relative importance of elastic, viscous and plastic contributions.1 Depending on the driving conditions, these materials exhibit both a solid-like and liquid-like regime: for vanishingly small strain amplitude, the material's response is linear and can be characterized by an elastic storage modulus and a loss modulus – in solids the former exceeds the latter at low frequencies and the material behaves elastically. In contrast, for sufficiently large strain amplitudes the materials yields and flows. Near the yield strain, the elastic modulus drops and, in many cases, the loss modulus peaks. What are the rheological scenarios that connect the small and large strain regimes? What are the microscopic signatures associated with increased driving strains? Which aspects of these scenarios depend on material properties, and which aspects are universal? Here we use extensive numerical simulations of particle-based models of non-Brownian amorphous solids to disentangle how the pre- and post-yielding regimes are connected. We evidence that there are two qualitatively distinct scenarios for the strain dependent response of soft glassy materials, depending on the rigidity of the jammed state of the material at rest.
The jamming transition has in recent years been shown to play an important organizing role for the response of soft repulsive sphere packings, which are an effective model for foams, emulsions, suspensions and granular media.2–5 First, there is overwhelming evidence that the distance to the critical jamming point, as measured by e.g. the confining pressure P, is the key control parameter governing a packing's quasistatic, linear elastic response,3,6–9 and more recent work has extended these findings to the linear viscoelastic response at finite frequency.8,10–12 Second, the distance to jamming has also been found to play a key role in organizing the steady state rheology of a wide range of soft materials.13–17 As linear response and steady state rheology are connected to the limits of zero and infinite strain amplitude in oscillatory shear, the distance to jamming can be expected to play a crucial role at finite strains as well. Moreover, several characteristic scales that limit the range of linear behavior all scale with the distance to jamming: when the pressure is lowered towards the critical point, the material becomes dominated by nonlinear response,8,11,18–21 and both the yield stress13–15 and the range of strains that are free of microscopic contact breaking events8,22–26 all vanish.
To fill in the gap between zero and infinite strain amplitudes and shed light on the rheological scenarios and microscopic mechanisms of yielding, we perform simulations of packings under oscillatory shear at varying strain amplitude γ0, pressure P, and number of particles N, focusing on the low frequency regime. Macroscopically, we identify not one but two distinct crossover strain scales. We find that linear response gives way to softening above a strain scale γs, after which the material's response reaches a new plateau before the material yields at a scale γy. Unlike prior observations of two-step yielding,27–29 this scenario does not require interparticle attraction. Near jamming softening and yielding scales differ in their pressure dependence: while γy is essentially constant, the softening strain γs vanishes linearly with P. Far above jamming the scales merge, suggesting the existence of a characteristic pressure that distinguishes jamming-like and dense systems. The relation between these rheological phenomena and the microscopic particle motion is complex. Whereas yielding is associated with the onset of diffusive particle motion, the relation between softening and microscopic rearrangements is far more subtle. While rearrangements destroy strict reversibility in the particles' trajectories, bulk properties such as the storage and loss moduli remain linear long after the first rearrangements – leading to a regime where particles exhibit irregular, trapped motion but the bulk response appears linear. Bulk softening only becomes apparent after an extensive amount of contact breaking events; the sum of many of these singular events leads to non-trivial power law scaling of the elastic modulus with strain amplitude.
These findings provide a fresh perspective on the physics of yielding, evidence a characteristic pressure scale that distinguishes jamming-dominated systems (such as granular media and wet foams) and dense systems (such as dry foams), and suggest that these two qualitatively different classes of soft glassy materials can be distinguished by their experimentally accessible rheological fingerprint.
Macroscopic rheology: softening and yielding
We use oscillatory rheology to show that there are three distinct flow regimes, which we refer to as the linear response, softened, and yielding regimes. A time-varying shear strain γ = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) is applied to soft sphere packings consisting of N particles that are at pressure P when unsheared, and the resulting shear stress σ is measured (see Appendix A). In the linear response regime, σ is proportional to γ0, and the in-phase and out-of-phase components of σ/γ0 are called the storage and loss moduli G′ and G′′, respectively; they characterize elastic stiffness and viscous damping. For finite strain amplitudes, the stress response ceases to be purely sinusoidal (see Appendix C), and the first harmonic terms in the Fourier expansion of σ are used to define the storage and loss moduli, which now depend on γ0. We focus on data taken at the low frequency ω = 10−3 in units constructed from the microscopic stiffness and damping coefficients; in Appendix D we demonstrate that our conclusions are unchanged at the higher frequency 10−2. Moduli are reported for data recorded after the passage of an initial transient, which can be identified from the cycle-to-cycle diffusion statistics (see below).
sin(ωt) is applied to soft sphere packings consisting of N particles that are at pressure P when unsheared, and the resulting shear stress σ is measured (see Appendix A). In the linear response regime, σ is proportional to γ0, and the in-phase and out-of-phase components of σ/γ0 are called the storage and loss moduli G′ and G′′, respectively; they characterize elastic stiffness and viscous damping. For finite strain amplitudes, the stress response ceases to be purely sinusoidal (see Appendix C), and the first harmonic terms in the Fourier expansion of σ are used to define the storage and loss moduli, which now depend on γ0. We focus on data taken at the low frequency ω = 10−3 in units constructed from the microscopic stiffness and damping coefficients; in Appendix D we demonstrate that our conclusions are unchanged at the higher frequency 10−2. Moduli are reported for data recorded after the passage of an initial transient, which can be identified from the cycle-to-cycle diffusion statistics (see below).
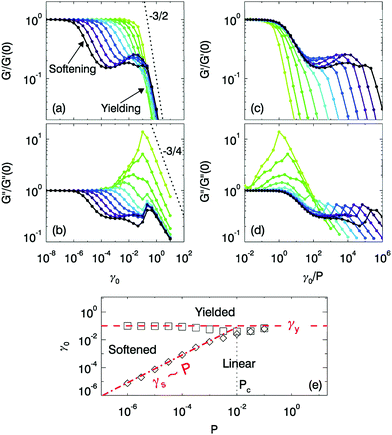
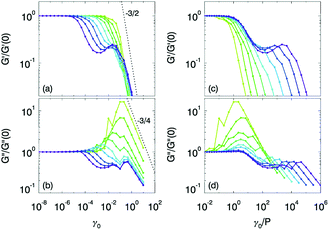
Our simulations uncover surprisingly rich rheological scenarios, as shown in Fig. 1a and b, which display the variation of the rescaled storage modulus G′(γ0,P)/G′(0,P) and the loss modulus G′′(γ0,P)/G′′(0,P) as a function of strain – in Appendix B we demonstrate that the linear response quantities scale with pressure and frequency consistent with earlier predictions.10 Our data evidences three different rheological regimes. (i) Linear response: for each pressure there is a finite strain range for which the moduli are essentially constant and equal to G′(0) and G′′(0), indicative of linear response. (ii) Softening: surprisingly, for low pressures and intermediate strains, both moduli fall below their linear response values but then reach new plateau values. We call this softening, to distinguish it from yielding, and associate a strain scale γs with its onset. (iii) Yielding: at sufficiently large strain amplitudes, the elastic modulus rapidly decays, while the loss modulus peaks. We refer to this as yielding, with an associated yield strain γy that does not strongly vary with P. For large strains the storage and loss moduli fall off rapidly as 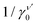 and
and 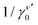 , respectively, with ν′ ≈ 1.5 and ν′′ ≈ ν′/2.30,31
, respectively, with ν′ ≈ 1.5 and ν′′ ≈ ν′/2.30,31
Softening and yielding are distinct phenomena, each with their unique rheological signature and pressure dependence. First, the loss modulus goes down at softening, and up at yielding, signaling a qualitative difference between these two phenomena. Second, systems at lower pressures clearly soften at smaller strain amplitude, whereas the yielding strain appears pressure independent. To characterize the pressure dependence of γs, we replot the data of Fig. 1a and b as a function of the rescaled strain γ0/P in Fig. 1c and d. We find excellent collapse in the linear response and softening regimes of both the storage and the loss moduli for P up to 10−2. Recently, several works have presented conflicting evidence for the scaling of the softening transition with pressure,8,19,32,33 and both γs ∼ P and γs ∼ P3/4 have been suggested – our data is inconsistent with an exponent 3/4.
We summarize our findings of a pressure-dependent softening transition, and a pressure-independent yielding transition in Fig. 1e. Here the red dot-dashed line indicates the softening crossover at γs ∼ P, the red dashed line indicates the yielding crossover at γy, and these lines meet at a characteristic pressure Pc. We note that many scaling laws near jamming break down when P becomes of order 10−2,34 and consistent with this our data suggests that γy ≈ 10−1 and Pc ≈ 10−2. Whereas such breakdown of scaling can be expected sufficiently far away from any critical point, we suggest that our data shows that there is a clear crossover pressure scale which separates the near-jamming and dense regimes; in the latter the physics is essentially pressure independent, and no longer controlled by the critical jamming point. Moreover, oscillatory rheology provides a specific experimental protocol to test which asymptotic regime is relevant for a given system: the jamming phenomenology is important when softening and yielding can be distinguished.
Reversible, trapped and diffusive dynamics
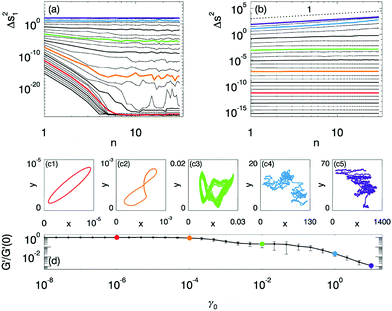
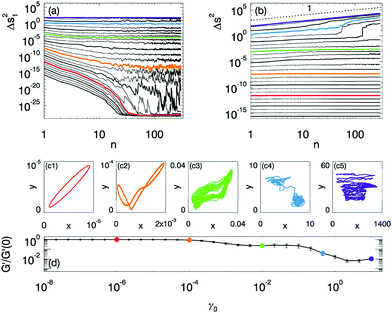
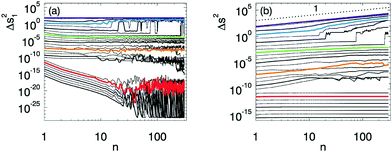
To shed light on the microscopic signatures of the rheological softening and yielding transitions, we now probe the microscopic particle trajectories. Recent years have seen considerable effort directed towards understanding the transition from reversible to irreversible particle trajectories under cyclic driving.35–41 With few exceptions,42 this work has been restricted to systems far from jamming, where the two step softening/yielding scenario identified here is absent. In that case the onset of irreversibility is found to correlate with macroscopic yielding. Here we characterize particle trajectories by stroboscopically sampling all particles at zero strain as a function of cycle number n. From these stroboscopic trajectories we compute the cycle-to-cycle squared displacements Δs12, and the cumulative squared displacements Δs2 (see Appendix A).Our data evidences three different dynamical regimes. (i) Reversible dynamics: particle trajectories at sufficiently small strain amplitudes are reversible: Δs12 decays to the noise floor after an initial transient, and particles trace out ellipses in space consistent with a strictly linear response (Fig. 2c1). (ii) Trapped dynamics: at intermediate strains the particle trajectories are trapped: both Δs12 and Δs2 reach a finite plateau at large n. The particle trajectories do not form closed orbits, but remain bounded (Fig. 2c2 and c3). (iii) Diffusive dynamics: for high strain amplitudes, Δs2 grows linearly with n and the particle motion becomes diffusive (Fig. 2c4 and c5).
We have verified (via the total harmonic distortion, see below) that in the reversible regime no contact changes take place during the oscillatory driving, and that the transition from reversible to trapped dynamics occurs when contacts are broken and created during the strain oscillations. Trapped dynamics is reminiscent of caging in hard sphere glasses, although there is no ballistic motion at short times and particles generally remain in contact with multiple neighbors. We note that the loss of microscopic reversibility after a single contact change suggests that the transition from reversible to caged dynamics is a finite size effect, as the strain needed to change one contact is O(1/N) in large systems (verified below). Directly obtaining the characteristic strain where the first contact changes from oscillatory rheology is numerically prohibitive, as it entails scans over N, P and γ0. However recent simulations of quasistatically sheared soft spheres determined the typical strain scale γcc at which the first contact change occurs and found that it obeys finite size scaling in the linear response regime:8,24,25
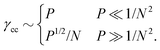 | (1) |
Our data for contact changes under oscillatory driving is consistent with this scaling, and we thus conjecture that the same scaling governs the strain scale where the transition from reversible to caged dynamics takes place.
The pressure dependence of the transition to diffusive dynamics can be deduced from the behavior of Δs12 and Δs2 as function of n; we find that the transition is essentially pressure-independent. In Fig. 3a we plot the large n plateau of Δs12 as a function of γ0 for varying pressures. While the initial growth of Δs12, associated with contact changes, depends on P – consistent with eqn (1) and observations that contact breaking near jamming depends on P8,23–26 – the asymptotic value of Δs12 becomes independent of P for large γ0. This increase signals a pressure-independent transition to diffusive motion, as is further evidenced by inspecting our data for Δs2 for all pressures, and fitting our data for Δs2 as nα. As Fig. 3b shows, the scaling exponent α sharply increases with γ and reaches a diffusive (α = 1) regime for large strains in an essentially pressure-independent manner.
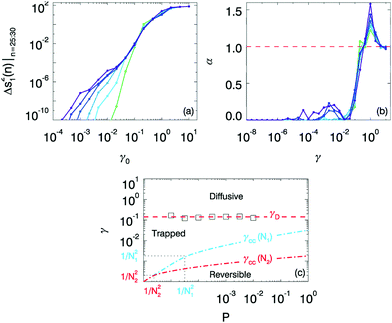 | ||
Fig. 3 Onset of diffusive motion for N = 128, ω = 10−3, and pressures from 10−5 (purple) to 3.2 × 10−3 (blue) in two steps per decade. (a) Plateau values for the median cycle-to-cycle second moment, Δs12, averaged over cycle n = 25–30. The characteristic strain of the initial rise of the plateau values of Δs12 increases with pressure, but the final rise is independent from P. (b) We estimate the onset of diffusive motion by fitting our data for Δs2 as nα (see Appendix A), and plotting the scaling α exponent as function of γ; α = 1 corresponds to diffusion. (c) Proposed state diagram indicating reversible, trapped and diffusive regimes as function of the control parameters P, γ0 and N. Symbols correspond to the onset of diffusive motion defined as the strain where α crosses 1; red dashed line is a guide to the eye at γ = 0.14. The dot-dashed lines indicate the prediction from eqn (1) for the transition from reversible to caged dynamics; here N2 > N1. The regime P < 1/N2 and γ0 < 1/N2 indicates the finite size regime where the first contact change arises at γcc ≈ P.43–45 Outside the finite scaling regime, 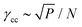 and thus vanishes for large N; hence the reversible regime disappears in the thermodynamic limit, where only the trapped and diffusive regimes play a role. and thus vanishes for large N; hence the reversible regime disappears in the thermodynamic limit, where only the trapped and diffusive regimes play a role. | ||
We summarize our picture for the microscopic behaviors in Fig. 3c, and now discuss the relation with the rheological behaviors shown in Fig. 1e. Our data fully supports identifying the transition to diffusive motion with rheological yielding – both are pressure-independent and their characteristic strains are close. The correspondence between the onset of diffusion and yielding is consistent with recent experimental and numerical findings that focus on concentrated emulsions.40,42 This link is reminiscent of the Lindemann melting criterion: once the relative particle motions reach a significant fraction of their separation at rest, structural information is lost, particles can freely diffuse, and macroscopic rigidity vanishes. A similar correspondence between diffusion and yielding also occurs in equilibrium systems, where the fluctuation-dissipation relation establishes the relation rigorously.
Surprisingly, the micro transition from reversible to trapped dynamics and the macroscopic softening are not directly linked. In fact, the transition from reversible to trapped dynamics is a finite-size artefact. This follows from the scaling of γcc with N, which dictates that in the limit of large N, the onset strain for trapped dynamics is vanishingly small so that the reversible regime vanishes. Hence, for large systems, the transition from reversible to trapped dynamics is irrelevant, which is reasonable as strict microscopic reversibility should be absent in the thermodynamic limit. As the critical strain for softening is independent of N, for large systems there is a wide parameter range where the microscopic dynamics is caged, but the rheology is still effectively linear.
Trapped motion and softening near jamming
In the remainder of this article, we will disentangle the relation between contact breaking and softening. Both are pressure-dependent, and both have characteristic strains that vanish when P → 0—they are thus connected to the jamming transition. The picture that will emerge is that contact changes have an![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/N) effect on G′, and occur at strains of order 1/N. Significant softening occurs after an extensive number of contact change events have happened, and this leads to a well-defined thermodynamic limit. Finally, the effect on the elastic modulus of contact breaks is cumulative, so that G′ decays linearly with |γ0|, thus signifying non-analytic behavior.
(1/N) effect on G′, and occur at strains of order 1/N. Significant softening occurs after an extensive number of contact change events have happened, and this leads to a well-defined thermodynamic limit. Finally, the effect on the elastic modulus of contact breaks is cumulative, so that G′ decays linearly with |γ0|, thus signifying non-analytic behavior.
We first note that the contact change strain provides a way to rationalize the linear dependence of the softening strain on P if we postulate that contact changes are necessary for softening, so γs ≥ γcc. This is plausible because the shear response of packings can be mapped directly onto a spring network for infinitesimal strains. However networks stiffen rather than soften at finite strains,46 which involve contact changes in packings but not in networks. We expect the lower bound on the softening strain will saturate for marginal packings that would unjam with the loss of just one contact. This marginal state is reached when P ∼ 1/N2.43,45,47 If we make the ansatz γs ∼ Pν, the value of the exponent ν is then determined by requiring γs ∼ γcc when P ∼ 1/N2. The result is ν = 1, consistent with the observed scaling of γs.
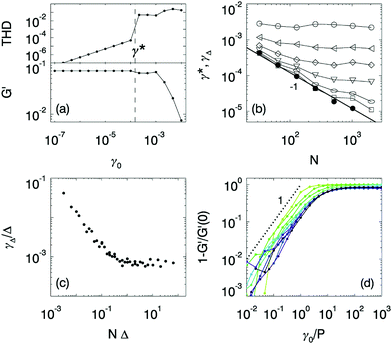
Returning to numerics, the link between contact changes and mechanical softening is illustrated in Fig. 4a, which focuses on a single packing. We detect contact changes via the sharp increase of anharmonic behavior of the time dependent stress signal, caused by abrupt changes in the contact stiffness when harmonic contacts open or close, and quantified by the total harmonic distortion 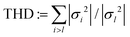 , where we have decomposed the stress signal in a Fourier series with coefficients σ1, σ2,…. At a characteristic strain γ*, Fig. 4a shows a sharp increase in the THD over several orders of magnitude, accompanied by a small decrease in G′. This corroborates our expectation that softening can only arise due to contact changes. Moreover, most of the softening of the storage modulus happens subsequent to, not at, the first contact break.
, where we have decomposed the stress signal in a Fourier series with coefficients σ1, σ2,…. At a characteristic strain γ*, Fig. 4a shows a sharp increase in the THD over several orders of magnitude, accompanied by a small decrease in G′. This corroborates our expectation that softening can only arise due to contact changes. Moreover, most of the softening of the storage modulus happens subsequent to, not at, the first contact break.
To uncover the link between contact changes and softening, we now explore the role of system size, and simulate oscillatory rheology for system sizes varying from N = 32 up to N = 2048 at fixed pressure P = 10−3, while varying the driving amplitude γ0 over many decades. We found that G′(γ0), in particular for small systems, exhibits significant fluctuations, which requires a careful procedure to obtain meaningful averages. For each packing, we therefore define γΔ as the smallest strain where the deviation in G′ from linear response, 1 − G′(γ)/G′(0) reaches a value Δ, and then take ensemble averages to obtain γΔ(N,Δ).
In Fig. 4b we compare the mean values of γ* (closed symbols) – obtained from detecting jumps in the THD – and γΔ for a range of Δ and N (open symbols). First, our data shows that γ* indeed decreases with system size, consistent with the 1/N of eqn (1). Second, for very small values of Δ, the data for γΔ closely approach γ*, consistent with the picture that any appreciable softening only arises after contact changes accumulate. Third, for large N or large Δ, γΔ becomes independent of N, evidencing a well defined continuum limit, where softening is due to an extensive number of contact changes.
As shown in Fig. 4c, all data for γΔ can be collapsed on a master curve by plotting γΔ/Δ as function of NΔ – data taken at different pressures shows the same trends (see Appendix D). This scaling collapse shows, first, that the typical effect of a single contact change on G′ is ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/N). Second, the behavior for NΔ ≪ 1 is consistent with γΔ/Δ ∼ (NΔ)−1, or γΔ ∼ 1/N: hence, for small Δ ≪ 1/N, γΔ scales as, and is close to, γ*. Third, the plateau for NΔ ≫ 1 confirms the existence of a well defined continuum limit, where γΔ, and hence the softening behavior, becomes independent of N and γΔ is linear in Δ. We conclude that softening first sets in once contacts start to break, only becomes significant when many contacts are changing, and is independent of system size for large N.
(1/N). Second, the behavior for NΔ ≪ 1 is consistent with γΔ/Δ ∼ (NΔ)−1, or γΔ ∼ 1/N: hence, for small Δ ≪ 1/N, γΔ scales as, and is close to, γ*. Third, the plateau for NΔ ≫ 1 confirms the existence of a well defined continuum limit, where γΔ, and hence the softening behavior, becomes independent of N and γΔ is linear in Δ. We conclude that softening first sets in once contacts start to break, only becomes significant when many contacts are changing, and is independent of system size for large N.
A final striking consequence of the softening being caused by the accumulation of independent contact changes is that the functional form of G′(γ0)/G′(0) is non-analytical. Our picture, backed up by the various scaling collapses, suggests that G′(γ0)/G′(0) should decrease linearly with the strain, or equivalently, that Δ = 1 − G′/G′(0) grows linearly with γ. In Fig. 4d we show data for Δ for large systems and a range of pressures, which confirms this linear deviation of the plateau value of G′ with strain. As Δ(γ0) needs to be an even function due to symmetry, this implies non-analytic behavior where Δ ∼ |γ0|. We note that similar non-analytic behavior has also been observed for strain stiffening in random spring networks at the rigidity transition46 – consistent with the usual association of non-analyticity with a phase transition. In contrast, the non-analytic behavior found here occurs at a finite distance from the jamming point, and we suggest that it is inherited from the purely repulsive contact forces between particles, which are themselves non-analytic at the point of contact.
Discussion
Simulating large amplitude oscillatory shear, we have found evidence for two qualitatively distinct yielding scenarios for soft glassy solids. In dense systems, such as highly concentrated emulsions and Lennard-Jones glasses,48 the macroscopic stress–strain response is linear up to the point of yielding, which occurs at a constant strain γy. In marked contrast, weakly jammed solids such as wet foams and emulsions first soften at a pressure-dependent strain γs, only to yield at a larger strain γy. The ratio of γs and γy determines a characteristic pressure on the order of 10−2 that marks the dividing line between these two material classes.Particle trajectories evidence an intricate link between microscopic and macroscopic behavior. The particle dynamics display just one clear transition that separates trapped and diffusive trajectories, and which corresponds to yielding. In contrast, softening has no sharp microscopic fingerprint, but results from the accumulation of an extensive number of contact changes leading to non-analytic rheological curves. Our measurements correspond well with recent experiments in emulsions42 and pastes.49 Softening is also observed in attractive glasses28 and granular media;20,50 however the characteristic strains scale differently, likely due to attraction, friction, and/or non-harmonic contact force laws. Our data for cycle-to-cycle diffusion (Fig. 2a) are strikingly similar to data from emulsions, which also show a swift rise that sharpens with increasing P.42
So far, we have focused on the behavior at a single driving frequency (ω = 10−3). However, our data for the characteristic strains and changes in diffusive behavior obtained at ω = 10−2 are very close, as we detail in Appendix D. In both cases, the elastic contributions to the stress are dominant and well separated from the viscous and (yet smaller) inertial contributions. This suggests that our scenario describes a rate independent, low frequency regime. We note that recent simulations of transient rheology find similarly rate-independent characteristic strains at these frequencies,8 and that the existence of rate independent characteristic strains is to be expected above jamming, when the system is solid.
Our findings clarify the notion of linear response.23,51 In sufficiently large systems, vanishingly small strains lead to contact changes, perfectly reversible trajectories are not to be found, and linear response in the strict sense, in which the microscopic equations of motion can be linearized about the initial condition, is violated as soon as the first contact change occurs.8,22–26,51,52 However, we have provided conclusive evidence that the breaking of contacts does not significantly influence the macroscopic behavior,8,11,24,51 leading to a well-defined effective linear response for macroscopic quantities.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A: numerical model
We perform MD simulations of 2D packings submitted to oscillatory shear. The initial packing configurations are so-called shear stabilized (SS) packings.44,45 Unlike algorithms that relax particles within a fixed box, SS packings are equilibrated in a purely isotropic stress state; the shear modulus is guaranteed to be positive, and there are no residual shear stresses. This is crucial, because packings with residual stress subjected to oscillatory driving are prone to long transients, making the use of SS packings crucial for numerical studies of oscillatory rheology.The shear is imposed using Lees-Edwards periodic boundary conditions, and Newton's Laws are integrated using a velocity-Verlet algorithm modified for velocity dependent forces. Our packings are composed of N soft spheres of radii linearly spaced from 1 to 1.4 and mass density ρ = 1. The spheres interact through contact elastic repulsion (amplitude fel = kδ, where δ is the overlap between two particles and k = 1), as well as viscous damping (![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) v = −bΔ
v = −bΔ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) , where Δ
, where Δ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) is their velocity difference at contact and b = 1).
is their velocity difference at contact and b = 1).
We measure the steady state stress tensor
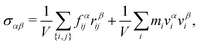 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt). The first sum is over contacts,
sin(ωt). The first sum is over contacts, ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) ij is the sum of elastic and viscous contact forces between particles i and j, and
ij is the sum of elastic and viscous contact forces between particles i and j, and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij points between their centers. The second sum gives the kinetic stress, where mi is mass and
ij points between their centers. The second sum gives the kinetic stress, where mi is mass and ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) i is velocity. In the low-frequency parameter regimes we explore, the kinetic stress is orders of magnitude below the viscous and elastic stresses, and the latter dominates.
i is velocity. In the low-frequency parameter regimes we explore, the kinetic stress is orders of magnitude below the viscous and elastic stresses, and the latter dominates.
We determine G* via the complex ratio of the first harmonic in the stress and strain signals, carefully checking that we reach stationarity. As our numerical model is deterministic and well behaved, statistical error bars are set by numerical noise and generally very small. However, it is well known that ensembles of finite size jammed systems at fixed pressure exhibit a considerable spread in quantities such as the static shear modulus.25,43–45 Our data for G′ and G′′, both in linear response and at finite strain, show concomitantly strong ensemble fluctuations, and we report mean values 〈G′(γ)/G′(0)〉 and 〈G′′(γ)/G′′(0)〉.
Diffusivity
Our local dissipation law is numerically expensive but crucial to capture the correct physics,15 and to properly resolve each oscillatory cycle, a large number of simulation steps are needed, in particular near jamming. Therefore, these simulations are numerically expensive, and pushing our numerical capacities, to obtain particle tracks we have simulated 33 realizations of systems of N = 128 particles for each value of P, Γ0 and two values of ω; for ω = 10−3 we have simulated 30 cycles, and for ω = 10−2, where transients are longer-lived, 300 cycles.For each realization we calculate the second moment ds2(n,m) = 〈(xin − xim)2 + (yin − yim)2〉, where m, n are cycle numbers and 〈·〉 is the average over the non-rattler particles. These measures are highly sensitive to rattlers and drift in the center of mass, which is a Goldstone mode. Before processing the position data, we first carefully identify the rattling particles at each time step and remove them from any analysis, then compute the Goldstone mode and remove it from the non-rattler positions. Nevertheless, some runs still exhibit residual drift or rattlers. As the reported second moments vary over 30 decades, drift makes the main trends less easy to observe. Therefore we focus on the median of the distributions of ds2(n,m), in particular the cycle-to-cycle second moment Δs12(n) := [ds2(n − 1,n)] and squared displacements Δs2(n) := [ds2(0,n)], where square brackets denote the median. In Appendix D we also show results for the mean, which show more fluctuations but do not lead to a different interpretation.
Determination of softening, yielding and diffusive onsets
We determine the data points for softening and yielding shown in Fig. 1e as follows. First, from our rheological data we estimate the strain where G′/G′(0) dips below 0.3 and 0.03 respectively. Second, to obtain an estimate of the critical strains that does not strongly depend on the choice of this cutoff, we assume that G′/G′(0) ∼ γ−3/2, and determine the strain where G′/G′(0) = 1, which then gives the hypothetical intersection of the plateau at low strains and power law decay at larger strains. To determine the onset of diffusive motion shown in Fig. 3c, we take data for Δs2 as function of n, and perform linear fits to log(Δs2) as α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(n), focusing on 3 ≤ n ≤ 30. We have checked that such fits are close to the data. The overshoot of α for intermediate strains is likely due to transients and is not expected to persist for larger n.
log(n), focusing on 3 ≤ n ≤ 30. We have checked that such fits are close to the data. The overshoot of α for intermediate strains is likely due to transients and is not expected to persist for larger n.
Appendix B: scaling of G*
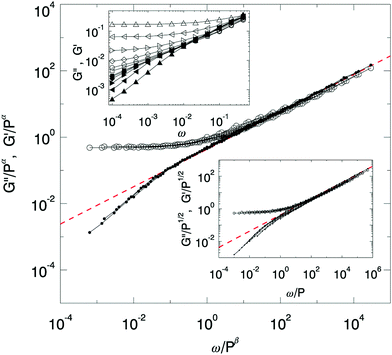
We report here our numerical results for the linear elastic and loss moduli, measured at γ0 = 10−10. Here the stress signal is well described by a simple harmonic response of the form σxy = G*γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iωt) + c.c. In this regime, recent theoretical arguments predict precise scaling laws for G′ and G′′ as function of P and ω.10,12 In Fig. 5 we show our rheological data for a range of pressures and frequencies for a system of N = 1024 particles. Our data is in good agreement with the aforementioned scaling arguments: (1) all data collapses when plotted as function of ω/P; (2) for small values of ω/P, the elastic modulus G′ ∼ P1/2
exp(iωt) + c.c. In this regime, recent theoretical arguments predict precise scaling laws for G′ and G′′ as function of P and ω.10,12 In Fig. 5 we show our rheological data for a range of pressures and frequencies for a system of N = 1024 particles. Our data is in good agreement with the aforementioned scaling arguments: (1) all data collapses when plotted as function of ω/P; (2) for small values of ω/P, the elastic modulus G′ ∼ P1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,34 and the loss modulus vanishes linearly with ω as G′′ ∼ ω/P1/2;9,10 at large ω/P, both G′ and G′′ exhibit nontrivial scaling with
3,34 and the loss modulus vanishes linearly with ω as G′′ ∼ ω/P1/2;9,10 at large ω/P, both G′ and G′′ exhibit nontrivial scaling with 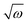 .8–10
.8–10
We note that we can improve on the quality of the data collapse when we plot G*/Pαvs. ω/Pβ, and find the best collapse for β = 0.8, α = 0.45. We do not believe that this constitutes a significant deviation from the theoretical mean field exponents α = 1/2, β = 1 – even linear response calculations show slight deviations,10 and data in 2D may suffer from log corrections, as 2 is believed to be the upper critical dimension for jamming.43 Moreover, our value of β is strongly influenced by the data at the lowest ω, for which simulations are expensive and we only have a limited number of oscillation cycles. Furthermore, several effects limit our scaling range. First, for P > 0.1 we see substantial deviations from scaling, as is the case for many static properties near jamming, while for P < 10−6 finite size effects start to dominate for our case of N = 1024 particles.8,12,43–47 Second, for our choice of microscopic parameters, inertial effects become detectable for ω ⪅ 0.05—if we limit our data to a smaller range of ω and P, the collapse becomes better but the scaling range shrinks.
Appendix C: nonlinearity of response
To illustrate the nonlinearity of the large amplitude oscillatory shear response, in Fig. 6 we present Lissajous curves (stress–strain plots parameterized by time) for the same strain amplitudes presented in Fig. 2c. Anharmonic contributions are clearly visible for large strain amplitudes, but are by no means dominant, so that G′ and G′′ remain meaningful.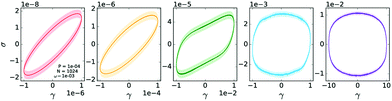 | ||
| Fig. 6 Lissajous curves for P = 10−4, N = 1024 and ω = 10−3. Averages are shown as thick curves, and the broader, fainter band indicates the standard deviation. | ||
Appendix D: robustness of results
To show that the separation of softening and yielding is robust to changes in particle number and frequency, in Fig. 7 and 8 we show our data for G′ and G′′ for N = 128 and both ω = 10−3 and ω = 10−2 – all features shown in Fig. 1 for N = 1024, ω = 10−3 are also present here.Diffusion
In Fig. 9 we show examples of the median cycle-to-cycle squared displacements Δs12, and the cumulative squared displacements Δs2 for ω = 10−2, illustrating that all features shown in Fig. 2 for ω = 10−3 are also present here. We note that the jumps visible in a few datasets are due to the large packing-to-packing fluctuations in the transition from trapped to diffusive particle dynamics. In Fig. 10 and 11 we show the mean cycle-to-cycle squared displacements Δs12 and the cumulative squared displacements Δs2 for ω = 10−2 and ω = 10−3—even though the mean is more sensitive to fluctuations, in particular for the smallest squared displacements (notice the large dynamical range), we stress that all essential features are similar in mean and median data.Acknowledgements
S. D.-B. acknowledges funding from the Dutch physics foundation FOM. E. S. was supported by the Hungarian National Research, Development and Innovation Office NKFIH under grant OTKA K 116036. B. P. T. and M. v. H. acknowledge financial support from the Netherlands Organization for Scientific Research (NWO).References
- H. A. Barnes and J. F. Hutton, An Introduction to Rheology, Elsevier, 1989 Search PubMed.
- D. J. Durian, Phys. Rev. Lett., 1995, 75, 4780–4783 CrossRef CAS PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef PubMed.
- G. Katgert and M. van Hecke, EPL, 2010, 92, 34002 CrossRef.
- T. S. Majmudar, M. Sperl, S. Luding and R. P. Behringer, Phys. Rev. Lett., 2007, 98, 058001 CrossRef CAS PubMed.
- M. Wyart, S. R. Nagel and T. A. Witten, EPL, 2005, 72, 486 CrossRef CAS.
- W. G. Ellenbroek, E. Somfai, M. van Hecke and W. van Saarloos, Phys. Rev. Lett., 2006, 97, 258001 CrossRef PubMed.
- J. Boschan, D. Vågberg, E. Somfai and B. P. Tighe, Soft Matter, 2016, 12, 5450–5460 RSC.
- K. Baumgarten, D. Vågberg and B. P. Tighe, Phys. Rev. Lett., 2017, 118, 098001 CrossRef PubMed.
- B. P. Tighe, Phys. Rev. Lett., 2011, 107, 158303 CrossRef PubMed.
- J. Boschan, S. A. Vasudevan, P. E. Boukany, E. Somfai and B. P. Tighe, Soft Matter, 2017, 13, 6870–6876 RSC.
- K. Baumgarten and B. P. Tighe, Soft Matter, 2017, 13, 8368–8378 RSC.
- P. Olsson and S. Teitel, Phys. Rev. Lett., 2007, 99, 178001 CrossRef PubMed.
- C. Heussinger and J.-L. Barrat, Phys. Rev. Lett., 2009, 102, 218303 CrossRef PubMed.
- B. P. Tighe, E. Woldhuis, J. J. C. Remmers, W. van Saarloos and M. van Hecke, Phys. Rev. Lett., 2010, 105, 088303 CrossRef PubMed.
- K. N. Nordstrom, E. Verneuil, P. E. Arratia, A. Basu, Z. Zhang, A. G. Yodh, J. P. Gollub and D. J. Durian, Phys. Rev. Lett., 2010, 105, 175701 CrossRef CAS PubMed.
- A. Ikeda, L. Berthier and P. Sollich, Soft Matter, 2013, 9, 7669–7683 RSC.
- L. R. Gómez, A. M. Turner, M. van Hecke and V. Vitelli, Phys. Rev. Lett., 2012, 108, 058001 CrossRef PubMed.
- M. Otsuki and H. Hayakawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042202 CrossRef PubMed.
- C. Coulais, A. Seguin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 198001 CrossRef CAS PubMed.
- I. Srivastava and T. S. Fisher, Soft Matter, 2017, 13, 3411–3421 RSC.
- G. Combe and J.-N. Roux, Phys. Rev. Lett., 2000, 85, 3628 CrossRef CAS PubMed.
- C. F. Schreck, T. Bertrand, C. S. O'Hern and M. Shattuck, Phys. Rev. Lett., 2011, 107, 078301 CrossRef PubMed.
- M. S. van Deen, J. Simon, Z. Zeravcic, S. Dagois-Bohy, B. P. Tighe and M. van Hecke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 020202 CrossRef PubMed.
- M. S. van Deen, B. P. Tighe and M. van Hecke, Phys. Rev. E, 2016, 94, 062905 CrossRef PubMed.
- E. Lerner, G. Düring and M. Wyart, Soft Matter, 2013, 9, 8252–8263 RSC.
- K. Pham, G. Petekidis, D. Vlassopoulos, S. Egelhaaf, P. Pusey and W. Poon, EPL, 2006, 75, 624 CrossRef CAS.
- N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456–2470 RSC.
- J. Segovia-Gutiérrez, C. Berli and J. De Vicente, J. Rheol., 2012, 56, 1429–1448 CrossRef.
- H. M. Wyss, K. Miyazaki, J. Mattsson, Z. Hu, D. R. Reichman and D. A. Weitz, Phys. Rev. Lett., 2007, 98, 238303 CrossRef PubMed.
- S. S. Datta, D. D. Gerrard, T. S. Rhodes, T. G. Mason and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041404 CrossRef PubMed.
- D. Nakayama, H. Yoshino and F. Zamponi, J. Stat. Mech.: Theory Exp., 2016, 2016, 104001 CrossRef.
- C. P. Goodrich, A. J. Liu and J. P. Sethna, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9745–9750 CrossRef CAS PubMed.
- M. van Hecke, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef CAS PubMed.
- I. Regev, T. Lookman and C. Reichhardt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062401 CrossRef PubMed.
- D. Fiocco, G. Foffi and S. Sastry, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 020301 CrossRef PubMed.
- N. C. Keim and P. E. Arratia, Phys. Rev. Lett., 2014, 112, 028302 CrossRef PubMed.
- I. Regev, J. Weber, C. Reichhardt, K. A. Dahmen and T. Lookman, Nat. Commun., 2015, 6, 8805 CrossRef CAS PubMed.
- N. V. Priezjev, Phys. Rev. E, 2016, 93, 013001 CrossRef PubMed.
- T. Kawasaki and L. Berthier, Phys. Rev. E, 2016, 94, 022615 CrossRef PubMed.
- P. Leishangthem, A. D. Parmar and S. Sastry, Nat. Commun., 2017, 8, 14653 CrossRef PubMed.
- E. D. Knowlton, D. J. Pine and L. Cipelletti, Soft Matter, 2014, 10, 6931–6940 RSC.
- C. P. Goodrich, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2012, 109, 095704 CrossRef PubMed.
- S. Dagois-Bohy, B. P. Tighe, J. Simon, S. Henkes and M. van Hecke, Phys. Rev. Lett., 2012, 109, 095703 CrossRef PubMed.
- C. P. Goodrich, S. Dagois-Bohy, B. P. Tighe, M. van Hecke, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022138 CrossRef PubMed.
- M. Wyart, H. Liang, A. Kabla and L. Mahadevan, Phys. Rev. Lett., 2008, 101, 215501 CrossRef CAS PubMed.
- B. P. Tighe and T. J. H. Vlugt, J. Stat. Mech.: Theory Exp., 2011, P04002 Search PubMed.
- D. Fiocco, G. Foffi and S. Sastry, Phys. Rev. Lett., 2014, 112, 025702 CrossRef PubMed.
- N. C. Keim, J. D. Paulsen and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032306 CrossRef PubMed.
- M. Otsuki and H. Hayakawa, Phys. Rev. E, 2017, 95, 062902 CrossRef PubMed.
- C. P. Goodrich, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022201 CrossRef PubMed.
- C. P. Goodrich, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2014, 112, 049801 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |