Gas bubble dynamics in soft materials†
J. M.
Solano-Altamirano
*,
John D.
Malcolm
and
Saul
Goldman
Dept. of Chemistry, The Guelph-Waterloo Centre for Graduate Work in Chemistry and The Guelph-Waterloo Physics Institute, University of Guelph, Guelph, Ontario N1G 2W1, Canada. E-mail: jmsolanoalt@gmail.com; malcolmj@uoguelph.ca; sgoldman@uoguelph.ca; Fax: +1 5197661499; Tel: +1 5198244120 ext. 53830
First published on 3rd November 2014
Abstract
Epstein and Plesset's seminal work on the rate of gas bubble dissolution and growth in a simple liquid is generalized to render it applicable to a gas bubble embedded in a soft elastic solid. Both the underlying diffusion equation and the expression for the gas bubble pressure were modified to allow for the non-zero shear modulus of the medium. The extension of the diffusion equation results in a trivial shift (by an additive constant) in the value of the diffusion coefficient, and does not change the form of the rate equations. But the use of a generalized Young–Laplace equation for the bubble pressure resulted in significant differences on the dynamics of bubble dissolution and growth, relative to an inviscid liquid medium. Depending on whether the salient parameters (solute concentration, initial bubble radius, surface tension, and shear modulus) lead to bubble growth or dissolution, the effect of allowing for a non-zero shear modulus in the generalized Young–Laplace equation is to speed up the rate of bubble growth, or to reduce the rate of bubble dissolution, respectively. The relation to previous work on visco-elastic materials is discussed, as is the connection of this work to the problem of Decompression Sickness (specifically, “the bends”). Examples of tissues to which our expressions can be applied are provided. Also, a new phenomenon is predicted whereby, for some parameter values, a bubble can be metastable and persist for long times, or it may grow, when embedded in a homogeneous under-saturated soft elastic medium.
1 Introduction
More than sixty years ago, Epstein and Plesset published a seminal article in which they showed how to semi-quantitatively estimate the rate of gas bubble growth or dissolution, for a bubble embedded in a liquid medium containing the dissolved gas of which the bubble is comprised.1 They applied their expressions to air bubbles suspended in water, containing dissolved air. Their rate expressions have been experimentally found to be largely correct, and the precise degree of validity of their model remains the subject of active research.2–4 For small dissolving bubbles, the predictions of Epstein and Plesset's model were found to be within about 9% of the observed values for the surface tension and saturation level dependencies2 when the surrounding medium is a simple liquid.Their work was subsequently applied to a variety of problems that arise in volcanology,5–7 cavitation in liquids8,9 and physiology.10,11 Here we extend Epstein and Plesset's approach to a gas bubble embedded in a soft slightly compressible elastic solid. This extension is required in order to correctly model gas bubble growth and dissolution in soft extravascular tissue in the human body. The latter application arises in the problem of Decompression Sickness, which is of interest to us.11,12
Decompression Sickness arises due to the growth of gas bubbles in blood and tissues, as a consequence of an overly rapid decompression (i.e., drop in external pressure), which may arise from an overly rapid ascent from a scuba dive, or from too rapid a drop in external pressure in aviation or space exploration. Two basic causative mechanisms of Decompression Sickness are currently distinguished, depending on whether the expanding bubbles are in arterial circulation, or whether they are lodged in extravascular tissue.13 The expansion of gas bubbles that get into arterial circulation – Arterial Gas Emboli (AGEs) – is believed to initiate cerebral, spinal, inner ear, and skin Decompression Sickness, while the expansion of extravascular (or “autochthonous”) bubbles is believed to be responsible for joint and musculoskeletal pain (colloquially, “the bends”).13 In an earlier article11 we applied Epstein and Plesset's work to AGEs in relation to their connection to Inner Ear Decompression Sickness. We would like to extend our work to include the dynamics (growth and dissolution) of gas bubbles lodged in soft extravascular tissues. Consequently, we focus here on developing the theoretical tools needed to do this. These bubbles will be considered to be lodged in a medium such as muscle or cartilage, which much more closely resembles a soft elastic solid than it does an inviscid liquid (such as water, which has no shear resistance or intrinsic shape). While Epstein and Plesset's work was essentially directly applicable to AGEs (since arterial blood is a liquid medium much like water), it must be significantly modified before it can be applied to a gas bubble lodged in soft tissue.
Of course, soft matter includes a broad range of material types, whose properties may differ considerably from one another. Since our interest here is in materials such as muscle and cartilage, we will use as their model a soft elastic solid. Soft elastic solids differ profoundly, for example, from viscoelastic fluids such as polymer melts, which we don't consider. Specifically, a soft elastic solid has a non-zero shear resistance and manifests a definite intrinsic shape, but its constituent particles (actually, small cells of its constituent material) are assumed to not undergo re-arrangement, in response to processes occurring within the medium—such as bubble growth or dissolution. A bubble growing or dissolving in a viscoelastic fluid however, will be accompanied by a molecular re-arrangement in the surrounding medium, and this fundamental difference will be reflected in the different equations that describe the respective systems.
We derive generalized rate equations that take into account the influence of a non-zero shear modulus in the medium, under the assumption that the medium has the properties of a soft elastic solid. The non-zero shear resistance manifests itself both on the magnitude of the internal gas bubble pressure and on the diffusion equation used for the medium. We illustrate our expressions by using them to predict the dynamics of growth and dissolution of an embedded gas bubble in a soft material with properties similar to soft tissues in the human body believed implicated in joint and musculoskeletal Decompression Sickness. We also very briefly compare our work with earlier work on gas bubbles in various other types of media, including viscoelastic media.
2 Theory
Epstein and Plesset's rate laws for gas bubble growth and dissolution are obtained from eqn (1)–(3) and (5), given below. Combining eqn (1)–(3) provides the relation between dR/dt and (∂c/∂r)R, and the solution of eqn (5) provides the expression(s) for (∂c/∂r)R.The Young–Laplace equation for the gas pressure inside a bubble embedded in an inviscid liquid (i.e. one without shear forces) is:
 | (1) |
Fick's law for the rate of solute transfer across a spherical interface is given by:
 | (2) |
Henry's law is assumed to apply at all the boundaries of the system:
 | (3) |
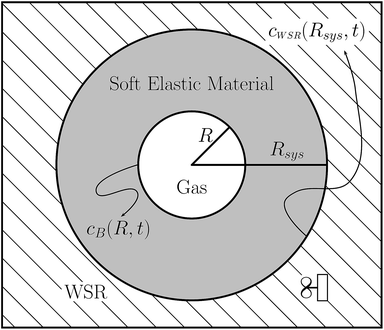
Here R* represents the distance from the center of the system to any of the boundaries (see Fig. 1), c(R*, t) is the dissolved gas concentration at (R*, t) (in units mol l−1), KH the Henry's constant for the gas dissolved in the medium and contained in the bubble, and P(R*, t) is the dissolved gas partial pressure at the boundary whose distance is R* from the system center. KH is an equilibrium constant that is related to the solubility of the gas in the medium.14 It gives the ratio of the gas partial pressure to its concentration in solution at equilibrium.
To derive an expression(s) for (∂c/∂r)R, we start by considering the full diffusion equation for a two-component fluid in the absence of elastic effects:15
 | (4) |
Here ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) is the flux of dissolved material within a differential volume element of the elastic medium, and
is the flux of dissolved material within a differential volume element of the elastic medium, and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) is the velocity of the volume element relative to the bubble. In eqn (4) it is assumed that any change in density stemming from a change of concentration of the dissolved substance can be neglected. The second term on the right of eqn (4) provides the contribution to ∂c/∂t due to any motion of the volume element (e.g. convective motion due to mixing or flow) relative to the bubble.
is the velocity of the volume element relative to the bubble. In eqn (4) it is assumed that any change in density stemming from a change of concentration of the dissolved substance can be neglected. The second term on the right of eqn (4) provides the contribution to ∂c/∂t due to any motion of the volume element (e.g. convective motion due to mixing or flow) relative to the bubble.
In order to derive analytic expressions for the rate of bubble growth/dissolution, Epstein and Plesset made two fundamental assumptions. One was to omit the contribution due to relative motion of the medium i.e., they took ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) in eqn (4) to be zero. The other involved a separation of time scales. This arose through their (tacit) assumption that any perturbation in the system—specifically, the transfer of a small amount of solute across the bubble interface—is followed by an instantaneous re-equilibration of the solute distribution in the entire system—i.e. both in the bubble and in the medium. Thus, eqn (1)–(3) are taken apply at all times. We will here refer to their second approximation as the “quasi-static approximation”, since it approximates the bubble as static (or growing infinitesimally slowly), relative to the very rapid re-distribution rate of the solute within the bubble and the surrounding medium. As mentioned above, the overall error that results from both of these approximations, made simultaneously, is within about 9% for the predicted dissolutions times for small bubbles in an under-saturated medium.2 Bubble growth in slightly super-saturated solutions also appears to be driven mostly by diffusive processes.4 Hence, the quasi-static approximation is in fairly good agreement with experimental observations both for slightly super-saturated and slightly under-saturated solutions. Good reviews that critically analyze the physical conditions under which the approximations made by Epstein and Plesset are viable and/or useful are provided in ref. 6 and 7.
in eqn (4) to be zero. The other involved a separation of time scales. This arose through their (tacit) assumption that any perturbation in the system—specifically, the transfer of a small amount of solute across the bubble interface—is followed by an instantaneous re-equilibration of the solute distribution in the entire system—i.e. both in the bubble and in the medium. Thus, eqn (1)–(3) are taken apply at all times. We will here refer to their second approximation as the “quasi-static approximation”, since it approximates the bubble as static (or growing infinitesimally slowly), relative to the very rapid re-distribution rate of the solute within the bubble and the surrounding medium. As mentioned above, the overall error that results from both of these approximations, made simultaneously, is within about 9% for the predicted dissolutions times for small bubbles in an under-saturated medium.2 Bubble growth in slightly super-saturated solutions also appears to be driven mostly by diffusive processes.4 Hence, the quasi-static approximation is in fairly good agreement with experimental observations both for slightly super-saturated and slightly under-saturated solutions. Good reviews that critically analyze the physical conditions under which the approximations made by Epstein and Plesset are viable and/or useful are provided in ref. 6 and 7.
With these approximations, the full diffusion eqn (4) is reduced to the familiar diffusion equation:
 | (5) |
In this work, we also make both of these assumptions, for the same reasons as in Epstein and Plesset's work. In addition, neglect of the medium's motion is further necessitated by our application of linear elasticity theory, which requires that our system undergoes only coherent deformations. By a “coherent deformation” is meant that the coordinates of the deformed body are isomorphic functions of the coordinates of the un-deformed body.16
In order to allow for the effects of a non-zero shear modulus in the medium we need, in addition to the above approximations, extensions of eqn (1) and (5). The extension of eqn (5) for describing the diffusion of a gas within a solid has been known for some time (see ref. 17 and references therein):
 | (6a) |
| D* = D + Nσ. | (6b) |
In eqn (6), M and N are phenomenological constants characteristic of the medium, σ is the trace of the stress tensor of the medium, and D* is an effective diffusion constant. However, for the isotropic elastic media which are considered here, these equations simplify. Since the trace of the stress tensor in an isotropic medium of arbitrary shape is a constant,18,19 the second term on the right-hand side of eqn (6a) vanishes for isotropic media. The resultant equation is:
 | (7) |
In what follows, we provide the extension of eqn (1), and subsequently use it to derive a generalization of Epstein and Plesset's solution for a soft elastic medium.
We consider a gas bubble embedded in an elastic medium, as illustrated in Fig. 1. This physical model is identical to the one introduced by Epstein and Plesset, except that we here allow for a positive shear resistance in the diffusive medium. The general purpose of the approximate model shown in Fig. 1 is to simplify the problem by physically separating the regions wherein diffusion and convection (or mixing) are presumed to occur. Diffusion alone is presumed to occur in the diffusive region via a concentration gradient within this region. The well-stirred region, which is comprised of the same elastic material as that of the diffusive region, is presumed to be perfectly well-mixed, i.e. it has no solute concentration gradient(s).
The entire system is taken to be in a quasi-static state at all times. Dissolved gas diffuses either toward or away from the bubble due to a solute concentration gradient within the diffusion shell that surrounds the bubble. This gradient stems from the solute concentrations at Rsys and at R being different. The concentration is fixed at the constant value cWSR at Rsys, and it is determined by the bubble pressure PB, and Henry's law, at R. Since PB is a function of R (see eqn (8a), (9), and (10)), and R varies with t, cB will vary as the bubble shrinks or grows. The bubble will dissolve if cB > cWSR, it will grow if cB < cWSR, and it will be stable or meta-stable, and persist for relatively long times (or indefinitely) if cB = cWSR.
2.1 Modification of the diffusion equation to allow for elastic effects
Recently, Goldman generalized the Young–Laplace equation by considering the effect of an elastic body on the internal pressure of a gas bubble embedded within it.20 For a spherical elastic shell containing a spherical embedded gas bubble at its center, the result was found to be given by the system of coupled equations: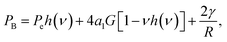 | (8a) |
 | (8b) |
 | (8c) |
| Rsys3 = R3 + (3V(el)in/4π)(1 + 3a2), | (8d) |
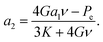 | (8e) |
Here, V(el)in is the initial volume of the elastic shell (i.e. prior to compression by the application of non-zero pressures to its surfaces), G is the shear modulus of the elastic medium, K is its modulus of compression (aka bulk modulus), Pe (as in eqn (1)) is the external pressure applied at the outer radius of the spherical shell, and a1 is a constant related to the volumetric change of the gas in the bubble due to compression. For ideal gases, or real gases at low-to-moderate pressures, a1 = −1/3.20
“a1” which is closely related to the compressibility of the gas bubble through 3a1 = ΔV (bubble)/V0 (bubble),20 plays a very important role here. Specifically, the magnitude of the effect stemming from the shear resistance G of the medium on the bubble's internal pressure is proportional to this term (see eqn (8a), (9), and (10)). It will be shown that the bubble's pressure profoundly effects its rate of growth or dissolution. Therefore a small condensed phase-like compressibility (such as a1 ≈ −(10−4–10−5)), which would apply if the gas bubble were replaced by a liquid bubble, would almost totally eliminate our elastic effect on the dynamics. In fact, the effects found and reported in this work arise almost entirely from the combination of the high compressibility of the bubble, together with the soft elastic properties of the surrounding medium.
For reasons given below we will, in this work, focus on soft elastic materials that are only slightly rigid. Specifically, we will only consider materials for which 0 < G ≪ K. Under these conditions, a2 ≅ 0, δ ≅ 0, h(ν) ≅ 1, and the above system of coupled equations are reduced to a single equation. We find:
| PB = Pe − (4G/3)(1 − ν) + 2γ/R | (9) |
 | (10) |
One can rewrite eqn (9) to define an effective surface tension:
 | (11) |
 | (12) |
Since 2GR(1 − ν)/3 ≥ 0 for all R, we see that the non-zero shear resistance of the elastic medium lowers the effective surface tension acting on the bubble. This holds for either a finite or an infinite elastic medium, but is specific to the type of elastic materials we consider here (i.e. only those which are compressible, and for which K ≫ G).
2.2 Generalization of Epstein and Plesset's solution
Fick's law (eqn (2)) is used in order to obtain the formal growth/dissolution rate expression for a gas bubble embedded in an isotropic elastic medium. Using the Ideal Gas law, we find: | (13) |
Substituting the expression for PB given by eqn (10) into eqn (13), gives
 | (14) |
In the limit G → 0, eqn (14) can be shown to reduce to Epstein and Plesset's rate expressions for γ ≥ 0.
2.3 The (∂c/∂r)R expressions
The working rate equations are obtained by replacing (∂c/∂r)R by the expressions obtained for it from the solution of the diffusion equation. We will consider the expressions for (∂c/∂r)R that arise both from the diffusion equation, and from its steady-state approximation, the Laplace equation.It is perhaps not superfluous to point out the distinction between the “steady-state” and the “quasi-static” approximations, both of which arise in this work. The former entails setting ∂c/∂t = 0 in the diffusion equation, which removes its explicit time-dependence. The time-dependence is then carried implicitly by constants (r-independent parameters) determined from the time-dependent boundary conditions (see eqn (19)). The quasi-static approximation, on the other hand, involves assuming an instantaneous re-equilibration of the solute distribution in the system, following each incremental gas transfer between the bubble, the surrounding medium, and the WSR. The quasi-static approximation is applicable both to the diffusion equation and to its steady-state approximation (the Laplace equation).
By solving the diffusion equation, Epstein and Plesset found:
 | (15) |
 | (16) |
In going from eqn (15) to eqn (16), we used cWSR ≡ fcsat = fPe/KH, where csat is the dissolved solute concentration in the well-stirred region of the medium at equilibrium, and f is the relative solute concentration to its equilibrium value (aka the “supersaturation ratio”) in the well-stirred region.
Epstein and Plesset noticed that the  term varied more rapidly with time than 1/R(t), and they consequently neglected it in order to derive an approximate analytic expression for the time evolution of the bubble radius (their work preceded the computer era so that the numerical procedures that we take for granted were then not an option).
term varied more rapidly with time than 1/R(t), and they consequently neglected it in order to derive an approximate analytic expression for the time evolution of the bubble radius (their work preceded the computer era so that the numerical procedures that we take for granted were then not an option).
An alternate route to these analytic expressions for the concentration gradient is to solve the Laplace equation:
| ∇2c(r, t) = 0 | (17) |
| c(Rsys = ∞) = cWSR; c(R, t) = cB(t). | (18) |
The solution of the Laplace equation under spherical symmetry has the general form
 | (19) |
From eqn (18) and (19), the concentration gradient at the bubble surface, obtained from the solution of the Laplace equation, is readily found to be
| (∂c/∂r)R = (fcsat − cB(t))/R(t). | (20) |
Notice that eqn (16) reduces to eqn (20), after dropping the second term in eqn (16).
3 Integration of the rate equations
The rate equation obtained on combining eqn (14) and (16) involves a numerical instability due to the infinite slope at t = 0. This problem can be eliminated by transforming to t1/2 as the time variable. It is also more convenient to work with the equations in dimensionless form.Therefore we define dimensionless (or reduced) variables for time, and for the bubble radius as:
 | (21) |
In eqn (21)R0 is the initial bubble radius, and to keep the notation simple, the time-dependencies of x2, R, and ρ are not explicitly written but are to be understood.
The semi-regularized dimensionless rate equations are obtained by combining eqn (14) with (16), and (14) with (20). The results are:
 | (22) |
 | (23) |
| α ≡ 4G/(3Pe), β ≡ 2γ/(3R0Pe), | (24a) |
 | (24b) |
Eqn (22) and (23), as written, are not fully regularized since they may become singular as ρ → 0 (the point at which the bubble dissolves). While this is irrelevant with respect to the Laplace-based eqn (23), which can be integrated analytically (below), it does create a problem for dealing with eqn (22), which can only be integrated numerically. Therefore, for this numerical integration we adopted a modified Runge–Kutta integration scheme, wherein the behavior of ρ is monitored at the intermediate steps of the integration procedure. The modification involved stopping the calculation and returning the values ρ = 0 and τ = τd as the intermediate values of ρ and τ, whenever negative ρ values were encountered. The validity of the method was confirmed by checking it against the analytical solution for the Laplace-based equation (below). The method yielded results whose relative errors oscillated around the errors expected for the traditional 4th-order Runge–Kutta integration scheme: O(10−4) − O(10−5).
As indicated above, eqn (23) can be integrated analytically, and the final expression obtained is well-behaved. Using a dimensionless time
 | (25) |
(x2 = τ) the result is:
 | (26) |
The dissolution time τd is found from:
| τd = τ(ρ = 0). | (27) |
4 Results
We first identify some actual materials for which G ≪ K, some of which are relevant to our interest in modeling gas bubble dynamics in soft extravascular tissue. These include solutions of gelatin in water, and a number of soft, largely aqueous tissues in humans and animals. The shear modulus for gelatin solutions can be made to have a variety of different values by adjusting the concentration of the polymeric gelatin solute, the temperature, the pH, and the concentration of any other solutes that may be present.21,22 Partly for this reason, aqueous gelatin solutions have been used extensively to model the influence of shear resistance effects in volcanology,23,24 and in studies related to Decompression Sickness.25In Table 1, we list values for the shear modulus for gelatin solutions under different conditions, and for a variety human and animal soft tissues. This list is by no means exhaustive, but it illustrates the approximate magnitudes of the reported G values, and some materials to which our expressions would be applicable. The entries at the bottom of the table for limb, muscle and cartilage are probably the most relevant to our interest in modelling gas bubbles responsible for joint pain and for musculoskeletal Decompression Sickness.
| Material | G (atm) | Ref. |
|---|---|---|
| Gelatin solution | 0.083–0.434 | 21 |
| Gelatin solution | 0.0002–0.0004 | 22 |
| Gelatin/agar | 0.07 | 26 |
| Neural retina | ∼9.87 × 10−4 | 27 |
| Liver | 0.001–0.003 | 28 |
| Liver (bovine) | 0.10 | 26 |
| Liver | 0.001 | 27 |
| Heart | 0.001 | 27 |
| Fat (porcine) | 0.46 | 26 |
| Breast (turkey) | 0.10 | 26 |
| Limb | 0.01 | 27 |
| Muscle | 0.005–0.010 | 28 |
| Articular cartilage | 0.33–5.26 | 29 |
| Knee cartilage | 2.0–4.0 | 30 |
The large ranges for some of the entries provided in Table 1 reflect different ways in which the shear resistance was measured, the specific tissue used, and the condition (degree of stress and strain) of the sample at the time of measurement.
The bulk modulus of dilute gelatin solutions will be dominated by the bulk modulus of water, which is known to be ∼2.14 × 104 atm, and actual measurements suggest that the shear and bulk moduli of such gelatin solutions differ by three orders of magnitude (Poisson ratio of 0.4996).31 Also, the compressibility modulus of soft tissues is usually several orders of magnitude greater than their shear modulus (see ref. 32 and references therein). Consequently, for both dilute gelatin solutions, and for the soft tissues listed in Table 1, the condition G ≪ K is fully satisfied.
It is well known that some materials such as gelatin, which have solid-like properties at low applied stresses, can behave as liquids if the magnitude of the applied stress exceeds the material's “yield stress”. However, since our main interest is in applications to soft tissues in human body that always have solid-like properties, regardless of the magnitude of the applied stress, the issue of yield stress will here not arise. In other words, we assume that the stresses applied to the material are always smaller than its yield stress.
The parameter values chosen for our calculations were further constrained by two considerations.
First, the requirement that the bubble pressure be non-negative requires that G ≤ 3Pe/4 (see eqn (10)). This requirement stems from the fact that gas bubbles with negative pressures, embedded in a medium with a positive pressure, are unstable on a thermodynamic time scale. Since Pe is here 1 atm, this produces the constraint G ≤ 0.75 atm in this work. This requirement is satisfied by many soft elastic materials, including most of those listed in Table 1, or by any other material for which G ≪ K. For materials which do not satisfy this requirement, but do satisfy our other requirements, and whose bubble pressure is non-negative, the system can be studied by numerically integrating the rate equations, and iteratively solving the system of coupled eqn (8) at each time step.
Second, it is known that as the thickness of the elastic material becomes reduced, the linear response approximation, which we assumed to hold for the relation between the stress and strain tensor components20 loses accuracy.33–35 Quadratic and possibly higher-order terms must then be included.36 Consequently, we will restrict our calculations to a finite-sized bubble surrounded by an infinite elastic shell.
Our results are given graphically in Fig. 2–4, for which the fixed parameter values were: T = 298.15 K, Pe = 1 atm, D* = 2900 μ2 s−1, γ = 0.7 μ atm (70 dynes cm−1), and KH = 1614 l atm mol−1. The values for D*, γ, and KH, correspond to the diffusion constant of air in water (for the purposes of this paper, we ignore the shift in the diffusion constant due to shear resistance, since any effect due to this shift would not change the overall behavior of our system), the surface tension of water, and the reciprocal of the solubility of air in water at 1 atm, respectively. We use these values to illustrate the general form of our solutions for soft elastic materials of the kind shown in Table 1.
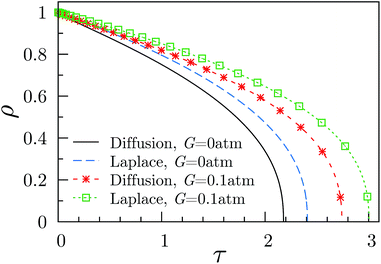 | ||
| Fig. 2 Reduced bubble radius as a function of reduced time for a dissolving bubble. The results are for the diffusion and Laplace equations, for fluids with G ≥ 0. The initial bubble radius was the same (R0 = 10 μ) for all four plots. The plots were obtained using eqn (22) and eqn (26), for the Diffusion and Laplace equations, respectively. The supersaturation ratio “f” was here set equal to 0.75 for all the plots. | ||
For purposes of checking and benchmarking, additional numerical values of dissolving times are provided in greater detail in tables, in the separate section “ESI†”.37
4.1 The effects on bubble growth or dissolution of shear modulus, surface tension, initial bubble radius, and external solute concentration
In Fig. 2 we show the radius vs. time dissolution plots obtained by using either the diffusion or the Laplace equations, and the effect of a non-zero value of the shear modulus, with both equations. Clearly, using the diffusion equation, as opposed to its steady-state approximation (the Laplace equation) produces a more rapid dissolution, for a given G. This is readily understood from eqn (16) and (20), from which it is seen that the steady-state approximation, by omitting the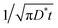 term, results (at all times, and particularly short times) in an insufficiently negative value of the surface gradient term (∂c/∂r)R. The latter controls the dissolution rate through eqn (13) and (14).
term, results (at all times, and particularly short times) in an insufficiently negative value of the surface gradient term (∂c/∂r)R. The latter controls the dissolution rate through eqn (13) and (14).
It is also evident from Fig. 2, that a non-zero shear modulus reduces the rate of dissolution (for either equation), and this is also easily understood. From eqn (3) and (10), cB (G > 0) < cB (G = 0), so that for a dissolving bubble, for which (∂c/∂r)R < 0, (∂c/∂r)R for G > 0, is less negative than (∂c/∂r)R for G = 0. Consequently (from eqn (14)), dR/dt is less negative for G > 0, so that we get a slower dissolution rate for G > 0, and this remains true whether one is using the Laplace equation or the diffusion equation.
In Fig. 3 we illustrate the effect of the variables (f, G, R0) on bubble growth and dissolution. The surface shown was obtained by setting the numerator in either eqn (22) or (23) to zero, setting ρ = 1, and solving the resultant equation for (f, G, R0). A bubble will grow or shrink depending on the sign of (f − 1) + α − 3β. As shown (and as expected), bubble dissolution is favored by a small initial radius, a small G, and a small f, while bubble growth is favored by a large initial radius, a large G, and a large f.
In Fig. 4 we show that a bubble whose elastic diffusion shell is embedded in an under-saturated medium will grow, if the shear modulus of the medium is sufficiently large. The exact value of G for which the transition from dissolution to growth occurs is given by the solution of (f − 1) + α − 3β = 0. For the parameters used in Fig. 4, this occurs at G = 0.2925 atm. For this value of G, f = 0.75, and the other parameter values given previously, a 10 μ bubble will be metastable, and may persist at that radius for a significant period of time (Fig. 4, black solid line). To the best of our knowledge, this is the first time that such behavior—bubble growth or meta-stability in an under-saturated medium—has been theoretically proposed for bubbles surrounded by a homogeneous diffusive medium. Stable bubbles in under-saturated media have been experimentally observed at the liquid–solid interface of some systems (see for example ref. 38). However, to the best or our knowledge, the meta-stability of bubbles in a homogeneous diffusive medium, which is under-saturated with respect to the dissolved gas in the bubble, has not been theoretically proposed elsewhere. The physical basis for this unusual behavior is the negative effect on the gas bubble pressure that arises for the parameter values: 0 < G < 3Pe/4; Pe ≈ O (1 atm) (see eqn (10), and ref. 20).
 | ||
| Fig. 4 The effect of the shear modulus on the evolution of a 10 μ bubble embedded in an under-saturated medium (f = 0.75). The plots were obtained from eqn (22). They can be taken to represent the form of the predicted dynamics of a bubble embedded in gelatin solutions, and/or in most of the soft tissues listed in Table 1. | ||
It is worth noting that the growth illustrated in Fig. 4 is strictly valid only for short times and for a bubble embedded in an infinite elastic medium. For real physical systems and long times, the results we show are approximate limiting values, and the dynamics will deviate somewhat from what is shown here. This is because in a real system, the elastic medium is not infinite, and after the bubble has grown sufficiently, non-linear effects will start to make themselves manifest.
Some further comments regarding actual bubble dissolution within a real physical system, and how it relates to our treatment are worthwhile. If the initial bubble radius were large enough, the elastic medium may experience wrinkling and/or crumbling in the final stages of the dissolution process, which we didn't consider. Thus, the validity of our treatment is limited to small bubbles (a few tens of microns), or alternately, to large bubbles constrained to dissolve by a few tens of microns. Under these constraints our neglect of wrinkling and crumbling instabilities39 is justified.
Also, it should be borne in mind that our initial state, by definition, had a pre-existing bubble lodged in the un-deformed medium, and its evolution is carried out starting from this un-deformed state. Therefore, the initial size of the bubble is not the main constraint; rather it is the difference between the initial and final size of the bubble, ΔR = R(tf) − R(t0), which is constrained to be of a few tens of microns.
4.2 Approximate asymptotic growth law for large bubbles
For bubbles sufficiently large so that the surface tension term can be neglected, β can be approximated by zero in eqn (23), so that the bubble's radius grows or shrinks, approximately, according to: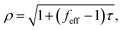 | (28) |
| feff = f/(1 − α). | (29) |
From eqn (28), we see that the sign of (feff − 1) determines whether a large bubble in an elastic medium contracts or expands. It will expand if this function is positive; otherwise, it will contract. Also, it is seen from these equations, that the shear resistance in the elastic medium can be thought of as increasing the value of the effective dissolved solute concentration in the well-stirred region from fcsat to feff·csat.
5 Relation to previous work on visco-elastic materials
There exists a body of previous work on the elastic effects of a medium on the dynamics of an embedded gas bubble, but significant differences exist on exactly what was meant by the term “elastic effects”. A particular focus in the past was the dynamics of a bubble in a foam. These studies on foams also differed from one another, depending on the nature of the elastic shell surrounding the bubble;40–42 or by requiring the medium to be an infinite viscous liquid,42,43 or an elastic-plastic material.44 Furthermore, in some cases, the mathematical form of the growth law for the bubble was imposed as an a priori assumption.40 Also, in some of the previous work it was assumed that the bubble pressure is affected by an ad-hoc polynomial term,45 or by postulated phenomenological rules.44In this work we used a functional form for the bubble pressure which arises entirely from the general theory of elasticity, in the limit of the linear response regime.19 In addition, all the previous work of which we are aware has ignored the effect of the medium's compression on the diffusion of the dissolved gas within it. We formally included this effect by using Aifantis' fundamental diffusion equation for elastic solids.17
Despite our somewhat more fundamental approach, and significant differences in the nature of the elastic materials considered, it is noteworthy that we obtained qualitatively similar results for the effect of elasticity of the medium on the bubble dynamics—for example, a reduction of the bubble's dissolution rate—as was reported in some of the earlier work (e.g., compare Fig. 2 (above), with ref. 42).
6 Summary
By extending the diffusion equation to allow for elastic effects, and using a recently derived generalized Young–Laplace equation to account for the effect of shear resistance on the pressure in an embedded gas bubble, we derived a generalization for the bubble's growth/dissolution rate equations that is applicable to gas bubbles embedded in soft elastic materials with properties resembling those of many soft tissues in the body. It was shown that if the shear modulus is sufficiently large (but less than 3Pe/4, for Pe ≈ O (1 atm)), a gas bubble may be meta-stable and remain at a constant size for some time, or it may grow, in a medium that is under-saturated with respect to the dissolved gaseous solute. To the best of our knowledge, this is the first report of the possibility of gas bubble meta-stability or growth in a homogeneous under-saturated medium. Also, this indicates that gas bubbles in extravascular soft tissue in the body arising from decompression will tend to persist for longer times than they would if they were suspended in a simple (non-elastic) liquid containing the same dissolved gas partial pressure. This has implications for the duration of symptoms of “the bends”.Acknowledgements
We are grateful to the Natural Sciences and Engineering Research Council of Canada (NSERC) for financial support in the form of a Discovery Grant (6831-2011) to one of us (SG). We also thank Simon Mitchell for his very helpful comments on arterial vs. extra-vascular forms of Decompression Sickness, and the anonymous reviewers of this article whose insightful comments improved it.References
- P. Epstein and M. Plesset, J. Chem. Phys., 1950, 18, 1505–1509 CrossRef CAS.
- P. B. Duncan and D. Needham, Langmuir, 2004, 20, 2567–2578 CrossRef CAS PubMed.
- P. B. Duncan and D. Needham, Langmuir, 2006, 22, 4190–4197 CrossRef CAS PubMed.
- O. R. Enríquez, C. Hummelink, G. W. Bruggert, D. Lohse, A. Prosperetti, D. van der Meer and C. Sun, Rev. Sci. Instrum., 2013, 84, 065111 CrossRef PubMed.
- E. B. Watson, M. A. Sneeringer and A. Ross, Earth Planet. Sci. Lett., 1982, 61, 346–358 CrossRef CAS.
- A. E. Kuchma, G. Y. Gor and F. M. Kuni, Colloid J., 2009, 71, 520–528 CrossRef CAS.
- G. Y. Gor and A. E. Kuchma, J. Chem. Phys., 2009, 131, 034507 CrossRef PubMed.
- M. S. Plesset and A. Prosperetti, Annu. Rev. Fluid Mech., 1977, 9, 145–185 CrossRef CAS.
- E. A. Neppiras, Phys. Rep., 1980, 61, 159–251 CrossRef.
- R. S. Srinivasan, W. A. Gerth and M. R. Powell, J. Appl. Physiol., 1999, 86, 732–741 CAS.
- J. M. Solano-Altamirano and S. Goldman, Math. Biosci., 2014, 252, 27–35 CrossRef CAS PubMed.
- S. Goldman, J. Appl. Physiol., 2007, 103, 484–493 CrossRef PubMed.
- T. J. R. Francis and S. J. Mitchell, Bennett and Elliot's Physiology and Medicine of Diving, Saunders, 5th edn, 2003, ch. 10.4, pp. 530–556 Search PubMed.
- J. Hildebrand and R. Scott, The solubility of nonelectrolytes, Dover, 3rd edn, 1964 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Course of theoretical physics: fluid mechanics, Pergamon Press, 1959 Search PubMed.
- I. S. Sokolnikov, Mathematical theory of elasticity, McGraw-Hill Book Company Inc., 1956 Search PubMed.
- E. C. Aifantis and W. W. Gerberich, Acta Mech., 1978, 29, 169–184 CrossRef.
- S. Timoshenko and J. N. Goodier, Theory of Elasticity, McGraw-Hill, 1951 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Course of theoretical physics: elasticity theory, Pergamon Press, 3rd edn, 1989 Search PubMed.
- S. Goldman, J. Chem. Phys., 2009, 131, 184502 CrossRef PubMed.
- K. te Nijenhuis, in Thermo-reversible networks: viscoelastic properties and structure of gels, Adv. Polym. Sci., 1997, vol. 130, ch. 10 Search PubMed.
- S. Hui Hsu and A. M. Jamieson, Polymer, 1993, 34, 2602 CrossRef.
- E. D. Giuseppe, F. Funiciello, F. Corbi, G. Ranalli and G. Mojoli, Tectonophysics, 2009, 473, 391–403 CrossRef.
- J. L. Kavanagh, T. Menand and K. A. Daniels, Tectonophysics, 2013, 582, 101–111 CrossRef CAS.
- D. Yount, in Mechanisms and Physics of Bubbles in Liquids, ed. L. V. Wijngaarden and Martinus Nijhoff, 1982, ch. Bubble nucleation in aqueous media: implications for diving physiology, pp. 37–44 Search PubMed.
- T. Glozman and H. Azhari, J. Ultrasound Med., 2010, 29, 387–398 Search PubMed.
- G. Forgacs, R. A. Foty, Y. Shafrir and M. S. Steinberg, Biophys. J., 1998, 74, 2227–2234 CrossRef CAS PubMed.
- E. Chen, J. Novakofski, W. K. Jenkins and J. W. D. O'Brien, IEEE Trans. Ultrason. Ferroelectrics Freq. Contr., 1996, 43, 191–194 CrossRef.
- J. Töyräs, T. Lyyra-Laitinen, M. Niinimäki, R. Lindgren, M. T. Nieminen, I. Kiviranta and J. S. Jurvelin, J. Biomech., 2001, 34, 251–256 CrossRef.
- B. L. Wong, W. C. Bae, J. Chun, K. R. Gratz, M. Lotz and R. L. Sah, Arthritis Rheum., 2008, 58, 2065–2074 CrossRef PubMed.
- J. C. L'Esperance, B. P. Boudreau, M. A. Barry and B. D. Johnson, Geo-Mar. Lett., 2013, 33, 75–81 CrossRef.
- A. P. Sarvazyan, O. V. Rudenko, S. D. Swanson, J. B. Fowlkes and S. Y. Emelianov, Ultrasound Interact. Biol. Med., 1998, 24, 1419–1435 CrossRef CAS.
- J. J. Stoker, Nonlinear elasticity, Gordon and Breach, 1968 Search PubMed.
- R. W. Ogden, Non-linear elastic deformations, Dover Publications, 1997 Search PubMed.
- Nonlinear elasticity: theory and applications, ed. Y. B. Fu and W. Ogden, Cambridge University Press, 2001 Search PubMed.
- J. E. Adkins, Philos. Trans. R. Soc., A, 1964, 256, 301–316 CrossRef.
- See ESI† for additional dissolving time values.
- J. R. T. Seddon and D. Lohse, J. Phys.: Condens. Matter, 2011, 23, 133001 CrossRef PubMed.
- H. King, R. D. Schroll, B. Davidovitch and N. Menon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9716–9720 CrossRef CAS PubMed.
- E. Ruckenstein and E. J. Davis, J. Colloid Interface Sci., 1970, 34, 142–158 CrossRef CAS.
- M. M. Fyrillas, W. Kloek, T. van Vliet and J. Mellema, Langmuir, 2000, 16, 1014–1019 CrossRef CAS.
- W. Kloek, T. van Vliet and M. Meinders, J. Colloid Interface Sci., 2001, 237, 158–166 CrossRef CAS PubMed.
- J. R. Street, Trans. Soc. Rheol., 1968, 12, 103–131 CrossRef.
- T. D. Kunkle, Med. Phys., 1982, 10, 184–190 CrossRef.
- G. Terrones and P. A. Gauglitz, Q. J. Mech. Appl. Math., 2003, 56, 513–525 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm02037e |
| This journal is © The Royal Society of Chemistry 2015 |