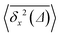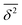Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of polymer looping with macromolecular crowding: effects of volume fraction and crowder size†
Jaeoh
Shin
a,
Andrey G.
Cherstvy
a and
Ralf
Metzler
 *ab
*ab
aInstitute for Physics & Astronomy, University of Potsdam, D-14476 Potsdam-Golm, Germany. E-mail: rmetzler@uni-potsdam.de
bDepartment of Physics, Tampere University of Technology, FI-33101 Tampere, Finland
First published on 20th October 2014
Abstract
The looping of polymers such as DNA is a fundamental process in the molecular biology of living cells, whose interior is characterised by a high degree of molecular crowding. We here investigate in detail the looping dynamics of flexible polymer chains in the presence of different degrees of crowding. From the analysis of the looping–unlooping rates and the looping probabilities of the chain ends we show that the presence of small crowders typically slows down the chain dynamics but larger crowders may in fact facilitate the looping. We rationalise these non-trivial and often counterintuitive effects of the crowder size on the looping kinetics in terms of an effective solution viscosity and standard excluded volume. It is shown that for small crowders the effect of an increased viscosity dominates, while for big crowders we argue that confinement effects (caging) prevail. The tradeoff between both trends can thus result in the impediment or facilitation of polymer looping, depending on the crowder size. We also examine how the crowding volume fraction, chain length, and the attraction strength of the contact groups of the polymer chain affect the looping kinetics and hairpin formation dynamics. Our results are relevant for DNA looping in the absence and presence of protein mediation, DNA hairpin formation, RNA folding, and the folding of polypeptide chains under biologically relevant high-crowding conditions.
I. Introduction
Molecular reactions in living biological cells are running off in a highly complex environment, that is compartmentalised by membrane structures and crowded with macromolecules and structural cytoskeletal networks. Macromolecular crowding (MMC) makes up a “superdense”1 environment modulating the kinetics of various biochemical processes in cells. Inter alia, this mechanism is employed biologically to tune the DNA accessibility in the cyto- and nucleoplasm. MMC non-trivially influences the levels of gene expression, and the size of the crowders dramatically modifies the response of genetic elements.2 In particular, it was found that in solutions of small crowders the rate of gene expression only varies slightly with the volume fraction ϕ of the crowders, while large crowders boost the expression levels many-fold.2More specifically, MMC constitutes a non-specific environment controlling the looping properties of biopolymers such as nucleic acids and polypeptides. Polymer looping is indeed a ubiquitous mechanism of DNA protection, compaction, and gene regulation in both bacteria and higher organisms.3 DNA looping is vital for the regulation of transcription and effects the robustness of bio-switches.4 The effects of MMC on kinetics of DNA looping are of paramount importance for the speed, efficiency, and precision of gene regulatory networks.2,5,6 Inspired by the impressive body of experimental evidence for the relevance of MMC on biochemical processes, we here scrutinise the key role of the crowder size for the kinetics and thermodynamics of polymer looping.
The quantitative study of the diffusion-limited encounter of the end monomers of a polymer chain in a mixture of crowders of varying sizes and the analysis of the effective viscosity of the solution are formidable theoretical problems. Despite the progress of the understanding of polymer looping and cyclisation under dilute solvent conditions by theoretical approaches7–10 and by simulations,11–17 polymer looping in the presence of MMC18–20 still poses a number of challenges, which are our main targets here.
It is known that MMC generally facilitates the association of proteins via volume exclusion effects and favours more compact states.21 Polymer looping, however, involves the diffusion of an extended and chain length-dependent fragment of the polymer in crowded solutions. This non-locality effect renders the trends of the inhibition or facilitation of polymer looping kinetics in the presence of MMC less intuitive. Looping is a fundamental dynamic property of polymers which can be directly probed by methods such as fluorescence energy transfer.22 A comprehensive theory of polymer looping under crowded conditions is not straightforward. We here employ extensive crowder-explicit simulations of polymer looping including a number of important physical and biochemical ingredients.
Polymer organisation in the presence of MMC and spatial confinement is a common theme in biophysics.23 It affects, for instance, the segregation of DNA rings in dividing bacteria cells24,25 as well as the territorial organisation of DNA inside eukaryotic nuclei26 and bacteria.27 Of particular interest is polymer looping and knotting in MMC-dominated solvents.28–30 The highly crowded environments of real biological cells feature volume occupancies of up to ϕ ∼ 30%.31,32In vitro, concentrated solutions of naturally occurring proteins, globular and branched polymers (lysozyme, serum albumin, PEG, dextran, Ficoll, etc.) mimic MMC conditions in a more controlled environment.33,34 On top of MMC volume exclusion, the eukaryotic cytoskeleton forms a spatial mesh with a period of several tens of nm affecting the diffusion of cellular components.
Excluded-volume interactions by crowders favour molecular association reactions,35 speed up the folding of proteins into their native structures,36–40 and facilitate the assembly of virus capsids.41 The effects of the crowder size were studied for polypeptide folding42 and protein fibrillisation.35 We note that apart from MMC in the cytosol of biological cells, crowding is also an important ingredient for the diffusional dynamics of embedded proteins and lipid molecules in biological membranes.43–45 Also note that the thermodynamics and the demixing transitions in the mixtures of colloidal particles and linear polymers have been explored,47 in particular in the limit of long polymers (the so-called “protein limit”).46
The biological relevance for the study of polymer looping is due to its central role in gene regulation, for instance, in the formation of DNA loops induced by transcription factor proteins such as Lac or λ repressor.48–50 The inter-segmental protein jumps along DNA made possible via looping facilitates protein diffusion in DNA coils51,52 and affects MMC-mediated gene regulation.2,5,53,54 Another example is the dynamics of the DNA chain itself on various levels of DNA structural organisation ranging from bare DNA, via chromatin fibres, to complex chromosomal filaments.3,55 We also mention protein-56 and RNA-folding57 reactions.
Experimentally, the effects of polymeric crowders on the opening–closing dynamics of ssDNA hairpins with complementary sticky ends58,59 were studied in detail.60 It was demonstrated in ref. 60 that ssDNA hairpin formation dynamics is dramatically slowed down in highly crowded solutions of dextran and PEG of varying molecular weights (MWs), MW ∼ 0.2–10 kDa. Also, the fraction of open hairpins gets reduced substantially by relatively large crowders, in contrast to low-MW solutions of sucrose. In the latter, the similarly slowed-down DNA hairpin dynamics due to a higher viscosity of the medium, the fraction of hairpins remained nearly constant with crowding. Note that the experimental setup of ref. 60 only allowed the measurement of the geometric average of looping–unlooping times τK. A separate measurement of looping Tl and unlooping Tul times of the cohesive chain ends as a function of MMC fraction ϕ was not feasible. The fraction of time the hairpins are in a looped state was also measured.60
Some effects of MMC on polymer looping were analysed recently.11,19 For instance, for implicit attractive depletion potentials between polymer segments (mimicking MMC) the polymer looping (Tl) and unlooping (Tul) times (see below) for ϕ = 0.15 and fixed size of crowders were quantified by simulations.11 For long chains, the increase of the looping time Tl obeys the scaling relation
| Tl(n) ∼ n2ν+1 ∼ n2.2 | (1) |
In contrast, the unlooping time Tul exhibits only a weak dependence on the chain length.11 A finite cohesive energy of polymer ends, εs > 0, gives rise to more extended “looped” periods and longer unlooping times.11 The looping time, the time separating the extended and looped states of the chain, becomes shorter due to “depletion-based crowding” for longer chains, i.e., more compact polymer states are favoured, effecting a slow-down of the unlooping dynamics.11
We here report results from extensive Langevin dynamics simulations of the looping of Rouse-like flexible polymers in solutions of explicit nearly hard-sphere crowders (see Fig. 1). We examine the effects of the crowding volume fraction ϕ, the crowder diameter dcr, the stickiness εs of the end monomers, and the chain length nσ, where σ is the monomer diameter. We showed recently25 that for two polymer rings under confinement and crowding conditions the contact properties have been non-monotonic in the crowding fraction ϕ. Here, we demonstrate that MMC has unexpected effects on the looping dynamics as well, due to the competition between depletion effects facilitating looping and an increased effective solution viscosity slowing down the looping kinetics, see Fig. 1 and 2.
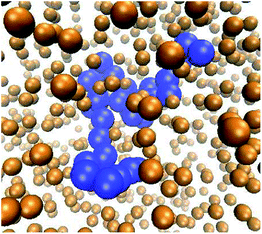 | ||
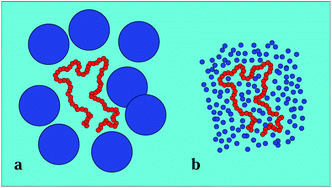
| Fig. 1 Typical polymer conformation in the presence of MMC. The polymer chain (blue spheres) consists of n = 32 monomers, the fraction of crowders (golden spheres, rendered smaller for better visibility of the polymer) is ϕ = 0.1, and the size of the crowders is dcr = 1σ in terms of the monomer diameter σ of the polymer chain. Video-files illustrating the looping dynamics of polymer chains for small and big crowders are included in the ESI.† | ||
II. Model and methods
To study polymer–nanoparticle mixtures by computer simulations, Monte-Carlo and molecular dynamics investigations were conducted in the literature to elucidate the static and dynamical behaviour of binary mixtures of polymers and crowders. Important ingredients were included in simulations to render the results applicable to realistic situations, for instance, in cells. Thus, the effects of compressible polymers,61 non-spherical62 and charged crowding nanoparticles63,64 on polymer–crowder demixing as well as the implications of confinement65,66 and viscoelastic effects68 on polymer looping kinetics were studied.Computer simulations11 revealed e.g. that the unlooping time Tul remains nearly constant with chain length n and increases 3–4 times as the crowding fraction grows from ϕ = 0 to 0.15. Note that because of the limited applicability of the effective depletion potentials used, only moderate ϕ values were studied in ref. 11. The unlooping time Tul is defined in our study as the time required for the chain to expand from the close-end to the equilibrium state, somewhat different from the definition used in ref. 11, see Fig. 3.
A. Potentials and approximations
Performing Langevin dynamics simulations of flexible polymers, we here examine the looping probabilities of the chain ends in the presence of MMC. The polymer chain is modelled within the bead-spring model with finitely extensible nonlinear elastic (FENE) potentials,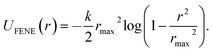 | (2) |
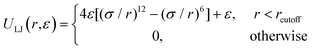 | (3) |
The chain monomer diameter is set in simulations to σ = 4 nm, determining the polymer thickness and its effective viscosity in the crowded solution, η. The diameter dcr of mono-disperse hard-core repulsive crowding particles varies in simulations in the range 0.75 ≤ dcr ≤ 8σ. The mass density is kept constant for all crowder sizes, fixed to the value known for average cytoplasm-crowding macromolecules.18 Thus, for the varying crowder sizes its mass grows as mcr ∼ dcr3 and the friction coefficient increases according to the “effective” Stokes–Einstein law as ξcr ∼ dcr, similar to the procedure of ref. 76. We use a cubic simulation box with volume V = L3 and periodic boundary conditions. The volume fraction of crowders is ϕ = NcrVcr/V, where Ncr is the number of crowders and 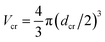 the volume of each crowding particle. The characteristic time scale for a crowder with dcr = 1σ and mcr = 67.7 kDa (ref. 18) is
the volume of each crowding particle. The characteristic time scale for a crowder with dcr = 1σ and mcr = 67.7 kDa (ref. 18) is 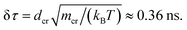 The times presented in the figures below are in the units of this elementary time step δτ. The features of the crowder size we observe with this explicit simulation scheme would not be visible in more coarse-grained models of crowded media employed previously, including those with effective depletion potentials.
The times presented in the figures below are in the units of this elementary time step δτ. The features of the crowder size we observe with this explicit simulation scheme would not be visible in more coarse-grained models of crowded media employed previously, including those with effective depletion potentials.
The dynamics of the position ri(t) of the chain monomers is described by the Langevin equation
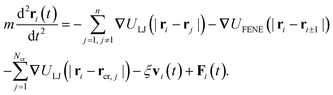 | (4) |
The terminal monomers interact with the energy εs which mimics e.g. the energetic profit for the formation of closed ssDNA hairpin structures via hydrogen-bonding pairing interactions between the complementary bases on the end DNA fragments. Although we simulate flexible polymers, via corresponding rescaling of the effective monomer size, the results can be applicable to looping of semi-flexible dsDNA as well, where the loop/ring joining reaction is often supported by ligation enzymes.70,71 The number of the chain monomers n in the simulations varies in the range 10 ≤ n ≤ 256. The pairing energy of εs = 5kBT used in the majority of results below can be considered as a good estimate for the pairing propensity in DNA hairpins with not too long complementary ends, see ref. 60. We examine the range of chain end cohesiveness of 0 ≤ εs ≤ 10kBT.
We simulate the attractive end-to-end interactions via the same LJ potential, eqn (3), but with a larger cutoff distance and bond intensity εs, namely Uattr(r) = ULJ(r, εs) + CLJ and rcutoff = 3σ. Along with this longer cutoff distance we shift the entire LJ potential in the vertical direction by the constant CLJ so that at r = rcutoff the potential becomes continuous with the zero-value branch at r > rcutoff. The volume fraction of mono-disperse crowders is varied in our simulations up to ϕ = 0.3; see ref. 72 for even denser colloidal systems.
The free energy of ssDNA hairpin formation contains two contributions: the favourable pairing of the helical dsDNA part and the entropic penalty of the looped part. The sum of the two for real DNAs is a complicated function of the DNA sequence and other model parameters73,75 amounting to ∼−2.1 kcal mol−1 ≈−3.5kBT for about 20 bp long DNA hairpins used in ref. 60. Longer complementary paired stem parts result in more stable hairpins, which we mimic in simulations via larger values of end-to-end cohesive energy εs.
We neglect long-range interactions between polymer segments, including electrostatic forces, that is a reasonable approximation for long chains at physiological salt concentrations. In low-salt solutions, however, in application to DNA, the charge–charge interactions will become important for the loop-closure probability and dynamics.77 We assume that polymer–solvent interactions remain unaltered at increasing volume occupancies by crowders (see ref. 78 for possible effects of MMC on the properties of nucleic acid solutions at reduced solvent activity).
Hydrodynamic interactions are also neglected below (i.e., we use the Rouse polymer model), see ref. 79–81 for some implications. The effects of hydrodynamic interactions on end-monomers dynamics of dsDNA have been studied by fluorescence correlation spectroscopy experimentally in ref. 82 and 83. Theoretically, the Rouse versus Zimm chain dynamics has been examined for semi-flexible polymers in solutions,84,85 confined spaces,86 and near surfaces.87 In the latter situation e.g. it was clearly demonstrated, based on hydrodynamic Brownian simulations and mean-field hydrodynamic theory, how the Zimm dynamics turns into the Rouse one as the polymer chain approaches the no-slip surface.87 In particular, for the end-to-end distance of the chain near the interface, the influence of hydrodynamic interactions screened as ∝1/r with the inter-particle distance was shown to be marginal.‡
B. Parameters and data analysis
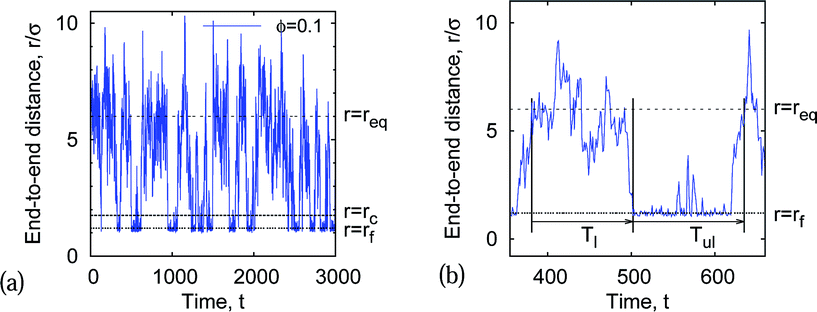
We compute the end-joining statistics from the time series of the polymer end-to-end distance generated in simulations as follows. For looping, we start with the most probable end-to-end chain extension (the minimum of the free energy F(r), see eqn (5) and Fig. 4, r = req) and let the chain ends diffuse to the final extension r = rf ≈ 1.2σ. (The contact distance between the terminal chain beads in the folded state implemented in ref. 11 was somewhat different, rf = σ + dcr.) The looped state distance rf corresponds to the minimum of the LJ potential in eqn (3) and remains nearly constant in the whole range of model parameters used here.The time required for the chain to join its ends is defined as the looping time Tl, see Fig. 3. The unlooping time Tul is defined as the time required for the chain to expand back, from the jointed-ends state with r = rf to the equilibrium state at r = req. This distance is a function of all model parameters, in particular of the chain length l = nσ and the MMC fraction, that is accounted for in simulations below. The closing time Tcl is defined as the average time the polymer needs to diffuse from the last moment its end-to-end extension was r = req to the first moment with the close-contact distance of r ≈ rf. The opening time Top is the minimal time for the chain ends to diffuse from the closed state r = rf to the first state with r = req. In Fig. 3 we illustrate on a real end-to-end diffusion trace the definitions of the looping/unlooping and opening/closing times.
Likewise, the critical distance of rc = 1.75σ used below to define the occurrence of end-monomer contacts remains nearly constant. It approximately denotes the end-monomer separation at which the free energy barrier emerges which separates the close-looped and equilibrium states of the polymer, see Fig. 4. This critical distance rc is used below to compute the looping probability Pl. One can think of other choices for rc to mimic somewhat longer-ranged nature of end–end contacts.§
We study the end-to-end joining statistics; the implications of MMC on looping kinetics of inner polymer monomers is beyond the scope of this study and will be presented elsewhere. The simulation time for the chains of n = 8, 32, and 128 monomers on a standard 3–3.5 GHz core machine is about 3, 4, and 60 h, respectively. The typical number of the looping events used for an averaging procedure for these chain lengths is about 2000, 500, and 200, correspondingly. In some cases we use traces, that are twice as long, for a better statistics. The number of crowding molecules of size dcr = 1σ in the simulation box used to perform simulations of the polymer chains of these lengths is Ncr ≈ 1000, 3000, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively. Moreover, we remark that instead of averaging over the ensemble of initial chain configurations, we rather analyse the individual simulated time traces of the end-to-end distance r(t) to compute the chain looping characteristics.
000, respectively. Moreover, we remark that instead of averaging over the ensemble of initial chain configurations, we rather analyse the individual simulated time traces of the end-to-end distance r(t) to compute the chain looping characteristics.
We analysed the r(t) data obtained from either single or multiple simulation runs, depending on the total computation time used. The typical running time, t ∼ 105…7 × δτ, is chosen much longer than all the time scales in the system, in order to avoid a bias in sampling of end-joining events. To perform the error analysis, we use different methods for the dynamic and static quantities. As looping events are rare, the time intervals between them are of the order of the chain relaxation time, and the events can be considered independent. Thus, we use the standard error of the mean to compute the error bars for the looping (unlooping) and opening (closing) times. For the static quantities, such as the radius of gyration of the polymer, we split the entire trajectory into ten sub-series, calculate the values for each of them, and then compute the standard deviations of those pre-averaged values to get the final error bar. Previously25 we also used the so-called “blocking method” for the error analysis in correlated sets of data. Here we compare the two methods for a number of quantities and the differences in the sizes of the error bar were ≲30%.
We need to distinguish the MMC effects for small (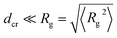 ) and large crowders (dcr ≳ Rg) as compared to the polymer’s radius of gyration. Large crowders creates voids/cages between themselves which facilitate compaction of relatively short polymers and facilitate looping. The reader is referred to Section III G for the quantitative analysis of caging effects in our polymer–crowder mixtures. For longer chains, which do not fit into a single cavity and need to occupy the neighbouring voids, the effect of crowders on looping probability can be inverted. A similar effect occurs in MMC-mediated protein folding, when small crowders favour the compact state of a protein, while larger ones can promote protein unfolding.88 The systematic investigation of crowder surface properties is the subject of our future investigation.89
) and large crowders (dcr ≳ Rg) as compared to the polymer’s radius of gyration. Large crowders creates voids/cages between themselves which facilitate compaction of relatively short polymers and facilitate looping. The reader is referred to Section III G for the quantitative analysis of caging effects in our polymer–crowder mixtures. For longer chains, which do not fit into a single cavity and need to occupy the neighbouring voids, the effect of crowders on looping probability can be inverted. A similar effect occurs in MMC-mediated protein folding, when small crowders favour the compact state of a protein, while larger ones can promote protein unfolding.88 The systematic investigation of crowder surface properties is the subject of our future investigation.89
III. Results: crowding and polymer dynamics
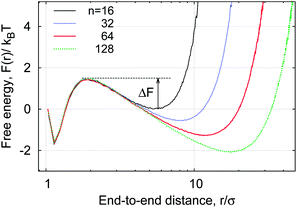
The equilibrium statistical behaviour of a linear flexible polymers with sticky ends is governed by the tradeoff between the enthalpically favourable pairing of the sticky ends and the entropy loss in the more compact looped state. In what follows we first rationalise the effects of MMC on the static properties of polymer looping. We then examine the kinetics of loop closure and opening as functions of the details of the crowders such as the crowding fraction and crowder size.A. Distribution function p(r) and free energy
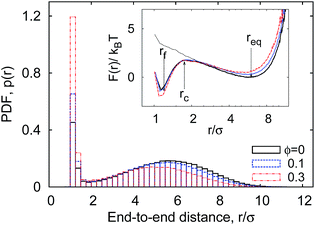
Our simulations generate time traces of the end-to-end distance r(t) between the two extremities of the linear polymer. These two end monomers interact through an attractive LJ potential with cohesiveness εs which is varied in the range 0 ≤ εs ≤ 10kBT, see the specification of the system in the preceding section. The recorded dynamics for r(t) exhibits the highly erratic dynamics shown in Fig. 3. We first focus on the one-dimensional probability density function (PDF) p(r) of the end-to-end distance, as shown in Fig. 4.The relative motion of terminal monomers is subject to the free energy potential F(r) that can be obtained from the PDF of the end-to-end distance p(r) (see Fig. 4) via the inverse Boltzmann relation as
F(r) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[p(r)]. log[p(r)]. | (5) |
 | ||
| Fig. 5 Looping probability Pl(ϕ) (panel a) and polymer radius of gyration Rg(ϕ) (panel b) computed from simulations for εs = 5kBT, n = 16. Experimental data60 for the fraction of closed ssDNA hairpins is shown in panel (c). Here and below the simulation data for dcr = 1σ are presented as small red circles, big blue circles correspond to dcr = 4σ. Note that the weaker effect of larger (dcr = 4σ) crowders on the dimensions of the polymer coil shown in panel (b) may be due to the matching of sizes (Rg ∼ dcr) for the relatively short chains considered here. | ||
 | ||
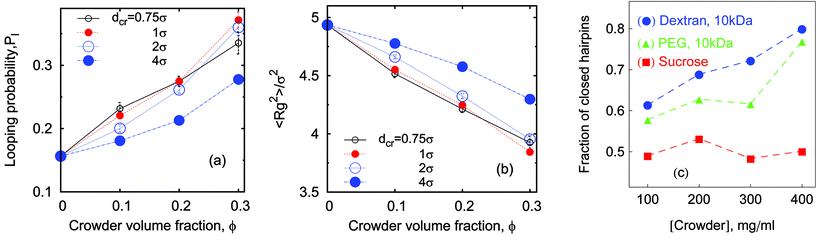
| Fig. 7 Average looping (panel a) and unlooping (panel b) times versus the chain length. The asymptote (1) of Tl(n) ∼ n2ν+1 in the absence of crowders is shown by the dashed line in panel (a). Parameters are the same as in Fig. 6. The shown error bars are often smaller than the symbol size. | ||
 | ||
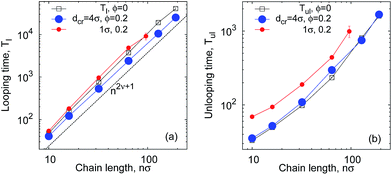
| Fig. 8 Characteristic time τK given by eqn (10) and computed from simulations (a) for n = 16 and εs = 5kBT. (b) Experimental data60 for ssDNA hairpin formation kinetics in solutions of different crowders. Both graphs are in log-linear scale. | ||
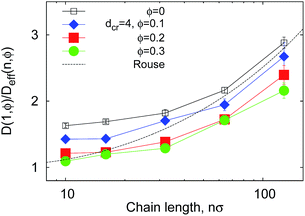 | ||
| Fig. 9 Reciprocal effective diffusivity D(1, ϕ)/Deff(n, ϕ) of polymer ends, obtained from fit of the Tl data in Fig. 7 with eqn (12). The Rouse chain result DR(n, 0) given by eqn (13) with D(1, 0) = 1/2 as used in simulations is the dashed curve. | ||
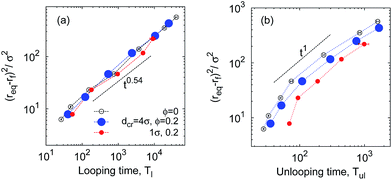 | ||
| Fig. 11 Diffusion law of eqn (18) for looping and unlooping times of the chain ends necessary to bridge the distance 〈δr(n)2〉. The asymptote of eqn (19) is the dotted line in panel (a); a linear scaling in panel (b) is included as a guide for the eye. Parameters are the same as in Fig. 7 and ϕ = 0.2. | ||
B. Looping probability and polymer size
From p(r)—which is a function of the number of monomers n—we compute the probability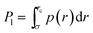 | (6) |
Fig. 5a demonstrates that the looping probability Pl grows with the crowding fraction ϕ. This is in accordance with the recent results of ssRNA tertiary folding–unfolding dynamics57 as well as ssDNA hairpin formation measurements60 in crowded polymeric solutions. In the latter experiment, fluorescence correlation spectroscopy data indicated a linear increase of the fraction of closed ssDNA hairpins as a function of ϕ,
| Pl(ϕ) ∼ A + Bϕ, | (7) |
Consider now the PDF p(r) shown in Fig. 4. It has a bimodal structure, reflecting the proximity between the sticky ends with end-to-end distances r ≈ σ and a broad distribution of r values reflecting the diffusive nature of the chain ends in the extended state. As can be seen in Fig. 4, the presence of MMC favours more compact polymer states: with increasing crowding fraction ϕ the polymer radius of gyration Rg decreases, in accordance with common MMC effects.21,56 The significant shift of the distribution to shorter r values is particularly visible when the peak around r ≈ σ is considered.
For completeness we mention that, as expected a priori, stronger cohesiveness of the sticky ends favours higher looping probabilities Pl, reaching unity at εs ≫ 1kBT (see Fig. 14) and yields progressively longer unlooping times. This fact also agrees with the experimental data on ssDNA hairpin formation in solutions of polymeric crowders of different MWs shown in Fig. 8. Interestingly, we find that for crowder molecules with a larger diameter dcr the looping probability Pl becomes less sensitive to ϕ, as demonstrated in Fig. 5a (smaller values of B in eqn (7)). To map the detailed parametric dependence of the looping statistics as a function of chain length n, crowder size dcr, and fraction ϕ is a major challenge for simulations. We examine all these effects below.
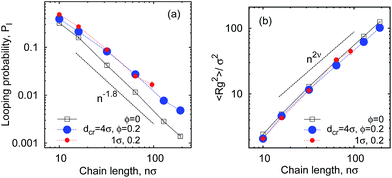
As shown in Fig. 6 for both small and large crowders the looping probability Pl decreases with the chain length n as
| Pl(n) ∼ n−1.8. | (8) |
The simulations yield instructive shapes for the polymer free energy F(r) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[p(r)] as shown in the insets of Fig. 4 and in Fig. 13. We find a clear trend for the free energy barriers ΔF(n): for the transition from the unlooped to the looped state the barriers become higher for longer chains, as shown in Fig. 13. This effect is due to the higher entropic penalty upon looping for longer polymers. In contrast, the barriers for a transition from the looped to the unlooped state are fairly insensitive to n, reflecting that unlooping is a local activation effect of dissolving the bond between the terminal monomers. This important feature gives rise to a more pronounced chain-length effect on the looping time Tl as compared to the analogous dependence of the unlooping time Tul, as seen in Fig. 7. We now study the (un)looping times in more detail.
log[p(r)] as shown in the insets of Fig. 4 and in Fig. 13. We find a clear trend for the free energy barriers ΔF(n): for the transition from the unlooped to the looped state the barriers become higher for longer chains, as shown in Fig. 13. This effect is due to the higher entropic penalty upon looping for longer polymers. In contrast, the barriers for a transition from the looped to the unlooped state are fairly insensitive to n, reflecting that unlooping is a local activation effect of dissolving the bond between the terminal monomers. This important feature gives rise to a more pronounced chain-length effect on the looping time Tl as compared to the analogous dependence of the unlooping time Tul, as seen in Fig. 7. We now study the (un)looping times in more detail.
C. Looping and unlooping times
Fig. 3 shows how we extract the average looping and unlooping times Tl and Tul from the time series r(t) of the end-to-end distance. Namely, Tl is counted from the point when—after a previous looped state—the chain ends reach their equilibrium distance req until they touch close to the minimum of the attractive LJ potential. By definition, the equilibrium distance req corresponds to the free energy minimum for the extended chain conformations. From that moment, Tul is counted until the chain ends are separated by the distance req again. The computation of Tl thus involves extensive chain rearrangements and thus non-trivially depends on the crowder fraction ϕ, which favours more compact states. In our analysis Tl and Tul are then averaged over many looping events, the results being shown in Fig. 15 for a fixed chain length.The distribution of looping times is found to be nearly exponential, and the characteristic time is shorter in more crowded solutions of bigger crowders, see Fig. 16. The full statistics and fluctuations of Tl can be envisaged from the PDFs presented in Fig. 16. We fitted the p(Tl) functions by two-parametric Weibull distributions of the form
| p(Tl) ∼ Tlγ−1exp[−(Tl/T*l)γ]. | (9) |
We also consider the opening and closing times Top and Tcl (Fig. 3). Top is the time for the chain ends to open up from a closed state and first reach the equilibrium distance req. Tcl measures the time from the last occurrence of req before a new looping event with r < rc. Both Top and Tcl grow with ϕ, as shown in Fig. 17. These times are, as expected, much shorter than the looping and unlooping times. For Top and Tcl we detect no significant difference in their ϕ dependence, consistent with theoretical93 and experimental94 results.
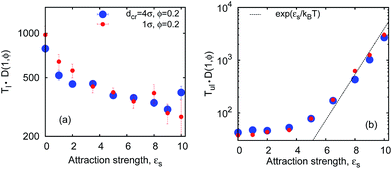
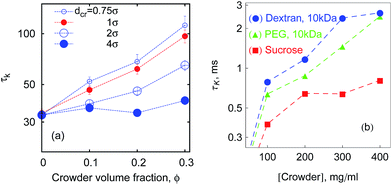
So what about the dependence on the crowder size? Fig. 7 demonstrates that for small crowders the looping kinetics is somewhat inhibited and Tl increases with ϕ. For large crowders, however, we observe the opposite and stronger trend: polymer looping is facilitated. As detailed in Fig. 15a, Tl indeed decreases with ϕ up to dcr = 4σ, however, for even larger crowders it starts to increase again, see Fig. 15b. For very large crowders Tl appears to approach the looping time in the absence of crowders, indicated by the dashed line in Fig. 15b. Fig. 18 reveals that the solution viscosity increases more strongly with ϕ for small crowders, slowing down the chain dynamics and reducing the looping rates. This non-trivial behaviour illustrated in Fig. 7 is our first key result.
Apart from the viscosity dependence, in Fig. 2 we highlight another important crowding-mediated effect. Namely, when the crowders are small, entropic effects favour a good mixing of crowders and chain monomers with little implications of the chain connectivity. When the crowders become larger, however, depletion effects become increasingly dominant. The chain becomes confined in a “cage”. We emphasise here that the cage is not static but rather a dynamic entity, because of perpetual diffusion of crowders. Only at very high ϕ values or with possible attractions between the crowders the cage becomes static, as studied in ref. 74. In this confined state, the looping probability is significantly increased and thus the looping dynamics gets facilitated. As shown in Fig. 7 the depletion effect just outweighs the increased viscosity for larger crowders. The dynamics of crowders remains Brownian even at high volume fractions of ϕ ∼ 0.3, see below.
The unlooping time Tul, in contrast, typically increases with ϕ. As shown in Fig. 7 and 15c, while the dependence of Tul on ϕ is very weak for large crowders, it becomes quite sizable for smaller crowders. The effect on Tul is due to both the higher viscosity induced by MMC and the impeded chain opening imposed by the caging effects. For the unlooping process both effects do not lead to an inversion of the ϕ-dependence of Tul inhibiting chain opening. The unlooping time is a monotonically decreasing function of the crowder size, see Fig. 15d.||
D. Comparison with DNA hairpin formation experiments
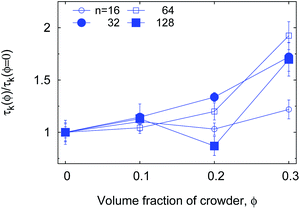
Ref. 60 reports experimental data from fluorescence correlation measurements of ssDNA hairpin formation. The characteristic time τK for the measured fluorescent blinking is given by the harmonic mean,60| τK = TlTul/(Tl + Tul). | (10) |
| τK(ϕ) ≃ exp(ζϕ) | (11) |
For a quantitative comparison of our results for τK to the experimentally observed τK(ϕ) enhancement,60 one needs to compare the relative sizes of polymers and crowders (experiment versus simulations). Namely, 10 kDa PEG polymers have Rg,PEG ≈ 2.8 nm, while for 21-bp long DNA hairpins Rg ∼ 7 nm.60 In simulations, for n = 16 chains, see Fig. 15, the gyration radius is Rg ≈ 2.5σ (Fig. 5b), so the crowders of diameter dcr ≈ 2σ are in the same relation to the polymer size in simulations as 21-bp DNA hairpins to 10 kDa PEG in experiments.60 Note that 10 kDa branched dextran polymers are smaller than 10 kDa PEG60 and the dynamics of DNA hairpin formation is slower in dextran solutions. The physical reason for this behaviour, as proposed in ref. 60, is a pronounced sub-diffusion of DNA hairpins in solutions of dextran with scaling exponent of 0.7 < β < 0.85, in stark contrast to the sucrose and PEG solutions where the hairpin diffusion is nearly Brownian (0.9 < β < 1), see also below.
E. Length dependence and effective diffusivity
The observed tradeoff between facilitation and inhibition is a fundamental feature of the looping kinetics for all chain lengths. Fig. 7 illustrates that the looping rate is systematically facilitated for larger crowders and impeded for smaller crowders. Concurrently, the scaling of the looping time with n given by eqn (1) does not change appreciably in crowded solutions compared to the dilute case ϕ = 0, as shown in Fig. 7. This is our second important result.Note that for longer polymers the accessible space inside the coil increases and at some point even large crowders can be accommodated therein, thus the reverting effect of polymer compaction by MMC. However, the gyration radius of our longest chains with n ≈ 200 monomers is still too small to see this happen for the larger crowders (dcr = 4σ) studied. Thus, the Tl(n) scaling behaviour for even longer chains remains similar to the situation in the absence of crowders. We observe a slightly more pronounced looping time variation with ϕ for longer polymers in crowded solutions, in agreement with the well-established results, for instance, in protein–DNA interactions.2 The unlooping times vary substantially with the polymer length (in stark contrast to the observations of ref. 11). This indicates that unlooping is not a purely local unbinding process, but it needs the cooperative motion of the polymer.**
In Fig. 9 we study how many chain monomers are involved in looping events by quantifying the inverse effective position-independent diffusivity 1/Deff of the end monomers. We use the data of Fig. 7 for Tl and the general expression for mean first-passage (i.e., looping) times
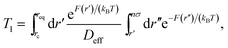 | (12) |
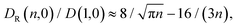 | (13) |
The effective number of monomers involved in the looping dynamics neff ∝ D(1,ϕ)/Deff(n, ϕ) increases slightly with n both for large and small crowders, as shown in Fig. 9. This figure illustrates that the number of chain monomers participating in looping slightly but systematically decreases with the MMC fraction ϕ. The functional dependence of Deff is qualitatively similar to that of Rouse chains at larger n, see eqn (13), but with somewhat smaller Deff values. For smaller n, however, a plateau of Deff is observed for all chain lengths in the simulations. For severe crowding we find that less monomers are involved in looping, compare the curves in Fig. 9. This analysis rationalises the cooperativity between the polymer extremities and the vicinal crowding particles. The ϕ-dependent chain end diffusivity is our third main result.††
F. Effects of the binding affinity
For ssDNA hairpins, the enthalpy gain of base-pairing upon looping is partly counter-balanced by the entropic penalty.104,105 For instance, for the 21-bp hairpin with CCCAA/GGGTT termini in ref. 60 the free energy of hairpin formation is ∼5kBT.73 This value is used in our simulations for the end-to-end binding energy εs, except for Fig. 10 where we vary εs in the broad range 0 ≤ εs ≤ 10kBT. Larger εs values represent ssDNA hairpins with longer and thus more adhesive complementary end sequences. We observe a moderate, monotonic decrease of the looping time with εs. Moreover, for all εs values longer looping times are obtained for smaller crowders and faster looping is detected for larger crowders (Fig. 10 and 20). This implies that our claims regarding the effects of crowding on the polymer looping dynamics are robust to changes of the model parameters.Both looping and unlooping times can be rescaled by the effective solution viscosity η ∼ 1/D(1,ϕ) to yield universal dependencies for different crowder sizes as demonstrated in Fig. 10b. Fig. 20 shows the unscaled looping and unlooping data, together with the results for in the absence of crowding, revealing the same trends for Tl,ul with the crowder size as those presented for a fixed end-monomer affinity in Fig. 7b. The viscosity-based rescaling works particularly well for the unlooping. As expected, for large end-to-end attraction εs the unlooping time grows and exhibits Arrhenius-like kinetics,
| Tl(εs) ∼ exp[εs/(kBT)], | (14) |
G. Cavity and caging
To quantify the already mentioned caging effects imposed by the crowders on the polymer coil, we explicitly compute the distribution of crowders around the polymer, as illustrated in Fig. 21. It shows that crowding particles of size comparable to the chain monomers diffuse quite substantially inside the coil volume. In contrast, crowders, whose sizes are much larger than the polymer monomers, are essentially excluded/depleted from the volume occupied by the polymer, thus facilitating polymer compaction and looping. Here, the reader is also referred to the investigation of caging effects in colloidal glasses.74We also evaluated the correlation characteristics of the number of contacts mcr–p(t) that the polymer chain establishes with the neighbouring crowders in the course of time, see Fig. 22 for relatively large crowders. We define the normalised auto-correlation function of polymer–crowders contacts as25
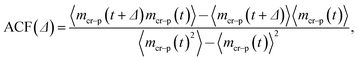 | (15) |
We observe that, after an initial fast decrease of the number of contacts established, the further decay of the correlation function becomes nearly exponential, ACF(Δ) ∼ exp[−Δ/T*], see Fig. 22. The corresponding decay length T* increases for longer polymers, partly due to a larger number of overall contacts mcr–p established. The characteristic time scale T* we obtain here is substantially shorter than the polymer looping time Tl under the same conditions, compare Fig. 7 and 22.‡‡
IV. Results: diffusion
A. Subdiffusion of polymer ends
MMC may impede the folding dynamics of short polypeptides due to a higher solution viscosity97 overwhelming the looping-facilitating caging effects. A size-dependent diffusivity emerges:97 the diffusion of longer chains is impeded more strongly. Fig. 11 based on our simulations shows a similar effect for the mean squared looping distance versus the looping and unlooping times. This quantifies the diffusion law for looping events, i.e., the diffusive bridging of the distance| δr = req − rc | (16) |
| 〈δr(n)〉2 ∼ n2ν | (17) |
| 〈δr(n)2〉 = 2Dαl〈Tl(n)〉αl = 2Dαul〈Tul(n)〉αul. | (18) |
Fig. 11a illustrates that at large ϕ the looping dynamics is subdiffusive with 0.5 ≲ αl ≲ 0.6. This is but the standard result for polymer looping, as seen from combination of eqn (1) and (18),
| 〈δr(n)2〉 ∼ Tl(n)2ν/(2ν+1) ∼ Tl(n)0.54. | (19) |
These observations can be rationalised as follows. Once a thermal fluctuation breaks the bond between the sticky ends, the separation r of the polymer ends drifts downhill in the free energy landscape F(r) discussed above, quickly assuming larger values. In contrast, the looping time depends strongly on n: to loop, the polymer needs to overcome an entropic penalty to get from req to the contact distance rc, see Fig. 13. Thus, for looping it takes much longer to bridge the distance δr(n) and involves interactions with a larger number of surrounding crowders, effecting the power law (19) with the small value αl = 0.54.
B. Diffusion of a tracer particle
The size of the obstacles controls the facilitation or inhibition of polymer looping in crowded environments. Additionally, we exploit how fast the polymer ends join one another from the extended equilibrium state and reveal the regime of anomalous diffusion for the looping times with the scaling exponent of ≈0.54, see eqn (19). Here we briefly examine whether this sub-diffusive behaviour of extended polymer extremities is connected to any subdiffusion of a tracer particle in the crowded solutions simulated.We compute the mean square displacement (MSD) for the diffusion of a single monomer of the chain (tracer particle), 〈s2(t)〉, in crowded solutions with varying MMC fraction ϕ and crowder diameter dcr. Namely, we use the anomalous diffusion law98–101
| 〈s2(t)〉 ∼ tβ | (20) |
| β(t) = d[log(〈s2(t)〉)]/d[log(t)] | (21) |
We find that the viscosity of solutions of smaller crowders grows with ϕ faster than for larger obstacles, see Fig. 18. In this figure, the diffusivity has been extracted from the time averaged MSD along the x-direction,
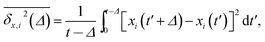 | (22) |
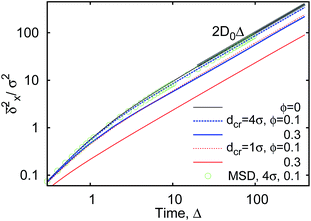
The ensemble averaged and time averaged MSD  traces are identical in the long-time limit, see Fig. 12, with the long-time exponent β being close to unity (Brownian motion). This indicates the ergodic tracer diffusion in the crowded solutions implemented in our simulations yields subdiffusive motion of the chain ends. In Fig. 12 we also show the ensemble and time averaged MSDs of a tracer particle with unit diameter in the crowded solutions. The diffusion exponent is nearly unity and no disparity of ensemble and time averaged displacements is detected, i.e., the motion is ergodic.99,101
traces are identical in the long-time limit, see Fig. 12, with the long-time exponent β being close to unity (Brownian motion). This indicates the ergodic tracer diffusion in the crowded solutions implemented in our simulations yields subdiffusive motion of the chain ends. In Fig. 12 we also show the ensemble and time averaged MSDs of a tracer particle with unit diameter in the crowded solutions. The diffusion exponent is nearly unity and no disparity of ensemble and time averaged displacements is detected, i.e., the motion is ergodic.99,101
V. Discussion
MMC non-specifically favours more compact conformations of proteins and speeds up their folding kinetics,21 as well as stabilises the proteins against thermal denaturation.95 MMC may also reduce the occurrence of mis-folded states via reduction of the conformational space.38 The degree of crowding in living cells is heterogeneous and the crowders are polydisperse in size,107 giving rise to a micro-compartmentalisation of the cellular cytoplasm.106,108,109 These effects pose the questions whether other fundamental elements of gene expression in biological cells are equally affected by MMC.Specifically, recent gene-regulation experiments2 have shown that bigger dextran molecules increase the rates of gene expression by RNA polymerase to a higher-fold as compared to smaller ones.2 Bigger dextran molecules both reduce the diffusivity of RNA polymerase and enhance the number of binding events to the promoters (enhancing the association and reducing the dissociation rates). In solution of small crowders the impact of ϕ on gene expression rates is non-monotonic (due to a compensation of moderate effects of MMC on the polymerase diffusivity and on its association rate to the DNA sites). In contrast, in solution of bigger crowders the expression rate grows monotonically and strongly with the ϕ fraction.2
Here we show that indeed the looping kinetics of polymers such as DNA is highly sensitive to the volume fraction and size of crowders in a non-trivial way, and quantitative knowledge of this effect is necessary for the understanding of the molecular biological function of DNA based on looping. From extensive Langevin dynamics simulations we demonstrated that polymer looping is facilitated in the presence of large crowders, mainly due to depletion-based chain compaction. In contrast, for small crowders the dominant effect is the larger effective viscosity impeding the looping dynamics. The exact tradeoff between the two effects critically depends on the system parameters.
Our results are applicable to generic DNA looping and RNA folding dynamics in crowded systems,110 particularly, the formation of ssDNA hairpins with in vitro crowders.60 Here, our predictions for the crowder size and binding affinity effects can be tested directly in experiments. We already have showed that some predictions of our model indeed capture the experimental behaviour.60 As targets for future studies, crowders of particular surface properties, non-inert poly-disperse and aspherical crowders will be studied.89
In addition, the simulations of semi-flexible instead of flexible polymers in the presence of both MMC and external spherical confinement are expected to reveal a number of novel features. For instance, in contrast to free-space flexible chains studied here, the presence of spacial restrictions and finite bending energy penalty upon polymer looping yields a quasi-periodic but highly erratic dependence of the looping characteristics on the chain length nσ. Strong anti-correlation of the looping time and looping probability versus the polymerisation degree, pertinent for flexible chains, as those presented in Fig. 6a and 7a, become more profound for the dynamics of cavity-confined semi-flexible polymers, see ref. 89. We hope that our current investigation triggers new theoretical and experimental developments of static and dynamical properties of polymers in the crowded realm characteristic of the interior of living cells.§§
VI. Appendix A
In this Appendix we present the supplementary figures explaining the details of our main-text results.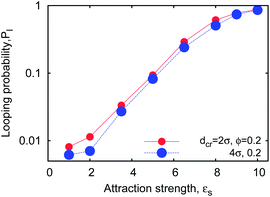 | ||
| Fig. 14 Looping probability versus terminal monomer stickiness, computed for n = 32 chains at different crowder sizes at ϕ = 0.2. | ||
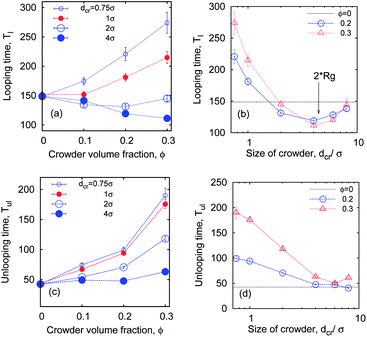 | ||
| Fig. 15 Looping and unlooping times versus ϕ, computed for a varying crowder size dcr, for short chains with n = 16 monomers, and εs = 5kBT. | ||
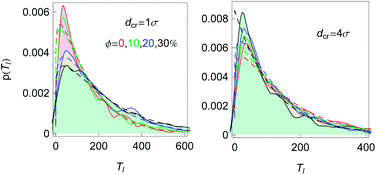 | ||
| Fig. 16 The PDFs of looping times for n = 16, εs = 5kBT and crowder sizes and fractions as indicated. Smoothed histograms are the simulations data and the dashed curves of the respective colour are the fits by eqn (9). The slight bumpiness of the histograms is due to the limited statistics of the generated looping events. | ||
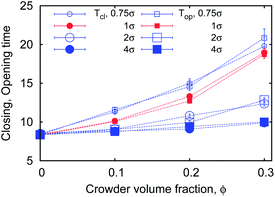 | ||
| Fig. 17 Opening and closing times Top,clversus MMC fraction ϕ for varying crowder sizes. Parameters are the same as in Fig. 15. | ||
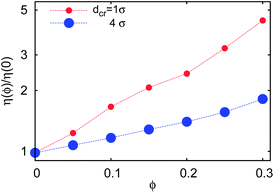 | ||
| Fig. 18 Effective solution viscosity η(ϕ) = kBT/(3πσD(1, ϕ)) for a tracer of diameter 1σ in solutions with varying crowder diameter dcr, as extracted from the analysis of time averaged MSD traces. | ||
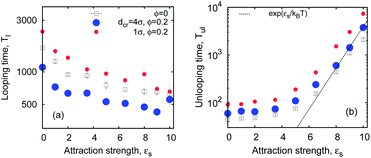 | ||
| Fig. 20 The same data as in Fig. 10 but without normalisation by the effective viscosity of the solution, η(ϕ) ∼ 1/D(1,ϕ). The data-set for the uncrowded solution is also included (open symbols). | ||
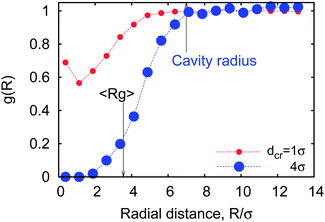 | ||
| Fig. 21 The radial distribution function of relatively small (red dots) and large (blue dots) crowders around a polymer coil with n = 32 monomers at MMC fraction of ϕ = 0.1. | ||
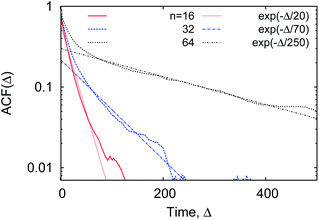 | ||
| Fig. 22 The auto-correlation function of the polymer–crowders contact number (15), computed for polymers of varying length, at ϕ = 0.2 and dcr = 4σ. The corresponding exponential asymptotes are shown as the dotted lines. | ||
VII. Abbreviations
| MMC | Macromolecular crowding |
| Probability density function | |
| LJ | Lennard-Jones |
| FENE | Finitely-extensible non-linear elastic |
| PEG | Polyethelene glycol |
| ssDNA | Single-stranded DNA |
| dsDNA | Double-stranded DNA |
| MW | Molecular weight |
| MSD | Mean squared displacement |
Note from the authors
After this paper was accepted, a number of relevant studies on this timely topic appeared. In particular, (i) the reader is referred to an extended review of Saxton [M. J. Saxton, J. Phys. Chem. B, 2014, 118, 12805] on the properties of various crowders used in vivo. (ii) The implications of crowders of varying size onto the asphericity of polymer chains in polymer-nanoparticle mixtures were examined by Monte-Carlo simulations by W. K. Lim and A. R. Denton, J. Chem. Phys., 2014, 141, 114909. (iii) The ring closure and loop formation reactions in the presence of reactive end groups of the polymer were examined by D. Sarkar, S. Thakur, Y. Tao and R. Kapral, Soft Matter, 2014, 10, 9577; there, the different scaling behaviour for the end-capture time with the polymer length was studied. (iv) Effects of loop stacking interactions and temperature on the thermodynamics of DNA hairpin formation were examined by M. Mosayebi et al., E-print arXiv:1410.1218. Similarly to our observations for the polymer looping time, the hairpin closing time was shown to be exponentially distributed. The variation of the hairpin closing time with temperature was shown to reveal a non-monotonic dependence, with a minimum close to the DNA melting temperature. This non-Arrhenius behavior is consistent with the experimental observations on DNA hairpin formation kinetics reported previously by M. I. Wallace, et al., Proc. Natl. Acad. Sci. USA, 2001, 98, 5584.Acknowledgements
We thank D. Jost for discussions on hairpin formation and M. Weiss for providing the experimental data for Fig. 5c and 8b. We acknowledge funding from the Academy of Finland (FiDiPro scheme to RM), the Deutsche Forschungsgemeinschaft (DFG Grant CH 707/5-1 to AGC), and the Federal Ministry of Education and Research (BMBF Project to JS). We are particularly grateful to an anonymous referee for the insightful comments which improved our understanding of the subject.References
- I. Golding and E. C. Cox, Physical nature of bacterial cytoplasm, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed.
- C. Tan, S. Saurabh, M. P. Bruchez, R. Schwartz and P. LeDuc, Molecular crowding shapes gene expression in synthetic cellular nanosystems, Nat. Nanotechnol., 2013, 8, 602–608 CrossRef CAS PubMed.
- R. Philips, J. Kondev, J. Theriot and H. Garcia, Physical Biology of the Cell, Garland Science, New York, 2012 Search PubMed.
- M. J. Morelli, P. R. ten Wolde and R. J. Allen, DNA looping provides stability and robustness to the bacteriophage λ switch, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(20), 8101–8106 CrossRef CAS PubMed.
- G. W. Li, O. G. Berg and J. Elf, Effects of macromolecular crowding and DNA looping on gene regulation kinetics, Nat. Phys., 2009, 5(4), 294–297 CrossRef CAS.
- H. Matsuda, G. G. Putzel, V. Backman and I. Szleifer, Macromolecular Crowding as a Regulator of Gene Transcription, Biophys. J., 2014, 106(4), 1801–1810 CrossRef CAS PubMed.
- G. Wilemski and M. Fixman, Diffusion-controlled intrachain reactions of polymers, J. Chem. Phys., 1974, 60(3), 866–877 CrossRef CAS PubMed.
- T. Guérin, O. Bénichou and R. Voituriez, Reactive conformations and non-Markovian cyclization kinetics of a Rouse polymer, J. Chem. Phys., 2013, 138(9), 094908 CrossRef PubMed.
- T. Guérin, O. Bénichou and R. Voituriez, Non-Markovian polymer reaction kinetics, Nat. Chem., 2012, 4(7), 568–573 CrossRef PubMed.
- A. Szabo, K. Schulten and Z. Schulten, First passage time approach to diffusion controlled reactions, J. Chem. Phys., 1980, 72(8), 4350–4357 CrossRef CAS PubMed.
- N. M. Toan, D. Marenduzzo, P. R. Cook and C. Micheletti, Depletion effects and loop formation in self-avoiding polymers, Phys. Rev. Lett., 2006, 97(17), 178302 CrossRef CAS.
- J. Shin and W. Sung, Effects of static and temporally fluctuating tensions on semiflexible polymer looping, J. Chem. Phys., 2012, 136(4), 045101 CrossRef PubMed.
- M. Fritsche and D. W. Heermann, Confinement driven spatial organization of semiflexible ring polymers: implications for biopolymer packaging, Soft Matter, 2011, 7, 6906–6913 RSC.
- J. Stampe and I. M. Sokolov, Cyclization of a polymer with charged reactive end groups, J. Chem. Phys., 2001, 114(11), 5043–5048 CrossRef CAS PubMed.
- R. R. Cheng and D. E. Makarov, Failure of one-dimensional Smoluchowski diffusion models, J. Chem. Phys., 2011, 134(8), 085104 CrossRef PubMed.
- N. M. Toan, G. Morrison, C. Hyeon and D. Thirumalai, Kinetics of loop formation in polymer chains, J. Phys. Chem. B, 2008, 112(19), 6094–6106 CrossRef CAS PubMed.
- K. V. Klenin and J. Langowski, Modeling of intramolecular reactions of polymers: an efficient method based on Brownian dynamics simulations, J. Chem. Phys., 2004, 121(10), 4951–4960 CrossRef CAS PubMed.
- J. S. Kim, V. Backman and I. Szleifer, Crowding-induced structural alterations of random-loop chromosome model, Phys. Rev. Lett., 2011, 106(16), 168102 CrossRef.
- D. Marenduzzo, K. Finan and P. R. Cook, The depletion attraction: an under-appreciated force driving cellular organization, J. Cell Biol., 2006, 175(5), 681–686 CrossRef CAS PubMed.
- D. Marenduzzo, C. Micheletti and P. R. Cook, Entropy-driven genome organization, Biophys. J., 2006, 90(10), 3712–3721 CrossRef CAS PubMed.
- H. X. Zhou, G. Rivas and A. P. Minton, Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef CAS PubMed.
- C. Bräuchle, D. C. Lamb and J. Michaelis, Single Particle Tracking and Single Molecule Energy Transfer, Wiley-VCH, Weinheim, Germany, 2012 Search PubMed.
- C. Micheletti, D. Marenduzzo and E. Orlandini, Polymers with spatial or topological constraints: theoretical and computational results, Phys. Rep., 2011, 504(1), 1–73 CrossRef CAS PubMed.
- J. Dorier and A. Stasiak, Modelling of crowded polymers elucidate effects of double-strand breaks in topological domains of bacterial chromosome, Nucleic Acids Res., 2013, 41(14), 6808–6815 CrossRef CAS PubMed.
- J. Shin, A. G. Cherstvy and R. Metzler, Mixing and segregation of ring polymers: spatial confinement and molecular crowding effects, New J. Phys., 2014, 16, 053047 CrossRef.
- T. Cremer and M. Cremer, Chromosome territories, Cold Spring Harbor Perspect. Biol., 2010, 2(3), a003889 Search PubMed.
- T. B. Le, M. V. Imakaev, L. A. Mirny and M. T. Laub, High-resolution mapping of the spatial organization of a bacterial chromosome, Science, 2013, 342(6159), 731–734 CrossRef CAS PubMed.
- A. R. Denton, Crowding in polymer-nanoparticle mixtures, Int. Rev. Cell Mol. Biol., 2014, 307, 27–71 CAS.
- F. Höfling and T. Franosch, Anomalous transport in the crowded world of biological cells, Rep Prog Phys, 2013, 76(4), 046602 CrossRef PubMed.
- M. Weiss, Crowding, Diffusion, and Biochemical Reactions, Int. Rev. Cell Mol. Biol., 2014, 307, 383–417 CAS.
- S. B. Zimmerman and A. P. Minton, Macromolecular crowding: biochemical, biophysical, and physiological consequences, Annu. Rev. Biophys. Biomol. Struct., 1993, 22(1), 27–65 CrossRef CAS PubMed.
- S. R. McGuffee and A. H. Elcock, Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm, PLoS Comput. Biol., 2010, 6(3), e1000694 Search PubMed.
- J. Szymanski and M. Weiss, Elucidating the origin of anomalous diffusion in crowded fluids, Phys. Rev. Lett., 2009, 103, 038102 CrossRef.
- W. Pan, L. Filobelo, N. D. P. Pham, O. Galkin, V. V. Uzunova and P. G. Vekilov, Viscoelasticity in homogeneous protein solutions, Phys. Rev. Lett., 2009, 102, 058101 CrossRef.
- C. K. Hu and M. S. Li, Dual effect of crowders on fibrillation kinetics of polypeptide chains revealed by lattice models, J. Chem. Phys., 2013, 138(18), 185101 CrossRef PubMed.
- G. Schreiber, G. Haran and H. X. Zhou, Fundamental aspects of protein-protein association kinetics, Chem. Rev., 2009, 109(3), 839–860 CrossRef CAS PubMed.
- M. Erlkamp, S. Grobelny and R. Winter, Crowding effects on the temperature and pressure dependent structure, stability and folding kinetics of Staphylococcal Nuclease, Phys. Chem. Chem. Phys., 2014, 16(13), 5965–5976 RSC.
- M. S. Cheung, D. Klimov and D. Thirumalai, Molecular crowding enhances native state stability and refolding rates of globular proteins, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(13), 4753–4758 CrossRef CAS PubMed.
- C. Hyeon and D. Thirumalai, Capturing the essence of folding and functions of biomolecules using coarse-grained models, Nat. Commun., 2011, 2, 487 CrossRef PubMed.
- M. Guo, Y. Xu and M. Gruebele, Temperature dependence of protein folding kinetics in living cells, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(44), 17863–17867 CrossRef CAS PubMed.
- M. del Alamo, G. Rivas and M. G. Mateu, Effect of macromolecular crowding agents on human immunodeficiency virus type 1 capsid protein assembly in vitro, J. Virol., 2005, 79(22), 14271–14281 CrossRef CAS PubMed.
- N. A. Denesyuk and D. Thirumalai, Crowding promotes the switch from hairpin to pseudoknot conformation in human telomerase RNA, J. Am. Chem. Soc., 2011, 133(31), 11858–11861 CrossRef CAS PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(16), 6438–6443 CrossRef CAS PubMed.
- J. H. Jeon, H. M. S. Monne, M. Javanainen and R. Metzler, Anomalous diffusion of phospholipids and cholesterols in lipid bilayer and its origins, Phys. Rev. Lett., 2012, 109, 188103 CrossRef.
- M. Javanainen, H. Hammaren, L. Monticelli, J. H. Jeon, R. Metzler and I. Vattulainen, Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes, Faraday Discuss., 2013, 161, 397–417 RSC.
- N. A. Mahynski, B. Irick and A. Z. Panagiotopoulos, Structure of phase-separated athermal colloid-polymer systems in the protein limit, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022309 CrossRef.
- P. Paricaud, S. Varga and G. Jackson, Study of the demixing transition in model athermal mixtures of colloids and flexible self-excluding polymers using the thermodynamic perturbation theory of Wertheim, J. Chem. Phys., 2003, 118(8), 8525–8536 CrossRef CAS PubMed.
- D. Swigon, B. D. Coleman and W. K. Olson, Modeling the Lac repressor-operator assembly: the influence of DNA looping on Lac repressor conformation, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(26), 9879–9884 CrossRef CAS PubMed.
- D. G. Priest, L. Cu, S. Kumar, D. D. Dunlap, I. B. Dodd and K. E. Shearwin, Quantitation of the DNA tethering effect in long-range DNA looping in vivo and in vitro using the Lac and λ repressors, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(1), 349–354 CrossRef CAS PubMed.
- Z. Hensel, X. Weng, A. C. Lagda and J. Xiao, Transcription-factor-mediated DNA looping probed by high-resolution, single-molecule imaging in live E. coli cells, PLoS Biol., 2013, 11(6), e1001591 CAS.
- B. van den Broek, M. A. Lomholt, S. M. Kalisch, R. Metzler and G. J. Wuite, How DNA coiling enhances target localization by proteins, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(41), 15738–15742 CrossRef CAS PubMed.
- M. A. Lomholt, B. van den Broek, S. M. J. Kalisch, G. J. L. Wuite and R. Metzler, Facilitated diffusion with DNA coiling, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(20), 8204–8208 CrossRef CAS PubMed.
- P. R. ten Wolde and A. Mugler, Importance of crowding in signaling, genetic, and metabolic networks, Int. Rev. Cell Mol. Biol., 2013, 307, 419–442 Search PubMed.
- M. Tabaka, T. Kalwarczyk and R. Holyst, Quantitative influence of macromolecular crowding on gene regulation kinetics, Nucleic Acids Res., 2014, 42(2), 727–738 CrossRef CAS PubMed.
- A. G. Cherstvy and V. B. Teif, “Structure-driven homology pairing of chromatin fibers: the role of electrostatics and protein-induced bridging”, J. Biol. Phys., 2013, 39(3), 363–385 CrossRef CAS PubMed.
- H. X. Zhou, Protein folding in confined and crowded environments, Arch. Biochem. Biophys., 2008, 469(1), 76–82 CrossRef CAS PubMed.
- N. F. Dupuis, E. D. Holmstrom and D. J. Nesbitt, Molecular-crowding effects on single-molecule RNA folding/unfolding thermodynamics and kinetics, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(23), 8464–8469 CrossRef CAS PubMed.
- G. Bonnet, O. Krichevsky and A. Libchaber, Kinetics of conformational fluctuations in DNA hairpin-loops, Proc. Natl. Acad. Sci. U. S. A., 1998, 95(15), 8602–8606 CrossRef CAS.
- R. Frederickx, T. in't Veld and E. Carlon, Anomalous Dynamics of DNA Hairpin Folding, Phys. Rev. Lett., 2014, 112, 198102 CrossRef CAS.
- O. Stiehl, K. Weidner-Hertrampf and M. Weiss, Kinetics of conformational fluctuations in DNA hairpin-loops in crowded fluids, New J. Phys., 2013, 15(11), 113010 CrossRef.
- B. Lu and A. R. Denton, Crowding of polymer coils and demixing in nanoparticle-polymer mixtures, J. Phys.: Condens. Matter, 2011, 23(28), 285102 CrossRef PubMed.
- A. Kudlay, C. Hyeon and D. Thirumalai, Influence of the Shape of Crowding Particles on the Structural Transitions in a Polymer, J. Phys. Chem. B, 2012, 116(29), 8513–8522 CrossRef CAS PubMed.
- A. R. Denton and M. Schmidt, Mixtures of charged colloid and neutral polymer: Influence of electrostatic interactions on demixing and interfacial tension, J. Chem. Phys., 2005, 122(24), 244911 CrossRef PubMed.
- A. R. Denton, Crowding in polymer-nanoparticle mixtures, Int. Rev. Cell Mol. Biol., 2014, 307, 27–71 CAS.
- N. K. Lee, C. F. Abrams and A. Johner, Optimal confinement for internal polymer binding, EPL, 2005, 72(6), 922–928 CrossRef CAS.
- C. F. Abrams, N. K. Lee and A. Johner, Diffusion-reaction in confined polymer chains, Macromolecules, 2006, 39(10), 3655–3663 CrossRef CAS.
- K. Kremer and G. S. Grest, Dynamics of entangled linear polymer melts: A molecular dynamics simulation, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS PubMed.
- P. Bhattacharyya, R. Sharma and B. J. Cherayil, Confinement and viscoelastic effects on chain closure dynamics, J. Chem. Phys., 2012, 136(23), 234903 CrossRef PubMed ; compare also R. Chakrabarty, Physica A, 2014, 391, 5326–5331 CrossRef PubMed.
- J. Shin, A. G. Cherstvy and R. Metzler, Sensing viruses by mechanical tension of DNA in responsive hydrogels, Phys. Rev. X, 2014, 4, 021002 Search PubMed.
- D. Shore, J. Langowski and R. L. Baldwin, DNA flexibility studied by covalent closure of short fragments into circles, Proc. Natl. Acad. Sci. U. S. A., 1981, 78(8), 4833–4837 CrossRef CAS.
- A. Vologodskii and M. D. Frank-Kamenetskii, Strong bending of the DNA double helix, Nucleic Acids Res., 2013, 41(14), 6785–6792 CrossRef CAS PubMed.
- N. A. Mahynski, A. Z. Panagiotopoulos, D. Meng and S. K. Kumar, Stabilizing colloidal crystals by leveraging void distributions, Nat. Commun., 2014, 5, 4472 Search PubMed.
- D. Jost and R. Everaers, A Unified Poland-Scheraga Model of Oligo-and Polynucleotide DNA Melting: Salt Effects and Predictive Power, Biophys. J., 2009, 96(3), 1056–1067 CrossRef CAS PubMed.
- E. Zaccarelli and W. C. K. Poon, Colloidal glasses and gels: The interplay of bonding and caging, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(36), 15203–15208 CrossRef CAS PubMed.
- J. SantaLucia Jr, A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics, Proc. Natl. Acad. Sci. U. S. A., 1998, 95(4), 1460–1465 CrossRef CAS.
- Y. Chen and K. Luo, Dynamics of polymer translocation through a nanopore induced by different sizes of crowding agents, J. Chem. Phys., 2013, 138(20), 204903 CrossRef PubMed.
- A. G. Cherstvy, DNA cyclization: suppression or enhancement by electrostatic repulsions?, J. Phys. Chem. B, 2011, 115(15), 4286–4294 CrossRef CAS PubMed.
- S. I. Nakano, D. Miyoshi and N. Sugimoto, Effects of Molecular Crowding on the Structures, Interactions, and Functions of Nucleic Acids, Chem. Rev., 2013, 114(5), 2733–2758 CrossRef PubMed.
- T. Ando, E. Chow and J. Skolnick, Dynamic simulation of concentrated macromolecular solutions with screened long-range hydrodynamic interactions: algorithm and limitations, J. Chem. Phys., 2013, 139(12), 121922 CrossRef PubMed.
- R. G. Winkler, Analytical calculation of the relaxation dynamics of partially stretched flexible chain molecules: necessity of a worm-like chain description, Phys. Rev. Lett., 1999, 82(9), 1843–1846 CrossRef CAS.
- R. G. Winkler, S. Keller and J. O. Rädler, Intramolecular dynamics of linear macromolecules by fluorescence correlation spectroscopy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73(4), 041919 CrossRef CAS.
- R. Shusterman, S. Alon, T. Gavrinyov and O. Krichevsky, Monomer Dynamics in Double- and Single-Stranded DNA Polymers, Phys. Rev. Lett., 2004, 92(4), 048303 CrossRef.
- E. P. Petrov, T. Ohrt, R. G. Winkler and R. Schwille, Diffusion and segmental dynamics of double-stranded DNA, Phys. Rev. Lett., 2006, 97(25), 258101 CrossRef CAS.
- D. E. Smith and S. Chu, Response of Flexible Polymers to a Sudden Elongational Flow, Science, 1998, 281(5381), 1335–1340 CrossRef CAS.
- T. T. Perkins, S. R. Quake, D. E. Smith and S. Chu, Relaxation of a single DNA molecule observed by optical microscopy, Science, 1994, 264(5160), 822–826 CAS.
- Y. R. Chemla and T. Ha, Ultraslow relaxation of confined DNA, Science, 2014, 345(6195), 380–381 CrossRef PubMed.
- Y. von Hansen, M. Hinczewski and R. R. Netz, Hydrodynamic screening near planar boundaries: Effects on semiflexible polymer dynamics, J. Chem. Phys., 2011, 134, 235102 CrossRef PubMed.
- G. Schreiber, G. Haran and H. X. Zhou, Fundamental aspects of protein-protein association kinetics, Chem. Rev., 2009, 109(3), 839–860 CrossRef CAS PubMed.
- J. Shin, A. G. Cherstvy and R. Metzler, work in progress.
- A. Y. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, Woodbury, NY, 1994 Search PubMed.
- X. Li and A. B. Kolomeisky, Mechanisms and topology determination of complex chemical and biological network systems from first-passage theoretical approach, J. Chem. Phys., 2013, 139(14), 144106 CrossRef PubMed.
- A. Valleriani, X. Li and A. B. Kolomeisky, Unveiling the hidden structure of complex stochastic biochemical networks, J. Chem. Phys., 2014, 140(6), 064101 CrossRef PubMed.
- H. S. Chung, J. M. Louis and W. A. Eaton, Experimental determination of upper bound for transition path times in protein folding from single-molecule photon-by-photon trajectories, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(29), 11837–11844 CrossRef CAS PubMed.
- K. Neupane, D. B. Ritchie, H. Yu, D. A. Foster, F. Wang and M. T. Woodside, Transition path times for nucleic acid folding determined from energy-landscape analysis of single-molecule trajectories, Phys. Rev. Lett., 2012, 109(6), 068102 CrossRef.
- K. W. Minton, P. Karmin, G. M. Hahn and A. P. Minton, Nonspecific stabilization of stress-susceptible proteins by stress-resistant proteins, Proc. Natl. Acad. Sci. U. S. A., 1982, 79(23), 7107–7111 CrossRef CAS.
- N. G. Van Kampen, Stochastic Processes in Physics and Chemistry, North Holland, 3rd edn, 2007 Search PubMed.
- S. Mukherjee, M. M. Waegele, P. Chowdhury, L. Guo and F. Gai, Effect of macromolecular crowding on protein folding dynamics at the secondary structure level, J. Mol. Biol., 2009, 393(1), 227–236 CrossRef CAS PubMed.
- R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 2000, 339(1), 1–77 CrossRef CAS.
- E. Barkai, Y. Garini and R. Metzler, Strange kinetics of single molecules in living cells, Phys. Today, 2012, 65(8), 29–35 CrossRef CAS PubMed.
- R. Metzler and J. Klafter, The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, J. Phys. A: Math. Gen., 2004, 37(31), R161–R208 CrossRef.
- R. Metzler, J. H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- A. B. Goins, H. Sanabria and M. N. Waxham, Macromolecular Crowding and Size Effects on Probe Microviscosity, Biophys. J., 2008, 95(11), 5362–5373 CrossRef CAS PubMed.
- A. P. Minton, Hard Quasi-spherical Particle Models for the Viscosity of Solutions of Protein Mixtures, J. Phys. Chem. B, 2012, 116(31), 9310–9315 CrossRef CAS PubMed.
- S. V. Kuznetsov, Y. Shen, A. S. Benight and A. Ansari, A Semiflexible Polymer Model Applied to Loop Formation in DNA Hairpins, Biophys. J., 2001, 81(5), 2864–2875 CrossRef CAS.
- M. T. Woodside, et al. Nanomechanical measurements of the sequence-dependent folding landscapes of single nucleic acid hairpins, Proc. Natl. Acad. Sci. U. S. A., 2005, 103(16), 6190–6195 CrossRef PubMed.
- Microcompartmentation and Phase Separation in Cytoplasm, A Survey of Cell Biology, ed. H. Walter, D. Brooks and P. Srere, 1999, Intl. Rev. Cell & Mol. Biol. 192 Search PubMed.
- S. K. Ghosh, A. G. Cherstvy, R. Metzler, work in progress.
- C. A. Strulson, et al., RNA catalysis through compartmentalization, Nat. Chem., 2012, 4, 941–946 CrossRef CAS PubMed.
- H. Walter and D. E. Brooks, Phase separation in cytoplasm, due to macromolecular crowding, is the basis for microcompartmentation, FEBS Lett., 1995, 361, 135–139 CrossRef CAS.
- N. F. Dupuis, E. D. Holmstrom and D. J. Nesbitt, Molecular-crowding effects on single-molecule RNA folding/unfolding thermodynamics and kinetics, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(23), 8464–8469 CrossRef CAS PubMed.
- H. Kang, P. A. Pincus, C. Hyeon and D. Thirumalai, 2014, Effects of macromolecular crowding on the collapse of biopolymers, arXiv:1409.5663.
- I. Oh, S. Choi, Y. J. Jung and J. S. Kim, Unusual size-dependence of effective interactions between collapsed polymers in crowded environments, Soft Matter, 2014, 10, 9098–9104 RSC.
- T. N. Shendruk et al., Simulating the Entropic Collapse of Coarse-Grained Chromosomes, 2014, arXiv:1407.2850.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm02007c |
| ‡ In highly-crowded systems, which are the main targets of the current study, the polymer chain experiences collisions with many crowders around in the course of diffusion-limited looping. We thus believe hydrodynamic interactions to be of secondary importance for the static and dynamical effects considered here, likely just re-normalising the effective viscosity of the solution. As we demonstrate, rather the size of thermally-agitated crowders, which are to be displaced to ensure polymer looping, and their volume fraction are the dominant effects. |
| § Note that starting from randomised chain configurations, in simulations of ref. 11 the looping time was computed till the chain ends are closer than a “critical” distance rc. The latter is an important parameter that depends on the type of interactions which act between the chain ends. It has a meaning of effective inter-segmental distance at which e.g. DNA–protein–DNA contacts can be established, ≈3–5 nm for a typical transcription factor. |
| ¶ Note that the one-dimensional end-monomer distribution function p(r) does not involve a Jacobian to recover the free energy profile F(r) since our end-to-end distance measurements already account for the spatial dilation. |
| || The unlooping time is much shorter than the looping time and Tul shows a weaker growth with n than Tl, compare the two panels in Fig. 7. One possible reason is as follows. A looping event is the end-monomer encounter reaction that becomes progressively slower for larger polymer coils. The unlooping time in contrast is related to the (only moderately perturbed) diffusion of the polymer ends on the length-scale of the polymer coil, req(n) ∼ Rg(n). |
| ** Such a statement is valid for relatively weak cohesion strength of the terminal monomers. In contrast, for very large end-to-end binding energies the unbinding kinetics is dominated by the dynamics of terminal monomers only, as illustrated by the Arrhenius-like behaviour for the unbinding events in Fig. 10. The motion of the polymer chain enables the accumulation of the energies ≳kBT required to disrupt the bond between the polymer ends. |
| †† Note that eqn (12) provides a satisfactory description of the looping times.12 Polymer looping is a prolonged barrier-crossing process in which the chain is close to equilibrium. For the reverse process of polymer unlooping, the disjoining of the end monomers takes place over a very short distance and spontaneous free-energy-downhill chain opening events occur (a process, which is inherently out of equilibrium). This is the main reason not to use the free energy-based eqn (12) to evaluate the times of chain unlooping. The latter consists of two terms, the time of disjoining the end monomers and their diffusion from a close distance to the separation req. Depending on the attraction strength εs, the relative contribution of the two terms to Tul varies. For large εs values, for instance, the first contribution dominates so that the unlooping time exhibits the Arrhenius-like kinetics, see eqn (14) and Fig. 10. |
| ‡‡ The reason is as follows. The decay time characterising ACF(Δ) is related to the dynamics of individual monomer–crowder contacts. The interplay of these local fluctuations defines the life-time of a cage mediated by larger crowders for the entire polymer. The looping time is, on the other hand, a target-search problem for the encounter reaction of the two polymer ends in the same small region of space. Being impeded by a topological polymer structure chain looping takes place typically on much longer time scales than T*. |
| §§ After submitting the current manuscript, we became aware of the recent studies of the crowder size.111,112 A stabilisation of intrinsically-disordered proteins and stabilisation of coil-to-globule transitions by crowding was discussed in ref. 111, based on computer simulations of an MMC-induced compaction of polymers. It was shown e.g. that smaller crowders exerting a higher osmotic pressure onto the polymer compact it to a larger extent, as compared to the bigger ones. In contrast to our observations, particularly small crowders are excluded from the space occupied by the self-avoiding polymer. Similar to our results, ref. 111 indicated that the size of the polymer coil reduces monotonically with ϕ. A slight non-monotonic Rg(ϕ) dependence obtained for the same system based on a phenomenological depletion potentials18 is thus rendered to be an artifact.111 The effects of MMC in our system are weaker than in ref. 111 (we have the Flory-like scaling of polymer dimensions and no coil-to-globule transitions occur). The difference may be due to a smaller size of crowders in ref. 111, as compared to the polymer monomers. Similar to our results presented in Fig. 5b, in ref. 113 smaller crowders were shown to be more efficient in compacting the polymer chain. Lastly, in ref. 112 the effects of the crowder size was investigated regarding the strength of depletion interactions between the two polymers. The strength of effective polymer–polymer attraction was shown to be reduced as the crowder size decreases (at a constant ϕ fraction). |
| This journal is © The Royal Society of Chemistry 2015 |