Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymer conformations in polymer nanocomposites containing spherical nanoparticles†
Argyrios
Karatrantos
a,
Nigel
Clarke
*a,
Russell J.
Composto
b and
Karen I.
Winey
b
aDepartment of Physics and Astronomy, University of Sheffield, Sheffield S3 7RH, UK. E-mail: n.clarke@sheffield.ac.uk
bDepartment of Materials Science and Engineering, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA
First published on 29th October 2014
Abstract
We investigate the effect of various spherical nanoparticles on chain dimensions in polymer melts for high nanoparticle loading which is larger than the percolation threshold, using molecular dynamics simulations. We show that polymer chains are unperturbed by the presence of repulsive nanoparticles. In contrast polymer chains can be perturbed by the presence of attractive nanoparticles when the polymer radius of gyration is larger than the nanoparticle radius. At high nanoparticle loading, chains can be stretched and flattened by the nanoparticles, even oligomers can expand under the presence of attractive nanoparticles of very small size.
I. Introduction
The radius of gyration is fundamental to both structure and dynamics in polymeric systems. The addition of nanoparticles to a polymer matrix can result in materials with improved electrical, rheological and tribological properties1 relative to a polymer melt. In this paper, we explore how spherical nanoparticles affect polymer dimensions in nanocomposites in the cases when the polymer radius of gyration (Rg) is larger or of the order of the nanoparticle radius (R).There is controversy as to whether the addition of nanoparticles to a polymer melt alters the polymer conformation. In particular, neutron scattering of a polystyrene (PS) chains/crosslinked PS nanoparticle (R = 2–4 nm) nanocomposite2 showed a polymer chain expansion (20% expansion of entangled polymers at nanoparticle volume fraction ϕ = 10%) for polymer chains with radius of gyration larger than the nanoparticle radius (Rg/R = 1.6–5.7), which is contrary to recent studies of PS/silica (R = 6.5 nm) nanocomposite3–5 for Rg/R = 1.9–3.9,5 and poly(ethylene–propylene) (PEP)/silica nanocomposite (R = 5–7.5 nm)6 where the polymer chains were unperturbed. Moreover in a study of a poly(dimethylsiloxane)/polysilicate (R = 1 nm) nanocomposite,7 a significant increase of the polymer chain dimensions (reaching 60% expansion at nanoparticle volume fraction (ϕ = 40%)) was observed for Rg/R = 6–8 (which is in agreement with the observations of Mackay2) and a decrease in polymer dimensions for Rg ≈ R. The quality of nanoparticle dispersion3,4 can have an important effect on the polymer chain dimensions and this depends on the nanoparticle–polymer interaction, nanoparticle–polymer size ratio,8 size of nanoparticles and nanoparticle volume fraction. In the recent study of PS/silica,5 where the nanoparticles (R = 6.5 nm) were well dispersed, no changes in polymer dimensions were observed. However we need to note that in the experimental area of polymer nanocomposites containing spherical nanoparticles, the role of monomer–nanoparticle interactions on polymer conformations is not yet clear.9
Nevertheless, by using the self-consistent polymer reference interaction site model (SC/PRISM),9 it was observed that spherical nanoparticles, smaller than the polymer chains and attracted to them, perturbed the polymer chain dimensions. The nanoparticles cause an increase in the radius of gyration with an increase in the nanoparticle volume fractions in accordance to the (PS) nanoparticle system,2,8 although there are significant differences between the theoretical model system and the experimental one. Some of the expansion is due to the effects of the excluded volume created by the nanoparticles, the nanoparticles act as good solvents to swell the polymers. From a simulation point of view, there is also controversy as to whether the addition of attractive nanoparticles to a polymer melt causes polymer chains either to expand,10–14 remain unaltered15–20 or reduce their dimensions21–23 compared to their size in the bulk. While most of these simulation studies were performed for low volume fraction of filler12–14,16,17,23 and for nanoparticle size similar to the polymer size,12,14,16 it is well recognized3,5–8 that in the case of polymer–nanoparticles mixtures, the polymer dimensions can be influenced by the characteristics of the nanoparticles (e.g. size, type of nanoparticle surface, dispersion, volume fraction of nanoparticles). To the best of our knowledge there are no studies that have addressed polymer dimensions in nanocomposites above the percolation threshold (ϕc = 31%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24), except the work of Vacatello22 that was implemented at constant density and for spatially frozen nanoparticles of size R = 4–8 nm.
24), except the work of Vacatello22 that was implemented at constant density and for spatially frozen nanoparticles of size R = 4–8 nm.
The rest of this paper is organized as follows. In Section II, we present the general features of the simulation methodology and the simulation details that were used to investigate the polymers in melts and nanocomposites. Subsequently, in Section III, we investigate first the polymer and nanoparticle structure and secondly we calculate the radius of gyration for both unentangled and entangled polymers in nanocomposites as a function of nanoparticle loading, monomer–nanoparticle interaction and nanoparticle size. Finally in Section IV, conclusions are presented.
II. Simulations methodology
To address this fundamental question we use the molecular dynamics method25–28 of a Kremer–Grest model.29 The classical Newton–Langevin equations that govern the motion of the particles is:25,29 | (1) |
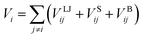 | (2) |
The Lennard-Jones (LJ) potential VLJij, acting along the line between the centres of mass of two particles force30 is given by:
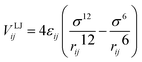 | (3) |
 ), and rij represents the distance between particles i and j. For monomer (m)-nanoparticle (p) interactions the combination rules: εmp = (εmεp)1/2, σmp = (σm + σp)/2 were used.30 The monomers (or nanoparticles) are modeled with the repulsive only part of eqn (3), shifted and truncated with a cut off radius at rc = 21/6σm (rc = 21/6σp for nanoparticles). For attractive monomer–nanoparticle interaction (attractive nanoparticles) the cut off radius is rc = 2.4σmp, and for repulsive monomer–nanoparticle interaction (repulsive nanoparticles) rc = 21/6σmp. Also, the monomers were connected using FENE potential:29
), and rij represents the distance between particles i and j. For monomer (m)-nanoparticle (p) interactions the combination rules: εmp = (εmεp)1/2, σmp = (σm + σp)/2 were used.30 The monomers (or nanoparticles) are modeled with the repulsive only part of eqn (3), shifted and truncated with a cut off radius at rc = 21/6σm (rc = 21/6σp for nanoparticles). For attractive monomer–nanoparticle interaction (attractive nanoparticles) the cut off radius is rc = 2.4σmp, and for repulsive monomer–nanoparticle interaction (repulsive nanoparticles) rc = 21/6σmp. Also, the monomers were connected using FENE potential:29 | (4) |
The stiffness of the polymer chains is controlled by a cosine harmonic bending potential,31 which acts on three consecutive beads along the chain. By increasing the intramolecular stiffness of the polymer chain the entanglement length is decreased to a value of Ne ≈ 58.
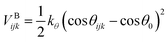 | (5) |
The simulations of the polymer melt were performed at a monomer density ρ* = Nt/V = 0.85 in a simulation cell of total Nt = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 monomers in the simulation box (48
000 monomers in the simulation box (48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 monomers were used for N = 80, 160 polymers), using the NVT ensemble. For equilibration of polymer melts the fast push off method was applied.32 The pressure calculated for the N = 200 polymer melt was P* = Pσm3/εm = 4.864. That pressure was used to perform all the nanocomposite systems simulations in the NPT ensemble. The length of the simulation cell was always larger than the end-to-end distance of the polymer chains. To set the temperature at
000 monomers were used for N = 80, 160 polymers), using the NVT ensemble. For equilibration of polymer melts the fast push off method was applied.32 The pressure calculated for the N = 200 polymer melt was P* = Pσm3/εm = 4.864. That pressure was used to perform all the nanocomposite systems simulations in the NPT ensemble. The length of the simulation cell was always larger than the end-to-end distance of the polymer chains. To set the temperature at  and pressure at P* = 4.864 the Langevin thermostat with a friction constant Γ = 0.5τ−1 and the Berendsen barostat were used with time constant τp = 2τ, respectively. The equations of motion were integrated using the Leap frog algorithm33 with a time step equal to 0.005τ for polymer melts (a time step of 0.004τ was used for nanocomposite simulations), where τ = (mσm2/(kBT))1/2 is the LJ time unit.
and pressure at P* = 4.864 the Langevin thermostat with a friction constant Γ = 0.5τ−1 and the Berendsen barostat were used with time constant τp = 2τ, respectively. The equations of motion were integrated using the Leap frog algorithm33 with a time step equal to 0.005τ for polymer melts (a time step of 0.004τ was used for nanocomposite simulations), where τ = (mσm2/(kBT))1/2 is the LJ time unit.
For nanocomposites, we consider systems of spherical nanoparticles in a dense polymer melt. The starting structures were created by an ensemble of polymers with N = 200 and nanoparticles inserted at random positions within a large simulation box. Subsequently, the NPT ensemble was used at melt pressure of P* = 4.864 to gradually squeeze the simulation box to a dense polymer melt. The equilibration time is long enough for the polymer to move more than twice the radius of gyration of the bulk polymer, Rg, which is the standard equilibration criterion.16,34 Specifically, for polymer matrices N = 200, the equilibrium time was 6 × 105τ ≈ 3τR (where τR = 2 × 105τ is the Rouse time for N = 350 semiflexible polymers35) which is sufficient time to evolve the entanglement density.36 All the types of nanoparticles have reached their diffusive regime (where the mean square displacement of nanoparticles scales linearly with time). The duration of the simulation production runs were between 0.5–3.5 × 105τ depending on the length of molecules and nanoparticles. In the nanocomposite systems studied, a total number of Nt = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 monomers were used in a cubic cell for systems with nanoparticles radius of R/σm = 1 and R/σm = 2, and Nt = 9440 monomers for nanoparticle radius of R/σm = 4. The nanoparticle volume fraction,37
600 monomers were used in a cubic cell for systems with nanoparticles radius of R/σm = 1 and R/σm = 2, and Nt = 9440 monomers for nanoparticle radius of R/σm = 4. The nanoparticle volume fraction,37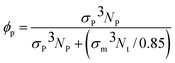 is set by varying the number of particles, Np. Details of the nanocomposite systems studied (nanoparticle volume fraction: ϕ(%), number of nanoparticles: Np of radius R) are summarized in Table 1.
is set by varying the number of particles, Np. Details of the nanocomposite systems studied (nanoparticle volume fraction: ϕ(%), number of nanoparticles: Np of radius R) are summarized in Table 1.
| volume fraction % | N p | N p | N p |
|---|---|---|---|
| R = 1 | R = 2 | R = 4 | |
| 10.3 | 400 | — | — |
| 18.7 | 800 | 100 | 5 |
| 25.7 | 1200 | — | — |
| 31.6 | 1600 | 200 | 10 |
| 40.9 | 2400 | 300 | 15 |
III. Results and discussion
A. Polymer and nanoparticle structure
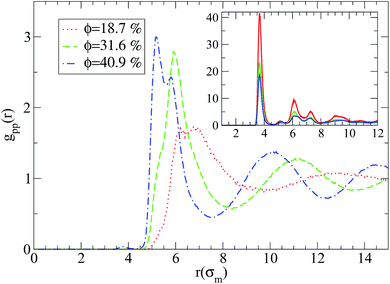
We first focus on the analysis of local polymer structure in nanocomposites. In Fig. 1 we show the monomer–nanoparticle radial distribution function gmp(r) for different nanoparticle loading with attractive or repulsive small nanoparticles (R = 1) respectively. As can be seen from Fig. 1, gmp(r) exhibits a three-layer structure. The high monomer density of the layers establish a well defined interface between nanoparticles and polymer melt whose structure differs from that of the amorphous polymer melt. By dispersing attractive nanoparticle in the polymer matrix the polymer density around the nanoparticles increases as can be seen by the enhanced first peak of gmp(r), comparing with gmp(r) of repulsive nanoparticles (inset in Fig. 1). Also, the nanoparticle loading increases the monomer density of polymers in contact with the nanoparticle surface. Similar behaviour appears in nanocomposites containing larger nanoparticles (R = 2–4) (results not shown).Regarding the nanoparticle structure an entire different behaviour for the two nanocomposite systems is observed as can be seen in Fig. 2. On one hand, when there is a repulsive monomer–nanoparticle interaction, there is a higher probability for the nanoparticles to be in contact with each other than in contact with monomers (inset of Fig. 2), while on the other hand attractive monomer–nanoparticle interaction leads the nanoparticles to be well dispersed in the polymer matrix. If the nanoparticle volume fraction is increased, there are more nanoparticle–nanoparticle contacts as can be seen from the first peak of gpp(r) in Fig. 2. By increasing the nanoparticle radius to R = 2 or R = 4, poor dispersion is observed for repulsive nanoparticles, especially in lowest nanoparticle loading (ϕ = 18.7%) the nanoparticles aggregate to one big cluster as can be seen by the high intensity first peak of gpp(r) in the inset of Fig. 3. Thus, in nanocomposites containing nanoparticles of radius to R = 2 or R = 4 the nanoparticles form aggregated clusters for repulsive monomer–nanoparticle interaction. Aggregation has been observed experimentally for polymer nanocomposites with weak interactions such as polystyrene–silica nanocomposite3,4 and possibly for the repulsive nanoparticle nanocomposite such as PEP–silica6 in which the TEM data were not reported. However, when the monomer–nanoparticle attraction is present there are no nanoparticle contacts for all the nanoparticles loading as can be seen from gpp(r) in Fig. 3. The nanoparticles are well dispersed in the polymer melt (the same behaviour is observed for nanoparticles of radius R = 4 – results not shown) in agreement with experimental observations for miscible systems such as PS chains-crosslinked PS nanoparticles.2
Attractive nanoparticles of radius R = 1 have diffused in the polymer matrix (N = 200) several times of Rg distance at high nanoparticle loading (ϕ = 40.9%) and its diffusivity is D = 4.4 × 10−4(σm2/τ). Thus, we can consider them as mobile. The diffusivity of large attractive nanoparticles (R = 2, 4) is small though due to their high mass, for example at ϕ = 40.9% (polymer matrics: N = 200 and N = 160 respectively), their diffusivity is D = 2.7 × 10−5 (for R = 2) and D = 4.39 × 10−6(σm2/τ) (for R = 4). Since the large nanoparticles of R = 2, 4 have not diffused a distance further than twice their diameter at high nanoparticle loading, in an entangled matrix, we consider them as immobile (see mean square displacement of nanoparticles R = 2 in the ESI† section).
B. Polymer dimensions
We now focus on the polymer dimensions analysis on melts and nanocomposites. The radius of gyration of a molecule, which is defined as the average squared distance between monomers in given conformation and the molecule's center of mass is given by:38,39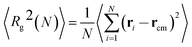 | (6) |
 is the center of mass of the chain. The radii of gyration of the polymer melt simulated systems are given in Table 2.
is the center of mass of the chain. The radii of gyration of the polymer melt simulated systems are given in Table 2.
| N | 10 | 20 | 40 | 50 | 80 | 100 | 160 | 200 |
|---|---|---|---|---|---|---|---|---|
| R g0 | 1.577 | 2.367 | 3.479 | 3.915 | 5.019 | 5.626 | 7.211 | 8.05 |
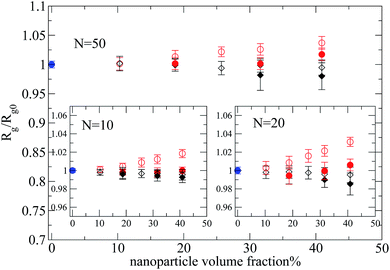
Let's first focus on polymer dimensions of nanocomposites with nanoparticles (R = 2) dispersed in polymer matrix (N = 100, 200). The trend is different between the two types of nanocomposites as can be seen in Fig. 4. In nanocomposites containing repulsive nanoparticles (black symbols), the polymers dimensions are not altered by the nanoparticle loading. The polymers are phase separated from the repulsive nanoparticles (of R = 2) in the nanocomposites, thus there is no change on radius of gyration values. On the other hand, in the nanocomposites containing attractive nanoparticles, the Rg increases, with increased nanoparticle loading, compared to its bulk value.
By reducing the nanoparticle radius of the nanocomposite to R = 1, similar trends can be observed as can be seen in Fig. 4. In this case, even though there are smaller clusters (inset of Fig. 2) than in the nanocomposites with large nanoparticles, there is no polymer swelling. When attractive monomer–nanoparticle interactions are present the overall polymer dimensions increase dramatically at high nanoparticle loading. In particular, the magnitude of expansion of polymer dimensions is larger for polymers with N = 200 following qualitatively the experimental data.7,8 In Fig. 4 we depict the relation Rg/Rg0 = (1 − ϕ)−1/3 (ref. 9) which predicts the polymer expansion due to the excluded volume introduced by the nanoparticles, assuming no change in density on mixing. The end-to-end distance data follow the same trend. All the polymers have a Gaussian conformation up to percolation threshold for all the nanocomposites. In nanocomposites (N = 160–200) above the percolation threshold the ratio 〈Ree〉2/〈Rg〉2 ≈ 6.1–6.22, so, we consider that the polymers still keep their Gaussian conformation. We also report the mean square internal distances for nanocomposite systems containing small nanoparticles (R = 1) in the ESI† section (data for larger nanoparticles have similar trends).
Hence polymer expansion appears in nanocomposites with attractive interactions and increases with the nanoparticle loading, the very small nanoparticles such as of radius R = 1 act as a good solvent and cause the polymer to expand. To further characterize the polymer structure, we calculated the principal moments (eigen values) of the gyration tensor, λ2i(i=1–3) (where Rg2 = λ12 + λ22 + λ32), for different nanoparticles volume fractions and depict these in Fig. 5. In our simulations for a polymer melt with chains of N = 200, the principal moments of the gyration tensor approach, λ12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ22
λ22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ32 = 12.1
λ32 = 12.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.7
2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.40 At high nanoparticle loading, ϕ ≥ 18.7%, the polymer chains are stretched and flattened by the nanoparticles, as can be seen from the λ12, λ22 values in comparison to the bulk values. Even oligomers (N = 20–50) are stretched and flattened at the highest nanoparticle loading (results not shown).
1.40 At high nanoparticle loading, ϕ ≥ 18.7%, the polymer chains are stretched and flattened by the nanoparticles, as can be seen from the λ12, λ22 values in comparison to the bulk values. Even oligomers (N = 20–50) are stretched and flattened at the highest nanoparticle loading (results not shown).
In the case of nanocomposites containing short polymers (N = 10, 20, 50) as matrix and repulsive nanoparticles, polymers remain unaltered compared with their melt values as can be seen in Fig. 6. Instead when attractive interactions are present the polymer dimensions increase compared with its melt value for small nanoparticles and loading ϕ ≥ 18.7% even for the smallest polymers studied (N = 10) (where Rg > R). This polymer expansion with nanoparticle loading becomes more abrupt for larger polymers (N = 50).
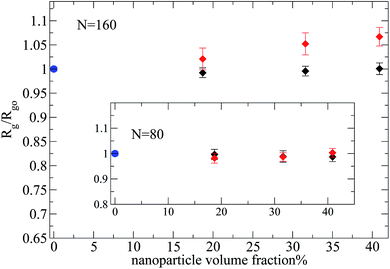
Then, we focus on the analysis of a nanocomposite system with larger nanoparticles of R = 4, in which the Rg of polymers chains with N = 160 (N/Ne ≈ 3) monomers is of the order of nanoparticle diameter ( ), which is made equivalent to the experimental repulsive nanocomposite by mixing PEP and hydrophobic modified silica.6 By such an increase of the nanoparticle radius at a constant nanoparticle volume fraction, we decrease the interfacial area. For the case of polymers (N = 80, 160) and repulsive nanoparticles the Rg remains unperturbed for all the nanoparticle loadings. Even for high nanoparticle loading we can not see any polymer contraction as was observed for entangled PEP polymers filled with silica nanoparticles6 (where there is a polymer contraction of 12% above percolation (ϕ = 50%)). This may arise either from the fact that in the large nanoparticles (R = 4) nanocomposites studied
), which is made equivalent to the experimental repulsive nanocomposite by mixing PEP and hydrophobic modified silica.6 By such an increase of the nanoparticle radius at a constant nanoparticle volume fraction, we decrease the interfacial area. For the case of polymers (N = 80, 160) and repulsive nanoparticles the Rg remains unperturbed for all the nanoparticle loadings. Even for high nanoparticle loading we can not see any polymer contraction as was observed for entangled PEP polymers filled with silica nanoparticles6 (where there is a polymer contraction of 12% above percolation (ϕ = 50%)). This may arise either from the fact that in the large nanoparticles (R = 4) nanocomposites studied  , whereas in Nusser's work
, whereas in Nusser's work  (ref. 6) or that the volume fraction studied is not high enough since above the percolation threshold (ϕc ≈ 31%) with increasing ϕ the geometrical confinement strongly gains importance.6 However, the monomer nanoparticle attraction does alter distinctively the polymer dimensions especially for high nanoparticle volume fraction as can be seen in Fig. 7. At nanoparticle loading ϕ = 18.7% the polymer chains remain unperturbed in agreement with the weakly interacting PS/silica nanocomposite5 which was investigated up to ϕ = 32% nanoparticle loading. Additionally, we have observed that the average radius of gyration of the short polymer chains (N = 10, 20, 40), in nanocomposites containing large nanoparticles of R = 4, does not change compared to its melt value for both repulsive and attractive nanoparticles at all volume fractions studied (results not shown). Thus we can conclude that short polymers in nanocomposites with Rg ≤ R, remain unperturbed as this result has also been observed experimentally in the PEP/silica nanocomposites.6,41
(ref. 6) or that the volume fraction studied is not high enough since above the percolation threshold (ϕc ≈ 31%) with increasing ϕ the geometrical confinement strongly gains importance.6 However, the monomer nanoparticle attraction does alter distinctively the polymer dimensions especially for high nanoparticle volume fraction as can be seen in Fig. 7. At nanoparticle loading ϕ = 18.7% the polymer chains remain unperturbed in agreement with the weakly interacting PS/silica nanocomposite5 which was investigated up to ϕ = 32% nanoparticle loading. Additionally, we have observed that the average radius of gyration of the short polymer chains (N = 10, 20, 40), in nanocomposites containing large nanoparticles of R = 4, does not change compared to its melt value for both repulsive and attractive nanoparticles at all volume fractions studied (results not shown). Thus we can conclude that short polymers in nanocomposites with Rg ≤ R, remain unperturbed as this result has also been observed experimentally in the PEP/silica nanocomposites.6,41
IV. Conclusions
To summarize, we investigated the conformations of polymers, for the first time in nanocomposites containing small spherical nanoparticles at high volume fraction, as depicted on the polymer radius of gyration in a broad size range 1.225 ≤ Rg/R ≤ 7.85 (for N = 80–200) for a range of nanoparticle loadings using molecular dynamics simulations. We find that in nanocomposites with repulsive monomer–nanoparticle interaction the polymers do not contract when taking into account the error margin. On the other hand, in nanocomposites with attractive monomer–nanoparticle interactions the polymers increase their size with the nanoparticle loading in qualitative agreement with the experimental data.2,7 We showed that in such nanocomposites with well dispersed small nanoparticles, the condition Rg > R is essential for polymer swelling in agreement with the observations of Nakatani7 and Tuteja–Mackay.2 In particular, this behaviour becomes more dramatic for the systems with the smallest nanoparticles (R = 1) dispersed in the polymer matrix where even short polymers can increase their dimensions slightly with nanoparticle loading when Rg > R, due to the high interfacial area following the observations of Nakatani7 and Tuteja–Mackay.2 Also, the fact that small nanoparticles of R = 1 are very mobile can also contribute on the chain expansion as reported in.42 In addition, the short polymer chains remain unperturbed from the nanoparticles when Rg ≤ R, in agreement with the experimental data.6In experiments only the nanocomposites systems by Nakatani7 and Tuteja2 contain very small nanoparticles of R = 1 nm and R = 2 nm, whereas in the work of Kumar3,5 in which no polymer expansion was observed, the nanoparticle size was R = 6.5 nm although the polymer radius of gyration was larger than R. Thus, we can conclude that the polymer–nanoparticle interaction, nanoparticle size and nanoparticle loading can play a major role in the polymer radius of gyration for nanocomposites in the size range of  and for very small nanoparticles which are well dispersed in the polymer matrix.
and for very small nanoparticles which are well dispersed in the polymer matrix.
Acknowledgements
This research was funded by the EPSRC/NSF Materials Network program EP/5065373/1 (EPSRC:NC, AK) and DMR-1210379 (NSF:KIW, RJC).References
- S. K. Kumar and R. Krishnamoorti, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 37 CrossRef CAS PubMed
.
- A. Tuteja, P. Duxbury and M. Mackay, Phys. Rev. Lett., 2008, 100, 077801 CrossRef
.
- S. Sen, Y. Xie, S. K. Kumar, H. Yang, A. Bansal, D. L. Ho, L. Hall, J. B. Hooper and K. S. Schweizer, Phys. Rev. Lett., 2007, 98, 128302 CrossRef
.
- N. Jouault, F. Dalmas, S. Said, E. Di Cola, R. Schweins, J. Jestin and F. Boue, Macromolecules, 2010, 43, 9881 CrossRef CAS
.
- M. K. Crawford, R. J. Smalley, G. Cohen, B. Hogan, B. Wood, S. K. Kumar, Y. B. Melnichenko, L. He, W. Guise and B. Hammouda, Phys. Rev. Lett., 2013, 110, 196001 CrossRef CAS
.
- K. Nusser, S. Neueder, G. J. Schneider, M. Meyer, W. Pyckhout-Hintzen, L. Willner, A. Radulescu and D. Richter, Macromolecules, 2010, 43, 9837 CrossRef CAS
.
- A. Nakatani, W. Chen, R. Schmidt, G. Gordon and C. Han, Polymer, 2001, 42, 3713 CrossRef CAS
.
- M. E. Mackay, A. Tuteja, P. M. Duxbury, C. J. Hawker, B. Van Horn, Z. Guan, G. H. Chen and R. S. Krishnan, Science, 2006, 311, 1740 CrossRef CAS PubMed
.
- A. L. Frischknecht, E. S. McGarrity and M. E. Mackay, J. Chem. Phys., 2010, 132, 204901 CrossRef PubMed
.
- F. W. Starr, T. B. Schroder and S. C. Glotzer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021802 CrossRef CAS
.
- J. Huang, Z. Mao and C. Qian, Polymer, 2006, 47, 2928 CrossRef CAS PubMed
.
- M. Goswami and B. G. Sumpter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041801 CrossRef
.
- G. G. Voyiatzis, E. Voyiatzis and D. N. Theodorou, Eur. Polym. J., 2011, 47, 699 CrossRef PubMed
.
- T. V. M. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Bohm and F. Müller-Plathe, Macromolecules, 2011, 44, 2316 CrossRef CAS
.
- G. D. Smith, D. Bedrov, L. Li and O. Byutner, J. Chem. Phys., 2002, 117, 9478 CrossRef CAS PubMed
.
- T. Desai, P. Keblinski and S. K. Kumar, J. Chem. Phys., 2005, 122, 134910 CrossRef PubMed
.
- P. J. Dionne, R. Osizik and C. R. Picu, Macromolecules, 2005, 38, 9351 CrossRef CAS
.
- A. Karatrantos, R. J. Composto, K. I. Winey and N. Clarke, Macromolecules, 2011, 44, 9830 CrossRef CAS
.
- A. Karatrantos, R. J. Composto, K. I. Winey, M. Kröger and N. Clarke, Macromolecules, 2012, 45, 7274 CrossRef CAS
.
- A. Karatrantos, N. Clarke, R. J. Composto and K. I. Winey, Soft Matter, 2013, 9, 3877 RSC
.
- M. Vacatello, Macromolecules, 2001, 34, 1946 CrossRef CAS
.
- M. Vacatello, Macromolecules, 2002, 35, 8191 CrossRef CAS
.
- M. Vacatello, Macromol. Theory Simul., 2003, 12, 86 CrossRef CAS
.
- M. J. Powell, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4194 CrossRef
.
- H. Bekker, H. J. C. Berendsen, E. J. Dijkstra, S. Achterop, R. van Drunen, D. van der Spoel, A. Sijbers, H. Keegstra, B. Reitsma and M. K. R. Renardus, Physics Computing 92, 1993, 252 Search PubMed
.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43 CrossRef CAS
.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306 CAS
.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. Mark and H. Berendsen, J. Comput. Chem., 2005, 26, 1701 CrossRef CAS PubMed
.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057 CrossRef CAS PubMed
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed
.
- M. Bulacu and E. van der Giessen, J. Chem. Phys., 2005, 123, 114901 CrossRef PubMed
.
- R. Auhl, R. Everaers, G. S. Grest, K. Kremer and S. J. Plimpton, J. Chem. Phys., 2003, 119, 12718 CrossRef CAS PubMed
.
- W. F. van Gunsteren and H. C. J. Berendsen, Mol. Simul., 1988, 1, 173 CrossRef
.
- J. Liu, Y. Wu, J. Shen, Y. Gao, L. Zhang and D. Cao, Phys. Chem. Chem. Phys., 2011, 13, 13058 RSC
.
- M. Pütz, K. Kremer and G. S. Grest, Europhys. Lett., 2000, 49, 735 CrossRef
.
- R. S. Hoy and M. O. Robbins, Phys. Review E, 2005, 72, 061802 CrossRef
.
- J. T. Kalathi, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2012, 109, 198301 CrossRef
.
-
P. Flory, Statistical Mechanics of Chain Molecules, Hanser Publishers, Munich, 1989 Search PubMed
.
-
M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed
.
- R. C. Picu and M. S. Ozmusul, J. Chem. Phys., 2003, 118, 11239 CrossRef CAS PubMed
.
- K. Nusser, G. I. Schneider, W. Pyckhout-Hintzen and D. Richter, Macromolecules, 2011, 44, 7820 CrossRef CAS
.
- F. M. Erguney, H. Lin and W. L. Mattice, Polymer, 2006, 47, 3689 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm01980f |
| This journal is © The Royal Society of Chemistry 2015 |