Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-assembly of biaxial discorectangular lead carbonate nanosheets into stacked ribbons studied by SAXS and HAADF-STEM tomographic tilt series†
J.
Zhang
a,
T.
Vad
b,
M.
Heidelmann‡
c,
T. E.
Weirich
cd and
W. F. C.
Sager‡
*a
aInstitute of Complex Systems, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: w.sager@fz-juelich.de
bInstitut für Textiltechnik, RWTH Aachen University, 52074 Aachen, Germany
cCentral Facility for Electron Microscopy, RWTH Aachen University, 52074 Aachen, Germany
dInstitute for Crystallography, RWTH Aachen University, 52074 Aachen, Germany
First published on 17th October 2014
Abstract
The self-assembling behaviour of 2.6 nm thin PbCO3 nanoplatelets with discorectangular shape and uniform width and thickness occurring after their formation in nonionic water-in-oil microemulsions has been investigated using synchrotron small angle X-ray scattering (SAXS) and (scanning) transmission electron microscopy ((S)TEM). The presence of attractive depletion forces originating from the ubiquitous microemulsion droplets triggers a new type of superstructure at low particle concentration. Instead of the universally observed formation of face-to-face assembled lamellar mesostructures, the nanosheets self-organise into extended ribbon structures, whereby each on top lying sheet is displaced by a constant shift in the length and width directions leading to a so far unprecedented staggered zigzag-type stack assembly with restricted height. This type of stacking gives rise to a complex interference pattern in the isotropic small angle scattering of the stacked ribbon assemblies (SRAs) in reverse micellar solution. Different to the, for lamellar-structured nanosheets typical, diffraction peaks at multiples of the wave vector corresponding to one particular repeat distance, the scattering peaks measured in this study are asymmetric, displaying a shoulder on their low wave vector side. The asymmetric shape of the observed face-to-face correlation peaks indicates that the SRAs do not extend in one direction only. Their scattering behaviour is analysed by expanding the Kratky–Porod structure factor for stacking plates into three dimensions. High-angle annular dark-field (HAADF)-STEM tilt series have complementary been acquired to retrieve three-dimensional structural information on the SRAs in the dry state and to confirm the model used for the refinement of the SAXS data.
1 Introduction
Anisometric inorganic nanoparticles with a well-defined shape have gained increasing interest in recent years not only due to the possibility to modulate the physical and chemical properties of nanomaterials by controlling their dimensionality (i.e., from zero-dimensional (0D) spheres to one-dimensional (1D) rods and wires to two-dimensional (2D) plates and sheets),1–5 but also due to their rising potential as building blocks in the modular assembly of nanostructured materials (nanocrystal superstructures) and their intrinsic ability to form mineral liquid crystals (MLCs). Current research in this area is focused on directing spontaneous organisation of matter into ordered arrangements and thus to develop new materials by designing and/or engineering their building blocks.6,7 A remaining challenge lies in predicting structure from constituent building blocks and to understand how self-assembling processes are governed by the shape (and topology) of the individual particles and the forces acting between them.8,9Biaxial (or board-like) particles display due to their dual nature a self-assembling behaviour in between rod-like (r) and plate-like (p) ordering. Hard rods and plates, i.e., particles having no interactions other than their inability to occupy the same region in space, can on pure entropic grounds spontaneously align and order into layers and columns at intermediate packing densities, provided that the structures formed increase the configurational space available to the particles.10 Due to the deviation from a cylindrical shape, biaxial hard particles exhibit a richer phase behaviour (mesophase polymorphism) than uniaxial rods and plates,11 when the appropriate conditions in shape, polydispersity and/or (directed) interparticle forces are met. Theoretical studies predict that with increasing packing density biaxial nematic (NB, with orientational order along three directors) and smectic (SmB, with in-layer orientational order) liquid crystalline (LC) phases form when the two aspect ratios of the particles, i.e., the length-to-width ratio (κ1) and the width-to-thickness ratio (κ2), become equal (κ1 ≈ κ2), while common uniaxial phases are stable for κ1 > κ2 (N(r)U and Sm(r)U) and κ1 < κ2 (N(p)U and Sm(p)U).11–13 The existence regions and phase sequence of the different mesophases are found to depend on particle geometry (e.g., rectangular, discorectangular or ellipsoidal cross-sectional shape),14 biaxial shape anisometry12,13 and particle polydispersity.15 The NB phase has been found to be stable for κ2 ≥ 2.5 and widens up with increasing κ2. For κ2 ≥ 5 the SmB phase and for κ2 ≥ 10 the NB phase splits additionally up into Sm(r)B and Sm(p)B and N(r)B and N(p)B regions, respectively.12§ Size polydispersity renders generally the establishment of long-distance positional ordering unfavourable, thus stabilising the NB phase with respect to smectic phases, but induces in this case also the formation of the NB phase if κ1 is slightly larger than κ2.15 Experimentally, the NB-phase has so far only been found for board-like goethite particles at κ1 ≈ κ2 ≈ 3.1 at size polydispersities >20%.16 The addition of small co-solutes (e.g., nonadsorbing polymers or micelles) to a stable particle dispersion gives rise to entropic short-range depletion attractions17,18 and allows such tuning of the effective attraction between the particles by the depletant density. Since the depletant entropy is maximized if the total volume available to the depletant is maximal, favouring thereby states that increase the overlap between the depletion regions of the particles, depletion forces become directional for anisometric particles.19,20 In the case of board-like particles the depletants induce attraction perpendicular to the largest faces favouring plate-like ordering.21 As biaxial phases form at the crossover between rod- and plate-like behaviour, the NB phase can become stable with increasing depletion density for boards with κ1 > κ2. Increasing depletant density reduces the stability of the LC phases resulting in a direct isotropic-solid transition.
Besides delamination from materials with layered structures,22 colloidal synthesis routes for thin free-standing nanosheets have increasingly been developed over the last five years due to the rising potential that 2D crystals offer (e.g., as multiple quantum well structures for semiconductor materials). These include routes that make use of subtle energy differences among the possible facets to facilitate growth along only one specific facet,23 soft template methods24 and oriented attachment of smaller nanocrystals.25,26 So far only 1D assembly of the sheets into lamellar stacks has been observed, whereby SAXS has mainly been used to determine the spacing between the constituting nanosheets.22,23,25,27
Here, we employ nonionic water-in-oil (w/o) microemulsions at low water content to synthesize well-defined lead carbonate nanosheets of biaxial shape that are characterised by a narrow width and thickness distribution and κ1 and κ2 values of about 2.7 and 5.5, respectively. At low particle concentrations we observe for the first time a transition of the self-assembling behaviour of the sheets from the commonly observed one-dimensional (1D) lamellar mesostructures to a novel type of superstructure, i.e., extended stacked ribbon assemblies of restricted height. The new structure is analysed by SAXS experiments with synchrotron radiation performed at the X33 beam line at the Doris III storage ring (DESY, Germany) and electron tomographic tilt series using high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) as imaging technique. Modelling the SAXS data using a Kratky–Porod type structure factor28 for stacking platelets that we expand into three-dimensions, we demonstrate that the obtained SRAs consist of face-to-face stacked sheets, whereby consecutive sheets are displaced by a constant shift in the width and length directions of the sheets. This leads to a well-defined staggered zigzag-type stack assembly and thus to ribbons that show extended growth in the length direction of the sheets while their height (stacking direction) is nearly constant.
2 Methods
Nanoparticles preparation
PbCO3 nanosheets were synthesized by mixing two water-in-oil microemulsions containing either 0.3 M Pb(NO3)2 or 0.3 M NaHCO3 as aqueous phase at 306 K. The microemulsions were made of appropriate amounts of Igepal CO-520 (ethoxylated nonylphenol with on average 5 ethylene oxide groups, Sigma-Aldrich), aqueous phase and cyclohexane (p.a., Merck) to yield a water-to-surfactant ratio (W/S) of 0.2 at concentrations of 13.6% and 6.8% Igepal in cyclohexane. Salts were purchased at their highest commercially available grade and water was purified using a Millipore purification unit (Milli-Q). The reaction was started by combining both microemulsions at 306 K and kept under stirring. For observation by TEM, samples were periodically taken from the reacting microemulsion. One drop of the collected particle-containing microemulsion was placed on a TEM-grid, which was then dried in an oven at 333 K. For inspection by SAXS, water was removed after 2 h from the reacting microemulsion by azeotropic distillation. Cyclohexane was added to regain the original volume. The particle suspension was vigorously shaken to ensure homogeneity prior to the SAXS measurements.Transmission electron microscopy
TEM-images were acquired from dried particle dispersions on carbon or silicon oxide coated copper grids with a Philips CM200 transmission electron microscope operating at 200 kV, equipped with a LaB6 cathode as electron source and an SIS Morada 11 megapixel side mounted CCD camera (Olympus Soft Imaging Solutions).HAADF-STEM tilt series
To reduce organic contamination in the TEM, dried up surfactant was removed from the TEM-grids by rinsing the grids with a few drops of n-hexane followed by plasma cleaning. Tomographic tilt series were recorded with a 200 kV FEI Tecnai F20 TEM using a Fischione high-angle annular dark-field (HAADF) detector for Z-contrast imaging in STEM mode. The HAADF-STEM signal was collected using a small camera length of 70 mm corresponding to a minimum scattering angle of 87 mrad. Acquisition of the tilt series was performed with a Gatan 916 single-tilt tomography holder allowing a maximum tilt angle of 80°. For automated data collection of the tilt series the Gatan 3D tomography-acquisition software was employed, correcting for specimen movement and focus change after tilting. Data post processing, e.g., tomographic alignment of the tilt series and subsequent 3D reconstruction using WBP (weighted back-projection) and SIRT (simultaneous iterative reconstruction technique) as reconstruction algorithms were carried out within the Gatan software package. The reconstructions allowed, however, the 3D visualization of the individual nanosheets but did not give detailed metric information on the stacks. One reason for this limitation is that the surfactant molecules that reside between the sheets are not stable under the electron beam and cause thus a non-constant background that cannot easily be subtracted. Additionally the complex nanoscale stacking of the sheets is difficult to resolve within a formed SRA. Therefore, the open source 3D rendering software Blender (Blender Foundation, The Netherlands, http://www.blender.org) was used to explore the origin of the experimentally observed contrast features in the tilt series by modelling two stacks consisting of 10 semi-transparent sheets using the parameters from the SAXS-refinement given in Table 1. Semi-transparency was applied to mimic the interference patterns originating from the experimental HAADF thickness contrast.Small angle X-ray scattering
The SAXS measurements were performed at the European Molecular Biology Laboratory (EMBL) X33 beam line at the Doris III storage ring (Deutsches Elektronen Synchrotron (DESY), Hamburg, Germany). The samples were filled into a 100 μl thermostated flat in-air cell with mica windows. The data were recorded at room temperature using a 1M Pilatus detector (DECTRIS) at a sample-to-detector distance of 2.7 m and a wavelength of 0.15 nm, covering a range of momentum transfer of 0.07 ≤ q ≤ 6 nm−1 (q = 4πsin(θ)/λ is the modulus of the scattering vector, 2θ is the scattering angle and λ is the wavelength). After normalisation to the intensity of the transmitted beam the collected data were radially averaged.29 For both particle dispersion and reverse micellar solution, the scattering of the solvent was subtracted prior to data analysis.Modelling of the small angle X-ray scattering intensities
Least-squares fitting of the model-curve to the observed SAXS data was performed with a self-written Fortran90 program, employing the Levenberg–Marquardt routines MRQMIN and MRQCOF.30,31 Broadening of the peaks due to smearing by the instrumental resolution function has not been taken into account, since it was found to be smaller than the broadening caused by the experimental uncertainties.Background scattering
The background scattering intensity Ibg(q) can be expressed by a power law of the form Ibg(q) = A/qp, which describes the scattering contribution from probably larger SRAs on swollen mica-windows of the sample cell.Average structure factor
The average or effective structure factor32 depicted in Fig. 5D is defined by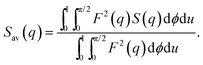 | (1) |
3 Results and discussion
3.1 Formation of stacked ribbon assemblies (SRAs)
In this study a nonionic water-in-oil microemulsion has been employed as reaction medium for the formation of the discorectangular nanosheets and their self-assembly into the stacked ribbon structures. Microemulsions are thermodynamically stable mixtures of water (or aqueous phase), oil and surfactant(s). They consist of nanosized water and/or oil domains that are separated by a surfactant monolayer and display, upon varying composition and temperature, a rich phase behaviour, whereby spherical and cylindrical droplets as well as bicontinuous structures form. In the case of w/o microemulsions, that have widely been used to synthesize inorganic nanoparticles, exchange of matter (e.g., ions or water-soluble species) between the water pools takes place when the droplets collide, allowing in principle control of nucleation and growth processes of the solid phase being formed.33–36 Adjusting the conditions of the microemulsion can – even for the same precursor salt system – facilitate, in addition to changes in particle size, also different particle morphologies and crystal structures.34,37For the synthesis of the PbCO3 nanosheets, we used an aqueous phase – Igepal CO-520 – cyclohexane system. The microemulsions were prepared with 13.6% Igepal (a nonionic surfactant of the ethoxylated arylether type with nonylphenol as hydrophobic moiety and on average 5 ethylene oxide groups) in cyclohexane at a low content of aqueous phase (water-to-surfactant ratio (W/S) of 0.2), see Methods for the details of the preparation. A nonionic surfactant has been chosen to reduce the influence of salt added to the aqueous phase on the phase behaviour and microstructure of the formed microemulsions (see (ESI†)) and to minimize specific interactions between the surfactant molecules and certain (charged) particle faces that could lead to a blocking of given growth directions as in the case of ionic surfactants. The microemulsion system with water as aqueous phase contains repelling spherical droplets with a radius of 3.8 nm and a size polydispersity of 18%.38 The water pool radius of 1 nm is quite small, but the pools contain still 50% of bulk-like water. The size and properties of the water droplets do in this case not significantly change due to the addition of the salts utilised for the synthesis of the lead carbonate nanosheets (see ESI† for additional SAXS experiments). The parental microemulsions (i.e., otherwise identical microemulsions that contain either lead or carbonate ions in their interior water pools) encompass for the applied concentration of 0.3 M precursor salt in the aqueous phase thus on average 3 ions in 4 microemulsion droplets. This shows that the formation of the PbCO3 nuclei is governed by the exchange kinetics between colliding droplets.36 The preparation conditions were selected such that uniform lathlike nanosheets form after mixing the two parental microemulsions that self-assemble into the novel type of stacked ribbons assemblies (SRAs) instead of 1D lamellar mesostructures. The resultant final volume fraction of the PbCO3 sheets is with 0.013% (0.106% weight fraction) very low. Since the major part of the microemulsion droplets stays intact during the nanosheet formation (see ESI†), they act as depletants and evoke attractive forces between the sheets. The calculated contact energy19 for the depletion attraction lies at −14 kBT. The high value is thus responsible for the self-aggregation of the nanosheets at the low particle concentration employed. Additionally performed dynamic light scattering measurements and optical light microscopy on the SRA-containing microemulsions in the liquid state confirm the formation of larger self-assembled structures within the microemulsions. These are presented in the ESI (see Fig. S1C and S1D†).
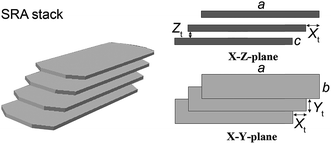
Fig. 1 shows bright-field TEM-images of the SRAs at different formation time and magnification. Most of the discorectangular sheets are building up within the first 30 min of the reaction. Individual and as such non-stacked singly lying nanosheets can be seen on the right side of Fig. 1E and G. They are quite regular in shape and display a width of 44 ± 2 nm and a length of 121 ± 14 nm. Their thickness that can only be judged if the sheets stand on one of their side faces (see, e.g., Fig. 1B and D), is very uniform and is of the order of 2–3 nm. Once the sheets have gained in size and number they start from about 30 min onwards to assemble face-to-face into – so far – unprecedented long straight ribbons that display a restricted height. The smaller assemblies observed at 30 min (Fig. 1B) and 1 h (Fig. 1F) reveal that while extended growth of the individual ribbons carries on in the length direction of the sheets, concomitant side-by-side arrangements of the ribbons takes place. During the assembling process the ribbon height, which corresponds to the stacking direction, stays nearly constant. The uniform thickness of the sheets and the regular stacking in the height direction can be seen in Fig. 1D, which displays three neighbouring ribbons from the short side of the sheets. A detailed view of an outgrown SRA at 2 h (Fig. 1E) that faces the platelet stacks from the top, unravels the origin of the extended ribbon growth. Each on top lying sheet in the stack is displaced by a constant shift in the length direction. At the upper end of the SRA the contours of the individual sheets are seen. Each consecutive sheet can be identified by its rounded edges and the increased contrast due to thickness multiplication. The small angle diffraction pattern obtained by Fourier transformation (FFT) of the same SRA micrograph demonstrates (with 7 reflexes on each side) the high regularity of the side-by-side arrangement of the ribbons. Overview images of outgrown SRAs display the distinct band structure and the cooperative bending of the ribbons on larger scales (Fig. 1A and G). The commonly observed (cooperative) bending of the ribbons is a hint for the existence of an additionally occurring shift of the stacking sheets in their width direction. The structure of the resultant SRAs is described in detail in the next section.
 | ||
| Fig. 1 TEM bright-field micrographs of PbCO3 stacked ribbon assemblies, formed in nonionic w/o microemulsions stabilised by 13.6% Igepal at W/S = 0.2, at different formation times as displayed in the upper right corners. The onset of the SRA formation is shown in (B) and (F), whereas larger SRAs can be seen in (A) and (G) for an overview and in (E) for more detailed information. (C) Digital small angle diffractogram of (E). The different reflexes correspond to multiples of the distance between two neighbouring ribbons in the SRA. (D) Detail of three neighbouring ribbons viewed from their short side. A schematic drawing of the SRAs is given in Fig. 4. The scale bars correspond, if not stated otherwise, to 200 nm. | ||
In order to find out whether it is possible to influence the type of platelet stacking, we also performed the same reaction at a surfactant concentration of 6.8% and thus at about half the droplet and particle concentrations. Under these conditions identical nanosheets are formed, but most of the sheets align face-to-face in the common way into 1D lamellar stacks as shown in Fig. 2A and B. In this case the stacking direction is also the growth direction, which lies perpendicular to the platelet face (lateral dimensions). This requires a higher number of sheets than for the SRAs to extend by the same distance. In addition to the 1D mesostructures a small number of single ribbons of the SRA type are found (Fig. 2D) that extend over more than 1 μm in length while consisting of less than 50 sheets. The highly regular SRAs occupy less space, hinting presumably at the formation of nuclei of a (new) solid mesophase in solution. The surfactant molecules themselves will probably not play a key role for the type of new platelet ordering, since they exceed the number of ions by a factor of 40.
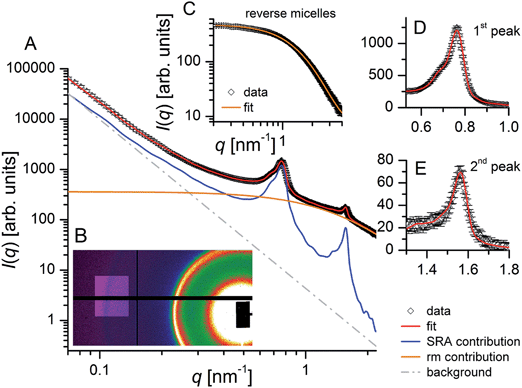
3.2 Small angle X-ray scattering from SRA suspensions
In order to analyse the scattering behaviour of the stacked ribbon assemblies we first need a model that describes the characteristics of the assemblies within the size range covered by the small angle X-ray measurements performed. Fig. 3 displays the measured small angle scattering intensities from a suspension of the SRAs in reverse micellar solution after removing water from the w/o microemulsion, used as precipitation medium, by azeotropic distillation. The covered scattering vector-range from 0.07 ≤ q ≤ 6 nm−1 (q = 4π sin(θ)/λ is the modulus of the scattering vector, 2θ is the scattering angle and λ is the wavelength) facilitates probing a size range between 1 and 90 nm and enables obtaining information on the dimensions of the constituting nanosheets and their arrangement within the SRAs. The two-dimensional scattering pattern shown in Fig. 3B is isotropic indicating a random distribution of the SRAs in solution and displays two sharp rings at intermediate and high q. The radially averaged scattering curve in Fig. 3A reveals a prominent first order structure factor peak at q = 0.768 nm−1 and an approximately 20 times smaller second peak at q = 1.569 nm−1. The peaks evidence in principle the stacking behaviour of the sheets and can thus be attributed to face-to-face interparticle correlations. The inter-sheet separation (dr) of 8.18 nm estimated from the peak position qmax using dr = 2π/qmax coincides with the spacing between neighbouring sheets found sparingly on the TEM bright-field images, when the sheets are viewed along the surface normal to the a–c and b–c side planes (see Fig. 4 for the model). Only a marginal number of assembled ribbons have fallen on the grid in such a way that it is possible to look through the space between the standing sheets (lamellae) either perpendicular (see Fig. 1D) or parallel to their long side.The exceptional, and to our knowledge unprecedented, asymmetric shape of the peaks, with the peaks displaying a shoulder on their low q side, indicates that the sheets do not form a one-dimensional or columnar stack. From the TEM-images we know that we are not dealing with a common assembly of parallel aligned platelets along one axis as in the case of the generally observed lamellar depletion stacks (see Fig. 2A and B). The SRA ribbons form because each on-top lying sheet is stepwise displaced by a clearly visible shift along the long axis of the sheet (x-direction, Fig. 1E). The fact that – especially in multi-ribbon assemblies – the formed ribbons tend to bend commonly over length scales of a few hundred nanometres (see Fig. 1A and G) is a hint for an additional, but smaller, shift per sheet along the short sheet axis (y-direction) forming a staggered zigzag-type of assembly (see Fig. 4). At low q (0.08 ≤ q ≤ 0.2 nm−1), no additional correlation peaks are visible that would make it necessary to take interactions between neighbouring ribbons within one SRA into account.
To model the small angle scattering intensities I(q) we need to address the different contributions leading to the observed total scattering. In the present case I(q) = ISRA(q) + Irm(q) + Ibg(q), whereby the three terms describe the scattering from the stacked ribbons, the reverse micelles and a non-constant background, respectively. The latter, which becomes significant with decreasing q, can be expressed by a power law and is explained in more detail in Methods, whereas the reverse micellar scattering becomes dominant with increasing q (see Fig. 3A). Removal of the solubilised water from the SRA-containing microemulsion prior to the SAXS measurements has been performed to stop ongoing reaction processes and to mainly reduce the dominant scattering contribution from the microemulsion droplets without changing the characteristics of the SRAs (see Fig. S1E in the ESI†). Due to the transformation of the microemulsion droplets to reverse micellar surfactant aggregates, their scattering contribution is lowered in intensity by one order of magnitude and shifted to higher scattering vectors, allowing thus to uncover the underlying characteristic features of the SRAs (see Fig. S1B in the ESI†). Since the concentration of the Igepal reverse micelles in the SRA-containing micellar solution is, due to the preparation, not accurately known, it is not possible to subtract a measured scattering curve of Igepal reverse micelles with same concentration (binary system) from the scattering curve of the SRA suspension prior to the data analysis. We, therefore, measured a reverse micellar solution of 13.6% Igepal in cyclohexane to determine the size and size distribution of the reverse micelles independently (Fig. 3C) and used their values as fixed parameters to fit the total scattering intensity. The scattering from the reverse micelles is described by 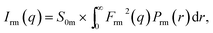 where Frm(q) is the particle form factor for a sphere39 with radius r and Prm(r) is the distribution function describing the radial polydispersity by a log-normal size distribution. S0m is the scaling factor for the contribution of the reverse micelles to the total scattering intensity. The refined values for the size and size distribution are given in Table 1. The small value for the reverse micellar radius of 0.63 ± 0.01 nm can be explained by the fact that the X-rays see, due to the similar electron density of the nonylphenol surfactant tail and the organic solvent (cyclohexane), only the ethylene oxide head group moiety and that the reverse micellar aggregates are less defined in the absence of water,40 which is also revealed by their relatively large polydispersity of 0.40.
where Frm(q) is the particle form factor for a sphere39 with radius r and Prm(r) is the distribution function describing the radial polydispersity by a log-normal size distribution. S0m is the scaling factor for the contribution of the reverse micelles to the total scattering intensity. The refined values for the size and size distribution are given in Table 1. The small value for the reverse micellar radius of 0.63 ± 0.01 nm can be explained by the fact that the X-rays see, due to the similar electron density of the nonylphenol surfactant tail and the organic solvent (cyclohexane), only the ethylene oxide head group moiety and that the reverse micellar aggregates are less defined in the absence of water,40 which is also revealed by their relatively large polydispersity of 0.40.
| Scattering contribution | Parameter | Refined value |
|---|---|---|
| a The fit has a crystallographic R-value of R = 1.9%, errors correspond to e.s.d.s. | ||
| Stacked sheets (SRAs) | Length a (nm) | 118 ± 2 |
| Width b (nm) | 43.52 ± 0.25 | |
| Thickness c (nm) | 2.62 ± 0.01 | |
| Shift in length Xt (nm) | 18.02 ± 0.4 | |
| Shift in width Yt (nm) | 5.20 ± 0.03 | |
| Inter-sheet space Zt (nm) | 5.19 ± 0.01 | |
| Uncertainty σx (nm) | 48 ± 1 | |
| Uncertainty σy (nm) | 0.62 ± 0.08 | |
| Uncertainty σz (nm) | 0.11 ± 0.07 | |
| Number of sheets/stack N | 15.0 ± 0.2 | |
| Scaling factor S0S (×104) | 8.84 ± 0.11 | |
| Reverse micelles | Radius rrm (nm) | 0.63 ± 0.01 |
| Polydispersity σrm | 0.40 ± 0.01 | |
| Scaling factor S0m | 18.77 ± 0.05 | |
| Background | Power law exp. p | 3.36 ± 0.4 |
| Power law const. A | 4.33 ± 0.4 | |
The scattering function for the stacked ribbon assemblies averaged over all orientations is
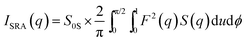 | (2) |
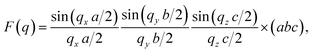 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Φ)(1−u2)1/2, qy = q
cos(Φ)(1−u2)1/2, qy = q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Φ)(1−u2)1/2, and qz = qu are the Cartesian components of the q-vector in spherical coordinates with u = cos(θ). To show that the shape of the platelets has no significant influence on the form factor, F2(q) is plotted in Fig. S2 for discorectangular and rectangular shaped plates in the ESI.† The scattering contribution arising from interplatelet interference within a one-dimensional stack is generally described by a short range structure factor S(q) of the Kratky–Porod type.28 For the specific arrangement of the SRAs, the originally one-dimensional Kratky–Porod structure factor needs to be evaluated for three dimensions, which finally leads to the expression
sin(Φ)(1−u2)1/2, and qz = qu are the Cartesian components of the q-vector in spherical coordinates with u = cos(θ). To show that the shape of the platelets has no significant influence on the form factor, F2(q) is plotted in Fig. S2 for discorectangular and rectangular shaped plates in the ESI.† The scattering contribution arising from interplatelet interference within a one-dimensional stack is generally described by a short range structure factor S(q) of the Kratky–Porod type.28 For the specific arrangement of the SRAs, the originally one-dimensional Kratky–Porod structure factor needs to be evaluated for three dimensions, which finally leads to the expression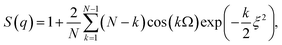 | (4) |
| Ω = |qxXt| + |qyYt| + |qz(c + Zt)| and ξ2 = qx2σx2 + qy2σy2 + qz2σz2 | (5) |
The quantities Xt, Yt, and (c + Zt) are the average components of the translation-vector in the respective directions, and, correspondingly, the σx, σy, and σz represent the uncertainties or Gaussian standard deviations of the vector components. The derivation of the SRA structure factor is given in detail in Section 3 of the ESI.† In order to minimize the complexity of eqn (2)–(5), we take due to their high electron density only the scattering from the PbCO3 sheets into account. The uncertainties σx, σy, σz include the polydispersities of the sheet dimensions in length (a), width (b) and thickness (c). Variation in the number of nanosheets per stack, which has been investigated for short stacks with N < 10 (typically 3–5),42 is not included, since this would require an additional integration in an already complex equation system.
The nonlinear least squares fit of the total scattering intensities is shown in Fig. 3A and the results of the refinement are summarized in Table 1. The comparison with the additionally displayed partial scattering intensities of the three contributions clearly shows that the characteristic features of the measured scattering curve, i.e., the two correlation peaks, stem from the scattering of the platelet stacks. At high q the scattering from the reverse micelles dominates the scattering curve. The shape of the observed structure factor peaks, which could both be well modelled (see Fig. 3D and E), indicates a complex interference pattern that needs to be further investigated. The refined values for the SRAs show that the found width (b(SAXS) = 43.52 ± 0.25 nm) and length (a(SAXS) = 118 ± 2 nm) of the PbCO3 nanosheets are in good agreement with those obtained from the TEM bright-field micrographs (b(TEM) = 44 ± 2 nm and a(TEM) = 121 ± 14 nm). As could already be seen from the TEM-images the sheets are rather thin having a thickness of c = 2.62 ± 0.01 nm, with c corresponding to only a small number of unit cell adequates (probably 3–5). The repeat distance (c + Zt = 7.81 ± 0.01 nm) is with an uncertainty σz = 0.11 ± 0.07 nm, and thus below 2%, the most defined entity of the SRAs. The value is slightly smaller than the d-spacing (dr = 8.18 nm) that one would obtain from the peak position qmax of the first peak for a one-dimensional stack. The interstitial space Zt is with 5.19 ± 0.01 nm about twice as large as the sheet thickness and does not seem to change significantly with drying. Its value suggests that the space is filled with adsorbed surfactant molecules that form a bilayer with interdigitated hydrocarbon tails, as observed for alkylated ethyleneoxide surfactants on silica43 or mica44 (the length per ethylene oxide monomer amounts to 3.5 Å for an extended zigzag chain45). For Igepal stabilised w/o microemulsions we found a value of 1.8 ± 0.2 nm for the hydrophilic head group shell thickness and a hydrophobic surfactant tail length of 0.91 ± 0.01 nm.38 Taking the adsorbed surfactant layer into account, one obtains a value of κ2 = 5.5 for the effective width-to-thickness ratio of the nanosheets. The shifts Xt and Yt correspond with 18.0 ± 0.4 nm and 5.20 ± 0.03 nm to 15% and 12% of the sheet length and width, respectively. The shift Yt in b-direction is quite defined with an uncertainty σy of 0.62 ± 0.08 nm but not visible in the bright-field images without tilting.
The shift Xt in a-direction is clearly visible but difficult to determine from the TEM-images, since it can be observed only at both ends of a ribbon. Towards the middle of a ribbon assembly, starting edges of a new stack overlap in the staggered configuration with ending edges of the former making it impossible to accurately assign the boundaries of one sheet in a ribbon (see Fig. 1E). With increasing number of sheets on top of each other, the difference in contrast fades further. The value determined by TEM with Xt(TEM) = 19 ± 6 nm agrees with the one found by SAXS Xt(SAXS) = 18.0 ± 0.4 nm. The rather large value of σx = 48 nm for the uncertainty in the shift along the a-direction arises from the fact that the length polydispersity of the particles is relatively large (see eqn (S14) in the ESI†). The refined value for the number of sheets per stack is N = 15, but one should keep in mind that we did not consider a distribution in N, which would lead to a smaller average value of Np = 11 plates per stacking unit (see eqn (S20) in the ESI†). From the TEM-images, we know that the ribbons reach the maximum height of less than 15 sheets. Estimations of N employing grey scale differences in STEM atomic number (Z)-contrast images reveal a lower limit of 8–10 and an upper limit of 12–15. This indicates that we see in the SAXS experiment the staggered assembly units that, therefore, form already in solution. These units build up to a few hundred nanometre long ribbons by end-to-end assembly of the stacked units, whereby the forming ribbons also assemble side-by-side (see Fig. 1).
In order to elucidate how the asymmetric shape of the observed structure factor peaks and thus the complex interference pattern evolves, we calculated the structure factor averaged over all orientations 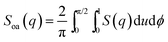 and the resulting scattering intensities I(q) for the different types of stacking possibilities for the sheets using the refined parameters given in Table 1. In Fig. 5 the scattering behaviour of (i) a 1D stack in z-direction without any offsets of the nanosheets in the x or y directions (c-stack), (ii) a bc-stack with an extra displacement along the short platelet axis in y-direction, and (iii) an ac-stack with an extra shift along the long platelet axis in x-direction are compared with that of (iv) the staggered zigzag-type abc-stack of the SRAs with both displacements in x and y directions. As can be seen in Fig. 5A–C, the shape and position of the inter-sheet correlation peaks is determined by the way the sheets stack. The experimentally observed asymmetric peak shape, with a shoulder on the low q-side, is except for the abc-stack of the SRAs observed for the bc-stacking only, manifesting that the shoulder emanates from a displacement in y-direction. The origin of the different scattering behaviour can be better explored by looking at the orientation averaged structure factor Soa(q) calculated with the uncertainties σx,y,z set to zero (Fig. 5E). This implies that all shifts (Xt, Yt and Zt) do not show a distribution and that the nanosheets themselves are (practically) monodisperse. The calculated peaks in Soa(q) are then not smeared out due to polydispersity. In this case the c-stack displays a regularly decaying saw-tooth pattern typical for a one-dimensional stack, with the peaks at multiples of the q-value corresponding to the repeat distance for c + Zt = 7.81 nm. The ac-stack pattern is made up by the interference between peaks that stem from repeat distances corresponding to the shifts in x-direction, Xt, and to c + Zt. Since Xt presents with 18 nm the largest observed repeat distance, the first peak appears already at about 0.35 nm−1 and the second peak corresponding to Xt/2 interferes with the c + Zt peak. For the bc-stack the peak corresponding to a repeat distance of Yt = 5.2 nm shows up at higher q-values than the c + Zt peak. The abc-stack pattern is then the result of the interference that stems from peaks of all three repeat distances. Fig. 5F displays Soa(q) with the refined σx,y,z (see Table 1). Due to the large value of the uncertainty in the x-direction (σx = 48 nm), the peaks originating from the Xt repeat distance are smeared out such that the curves for the ac and c-stacks and those of the abc and the bc-stacks differ significantly only at low q. For the bc-stack the peaks corresponding to the c + Zt repeat distance become as for the abc-stack the most dominant.
and the resulting scattering intensities I(q) for the different types of stacking possibilities for the sheets using the refined parameters given in Table 1. In Fig. 5 the scattering behaviour of (i) a 1D stack in z-direction without any offsets of the nanosheets in the x or y directions (c-stack), (ii) a bc-stack with an extra displacement along the short platelet axis in y-direction, and (iii) an ac-stack with an extra shift along the long platelet axis in x-direction are compared with that of (iv) the staggered zigzag-type abc-stack of the SRAs with both displacements in x and y directions. As can be seen in Fig. 5A–C, the shape and position of the inter-sheet correlation peaks is determined by the way the sheets stack. The experimentally observed asymmetric peak shape, with a shoulder on the low q-side, is except for the abc-stack of the SRAs observed for the bc-stacking only, manifesting that the shoulder emanates from a displacement in y-direction. The origin of the different scattering behaviour can be better explored by looking at the orientation averaged structure factor Soa(q) calculated with the uncertainties σx,y,z set to zero (Fig. 5E). This implies that all shifts (Xt, Yt and Zt) do not show a distribution and that the nanosheets themselves are (practically) monodisperse. The calculated peaks in Soa(q) are then not smeared out due to polydispersity. In this case the c-stack displays a regularly decaying saw-tooth pattern typical for a one-dimensional stack, with the peaks at multiples of the q-value corresponding to the repeat distance for c + Zt = 7.81 nm. The ac-stack pattern is made up by the interference between peaks that stem from repeat distances corresponding to the shifts in x-direction, Xt, and to c + Zt. Since Xt presents with 18 nm the largest observed repeat distance, the first peak appears already at about 0.35 nm−1 and the second peak corresponding to Xt/2 interferes with the c + Zt peak. For the bc-stack the peak corresponding to a repeat distance of Yt = 5.2 nm shows up at higher q-values than the c + Zt peak. The abc-stack pattern is then the result of the interference that stems from peaks of all three repeat distances. Fig. 5F displays Soa(q) with the refined σx,y,z (see Table 1). Due to the large value of the uncertainty in the x-direction (σx = 48 nm), the peaks originating from the Xt repeat distance are smeared out such that the curves for the ac and c-stacks and those of the abc and the bc-stacks differ significantly only at low q. For the bc-stack the peaks corresponding to the c + Zt repeat distance become as for the abc-stack the most dominant.
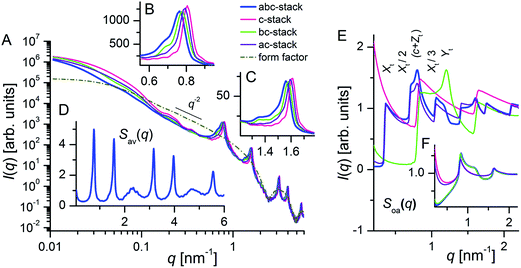 | ||
| Fig. 5 Calculated scattering intensities for the four different types of stacking that elucidate the origin of the asymmetric shape observed for the correlation peaks of the SRAs. (A) Scattering intensity I(q) of the stacks and form factor F2(q) of the nanosheets. (B–C) Enlargements of the peak regions. (D) Averaged structure factor Sav(q) for the abc-stack showing extinction of the 3rd and 5th order peak due to destructive interference with the form factor. (E) and (F) Orientation averaged structure factor Soa(q) with the uncertainties σx,y,z set to zero (E) and with the refined σx,y,z given in Table 1 (F). | ||
In Fig. 5A the form factor for the platelets is also displayed. The first minimum in F2(q) at q = 2.4 nm−1 corresponds to a nanosheet thickness of 2.62 nm. At intermediate q (0.2 ≤ q ≤ 1 nm−1) the form factor curve shows a q−2 power law decay characteristic for plate-like objects. At low q (<0.03 nm−1) the Guinier-region for the sheet length is reached. The I(q) curves show that the influence of the form factor at q < 0.5 nm−1 is significant only in the case of the c-stack. At large q the first minimum in the form factor coincides with the third order peak of the structure factor ((c + Zt)/3 = 7.81/3 nm = 2.6 nm) causing destructive interference. The extinction of every third structure factor peak can be better seen by plotting the averaged structure factor Sav(q) (Fig. 5D) that is weighted with the form factor (see eqn (1)).
3.3 Scanning transmission electron microscopic tilt series of dried SRAs
In order to retrieve complementary three-dimensional (3D) information of the nanostructured PbCO3 stacked ribbon assemblies we acquired tomographic tilt series on dried SRA samples using high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) as imaging technique. Due to nearly Rutherford scattering conditions HAADF-STEM imaging yields Z-contrast images, where the intensity is proportional to the projected sample thickness and approximately to the square of the atomic number (Z∼1.7).46,47 The latter gives in case of the SRAs rise to a higher contrast between the nanosheets, their surrounding surfactant molecules and the underlying carbon background of the coated TEM-grid.Even though a large number of individual SRAs can be viewed on the grid, only very few are deposited such that one of the stack axes (i.e. the x- and y-directions (see Fig. 4)) is parallel to the tilt axis of the single-tilt tomography holder. Selected HAADF-STEM micrographs of a tilt series performed on an SRA built up by four side-by-side assembled ribbons are displayed on the left side of Fig. 6. In this series, the tilt axis does not lie exactly parallel to the ribbon or band structure, but allows the sheets to be viewed as they rotate along their long axis. The series (see Movie S3 in the ESI†) has been acquired over an angular range of −66° to +66° with a minimum and maximum tilt increment of 1.8° and 4° at the high and low angles, respectively. Depending on the tilt angle not all images show a clear band structure as can be seen in Fig. 6J and M, revealing more complex interference patterns (Fig. 6D and G). Attempts to retrieve 3D information of the SRAs from the tilt series using state of the art reconstruction techniques (e.g., weighted back-projection (WBP) or simultaneous iterative reconstruction technique (SIRT))47,48 enabled a 3D visualization of the individual PbCO3 nanosheets, but did not provide detailed metric information of their stacking behaviour (see Methods). To gain insight into the different structures observed and to confirm the SAXS model developed, we, therefore, used the refined parameters given in Table 1 to construct two parallel assembled SRA building units consisting of ten semi-transparent sheets each and simulated their tilting behaviour (see Methods). For comparison with the acquired STEM-images, in which the SRAs already lie under a certain angle on the TEM-grid, we need a linchpin to define a common angle. The micrograph in Fig. 6A, which has been taken at a tilt angle of −65°, reveals sheets that are standing on their long (a–c) side with the electron beam passing through their full width. Here we define the angle that enables a view through the gaps between neighbouring lamellae as −90°, leading thus to an offset of the experimentally obtained tilt angle of −25°. One should, however, keep in mind that the short sheet axis may not be completely parallel to the incoming beam and that the ribbons do not lie exactly parallel to the tilt axis. Therefore, the comparison with the simulated tilting behaviour is only qualitative and the angles in Fig. 6 should not be taken as absolute.
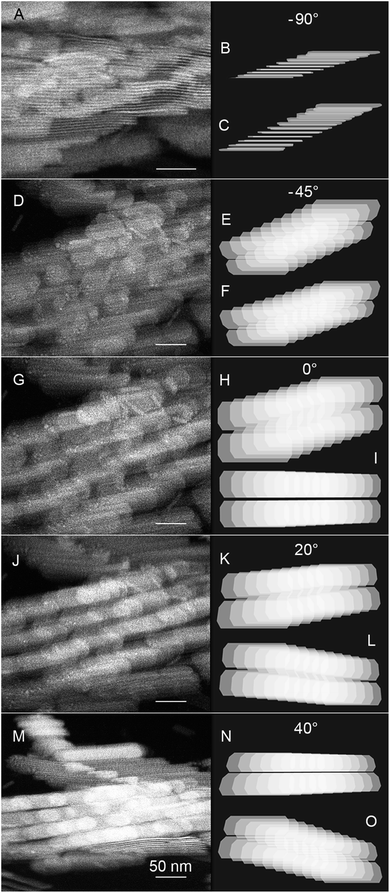 | ||
| Fig. 6 Selected HAADF-STEM images from an electron tomographic tilt series performed on an almost horizontal lying SRA built up of four side-by-side assembled ribbons together with simulated stacks ((B), (E), (H), (K), and (N) abc-stack; (C), (F), (I), (L), and (O) ac-stack) for comparison. The STEM-images were recorded at tilt angles of (A) −65°, (D) −20°, (G) +25° (J) +45° and (M) +65°. See also Movies S3–S5 in the ESI† for 3D animations of the complete tilt series. | ||
Fig. 6 displays on the right the predicted tilting behaviour of the SRAs, whereby the upper stack in each panel is produced taking all three shifts (abc-stack) into account (Fig. 6B, E, H, K and N) and the lower stack is constructed without the sideward shift (no Yt shift, ac-stack, Fig. 6C, F, I, L and O). The images show that the observed interference patterns can be qualitatively explained considering the interference between two neighbouring ribbons. With the tilt axis parallel to the ribbons the difference between the two types of stacking becomes most pronounced at the angle under which the band structure becomes observable and the perspective projection and/or real displacement in the b-direction diminishes. At −90° the ribbons are viewed from their long (a–c) side (Fig. 6A). The four consecutive bands cover a space of about 200 nm thus making it difficult to find an angle under which they collapse into one band. However, the fact that it is possible to see through the lamellae indicates already that the single sheets are interlocked and that the sideward displacement in the staggered SRA configuration proceeds at the same height to the neighbouring ribbon in the row. In the simulation (Fig. 6B and C) the stack is viewed from a finite angle leading to a perspective distortion and thus an apparent varied spacing between the sheets in the stack. Tilting into the direction, which enables viewing the individual nanosheets from the a–b side, induces interferences due to the existening electron transparency of the nanosheets. This leads, depending on the tilt angle, to the emergence of a third interjacent layer consisting of circular discs or segments of a circle, which can be seen in Fig. 6D and E at −45° and Fig. 6G and H at 0°, respectively. The interferences occurring also give the impression of two dogleg stairs with the front ribbon going down from left to right, while the back ribbon climbs up (see, e.g., Fig. 6E and H). The displacement per sheet in b-direction (Yt-shift) is best visible at 20° (Fig. 6J and K). For the ac-stack the band structure can be visualized at an angle of 0° (Fig. 6I), whereas the zigzag staggered SRA (abc) stack requires rotation by another 40° (Fig. 6M and N). The similarity between the STEM-images and the simulated abc-stack patterns corroborates the existence of the Yt-shift and thus the 3D nanostructure of the SRAs retrieved from the SAXS experiment.
In addition Fig. 7 reveals a tilt series of three side-by-side assembled ribbons with the tilt axis almost perpendicular to the band structure. The series (see Movie S6 in the ESI†) has been acquired from −65° to 65° with a tilt increment of 2.5°. The upper insets depict the simulated ac-stacks (without shift in b-direction) and the lower the abc-stacks. As for the SRAs in Fig. 6 we use the angle under which the sheets are viewed as standing in this case on their short (b–c) side as linchpin, leading thus to an offset of −20°. Without considering the Yt-shift the sheets and ribbons contract due to the projection only in length upon going from 0° to −82.5° (upper insets in Fig. 7B–E) until they are seen from their edges (Fig. 7A). For the abc-stack the reduction in the ribbon length is less pronounced (lower insets in Fig. 7). Instead the offset of the sheets in b-direction becomes evident, leading to the staggered band structure and the appearance of interference patterns between the ribbons that have already been observed in Fig. 6. The reader is encouraged to view the 3D animations over the full angular range for both tomographic tilt series, i.e. STEM-images as well as the simulated SRAs, online (Movies S3–S8 in the ESI†) for better visualization.
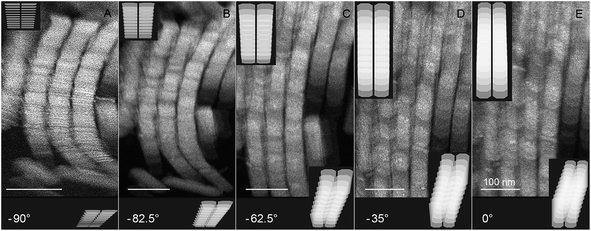 | ||
| Fig. 7 Selected HAADF-STEM images from an electron tomographic tilt series performed on an almost vertical lying SRA built up of three side-by-side assembled ribbons together with simulated stacks (upper insets ac-stack; lower insets abc-stack) for comparison. The STEM-images were recorded at tilt angles of (A) −70°, (B) −62.5°, (C) −42.5° (D) −15° and (E) +20°. See also Movies S6–S8 in the ESI† for 3D animations of the complete tilt series. | ||
4 Conclusions
In this work we show that biaxial discorectangular-shaped nanosheets can in the presence of attractive depletion forces assemble into a novel superstructure consisting of extended ribbons, whereby the central building unit is a three-dimensional stack in which each consecutive sheet is displaced by a constant shift in the width and length directions of the constituting platelets thus yielding a restricted band height. The formation of the highly ordered, staggered zigzag-type assemblies is achieved due to the low width- and thickness polydispersities (<5%) of the sheets. Besides the dimensions also the shifts for the displacements in these directions are well-defined, whereas both the increased polydispersity in length and the larger uncertainty in the shift along the long sheet axis do not constrain the organisation within the SRAs. The individual nanosheets are thus not placed on a regular lattice and, as a result of their face-to face alignment, are not free to rotate around their translational position (nonrotator phase).8 Theoretical studies on the self-assembling behaviour of biaxial (hard) particles have to our knowledge so far not taken anisotropy in the polydispersity into account (see, e.g., ref. 12 and 15), which will probably play a key role in the formation of the observed SRAs. We, therefore, hope that this study might foster investigations on possible sources of new types of ordering. A question that still remains of interest to us is to gain insight whether the formation of our SRA superstructures can be explained by the shape of the particles alone or whether, e.g., additionally building-up dipoles49 are necessary for obtaining the staggered zigzag structure of the SRAs.The superstructure of the SRAs leads to complex, and so far unprecedented, interference patterns when characterised by small angle X-ray scattering and electron tomographic tilt series. Expanding the Kratky–Porod structure factor for stacking plates into three dimensions, we demonstrate that the asymmetric shape of the two observed face-to-face correlation peaks originates from the interference stemming from the peaks of all three repeat distances, whereby the peaks are smeared out by the uncertainties in the corresponding shifts. Using the refined parameters from the SAXS measurements allows qualitative modelling of the STEM tilt series.
Acknowledgements
The authors would like to thank P. Konarev (EMBL-Hamburg) for his help in performing the SAXS experiments and S. de Waal for graphical assistance. The work of M.H. has been supported by the German Science foundation (DFG grant no. WE 2579/3-1).References
- C. Burda, X. B. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025–1102 CrossRef CAS PubMed.
- C. Pacholski, A. Kornowski and H. Weller, Angew. Chem., Int. Ed., 2002, 41, 1188–1191 CrossRef CAS.
- S. Kan, T. Mokari, E. Rothenberg and U. Banin, Nat. Mater., 2003, 2, 155–158 CrossRef CAS PubMed.
- S. Ithurria, M. D. Tessier, B. Mahler, R. P. S. M. Lobo, B. Dubertret and A. L. Efros, Nat. Mater., 2011, 10, 936–941 CrossRef CAS PubMed.
- S. Jeong, D. Yoo, J. T. Jang, M. Kim and J. Cheon, J. Am. Chem. Soc., 2012, 134, 18233–18236 CrossRef CAS PubMed.
- G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774 CrossRef CAS PubMed.
- M. R. Jones, K. D. Osberg, R. J. Macfarlane, M. R. Langille and C. A. Mirkin, Chem. Rev., 2011, 111, 3736–3827 CrossRef CAS PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS PubMed.
- M. P. Taylor and J. Herzfeld, Phys. Rev. A, 1991, 44, 3742–3751 CrossRef.
- Y. Martinez-Raton, S. Varga and E. Velasco, Phys. Chem. Chem. Phys., 2011, 13, 13247–13254 RSC.
- S. D. Peroukidis and A. G. Vanakaras, Soft Matter, 2013, 9, 7419–7423 RSC.
- Y. Martinez-Raton, S. Varga and E. Velasco, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031705 CrossRef.
- S. Belli, A. Patti, M. Dijkstra and R. van Roij, Phys. Rev. Lett., 2011, 107, 148303 CrossRef CAS.
- E. van den Pol, D. M. E. Thies-Weesie, A. V. Petukhov, D. V. Byelov and G. J. Vroege, Liq. Cryst., 2010, 37, 641–651 CrossRef CAS.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CAS.
- A. Vrij, Pure Appl. Chem., 1976, 48, 471–483 CrossRef CAS.
- T. G. Mason, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 060402 CrossRef CAS.
- P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2012, 6, 609–614 CrossRef CAS PubMed.
- S. Belli, M. Dijkstra and R. van Roij, J. Phys.: Condens. Matter, 2012, 24, 284128 CrossRef CAS PubMed.
- D. Yamaguchi, N. Miyamoto, S. Koizumi, T. Nakato and T. Hashimoto, J. Appl. Crystallogr., 2007, 40, S101–S105 CrossRef CAS.
- J. W. Seo, Y. W. Jun, S. W. Park, H. Nah, T. Moon, B. Park, J. G. Kim, Y. J. Kim and J. Cheon, Angew. Chem., Int. Ed., 2007, 46, 8828–8831 CrossRef CAS PubMed.
- J. S. Son, X. D. Wen, J. Joo, J. Chae, S. I. Baek, K. Park, J. H. Kim, K. An, J. H. Yu, S. G. Kwon, S. H. Choi, Z. W. Wang, Y. W. Kim, K. Kuk, R. Hoffmann and T. Hyeon, Angew. Chem., Int. Ed., 2009, 48, 6861–6864 CrossRef CAS PubMed.
- C. Schliehe, B. H. Juarez, M. Pelletier, S. Jander, D. Greshnykh, M. Nagel, A. Meyer, S. Foerster, A. Kornowski, C. Klinke and H. Weller, Science, 2010, 329, 550–553 CrossRef CAS PubMed.
- Z. Y. Tang, Z. L. Zhang, Y. Wang, S. C. Glotzer and N. A. Kotov, Science, 2006, 314, 274–278 CrossRef CAS PubMed.
- K. L. Young, M. R. Jones, J. Zhang, R. J. Macfarlane, R. Esquivel-Sirvent, R. J. Nap, J. S. Wu, G. C. Schatz, B. Lee and C. A. Mirkin, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2240–2245 CrossRef CAS PubMed.
- O. Kratky and G. Porod, J. Colloid Sci., 1949, 4, 35–70 CrossRef CAS.
- M. W. Roessle, R. Klaering, U. Ristau, B. Robrahn, D. Jahn, T. Gehrmann, P. Konarev, A. Round, S. Fiedler, C. Hermes and D. I. Svergun, J. Appl. Crystallogr., 2007, 40, S190–S194 CrossRef CAS.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in Fortran, Cambridge University Press, New York, 2nd edn, 1992, pp. 678–683 Search PubMed.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 CrossRef CAS.
- B. Weyerich, J. Brunner-Popela and O. Glatter, J. Appl. Crystallogr., 1999, 32, 197–209 CrossRef CAS.
- V. Uskokovic and M. Drofenik, Surf. Rev. Lett., 2005, 12, 239–277 CrossRef CAS.
- W. F. C. Sager, in Nanostructured Soft Matter: Experiments, Theory, Simulation and Perspectives, ed. A. V. Zvelindovsky, Springer, Dordrecht, 2007, pp. 3–44 Search PubMed.
- W. F. C. Sager, Curr. Opin. Colloid Interface Sci., 1998, 3, 276–283 CrossRef CAS.
- U. Natarajan, K. Handique, A. Mehra, J. R. Bellare and K. Khilar, Langmiur, 1996, 12, 2670–2678 CrossRef CAS.
- C. E. Nicholson, C. Chen, B. Mendis and S. J. Cooper, Cryst. Growth Des., 2011, 11, 363–366 CAS.
- T. H. van der Loop, M. R. Panman, S. Lotze, J. Zhang, T. Vad, H. J. Bakker, W. F. C. Sager and S. Woutersen, J. Chem. Phys., 2012, 137, 044503 CrossRef PubMed.
- G. Porod, in Small Angle X-Ray Scattering, ed. O. Glatter and O. Kratky, Academic Press, London, 1982, pp. 17–51 Search PubMed.
- M. J. Hollamby, R. Tabor, K. J. Mutch, K. Trickett, J. Eastoe, R. K. Heenan and I. Grillo, Langmuir, 2008, 24, 12235–12240 CrossRef CAS PubMed.
- P. Mittelbach and G. Porod, Acta Phys. Austriaca, 1961, 14, 185–211 CAS.
- C. Pizzey, S. Klein, E. Leach, J. S. van Duijneveldt and R. M. Richardson, J. Phys.: Condens. Matter, 2004, 16, 2479–2495 CrossRef CAS.
- A. Gellan and C. H. Rochester, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 2235–2245 RSC.
- J. P. Dong and G. Z. Mao, Langmuir, 2000, 16, 6641–6647 CrossRef CAS.
- V. Degiorgio, in Physics of Amphiphiles: Micelles, Vesicles and Microemulsions, ed. V. Degiorgio and M. Corti, North-Holland, Amsterdam, 1985, pp. 303–332 Search PubMed.
- E. J. Kirkland, Advanced Computing in Electron Microscopy, Plenum Press, New York, 1998, pp. 92–93 Search PubMed.
- C. Kübel, A. Voigt, R. Schoenmakers, M. Otten, D. Su, T. C. Lee, A. Carlsson and J. Bradley, Microsc. Microanal., 2005, 11, 378–400 CrossRef PubMed.
- A. Alpers, R. J. Gardner, S. Konig, R. S. Pennington, C. B. Boothroyd, L. Houben, R. E. Dunin-Borkowski and K. J. Batenburg, Ultramicroscopy, 2013, 128, 42–54 CrossRef PubMed.
- R. Kniep and P. Simon, Angew. Chem., Int. Ed., 2008, 47, 1405–1409 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary material (SRA-preparation from nonionic w/o microemulsions including additional SAXS and DLS measurements (Fig. S1), form factor for the discorectangular platelets (Fig. S2), derivations for the SRA structure factor, for the error term in a-direction within the SRA structure factor and for the average number of sheets per SRA stacking unit, as well as movies with the 3D animations of the experimental and simulated tilt series Movies (S3–S8)) is available in the online version of this article. See DOI: 10.1039/c4sm01935k |
| ‡ Present address: Ernst Ruska-Centre for Microscopy and Spectroscopy with Electrons and Peter Grünberg Institute, Forschungszentrum Jülich, 52425 Jülich, Germany. |
| § The Sm(r)B (Sm(p)B respectively) phase is a biaxial smectic phase that consists of particles arranged in layers with their long (short) particles axes perpendicular to the layers and with the secondary particles axes oriented in the layer planes. N(r)B and N(p)B denote biaxial nematic phases with rod- and plate-like ordering, respectively.12 |
| This journal is © The Royal Society of Chemistry 2014 |