 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multi-blob coarse graining for ring polymer solutions
Arturo
Narros
a,
Christos N.
Likos
*a,
Angel J.
Moreno
b and
Barbara
Capone
a
aFaculty of Physics, University of Vienna, Boltzmanngasse 5, A-1090, Vienna, Austria. E-mail: christos.likos@univie.ac.at
bCentro de Física de Materiales (CSIC, UPV/EHU), Materials Physics Center MPC, Paseo Manuel de Lardizabal 5, E-20018 San Sebastián, Spain
First published on 25th September 2014
Abstract
We present a multi-scale molecular modeling of concentrated solutions of unknotted and non-concatenated ring polymers under good solvent conditions. The approach is based on a multi-blob representation of each ring polymer, which is capable of overcoming the shortcomings of single-blob approaches that lose their validity at concentrations exceeding the overlap density of the solution [A. Narros, A. J. Moreno, and C. N. Likos, Soft Matter, 2010, 6, 2435]. By means of a first principles coarse-graining strategy based on analytically determined effective pair potentials between the blobs, computed at zero density, we quantitatively reproduce the single molecule and solution properties of a system with well-defined topological constraints. Detailed comparisons with the underlying, monomer-resolved model demonstrate the validity of our approach, which employs fully transferable pair potentials between connected and unconnected blobs. We demonstrate that the pair structure between the centers of mass of the rings is accurately reproduced by the multi-blob approach, thus opening the way for simulation of arbitrarily long polymers. Finally, we show the importance of the topological constraint of non-concatenation on the structure of the concentrated solution and in particular on the size of the correlation hole and the shrinkage of the rings as melt concentrations are approached.
1. Introduction
Ring polymers are the most characteristic prototype of topologically constrained molecules.1 Without any modifications of the chemistry, solvent quality or any other physical or building-block properties of the macromolecules, the mere operation of joining together the two free ends of a linear polymer chain has profound impact on the structural and dynamical properties of single molecules and concentrated solutions of the same alike. Interest in ring polymers dates from many decades ago, as is witnessed, e.g., in three pioneering papers on the subject: in the work of Frank-Kamenetskii et al.,2 the notion of the topological interaction between two rings has been introduced and analyzed quantitatively, which arises from the non-concatenation condition of the same; in the work of Grosberg et al.,3 the crumpled globule model of rings in the melt has been put forward, making a strong distinction between the structures of linear- and ring-polymer melts; and finally, Obukhov et al.4 have put forward an annealed lattice-animal picture of a ring polymer in a melt, deriving thereby novel scaling laws for the diffusion coefficient and the longest relaxation time of a ring, and thereby revising previous predictions.5,6 Despite their conceptual simplicity and their highly interesting characteristics, the study of ring polymers, both experimentally and theoretically, is confronted with many obstacles.7 From the theoretical point of view, the main difficulty of rings in comparison to their linear counterparts lies indeed in the treatment of the topological constraints, which, inter alia, prevents the formulation of the problem in terms of a field-theoretical approach8 that has proven extremely fruitful for the treatment of solutions or melts of linear chains. On the experimental side, the main problems are related to the difficulty of controlling the synthetic processes so as to obtain monodisperse rings of identical knotedness. Accordingly, computer simulations have emerged as an indispensable tool for the analysis of the static and dynamic properties of ring polymers and their solutions.7–32A great deal of interest in ring polymers is motivated by their biological relevance. Indeed, biopolymers such as DNA or chromosomes are often found in a topologically constrained state when they are packed within cells or eukaryotes.3,33–35 In 1993, Grosberg et al.3 demonstrated that molecules that have a topological constraint appear to be able to survive longer in an out-of-equilibrium state that allows for more compact structures, therefore hypothesizing that the long-lasting problem of packing of e.g., chromosomes in eukaryotes that could not be explained by packing of linear biopolymers could be solved by adding a topological constraint. Proteins and DNA display a rich variety of topological effects, both structural and dynamic. For example, the DNA of bacteria is present in the traditional double-helix form, but in contrast to what happens for eukaryotes, they have circular chromosomes contained in a DNA helix which is closed into a ring.36 Formation of knots along the backbone of DNA and their location depending on the varying rigidity along the backbone of the macromolecule in the bulk37 and in confinement38 are other manifestations of the importance of topological concepts for biologically relevant processes.
At the single-molecule level (equivalent to the infinite-dilution limit of a polymer solution), topology manifests itself in various ways. Although the infinite-dilution gyration radius of the rings, Rg,0, scales with monomer number N with the same, Flory exponent ν = 0.588 as that of the linear chains in athermal solvents (Rg,0 ∼ Nν), topology effectively expresses itself as a larger excluded-volume parameter, resulting in a lowering of the Θ-temperature of the rings in comparison to that of the linear polymers.30,39 A related, remarkable effect is the fact that in contrast to ideal (i.e., without excluded volume) linear polymers, ideal ring polymers experience an effective repulsion between molecules that is purely due to the additional topological constraint of closing each chain into a loop,31,40 leading to a scaling Rg,0 ∼ Nν that is identical to that of self-avoiding rings. The effects of topology become even stronger at higher concentrations and in particular at those exceeding the overlap density of the rings. Although the concentration screens out the excluded-volume interaction for linear chains, resulting in Gaussian statistics between the correlation blobs of the chains,41 the topological potential between different rings cannot be screened out. Accordingly, the size of flexible rings in semidilute solutions and melts scales with the molecular weight as Rg ∼ N1/3 for sufficiently long rings exceeding the entanglement length, but it is preceded by a crossover-scaling Rg ∼ N2/5 for shorter chains8,18,22 – see Section 4 for more details. Solutions of ring polymers present a melt viscosity that is lower by one order of magnitude with respect to a solution of linear chains in the same density and under the same solvent conditions.42–45 Investigations on melts of unknotted, non-concatenated rings7,10,12–14 have shown that they display a higher diffusivity7,10,12–14,23,46 and that the Rouse regime extends to larger scales than in their linear counterparts.19 Rheological experiments47 and simulations23 have revealed a power-law stress relaxation, instead of the usual reptation-like exponential behavior found for linear chains. Semiflexible rings, on the other hand, feature a particular form of self-organization in semidilute solutions, forming a disordered state of columnar clusters penetrated by other rings,31 and displaying an unusual dynamic scenario in which the coherent and the incoherent correlation functions are decoupled from one another, resulting in a state that has been termed cluster glass.32
It is evident, thus, that the properties of topologically constrained molecules in the semi-dilute regime are extremely difficult to access, both via theoretical approaches and computational studies. The difficulty of the latter increases with polymer size and density of polymers in solution, the larger the ring and more rings in solution, the more the topological tests required in order to preserve the original topology of the system. It therefore becomes of crucial importance to be able to analyze, simulate and access the semi-dilute regime for molecules with a ring architecture. A full-monomer detailed representation of semi-dilute solutions, due to both the high number of monomers that it would be necessary to simulate and the high number of topological checks that would be needed, appears to be quite prohibitive if simulations have to be performed for very large polymers in density regimes close and above the overlap concentration, and therefore a coarse-grained approach is called for.
The simplest coarse-graining strategy amounts to replacing the entire ring with a single effective coordinate, usually chosen to be the molecule's center of mass,20,21 in close analogy in the case of linear chains.48 This single-blob representation of the rings already expresses some of the distinct features related to the ring topology: the resulting effective interaction has a very different amplitude and shape with respect to the Gaussian effective interaction of linear chains,21 a feature that has been recently rationalized in terms of the strong asymmetry in the sizes of two interpenetrating ring polymers, stemming from the threading of one through the other.49 Further, the single-blob approach is sensitive to the type of knotedness of the rings, at least for moderate sizes of the same.21,49,50 Despite the fact that the single-blob representation of rings is carrying a clear signature of the closed-circle topology, it is inadequate to provide an accurate description of the solution structure in the semi-dilute and concentrated regimes.21,31 The reason lies in the multiple overlaps between the single-blobs that become dominant as the concentration increases, leading to a shrinking of the molecules. As the rings' size gets reduced and the circles tend to the crumpled-globule conformations induced by their mutual, unscreened topological interactions,22 the threading scenario leading to the zero-density center-of-mass effective potential becomes unlikely, and the overall shape of the rings is vastly different from the one at infinite dilution.49 Known also for the case of linear polymers,48,51,52 this failure of the single-blob effective pair potentials to account for the many-body properties in concentrated solutions is particularly severe for the case of rings: indeed, the zero-density ring–ring effective interaction is bound and it has a Fourier transform with negative parts (i.e., it is of the Q±-type53), implying therefore the emergence of stable clusters above the overlap concentration. This prediction, however, is in full contradiction with numerical and experimental evidence, leading to the unambiguous conclusion that the single-blob representation is inappropriate for concentrated ring polymer solutions, as it leads to qualitatively erroneous predictions.
In order to deeply explore the semi-dilute regime of a ring polymer solution, it appears therefore essential to develop a reliable multi-scale coarse-graining strategy, breaking the rings into a multitude of blobs that are free of mutual multiple overlaps. In this work, we set forward an extension of the soft effective segment (SES) or multi-blob (MB) representation to ring polymers. Such a multi-scale methodology has been recently introduced and proven to be reliable and quantitative in reproducing the properties of semi-dilute solutions of linear chains,54 diblock copolymers,55,56 molecules with a complex architecture and chemistry, such as telechelic star polymers,57 as well as homopolymer brushes.58 Introduction of topological constraints into the multi-blob approach has, however, not been attempted thus far. Our approach brings about a reduction of several orders of magnitude in the number of beads needed to represent a chain of underlying N ≥ 103 monomers (Kuhn segments). In this work, we will show that the MB coarse-graining procedure applied to ring polymers is quantitative in a wide density range. Single molecule properties, pair potentials and solution properties obtained both with a full-monomer representation and with a coarse-grained one have been analyzed, demonstrating the validity of the proposed methodology.
The rest of this paper is structured as follows. In Section 2, we present two different microscopic models used in our simulations of ring polymers as well as the procedure of the multi-blob coarse graining and the resulting multi-blob model. In Section 3, we demonstrate, by comparing the results between the microscopic and the coarse-graining procedures, that the multi-blob model leaves all single-molecule properties invariant and that it also preserves the effective potential and the topological potential between two ring polymers. In Section 4, we extend the analysis to ring polymer solutions deeply in the semi-dilute regime, demonstrating that the multi-blob approach reproduces very accurately the correlation functions between the rings. We also show the effects that the intermolecular topological interaction incurs on both the shrinkage of the rings and on the correlation functions by comparing with simulation results in which this interaction is (artificially) switched off. Finally, in Section 5 we summarize and draw our conclusions.
2. The microscopic models and their multi-blob coarse-graining
2.1 Correlation blobs and the central idea of the multi-blob representation
We begin by setting up the notation for the rest of the paper and by setting the stage of the multi-blob approach. We consider M polymer chains enclosed in the volume V; each chain consists of N (microscopic) monomers. The instantaneous radius of gyration of any ring at infinite dilution, where the effects of other rings can be ignored, is denoted as![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g,0 and its expectation value 〈
g,0 and its expectation value 〈![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g,0〉 as just Rg,0. At finite concentrations, the second subscript is dropped and the two quantities are denoted as
g,0〉 as just Rg,0. At finite concentrations, the second subscript is dropped and the two quantities are denoted as ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g and Rg, respectively. The latter values are, in general, density-dependent.
g and Rg, respectively. The latter values are, in general, density-dependent.
The chain density (concentration), ρ, is defined as ρ = M/V. It is also convenient to define the overlap density ρ* as
 | (1) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , one can also define the monomer concentration ϕ = Nρ and thus, from eqn (1), its value at chain overlap, ϕ* = Nρ*. Since Rg,0 ∼
, one can also define the monomer concentration ϕ = Nρ and thus, from eqn (1), its value at chain overlap, ϕ* = Nρ*. Since Rg,0 ∼ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) Nν, it follows eqn (1) that
Nν, it follows eqn (1) that| ρ* ∼ N−3ν; ϕ* ∼ N1–3ν, | (2) |
 | (3) |
Note also that ξ is independent of the degree of polymerization in the semidilute regime:
 | (4) |
 | (5) |
These ideas also play a crucial role in the development of the multi-blob representation of polymers; however, the latter is a more general approach. In particular, the idea behind the multi-blob coarse-graining is that the problem of many-body effective interactions can be circumvented if the coarse-grained entities are chosen to be sufficiently small so that only pair overlaps are significant. Accordingly, the polymer is rendered as a succession of nB blobs of g monomers and size rg ∼ gν each. At any given ratio ρ/ρ*, the blob is small enough so that it contains at most pair-contacts and at the same time big enough so that it contains a large number of monomers. From the above discussion, it follows that for the coarse-grained blobs, the mutually equivalent inequalities
| nB ≥ nξ; rg ≤ ξ; g ≤ gξ | (6) |
nB ≫ 1; rg ≫ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ; g ≫ 1. ; g ≫ 1. | (7) |
Whereas the concept of the correlation-blob is used extensively (and with great success) in scaling theory, where one makes use of this physical picture to derive some general power-law dependencies of e.g., thermodynamic quantities on the ratio ρ/ρ* the multi-blob approach is more detailed. One aims at renormalizing the monomer–monomer potentials at the level of blob–blob interactions and thus at describing the chains at a coarser, mesoscopic level. Starting, therefore, with some microscopic, monomer-resolved polymer model, successive sequences of g monomers (g ∼ rg1/ν) are grouped together to form a blob, whose size cannot exceed the linear dimension ξ of the correlation blob. Following a procedure to be described in detail in Section 2.3, effective interactions are derived between these blobs, both the disconnected ones and those that are tethered to one another. Provided that g is sufficiently large, these potentials are universal, i.e., independent of the details of the underlying microscopic model. The multi-blob approach is thus perfectly suited for the efficient study of polymer solutions with arbitrarily large degrees of polymerization N.
2.2 The full-monomer models
We consider exclusively unknotted, non-concatenated, and fully flexible homopolymer rings under athermal solvent conditions. At the microscopic level, we employ two different models that are already introduced elsewhere,21 which we repeat here for completeness.Model I. – here, monomers are modelled as hard-spheres of diameter d and the connections among them are implemented as threads of maximal surface-to-surface extension δd (δ > 1). Accordingly, the monomer–monomer interaction Vmm(r) and the bonding interaction Vbond(r), where r is the distance between the monomer centers, read as
 | (8) |
 | (9) |
Model II. – for the second full monomer level a soft sphere potential is employed. The monomer–monomer interactions are given by
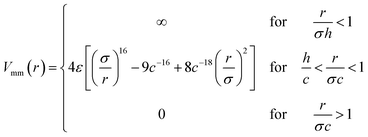 | (10) |
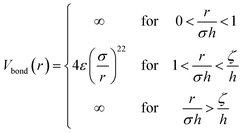 | (11) |
For both microscopic models, the preservation of topological constraints was additionally checked in the following way: an artificial, concatenated configuration between two rings was created, and subsequently each ring was pulled in opposite directions by opposite forces of increasing magnitude. Even at the strongest pulling forces, in which rings had deformed into straight-line ‘double-rods’, the two polymers remained linked to one another, confirming the non-crossing of bonds during simulation.
2.3 Multi-blob effective potentials and mapping between the monomer-resolved and the multi-blob models
A reliable coarse-graining, multi-blob methodology needs to be precise, to be back-tractable onto the microscopic system, and at the same time it has to provide access to large scale analyses both in terms of the number of molecules in solution as well as in terms of the number of microscopic constituents. The coarse-graining methodology used to address the problem at hand is a first-principles approach, which extends the considerations previously introduced successfully for the case of linear homopolymers,54 diblock copolymers,55,56 grafted homopolymeric brushes58 and telechelic star polymers.57 Chains are split into nB segments (blobs), containing a minimum number of g = 80 to 100 monomers, so that each segment is in the scaling regime, i.e., its properties are not affected by finite size scaling and follow general scaling laws. Each one of the segments will be represented via an effective potential that is extracted at zero density by simulating two chains, dividing them into dimers, computing the pair correlation functions between all dimers and inverting the analytical expansion that links the Meyer functions to the pair correlation functions.55,56,59 Once the effective potentials between the various sub-segments of the chain have been extracted, each ring polymer is simulated as a ring of blobs instead of as a ring of monomers.Blobs interact with one another via effective pair-potentials that are extracted from simulations of two linear chains. In principle, one would have to consider two chains of nB blobs each, and derive the effective potentials from those, by means of an inversion procedure. In practice, however, it turns out that considering two dimers consisting of two blobs each is sufficient. Accordingly, the extraction of the potentials between the blobs results in coupled integral equations that include contributions arising from up to four bodies.54,55 The set of effective interactions consists of a Gaussian shaped potential that acts between all blobs (tethered and untethered) and a tethering harmonic potential acting between bonded blobs. Such effective potentials are universal properties of the class of polymers analyzed, i.e., they are independent of the underlying model they have been extracted from.58
In the blob representation, each of the nB blobs has a radius of gyration, rg; since within each blob there are g monomers, it holds N = gnB. All the potentials acting between different blobs involve a single length scale, the radius of gyration of the blobs rg. In particular, the blob–blob potential Vb(r) acting between all blobs and the tethering potential φt(r) acting between bonded, adjacent blobs, take the forms:
βVb(r) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(γr/rg)2] + B exp[−(γr/rg)2] + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(δr/rg)2] exp[−(δr/rg)2] | (12) |
βφt(r) = C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(ζr/rg)2] + D(r/rg − r0)2. exp[−(ζr/rg)2] + D(r/rg − r0)2. | (13) |
In eqn (12) and (13), β ≡ (kBT)−1 and the parameters appearing have the numerical values A = 2.06, B = 0.02, γ = 0.81, δ = 0.10, C = 1.12, ζ = 0.83, D = 0.54 and r0 = 0.98.
Within an arbitrary microscopic model M having a fundamental length scale ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,† the radius of gyration of a ring polymer is given by
,† the radius of gyration of a ring polymer is given by
RMg,0 = αMR![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) Nν, Nν, | (14) |
| RBg,0 = αBRrgnνB. | (15) |
In eqn (15), the superscript B is an indicator that the blobbed representation has been used. Indeed, as rg is the only length scale there, it naturally appears on the right hand-side in lieu of the scale ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) of the M-representation in eqn (14), and, similarly, nB replaces N. Given the fact that each blob contains g original monomers that form a linear chain, the radius of gyration rg of the blobs is that of a linear polymer chain contained in a blob and thus it is expressed as:
of the M-representation in eqn (14), and, similarly, nB replaces N. Given the fact that each blob contains g original monomers that form a linear chain, the radius of gyration rg of the blobs is that of a linear polymer chain contained in a blob and thus it is expressed as:
rg = αML![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) gν, gν, | (16) |
RBg,0 = αBRαML![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) Nν. Nν. | (17) |
From a comparison of eqn (14) and (17), it follows that the multi-blob representation induces a rescaling of the zero-density radius of gyration by a factor 1/α of order unity, which results from a combination of the pre-factors αBR, αML and αMR as follows:
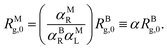 | (18) |
The proportionality factors αba (a = L and R; b = M and B) that link the radius of gyration Rg,0 to the number of monomers N in a polymer, contain information on the average number of contacts of the monomers with the solvent, on the excluded volume of the monomers, and on the solvent quality. They are therefore quantities that depend on the specific model chosen to represent the system. On the other hand, the scaling exponent ν that determines the scaling of Rg,0 with the number of monomers N within a chain is an universal constant that only depends on the solvent quality. When different representations have to be compared, it becomes hence crucial to rescale all lengths by the respective radius of gyration computed at zero density, therefore obtained results are universal and independent of the description chosen.
The two different proportionality factors can be clearly seen in the double-logarithmic plot of the radius of gyration of a ring polymer as a function of the length of the polymeric chain presented in Fig. 1. The two straight lines shown there run in parallel; it can be seen that αMR = 0.404 for Model I, whereas αBRαML = 0.282, their ratio yielding the conversion factor α = 1.433. Accordingly, when we analyze multi-blob simulation results and we wish to re-express quantities with the dimension of length in terms of the microscopic scale ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , we must perform an additional rescaling of the same by the factor α = 1.433 (Model I), in order to carry out a comparison with the monomer-resolved model. In such a way, we eliminate artificial discrepancies between the two. Alternatively, carrying out the rescaling in the reverse order, we can express results of any microscopic model on the length scale of the universal multi-blob model, and thus render the properties of the system completely model-independent. Finally, another option is to reduce the length scales of each model separately on the corresponding model-specific Rbg,0 (b = M and B), and compare the results from various models in this fashion. We will employ either possibility in presenting the results in the following section, choosing for each quantity the length scale most natural to it. Finally, we note that the pre-factors αba can be easily determined for any model from simulations of relatively short molecules.
, we must perform an additional rescaling of the same by the factor α = 1.433 (Model I), in order to carry out a comparison with the monomer-resolved model. In such a way, we eliminate artificial discrepancies between the two. Alternatively, carrying out the rescaling in the reverse order, we can express results of any microscopic model on the length scale of the universal multi-blob model, and thus render the properties of the system completely model-independent. Finally, another option is to reduce the length scales of each model separately on the corresponding model-specific Rbg,0 (b = M and B), and compare the results from various models in this fashion. We will employ either possibility in presenting the results in the following section, choosing for each quantity the length scale most natural to it. Finally, we note that the pre-factors αba can be easily determined for any model from simulations of relatively short molecules.
 | ||
| Fig. 1 Double-logarithmic plot of the dependence of the infinite-dilution gyration radius Rg,0 for flexible and unknotted ring polymers on the number N of microscopic monomers. Red circles correspond to the full-monomer Model I and black ×-symbols to the multi-blob model. Within the latter, different coarse-graining realizations resulting from various combinations of g and nB at fixed values of N = gnB are shown. Dashed lines are fits to a power law, eqn (14) and (17), with the Flory exponent ν = 0.588. | ||
3. One and two rings
Once the multi-blob procedure is set up, it is necessary to test the level of coarse graining necessary to represent a ring polymer without affecting its properties. In order to do this, single molecule properties, such as shape parameters and the distribution of the radius of gyration are computed both with the coarse-grained representation and the microscopic one, and compared to one another. The same is done for the center-of-mass effective interaction. The knowledge gained from these comparisons also serves as a basis for deciding which is the minimal number of blobs per ring necessary for a faithful representation of the properties of concentrated systems.We first consider single molecule properties. In order to assess the validity of the coarse graining procedure, we consider two characteristic quantities, namely the gyration tensor, which entails information on the shape of the rings, as well as the probability density P(![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g,0) of the instantaneous gyration radius
g,0) of the instantaneous gyration radius ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g,0 of the rings. Both quantities have been measured within Model I and within the multi-blob approach for vastly different values of N and blobbing fractions, with the number of blobs per ring, nB, employed in the latter lying in the range 10 ≤ nB ≤ 20.
g,0 of the rings. Both quantities have been measured within Model I and within the multi-blob approach for vastly different values of N and blobbing fractions, with the number of blobs per ring, nB, employed in the latter lying in the range 10 ≤ nB ≤ 20.
Analysis of the gyration tensor yields the set of the expectation values of its three eigenvalues30λ1 > λ2 > λ3. We compare these between the multi-blob and the full monomer representations as shown in Fig. 2. It can be seen that a small number of blobs, 10 ≤ nB ≤ 20, are sufficient to accurately reproduce the shape and the asymmetries of the molecule. Within the whole N-range and independent of the model used, the three eigenvalues are constant and agree across all descriptions of the rings. The distributions of the radius of gyration have been measured for Model I and for the multi-blob approach. For the former, monomer numbers N = 1000, 1500, 2000, 2500 and 3000 have been used, whereas for the latter five different values of nB, namely nB = 10, 12, 15, 17 and 20 have been employed. Selected results, with the gyration radius ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g,0 expressed on the microscopic length scale‡d, are shown in Fig. 3. The striking agreement obtained between the two representations for all N corroborates the validity of the multi-blob approach for isolated molecules and it establishes that a number of blobs as small as nB = 10 are already sufficient to reproduce the salient features of ring polymers. At the same time, as each blob contains at least g = 100 monomers, a very fast simulation of a 10-blob-ring brings forward the properties of ring polymers with at least N = 1000 true monomers.
g,0 expressed on the microscopic length scale‡d, are shown in Fig. 3. The striking agreement obtained between the two representations for all N corroborates the validity of the multi-blob approach for isolated molecules and it establishes that a number of blobs as small as nB = 10 are already sufficient to reproduce the salient features of ring polymers. At the same time, as each blob contains at least g = 100 monomers, a very fast simulation of a 10-blob-ring brings forward the properties of ring polymers with at least N = 1000 true monomers.
 | ||
Fig. 3 The distribution functions of the instantaneous radius of gyration ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g,0 of ring polymers at infinite dilution, obtained within Model I (full-monomer) and in the multi-blob representation at different levels of coarse graining. (a) N = 1000 monomers; (b) N = 2000 monomers; (c) N = 3000 monomers. The multi-blob results have been obtained using different numbers of blobs, as indicated in the legend of panel (a), which applies to all panels. Results from the multi-blob simulations have been re-expressed in units of d by using the rescaling in eqn (18). g,0 of ring polymers at infinite dilution, obtained within Model I (full-monomer) and in the multi-blob representation at different levels of coarse graining. (a) N = 1000 monomers; (b) N = 2000 monomers; (c) N = 3000 monomers. The multi-blob results have been obtained using different numbers of blobs, as indicated in the legend of panel (a), which applies to all panels. Results from the multi-blob simulations have been re-expressed in units of d by using the rescaling in eqn (18). | ||
We now turn our attention to a more detailed quantity that involves two rings and thus it is anticipated to be more sensitive to the number of blobs used to coarse-grain a ring, namely the effective interaction between their centers of mass,20,21Veff(R). Both the microscopic and multi-blob Hamiltonians of two ring polymers, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , have the general form:
, have the general form:
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 11({rN}) + 11({rN}) + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 22({sN}) + 22({sN}) + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 12({rN,sN}), 12({rN,sN}), | (19) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 12({rN,sN}) contains all the inter-ring interactions between the segments. The canonical and topologically faithful partition function
12({rN,sN}) contains all the inter-ring interactions between the segments. The canonical and topologically faithful partition function ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T is given as
T is given as![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T = ∫∫drNdsN T = ∫∫drNdsN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−β exp[−β![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ]T. ]T. | (20) |
Note the usage of the notation ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T and exp[−β
T and exp[−β![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ]T with the T-superscript. This indicates that, in addition to the usual Boltzmann weight, expressed in the exponential factor of the Hamiltonian, there is an explicit exclusion from the partition sum of all microstates that leads to concatenated rings. In what follows, a T-superscript will always be used to indicate the presence of this topological constraint, whereas its absence will denote a usual partition sum, in which concatenated configurations are allowed. Additional constraints on the coordinates can be formally handled by e.g. introducing appropriate δ-functions in the integrand of eqn (20). The separation between the centers of mass, for instance, can be formally fixed at a distance R = |R| to define the constrained partition function
]T with the T-superscript. This indicates that, in addition to the usual Boltzmann weight, expressed in the exponential factor of the Hamiltonian, there is an explicit exclusion from the partition sum of all microstates that leads to concatenated rings. In what follows, a T-superscript will always be used to indicate the presence of this topological constraint, whereas its absence will denote a usual partition sum, in which concatenated configurations are allowed. Additional constraints on the coordinates can be formally handled by e.g. introducing appropriate δ-functions in the integrand of eqn (20). The separation between the centers of mass, for instance, can be formally fixed at a distance R = |R| to define the constrained partition function ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T(R) as:
T(R) as:
 | (21) |
With the help of ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T(R) given in eqn (21), the effective interaction Veff(R) between the centers of mass of the molecules is defined as:
T(R) given in eqn (21), the effective interaction Veff(R) between the centers of mass of the molecules is defined as:
 | (22) |
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T(R → ∞) =
T(R → ∞) = ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (R → ∞). By multiplying and dividing the right-hand side with
(R → ∞). By multiplying and dividing the right-hand side with ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (R), one can decompose the effective interaction Veff(R) into its steric part Vsteric(R) and the topological potential VT(R):
(R), one can decompose the effective interaction Veff(R) into its steric part Vsteric(R) and the topological potential VT(R):| Veff(R) = Vsteric(R) + VT(R), | (23) |
 | (24) |
 | (25) |
The steric potential Vsteric(R), eqn (24), is thus expressed in the usual way in which effective interactions between macromolecular entities are defined in cases where topology plays no role. Eqn (23) demonstrates however, that for ring polymers, Vsteric(R) is only part of the full story: an additional, topological term VT(R) must be added to it to obtain the full effective potential Veff(R). Though, as it will be shortly shown, for two rings VT(R) is only a small fraction of Veff(R), in concentrated solutions where steric interactions are increasingly screened out, the topological interaction plays a very important role in determining the conformations of the molecules and the correlations between them.
To compute the two contributions to the effective pair potential in the simulation, we use a generalization of the Widom insertion algorithm.48,51,60 Our choice is guided by the fact that as R → ∞, and since the inter-monomer potentials are short-ranged, the interaction term ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 12({rN,sN}) vanishes identically and the denominator of eqn (22) factorizes into the product of the partition functions of two noninteracting rings. Concomitantly, eqn (22) can be re-expressed as
12({rN,sN}) vanishes identically and the denominator of eqn (22) factorizes into the product of the partition functions of two noninteracting rings. Concomitantly, eqn (22) can be re-expressed as
 | (26) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 of two independent rings:
0 of two independent rings:![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = 0 = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 11({rN}) + 11({rN}) + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 22({sN}). 22({sN}). | (27) |
It might appear at first sight paradoxical that one is capable of expressing a constrained free energy as the expectation value of some quantity. However, as eqn (22) readily shows, Veff(R) is a difference between two constrained free energies, one at separation R and the other at infinite separation. Free energy differences can indeed be calculated very efficiently using computer simulations.
Widom insertion51,60 takes advantage of eqn (27) in the following way. First, a very large number of independent and equilibrated single-ring configurations are generated. Thereafter, these are combined in pairs by simply pulling one of the two is such a way that its center of mass lies at a distance R from the center of mass of the other, i.e., one molecule is inserted at a distance R from the other. From the ensemble of these inserted pairs, the expectation value appearing in eqn (27) is computed. The method is simple and transparent; however, it is inefficient when the typical conformations of the interacting entities are markedly different from those generated within the non-interacting Hamiltonian. For instance, Widom insertion would not be appropriate to calculate the effective interaction of a dense polymer brush with a hard wall, since for close brush-wall approaches, the massive retraction of the brush hairs, enforced by the presence of the wall, would result in configurations that appear extremely rare in the free-brush case. However, Widom insertion is well-suited for fractal, open, and penetrable macromolecules, whose effective interactions do not exceed a few kBTs even at the closest approaches. It has been successfully employed to linear chains51 and it has also proven accurate and efficient also for the case at hand. At the same time, it must be emphasized that the arbitrary insertion of one ring into the neighborhood of another always entails the risk of producing a concatenated pair. Therefore, due care has to be taken a posteriori to exclude such cases from the calculation of the expectation value in eqn (27).
For the case at hand, we proceeded as follows. For each insertion step, we randomly select two molecules from an ensemble of L = 104 isolated ring equilibrium configurations. We then compute, for all possible ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = L(L − 1)/2 combinations of the equilibrium configurations, the probability
= L(L − 1)/2 combinations of the equilibrium configurations, the probability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) TS(R) of bringing the centers of mass of the two molecules at a distance R, under the condition that both the topological (T) and the steric (S) constraints are fulfilled. To this end, the following procedure has been followed. Each microstate μ(R) in which the centers of mass of the two rings are separated by R is first checked for steric interactions and it is provisionally accepted with a steric hindrance acceptance probability paccS(μ(R)) given by:
TS(R) of bringing the centers of mass of the two molecules at a distance R, under the condition that both the topological (T) and the steric (S) constraints are fulfilled. To this end, the following procedure has been followed. Each microstate μ(R) in which the centers of mass of the two rings are separated by R is first checked for steric interactions and it is provisionally accepted with a steric hindrance acceptance probability paccS(μ(R)) given by:
paccS(μ(R)) = exp[−β![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 12(μ(R))], 12(μ(R))], | (28) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) S(R) out of
S(R) out of ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) configurations survive the steric test.§
configurations survive the steric test.§
To account for inter-winding of the two rings, we compute the Gauss linking number, m, which is a measure of the degree of concatenation of two molecules.20,40 For any microstate μ(R), m is given by
 | (29) |
| paccTS(μ(R)) = δm,0paccS(μ(R)). | (30) |
In this way, the number of accepted configurations is further reduced from ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) S(R) to
S(R) to ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) TS(R) and the effective interaction is computed as
TS(R) and the effective interaction is computed as
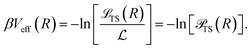 | (31) |
The steric part, Vsteric(R), is calculated as −kBT times the logarithm of the probability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) S(R) of passing the steric requirements, i.e.,
S(R) of passing the steric requirements, i.e.,
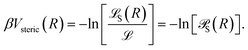 | (32) |
The topological potential is now easily obtained with the help of eqn (23), (31) and (32) as −kBT times the logarithm of the ratio of the number of configurations fulfilling the combination of T- and S-conditions over those fulfilling only S:
 | (33) |
In the last equation, we introduced the conditional probability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) T|S(R) that a given configuration will fulfill the topological constraints provided that it fulfills the steric ones. This follows immediately from eqn (31)–(33) as a corollary of the rule for calculating conditional probabilities:
T|S(R) that a given configuration will fulfill the topological constraints provided that it fulfills the steric ones. This follows immediately from eqn (31)–(33) as a corollary of the rule for calculating conditional probabilities:
 | (34) |
For purely repulsive monomers, the contribution Vsteric(R) is positive, since the proximity of the two molecules restricts the number of conformers for both, thereby reducing the entropy of the system. This is also evident from eqn (32), valid only for repulsive interactions, which expresses βVsteric(R) as minus the logarithm of a probability and it thus implies βVsteric (R) ≥ 0 for all R. However, in solvents of worsening quality, for which enthalpic terms would be present in the intermonomer interactions, this quantity can indeed develop attractive parts for some ranges of the intermolecular separation.30,51 The topological potential, on the other hand, is given as βVT(R) = −ln[![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T(R)/
T(R)/![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (R)], and the numerator of the ratio within the logarithm is always smaller than its denominator, since those microstates that violate the non-concatenation condition are included in the partition sum
(R)], and the numerator of the ratio within the logarithm is always smaller than its denominator, since those microstates that violate the non-concatenation condition are included in the partition sum ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (R) but excluded from
(R) but excluded from ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) T(R). Topology sets forth a constraint that inadvertently reduces the number of permissible microstates, therefore the topological contribution βVT(R) is non-negative at all R, independent of the microscopic details of the model. Still, a weak attractive, topological effective force FT(R) = −∇VT(R) can emerge between two rings at moderately small values of their separation, R ≤ Rg,0/2, see below.
T(R). Topology sets forth a constraint that inadvertently reduces the number of permissible microstates, therefore the topological contribution βVT(R) is non-negative at all R, independent of the microscopic details of the model. Still, a weak attractive, topological effective force FT(R) = −∇VT(R) can emerge between two rings at moderately small values of their separation, R ≤ Rg,0/2, see below.
Results for the effective and topological potentials Veff(R) and VT(R) are reported in Fig. 4 which are obtained from both the full-monomer representation (Model I) and the coarse-grained, multi-blob simulation. The latter has been performed at two levels of blobbing, i.e., representing each ring with nB = 20 and nB = 50 blobs. For the former, rings of N = 100 monomers have been chosen, so that the results are already in the scaling regime, i.e., independent of the degree of polymerization.21 It can be seen that already for nB = 20, the agreement between the full-monomer and the coarse-grained approaches is very good, discrepancies between the two models being at most of the order of 5%, whereas for nB = 50 the agreement is perfect. The characteristic plateau20,21,30,40 of Veff(R) for R ≤ Rg,0/2 is nicely reproduced by all approaches. We also note that the results for nB = 20 and nB = 50 compare much better with one another than the ones for N = 20 and N = 50 for Model I,21 which are not even in the scaling regime in that case. Soft segment interactions lead to a much more rapid approach to the scaling limit than hard ones.
The topological effective potentials obtained both with the two levels of coarse-graining in the multiblob representation and with the full-monomer model are quantitatively comparable to those predicted by Hirayama et al.,40 who employed the self-avoiding polygon model, by Bohn and Heermann,20 who performed lattice simulations, as well as by Narros et al.21 in their off-lattice simulations. As predicted by the various authors, VT(R) is positive and it displays a maximum at R ≅ Rg,0/2, which accounts for about 13% of the maximum value of the total effective potential.
As regards the performance of the coarse-graining procedure, while both levels of coarse graining are able to qualitatively reproduce the shape of the microscopic effective potential very accurately, the data obtained with a finer coarse graining show a truly excellent overlap with those extracted with a full monomer representation. As the effective pair potentials are extremely sensitive to the internal degrees of freedom of a molecule, it appears that even though single molecule properties are perfectly reproduced already with nB = 10 blobs (see Fig. 3), in order to quantitatively reproduce the many body contributions in the effective pair potential a finer coarse graining is required, namely nB = 50. A possible source for the discrepancies between the few-nB-results and the full-monomer ones may lie in the implicit assumption made in the calculation of the Gaussian linking number m that the soft blobs are connected with straight line segments with one another. When viewed not as an ad hoc model, however, but rather as a description emerging from a microscopic picture, it should be realized that each blob contains a large number of fluctuating monomers. Accordingly, whereas the assumption of straight-line connections between the blob centers might lead to concatenated conformations, there still exist underlying full-monomer microstates compatible with the blobbed conformation that are not concatenated and vice versa. This effect, which is stronger for small nB-numbers, manifests itself predominantly on the topological potential. Indeed, as it can be seen in Fig. 4, the nB = 20-result for VT(R) at the maximum of the same differs by its microscopically determined counterpart by about 13% and it accounts for the main part of the discrepancies for Veff(R) as well. To avoid the influence of such artifacts, we will, in what follows, always represent multi-blobbed ring polymers with nB = 50 blobs to explore the properties of semi-dilute solutions.
4. Concentrated solutions
Once ensured that both single molecule properties and effective pair potentials are reproduced by our coarse-graining methodology, we focus our attention on the properties of semi-dilute ring polymer solutions upon augmenting densities. To deeply explore the semi-dilute regime, we performed with both representations of Monte Carlo simulations of the microscopic Models I and II as well as of the multi-blobbed rings for a range of densities 0.5 ≤ ρ/ρ* ≤ 7. The highest density simulated with the microscopic models was ρ/ρ* = 4, while the multi-blob approach allows us to easily explore higher densities; we simulated up to ρ/ρ* = 7 in this work. For all densities and all models, a number of M = 350 rings have been simulated in![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) run = 16 independent simulation runs, employing periodic boundary conditions and different initial configurations, and adjusting the size of the simulation box to achieve the desired ratio ρ/ρ*.
run = 16 independent simulation runs, employing periodic boundary conditions and different initial configurations, and adjusting the size of the simulation box to achieve the desired ratio ρ/ρ*.
To grow the rings to their desired size and ascertain that no concatenations take place, we proceeded as follows. First, we randomly placed in the simulation box M = 350 small, unknotted and non-concatenated mini-rings consisting of four monomers each, i.e., rings much smaller than the required ones and thus presenting no difficulties in placing in the box. Second, we grew them to the desired size (N = 50 or 100 for Models I and II, and nB = 50 for the multi-blob model) by sequentially adding monomers to them during a Monte-Carlo simulation that serves exclusively to grow the rings up to their desired size. Concatenations after the addition of every single monomer were prevented using the algorithm presented in the Appendix of ref. 30. After the desired molecular size N(nB) for each molecule was reached, long MC simulations in each one of the ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) run boxes were performed to equilibrate the systems. Equilibrium is achieved when the statistical average of the gyration radii taken over all molecules in all simulation cells does not change any more across several saved configurations. The MC steps employed were single-monomer (blob) moves as well as three types of collective moves: simple- and double crankshaft-moves, as well as rigid translation of the ring as a whole.61,62 For an explanation of the crankshaft moves and the topology checks employed for the same, we refer the reader to the Appendix.
run boxes were performed to equilibrate the systems. Equilibrium is achieved when the statistical average of the gyration radii taken over all molecules in all simulation cells does not change any more across several saved configurations. The MC steps employed were single-monomer (blob) moves as well as three types of collective moves: simple- and double crankshaft-moves, as well as rigid translation of the ring as a whole.61,62 For an explanation of the crankshaft moves and the topology checks employed for the same, we refer the reader to the Appendix.
For Models I and II, topology is preserved under individual monomer moves for a sufficiently small displacement step. This is the case neither for the crank-shaft moves in the microscopic models nor for any type of move in the multi-blobbed model. To guarantee the absence of concatenations, we could have employed the Gaussian linking number m criterion used for the effective potential, but such a test becomes prohibitive when the number of molecules in solution is high. We therefore opted for the bond-crossing algorithm described in the Appendix of ref. 30, which, whenever two bonds meet, treats them as if they were hard. The advantage of this algorithm is that the checks performed are local around each bond for which an attempt has been made to be moved, whereas the Gaussian linking number requires the calculation of a double integral over both rings that need to be checked for being linked.
Furthermore, after an equilibrium state has been reached, we performed one additional test by enforcing an annealing/relaxation process as follows: we carried out additional MC simulations, in which we perturbed the rings by imposing harmonic center-of-mass potentials on each ring that expanded and compressed its molecular size away from the original state of assumed equilibrium. Subsequently, these potentials were switched off; we checked whether the rings relaxed back to their original size after this procedure, confirming that this was indeed the case. Moreover, we also checked that the molecules' ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g-distributions in each of the
g-distributions in each of the ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) run simulation runs were similar between the different boxes, i.e., they showed overlap within error bars. Any two saved configurations are separated by 3 × N × M collective moves plus 100 × N × M single-monomer moves, whereby, for the multi-blob model N is replaced by nB. Finally, we have saved 20 configurations for each simulation box, obtaining an ensemble of 20 ×
run simulation runs were similar between the different boxes, i.e., they showed overlap within error bars. Any two saved configurations are separated by 3 × N × M collective moves plus 100 × N × M single-monomer moves, whereby, for the multi-blob model N is replaced by nB. Finally, we have saved 20 configurations for each simulation box, obtaining an ensemble of 20 × ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) run × M = 112
run × M = 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibrated and statistically independent configurations for each density considered, which have been used to analyze the results.
000 equilibrated and statistically independent configurations for each density considered, which have been used to analyze the results.
Results from our simulations for the density-dependent radius of gyration Rg are shown in Fig. 5. The observed shrinking of the polymer size for ρ/ρ* > 1 can be understood in the framework of the correlation-blob-model sketched in Section 2.1. The polymer consists of nξ correlation blobs, each of size ξ, performing a random walk characterized by some exponent υ. Accordingly, the gyration radius of the polymer depends on ξ and nξ as
| Rg ∼ ξnυξ. | (35) |
Using eqn (3) and (5), eqn (35) yields a power-law dependence on density, namely
 | (36) |
 | (37) |
Note that in the melt, where ξ → ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and nξ → N, eqn (35) is valid for the polymer size at all scales.
and nξ → N, eqn (35) is valid for the polymer size at all scales.
If the correlation blobs also performed a self-avoiding random walk, we would have υ = ν and polymers would not shrink at all for ρ > ρ*. However, the concentration screens out the excluded volume interactions,41 and linear chains adopt in concentrated solutions Gaussian-walk conformations at scales larger than ξ. This implies υ = 1/2, leading viaeqn (37) to the well-known result x = −1/8 for linear polymers.41 For rings, things are different. The topological interactions between different rings cannot be screened out, thus the exponent υ cannot be the one corresponding to a Gaussian random walk. The value of this exponent has been an issue of a long debate. Previous theoretical arguments,5 supported thereafter by computer simulations7,9–13,15 seemed to converge to a value υ = 2/5 for this exponent. However, more recent simulations with longer chains as well as more sophisticated theoretical approaches8,11,17–19,22–25 show that the situation is a bit more subtle: for very long chains whose length N exceeds the entanglement length63Ne, the exponent is υ = 1/3, corresponding to a collapsed lattice animal. However, for N < Ne, a broad crossover regime that can cover several decades in N exists and for which a power-law dependence with the exponent υ = 2/5 is valid.
The results shown in Fig. 5 can now be discussed in this context. To begin with, the multi-blob approach yields results that are identical to those obtained from the monomer-resolved simulations from two different microscopic models, underlying once more the reliability of the former, now for a very broad range of concentrations. Going into a more detailed, quantitative analysis of the results, it can be seen that two power-law regimes emerge for the shrinkage of Rg as a function of the ratio ρ/ρ*. As pointed out also by Iyer et al.,16 there exists a concentration ρT > ρ* that marks a crossover between a regime in which topology is not effective in determining the shrinkage of the rings (for ρ* ≤ ρ ≤ ρT) and a regime where topology is dominant, ρ ≥ ρT. In our case, ρT ≅ 2ρ*. Indeed, the power-law decay of Rg can be fitted with a line of slope −1/8 up to ρT, consistent with a Gaussian random walk of the correlation blobs, and identical to the behavior of linear polymer chains. For ρ > ρT, on the other hand, the decay becomes much more rapid, the power-law switching over to a decay with an exponent −1/4, which is consistent with υ = 2/5. This value of υ corresponds to the broad, crossover regime for N < Ne mentioned above. Indeed, even at the highest density considered for the microscopic models, the monomer density never exceeds a typical value ϕmax ≅ 0.48![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) −3. Measurements and estimates for the entanglement length of similar models63 yield Ne ≅ 30 for ϕ = 0.85
−3. Measurements and estimates for the entanglement length of similar models63 yield Ne ≅ 30 for ϕ = 0.85![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) −3 and Ne ≅ 200 for ϕ = 0.23
−3 and Ne ≅ 200 for ϕ = 0.23![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) −3. We are, evidently, far away from the asymptotic regime N > Ne in which the υ = 1/3-exponent holds, probing instead the υ = 2/5-range, which, by virtue of eqn (37), results in x = −1/4 as the results in Fig. 5 demonstrate. The strong fulfillment of the inequality N < Ne at the ρ/ρ*-ratios considered here has been explicitly confirmed by the estimates of the entanglement length in ref. 26, ascertaining that there is no significant entanglement at the blob length scale.
−3. We are, evidently, far away from the asymptotic regime N > Ne in which the υ = 1/3-exponent holds, probing instead the υ = 2/5-range, which, by virtue of eqn (37), results in x = −1/4 as the results in Fig. 5 demonstrate. The strong fulfillment of the inequality N < Ne at the ρ/ρ*-ratios considered here has been explicitly confirmed by the estimates of the entanglement length in ref. 26, ascertaining that there is no significant entanglement at the blob length scale.
Our claim that topology is the single factor determining the ∼ (ρ/ρ*)−1/4-power law for the shrinkage of the star is unambiguously proven by performing simulations without the topology check, marked ‘no T’ in Fig. 5. Allowing for ring concatenations leads to the usual, ∼(ρ/ρ*)−1/8-power law over the whole density range explored, and there is no crossover to a new exponent at ρT any more: as far as their scaling properties are concerned, rings would behave as linear chains in the concentrated regime if concatenations were allowed. At the same time, it must be emphasized that rings would not be identical to linear chains in their more detailed properties, such as e.g. their infinite-dilution effective interaction Veff(R) or their pair distribution function g(r). The former is evident from the results shown in Fig. 4. Without the topological constraint, Veff(R) would be identical to Vsteric(R), i.e., Veff(R) → Veff(R) − VT(R), and the last expression results in a potential markedly different from the Gaussian interaction between polymer chains.
To investigate the effect of topology on the pair distribution function between the centers of mass, g(R), we have repeated the simulations without the topology check (‘no T’); the results are shown in Fig. 6. It can be seen that, in full consistency with the results for the radius of gyration, marked differences between the correlation functions with and without topological check arise from a density ρ ≥ ρT on. In particular, the degree of inter-penetration between the rings grows when concatenations are allowed, as expected. The effects of the topology are clearly visible in g(R) up to its main peak, R ≅ 7d, corresponding to ≅1.2Rg,0 or ≅1.6Rg at ρ/ρ* = 4 for N = 100. However, even in the absence of the topological constraint, the correlation hole is deeper and broader than for the case of linear chains at the same values of the concentration.48 Due to their cyclical architecture, even ‘ghost rings’ are less penetrable objects than linear chains.
We finally turn our attention to the pair distribution function g(R) between the rings' centers of mass, comparing the results from Model I and from the multi-blob representation as shown in Fig. 7. The excellent and parameter-free agreement between the two underlines the ability of the multi-blob approach to reproduce the structural correlations in concentrated ring polymer solutions. The clustering artifacts caused by the single-blob representation on the basis of Veff(R) alone are removed.21 No inversion procedure of g(R) is any more necessary to yield strongly density-dependent, single-blob effective potentials.21 Indeed, the latter is merely an expression of the increasingly strong many-body interactions that are obtained when one insists at describing mutually overlapping ring polymers as pairwise-interacting single blobs. Once the rings are divided into a sufficient number of smaller segments, each one still large enough to contain a large number of monomers, and these segments have overwhelmingly pair-contacts, the need to resort to density-dependent effective interactions is not present any more. The system can be described by means of fully transferrable, realistic and reliable pair interactions alone.
5. Concluding remarks
We have presented a multi-blob representation of unknotted and flexible ring polymers, which results in a description of ring polymers by means of effective potentials that are universal, i.e., independent of the microscopic details of the underlying model. The interactions are fully transferrable and they provide parameter-free agreement with microscopic results for a wide range of concentrations deeply into the semidilute regime. A length-rescaling involved in adjusting the results of the multi-blob representation back to the microscopic ones is neither arbitrary nor dependent on the concentration but rather an ingredient inherent in the multi-blob approach. The value of this numerical re-scaling factor of order unity can be determined a priori and independent of the finite-density simulations, on the basis of the scaling laws for moderately sized chains and rings in the microscopic and the multi-blobbed representations. With the help of the latter, arbitrarily long polymers can be simulated at a small fraction of the computational cost that would have been required in a full-monomer representation of the same.Efficient checks for the topological, no-concatenation constraints on the ring polymers have been introduced and successfully implemented, demonstrating the crucial role played by the latter in both the shrinkage and the correlations among rings in solution. At present, our work has been limited to flexible and unknotted ring polymers in athermal or good solvents. Future studies should focus on the extension of these ideas to solvents of varying qualities and also on the open issue of a proper accommodation of knotting in a multi-blob representation of ring polymers.
A Appendix: crankshaft algorithms
In this Appendix, we describe the simple- and double-crankshaft moves as well as the algorithm employed to make sure that no topological violation takes place for the accepted ones. What follows is valid both for the full-monomer and for the coarse-grained simulation.A.1 Simple crankshaft
This move selects two random monomers in the ring polymer and it rotates the shorter of the two portions of the ring by a random angle ω around the axis that connects the two monomers. In Fig. 8, we show a sketch of the move and the associated geometry. The algorithm for generating and accepting/rejecting the move is described below. | ||
| Fig. 8 Simple crankshaft move. The smaller portion of the ring polymer is rotated to an angle ω around the axis connecting two random monomers. | ||
1. Randomly select a monomer i in the chain.
2. Randomly select the second monomer j in the portion of the chain such that 2 <|i − j| < N/3. In the following notation i < j (the case i > j is symmetric by construction).
3. Define the rotation axis as R = ri − rj.
4. Select a random angle ω ∈ [α, −α]. Here, α is chosen under the constraint that the largest of the arc-lengths of the monomers generated by the rotation does not exceed the length of its chord by a certain threshold Δ, chosen in this case to be Δ = 1.1.
5. Calculate the new location of all monomers k ∈ (i, j) after the rotation ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (R,ω) as {r′i+1,…,r′j−1} =
(R,ω) as {r′i+1,…,r′j−1} = ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (R,ω){ri+1,…,rj−1}. The rotation generates a surface S spanned by the rotating bonds. Triangulate this surface by straight lines shown in Fig. 8 as red segments.
(R,ω){ri+1,…,rj−1}. The rotation generates a surface S spanned by the rotating bonds. Triangulate this surface by straight lines shown in Fig. 8 as red segments.
6. Compute the energy of the old and the new configurations, E and E′, and perform Metropolis Monte Carlo for the attempted move on the basis of ΔE = E′ − E.
• If the movement is (provisionally) accepted, continue to step 7.
• Otherwise go to step 1 (move REJECTED).
7. For each of the bonds around the surface S that could have crossed it during its generation, check whether this is the case for any of the triangles of S shown in Fig. 8. Employ the algorithm of the Appendix of ref. 30 for this check.
• If any of the checks is positive (there is crossing of links), the move is REJECTED and go to step 1.
• Otherwise the movement is ACCEPTED and continue to step 8.
8. Update the configuration and the total energy.
A.2 Double crankshaft
The double crankshaft move is a variation of the simple crankshaft in which a part of the rotated segment undergoes the inverse rotation. In this way, a part of the ring is just ‘lifted up’ as shown in Fig. 9.1. Randomly select a monomer i in the chain.
2. Randomly select the second monomer j in the portion of chain such that 2 < |i − j| < N/3. In the following notation i < j (the case i > j is symmetric by construction).
3. Define the first rotation axis as R1 = ri − rj and the second rotation axis R2 = r′i+1 − r′j−1, primes denoting the position vectors after the first rotation.
4. Select a random angle ω ∈ [α, −α] as before.
5. Perform the first crankshaft rotation, ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (R1,ω), bringing the monomers to the positions {r′i+1,…,r′j−1} =
(R1,ω), bringing the monomers to the positions {r′i+1,…,r′j−1} = ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (R1,ω){ri+1,…,rj−1} and the second one,
(R1,ω){ri+1,…,rj−1} and the second one, ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (R2,−ω), bringing the monomers to the positions {r′′i+2,…,r′′j−2} =
(R2,−ω), bringing the monomers to the positions {r′′i+2,…,r′′j−2} = ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (R2,−ω){r′i+2,…,r′j−2}. The combination of these generates a surface S that is triangulated as shown in Fig. 9 by the red segments.
(R2,−ω){r′i+2,…,r′j−2}. The combination of these generates a surface S that is triangulated as shown in Fig. 9 by the red segments.
6. Follow the same steps from step 6 as for the case of the simple crankshaft.
Acknowledgements
This work has been supported by the Austrian Science Fund (FWF), Grant 23400-N16. Computer time at the Vienna Scientific Cluster (VSC) is gratefully acknowledged.References
- C. Micheletti, D. Marenduzzo and E. Orlandini, Phys. Rep., 2011, 504, 1 CrossRef CAS.
- M. D. Frank-Kamenetskii, A. V. Lukashin and A. V. Vologodskii, Nature, 1975, 258, 398 CrossRef CAS PubMed.
- A. Grosberg, Y. Rabin, S. Havlin and A. Neer, Europhys. Lett., 1993, 23, 373 CrossRef CAS.
- S. P. Obukhov, M. Rubinstein and T. Duke, Phys. Rev. Lett., 1994, 73, 1263 CrossRef CAS PubMed.
- M. E. Cates and J. M. Deutsch, J. Phys., 1986, 47, 2121 CAS.
- M. Rubinstein, Phys. Rev. Lett., 1986, 57, 3023 CrossRef CAS PubMed.
- M. Müller, J. P. Wittmer and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 53, 5063 CrossRef.
- A. Y. Grosberg, Soft Matter, 2014, 10, 560 RSC.
- T. Pakula and S. Geyler, Macromolecules, 1988, 21, 1665 CrossRef CAS.
- M. Müller, J. P. Wittmer and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 4078 CrossRef.
- M. Müller, J. P. Wittmer and J.-L. Barrat, Europhys. Lett., 2000, 52, 406 CrossRef.
- S. Brown and G. Szamel, J. Chem. Phys., 1998, 108, 4705 CrossRef CAS.
- S. Brown and G. Szamel, J. Chem. Phys., 1998, 109, 6184 CrossRef CAS.
- S. Brown, T. Lenczycski and G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 052801 CrossRef CAS.
- K. Hur, R. G. Winkler and D. Y. Yoon, Macromolecules, 2006, 39, 3975 CrossRef CAS.
- B. V. S. Iyer, S. Shanbhag, V. A. Juvekar and A. K. Lele, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 2370 CrossRef CAS.
- T. Vettorel, A. Y. Grosberg and K. Kremer, Phys. Biol., 2009, 6, 025013 CrossRef PubMed.
- J. Suzuki, A. Takano, T. Deguchi and Y. Matsushita, J. Chem. Phys., 2009, 131, 144902 CrossRef PubMed.
- G. Tsolou, N. Stratikis, C. Baig, P. S. Stephanou and V. G. Mavrantzas, Macromolecules, 2010, 43, 10692 CrossRef CAS.
- M. Bohn and D. W. Heermann, J. Chem. Phys., 2010, 132, 044904 CrossRef PubMed.
- A. Narros, A. J. Moreno and C. N. Likos, Soft Matter, 2010, 6, 2435 RSC.
- J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204904 CrossRef PubMed.
- J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204905 CrossRef PubMed.
- T. Sakaue, Phys. Rev. Lett., 2011, 106, 167802 CrossRef PubMed.
- T. Sakaue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021806 CrossRef.
- A. Rosa, E. Orlandini, L. Tubiana and C. Micheletti, Macromolecules, 2011, 44, 8668 CrossRef CAS.
- A. Rosa and R. Everaers, Phys. Rev. Lett., 2014, 112, 118302 CrossRef PubMed.
- D. Michieletto, D. Marenduzzo, E. Orlandini, G. P. Alexander and M. S. Turner, ACS Macro Lett., 2014, 3, 255 CrossRef CAS.
- D. Michieletto, D. Marenduzzo, E. Orlandini, G. P. Alexander and M. S. Turner, Soft Matter, 2014, 10, 5936 RSC.
- A. Narros, A. J. Moreno and C. N. Likos, Macromolecules, 2013, 46, 3654 CrossRef CAS PubMed.
- M. Bernabei, P. Bacova, A. J. Moreno, A. Narros and C. N. Likos, Soft Matter, 2013, 9, 1287 RSC.
- M. Z. Slimani, P. Bacova, M. Bernabei, A. Narros, C. N. Likos and A. J. Moreno, ACS Macro Lett., 2014, 3, 611 CrossRef CAS PubMed.
- A. Rosa, Biochem. Soc. Trans., 2013, 41, 612 CrossRef CAS PubMed.
- A. Rosa and R. Everaers, PLoS Comput. Biol., 2008, 4, e1000153 Search PubMed.
- D. Buck and E. Flapan, Applications of Knot Theory, J. Am. Math. Soc., 2008, 66, 47 Search PubMed.
- L. Postow, C. D. Hardy, J. Arsuaga and N. R. Cozzarelli, Gene Dev., 2004, 18, 1766 CrossRef CAS PubMed.
- R. Matthews, A. A. Louis and C. N. Likos, ACS Macro Lett., 2012, 1352 CrossRef CAS PubMed.
- P. Poier, C. N. Likos and R. Matthews, Macromolecules, 2014, 47, 3394 CrossRef CAS PubMed.
- A. Takano, Y. Kushida, Y. Ohta, K. Masuoka and Y. Matsushita, Polymer, 2009, 50, 1300 CrossRef CAS.
- N. Hirayama, K. Tsurusaki and T. Deguchi, J. Phys. A: Math. Theor., 2009, 42, 105001 CrossRef.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, 2003 Search PubMed.
- J. Roovers, Macromolecules, 1985, 18, 1359 CrossRef CAS.
- J. Roovers, Macromolecules, 1988, 21, 1517 CrossRef CAS.
- G. B. McKenna, G. Hadziioannou, P. Lutz, G. Hild, C. Strazielle, C. Straupe, P. Rempp and A. J. Kovacs, Nat. Mater., 1987, 20, 498 CrossRef CAS.
- D. F. Hodgson and E. J. Amis, J. Chem. Phys., 1991, 95, 7653 CrossRef CAS.
- K. Hur, C. Jeong, R. G. Winkler, N. Lasevic, R. H. Gee and D. Y. Yoon, Macromolecules, 2011, 44, 2311 CrossRef CAS.
- M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hinzen, D. Richter, D. Cho, T. Chang and M. Rubinstein, Nat. Mater., 2008, 7, 997 CrossRef CAS PubMed.
- P. G. Bolhuis, A. A. Louis, J. P. Hansen and E. J. Meijer, J. Chem. Phys., 2001, 114, 4269 CrossRef.
- A. Narros, A. J. Moreno and C. N. Likos, Macromolecules, 2013, 46, 9437 CrossRef CAS PubMed.
- A. Narros, A. J. Moreno and C. N. Likos, Biochem. Soc. Trans., 2013, 41, 630 CrossRef CAS PubMed.
- V. Krakoviack, J.-P. Hansen and A. A. Louis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 041801 CrossRef CAS.
- G. D’Adamo, A. Pelissetto and C. Pierleoni, Soft Matter, 2012, 8, 5151 RSC.
- C. N. Likos, A. Lang, M. Watzlawek and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031206 CrossRef CAS.
- C. Pierleoni, B. Capone and J.-P. Hansen, J. Chem. Phys., 2007, 127, 171102 CrossRef PubMed.
- B. Capone, J.-P. Hansen and I. Coluzza, Soft Matter, 2010, 6, 6075 RSC.
- B. Capone, I. Coluzza and J.-P. Hansen, J. Phys.: Condens. Matter, 2011, 23, 194102 CrossRef PubMed.
- B. Capone, I. Coluzza, F. Lo Verso, C. N. Likos and R. Blaak, Phys. Rev. Lett., 2012, 109, 238301 CrossRef PubMed.
- I. Coluzza, B. Capone and J.-P. Hansen, Soft Matter, 2011, 7, 5255 RSC.
- B. M. Ladanyi and D. Chandler, J. Chem. Phys., 1975, 62, 4308 CrossRef CAS.
- B. M. Mladek and D. Frenkel, Soft Matter, 2011, 7, 1450 RSC.
- S. K. Kumar, M. Vacatello and D. Y. Yoon, J. Chem. Phys., 1988, 89, 5206 CrossRef CAS.
- F. A. Escobedo and J. J. de Pablo, J. Chem. Phys., 1995, 102, 2636 CrossRef CAS.
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823 CrossRef CAS PubMed.
Footnotes |
† In our case, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = d for Model I and = d for Model I and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = σ for Model II. = σ for Model II. |
| ‡ Here, also the expectation value Rg,0 could have been used to scale the horizontal axes but in this case all curves would practically collapse onto one another, independent of the value of N. |
| § Note that for Model I the exponential factor at the right-hand side of eqn (28) is either zero, if any two monomers of the two rings overlap, or unity, otherwise, and thus the survival of a microstate is not any more a matter of chance. |
| ¶ This is not entirely correct. Although m ≠ 0 always implies the existence of concatenation, the opposite is not true, since there are some particular situations, such as the Whitehead link, for which m = 0. We have ignored these special cases here. |
| This journal is © The Royal Society of Chemistry 2014 |







