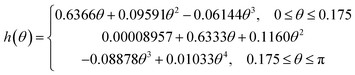Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaporation of a capillary bridge between a particle and a surface†
Michael J.
Neeson
ab,
Raymond R.
Dagastine
bcd,
Derek Y. C.
Chan
abe and
Rico F.
Tabor
*f
aDepartment of Mathematics and Statistics, University of Melbourne, Parkville 3010, Australia
bParticulate Fluids Processing Centre, University of Melbourne, Parkville 3010, Australia
cDepartment of Chemical and Biomolecular Engineering, University of Melbourne, Parkville 3010, Australia
dMelbourne Centre for Nanofabrication, 151 Wellington Road, Clayton 3168, Australia
eDepartment of Chemistry and Biotechnology, Swinburne University of Technology, Hawthorn 3122, Australia
fSchool of Chemistry, Monash University, Clayton 3800, Australia. E-mail: rico.tabor@monash.edu; Fax: +61 3 9905 4597; Tel: +61 3 9905 4558
First published on 5th September 2014
Abstract
The liquid bridge that forms between a particle and a flat surface, and the dynamics of its evaporation are pertinent to a range of physical processes including paint and ink deposition, spray drying, evaporative lithography and the flow and processing of powders. Here, using time-lapse photography, we investigate the evaporative dynamics of a sessile liquid bridge between a particle and a planar substrate. Different wetting characteristics of the particle and substrate are explored, as well as the effects of contact line pinning and stick-slip boundary conditions. A theoretical framework is developed to quantify and analyse the experimental observations. For the size range of particles and drops used in this study, gravity is by far the smallest force in the system when compared to the surface tension and capillary interactions that are present, but in certain circumstances it dictates the key evolution stages of the geometry of the particle-drop-substrate systems. Analysis of evaporation dynamics and capillary forces indicate that at low Bond numbers, surface tension forces dominate and provide unique opportunities for the control of particles on surfaces.
The existence of liquid bridges between solids – either as particles or extended flat surfaces – is of considerable interest and importance in a range of fields, which can be crudely separated into three classes based on their geometry: (i) one or more small particles can sit at the interface of a much larger drop, (ii) a small liquid volume sits between two solid surfaces forming a ‘capillary bridge’ and (iii) the transitional case where the sizes of the drop and particle are of comparable magnitude.
The limit in which the particle radius is much smaller than the drop radius has been investigated extensively, primarily in the context of Ramsden or Pickering emulsions,1,2 foams, ‘dry water’3 and liquid marbles,4–6 where many particles are adsorbed at a liquid interface to confer stability.7,8 The force between a small particle and a drop (or bubble) interface has been investigated by various groups using the atomic force microscope, and the observed behaviour analysed in terms of wetting and capillarity.9–13 Using a perturbation analysis, the lateral capillary interactions between particles in a Pickering emulsion were theoretically investigated.14
For the case of multiple particles joined by liquid capillary bridges, each bridge can be defined geometrically by its volume and the contact angle at the particle surfaces. This case is of interest when powders are processed and handled, particularly in moist environments or where hygroscopic materials are involved.15,16 Common examples include minerals and ceramics processing, foods (e.g. starch and whey powders) and permeation and moisture retention in soils and sediments.17,18 Recently it was shown that the addition of a tiny amount of a secondary fluid to a suspension causes large capillary networks, greatly altering its bulk rheological behaviour.19
Capillary bridges are of particular importance since they give rise to the capillary force, which has wide-ranging implications in the study of interfacial forces in atomic force microscopy20 and particle adhesion21–23 through to nanoscale applications such as dip-pen lithography24 and micro-manipulation.25 Several studies have experimentally investigated the forces arising from small capillary bridges between a particle and a surface.26
Orr et al.27 provided a comprehensive theoretical treatment of an axisymmetric capillary bridge between a spherical particle and a flat substrate. More recently Guzowski et al.28 considered the capillary force that acts on a particle attached to an initially spherical interface when subjected to an asymmetric displacement of the particle.
When multiple particles sit on a flat liquid surface, the local interface near each particle is deformed, resulting in a lateral capillary force between particles that can be either attractive or repulsive. The attractive lateral capillary force facilitates the self-assembly of large two-dimensional crystal arrays.29–31 Alternatively, colloidal self-assembled arrays can be formed by initially suspending multiple particles inside a drop and subsequently evaporating the supporting drop.32–36 Since these capillary forces are extremely large when compared to, for example, particle weights, they provide surprising and useful behaviours such as adhesives that mimic gecko adhesion37 and insects that are able to climb ‘uphill’ at liquid menisci.38
Although the behaviour of both a small particle on a much larger spherical drop, class (i), and a small liquid bridge between a large particle and a surface, class (ii), have both been studied extensively, the same cannot be said for the intermediate class (iii), where the characteristic dimensions of both the particle and the drop are comparable. Such configurations share similarities with those for which the particle is replaced by a third mutually immiscible fluid.39
In this paper we consider, both theoretically and experimentally, the capillary bridge formed between a spherical particle and a planar substrate. We analyse the cases of pinned contact line as well as constant contact angle boundary conditions at both fluid–fluid-surface contacts, as it is seen that both boundary conditions are observed in the presented experiments.
By comparing the Gibbs free energy for each configuration, we are able to determine the energetically favoured configuration, revealing an important critical volume below which an axisymmetric collar is formed around the base of the particle, exerting an attractive force between the particle and the substrate, whereas above this critical volume the interface is spherical with no capillary force acting between the particle and the substrate.
Having developed a theoretical solution for an equilibrium capillary drop interface, we present a series of experiments with a small particle at the air–water interface of a water sessile or pendant drop. By allowing the drop to evaporate and tracking the evolution of the drop shape by time-lapse photography, we are able to investigate the dependence of system geometry on volume as well as hysteresis effects, using the theoretical model to obtain relevant physical parameters for comparison.
1 Theory
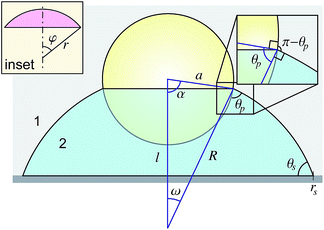
When a spherical particle of radius a is placed at the interface of a sessile drop of fluid 2, surrounded by an outer fluid 1, a liquid capillary bridge is formed between the particle, p and the substrate, s (Fig. 1). The characteristic dimension of the drop over which gravitational force can deform the interface is the capillary length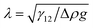 , where γ12 is the interfacial tension of the 12-fluid interface, Δρ is the density difference between the two fluid phases and g is the gravitational acceleration. For drop dimensions well below the capillary length (∼2.7 mm for a water drop in air) its shape will be determined by the Young–Laplace equation without the gravitational term,
, where γ12 is the interfacial tension of the 12-fluid interface, Δρ is the density difference between the two fluid phases and g is the gravitational acceleration. For drop dimensions well below the capillary length (∼2.7 mm for a water drop in air) its shape will be determined by the Young–Laplace equation without the gravitational term,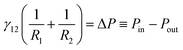 | (1) |
The solution for the drop shape is determined by the drop volume and by the physical condition at the three-phase contact lines at the substrate and at the particle. In the present context of how the shape of the liquid bridge evolves as the drop evaporates, we consider two possibilities: (I) the contact angle at the three-phase contact line remains constant as evaporation progresses and is given by θP at the particle and by θs the substrate, according to the Young–Dupré equation, or (II) the position of the contact line is fixed during evaporation. In the latter case, the position of the pinned contact line is prescribed by the angle, α, subtended at the centre of the particle and by the radial position, rs, of the contact line measured along the substrate (see Fig. 1).
We can now consider the two possible drop or liquid bridge shapes that can form depending on the location of the particle relative to the sessile drop and the substrate. The characteristic dimension of the drop or liquid bridge is assumed to be small compared to the capillary length so that gravity does not affect the drop shape through the Young–Laplace equation. However, as we shall see, the small gravitational force plays an important role in determining the position of the particle in relation to the substrate through density difference between the particle and the fluid phases.
1.1 Spherical drop interface
If the spherical particle does not make contact with the substrate and is located in a symmetrical position about the apex of the sessile drop (Fig. 1), the drop interface will be a portion of a sphere with radius R1 = R2 ≡ R = 2γ12/ΔP, the Laplace radius, see eqn (1). The particle can be maintained in this symmetrical position by gravitational force that is negligible in deforming the interface. We now show that this solution can also satisfy the required boundary conditions at the particle and the substrate.The spherical liquid interface makes contact with the substrate at the contact radius rs where the contact angle is θs and also from the cosine rule for the triangle formed between the centre of the particle, centre of the spherical interface and the three phase contact line at the particle we can obtain the following equations, see Fig. 1,
rs = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs θs | (2a) |
l2 = a2 + R2 − 2aR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp θp | (2b) |
R2 = a2 + l2 − 2al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α | (2c) |
A useful relation between the angles θp and α can be found by equating the radius of the meniscus contact with the sphere, giving R sin[π − (α + θp)] = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α. Using eqn (2a) allows R to be eliminated, giving
α. Using eqn (2a) allows R to be eliminated, giving
rs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin[π − (α + θp)] = a sin[π − (α + θp)] = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs. θs. | (3) |
There exist a critical minimum drop or liquid bridge volume at which the particle can remain at the apex of a spherical drop, while it is also in contact with the substrate. If the drop volume is above this critical volume, the drop interface will be a segment of a sphere and the particle can be located at any point on the interface without affecting the interfacial energy of the system. Thus, the gravitational energy will determine the position of the particle, with the particle either touching the substrate or be located at the apex, depending on the densities of both phases and the particle.‡ An expression to determine the position of the particle is given in the ESI.† The volume of the drop and the surface areas of the 12-, 2s- and 2p-interfaces can then be written in terms of those of a spherical cap
| Vs = vcap(R, θs) − vcap(R, ω) − vcap(a, α) | (4a) |
| As12 = scap(R, θs) − scap(R, ω) | (4b) |
As2s = π(R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs)2 θs)2 | (4c) |
| As2p = scap(a, α) | (4d) |
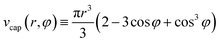 | (5) |
scap (r, φ) ≡ 2πr2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ). φ). | (6) |
If the particle is located at the apex of the drop, the distance of closest approach, h0, between the particle and the substrate is
h0 = l − (a + R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs). θs). | (7) |
As the volume of the supporting drop decreases, the particle will eventually come into contact with the substrate. This volume is the minimal drop volume for which a spherical configuration can exist. Below this, the drop shape will be an axisymmetric collar that we consider next.
1.2 Axisymmetric collar
The shape of an axisymmetric capillary bridge between a particle and substrate has been considered by Orr et al.27 By writing the r and z variables with respect to the angle ϕ between the meniscus and the horizontal, they presented the solution in terms of elliptic integrals. The form of their solution required a choice of sign that is related to the meridional curvature (defined below). For an interface where the meridional curvature changes sign, careful use of limits is required. Here we find it more convenient to parameterise the drop shape with respect to the arc length s, although the result is mathematically identical to the solution of Orr et al.27In Fig. 2 we show a spherical particle in contact with a substrate with a liquid bridge in the form of an axisymmetric collar around its base. The angle α locates the position of the three phase contact line on the particle surface. In this case, it is convenient to work with the mean curvature H ≡ ΔP/2γ12 of the interface that is initially positive and decreases continuously as the drop volume decreases, passing through zero before becoming negative.
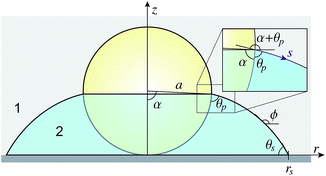 | ||
| Fig. 2 A schematic representation of the three-phase contact region of an axisymmetric collar formed around particle-substrate contact. | ||
The meridional curvature, 1/R1 = −dϕ/ds and the azimuthal curvature, 1/R2 = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ/r can be expressed in terms of the tangent angle ϕ, and trigonometry gives dr/ds = −cos
ϕ/r can be expressed in terms of the tangent angle ϕ, and trigonometry gives dr/ds = −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and dz/ds = −sin
ϕ and dz/ds = −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ. The origin of the arc length s = 0 is at the particle, with s increasing away from the particle. Using eqn (1) we obtain a system of 3 ordinary differential equations
ϕ. The origin of the arc length s = 0 is at the particle, with s increasing away from the particle. Using eqn (1) we obtain a system of 3 ordinary differential equations
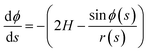 | (8a) |
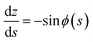 | (8b) |
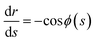 | (8c) |
p: ϕ = α + θp, r = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, z = a (1 − cos α, z = a (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α), s = 0 α), s = 0 | (9a) |
| s: ϕ = π − θs, r = rs, z = 0, s = smax. | (9b) |
The volume Vc of the collar, and the surface areas of the 12-, 2s- and 2p-interface (Ac12, Ac2s, Ac2p respectively) can be calculated from
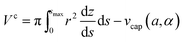 | (10a) |
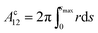 | (10b) |
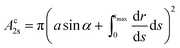 | (10c) |
| Ac2p = scap(a, α). | (10d) |
An iterative method is required to solve the coupled differential equations in order to determine the unknown H that is consistent with the prescribed volume and either the prescribed contact positions or contact angles at the two three phase contacts.
We outline an iterative method for generating interfaces for the case where both contact angles are constant. To begin, we pick a value for α and choose an initial value for the mean curvature H0. An interface can now be generated by solving eqn (8), subject to the initial conditions (9a). The differential equations are solved numerically until z = 0, with the arc length at this point being denoted smax. We now form an objective function based on the boundary condition, in this case g(H) = ϕ (smax) − (π − θs), which we require to be zero. The quantity Hi can now be updated using the secant method. This process is repeated until the boundary condition at the substrate is satisfied to within a specified tolerance. Changing the filling angle α results in interfaces corresponding to different drop volumes.
1.3 Evaporation dynamics
The evaporation rate for a sessile drop undergoing diffusion-driven evaporation was first solved by Picknett and Bexon.40 By drawing an analogy between the equations governing diffusion-driven evaporation and electrostatic potential, they developed a differential equation for the evaporation rate which involved a contact angle dependant parameter h(θ) ≡ C(θ)/R, with C(θ) being the capacitance of a lens of the same shape that can be expressed analytically as an infinite series. For numerical work, Picknett and Bexon40 presented an approximate polynomial expression for the capacitance of the scaled lens in terms of the angle θ,that is accurate to within 0.2% of the analytical result. The evaporation rate can then be expressed as
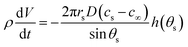 | (11) |
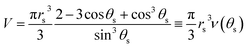 | (12) |
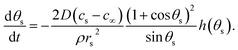 | (13) |
Taking the time scale ts = ρrs2/2D(cs − c∞), and tf as the time when the drop vanishes, the solution of eqn (13) can be written as
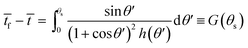 | (14) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = t/ts is the scaled time. For more details see Dash and Garimella41 and Gelderblom et al.42
= t/ts is the scaled time. For more details see Dash and Garimella41 and Gelderblom et al.42
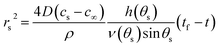 | (15) |
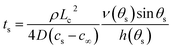 | (16) |
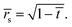 | (17) |
Thus the result in eqn (14) gives the variation of the contact angle at the substrate with time as the drop evaporates under the pinned contact line condition, whereas the result in eqn (17) gives the variation of the position of the contact line at the substrate with time as the drop evaporates under the constant contact angle condition.
2 Materials and methods
Water was obtained from a Millipore Direct-Q 5 system (minimum resistivity 18.4 MΩ cm). Polystyrene spheres (Amberlite XAD-4, Sigma) with a radius of ∼150 μm were used as received. Glass microparticles with radii 100–400 μm were obtained from Polysciences, Inc (#18903) and used as received. Poly(methyl methacrylate) (PMMA, 99%, Sigma) was spin-coated onto glass microscope slides at 3000 rpm from a 20 mg mL−1 solution in chloroform. Gold surfaces were generated by sputtering 5 nm of chromium (as an adhesion layer) and 50 nm of gold using a Quorum Q150T-S sputter coater. A polystyrene tissue culture dish was used as the polystyrene substrate and a poly(tetrafluoroethylene) (PTFE) surface was made by stretching a length of PTFE tape over a glass microscope slide.For each experiment a water pendant or sessile drop was formed on the required substrate. The small gravitational force was used to ensure the initial position of the particle is at the apex of the pendent or sessile drop on the substrate. The evaporation rate depends on the combination of the parameters D(cs − c∞) that varies with temperature and relative humidity (see eqn (14) and (17)). However, no special steps were taken to control these values in the laboratory.
Experiments were visualised using a CCD camera (Flea3, Point Grey, Richmond, BC, Canada) coupled to a Kozo XJP-300 microscope. The optical system was calibrated with a known size standard, measured using laser diffraction. Diffuse illumination was provided using a white LED source and a diffuser. Each experimental image was first binarised to extract the drop-particle profile, and then a routine developed in Mathematica (Wolfram Research) was used to fit the theoretical solution. A Levenberg–Marquardt optimisation routine was used to ensure rapid convergence of the experimental and theoretical drop profiles. Physical quantities were then extracted from the optimised parameters.
3 Results and discussion
Here we present and discuss the geometric and evaporative characteristics of four key systems that serve to illustrate the complex range of behaviours available to particle-drop-substrate systems. Material combinations were chosen to provide a range of different surface wettabilities, in order to explore conditions in which the droplet contact angle and solid–water–air van der Waals force (relevant to the wetting behaviour) vary widely:1. Silica–water–poly(tetrafluoroethylene), PTFE: the water droplet adopts a spherical solution throughout, and the silica particle does not come into contact with the substrate until the end of the evaporation process.
2. Silica–water–gold: the water droplet transitions from a spherical to axisymmetric collar configuration.
3. Polystyrene–water–polystyrene: the water droplet adopts a collar configuration throughout, including geometries where the meridional curvature of the interface changes sign resulting in an inflection in the function z(r).
4. Silica–water–poly(methyl methacrylate), PMMA: the water droplet transitions from an asymmetric spherical solution to an axisymmetric collar configuration.
In each experiment, a water drop was deposited onto the substrate, forming either a pendant (experiments 1 and 2) or a sessile (experiments 3 and 4) drop depending on the orientation of the substrate. A particle was then placed onto the immobilised drop, resulting in either a collar or a spherical configuration. Fig. 3 shows time-lapse photographs of the evaporation process for experiments 1–3. Videos of evaporation experiments are available in the ESI.† As discussed later, the evaporation time-scale is sufficiently slow that each instantaneous configuration can be accurately described by the equilibrium Young–Laplace equation.
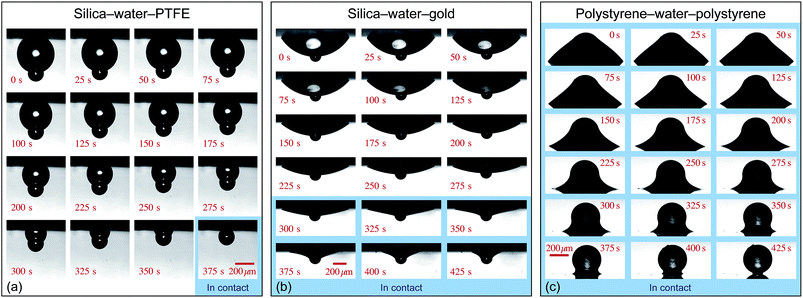 | ||
| Fig. 3 Time-lapse images of the evolution of three different axisymmetric particle-drop-substrate systems. (a) A water pendant drop hanging from a hydrophobic PTFE substrate with a silica particle resting at the apex of the drop, with the particle touching the substrate in the final frame. (b) A water pendant drop hanging below a gold substrate, with a silica particle initially at the apex of the drop. The particle touches the substrate after 285 seconds, after which an axisymmetric collar rests around the particle-substrate contact. (c) A polystyrene particle in contact with a polystyrene substrate with an axisymmetric collar formed around the contact for the duration of the experiment. The blue shaded regions denote the experimental images for which the particle is in contact with the substrate. See ESI† for videos of each experiment. | ||
Time-lapse images were compared to interfacial profiles predicted by the Young–Laplace equation. The accuracy of the fit was demonstrated by overlaying predicted interfaces on top of time-lapse photographs, as shown in Fig. 4.
 | ||
| Fig. 4 Two representative experimental drop profiles for each of the four experiments are compared to the Young–Laplace solution. | ||
The extracted data allows the contact radii and contact angles to be calculated at both the particle and the substrate, together with the drop volume, air–water interfacial area and Laplace pressure. Using these quantities, it is then possible to calculate the capillary force Fcapillary between the particle and the substrate
Fcapillary = Finterfacial tension − Fpressure = (2πrs)(γ12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs) − (ΔP)(πrs2), θs) − (ΔP)(πrs2), | (18) |
3.1 Initial configuration
When a particle is placed at the interface of a sessile drop, the analysis presented in Section 1 predicts that one of two basic configurations will be assumed. If the sessile drop volume is less than the critical volume for spherical drop formation, then an axisymmetric collar around the particle-substrate contact will form, whereas if the volume is above the critical volume the air–water interface will be spherical. This spherical case can be split into energetically equivalent but geometrically resolved homologues, as the particle can sit at any point on the interface without energetic penalty. Therefore the effects of gravity (i.e. buoyancy) must be considered, even though the gravitational force is several orders of magnitude smaller than the capillary force (gravitational force/capillary force = Bond number ∼ 0.01).§When the particle is more dense than both liquid phases, the particle will experience a downward net force, positioning it either axisymmetrically at the nadir of a pendant drop, or asymmetrically to the side of a sessile drop. This effect is demonstrated in Fig. 3 and 5, where experiments 1 and 2 (Fig. 3a and b) show a heavy silica particle at the apex of a pendant drop, while Fig. 5 shows the particle at the base of a spherical sessile drop. The reverse is true for a particle less dense than both liquid phases. For the intermediate case, it is possible to find a volume dependant expression to determine the particle position. Details of this calculation are provided in ESI.†
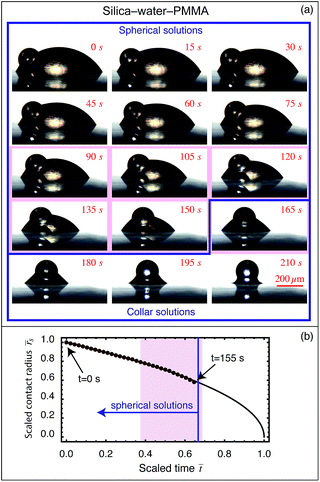 | ||
| Fig. 5 (a) A silica particle on a PMMA coated substrate with a water drop around the base. Time-lapse images taken 15 s apart show the progress of the evaporation. The system is initially asymmetric due to the density of silica being greater than water. As the volume of the drop decreases, the system evolves towards an axisymmetric collar, which is achieved at approximately 160 s into the experiment. Thereafter, the system remains in the axisymmetric collar configuration until the water completely evaporates. The shaded red region denotes the region where the experimental interfaces deviate from the theoretically predicted interfaces due to surface non-ideality, while the blue line delimits the region where the interfaces are spherical from those which are axisymmetric collar. (b) The scaled substrate contact radius evolution versus scaled time (brown symbols) for which the interfaces are spherical interfaces. The black line represents the theoretical evolution of the contact radius for diffusion-driven evaporation neglecting the presence of the particle. See ESI† for a video. | ||
It is clear that the initial condition adopted is a direct result of both the relative volumes of particle and drop, and the system surface chemistry (that is, the contact angle on both the substrate and particle). Exemplar are the cases of a silica particle and water drop on a PTFE or polystyrene surface (Fig. 3a and c). Due to the high water contact angle of the PTFE substrate, a spherical interface with small contact radius is favoured throughout, whereas the less hydrophobic polystyrene results in collars with large contact radii.
3.2 Boundary conditions
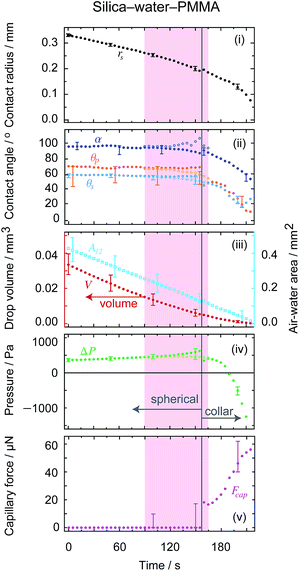
The theory presented above was derived for the boundary condition of either a pinned contact line where the initial liquid–solid contact line is fixed and evaporation results in a change in air–water–solid contact angle; or a constant contact angle where the liquid–solid contact line is free to move and retain the thermodynamically favoured air–water–solid contact angle. In reality however, the boundary condition for a given system depends largely on the microscopic geometry and surface chemistry of both surfaces, and a combination of both pinned contact line and constant contact angle cases may be observed within the same experiment. For the systems explored here, the situation is further complicated by the different solid geometries (i.e. a curved particle and flat substrate) and dissimilar material combinations chosen to emphasise the importance of wetting effects.For the axisymmetric systems presented, throughout the spherical evaporation process the three-phase contact at the substrate has a pinned contact line (see uppermost panels in Fig. 6), while the particle contact condition is not as easily determined with the same precision due to its geometry and freedom of rotation. Given that the particle contact radius remains constant well into the collar mode of evaporation, it appears that the contact line at the particle is also pinned.
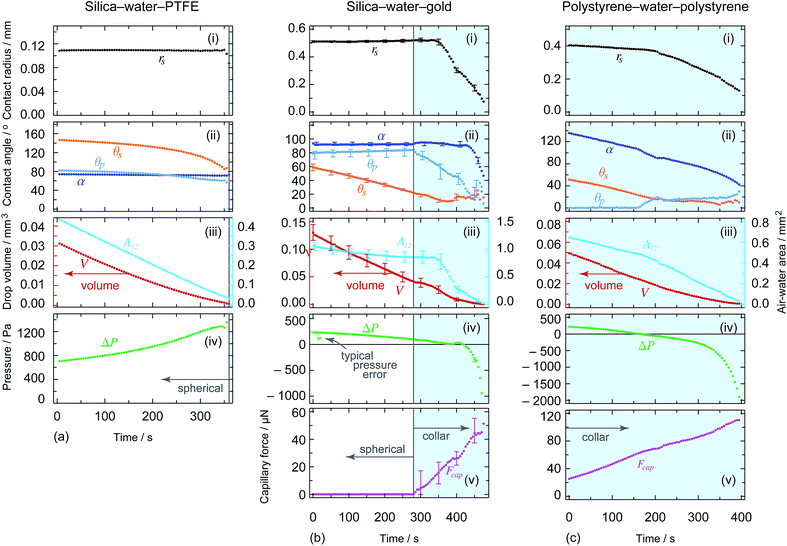 | ||
| Fig. 6 Time variations of (i) the drop substrate contact radius, (ii) the contact angles at both the substrate θs and particle θp together with the filling angle α which the meniscus makes with the centre of the particle measured through the water, (iii) the volume of the water drop (left hand axes) and the air–water interfacial area (right hand axes), (iv) the Laplace pressure across the interface and (v) the (attractive) capillary force between the particle and the substrate for each of the three experiments presented in Fig. 3. From left to right, the extracted quantities correspond to the experiments shown in Fig. 3a–c, respectively. All quantities were extracted by fitting the theoretical solution to the experimental photographs (the blue shaded region represents the evaporation regions where the drop is an axisymmetric collar around the particle-substrate contact). Representative error bars are shown on the centre column plots. | ||
Perhaps the clearest case is that of silica–water–PTFE (experimental images shown in Fig. 3a, with the extracted physical quantities shown in Fig. 6a), where the drop contact radius on the substrate is effectively constant throughout the entire evaporation process, resulting in an increasingly pronounced decrease in substrate contact angle as evaporation proceeds. Similar behaviour is seen for the early, spherical stages of the silica–water–gold experiment (experimental images and extracted physical quantities shown in Fig. 3b and 6b, respectively), although after the particle touches the substrate and collar configurations become applicable, accompanied with significant changes in the position of the contact line. Most notably, the drop contact line on the substrate de-pins, with the substrate contact condition transitioning to a constant contact angle (∼15°).
In the case of polystyrene–water–polystyrene (experimental images and extracted physical quantities shown in Fig. 3c and 6c, respectively), the boundary conditions are not as clearly defined during the experiment, as the contact angles and contact radius both change throughout. Perhaps most interestingly, there is a discontinuity in both of these parameters at a distinct point that appears to be consistent with the inversion of the droplet Laplace pressure from positive to negative. This results in a more rapid retraction of the contact radius, although this may also be connected to the low substrate contact angle (<20°) at this stage.
If the pinned contact line condition applies at both the particle and the substrate, it is possible to find the rate at which the contact angles at the substrate and particle vary with respect to each other by differentiating eqn (3), which gives
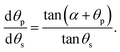 | (19) |
This useful relation predicts the direction of change of contact angle for given surface chemistries. Importantly, for the silica–water–gold experiment, dθp/dθs ∼ −0.1, which implies that for θs to decrease by 40°, the particle contact angle will increase by 4°, accurately matching the presented theory. This relationship also predicts that for the silica–water–PTFE experiment the particle contact angle decreases with decreasing substrate contact angle (dθp/dθp ∼ 0.6), which matches experimental data.
Perhaps most curiously, the case of a silica particle-sessile water drop composite on a spun coated poly(methylmethacrylate) (PMMA) surface (Fig. 5) shows a constant contact angle during most of its evaporation process, and for all of the states in which the drop adopts a spherical interface (Fig. 7). However, the contact angles at both particle and surface appear to pin at the point when collar geometries are formed, associated with both a decrease and sign change in Laplace pressure and a strong capillary force between the particle and surface. The reasons for this change in boundary condition are not entirely clear, but appear to be associated with the evaporation dynamics, as the volume and surface area continue to change smoothly despite the abrupt changes in contact angle and capillary force. It is conceivable that in diffusion-driven evaporation, the system contact angles must adjust to maintain the correct pressure-to-surface area ratio, although further experiments would be required to understand this more fully. A more decisive analysis is thwarted by minor deviations from ideality (shown as the shaded region in Fig. 7) wherein uncertainties arise due to minor asymmetric pinning of both the particle and substrate contact lines.
3.3 Capillary force
When the drop interface is spherical, there is no force acting on the particle. For an axisymmetric collar, however, the interface exerts a force on the particle. Orr et al.27 showed theoretically that depending on the drop volume, the resulting capillary force could be either attractive or repulsive. The spherical solution separates these two cases, as it results in no capillary force.As shown in the theory section, when the drop volume is above the critical volume, the configuration can either form a spherical interface, or a collar interface exerting a repulsive capillary force on the particle. Clearly the case of a repulsive capillary force is only physical in the instance that the particle is ‘held’ onto the surface, otherwise the system will revert to the energetically favoured spherical interface.
We can compare the surface energies of the two configurations by first taking the particle to sit axisymmetrically at the apex of a spherical drop. If the particle is then moved toward the substrate to form an axisymmetric collar, the potential energy, U, of the system has been increased since dU/dz = −Fcapillary with the capillary force acting in the opposite direction to the displacement. For an idealised system, conservation of energy results in an increase in the surface energy. Since each of the interfacial areas (and therefore the interfacial energies) for a spherical interface are independent of the position of the particle at the apex or base of the drop, we find the important result that the spherical drop interface is more energetically favourable than the axisymmetric collar for drop volumes above the critical volume. Therefore for a drop volume above the critical volume, a spherical interface will be formed with no capillary force acting on the particle. As the drop volume decreases below the critical volume, an axisymmetric collar is formed with an attractive capillary force between the particle and the substrate.
The capillary force for evaporating particle-drop-substrate geometries analysed here follows expected behaviour based on interfacial curvature (Fig. 6). For silica–water–PTFE, the large substrate contact angle results in drop geometries that are spherical and convex until the final experimental photograph shown. It is possible that a very small liquid bridge (that cannot be visually resolved) still remains between the particle and the surface at the end of the experiment. This would explain why the particle remains adhered to the substrate despite the gravitational force acting to remove it. Such microscopic capillary bridges have been indicated before as an explanation for large adhesion forces seen for particles at substrates.44 For silica–water–gold where the drop is pendant, the system transitions from a spherical interface to a collar, and in doing so experiences an attractive capillary force that rises approximately linearly from 0 to ∼50 μN. The same is true for a silica particle on a sessile drop upon a PMMA substrate (Fig. 7). For polystyrene–water–polystyrene, the droplet configuration is an axisymmetric collar throughout, and thus the particle experiences a continual attractive capillary force, again with a nearly linearly increasing trajectory from ∼20 − 110 μN.
Orr et al.27 calculated the capillary force between a particle and a surface for a liquid bridge whose volume tends to zero. They calculated the maximal capillary force
Fmaxcapillary = 2πγa(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θs + cos θs + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp) ≤ 4πγa θp) ≤ 4πγa | (20) |
For comparison, the force on the silica particle due to gravity (i.e. the weight) F = ρVg ∼ 50 nN, which is 3 orders of magnitude smaller than the capillary force. Thus for the length-scales studied here (and below these dimensions), capillary interactions are enormous compared to gravitational interactions, and even more so for very small capillary bridges. This explains how a comparatively massive particle can be held up by a pendant drop that is a small fraction of its volume. The relative strengths of these interactions are undoubtedly important in the precise evaporative (self) assembly of colloidal particles.
3.4 Evaporation dynamics
Having developed a comprehensive theoretical understanding of the configuration of a static particle-drop-substrate system, it is pertinent to extend this to explore the dynamics of the droplet evaporation, a central theme for real-life systems in which particle-drop-surface attachments are encountered.Starting from the analysis of a ‘naked’ sessile drop evaporating under diffusion-limited conditions as provided by Picknett and Bexon,40 we can compare our experiments wherein a particle is placed at the interface. For the pinned contact line case, eqn (14) gives a universal curve for the contact angle θs in terms of the scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) . By taking the time when the drop vanishes to be 0 then gives θs(
. By taking the time when the drop vanishes to be 0 then gives θs(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = G−1(−
) = G−1(−![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), which allows the evolution of θs for the spherical drops in Fig. 3a and b to be compared to the theory for a naked sessile drop. For each experiment, the initial and final contact angles set the initial and final scaled time and hence the time scale, ts. The substrate contact angle evolution with respect to the scaled time is presented in Fig. 8, showing good agreement between theory and both the silica–water–PTFE and silica–water–gold. Similarly, the evolution of the substrate contact radius for the constant contact angle case can be compared to eqn (17), and is presented in Fig. 5b. Both time scale expressions comprise the unconstrained diffusion rate parameter, D(cs − c∞), with the values used in scaling each of the experiments shown in Table 1. It is clear that within the experimental uncertainty inherent in the extraction of parameters from image fitting, the evaporation dynamics of spherical interfaces with a particle present are indistinguishable from the equivalent ‘naked’ sessile or pendant drops for both gold and PTFE surfaces.
), which allows the evolution of θs for the spherical drops in Fig. 3a and b to be compared to the theory for a naked sessile drop. For each experiment, the initial and final contact angles set the initial and final scaled time and hence the time scale, ts. The substrate contact angle evolution with respect to the scaled time is presented in Fig. 8, showing good agreement between theory and both the silica–water–PTFE and silica–water–gold. Similarly, the evolution of the substrate contact radius for the constant contact angle case can be compared to eqn (17), and is presented in Fig. 5b. Both time scale expressions comprise the unconstrained diffusion rate parameter, D(cs − c∞), with the values used in scaling each of the experiments shown in Table 1. It is clear that within the experimental uncertainty inherent in the extraction of parameters from image fitting, the evaporation dynamics of spherical interfaces with a particle present are indistinguishable from the equivalent ‘naked’ sessile or pendant drops for both gold and PTFE surfaces.
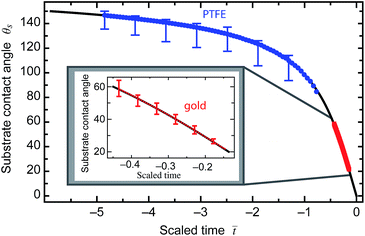 | ||
| Fig. 8 The evolution of the substrate contact angle θs for a ‘naked’ sessile drop with a pinned contact line undergoing diffusion-driven evaporation. The black curve represents the universal curve presented in eqn (14). The blue symbols are the substrate contact angles for the silica–water–PTFE experiment and the red symbols are the substrate contact angles for the silica–water–gold experiment, showing good agreement between the functional form of the drop-particle substrate contact evolution and that of a plain sessile drop. | ||
| Experiment | PCL/CCA | D(cs − c∞)/kg m−1 s−1 |
|---|---|---|
| Silica–water–PTFE | PCL | 0.7 × 10−7 |
| Silica–water–gold | PCL | 1.3 × 10−7 |
| Silica–water–PMMA | CCA | 1.3 × 10−7 |
Having established that the evaporation of the liquid bridge can be described by the evolution of a ‘naked’ sessile drop, we consider the evaporation when the liquid bridge is in an axisymmetric collar configuration. The silica–water–gold and silica–water–PMMA experiments demonstrate both spherical and collar configurations at different drop volumes, and illustrate the differences between the two modes of evaporation. During the silica–water–gold experiment, both the particle and substrate contact lines are pinned, with the substrate contact angle decreasing linearly, while the particle contact angle variation is well described by eqn (19). Once the particle makes contact with the substrate, the particle contact angle rapidly decreases with both contact lines initially remaining pinned. Soon thereafter, as the pressure decreases to zero, the system reconfigures itself, with the substrate contact radius rapidly decreasing with a concomitant decrease in the air–water interfacial area. Finally, the Laplace pressure changes sign with the particle contact depinning. Throughout the collar phase, the capillary force acting on the particle increases in magnitude.
The polystyrene–water–polystyrene experiment illustrates the collar evaporation further, however the particle contact condition is different. Initially, the polystyrene is completely wetted by the particle, with the contact radius on the particle moving. Similar key behaviours are again observed; namely, the Laplace pressure decreasing to zero causes the system to reconfigure itself, after which point both contact angles remain relatively constant. The capillary force between the particle and the substrate is also attractive and increasing in magnitude.
For the silica–water–PMMA experiment, the initial configuration is a spherical interface with the particle in contact with the substrate. The substrate contact angle is initially constant (θs ∼ 60°) with both the particle contact angle and radius remaining constant within experimental uncertainty. Interestingly, 90 s into the evaporation process the experimental interface deviates from the spherical interface, however the interface is clearly not an axisymmetric collar either. This is apparently caused by pinning at both particle and substrate contacts, together with non-zero horizontal forces between the particle and the substrate, presumably resulting from surface non-ideality. For the frames between 90 s and 155 s, fitting spherical interfaces to these frames provides a broadly accurate estimate of the volume and interfacial area, but does not accurately capture local behaviour such as the contact angles and the curvature (and hence the Laplace pressure). To obtain a more accurate estimate of the contact angle and Laplace pressure, the curvature of the drop profile to the right of the particle was calculated (as pinning occurred primarily on the left side of the silica particle). These extracted quantities are plotted in open circles on both plots, with the pinning region indicated by the shaded red in Fig. 5 and 7.
The interfacial area decreases linearly with time for the entirety of the experiment, and is notably independent of the Laplace pressure which, unlike a ‘naked’ sessile drop, changes sign.
3.5 Implications and opportunities for surface chemistry
Having analysed the possible geometries available to particle-drop-surface composites, and the dynamics of their evolution as the drop evaporates, it becomes pertinent to highlight the opportunities that are apparent in system design and control.Clearly surface chemistry and morphology is of overriding importance in determining the parameters that control the drop geometry – that is, contact angles via surface chemistry. However, the substrate also acts to determine the boundary condition – either pinned contact line (with a varying contact angle) or constant contact angle (with the contact line free to move). In the cases examined experimentally here we did not purposefully select materials with the expectation of different boundary conditions. For greater precision, it would be possible to use patterned or micro-engineered substrates to introduce surface chemical or physical heterogeneities in order to facilitate contact line pinning of the drop at a certain position. Similarly, particles with hemispheres that exhibit different wettabilities (Janus particles) could be advantageous in controlling the contact line and obtaining specific geometric characteristics.
4 Conclusion
We have analysed experimentally and theoretically the configurations available to a particle-droplet-substrate system. The preferred state can be easily predicted for any combination of fluid and particle densities, contact angles and volume ratios. An understanding of this behaviour is of great importance when designing systems that can take advantage of such composite colloids, such as evaporative lithography and microelectromechanical systems.When comparing the measured geometry of real systems to the theoretical expectation, the effects of non-ideality become clear, and the extent of these departures from prediction vary depending on the surface chemistry of the systems used. In particular, the effects of liquid contact line pinning due to surface inhomogeneities are significant and have a strong influence over the geometries observed. In most cases, despite the effects of pinning, the theory can still be applied to obtain physical parameters with sufficient accuracy for most purposes. Significantly, for all systems, a critical volume is determined, below which a strongly attractive capillary force is ‘switched on’, providing unique opportunities for surface modification and assembly. In all cases explored here, and indeed for all low Bond numbers, surface tension forces dominate the behaviour of liquid bridges; however, when all other forces are balanced, gravity can still play a role in determining the geometry of the system (i.e. whether the particle rests at the base or apex of the drop).
Interestingly, an analysis of the liquid evaporation of these systems indicates that the presence of a particle at the interface has very little influence on the evaporation rate when compared to a ‘naked’ sessile drop, providing access to a well-understood description of evaporation dynamics. The existence of a remaining microscopic capillary bridge between the particle and surface that cannot be visualised in these experiments is posited, and remains to be experimentally investigated.
References
- S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001–2021 RSC.
- W. Ramsden, Proc. R. Soc. London, 1903, 72, 156–164 CrossRef CAS.
- B. P. Binks and R. Murakami, Nat. Mater., 2006, 2, 865–869 CrossRef PubMed.
- P. Aussillous and D. Quéré, Nature, 2001, 411, 924–927 CrossRef CAS PubMed.
- E. Bormashenko, Curr. Opin. Colloid Interface Sci., 2011, 16, 266–271 CrossRef CAS PubMed.
- G. McHale and M. I. Newton, Soft Matter, 2011, 7, 5473–5481 RSC.
- R. Aveyard, B. D. Beake and J. H. Clint, J. Chem. Soc., Faraday Trans., 1996, 92, 4271–4277 RSC.
- S. Komura, Y. Hirose and Y. Nonomura, J. Chem. Phys., 2006, 124, 241104 CrossRef CAS PubMed.
- H.-J. Butt, J. Colloid Interface Sci., 1994, 166, 109–117 CrossRef CAS.
- P. Mulvaney, J. M. Perera, S. Biggs, F. Grieser and G. W. Stevens, J. Colloid Interface Sci., 1996, 183, 614–616 CrossRef CAS.
- B. A. Snyder, D. E. Aston and J. C. Berg, Langmuir, 1997, 13, 590–593 CrossRef CAS.
- M. Preuss and H.-J. Butt, Int. J. Miner. Process., 1999, 56, 99–115 CrossRef CAS.
- G. E. Yakubov, O. I. Vinogradova and H.-J. Butt, J. Adhes. Sci. Technol., 2000, 14, 1783–1799 CrossRef CAS PubMed.
- J. Guzowski, M. Tasinkevych and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031401 CrossRef CAS.
- Z. Fournier, D. Geromichalos, S. Herminghaus, M. Kohonen, F. Mugele, M. Scheel, M. Schulz, B. Schulz, C. Schier, R. Seemann and A. Skudelny, J. Phys.: Condens. Matter, 2005, 17, S477 CrossRef CAS.
- C. Gögelein, M. Brinkmann, M. Schröter and S. Herminghaus, Langmuir, 2010, 26, 17184–17189 CrossRef PubMed.
- R. K. Niven, J. Pet. Sci. Eng., 2006, 52, 1–18 CrossRef CAS PubMed.
- T. K. Tokunaga, Water Resour. Res., 2011, 47, 8514 CrossRef.
- E. Koos and N. Willenbacher, Science, 2011, 331, 897–900 CrossRef CAS PubMed.
- T. Stifter, O. Marti and B. Bhushan, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13667–13673 CrossRef CAS.
- J. S. McFarlane and D. Tabor, Proc. R. Soc. London, Ser. A, 1950, 202, 224–243 CrossRef CAS.
- H. Schubert, Powder Technol., 1984, 37, 105–116 CrossRef.
- Y. I. Rabinovich, J. J. Adler, M. S. Esayanur, A. Ata, R. K. Singh and B. M. Moudgil, Adv. Colloid Interface Sci., 2002, 96, 213–230 CrossRef CAS.
- R. D. Piner, J. Zhu, F. Xu, S. Hong and C. A. Mirkin, Science, 1999, 283, 661–663 CrossRef CAS.
- K. J. Obata, T. Motokado, S. Saito and K. Takahashi, J. Fluid Mech., 2004, 498, 113–121 CrossRef.
- H.-J. Butt and M. Kappl, Adv. Colloid Interface Sci., 2009, 146, 48–60 CrossRef CAS PubMed.
- F. M. Orr, L. E. Scriven and A. P. Rivas, J. Fluid Mech., 1975, 67, 723–742 CrossRef.
- J. Guzowski, M. Tasinkevych and S. Dietrich, Eur. Phys. J. E, 2010, 33, 219–242 CrossRef CAS PubMed.
- N. D. Denkov, O. D. Velev, P. A. Kralchevsky, I. B. Ivanov, H. Yoshimura and K. Nagayama, Langmuir, 1992, 8, 3183–3190 CrossRef CAS.
- N. D. Denkov, O. D. Velev, P. A. Kralchevsky, I. B. Ivanov, H. Yoshimura and K. Nagayama, Nature, 1993, 361, 26 CrossRef.
- P. A. Kralchevsky and K. Nagayama, Adv. Colloid Interface Sci., 2000, 85, 145–192 CrossRef CAS.
- I. U. Vakarelski, D. Y. C. Chan, T. Nonoguchi, H. Shinto and K. Higashitani, Phys. Rev. Lett., 2009, 102, 058303 CrossRef.
- I. U. Vakarelski, J. O. Marston and S. T. Thoroddsen, Langmuir, 2013, 29, 4966–4973 CrossRef CAS PubMed.
- V. N. Manoharan, M. T. Elsesser and D. J. Pine, Science, 2003, 301, 483–487 CrossRef CAS PubMed.
- F. Fan and K. J. Stebe, Langmuir, 2004, 20, 3062–3067 CrossRef CAS.
- S. Watanabe, K. Inukai, S. Mizuta and M. T. Miyahara, Langmuir, 2009, 25, 7287–7295 CrossRef CAS PubMed.
- A. K. Geim, S. V. Dubonos, I. V. Grigorieva, K. S. Novoselov, A. A. Zhukov and S. Y. Shapoval, Nat. Mater., 2003, 2, 461–463 CrossRef CAS PubMed.
- D. L. Hu and J. W. M. Bush, Nature, 2005, 437, 733–736 CrossRef CAS PubMed.
- M. J. Neeson, R. F. Tabor, F. Grieser, R. R. Dagastine and D. Y. C. Chan, Soft Matter, 2012, 8, 11042–11050 RSC.
- R. Picknett and R. Bexon, J. Colloid Interface Sci., 1977, 61, 336–350 CrossRef CAS.
- S. Dash and S. V. Garimella, Langmuir, 2013, 29, 10785–10795 CrossRef CAS PubMed.
- H. Gelderblom, A. G. Marín, H. Nair, A. van Houselt, L. Lefferts, J. H. Snoeijer and D. Lohse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 026306 CrossRef.
- G. McHale, S. M. Rowan, M. I. Newton and M. K. Banerjee, J. Phys. Chem. B, 1998, 102, 1964–1967 CrossRef CAS.
- J. C. Contreras-Naranjo and V. M. Ugaz, Nat. Commun., 2013, 4, 1919 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Ancillary results and videos of evaporating drops on different substrates. See DOI: 10.1039/c4sm01826e |
| ‡ The particle will not sit at an intermediate point for the same reason a particle submersed in a volume of water will either rise or sink. |
| § Bond number = (L/λ)2, where λ is the capillary length and L is a typical length scale for the system (L ∼ 200 μm). |
| This journal is © The Royal Society of Chemistry 2014 |