Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymer translocation: the first two decades and the recent diversification
Vladimir V.
Palyulin
a,
Tapio
Ala-Nissila
b and
Ralf
Metzler
 *ac
*ac
aInstitute for Physics & Astronomy, University of Potsdam, D-14476 Potsdam-Golm, Germany. E-mail: rmetzler@uni-potsdam.de
bDepartment of Applied Physics and COMP CoE, Aalto University School of Science, FI-00076, Espoo, Finland
cPhysics Department, Tampere University of Technology, FI-33101 Tampere, Finland
First published on 19th September 2014
Abstract
Probably no other field of statistical physics at the borderline of soft matter and biological physics has caused such a flurry of papers as polymer translocation since the 1994 landmark paper by Bezrukov, Vodyanoy, and Parsegian and the study of Kasianowicz in 1996. Experiments, simulations, and theoretical approaches are still contributing novel insights to date, while no universal consensus on the statistical understanding of polymer translocation has been reached. We here collect the published results, in particular, the famous–infamous debate on the scaling exponents governing the translocation process. We put these results into perspective and discuss where the field is going. In particular, we argue that the phenomenon of polymer translocation is non-universal and highly sensitive to the exact specifications of the models and experiments used towards its analysis.
| Tapio Ala-Nissila Tapio Ala-Nissilä is a Professor of Physics at the Department of Applied Physics, Aalto University School of Science (Aalto SCI), Espoo, Finland, and Adjunct professor of Physics at the Department of Physics, Brown University, Providence, USA. He is the head of the Multiscale Statistical Physics (MSP) group of about 15 researchers, which is part of the Computational Nanoscience Center of Excellence at Aalto SCI. The MSP group focuses on multiscale theoretical and computational modeling of nanoscale phenomena in condensed matter and soft matter physics, including nanoplasmonics, self-organization in strained systems, polymer dynamics, escape and translocation, and stochastic thermodynamics in small classical and quantum systems. |
I. Introduction
The basic idea is simple. Suppose you put up your tent at the camp site and discover that there is a hole in the roof of the tent, while dark rain clouds are building up in the sky. As a quick fix you stuff a crumpled-up plastic bag or the cork of the just-opened wine bottle in the hole. Obviously, depending on how good the plug fits the hole, more or less rain will seep through. Two decades ago, this simple principle was demonstrated to apply to molecular systems, as well. Take a membrane consisting of a bilayer of lipid molecules that contains a hole in the form of an embedded protein channel—biological cells in fact naturally contain thousands of them. Apply a voltage difference across the membrane. You will then measure a certain current going through the channel. If you now clog up this molecular channel with a polymer, for instance, a single-stranded DNA or an RNA chain, the ions in the solution cannot be driven through the channel that easily any more and the electrical current will drop considerably. Once the clogging chain slips out of the pore again, the ions can pass easily and the current jumps up to its previous value. It turns out that such a system is indeed sufficiently sensitive to the type of monomer of the clogging chain, i.e., its nucleotides, that the scientists involved in this project immediately started thinking about how they could use this effect to decipher the sequence of nucleotides, the genetic code written on the chain. This is the story of the physics of the passage of polymer chains across a small channel in a membrane, the so-called translocation process.On a larger scale, the principle had been around for some time. The Coulter counter originally developed by Wallace Coulter in the 1940ies and eventually patented in 1953 (ref. 1) and its improved versions are based on the measurable change of the impedance proportional to the size of an object that is passing an orifice and displaces (part of) the electrolyte carrying the current through the orifice in an electrical field. The Coulter counter is typically used to count blood cells in a sample but was also shown to allow the counting of submicron particles such as viruses.2 A breakthrough came with the study of Bezrukov, Vodyanoy, and Parsegian in 1994 which showed that one can count poly(ethylene oxide) molecules from the ionic current time trace through an alamethicin channel.3 Shortly after this discovery, in 1996 Kasianowicz, Brandin, Branton, and Deamer demonstrated that the ionic current through an α-hemolysin channel suspended in a lipid bilayer depends on the nucleotide sequence of an RNA chain threading through the channel.4 The technological potential of these initial results prompted a long string of publications, making the field of polymer translocation one of the most active in soft matter and biological physics research.
Apart from the idea of the sequencing, we note that nanopores are used to measure concentrations and types of small analytes,5,6 to determine the distribution of masses (“mass spectrum”) of a mixture of polymers,7 to identify stereoisoforms of a common drug,8 to sort proteins,9,10 and to detect microRNA molecules.11 Still, the major driving force behind the interest in polymer translocation remains its possible use as an efficient and cheap sequencing method.12–14 Due to the relation of the sequence of a nucleotide chain and the local friction on the translocating chain due to interactions with the pore, this technology is at times also referred to as nanopore force spectroscopy.
The majority of previous review articles on polymer translocation focus on the experimental context.11,12,15–22 The reviews oriented towards theoretical and simulation approaches concentrate on computer simulations of the ionic current blockade phenomenon,23 or mainly summarise the scaling behaviour of the translocating polymer.24,25 The recent book by Muthukumar provides a broad introduction to the topic and outlines the quasi-equilibrium approach to polymer translocation.26 Our goal here is to address the development of the scaling approach, large scale simulations, as well as directions of translocation research involving different translocation techniques, the influence of the chain sequence, the rigidity of the chain, and complex interactions with the pore.
We first briefly address in Section II the technological questions of the current measurement to detect the presence of a (partial) blockage of a nanopore across a membrane when a different voltage is applied to either side of the membrane. We then summarise the typical kinds of pores used in experiments in Section III. Section IV then reviews the various results obtained for the free translocation in absence of a driving force, followed by the forced translocation process in Section V. Some specifics about polyelectrolyte translocation are collected in Section VI. Section VII considers the effects of interactions between the translocating chain and the pore. The entropic driving or resistance against chain passage through the pore due to confinement are addressed in Section VIII. Finally, Section IX collects some results on the translocation in the presence of binding proteins, that partially rectify the motion of the chain through the pore. We present a short summary and outlook in Section X. Readers not interested in technical details of polymer translocation may skip Sections II and III without loss of context in the subsequent sections.
II. Picoampere current variations
As mentioned above, the information on the polymer translocation process stems from ionic current variations across a channel. While in the original setups of the Coulter counter the channel was embedded in a glass pane and the width of the channel (pore) was in the range of micrometres, modern translocation experiments use biological or artificial channels embedded in supported lipid or engineered solid state membranes. The channel widths are of the order of a few nanometres. The membrane separate two chambers containing a low-molecular electrolyte solution with high ionic strength. Typical experiments use of the order of 1 M potassium chloride. Due to the specific physical properties of such translocation systems, the electric current can be measured at high bandwidth at picoampère resolution and at frequencies of around 102 Hertz.An external electric field is applied to the system across the membrane, with a voltage of typically around 102 millivolts. The current flowing through the channel is remarkably stable at levels of 100 picoampère, with fluctuations in the range of 5 picoampère. In the presence of the polymer chain in the channel, the channel is almost fully blocked by the chain and the current drops down to some 10 picoampère. As demonstrated in a typical current-time trace in Fig. 1, the detection of single translocation events is significant in such setups. The precise signatures of the ionic current traces provide implicit information about the length and sequence of the translocating polymers. The phenomenon of ionic current blockade is quite complex, involving the geometric properties of the pore as well as electrostatic and hydrodynamic interactions. It thus depends on many parameters, which need to be meticulously calibrated, as reviewed by Aksimentiev.23
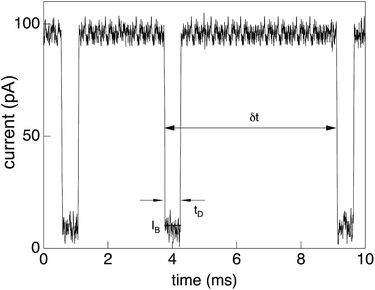 | ||
| Fig. 1 Current trace showing distinct drops from the free-pore value of about 102 picoampère to around 10 picoampère due to partial blockade of the α-hemolysin pore for low-molecular electrolytes by a translocating single-stranded DNA chain. Three distinct translocation events are shown, each with a duration of few milliseconds. Reprinted with permission from ref. 30. | ||
DNA and RNA are highly negatively charged, and the electrical field gradients in the vicinity of the channel pore assist the chain in threading into the pore and passing from the cis to the trans side of the membrane. If the electrical field is applied during the entire process, the translocation is thus driven, that is, the chain forced through the channel. Based on the information provided by the current trace, experimentalists can also completely switch off the electric field once the chain is just threaded into the pore to measure unforced translocation. Of course, in the latter case the chain may also retract from the pore to its original (cis) side.
A polymer molecule approaches the pore in different configurations for every translocation event. In order to average the passage properties over configurations Gershow and Golovchenko proposed to recapture the same molecule in a solid state nanopore by changing the voltage polarity before the molecule diffuses too far astray and repeating this procedure a few times.27 This method also proves that the electronic signal comes from a passage of a single translocating molecule. In ref. 28 the recapture process of linear and double-stranded λ DNA through a large, 20 nm wide pore in an SiN membrane was scrutinised. Up to 1000 re-translocations were observed. This allowed to plot current blockade histograms for each individual molecule. Since the translocation process runs off very fast DNA does not have time to equilibrate before it shuttles back through the hole. Thus it does not proceed in a ”head-to-tail” fashion, but in a very folded configuration. For the particular setup the authors observed up to 13 ds-DNA strands within the nanopore. In order to study a relaxed DNA long recapture times are needed which however considerably increases the chances of losing the molecule.
In the case when either one or two DNA strands of linear ds-DNA could pass through a pore the observations of a current trace allowed to gather statistics of capture locations 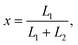 where L1 and L2 are the lengths of strands measured from the part of DNA which first entered the pore.29 The associated theoretical model showed that purely due to configurational entropy considerations DNA chains are most likely to enter the pore near their ends, i.e., almost in a ”head-to-tail” fashion.
where L1 and L2 are the lengths of strands measured from the part of DNA which first entered the pore.29 The associated theoretical model showed that purely due to configurational entropy considerations DNA chains are most likely to enter the pore near their ends, i.e., almost in a ”head-to-tail” fashion.
III. Pore types
To work as a precise measuring tool the translocation process needs to be controlled and predictable. Hence suitable nanopores are critical. Obtaining a single pore in a thin membrane is not straightforward experimentally. Thus in the first setups biological pores were used.4 In the membranes of eukaryotic and prokaryotic cells there exist a large variety of membrane pore proteins. However only few of them are stable for hours and provide a sufficiently large diameter to allow passage of DNA molecules. The most widely used bio-nanopore so far is the pore-forming toxin α-hemolysin.15Fig. 2a shows a cross-section of an α-hemolysin pore embedded in a lipid membrane. α-hemolysin is secreted by the bacterium Staphylococcus aureus and causes cell death by binding with the outer membrane and subsequent release of vital molecules such as ATP, as well as cell depolarisation etc. In the narrowest part the α-hemolysin pore has a width of 1.4 nm. Application of a voltage of 100 mV across the membrane produces a current of about 100 pA.17,18 When single-stranded DNA occupies the pore the current depends on the nucleotide content. Usually the translocation proceeds rather quickly. A single-stranded DNA chain of 100 Cytosine bases (nucleotides) will pass in about 0.1 msec, corresponding to about 1 μsec per base33 (compare Fig. 1). In other experiments velocities of 10−1–103 nucleotides per second were obtained (see Fig. 1 in ref. 34). Experiments with α-hemolysin revealed remarkable results. For instance, poly-adenine RNA molecules moved an order of magnitude slower through the pore than poly-cytosine or poly-uracil, due to the secondary structure assumed by the former. This structure needs to be unravelled before the chain can thread through the pore35 (see also the recent 2D simulation on the influence of coil–helix transition on the translocation36). Another interesting feature is that the translocation speed depends on the orientation of the single-stranded DNA molecule. DNA which enters the pore with its 3′ end passes two times slower than those which enter with their 5′ end first.37 The channel made up of an α-hemolysin molecule is too long to show current variations due to particular nucleotides of a translocation DNA. An alternative came with the use of MspA porin.32 This channel protein from the bacterium Mycobacterium smegmatis is shown in an all atom resolution top view and cross section in Fig. 2b. Unlike α-hemolysin, MspA has a rather short effective length of about 0.5 nm for the narrow pore part. MspA needs to be modified to prevent gating, i.e., the change of the channel structure due to ionic current variation. As a result it can significantly distinguish trinucleotide sets (AAA, CCC etc.).38 Another practically important example for bio-pores is the phi29 viral packaging motor, which was used to transporting dsDNAs.39 More details on pore types can be found in ref. 15. | ||
| Fig. 2 Pore types used in polymer translocation. (a) Translocation setup using the α-hemolysin pore of Staphylococcus aureus (Image courtesy A. Aksimentiev, University of Illinois at Urbana-Champaign), see details in ref. 23 and 31. (b) MspA porin from Mycobacterium smegmatis32 (Image copyright PNAS). (c) Solid state nanopore and the potential to produce different shapes and arrangements (Image courtesy C. Dekker, Delft University of Technology), (d) DNA origami nanopore. Scale bars on the TEM images on the right are 20 nm (image courtesy H. Dietz, Technical University of Munich). Note that the protein pores shown here only allow the passage of single-stranded DNA, while artificial pores such as those shown in panels (c) and (d) are almost exclusively used for the passage of double-stranded DNA. For more details, see ref. 15. | ||
The advantages of biological nanopores include the atomic precision of their assembled structure and the opportunity to tune them through genetic modification.22 Conversely, biological pores rarely exceed 2 nm in diameter, which is wide enough only for single-stranded DNA or RNA as well as unfolded protein chains. Another disadvantage is that these bio-pores can lose stability when pH, temperature, and other parameters are varied. In order to solve these issues, a major goal was the engineering of synthetic pores.
Solid state nanopores represent a technological alternative to bio-pores.17 They are significantly more resistant and durable, their width can be fine-tuned with subnanometre precision,34,40 and they have improved mechanical, chemical, and thermal characteristics.16 Solid state nanopores can also be integrated with electronic41 and optical readout techniques.42 The first demonstration of the viability of the solid state nanopore approach was achieved by Golovchenko et al.43 They used an ion-beam sculpting technique to produce nanopores with well-defined sizes in SiN membranes. By tuning of the ion rate and temperature both increase and shrinkage of the pore diameter can be achieved.
Dekker and co-workers chose a different approach.40 They also started with silicon-based membranes (Si, SiN, and SiO2). Then a combination of electron beam lithography with etching techniques was used. The holes obtained in this fashion were about 20 nm wide and the diameter could be decreased to below 10 nm if necessary, see the examples shown in Fig. 2c. The nanopore size was modified by application of high-intensity wide-field illumination using transmission electron microscopy (TEM). In that course, large pores were demonstrated to grow in size, while small pores shrank. An alternative way is to drill through a membrane by a locally focused electron beam in a TEM setup.44–46 Ångstrom-level thickness of the membrane was achieved by atomic-layer deposition of Al2O3.47 In the process of membrane piercing by a focused electronic beam a part of the insulating Al2O3 were shown to turn into conducting Al. At the same time different nanocrystalline domains were formed in a dose-dependent way.48 Control over the charge density in the area of the nanopore helps reducing DNA translocation velocities as well as the magnitude of 1/f noise.49 However, the fabrication of these ultrathin membranes come along with ionic current leakages through the pinholes.16
One solution of the aforementioned problems is the use of graphene sheets as membranes, as generally these have suitable electrical and mechanical properties. In 2010 the groups of Golovchenko,50 Drndic,51 and Dekker52 succeeded in performing double-stranded DNA translocation through a pore in graphene. Changes of the ionic current indicated that translocation events occurred both for folded and unfolded DNA chains. The best resolution in ref. 50 was achieved for an effective membrane thickness of ∼0.6 nm, that is, for a thickness comparable to the size of a single nucleotide of single-stranded DNA. This means that a single nucleotide will affect the ionic current at a given point of time. In ref. 50 the speed of the translocation was about 10 to 100 nucleotides per millisecond, which is too quick for the detection of single nucleotides. Since this is a new type of solid state pore, many questions still remain unanswered. For instance, it is not clear so far whether indeed single nucleotide specificity can be achieved. Another important issue is the selectivity of graphene pores.16
The lack of chemical specificity of solid state nanopores can be mended by adding modifications, which target the differences between the analytes. Thus, hybrid nanopores can be synthesised, for instance, by attaching nucleotide chains with a hairpin loop to the nanopore surface.53 In such a setup, nucleotide chains complementary to the hairpin attach preferentially and thus translocate quicker. Even a single mismatch in the sequence can lead to longer pulses and smaller amounts of translocation events. In ref. 54 for the identification of proteins lipid-covered SiN pores were used. The introduction of mobile ligands into the lipid layer added chemical specificity to the nanopore and slowed the translocation of the target proteins. In another experiment α-hemolysin was inserted into a solid-state nanopore in an SiN membrane55 and thus combined the specificity and exact reproducibility of a biological pore with good integrability of a solid state membrane in nanodevices. This appears as a promising step towards the realisation of wafer-scale parallel arrays for sequencing.
There are many other alternative setups to translocation. For example, Sean Ling and collaborators56 suggested the so-called reverse or double-force translocation setup, where in addition to the pore-driven field there is an opposing force at the trans end of the chain. In such a setup the effective diffusion constant of the DNA is significantly reduced, thereby suppressing thermal smearing effect due to diffusion in the positional measurements of DNA sequences.
We mention two more approaches to translocation setups. Ref. 57 and 58 showed that glass nanocapillaries with diameters down to 27 nm can in fact detect a folding state of a single λ-phage DNA. Another interesting technology involves the use of DNA origami structures as a scaffold. DNA origami involves designed DNA sequences, which self-assemble into pre-determined shapes.59,60 Origami structures of the kind shown in Fig. 2 were put onto the pore61,62 in a manner resembling the α-hemolysin pore.55 Translocation of λ-phage DNA was detected for a conical origami pore,61 which was made of a solid-state pore and a DNA origami cone inset. In another experiment it was found that DNA origami nanoplates can be electrically assembled into nanopores.62 It was shown that they can be devised to become chemically selective. A piece of ssDNA was tethered to the origami structure as a so-called “bait”. This allowed to selectively catch molecules with complementary sequences to the pore.
IV. Unforced translocation
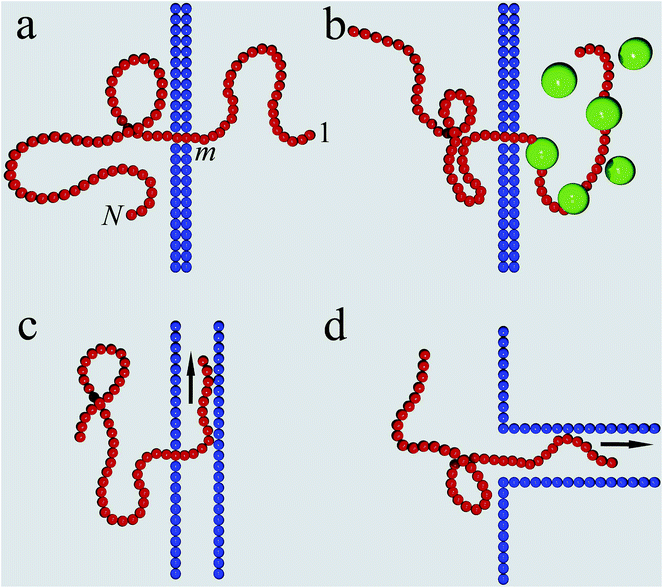
Different scenarios for polymer translocation are sketched in Fig. 3. In most of the review we will focus on case (a), in which the chain translocates through a channel across a membrane. The other scenarios are discussed further below.Before a chain starts to translocate through a pore it first needs to be guided towards the pore and threaded inside. Both steps make up the so-called capture process. The capture of a polymer depends mainly on the concentration of macromolecules in the electrolyte solution, the bias voltage, and the salt concentration. The probability that a capture event will occur in the absence of an external field can be estimated from the ratio of the partition functions of a tethered chain, 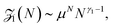 and a free chain in the bulk
and a free chain in the bulk 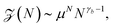 63 where μ is the non-universal connectivity factor (for instance, μ = 6 in a cubic lattice), and γ1 and γ are critical configuration exponents. The values of the latter two exponents are γ1 ≈ 0.680 for a linear self-avoiding chain—a good model for polymer chains at good solvent conditions—tethered to a wall and γ ≈ 1.12 for a chain in the bulk. The probability to find the chain tethered to the wall, i.e., with one end sticking in the pore, then becomes under equilibrium conditions.
63 where μ is the non-universal connectivity factor (for instance, μ = 6 in a cubic lattice), and γ1 and γ are critical configuration exponents. The values of the latter two exponents are γ1 ≈ 0.680 for a linear self-avoiding chain—a good model for polymer chains at good solvent conditions—tethered to a wall and γ ≈ 1.12 for a chain in the bulk. The probability to find the chain tethered to the wall, i.e., with one end sticking in the pore, then becomes under equilibrium conditions.
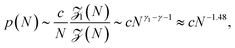 | (1) |
Without maintaining a forcing gradient across the membrane, once the first monomer is threaded into the pore, the chain will likely retract into the bulk on the cis side, and a new chain then needs to be recruited. However, in the study of unforced translocation the problem is often split up into the sole consideration of the capture and the translocation process. When focusing on the latter, a reflecting boundary condition is implemented both in simulations and theoretical approaches. The progress of the chain during the translocation process is measured in terms of the co-ordinate m counting the monomers that have passed through the pore, see Fig. 3a. The number m is the natural reaction co-ordinate for the translocating chain. In the following, N denotes the length of the translocating chain.
The theoretical approach to unforced polymer translocation started with the pioneering work of Sung and Park in 1996.69 They suggested to consider polymer translocation as a quasi one-dimensional diffusion problem, where the number m is taken as the fundamental variable in the description. Another important assumption was the idea that a chain threads slowly enough to be sufficiently close to its equilibrium during the translocation process. This allows one to deduce the free energy of the chain as the sum of the configurational entropies of two separate polymer chains of length m and N – m attached to a flat stiff wall. Sung and Park considered Gaussian chains. Here, we report the more general form suggested by Muthukumar using the exponents for self-avoiding chains70
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (m) ≃ −T(γ1 − 1)ln[m(N − m)] + mΔμ + const., (m) ≃ −T(γ1 − 1)ln[m(N − m)] + mΔμ + const., | (2) |
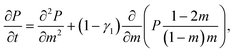 | (3) |
As pointed out by Chuang, Kantor, and Kardar, the last argument leads to a contradiction in the following sense.71 The Rouse equilibration time for a free polymer can be estimated as the time during which the polymer diffuses over a distance of its own size, i.e.,
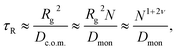 | (4) |
To address this issue Chuang et al. performed Monte Carlo simulations of spontaneous translocation using the fluctuating bond (FB) lattice model in 2D.71 However, due to computational limitations these authors had to artificially constrain the dynamics such that the chain was not able to escape from the pore before fully passing to the trans side of the membrane during the simulations. As they already noted, to impose such a reflecting boundary condition causes a systematic error in the scaling of the translocation time τ, an argument which pertains to virtually all simulation studies using this type of boundary condition. Despite this, Chuang et al. concluded that their data were consistent with the simple argument of eqn (4) that τ ∼ N1+2ν. The problem with the artificial reflecting boundary condition was resolved by Luo, Ala-Nissila, and Ying,75 who suggested that the polymer be placed inside the pore exactly halfway, such that it sits on top of the entropic barrier. A concept similar to this two-sided translocation was considered in ref. 76, in which the half-way unthreading time is considered, i.e., the process of spontaneous escape to either the cis or trans side. Using this setup and the FB model Luo et al. confirmed the exponent α = 2.5 in 2D.75 Several other numerical studies based on different simulation models are consistent with the 1 + 2ν scaling both in 2D and 3D.63,77–80 The whole range of proposed exponents α for the scaling of the mean translocation time as function of the chain length,
| τ ∼ Nα, | (5) |
| α value | Model | Reference |
|---|---|---|
| Rouse translocation | ||
| 1+2ν2D = 2.5 | 2D MC | Chuang,71 Luo75 |
| 1+2ν | 2D FB | Panja81 |
| 2.4 | 3D MC | Wolterink76 |
| 2.23 ± 0.04 | 3D MC | Milchev63 |
| 1 + 2ν | 2D, 3D MD | Wei78 |
| 2ν + 2 − γ1 | 3D MC | Dubbeldam82 |
| 2 + ν | 2D, 3D MC | Panja83,84 |
| 2.44 ± 0.03 | 2D MD | Luo79 |
| 2.22 ± 0.06 | 3D MD | Luo79 |
| 2.17 ± 0.06 | 3D LD | Mondaini80 |
| 2.48 ± 0.07 | 2D LD | Huopaniemi77 |
| 2.55 ± 0.05 | 2D LD | Lehtola85 |
| 2.33 ± 0.05 | 3D LD | Lehtola85 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Zimm translocation | ||
| 2.27 ± 0.04 | 3D MD | Guillouzic86 |
| ≈2.3 | 3D MD | Gauthier87 |
| 2.30 ± 0.07 | 3D SRD | Lehtola85 |
| 2.24 ± 0.03 | 3D DPD | Kapahnke88 |
| 1 + 2ν | 3D theory | Panja83 |
| 2.516 | 3D LD | de Haan89 |
The immediate important implication of the above scaling argument is that the dynamics of polymer translocation as function of time is anomalous. To see this, we follow Chuang et al. and assume the Flory scaling Rg ∼ Nν of the radius of gyration, combined with the Rouse equilibration time τR ∼ N1+2ν.71 The argument then assumes that the mean squared displacement (MSD) of the monomer co-ordinate m in the pore, i.e., a measure for the progress of the translocation, evolves in power-law form according to
| 〈Δm2 (t)〉 ∼ tβ, | (6) |
One of the earlier suggestions to capture the anomalous nature of this anomalous diffusion was to describe the stochastic motion of the translocating chain via the fractional Fokker–Planck equation,90–92 which is a direct generalisation of eqn (3). It represents a mathematically convenient way to combine the subdiffusive motion (6) with the potential of the driving force.82,90,93 For a constant driving force the distribution of passage times in this model scales as ≃t−1−β, and in absence of any driving as ≃t−1−β/2.90 From scaling considerations Dubbeldam et al. estimated the anomalous exponent in this fractional Fokker–Planck equation model to be β = 2/(2ν + 2 − γ1) ≈ 0.801 and reported good agreement of this prediction with their Monte Carlo simulations. The authors used the one-sided setup with constrained dynamics in their simulations. However, these simulations results are at variance with other numerical studies. Anomalous dynamics in a sawtooth potential as a model for the DNA passage was considered in ref. 94. The authors discussed the scaling for the mean first passage time and found that it scales as ≃N2/β = N2ν+2−γ1.
Several other suggestions for the scaling exponents associated with unbiased translocation based on scaling arguments were reported.76,83,84,95–97 It was argued in ref. 76 that τ ≃ N1+2νϕ(b/L), where b is the diameter of a pore and L its width, and the scaling function ϕ (x) ≃ x−0.38±0.08. Hence this approach gives α = 2.40 ± 0.08 in 3D, which was also supported by 3D lattice model Monte Carlo (MC) simulations in ref. 76. More recently,83 a different argument was presented. During translocation the polymer segments move from one side of the membrane to the other, and it was assumed that the motion of one of the monomers creates a tension, which needs a finite time for relaxation—the Rouse equilibration time τR ≃ N1+2ν. The relaxation time was proposed to scale as 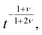 which leads to the mean squared displacement
which leads to the mean squared displacement 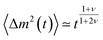 of the translocation co-ordinate for times shorter than τR, and normal diffusion for larger times, i.e., 〈Δm2 (t)〉 ≃ t. For the overall translocation (or unthreading) time this leads to the scaling τ ≃ N2+ν, i.e., the scaling exponent is ≈ 2.59 in 3D and 2.75 in 2D. For the Zimm regime with its characteristic relaxation time scaling τZ ∼ N3ν an analogous derivation leads then to the scaling τ ≃ N1+2ν. These predictions were corroborated by 3D lattice model simulations based on the same model as in ref. 76, where different results were obtained. The validity of this approach were discussed in a comment and the followup reply.98,99
of the translocation co-ordinate for times shorter than τR, and normal diffusion for larger times, i.e., 〈Δm2 (t)〉 ≃ t. For the overall translocation (or unthreading) time this leads to the scaling τ ≃ N2+ν, i.e., the scaling exponent is ≈ 2.59 in 3D and 2.75 in 2D. For the Zimm regime with its characteristic relaxation time scaling τZ ∼ N3ν an analogous derivation leads then to the scaling τ ≃ N1+2ν. These predictions were corroborated by 3D lattice model simulations based on the same model as in ref. 76, where different results were obtained. The validity of this approach were discussed in a comment and the followup reply.98,99
Kantor, Kardar, and coworkers noted some additional issues with the anomalous dynamics.100–102 They pointed out that in the case of the fractional Fokker–Planck approach the mean translocation time is infinite, however, simulations obviously provide well defined averages.† More significantly, numerics and 2D FB simulations showed that the distribution of translocation times has an exponential decay ≃ exp(−t/τ) rather than the power-law behaviour predicted by the fractional Fokker–Planck equation, compare also ref. 104. In addition, the probability distribution of the translocation co-ordinate m was found to be Gaussian, but with the anomalous time dependence (6) of the mean squared displacement. As known now the natural description of the translocation process is provided in terms of the generalised Langevin equation (GLE) with power-law memory kernel,105,106 or in terms of fractional Brownian motion,107,108 whose behaviour is identical with the overdamped limit of the GLE with power-law kernel, see the discussion in ref. 109–111.
Further simulation results were reported by Slater and coworkers.87,89,112,113 These works are based on MD simulations of translocation both with87 and without explicit solvent.112 The authors find that the scaling exponent for the translocation time strongly depends on the pore width for the range of chain lengths N they studied—in ref. 87 the largest value was N = 31, while in ref. 112N varied between 19 and 299. The reported effective scaling exponent α varies between two and three with increase of the pore width from 1 to 10 times the size of the monomer beads.114 This large range in fact covers the values of the scaling exponent α obtained from all numerical simulations reported by other authors. Slater and company also systematically studied the influence of the viscosity of the surrounding medium89,113 and obtained a crossover from α = 2 for vanishing viscosity, η = 0, up to the value α ≈ 2.55 for high effective viscosities—with chain lengths up to 99 beads.89 The latter α value is in fact relatively close to the proposed value 2 + ν from ref. 83. The former value was recovered in ref. 115 for small viscosities and relatively short chain lengths—in this case it is expected that the chains are fairly close to equilibrium and the simple Fokker–Planck description of spontaneous translocation may be a good approximation.
Despite the considerable numerical and theoretical effort spent on the study of unforced polymer translocation dynamics, there is no consensus on a unified statistical description of this process. High-accuracy MD simulations with the longest microscopic bead-spring chains to date (N = 400 in ref. 79) support the form α = 1 + 2ν for the scaling exponent, predicted by Chuang, Kantor, and Kardar, with high accuracy, and the same result was found by several other groups. In a recent paper, Panja and Barkema81 presented further simulation results for the 2D FB model by extending the chain lengths to N = 1000. They report a crossover from α = 1 + 2ν to 2 + ν in accordance with their scaling arguments. However, the FB model chains approach the continuum limit relatively slowly—about six fluctuating bonds correspond to one bead in MD for chain diffusion—and thus the MD data in ref. 79 may be considered more reliable. The extreme sensitivity of the (effective) scaling exponents to the pore width shows that the pore friction plays an important role for the translocation dynamics, and similar to the forced translocation case discussed below may indicate significant finite-size effects for the relatively short chains studied in ref. 89 and many other simulation studies. Conversely, one may argue that translocation simulations are not truly universal due to the high sensitivity of the results to details of how the simulations are set up.
V. Forced translocation
Since one of the major motivations in the field of polymer translocation comes from the potential use of nanopore translocation as a fast and cheap sequencing tool for polynucleotides14 the study of driven translocation is technologically the more relevant problem. Most of the experiments considered an external electric field as the main driving force for the translocation of polymer chains. Yet there are many other possibilities, such as chaperone binding (see Section VIII), confinement at the cis-side (Section VII), polymer adsorption,63 difference in solvent conditions88,116 or in the size of crowding agents117 (for unbiased translocation in the presence of crowders see ref. 118 and 119), as well as different degrees of crowding disorder.120In comparison to the unbiased translocation problem, for driven translocation at least one more parameter enters the problem, and the scaling of the mean translocation time τ should be connected with both the polymer length N and the force amplitude f, that is, we consider
τ ≃ Nα/f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, δ, | (7) |
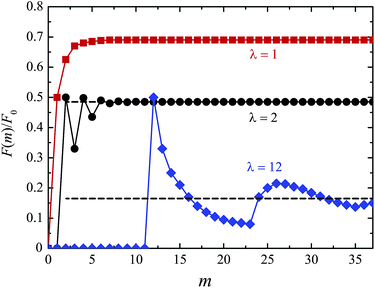
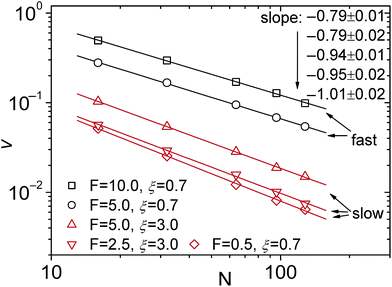
The oversimplified quasi-equilibrium picture of forced translocation was questioned by Kantor and Kardar,123 who performed Monte Carlo simulations with the 2D FB model. Their line of argument goes as follows. If there were no membrane at all, then one could assume that the shape of the polymer stays the same and can be described by its gyration radius Rg ∼ aNν. The force applied to the polymer is f, which leads to the centre of mass velocity v ∼ f/N. In order to get past this “virtual” membrane, the polymer should move a distance of the order of its gyration radius. Thus the hindrance-free scaling is τ ∼ N1+ν/f. If the chain were driven through a small hole in a real membrane, α cannot be smaller than this value. Similar to the unforced case discussed in the previous section, Kantor and Kardar concluded that the translocation dynamics is anomalous. By now a whole range of driven translocation studies either confirmed the exponent α = 1 + ν or contested it. Kantor and Kardar themselves found numerically that α = 1.45, which they attributed to finite chain length effects. In other simulations it was soon discovered that there can be a crossover for the scaling exponent depending on the length of the chain, the force amplitude, and the viscosity.77,124,125 For low bias Gauthier and Slater126,178 reported a value consistent with the Kantor–Kardar estimate 1 + ν. Dubbeldam et al.93 assumed anomalous dynamics and applied the fractional Fokker–Planck equation as they did for the undriven case.82 They found τ ∼ N2/α−1f−1, where α = 2/(2ν + 2 − γ1). These arguments were contested by Vocks et al.,95 who applied their memory function approach and obtained scaling 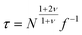 . A way to reconcile these contradictions were suggested by two of us in ref. 128. High accuracy Langevin dynamics simulations were performed to study the scaling τ ∼ Nα. We found that two distinct limiting regimes exist, namely those corresponding to slow and fast translocation. The slow translocation corresponds to small driving forces or high friction, and results in α = 1 + ν, which is in agreement with ref. 123, 127 and 129. The opposite regime of fast translocation is characterised by α ≈ 1.37 (see Fig. 4) in agreement with ref. 79 and 130. The argument of ref. 128 was that faster translocation results in a distinctly non-equilibrium translocation dynamics, as demonstrated by the deviation of the radius of gyration scaling and typical snapshots of the conformations of the translocating chain.
. A way to reconcile these contradictions were suggested by two of us in ref. 128. High accuracy Langevin dynamics simulations were performed to study the scaling τ ∼ Nα. We found that two distinct limiting regimes exist, namely those corresponding to slow and fast translocation. The slow translocation corresponds to small driving forces or high friction, and results in α = 1 + ν, which is in agreement with ref. 123, 127 and 129. The opposite regime of fast translocation is characterised by α ≈ 1.37 (see Fig. 4) in agreement with ref. 79 and 130. The argument of ref. 128 was that faster translocation results in a distinctly non-equilibrium translocation dynamics, as demonstrated by the deviation of the radius of gyration scaling and typical snapshots of the conformations of the translocating chain.
 | ||
| Fig. 4 Scaling of the translocation time τ versus chain length N with varying trans-membrane force F and friction coefficient ξ. Reprinted with permission from.128 | ||
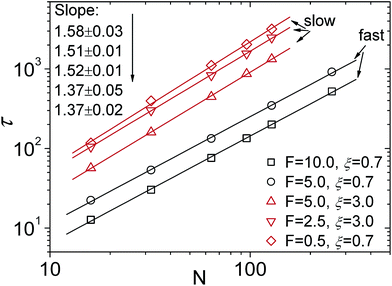
For the scaling dependence on the amplitude of the driving force most authors reported results consistent with or at least close to the inverse-force scaling τ ∼ 1/f. However, we found numerically that a crossover from τ ∼ 1/f to τ ∼ 1/f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 occurs when the driving force is increased beyond a certain value, as shown in Fig. 5, see also Fig. 4 in ref. 128. The large variation in the values of the scaling exponents obtained from different simulations is evidenced in Table 2. This indicates that the results are sensitive to the details of the actual simulations—such as the parameters defining the geometry and size of the pore, the magnitude of the driving force, etc.—another indicator that driven translocation may represent a distinctly non-equilibrium process. The key idea behind the physics in this process was provided by Sakaue and collaborators in a series of recent papers.137,143–146 The argument is based on the observation that when a chain starts threading through the pore the entire polymer does not feel the conformational changes at once. The portion of the chain which moves towards the pore on the cis side grows over time as the tension propagates along the chain, similar to a coiled garden hose being pulled from one end. Hence, Sakaue and coworkers split the chain into two separate parts: a moving one and another part, which is in equilibrium. The dynamics is determined by the motion of the boundary R(t) between these domains, as sketched in Fig. 6. The translocation time is then calculated from the relation R(t) ∼ Rg ∼ Nν. The authors differentiate between three different regimes for various force strengths: the trumpet regime, the stem-flower regime and the strong stretching regime.145 This treatment leads to the 1 + ν value for α and a value for force exponent δ which depends explicitly on the field strength. We note that a similar reasoning based on the original argument of Di Marzio, Guttman, and Hoffman147 was used in the context of shrinking single-stranded DNA denaturation bubbles.148,149
0.8 occurs when the driving force is increased beyond a certain value, as shown in Fig. 5, see also Fig. 4 in ref. 128. The large variation in the values of the scaling exponents obtained from different simulations is evidenced in Table 2. This indicates that the results are sensitive to the details of the actual simulations—such as the parameters defining the geometry and size of the pore, the magnitude of the driving force, etc.—another indicator that driven translocation may represent a distinctly non-equilibrium process. The key idea behind the physics in this process was provided by Sakaue and collaborators in a series of recent papers.137,143–146 The argument is based on the observation that when a chain starts threading through the pore the entire polymer does not feel the conformational changes at once. The portion of the chain which moves towards the pore on the cis side grows over time as the tension propagates along the chain, similar to a coiled garden hose being pulled from one end. Hence, Sakaue and coworkers split the chain into two separate parts: a moving one and another part, which is in equilibrium. The dynamics is determined by the motion of the boundary R(t) between these domains, as sketched in Fig. 6. The translocation time is then calculated from the relation R(t) ∼ Rg ∼ Nν. The authors differentiate between three different regimes for various force strengths: the trumpet regime, the stem-flower regime and the strong stretching regime.145 This treatment leads to the 1 + ν value for α and a value for force exponent δ which depends explicitly on the field strength. We note that a similar reasoning based on the original argument of Di Marzio, Guttman, and Hoffman147 was used in the context of shrinking single-stranded DNA denaturation bubbles.148,149
 | ||
| Fig. 5 Scaling of the translocation velocity v with chain length N with varying trans-membrane force F and friction coefficient ξ. Reprinted with permission from ref. 128. | ||
| α value | δ value | Method | First author and reference |
|---|---|---|---|
| Rouse translocation | |||
| 1 | — | 3D MC | Chern131 |
| 1 | — | Theory | Lubensky121 |
| 1 | — | Experiment | Meller30 |
| 1 | 1 | 3D BD | Tian132 |
| 1.65 ± 0.08 | — | 3D MC | Milchev63 |
| 1 + ν | 1 | Theory, 2D MC | Kantor123 |
| 1 + ν | — | Theory | Matsuyama133 |
| 1.60 | — | 3D MC | Tsuchiya134 |
| 1.46 ± 0.01 (short) | — | 2D FB | Luo124 |
| 1.72 ± 0.06 (long) | — | 2D FB | Luo124 |
| 1.50 ± 0.01 (short) | — | 2D LD | Huopaniemi77 |
| 1.69 ± 0.04 (long) | — | 2D LD | Huopaniemi77 |
| 2ν + 1 − γ1 | 1 | 3D MC | Dubbeldam93 |
| ≈ 1.9 | 0.94 ± 0.01 | 2D LD, theory | Huopaniemi135 |
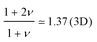
|
1 | 2D,3D Theory, MC | Panja,Vocks95,96 |
| 1.42 ± 0.01 | — | 3D MD | Luo79 |
| 1.36 ± 0.01 | — | 3D LD | Bhattacharya130 |
| 1.36 ± 0.03 | — | 3D LD | Fyta136 |
| 1 + ν (slow) | 1 | 3D LD | Luo128 |
| 1.37 ± 0.02 (fast) | 0.79 ± 0.02 | 3D LD | Luo128 |
| 1 + ν | 1 | Theory | Saito137 |
| 1 + ν | 0.9–1 (crossover to strong) | Theory | Ikonen138 |
| — | 0.90–0.95 (crossover to strong) | 3D LD and BD | Ikonen138 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Zimm translocation | |||
| 1.20 ± 0.01 | — | 3D DPD | Kapahnke88 |
| 1.28 ± 0.01 | — | 3D LB | Fyta136 |
| 1.28 ± 0.03 | — | 3D LB | Izmitli139 |
| 1.27 ± 0.03 | — | Experiment | Storm140 |
| 1.05 ± 0.02 (slow) | 0.994 ± 0.008 | 3D SRD | Lehtola141 |
| 1.18 ± 0.02 (fast) | 0.940 ± 0.013 | 3D SRD | Lehtola141 |
| 1 + ν | 1 (strong) | Theory | Saito, Ikonen137,142 |
| 1 + ν |

|
Theory | Saito137 |
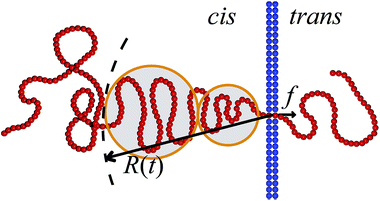 | ||
| Fig. 6 Illustration of the tension propagation along the translocating chain. The translocation force f acts inside the pore. The tension propagation front R(t) separates the part of the polymer that is dragged towards the pore from the part that so far is not influenced by the drag force. The latter part of the polymer chain is equilibrated. The tension blobs hypothesised by Sakaue are indicated.137,143–146 | ||
Rowghanian and Grosberg 150 modified the theory by Sakaue and coworkers by assuming that the flux of monomers is the same through any cross-section of the trumpet with respect to a line perpendicular to the membrane containing the pore. They called this the “iso-flux trumpet” approach and indeed obtained 1 + ν for the scaling exponent α. A result consistent with the iso-flux trumpet assumption was also reported for sufficiently large driving forces and/or long chains by Dubbeldam et al.151 in their consideration of the three regimes mentioned above, and different scaling expressions were found for the different cases. However, Ikonen and collaborators used the idea of tension propagation to develop a consistent theory of driven translocation based on the combination of a Brownian dynamics equation of motion for the reaction co-ordinate of the chain with the explicit dynamics of the tension front propagation in the chain, resulting in a time-dependent memory term.138,142,152
The Brownian dynamics-tension propagation (BDTP) theory138,142,152 predicts that α = 1 + ν asymptotically when N → ∞ in all the three regimes, and there is a crossover from δ ≈ 0.9 to δ = 1.0 with increasing driving force, the latter value being the asymptotic high-force limit.138 Most importantly, the BDTP theory explains the large variation in the numerically obtained values of the scaling exponents. First, there is a large correction-to-scaling term in the translocation time that is linear in N, which leads to effective exponents that are typically smaller than 1 + ν even for chain lengths up to 105–106 beads as shown in Fig. 7 and Table 3. Second, the BDTP theory also explains the sensitivity of the exponents to the various simulation parameters. A key role in this is played by the effective pore friction that the threading chain experiences, as it controls the magnitude of the correction-to-scaling term.142 Ikonen and collaborators showed that all existing MD computer simulation data for the exponent α, which was obtained using proper initial and boundary conditions—without the unphysical reflective boundary condition on the cis side—can be quantitatively reproduced by the BDTP model when pore friction and finite chain length effects are properly taken into account. The scatter in the exponent δ is partially explained by the relatively soft bonds and low values of the Langevin friction used in typical MD simulations, but most recent MD data seems to indicate that 0.9 ≲ δ ≲ 0.95 even for high forces, i.e. it does not seem to reach the asymptotic limit of unity as predicted by the BDTP theory. This may be due to the crowding effects of highly driven chains on the trans side, which have not been taken into account. Finally, Ikonen et al. have also generalised the BDTP theory to the case of Zimm friction including hydrodynamic effects for which the asymptotic exponent remains to be α = 1 + ν, but the finite chain length effects are even more severe than in the Rouse case.142
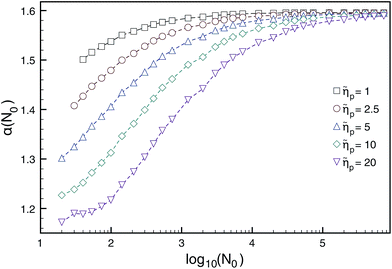 | ||
Fig. 7 Dependence of the translocation exponent α(N0) on polymer length N0 for different ratios of pore/solvent friction ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) p obtained from BDTP theory in ref. 138. Reprinted with permission from ref. 138. p obtained from BDTP theory in ref. 138. Reprinted with permission from ref. 138. | ||
| α (BDTP) | α (MD) | Dimension and parameter values |
|---|---|---|
| 2D, k B T = 1.2, ref. 77 | ||
| 1.51 ± 0.02 | 1.50 ± 0.01 | f = 5.0, γ = 0.7, 20 ≤ N ≤ 70 |
| 1.71 ± 0.02 | 1.69 ± 0.04 | f = 5.0, γ = 0.7, 500 ≤ N ≤ 800 |
| 1.52 ± 0.02 | 1.50 ± 0.02 | f = 2.4, γ = 0.7, 20 ≤ N ≤ 70 |
| 1.71 ± 0.02 | 1.65 ± 0.04 | f = 2.4, γ = 0.7, 500 ≤ N ≤ 800 |
| 1.66 ± 0.02 | 1.64 ± 0.01 | f = 5.0, γ = 3.0, 20 ≤ N ≤ 70 |
| 1.71 ± 0.02 | 1.67 ± 0.03 | f = 5.0, γ = 3.0, 500 ≤ N ≤ 800 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| 3D, k B T = 1.2, ref. 128 | ||
| 1.59 ± 0.02 | 1.58 ± 0.03 | f = 0.5, γ = 0.7, 16 ≤ N ≤ 128 |
| 1.35 ± 0.02 | 1.37 ± 0.05 | f = 5.0, γ = 0.7, 16 ≤ N ≤ 256 |
| 1.34 ± 0.02 | 1.37 ± 0.02 | f = 10.0, γ = 0.7, 16 ≤ N ≤ 256 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| 3D, k B T = 1.2, ref. 79 | ||
| 1.41 ± 0.01 | 1.42 ± 0.01 | f = 5.0, γ = 0.7, 40 ≤ N ≤ 800 |
| 1.39 ± 0.01 | 1.41 ± 0.01 | f = 5.0, γ = 0.7, 64 ≤ N ≤ 256 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| 3D, k B T = 1.0, ref. 153 | ||
| 1.46 ± 0.02 | 1.47 ± 0.05 | f = 3.0, γ = 11.7, 70 ≤ N ≤ 200 |
| 1.49 ± 0.02 | 1.50 ± 0.01 | f = 30.0, γ = 11.7, 200 ≤ N ≤ 800 |
An important yet often neglected indicator for the translocation dynamics is the distribution of waiting times measuring how long it takes individual monomers to pass the pore. In Fig. 8 it is demonstrated how the statistics of waiting times reveals the two distinct physical translocation regimes: increasing waiting times ascribed to the initial stage of tension propagation along the previously relaxed chain and the final stage of decreasing waiting times corresponding to the retraction of the, by now, stretched tail from the cis side.138 Similar analyses are reported in ref. 154–157.
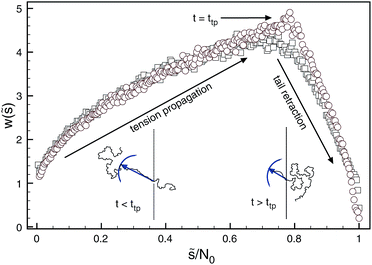 | ||
| Fig. 8 Distribution of waiting times generated for forced translocation through a pore by molecular dynamics (squares) and Brownian dynamics tension propagation (circles) techniques. The distribution clearly distinguishes the two stages of the translocation process. Reprinted with permission from ref. 138. | ||
The influence of the chain rigidity on the translocation properties for the driven case was investigated by Bhattacharya and Adhikar.154,158 They found that with increasing chain rigidity κb, the translocation time grows as 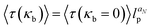 , where lp is the persistence length of the chain and aN moderately depends on the chain length—for N = 256 it was found that aN ≃ 0.32. The inequality α < 1 + ν was satisfied for all values of rigidity studied in ref. 158.
, where lp is the persistence length of the chain and aN moderately depends on the chain length—for N = 256 it was found that aN ≃ 0.32. The inequality α < 1 + ν was satisfied for all values of rigidity studied in ref. 158.
Long polymers can often become entangled and knotted; however, the probability of knotted configurations becomes significant only when the chain lengths are of the order of tens of thousands of monomers, or more.159 Apparently if a knotted polymer threads through a pore, knots should hamper the movement or, as one might assume, even completely halt it. Brownian dynamics simulations of knotted polymer translocation160 showed that below a certain threshold force knots add an effective friction, without jamming the process. However, for high pulling forces, knots become tight and the passage of a polymer basically stops.160 We note that knotting can become more relevant when the chain-to-be-translocated is confined, for instance, in virus capsids.161 The ejection of a knotted DNA chain from a virus would be significantly hampered. For the effects of knots in proteins, that translocate through mitochondrial pores, see ref. 162.
Instead of driving a polymer chain through the pore by an external force, another possibility—potentially useful for DNA sequencing—could be to pull the chain at one of its ends by optical tweezers using an end-attached colloidal particle.163 The polymer dynamics in the case of a double-force arrangement was analysed in detail by Ollila et al.164 The case when the polymer is only pulled from one end was first analysed by Kantor and Kardar.123 For moderate forces they predict that α = 2, and corroborated their prediction by MC simulations of the 2D FB model. In another work, Grosberg et al.129 argue that α = 2 and α = 1 + ν for elongated and coiled polymers, and verified their prediction by MD simulations of ideal chains. Huopaniemi et al.135 carried out a more detailed scaling analysis and obtained α = 2 both in the moderate and strong force regimes, while α = 1 + 2ν in the weak force limit (as in the spontaneous translocation case). They also performed 2D Langevin dynamics simulations to support their predictions. The weak force limit was subsequently contested by Panja and Barkema,96 who claim that α = 2 + ν, in analogy to their prediction to the spontaneous case. However, since the physics of pulled translocation for coiled chains must be controlled by tension front propagation similar to the pore-driven case, memory effects of the type considered in ref. 96 possibly do not hold in this case.
VI. Polyelectrolyte translocation
A major portion of translocation experiments are performed with an electric field as driving force. In a full description of the translocation process, one should therefore take charge effects of translocating polyelectrolytes such as DNA or RNA into account. We here provide a brief introduction into this field. The explicit consideration of charge effects affects both the capture process of the polymer chain by the pore and the potential barrier for the threading process. Concurrently, charge effects offer an opportunity to tune the process by change of the salt concentration of the ambient solution. The deformation of single stranded DNA chains on approaching the pore were recently investigated.166 For the translocation of DNA of 800–8000 base pairs through SiN pores Wanunu et al. found that a 20-fold salt gradient across the pore enhances the electric field such that the sensitivity to DNA concentration increases by a factor of 30 and allows the detection at picomolar DNA concentrations.67 In their experiment positive K+ ions went to the cis chamber and effectively polarised the vicinity of the pore. The field, in which DNA moves to the pore, is not created by immobile charges but comes from the conductivity of the salt solution. Current conservation focuses the field lines towards the pore and leads to an electrophoretic funnelling of the DNA into the pore.65 The expressions for the capture rates in ref. 65 and 165 were obtained by taking these electro-hydrodynamic effects into account. Surprisingly, the theoretical estimates show that the electro-osmotic flow through and around the coil is somewhat reduced but is not suppressed completely165 as it was supposed in the earlier model.67For biological pores the dependence of the capture rate on salt concentrations can be non-trivial due to additional interactions of the polymer with the pore charges.167 Thus, at high-pH conditions the repulsion between the sodium poly(styrene sulfonate) and the α-hemolysin pore resulted in a non-monotonous dependence of the capture rate on the salt concentration in the cis-compartment.167 As in the case of solid-state nanopores,67 an increase of the salt gradient across the pore led to a considerable growth of the capture rate167 —remarkably, for a ten-fold change csalt,trans/csalt,cis = 10 the translocation rate was up by two orders of magnitude. The capture rate depends non-trivially on the DNA length. For small lengths it grows rather steeply with N, while it is limited by a potential barrier at the pore and then becomes independent of the molecular weight, see Fig. 4a in ref. 165. The rate in the latter regime is limited by DNA diffusion time towards the pore.
Threading of a polyelectrolyte is also significantly affected by the electric potential. Under the assumption that the speed of the chain passage is determined by the balance of viscous and electrical forces, and the Debye length is vanishingly small, Ghosal168 computed the translocation velocity.§ In the case of counter-ion condensation the results agree with experiments by Storm et al.169 A weak dependence of the translocation speed on the polymer length found in the experiment was not featured in this relatively simple theoretical approach. In the case of a finite Debye layer thickness170 the translocation time was predicted to have a maximum at a certain salt concentration, which agree with experimental results for DNA translocation through solid-state nanopores of Smeets et al.171 The slowing down of the polymer motion in this case was due to the electro-osmotic flow in the direction opposite to threading generated next to the wall. The electro-osmotic flow was shown to play a crucial role in the screening of DNA charge:172 by MD simulations the authors estimated the magnitude of the stall force for the DNA—the force needed to stop the motion of DNA. The DNA effective charge was found to be 25% of its bare charge, which roughly corresponded to the Manning condensation assumption. However, it was also found that the stall force depends on the electrolyte viscosity and surface properties of the pore. Hence it was concluded that a decrease in the driving force in the pore is caused by hydrodynamic drag of the electro-osmotic flow rather than pure counterion condensation. This reduction of the DNA charge was observed independently in experiments, in which dextran sulfate sodium translocated through an α-hemolysin pore in a lipid bilayer.173,174 These experiments also revealed that for small voltages translocation was not observed due to the entropic barrier. Chains also did not translocate when the Debye screening lengths were smaller than the pore radius.
We also mention another experiment, also confirmed by MD simulations, which revealed that counter-ion size also plays a crucial role in the translocation process.175 There the conventionally used KCl electrolyte was compared with NaCl and LiCl electrolytes. Though similar in chemical nature the counterions Na+ and Li+ exhibited a stronger binding to DNA, which resulted in smaller effective DNA charge and significantly longer translocation times (up to 10 times for longer for 4 M LiCl versus 4 M KCl solutions).
Evidence of the dependence of the electroosmotic flow on the pore diameter was revealed in optical tweezers experiments.176 The threading force was measured by pulling λ-phage dsDNA through a silicon-nitride solid state pore of 41 nm diameter and through the same pore coated with lipids, which decreased the diameter by 10 nm. For smaller pores the electroosmotic flow is lower, that is, it does not strongly counteract the electrostatic force, resulting in a larger threading force. Theoretical calculations for this scenario were based on coupled Poisson, Nernst–Planck, and Stokes equations for a charged rod-shaped particle passing through an orifice.177 The comparison of experimental results and the theoretical model indicates that no-slip boundary conditions underestimate the value of the dragging force.176 However, hydrodynamic slip effects on the DNA surface with a length of 0.5 nm reproduced the experimental results remarkably well.
Yet another contribution to this complex picture comes from a difference in dielectric constants of water and membrane, for instance, for a lipid bilayer the dielectric constant ε ≈ 2. Meller et al.178 suggested that this difference may be a possible cause for the rather high energy barrier for polyelectrolyte translocation (over 10 kBT). Later on this assumption was supported by MD simulations.179 On the theoretical side, first steps have already been taken to develop a fully microscopic theory of electrostatic correlations in cylindrical membrane nanopores to account for the correlation effects induced by the surface charge, nanoconfinement of the electrolyte, and interfacial polarisation charges associated with a low permittivity membrane.180
Undoubtedly charge distributions along a pore play an important role. In ref. 181 3D Langevin dynamics simulations of a polyelectrolyte going through a channel with different charge distributions were performed. It was shown that certain distributions assist in the slowing down of the translocation process due to free-energy wells, which trap a polymer near its end. This effect could be beneficial with respect to increasing the accuracy in sequencing experiments.
VII. Pore–polymer interaction and sequence effects
Most of the theoretical and simulations studies of polymer translocation are based on homopolymers. However, essentially all biological polymers feature a heteropolymeric structure, which renders sequence effects important for the understanding of the actual sequencing possibilities. Sequence effects may show up for chains with different charges of monomers, which leads to variation in the driving force,182 different interaction strengths between the monomers and the pore,183,184 a mix of single and double stranded parts of DNA,185 or due to secondary structure of RNAs.186,187 The first study of heteropolymer translocation was undertaken by Muthukumar with a quasi-equilibrium approach.188 He proposed a solution based on the Fokker–Planck equation corresponding to the diffusion on an interval with reflecting boundary condition at one end and an absorbing boundary at the other. Kafri et al. considered translocation with sequence heterogeneity within a transition rate constant approach and predicted that heterogeneity itself can lead to anomalous dynamics.189Apparently the variation of the flexibility of a polymer along the molecule should significantly change the translocation patterns. Slater and de Haan190 demonstrated that structural information can be extracted from the translocation process for rod-coil copolymers. The passage speed for rod-parts was significantly higher than for coil-parts because it was not hindered by an entropic barrier, effected by the accessible degrees of freedom of a flexible polymer. Hence it was suggested that a rigid polymer can be “anchored” by addition of coils at both ends, as shown in Fig. 9. In concern of the use of nanopore force spectroscopy for single-stranded DNA and RNA chains it is important to remember that these molecules are prone to the formation of secondary structures such as loops and hairpins. If the pore diameter is so small that secondary structures cannot thread inside, these first need to unzip and therefore overcome additional kinetic barriers:191 the presence of hairpins increases the translocation time considerably. At the same time the formation of non-native base pairs on the trans-side slows down backsliding of the chain and effectively eases the substantial free energy barrier, which arises from unzipping on the cis-side.192 Estimation of the translocation exponent α for the length dependence of the translocation time for random RNA sequences was considered in ref. 186. The nature of the free energy barrier for random RNA with base-pairing patterns is different from the homopolymer case. Although this barrier has a logarithmic nature in both cases, for RNA translocation at low temperatures it dominates the translocation, leading to anomalous dynamics. The exponent α was found to depend on the base-pair matching energy and the values changed from 2.45 in the high temperature limit up to 6–14 for glassy states.186 Subsequent further development of this model allowed to calculate the distribution of exit times which showed quite good agreement with experimental data.187
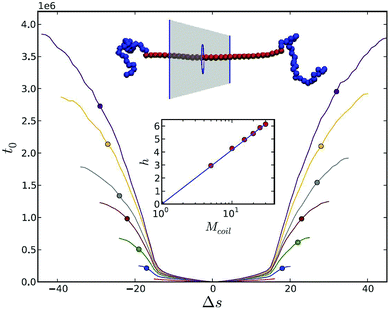 | ||
| Fig. 9 Anchoring of stiff polymer by addition of two terminal coiled blocks. The translocation process starts in the middle of the rod. t0 is an average first time for Δs segments to translocate for increasing coil lengths: Mcoil = 1 (red), 5 (blue), 10 (green), 15 (brown), 20 (grey), 25 (orange), 30 (purple) in the absence of a driving force. Reprinted from ref. 190 with permission from APS. | ||
In complex cases, when the interaction of a polymer with the pore is combined with time-dependent driving forces complex phenomena such as resonant activation can be found. In ref. 193 Langevin dynamics simulations showed that for the attractive pore case the translocation time for successful threading events might have a minimum at a certain frequency of the driving force. If there is no attraction, the passage time crosses over to a fast translocation regime with a drop in the frequency.
VIII. Translocation out of or into confinement
So far we considered the more generic case of translocation of polymer chains between two infinite semi-spaces. In this and the following sections we focus on two more specific topics of polymer translocation. In the following section we address the effective driving force due to binding proteins. Here we ask the question what happens if the chain starts in a confined space and then ejects to an unlimited volume, or vice versa, when it has to squeeze into a limited space. The first question is a generalisation of the problem of ejection of viral DNA or RNA from a bacteriophage into a bacteria cell.194 The process of DNA ejection is rather involved, because within the capsid five different pressure contributions can be found:195 the osmotic pressure of DNA and counterions, the direct pressure on the DNA, the hydrostatic pressure, the pressure experienced by the capsid, and the pressure coming from the chemical potential of the DNA ejection. One should also add to that effects of in vivo crowding inside the target cell: for the λ-phage in vivo and in vitro rates of DNA ejection differ by about two to three orders of magnitude.196The observation of these effects on viral ejection provided the motivation to start from a simpler problem, namely that of a purely entropy-based translocation from confined spaces. The presence of confinement then acts as a major driving force for translocation. In ref. 197 the authors considered translocation out of planar confinement in 3D and out of the confinement between two strings of atoms in 2D and used both scaling arguments and Langevin dynamics simulations. They found that the scaling of the translocation time with the dimension R of the confinement in 3D was τ ∼ Nβ+ν2DR1+(1−ν2D)/ν ∼ R1.34 from scaling arguments based on the blob picture198 compared to τ ∼ N1.43±0.10 in the simulations, where β is the scaling exponent for the mean velocity v ∼ Nβ. In 2D the exponents were τ ∼ Nβ+1R1 from scaling arguments and τ ∼ R1.04±0.01 from simulations. The results were different from previous attempts to solve the problem by Cacciuto and Luijten199 and Panja et al.,84 where the dependencies were τ ∼ N1+νR1/ν and τ ∼ N2ν2D, correspondingly. Cacciuto and Luijten assumed that the during translocation the polymer moves by its gyration radius, while they did not consider the fact that the polymer is deformed and effectively represents a string of blobs. More correctly it should therefore move by the size of the string of blobs in order to translocate.197 Recently Luo and Shenga simulated the escape of a ring polymer from a nanochannel,200 observing two regimes. For long chains the translocation time was smaller than for linear chains of identical length due to a larger pulling force, but for shorter chains the opposite trend was observed, due to the longer diffusion distance before the chain starts to experience this force.
The remarkable influence of the geometric shape of the chamber confining the polymer chain on the packaging and ejection time of a polymer was reported in ref. 201. It was observed that for flexible polymers a spherical shape leads to a quicker packaging but slower ejection than an ellipsoid. However, for semiflexible polymers such as DNA the spherical shape expedites both packaging and ejection. The authors suggest this effect as an explanation for the rather spherical shapes of viruses with pressure-driven ejection, such as bacteriophage T7, phage λ, etc.202 Linna et al. studied the escape of a polymer from a spherical cavity with Langevin dynamics simulations.203 They found that the scaling τ ∼ Nα was well fulfilled only for initial polymer densities in a capsid which were less than 0.25. The exponents α were different for various packaging densities ranging from α ≈ 1.22 (ρ = 0.2) to α ≈ 1.35 (small densities). Another important factor for viral ejection are topological constraints of viral DNA. Computer simulations by Marenduzzo et al. demonstrate that disordered entangled states of DNA packing effect long release times due to the constant readjustments to disentangle the chain.204 Addition of cholesteric interactions were shown to stimulate the chain packing in a spool fashion. The ejection time for this case drops significantly. For the most frequently occurring torus knots the unknotting proceeds by step-wise simplification of the topology.
Another way to control the polymer ejection was proposed by Evilevitch et al.205,206 These authors aimed at controlling DNA ejection in vitro from λ-phage by the osmotic pressure of polyethylene glycol in the outer solution. They found that ejection is completely suppressed by a pressure of 20 atmospheres, which as they note is not equal, but smaller than the pressure inside a natural capsid. Similar findings were discovered for other bacteriophages such as T5.207 Very recently the osmotic suppression technique proved an existence of a high internal pressure of tens of atmospheres within the eukaryotic human virus HSV-1.208 For HSV-1 an increase of the external osmotic pressure suppressed the ejection, which shows that the internal pressure is powering the ejection of the entire genome. Since eukaryotic and bacteriophage viruses are split by billions of years of separate evolution this finding supports the view that pressure-driven DNA ejection is a key mechanism for viral infection. It is important to stress that these results were obtained in vitro. The situation in vivo can in fact be substantially different:209 the osmotically stressed cellular cytoplasm can promote DNA ejection from the phage rather than suppress it. The enhancement of ejection occurs due to the condensation of DNA in the presence of crowding molecular agents as well as DNA-binding proteins.
The injection into a cavity was analysed in terms of Langevin dynamics simulations for 2D cases of circular210 and ellipsoidal211 shapes of confinement. Comparison of these two cases shows that anisotropic confinement increases the translocation time, and the time grows with increasing aspect ratio of the ellipsoid. For the translocation time in the circular case a non-universal dependence of τ ∼ Nα/(F − f(φ)) was found, where φ is a volume fraction of the polymer in confinement, where F is the driving force in the pore and f(φ) is an average resisting force of the whole translocation process. The exponent α decreased with φ from ∼1.5 for weak confinement to 1.3, and then increased again to 1.65 for φ = 0.45, showing an interesting non-monotonous dependence.
The problem of driving a polymer into a confined volume (“injection”) has both technological and biological relevance and is not a trivial one, considering the case quantitatively. The first experiments reported by the Bustamante group showed that bacteriophage ϕ29 packages 6.6 μm long dsDNA into a capsid of size 42 × 54 nm with the help of a portal complex molecular motor.212 Obviously this happens against a rapidly increasing electrostatic and bending energy cost as well as decrease of conformational entropy, leading to packaging forces of up to 57 pN. Theoretical modelling and Brownian MD simulations for the packaging of viral genome were developed in parallel.213–215 They showed that more than a 10-fold build-up of the loading force occurs roughly within the last 20–30 percent of the genome to be injected into the capsid, which agrees qualitatively with experiment.212 This build up plays a crucial role by creating the force for a subsequent ejection of viral DNA into bacterial cells.216
One possible source for the driving force translocating the chain can be a flow into the compartment, that the polymer is supposed to enter. The first approach to this problem dates back to the scaling theories in the classics of polymer theory.217,218 Later it was obtained that a chain can be sucked into the pore if the solvent current exceeds a certain threshold Jc ∼ kBT/η,219 where η is the solvent viscosity. These results were subsequently confirmed by mesoscale simulations,220 which showed that the critical velocity flux depends linearly on temperature but is independent of the polymer length. It should be noted, however, that in ref. 219 and 220 the time characteristics of the sucking process were not considered. This was studied in ref. 155 for the case of a flow into a pore channel, which is oriented perpendicular to the wall (Fig. 3d). Here the flow affects the motion of monomers, which are actually inside the channel. Hence the driving force is proportional to the number of units in the pore. The simple scaling relation τ ∼ N/F was found for the injection time in the case of the so-called steady state scenario, where N is the number of units in a polymer and F is the driving force. For small diameters of the channel the dependence on N and F was shown to be non-universal. The problem of injection into a laterally unbounded confined space (compare Fig. 3c) was considered in ref. 156 and 157. Unlike the case of translocation into unbounded domains, here the translocation time τ depends non-universally on the driving force F. Increase of the confinement size R first leads to a quick drop in translocation times, which then approach a plateau value.
IX. Chaperone-assisted translocation
Nature has come up with her very own solution to the translocation problem. Apart from trans-membrane potentials, a quite elegant way to effect a driving force for translocation is the presence of binding proteins called chaperones into the system.72 This happens, for instance, across the membrane of mitochondria.221 In the simplest case these proteins bind on the trans side, as sketched in Fig. 3b, and prevent backsliding of the chain when they are bound on the chain next to the pore exit. This creates an effective force for translocation. The chaperone binding-mechanism was first proposed for protein translocation in 1992 by Simon et al. as a Brownian ratchet with partial rectification of the chain motion through the pore.222 They considered a straight sequence of beads connected by harmonic strings and assumed that if the binding site gets out of the pore it is immediately occupied by a chaperone preventing backsliding of the chain. Thus the mean translocation time drops from L2/2D for the undriven case to L2/(2MD), where M is the number of binding sites, L is the length of the polymer, and D is the diffusion coefficient for the sliding motion through the pore: in this realisation of the chaperone-driven translocation the translocation time is reduced by a factor of M. The authors also pointed out that normally proteins have both adsorption and desorption rates and do not bind immediately.Subsequently, from experiments Matlack et al. found that BiP proteins function indeed as a molecular rachet during the translocation of secretory proteins via the prepro-α factor in the translocation through the channel constituted by the Sec complex.223 Elston compared the Brownian rachet model with experiments reported in ref. 223 and showed a good agreement for the fraction of the remaining prepro-α factor as a function of BiP chaperone concentrations.224 It should be noted that the power stroke model, which assumes that BiP changes its conformation and propels the chain also performed well in comparison with experiments.225 The passive chaperone mechanism also provides a reasonable explanation226 for the results of experiments of DNA uptake into the cell nucleus.227 In the experiment227 eggs of the African clawed frog were used to make cell-free nuclei extracts, which contain a full set of biochemical factors involved in the translocation process as well as providing access to nuclear pores. The combination of fluorescence microscopy and single-molecule manipulation showed that fluorescent DNA molecules gather in reconstructed nuclei and allowed to measure the rate of uptake of λ-phage DNA. The authors showed the consistency of the DNA uptake with a ratchet model.
The Brownian rachet model was studied in more detail by Brownian dynamics simulations and a solution of the corresponding Fokker–Planck equation.228 It was argued that the binding of the chaperones creates an effective pulling force, which can be adjusted in a way that leads to the decrease of the mean translocation time from that of unbiased translocation down to the translocation time for ideal ratcheting. This approach was extended and generalised in ref. 229 and 230. An analysis based on the partition function for the chaperone model showed the intuitive result that the back-sliding of the chain through the pore to the cis side is proportional to the probability that no chaperone is bound to the chain segment next to the pore exit. Simultaneously, a chaperone can bind to a site if it is unoccupied by already bound chaperones. Including the finite size of the polymer chain and the possible occurrence of chaperones on both sides of the membrane, the model's main feature is that chaperones occupy more than one monomer of the translocating chain. If there exists a mismatch in size of the chaperones and monomers to which they bind, then the so-called “parking lot” effect comes about.229 Assume that the size of a monomer is σ and the size of a chaperone is λσ. Then λ monomers need to translocate through the pore until the first chaperone can bind. Once the first chaperone sits on the chain, the same happens with the next λ monomers of the protruding chain. Moreover, if the chaperones do not site side by side, a chaperone can only bind between them if the space is large enough. These effects create oscillations in the effective pulling force, as shown in Fig. 10: no oscillations exist when λ = σ, while in the case λ = 12σ the oscillation are distinct. After a few oscillations the effect weakens considerably due to the possibility of multiple configurations. The force eventually reaches a plateau, whose height decreases with the less efficient partial ratcheting for larger chaperone binding sizes λ. A detailed analysis based on evolution equations was conducted in ref. 231 for both discrete and continuous representations and irreversible binding. This analysis allows to find the large deviation function, which contains information about the velocity, the diffusion coefficient, and the cumulants quantifying the process.
Analytical and Monte Carlo simulations studies of AB heteropolymer translocation for chaperone-driven translocation were reported by Abdolvahab et al.232–234 These authors found that the first two moments of the first passage time distribution can provide information not only about the length of a polymer but also its composition. Depending on the binding energy of chaperones for A and B units of the translocating chain the mean translocation time can substantially decrease with increasing mixing probability PAB—the probability that A and B segments occur next to each other in the polymer sequence. After PAB reaches 0.5 the mean translocation time reaches a plateau and does not change considerably further. In ref. 234 a dimensionless Péclet number was introduced, 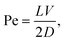 where L is the length of the copolymer, V is the average translocation speed, and D is the diffusivity. It was shown that this Péclet number completely characterises the translocation dynamics. The scaling exponent α of the translocation time as function of the chain length, τ ∼ Lα was found to decrease from 2 for vanishing Péclet number and asymptotically tends to unity for high Péclet number. In contrast, an increase of the effective binding energy leads to a growth of α from 1 to 2.
where L is the length of the copolymer, V is the average translocation speed, and D is the diffusivity. It was shown that this Péclet number completely characterises the translocation dynamics. The scaling exponent α of the translocation time as function of the chain length, τ ∼ Lα was found to decrease from 2 for vanishing Péclet number and asymptotically tends to unity for high Péclet number. In contrast, an increase of the effective binding energy leads to a growth of α from 1 to 2.
If one additionally takes into account that a chaperone increases the viscous frictional force of the chain once it binds, the increase in the volume fraction of the chaperones and the binding energy do not always lead to smaller translocation times, which was shown by 2D Langevin simulations for stiff chains.235 The initial decrease of the mean translocation time later turned to a weak growth. Thus, there should be an optimal concentration and binding affinity of chaperones during the translocation. The same effects were shown to hold for flexible chains.236
X. Summary
The field of (bio)polymer translocation started with much fanfare, heralding that sequencing of polynucleotides (DNA, RNA) or proteins were within reach. Despite the fact that most papers on translocation start with the technological vision of sequencing, this goal still has not been achieved. However, considerable progress in the field of translocation has been accomplished in experiments, simulations, and theory. Part of this development is witnessed in the large number of papers devoted to the field of translocation that we compiled here.On the experimental side, massive progress has been attained. Thus, starting from the original α-hemolysin pores much more complex and controllable pore types in well characterised membranes have been engineered. Additionally considerable knowledge has been accumulated on the various effects of system parameters such as charge effects, details of the driving force, or interactions of the translocating chains with the pore.
Theoretically and especially by extensive simulations it could be shown that the polymer translocation process—even in the limit of long translocating chains—is not characterised by few, universal scaling laws. Instead, certain details may strongly influence the specific translocation dynamics. While for the aesthetic mind of a theorist this is dissatisfactory, for potential technological applications this is not necessarily bad news. Indeed, the specificity of the process may enable a higher sensitivity and better ways of fine-tuning. In future textbooks of polymer physics surely polymer translocation will find its place.
Concurrently, the cacophony of different scaling theories leading to a rich multitude of scaling exponents such as α and δ for the typical translocation time τ ≃ Nα/fδ of a polymer containing N monomers and in the presence of a driving force f appears to converge to some unifying theories. These more recently developed approaches provide good explanations for the diversity of power laws obtained both in analytical theories and simulations. In particular, it is being acknowledged that in many if not most cases the translocation process is out of equilibrium. Whether the quantification of translocation in terms of the mean time τ is sufficient, or whether the knowledge of the entire distribution of translocation times is necessary, will depend on the details of the exact setup and will be one of the topics to be studied more concretely in the future.
Another contribution to the non-universal character of polymer translocation comes from the specific sequence of the chain-to-be-translocated. Thus, apart from the very sequence itself the local persistence may change along the chain, different local charge densities may occur, and the chain interacts specifically with ambient charges as well as with the pore and membrane surface. Again, it is to be expected that the resulting effects will be interesting, and potentially made good use of in future translocation assays.
There exists, however, an imbalance in the degree of theoretical understanding between forced and unforced translocation. Forced translocation is by now pretty well understood concerning both the scaling exponents themselves and the slow convergence to asymptotic scaling. Unforced translocation, as was shown in recent work,75,79,142 within error bars is consistent with a range of theoretical models. We believe that unforced translocation is indeed a major remaining challenge for theoretical modelling of polymer translocation. Due to the lack of a full understanding of unforced translocation, even statements concerning a continuous crossover from forced to unforced translocation need to be taken with a major grain of salt.
Other remaining challenges include hydrodynamic interactions: to what degree do they modify the results obtained in simulations and theory without taking them into consideration? What does it mean quantitatively that in the asymptotic limit they should not influence the scaling, is this limit reached for any reasonable simulations or experiments? How realistic is the pore-centred driving force? Could results be changed in realistic fields, especially due to the non-equilibrium character of the process? What about chain heterogeneities in the sense of sequence, knots, or hairpins in long and realistic chains with a finite persistence length? Finally, how can various types of interactions be included more realistically, such as intrachain interactions, counterions of various valency, or chain-pore interactions?
Ultimately, only improvements in experiments will help resolving all questions. While simulations as well as theories with their concrete predictions are indispensable, it is not clear whether they take into account all necessary features of the process. For experimentalists this is a challenge, as for a proper comparison between both worlds, chains with some 105 statistical units need to be studied. This is certainly hard to achieve in experiments, but may be resolved with the advances in the pore construction and the overall experimental setup of membranes and pores.
It will be interesting to see to what extent the original expectations of the technological possibilities of the translocation process will be achieved when we look back ten years from now.
Acknowledgements
VVP acknowledges financial support from Deutsche Forschungsgemeinschaft (Project number PA 2042/1-1). RM acknowledges financial support from the Academy of Finland (FiDiPro scheme). TAN acknowledges partial support by the Academy of Finland through its COMP Center of Excellence grant no. 251748.References
- W. H. Coulter, Means for counting particles suspended in a fluid, US pat. 2656508, 1953.
- R. W. DeBlois and C. P. Bean, Rev. Sci. Instrum., 1970, 41, 909 CrossRef.
- S. M. Bezrukov, I. Vodyanoy and V. A. Parsegian, Nature, 1994, 370, 279–281 CrossRef CAS PubMed.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Proc. Natl. Acad. Sci. U. S. A., 1996, 94, 13770–13773 CrossRef.
- L.-Q. Gu, O. Braha, S. Conlan, S. Cheley and H. Bayley, Nature, 1999, 398, 686–690 CrossRef CAS PubMed.
- S. M. Bezrukov, J. Membr. Biol., 2000, 174, 1–13 CrossRef CAS PubMed.
- J. W. F. Robertson, C. G. Rodrigues, V. M. Stanford, K. A. Rubinson, O. V. Krasilnikov and J. J. Kasianowicz, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8207–8211 CrossRef CAS PubMed.
- X. Kang, S. Cheley, X. Guan and H. Bayley, J. Am. Chem. Soc., 2006, 128, 10684–10685 CrossRef CAS PubMed.
- C. C. Striemer, T. R. Gaborski, J. L. McGrath and P. M. Fauchet, Nature, 2007, 445, 749–753 CrossRef CAS PubMed.
- A. J. Wolfe, M. Mohammad, S. Cheley, H. Bayley and L. Movileanu, J. Am. Chem. Soc., 2007, 129, 14034–14041 CrossRef CAS PubMed.
- L.-Q. Gu, M. Wanunu, M. X. Wang, L. McReynolds and Y. Wang, Expert Rev. Mol. Diagn., 2012, 12, 573–584 CrossRef CAS PubMed.
- D. Branton, et al. , Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS PubMed.
- R. F. Service, The Race for the $1000 Genome , Science, 311, 1544–1546 Search PubMed.
- E. A. Manrao, I. M. Derrington, A. H. Laszlo, K. W. Langford, M. K. Hopper, N. Gillgren, M. Pavlenok, M. Niederweis and J. H. Gundlach, Nat. Biotechnol., 2012, 30, 349–353 CrossRef CAS PubMed.
- M. Wanunu, Phys. Life Rev., 2012, 9, 125–158 CrossRef PubMed.
- B. M. Venkatesan and R. Bashir, Nat. Nanotechnol., 2011, 6, 615–624 CrossRef CAS PubMed.
- C. Dekker, Nat. Nanotechnol., 2007, 2, 209–215 CrossRef CAS PubMed.
- A. Meller, J. Phys.: Condens. Matter, 2003, 15, R581–R607 CrossRef CAS.
- L. Movileanu, Soft Matter, 2008, 4, 925–931 RSC.
- L. Movileanu, Trends Biotechnol., 2009, 27, 333–341 CrossRef CAS PubMed.
- S. Majd, E. C. Yusko, Y. N. Billeh, M. X. Macrae, J. Yang and M. Mayer, Curr. Opin. Biotechnol., 2010, 21, 439–476 CrossRef CAS PubMed.
- U. F. Keyser, J. R. Soc., Interface, 2011, 8, 1369–1378 CrossRef CAS PubMed.
- A. Aksimentiev, Nanoscale, 2010, 2, 468–483 RSC.
- A. Milchev, J. Phys.: Condens. Matter, 2011, 23, 103101 CrossRef PubMed.
- D. Panja, G. T. Barkema and A. B. Kolomeisky, J. Phys.: Condens. Matter, 2013, 25, 413101 CrossRef PubMed.
- M. Muthukumar, Polymer Translocation, CRC Press, Boca Raton, Florida, 2011 Search PubMed.
- M. Gershow and J. A. Golovchenko, Nat. Nanotechnol., 2007, 2, 775–779 CrossRef CAS PubMed.
- C. Plesa, L. Cornelissen, M. W. Tuijtel and C. Dekker, Nanotechnology, 2013, 24, 475101 CrossRef PubMed.
- M. Mihovilovic, N. Hagerty and D. Stein, Phys. Rev. Lett., 2013, 110, 028102 CrossRef PubMed.
- A. Meller and D. Branton, Electrophoresis, 2002, 23, 2583–2591 CrossRef CAS PubMed.
- A. Aksimentiev and K. Schulten, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 4337–4338 CrossRef CAS PubMed.
- T. Z. Butler, M. Pavlenok, I. M. Derrington, M. Niederweis and J. H. Gundlach, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20647–20652 CrossRef CAS PubMed.
- A. Meller, L. Nivon and D. Branton, Phys. Rev. Lett., 2001, 86, 3435–3438 CrossRef CAS PubMed.
- B. M. Venkatesan, B. Dorvel, S. Yemenicioglu, N. Watkins, I. Petrov and R. Bashir, Adv. Mater., 2009, 21, 2771–2776 CrossRef CAS PubMed.
- M. Akeson, D. Branton, J. J. Kasianowicz, E. Brandin and D. W. Deamer, Biophys. J., 1999, 77, 3227–3233 CrossRef CAS PubMed.
- K. Singh and A. Sain, Europhys. Lett., 2013, 104, 18007 CrossRef.
- J. Mathé, A. Aksimentiev, D. R. Nelson, K. Schulten and A. Meller, Orientation discrimination of single-stranded DNA inside the α-hemolysin membrane channel, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12377–12382 CrossRef PubMed.
- I. M. Derrington, T. Z. Butler, M. D. Collins, E. Manrao, M. Pavlenok, M. Niederweis and J. H. Gundlach, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16060–16065 CrossRef PubMed.
- D. Wendell, P. Jing, J. Geng, V. Subramaniam, T. J. Lee, C. Montemagno and P. Guo, Nat. Nanotechnol., 2009, 4, 765–772 CrossRef CAS PubMed.
- A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, Nat. Mater., 2003, 2, 537–540 CrossRef CAS PubMed.
- S.-W. Nam, M. J. Rooks, K.-B. Kim and S. M. Rossnagel, Nano Lett., 2009, 9, 2044–2048 CrossRef CAS PubMed.
- B. McNally, A. Singer, Z. Yu, Y. Sun, Z. Weng and A. Meller, Nano Lett., 2010, 10, 2237–2244 CrossRef CAS PubMed.
- J. Li, D. Stein, C. McMullan, D. Branton, M. J. Aziz and J. A. Golovchenko, Nature, 2001, 412, 166–169 CrossRef CAS PubMed.
- J. B. Heng, C. Ho, T. Kim, R. Timp, A. Aksimentiev, Y. V. Grinkova, S. Sligar, K. Schulten and G. Timp, Biophys. J., 2004, 87, 2905–2911 CrossRef CAS PubMed.
- D. Krapf, M.-Y. Wu, R. M. M. Smeets, H. W. Zandbergen, C. Dekker and S. G. Lemay, Nano Lett., 2006, 6, 105–109 CrossRef CAS PubMed.
- H. W. Zandbergen, R. J. H. A. van Duuren, P. F. A. Alkemade, G. Lientschnig, O. Vasquez, C. Dekker and F. D. Tichelaar, Nano Lett., 2005, 5, 549–553 CrossRef CAS PubMed.
- B. M. Venkatesan, B. Dorve, S. Yemenicioglu, N. Watkins, I. Petrov and R. Bashir, Adv. Mater., 2009, 21, 2771–2776 CrossRef CAS PubMed.
- B. M. Venkatesan, A. E. Shah, J. M. Zuo and R. Bashir, Adv. Funct. Mater., 2010, 20, 1266–1275 CrossRef CAS PubMed.
- D. P. Hoogerheide, S. Garaj and J. A. Golovchenko, Phys. Rev. Lett., 2009, 102, 256804 CrossRef PubMed.
- S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190–193 CrossRef CAS PubMed.
- C. A. Merchant, K. Healy, M. Wanunu, V. Ray, N. Peterman, J. Bartel, M. D. Fischbein, K. Venta, Z. Luo, A. T. C. Johnson and M. Drndic, Nano Lett., 2010, 10, 2915–2921 CrossRef CAS PubMed.
- G. F. Schneider, S. W. Kowalczyk, V. E. Calado, G. Pandraud, H. W. Zandbergen, L. M. K. Vandersypen and C. Dekker, Nano Lett., 2010, 10, 3163–3167 CrossRef CAS PubMed.
- S. M. Iqbal, D. Akin and R. Bashir, Nat. Nanotechnol., 2007, 2, 243–248 CrossRef CAS PubMed.
- E. C. Yusko, J. M. Johnson, S. Majd, P. Prangkio, R. C. Rollings, J. Li, J. Yang and M. Mayer, Nat. Nanotechnol., 2011, 6, 253–260 CrossRef CAS PubMed.
- A. R. Hall, A. Scott, D. Rotem, K. K. Mehta, H. Bayley and C. Dekker, Nat. Nanotechnol., 2010, 5, 874–877 CrossRef CAS PubMed.
- H. Peng and X. S. Ling, Nanotechnology, 2009, 20, 185101 CrossRef PubMed.
- L. J. Steinbock, C. Otto, C. Chimerel, J. Gornall and U. F. Keyser, Nano Lett., 2010, 10, 2493–2497 CrossRef CAS PubMed.
- I. J. Steinbock, C. Otto, D. R. Skarstam, S. Jahn, C. Chimerel, J. I. Gornall and U. F. Keyser, J. Phys.: Condens. Matter, 2010, 22, 454113 CrossRef PubMed.
- A. Kuzuya and M. Komiyama, Nanoscale, 2009, 2, 310–322 RSC.
- B. Sacca and C. M. Niemeyer, Angew. Chem., Int. Ed., 2012, 51, 58–66 CrossRef CAS PubMed.
- N. A. W. Bell, C. R. Engst, M. Ablay, G. Divitini, C. Ducati, T. Liedl and U. F. Keyser, Nano Lett., 2012, 12, 512–517 CrossRef CAS PubMed.
- R. S. Wei, T. G. Martin, U. Rant and H. Dietz, Angew. Chem., Int. Ed., 2012, 51, 4864–4867 CrossRef CAS PubMed.
- A. Milchev, K. Binder and A. Bhattacharya, J. Chem. Phys., 2004, 121, 6042–6051 CrossRef CAS PubMed.
- M. Muthukumar, J. Chem. Phys., 2010, 132, 195101 CrossRef CAS PubMed.
- A. Y. Grosberg and Y. Rabin, J. Chem. Phys., 2010, 133, 165102 CrossRef PubMed.
- P. Rowghanian and A. Y. Grosberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042722 CrossRef.
- M. Wanunu, W. Morrison, Y. Rabin, A. Y. Grosberg and A. Meller, Nat. Nanotechnol., 2010, 5, 160–165 CrossRef CAS PubMed.
- M. M. Hatlo, D. Panja and R. van Roij, Phys. Rev. Lett., 2011, 107, 068101 CrossRef PubMed.
- W. Sung and P. J. Park, Phys. Rev. Lett., 1996, 77, 783–786 CrossRef CAS PubMed.
- M. Muthukumar, J. Chem. Phys., 1999, 111, 10371–10374 CrossRef CAS.
- J. Chuang, Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 65, 011802 CrossRef.
- R. Metzler and K. Luo, Eur. Phys. J.: Spec. Top., 2010, 189, 119–134 CrossRef CAS.
- P. J. Park and W. Sung, J. Chem. Phys., 1998, 108, 3013–3018 CrossRef CAS.
- A. Yu. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, New York, 1994 Search PubMed.
- K. Luo, T. Ala-Nissila and S. C. Ying, J. Chem. Phys., 2006, 124, 034714 CrossRef PubMed.
- J. K. Wolterink, G. T. Barkema and D. Panja, Phys. Rev. Lett., 2006, 96, 208301 CrossRef PubMed.
- I. Huopaniemi, K. Luo, T. Ala-Nissila and S.-C. Ying, J. Chem. Phys., 2006, 125, 124901 CrossRef PubMed.
- D. Wei, W. Wang, X. Jin and Q. Liao, J. Chem. Phys., 2007, 126, 204901 CrossRef PubMed.
- K. Luo, S. T. T. Ollila, I. Huopaniemi, T. Ala-Nissila, P. Pomorski, M. Karttunen, S.-C. Ying and A. Bhattacharya, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 050901(R) CrossRef.
- F. Mondaini and L. Moriconi, Phys. Lett. A, 2012, 376, 2903–2907 CrossRef CAS.
- D. Panja and G. T. Barkema, J. Chem. Phys., 2010, 132, 014902 CrossRef PubMed.
- J. L. A. Dubbeldam, A. Milchev, V. G. Rostiashvili and T. A. Vilgis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 010801 CrossRef CAS.
- D. Panja, G. T. Barkema and R. C. Ball, J. Phys.: Condens. Matter, 2007, 19, 432202 CrossRef.
- D. Panja, G. T. Barkema and R. C. Ball, J. Phys.: Condens. Matter, 2008, 20, 075101 CrossRef.
- V. V. Lehtola, R. P. Linna and K. Kaski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031803 CrossRef CAS.
- S. Guillouzic and G. W. Slater, Phys. Lett. A, 2006, 359, 261–264 CrossRef CAS.
- M. G. Gauthier and G. W. Slater, Eur. Phys. J. E, 2008, 25, 17–23 CrossRef CAS PubMed.
- F. Kapahnke, U. Schmidt, D. W. Heermann and M. Weiss, J. Chem. Phys., 2010, 132, 164904 CrossRef PubMed.
- H. W. de Haan and G. W. Slater, J. Chem. Phys., 2012, 136, 154903 CrossRef PubMed.
- R. Metzler and J. Klafter, Biophys. J., 2003, 85, 2776–2779 CrossRef CAS PubMed.
- R. Metzler, E. Barkai and J. Klafter, Phys. Rev. Lett., 1999, 82, 3563 CrossRef CAS.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- J. L. A. Dubbeldam, A. Milchev, V. G. Rostiashvili and T. A. Vilgis, Europhys. Lett., 2007, 79, 18002 CrossRef.
- R. C. Lua and A. Y. Grosberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061918 CrossRef.
- H. Vocks, D. Panja, G. T. Barkema and R. C. Ball, J. Phys.: Condens. Matter, 2008, 20, 095224 CrossRef.
- D. Panja and G. T. Barkema, Biophys. J., 2008, 94, 1630–1637 CrossRef CAS PubMed.
- D. Panja, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011803 CrossRef.
- L. A. Dubbeldam, A. Milchev, V. G. Rostiashvili and T. A. Vilgis, J. Phys.: Condens. Matter, 2009, 21, 098001 CrossRef PubMed.
- D. Panja, G. T. Barkema and R. C. Ball, J. Phys.: Condens. Matter, 2009, 21, 098002 CrossRef PubMed.
- Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061121 CrossRef.
- C. Chatelain, Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021129 CrossRef.
- A. Amitai, Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011107 CrossRef.
- J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed.
- J. M. Polson and A. C. M. McCaffrey, J. Chem. Phys., 2014, 140, 184904 CrossRef PubMed.
- D. Panja, J. Stat. Mech.: Theory Exp., 2010, L02001 Search PubMed.
- D. Panja, J. Stat. Mech.: Theory Exp., 2010, P06011 Search PubMed.
- J. L. A. Dubbeldam, V. G. Rostiashvili, A. Milchev and T. A. Vilgis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011802 CrossRef CAS.
- D. Panja, J. Phys.: Condens. Matter, 2011, 23, 105103 CrossRef PubMed.
- I. Goychuk, Adv. Chem. Phys., 2012, 150, 187 CrossRef CAS.
- J.-H. Jeon, H. Martinez-Seara Monne, M. Javanainen and R. Metzler, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed; G. R. Kneller, K. Baczynski and M. Pasienkewicz-Gierula, J. Chem. Phys., 2011, 135, 141105 CrossRef PubMed.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC; R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys. 10.1039/C4CP03465A.
- H. W. de Haan and G. W. Slater, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051802 CrossRef.
- H. W. de Haan and G. W. Slater, J. Chem. Phys., 2012, 136, 204902 CrossRef PubMed.
- M. G. Gauthier and G. W. Slater, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021802 CrossRef.
- J. M. Polson and A. C. M. McCaffrey, J. Chem. Phys., 2013, 138, 174902 CrossRef PubMed.
- C. Loerscher, T. Ala-Nissila and A. Bhattacharya, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011914 CrossRef.
- Y. Chen and K. Luo, J. Chem. Phys., 2013, 138, 204903 CrossRef PubMed.
- W.-P. Cao, L.-Z. Sun, C. Wang and M.-B. Luo, J. Chem. Phys., 2011, 135, 174901 CrossRef PubMed.
- A. Gopinathan and Y. W. Kim, Phys. Rev. Lett., 2007, 99, 228106 CrossRef PubMed.
- H. W. de Haan and G. Slater, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 020601(R) CrossRef.
- D. K. Lubensky and D. R. Nelson, Biophys. J., 1999, 77, 1824–1838 CrossRef CAS PubMed.
- E. Slonkina and A. B. Kolomeisky, J. Chem. Phys., 2003, 118, 7112–7118 CrossRef CAS.
- Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021806 CrossRef.
- K. Luo, I. Huopaniemi, T. Ala-Nissila and S.-C. Ying, J. Chem. Phys., 2006, 124, 114704 CrossRef PubMed.
- K. Luo, T. Ala-Nissila, S.-C. Ying and A. Bhattacharya, J. Chem. Phys., 2007, 126, 145101 CrossRef PubMed.
- M. G. Gauthier and G. W. Slater, J. Chem. Phys., 2008, 128, 065103 CrossRef PubMed.
- M. G. Gauthier and G. W. Slater, J. Chem. Phys., 2008, 128, 205103 CrossRef PubMed.
- K. Luo, T. Ala-Nissila, S.-C. Ying and R. Metzler, Europhys. Lett., 2009, 88, 68006 CrossRef.
- A. Yu. Grosberg, S. Nechaev, M. Tamm and O. Vasilyev, Phys. Rev. Lett., 2006, 96, 228105 CrossRef PubMed.
- A. Bhattacharya, W. H. Morrison, K. Luo, T. Ala-Nissila, S.-C. Ying, A. Milchev and K. Binder, Eur. Phys. J. E, 2009, 29, 423–429 CrossRef CAS PubMed.
- S.-S. Chern, A. E. Cárdenas and R. D. Coalson, J. Chem. Phys., 2001, 115, 7772–7782 CrossRef CAS.
- P. Tian and G. D. Smith, J. Chem. Phys., 2003, 119, 11475–11483 CrossRef CAS.
- A. Matsuyama, J. Chem. Phys., 2004, 121, 8098 CrossRef CAS PubMed.
- S. Tsuchiya and A. Matsuyama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011801 CrossRef.
- I. Huopaniemi, K. Luo, T. Ala-Nissila and S.-C. Ying, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061912 CrossRef.
- M. Fyta, S. Melchionna, S. Succi and E. Kaxiras, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036704 CrossRef.
- T. Saito and T. Sakaue, Eur. Phys. J. E, 2012, 35, 125 CrossRef CAS.
- T. Ikonen, A. Bhattacharya, T. Ala-Nissila and W. Sung, J. Chem. Phys., 2012, 137, 085101 CrossRef CAS PubMed.
- A. Izmitli, D. C. Schwartz, M. D. Graham and J. J. de Pablo, J. Chem. Phys., 2008, 128, 085102 CrossRef PubMed.
- A. J. Storm, C. Storm, J. Chen, H. Zandbergen, J.-F. Joanny and C. Dekker, Nano Lett., 2005, 5, 1193–1197 CrossRef CAS PubMed.
- V. V. Lehtola, R. P. Linna and K. Kaski, Europhys. Lett., 2009, 85, 58006 CrossRef.
- T. Ikonen, A. Bhattacharya, T. Ala-Nissila and W. Sung, Europhys. Lett., 2013, 103, 38001 CrossRef.
- T. Sakaue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 021803 CrossRef.
- T. Sakaue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041808 CrossRef.
- T. Saito and T. Sakaue, Eur. Phys. J. E, 2011, 34, 135 CrossRef PubMed.
- T. Saito and T. Sakaue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061803 CrossRef.
- E. A. Di Marzio, C. M. Guttman and J. D. Hoffman, Faraday Discuss. Chem. Soc., 1979, 68, 210 RSC.
- T. Ambjörnsson and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 030901(R) CrossRef.
- T. Ambjörnsson and R. Metzler, J. Phys.: Condens. Matter, 2005, 17, S1841 CrossRef.
- P. Rowghanian and A. Y. Grosberg, J. Phys. Chem. B, 2011, 115, 14127–14135 CrossRef CAS PubMed.
- L. A. Dubbeldam, V. G. Rostiashvili, A. Milchev and T. A. Vilgis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041801 CrossRef.
- T. Ikonen, A. Bhattacharya, T. Ala-Nissila and W. Sung, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051803 CrossRef CAS.
- V. V. Lehtola, R. P. Linna and K. Kaski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061803 CrossRef CAS.
- R. Adhikari and A. Bhattacharya, J. Chem. Phys., 2013, 138, 204909 CrossRef PubMed.
- K. Luo and R. Metzler, J. Chem. Phys., 2011, 134, 135102 CrossRef PubMed.
- K. Luo and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 021922 CrossRef.
- K. Luo and R. Metzler, J. Chem. Phys., 2010, 133, 075101 CrossRef PubMed.
- A. Bhattacharya, Polym. Sci., Ser. C, 2013, 55, 60–69 CrossRef CAS.
- Y. Kantor, Pramana, 2005, 64, 1011–1017 CrossRef CAS.
- A. Rosa, M. Di Ventra and C. Micheletti, Phys. Rev. Lett., 2012, 109, 118301 CrossRef CAS PubMed.
- J. Arsuaga, M. Vázquez, S. Triguieros, D. W. Sumners and J. Roca, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5373 CrossRef CAS PubMed.
- P. Sczymczak, Biochem. Soc. Trans., 2013, 41, 620 CrossRef PubMed.
- H. Peng and X. S. Ling, Nanotechnology, 2009, 20, 185101 CrossRef PubMed.
- S. T. T. Ollila, K. Luo, T. Ala-Nissila and S.-C. Ying, Eur. Phys. J. E, 2009, 28, 385–393 CrossRef CAS PubMed.
- P. Rowghanian and A. Y. Grosberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042723 CrossRef.
- F. Farahpour, A. Maleknejad, F. Varnik and M. R. Ejtehadi, Soft Matter 10.1039/c2sm27416g.
- B. Jeon and M. Muthukumar, J. Chem. Phys., 2014, 140, 015101 CrossRef PubMed.
- S. Ghosal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 71, 051903 Search PubMed.
- A. J. Storm, J. H. Chen, H. W. Zandbergen and C. Dekker, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051903 CrossRef CAS.
- S. Ghosal, Phys. Rev. Lett., 2007, 98, 238104 CrossRef PubMed.
- R. M. M. Smeets, U. F. Keyser, D. Krapf, M.-Y. Wu, N. H. Dekker and C. Dekker, Nano Lett., 2006, 6, 89–95 CrossRef CAS PubMed.
- B. Luan and A. Aksimentiev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021912 CrossRef.
- G. Oukhaled, L. Bacri, J. Mathé, J. Pelta and L. Auvray, Europhys. Lett., 2008, 82, 48003 CrossRef.
- L. Brun, M. Pastoriza-Gallego, G. Oukhaled, J. Mathé, L. Bacri, L. Auvray and J. Pelta, Phys. Rev. Lett., 2008, 100, 158302 CrossRef CAS PubMed.
- S. W. Kowalczyk, D. B. Wells, A. Aksimentiev and C. Dekker, Nano Lett., 2012, 12, 1038–1044 CrossRef CAS PubMed.
- L. Galla, A. J. Meyer, A. Spiering, A. Sischka, M. Mayer, A. R. Hall, P. Reimann and D. Anselmetti, Nano Lett., 2014, 14, 4176–4182 CrossRef CAS PubMed.
- S. Getfert, T. Töws and P. Reimann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062710 CrossRef.
- D. Jan Bonthuis, J. Zhang, B. Hornblower, J. Mathé, B. I. Shklovskii and A. Meller, Phys. Rev. Lett., 2006, 97, 128104 CrossRef.
- S. Kesselheim, M. Sega and C. Holm, Soft Matter, 2012, 8, 9480–9486 RSC.
- S. Buyukdagli and T. Ala-Nissila, J. Chem. Phys., 2014, 140, 064701 CrossRef PubMed.
- H. H. Katkar and M. Muthukumar, J. Chem. Phys., 2014, 140, 135102 CrossRef CAS PubMed.
- M. G. Gauthier and G. W. Slater, J. Chem. Phys., 2008, 128, 175103 CrossRef PubMed.
- K. Luo, T. Ala-Nissila, S.-C. Ying and A. Bhattacharya, Phys. Rev. Lett., 2008, 100, 058101 CrossRef PubMed.
- J. A. Cohen, A. Chaudhuri and R. Golestanian, Phys. Rev. X, 2012, 2, 021002 Search PubMed.
- S. Kotsev and A. B. Kolomeisky, J. Chem. Phys., 2006, 125, 084906 CrossRef PubMed.
- M. McCauley, R. Forties, U. Gerland and R. Bundschuh, Phys. Biol., 2009, 6, 036006 CrossRef PubMed.
- S. Schink, S. Renner, K. Alim, V. Arnaut, F. C. Simmel and U. Gerland, Biophys. J., 2012, 102, 85–95 CrossRef CAS PubMed.
- M. Muthukumar, Electrophoresis, 2002, 23, 1417–1420 CrossRef CAS PubMed.
- Y. Kafri, D. K. Lubensky and D. R. Nelson, Biophys. J., 2004, 86, 3373–3391 CrossRef CAS PubMed.
- H. W. de Haan and G. W. Slater, Phys. Rev. Lett., 2013, 110, 048101 CrossRef PubMed.
- U. Gerland, R. Bundschuh and T. Hwa, Phys. Biol., 2004, 1, 19–26 CrossRef CAS PubMed.
- R. Bundschuh and U. Gerland, Phys. Rev. Lett., 2005, 95, 208104 CrossRef PubMed.
- T. Ikonen, J. Shin, W. Sung and T. Ala-Nissila, J. Chem. Phys., 2012, 136, 205104 CrossRef PubMed.
- I. J. Molineux and D. Panja, Nat. Rev. Microbiol., 2013, 11, 194–204 CrossRef CAS PubMed.
- D. Panja and I. J.Molineux, Phys. Biol., 2010, 7, 045006 CrossRef PubMed.
- P. Grayson and I. J. Molineux, Curr. Opin. Microbiol., 2007, 10, 401–409 CrossRef CAS PubMed.
- K. Luo, R. Metzler, T. Ala-Nissila and S.-C. Ying, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021907 CrossRef.
- P. G. de Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca, NY, 1979 Search PubMed.
- A. Cacciuto and E. Luijten, Phys. Rev. Lett., 2006, 96, 238104 CrossRef PubMed.
- J. Shenga and K. Luo, Soft Matter, 2012, 8, 367–374 RSC.
- I. Ali, D. Marenduzzo and J. M. Yeomans, Phys. Rev. Lett., 2006, 96, 208102 CrossRef CAS PubMed.
- T. S. Baker, N. H. Olson and S. D. Fuller, Microbiol. Mol. Biol. Rev., 1999, 63, 862–922 CAS.
- R. P. Linna, J. E. Moisio, P. M. Suhonen and K. Kaski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052702 CrossRef CAS.
- D. Marenduzzo, C. Micheletti, E. Orlandini and D. W. Sumners, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20081–20086 CrossRef CAS PubMed.
- A. Evilevitch, L. Lavelle, C. M. Knobler, E. Raspaud and W. M. Gelbart, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 9292–9295 CrossRef CAS PubMed.
- A. Evilevitch, M. Castelnovo, C. M. Knobler and W. M. Gelbart, J. Phys. Chem. B, 2004, 108, 6838–6843 CrossRef CAS.
- M. Castelnovo and A. Evilevitch, Eur. Phys. J. E, 2007, 24, 9–18 CrossRef CAS PubMed.
- D. W. Bauer, J. B. Huffman, F. L. Homa and A. Evilevitch, J. Am. Chem. Soc., 2013, 135, 11216–11221 CrossRef CAS PubMed.
- M. Jeembaeva, M. Castelnovo, F. Larsson and A. Evilevitch, J. Mol. Biol., 2008, 381, 310–323 CrossRef CAS PubMed.
- K. Zhang and K. Luo, J. Chem. Phys., 2012, 136, 185103 CrossRef PubMed.
- K. Zhang and K. Luo, Soft Matter, 2013, 9, 2069–2075 RSC.
- D. E. Smith, S. J. Tans, S. B. Smith, S. Grimes, D. L. Anderson and C. Bustamante, Nature, 2001, 413, 748–752 CrossRef CAS PubMed.
- J. Kindt, S. Tzlil, A. Ben-Shaul and W. M. Gelbart, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 13671–13674 CrossRef CAS PubMed.
- S. Tzlil, J. Kindt, W. M. Gelbart and A. Ben-Shaul, Biophys. J., 2003, 84, 1616–1627 CrossRef CAS PubMed.
- P. K. Purohit, M. M. Inamdar, P. D. Grayson, T. M. Squires, J. Kondev and R. Phillips, Biophys. J., 2005, 88, 851–866 CrossRef CAS PubMed.
- A. S. Petrov, S. S. Douglas and S. C. Harvey, J. Phys.: Condens. Matter, 2013, 25, 115101 CrossRef PubMed.
- F. Brochard and P. G. de Gennes, J. Chem. Phys., 1977, 67, 52–56 CrossRef CAS.
- S. Daoudi and F. Brochard, Macromolecules, 1978, 11, 751–758 CrossRef CAS.
- T. Sakaue, E. Raphaël, P.-G. de Gennes and F. Brochard-Wyart, Europhys. Lett., 2005, 72, 83–88 CrossRef CAS.
- A. P. Markesteijn, O. Berk Usta, I. Ali, A. C. Balazs and J. M. Yeomans, Soft Matter, 2009, 5, 4575–4579 RSC.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular biology of the cell, Garland Science, New York, 2008 Search PubMed.
- S. M. Simon, C. S. Peskin and G. F. Oster, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 3770–3774 CrossRef CAS.
- K. E. S. Matlack, B. Misselwitz, K. Plath and T. A. Rapoport, Cell, 1999, 97, 553–564 CrossRef CAS PubMed.
- T. C. Elston, Biophys. J., 2000, 79, 2235–2251 CrossRef CAS PubMed.
- T. C. Elston, Biophys. J., 2002, 82, 1239–1253 CrossRef CAS PubMed.
- Z. Farkas, I. Derényi and T. Vicsek, J. Phys.: Condens. Matter, 2003, 15, S1767–S1777 CrossRef CAS.
- H. Salman, D. Zbaida, Y. Rabin, D. Chatenay and M. Elbaum, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7247–7252 CrossRef CAS PubMed.
- R. Zandi, D. Reguera, J. Rudnick and W. M. Gelbart, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8649–8653 CrossRef CAS PubMed.
- T. Ambjörnsson and R. Metzler, Phys. Biol., 2004, 1, 77–88 CrossRef PubMed.
- T. Ambjörnsson, M. A. Lomholt and R. Metzler, J. Phys.: Condens. Matter, 2005, 17, S3945–S3964 CrossRef PubMed.
- P. L. Krapivsky and K. Mallick, J. Stat. Mech.: Theory Exp., 2010, P07007 Search PubMed.
- R. H. Abdolvahab, F. Roshani, A. Nourmohammad, M. Sahimi and M. Reza Rahimi Tabar, J. Chem. Phys., 2008, 129, 235102 CrossRef CAS PubMed.
- R. H. Abdolvahab, M. R. Ejtehadi and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011902 CrossRef.
- R. H. Abdolvahab, R. Metzler and M. R. Ejtehadi, J. Chem. Phys., 2011, 135, 245102 CrossRef PubMed.
- W. Yu, Y. Ma and K. Luo, J. Chem. Phys., 2012, 137, 244905 CrossRef PubMed.
- W. Yu and K. Luo, J. Am. Chem. Soc., 2013, 133, 13565–13570 CrossRef PubMed.
Footnotes |
| † This problem as such can be rectified by introduction of a cutoff in the power-law distribution of immobilisation times used in the derivation of the fractional Fokker–Planck equation, see the discussion in ref. 103. |
| ‡ Note that we use the scaling exponent α for the dependence of τ on N for both unforced and forced translocation. Tables 1and 2 list the values of α for the respective cases. |
| § It should, however, be stressed that the concept of Debye screening is delicate here, as the system is not in equilibrium and there flows an electric current through the electrolyte. |
| This journal is © The Royal Society of Chemistry 2014 |