Open Access Article
Open Access ArticleMolecular versus macroscopic perspective on the demixing transition of aqueous PNIPAM solutions by studying the dual character of the refractive index
Martine
Philipp
*a,
Ralitsa
Aleksandrova
b,
Ulrich
Müller
b,
Martin
Ostermeyer
c,
Roland
Sanctuary
b,
Peter
Müller-Buschbaum
a and
Jan K.
Krüger†
b
aTechnische Universität München, Physik-Department, Lehrstuhl für Funktionelle Materialien, James-Franck-Strasse 1, D-85748 Garching, Germany. E-mail: martine.philipp@tum.de; Tel: +49 89 289 12455
bUniversité du Luxembourg, Laboratoire de Physique des Matériaux, Campus Limpertsberg, 162A, avenue de la faïencerie, L-1511 Luxembourg, Luxembourg
cAnton Paar OptoTec GmbH, Albert-Einstein-Strasse 5, D-30926 Seelze-Letter, Germany
First published on 3rd July 2014
Abstract
The phase separation of aqueous poly(N-isopropyl acrylamide) (PNIPAM) solutions is known to strongly affect their volume expansion behaviour and the elastic moduli, as the latter are strongly coupled to the macroscopic order parameter. On the molecular scale, considerable changes in H-bonding and hydrophobic interactions, as well as in the structure govern the demixing process. However, the relationship between the molecular and macroscopic order parameters is unclear for such complex phase-separating solutions. We contribute to the clarification of this problem by relating optical to volumetric properties across the demixing transition of dilute to concentrated aqueous PNIPAM solutions. Far from the demixing temperature, the temperature dependence of the refractive index is predominantly determined by thermal expansion. In the course of phase separation, the refractive index is dominated by the anomalous behaviour of the specific refractivity, which reflects the spatio-temporally averaged changes in molecular interactions and the structural reorganization of the demixing solutions. Moreover, the presence of relaxation processes is studied by the complex expansion coefficient using the novel technique of temperature modulated optical refractometry.
A Introduction
Aqueous polymer solutions and gels might undergo phase separation upon heating.1–7 This phenomenon is denoted as a demixing transition, being of the lower critical solution temperature type (LCST). A classical and much-investigated polymer, possessing a particularly sharp LCST-type demixing transition in an aqueous environment, is poly(N-isopropyl acrylamide) (PNIPAM).5,8–15 The demixing transition of aqueous PNIPAM solutions typically spreads over a temperature range of a few °C above Tc ≈ 32 °C.1,2,16–19 The PNIPAM chains are enveloped by hydration layers in the homogeneous solution below the demixing temperature.9,10,13,20–29 The hydration number, which is the number of hydrated water molecules per NIPAM monomer, was estimated to be about 8 for concentrated PNIPAM solutions.24,25,28–30 The extent of the hydration shells might depend on the PNIPAM concentration of the solution. The phase separation results from important changes in the hydrogen bonds and hydrophobic interactions existing between the macromolecules and water molecules.20–23 Therefore a partial dehydration of the macromolecules accompanies the demixing process.21,28 Part of the amide groups of the PNIPAM side-chains are supposed to form still hydrogen bonds with water molecules, but not intra- or intermolecular hydrogen bonds with PNIPAM in the segregated state of the solution.20–23 Upon heating homogeneous PNIPAM solutions across Tc, the partially dehydrated macromolecules collapse and gel-like PNIPAM-rich agglomerates grow within the phase-separating solutions.8,31–37 The kinetics related to their growth typically occurs on the time scale of minutes to hours31,32,35,38–40 and depends much on the polymer concentration of the solution, the applied heating rate and the depth of the temperature jump above Tc.32,35,38,39 The attractive interactions between the emerging PNIPAM-rich clusters, as well as their elasticity, codetermine their finally achieved size and compactness.The difference in polymer concentration within a phase-separating solution is considered as being the macroscopic order parameter of the LCST-type demixing transition.2,11,41 The specific volume ν(T) is a related quantity, which distinctly increases above the demixing temperature of PNIPAM solutions.9,10,24,28 Positive excess volumes are observed for the phase separation of PNIPAM solutions. As the intrinsic volume of the macromolecules is expected to remain constant during demixing,9,10,24,28 the excess volumes of phase-separating solutions are mainly attributed to the water molecules, which are expelled from the hydration shells of PNIPAM. The volume expansion coefficient α(T) = ν(T)−1 × ∂ν(T)/∂T is the macroscopic order parameter susceptibility, being particularly sensitive to the LCST-type demixing transition.
A frequently applied experimental technique to determine the demixing temperature of phase-separating polymer solutions is turbidimetry.1,2,10,42,43 The cloud point determined with such a technique can be attributed to the onset of opaqueness of a segregating solution. Its opaqueness is due to quasi-static fluctuations of the refractive index, which exist in the range of a few 100 nm, and lead to strong elastic scattering of light. These optical heterogeneities stem from the differences in refractive index that exist between the polymer-rich clusters and their water-rich environment. Hence, turbidimetry clearly demonstrates how sensitive optical refraction techniques are to the phase separation of thermo-responsive polymer solutions. In turn, Abbe refractometry can help to gain deeper insight into the evolution of the refractive index versus temperature during the early stages of the demixing process.36 The quantitative evaluation of the refractive index of the phase-separating solution is indeed possible as long as the solution behaves homogeneous on the probed length scale of a few 100 nm.
It is known since long ago that the refractive index and the specific volume are closely related to each other.44–47 This is due to the fact that the refractive index basically probes the number density of electronic dipoles present in matter. The Lorentz–Lorenz relationship is frequently used to describe this relationship between the specific volume and the refractive index, where the specific refractivity is introduced in order to account for the molecular polarisabilities.44–47 The refractive index hence possesses a dual nature: on the one hand it is related to the specific volume, which is a macroscopic quantity, and on the other hand to molecular bond polarisabilities, as represented by the specific refractivity. For many materials within a given phase the specific refractivity is almost constant in dependence of temperature or pressure.44–47 However, it can be expected to strongly vary in a material undergoing phase separation, as the bond polarisabilities are then changed considerably.
Combining studies of refractive indices and specific volumes in the present work, we provide valuable insight into the microscopic and macroscopic order parameters of the LCST-type demixing transition covering a large concentration range of dilute to concentrated PNIPAM solutions. The specific volume, being closely related to the macroscopic order parameter, visibly reflects the macroscopic cooperativity of the transition phenomenon.11,28 We investigate how far the cooperativity of this demixing transition is already established at the molecular level. This is indirectly studied by probing the specific refractivity, which is highly sensitive to the changes in the structure and intermolecular interactions existing within phase-separating PNIPAM solutions. Moreover, the existence of relaxation processes, probed by the complex expansion coefficient, and of low frequency order parameter fluctuations is investigated by using a novel type of refractometry, namely temperature modulated optical refractometry (TMOR).
B Experimental
B.1 Sample preparation
Poly(N-isopropylacrylamide) (PNIPAM) was purchased from Sigma-Aldrich Chemie GmbH, Taufkirchen, Germany. The number average molecular weight of this PNIPAM homopolymer is equal to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–25
000–25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1. This corresponds to a degree of polymerization of about 200. Distilled water was used for preparing dilute to concentrated aqueous PNIPAM solutions with concentrations varying from 0.3 to 30 mass%. For each PNIPAM concentration at least 4 ml of solution were prepared, which was sufficient for investigating its mass density and refractive index. The studied PNIPAM concentrations of all solutions lie below the critical concentration.
000 g mol−1. This corresponds to a degree of polymerization of about 200. Distilled water was used for preparing dilute to concentrated aqueous PNIPAM solutions with concentrations varying from 0.3 to 30 mass%. For each PNIPAM concentration at least 4 ml of solution were prepared, which was sufficient for investigating its mass density and refractive index. The studied PNIPAM concentrations of all solutions lie below the critical concentration.
B.2 Refractometry and temperature modulated optical refractometry
The refractive indices of pure water and the aqueous PNIPAM solutions were measured between 20 and 40 °C using the high precision, computer-controlled Abbe refractometer Abbemat from Anton Paar OptoTech GmbH, Seelze, Germany. This type of refractometer exactly determines the limit of total reflection of a divergent light beam impinging from the prism onto the sample.36,48 Monochromatic light with a vacuum wavelength of 589 nm (sodium D-line) is used. The refractometer possesses the high absolute accuracy of 2 × 10−5 and a relative accuracy of 10−6. The temperature accuracy at the position of the sample is better than 10−2 °C.The Abbemat refractometer does not only offer the possibility of linear temperature rates. In analogy to temperature modulated differential scanning calorimetry (TMDSC),49 the temperature of the sample can also be perturbed in a sinusoidal manner in the case of Abbemat refractometers. For this novel experimental technique called temperature modulated optical refractometry (TMOR),48 low frequency dynamics of the refractive index and thus of the volume expansion coefficient, induced by the perturbation of temperature, are accessible. TMOR is thus able to provide an alternative view on molecular relaxations, since it couples to fluctuations of the electrical polarization, instead to fluctuations of entropy as TMDSC does. Note that these discussed loss processes are not related to the absorption of light by the sample, but due to low-frequency relaxation processes induced by the temperature perturbation lying in the mHz frequency range.
The temperature of the sample Tω(t), which is modulated in a sinusoidal manner at an average temperature of Tav, can be expressed as:
Tω(t) = Tav(t) + AT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt), sin(ωt), | (1) |
|n*D,ω(t)| = nD,av(t) + |∂n*D,ω/∂T|AT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt − Φ), sin(ωt − Φ), | (2) |
| |∂n*D,ω/∂T| = An,ω/AT, | (3) |
Abbe refractometers are in principle highly sensitive to the adsorption and sedimentation of PNIPAM-rich agglomerates on the sapphire prism of the refractometer in the phase-separating solutions. This is due to the fact that Abbe refractometry is a surface-sensitive technique, where the probed sample volume (of a few 100 nm thickness) lies next to the prism.36 In order to avoid sedimentation of PNIPAM-rich agglomerates onto the prism of the Abbemat, it was placed upside down for all investigations. According to our investigations, the adsorption of PNIPAM molecules on the prism increases with the polymer concentration of the solution, for identical heating rates. Only reliable datasets are shown, which are not falsified by elastic light scattering and adsorption of PNIPAM on the prism. The refractive index values are only given for the initial stage of demixing, for which the phase-separating solution still behaves homogeneously on the probed length scale of a few 100 nm.
B.3 Dilatometry
The evolution of specific volume versus temperature was investigated for the aqueous PNIPAM solutions and pure water using a DMA 5000 M dilatometer from Anton Paar, Austria. The measurement principle relies on the determination of the resonance frequency of an oscillating glass tube filled with sample, which depends on the latter's specific volume. The dilatometer provides the accuracy of 5 × 10−6 g cm−3 within the used range of mass densities. A temperature accuracy of 0.01 °C is guaranteed by means of a built-in Peltier thermostat. Dilatometry is less sensitive to adsorption and sedimentation phenomena compared to refractometry since the specific volume is determined for the whole sample volume.C Theoretical background
C.1 The dual character of the refractive index
The electric field of visible light interacts with the dipoles of matter through electronic polarization and atomic polarization. This means that on the one hand, the refractive index is co-determined by the number density of electronic dipoles present in matter. On the other hand, the molecular polarisability, the local arrangement and the interactions between dipoles (being relevant at optical frequencies) contribute to the refractive index. Different theoretical approaches exist in order to describe this dual character of the refractive index of macroscopically isotropic samples (see e.g.ref. 44–47 and 51). Generally these theories relate the refractive index to the specific volume and a phenomenological quantity, which is called the specific refractivity r. The specific volume is a purely macroscopic property of condensed matter. On the contrary, the specific refractivity reflects molecular properties, like molecular polarisability, the local arrangement and the interactions between dipoles.44–47,51 All of the proposed models include considerable approximations concerning the local dielectric environment of a considered molecule, which in turn yields that these models are generally only correct within a margin of error of a few percent.44–47,51 Lorentz and Lorenz used a mean field approximation in order to calculate the local electric field acting on a molecule placed within a dielectric continuum.45,47 The resulting Lorentz–Lorenz relationship relates the refractive index nD (D stands for the sodium D line of 589 nm) to the specific volume ν, according to:| (nD2 − 1)/(nD2 + 2) = r/ν. | (4) |
If the refractive index and the specific volume are determined under the same conditions by independent experimental techniques, then the specific refractivity r can be calculated using eqn (4). However, the restrictive assumptions needed to derive the Lorentz–Lorenz relationship imply that the applicability of this relationship to phase-separating PNIPAM solutions is not at all trivial.
The quasi-static thermo-optical coefficient ∂nD/∂T can be derived from the Lorentz–Lorenz relationship, according to:
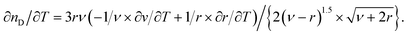 | (5) |
If the relative changes with respect to the temperature of the specific refractivity are small as compared to those of the specific volume ν, the volume expansion coefficient α can be deduced from eqn (5), according to:
| α(T) = −6nD(T)/{[nD2(T) + 2][nD2(T) − 1]} × ∂nD(T)/∂T. | (6) |
Note that in contrast to the Lorentz–Lorenz relationship, this relationship between the volume expansion coefficient and the thermo-optical coefficient does not depend on the specific refractivity.
C.2 TMOR and the complex volume expansion coefficient
As explained in Section B.2, TMOR allows for calculating the complex refractive index, being the dynamical response of the sample to a sinusoidal perturbation of its temperature. The complex volume expansion coefficient can be extracted from the thermo-optical coefficient determined by TMOR, by combining eqn (2), (3) and (6):48| |α*ω(T)| = |∂n*D,ω(T)/∂T| × {−6nD,av/[(nD,av2 + 2)(nD,av2 − 1)]}. | (7) |
A prerequisite of eqn (7) is that the temperature dependence of the specific refractivity is negligible in comparison to that of the specific volume. This condition is verified for many materials, but is expected to break down close to phase transitions. Since the TMOR technique can be performed with small amplitudes AT, being considerably smaller than 1 °C, the almost constancy of the specific refractivity can be realized in many cases.
Knowing the amplitude of the refractive index response An,ω and the phase angle Φ between the temperature signal Tω(t) and the complex refractive index, the real and imaginary parts of the complex volume expansion coefficient can be deduced from eqn (7), according to:
| α′ω(T) = |α*ω(T)|cos(Φ) | (8) |
| α′′ω(T) = |α*ω(T)|sin(Φ). | (9) |
Eqn (8) and (9) permit us to identify thermo-optical and mechanical relaxation processes, which are provoked by the perturbation of the temperature of the sample. In the case that such relaxation processes are absent, i.e. α′′ω(T) = 0 and that the Lorentz–Lorenz relationship is applicable, then the real part of the complex volume expansion coefficient α′ω(T) is equal to the static volume expansion coefficient (as measured independently by dilatometry).
D Results and discussion
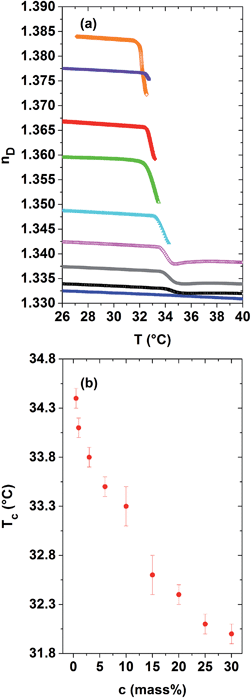
As discussed in Section C.1, the refractive index is related to the quotient of the specific refractivity and the specific volume, r/ν, where the specific refractivity depends amongst others on molecular bond polarisabilities. The aim of this article is to investigate the relevance of both contributions for phase-separating PNIPAM solutions in a wide concentration range. The evolution of their refractive indices and specific volumes versus temperature was measured across Tc by two independent techniques, namely Abbe refractometry and dilatometry. The related curves are displayed in Fig. 1 and 2 for dilute to concentrated aqueous PNIPAM solutions, possessing PNIPAM concentrations ranging from 1 to 30 mass%. The related values are also shown for distilled water as a reference. As depicted in Fig. 1(a), the refractive index of the solutions increases with the PNIPAM concentration for a given temperature within the homogeneous low temperature phase. A qualitative explanation of this observation is that the refractive index of the pure, amorphous polymer (1.495) is at room temperature considerably higher than that of water (1.333). However, a simple linear mixing rule utilizing the properties of bulk water and the amorphous PNIPAM fully neglects the presence of any hydration shell water, which envelops the PNIPAM molecules and might act as a third component. For a given PNIPAM solution the refractive index nD(T) shows an almost kink-like behaviour at the demixing temperature. This kink becomes progressively pronounced in dependence of the PNIPAM concentration. Representing the demixing temperatures versus PNIPAM concentration leads to the LCST-type demixing phase diagram shown in Fig. 1(b). In agreement with our findings, the LCST of aqueous PNIPAM homopolymer solutions is expected to lie at about 40 mass%.1,40,42,43As depicted in Fig. 1(a), for dilute to semi-dilute PNIPAM solutions with PNIPAM concentrations of maximal 6 mass%, the evolution of the refractive index can be exactly probed until 40 °C. Within a temperature range of a few °C above Tc, a minimum of the refractive index is observed. In agreement with our studies of the longitudinal elastic modulus,34–36 the macroscopic order parameter saturates in this temperature range. In the established high-temperature phase, the refractive index shows again its usual, positive temperature dependence. For PNIPAM concentrations above 6 mass%, the refractive index could only be quantified in a reliable manner for a temperature range with a limited width of about 1 or 1.5 °C above Tc. At higher temperatures, the data evaluation might be significantly affected by adsorption of PNIPAM on the prism. Another reason for inaccurate data evaluation in this range of temperature and PNIPAM concentration is the elastic scattering of the incident light by the optical heterogeneities within the rather concentrated phase-separating PNIPAM solutions. The latter effect becomes relevant as soon as the PNIPAM-rich agglomerates have grown larger in diameter than a few 100 nm, so that the solution behaves heterogeneous on the length scale probed by the refractometer.34–36
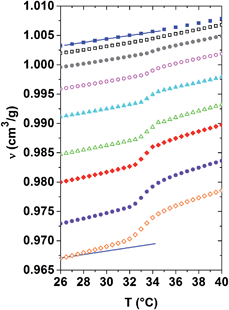
Using dilatometry, the evolution of the specific volume versus temperature ν(T) is probed across the demixing transition for the same dilute to concentrated aqueous PNIPAM solutions. As shown in Fig. 2, the higher the PNIPAM concentration of a given homogeneous solution, the lower its specific volume. Neglecting the presence of hydration shells enveloping the PNIPAM molecules below Tc, this effect can be explained in a qualitative manner by the higher mass density of PNIPAM as compared to that of water. As indicated by the two parallel straight lines next to the datasets of distilled water and the 30 mass% solution in Fig. 2, the slope of the ν(T)-curves increases with the polymer concentration deep within both phases. It follows from these curves that the volume expansion coefficient increases as a function of PNIPAM concentration. In general, the volume expansion coefficient probes the anharmonicity of the spatio-temporally averaged molecular interaction potentials of an isotropic solution, and as such permits quantifying the nonlinear behaviour of matter. It follows from the above that within both phases the anharmonicity of the average molecular interaction potential increases with the PNIPAM concentration of the solutions.
The ν(T)-curves of all PNIPAM solutions increase steeper in the range of the demixing transition, spreading typically over a temperature range of 3 °C above Tc, than in the homogeneous phase. As the total number of molecules is also conserved during these dilatometric investigations, the indicated ν(T)-values correspond to spatial averages over the PNIPAM-rich and the PNIPAM-poor phases in the demixing solutions. Obviously, on average the molecules are packed in a denser way in the demixed state than in the homogenous phase of a given PNIPAM solution. The changes in volume observed during phase separation are actually not attributed to variations of the intrinsic volume of the macromolecules. Indeed, they can be related to changes in the specific volume of the water molecules, which are expelled from the hydration shells during phase separation. The significantly nonlinear increase of the specific volume at Tc corresponds to positive excess volumes, which strongly increase with the PNIPAM concentration of the solution.28 These excess volumes are related to the temperature evolution of the order parameter.
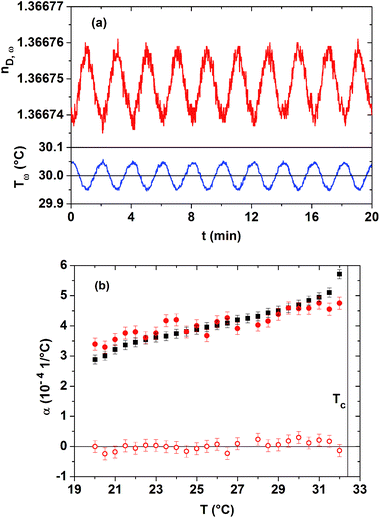
The presence of kinetic processes and of low frequency fluctuations of the macroscopic order parameter is studied within the homogeneous phase of the 20 mass% PNIPAM solution. Employing the novel technique of TMOR, we can moreover verify the applicability of the Lorentz–Lorenz relationship. A step-wise temperature increase with step widths of 0.5 °C between 20 and 32 °C is used. After each step-wise temperature change, the temperature of the sample is modulated in a sinusoidal manner using the absolutely small amplitude of 0.05 °C and a period of 2 min. A corresponding temperature profile is displayed in the bottom panel of Fig. 3(a), with the average temperature lying at 30.00 °C. Only due to the high resolution of the used refractometer, a time-dependent, almost sinusoidal response of the refractive index of the PNIPAM solution can be resolved for such a low amplitude temperature modulation. As shown in the top panel of Fig. 3(a), the amplitude of this sinusoidal nD(t)-response is about 1 × 10−5, so that the statistical data scatter lies close to the resolution limit of the instrument. Since the average refractive index is constant over time at each temperature plateau, we conclude that no measurable kinetic processes are present within the homogeneous low temperature phase close to Tc. This result is in agreement with the literature, where major kinetic processes are only discussed for the phase separation process above Tc. Moreover, also slow fluctuations of the order parameter cannot be discriminated on time scales of 20 min.
Furthermore, the sinusoidal perturbation of the temperature of the sample permits probing the dynamics of the complex volume expansion coefficient present at an excitation frequency of 9 mHz. As explained in Section C, a prerequisite for doing so is that the Lorentz–Lorenz relationship is applicable and that the specific refractivity of the sample shows no significant dependence on temperature. The real and imaginary parts of α*ω(T), extracted from the TMOR investigations, are given in Fig. 3(b). The statistical relevance of α*ω(T)-datasets increases with the number of temperature modulations at constant Tav, i.e. with the time employed for recording each α*ω(T)-data point. Due to this fact, the determination of complex expansion coefficients is highly impeded by kinetic processes that occur for the phase-separating PNIPAM solution above Tc.
Since according to Fig. 3(b) the imaginary part α′′ω(T) is equal to zero within the margin of error, no thermo-mechanical dissipation processes are excited at mHz frequencies in the low temperature phase of the 20 mass% PNIPAM solution. As in addition the real part of the volume expansion coefficient α′ω(T) coincides with the classical, static volume expansion coefficient (extracted from dilatometry, see Fig. 2) within the margin of error, the Lorentz–Lorenz relationship is applicable within the low temperature phase of the aqueous PNIPAM solution. There exists no reason why the Lorentz–Lorenz relationship should break down above Tc, as long as the electrodynamic theory for homogeneous systems can be applied at the used optical wavelength. This observation confirms that the specific refractivities can be safely estimated by employing the Lorentz–Lorenz relationship to the independently determined nD(T)- and ν(T)-datasets of the PNIPAM solutions.
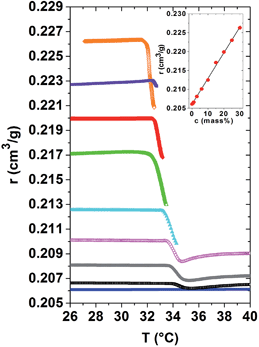
A central question of this article is how the local and macroscopic cooperativity of the demixing transition develops above Tc. As the specific refractivity reflects molecular optical properties, they are calculated for a large concentration range, using the datasets of the refractive indices and the specific volumes given in Fig. 1(a) and 2. The respective specific refractivity curves are provided in Fig. 4. Within the homogeneous low temperature phase, the specific refractivity is almost constant for a given PNIPAM concentration. This observation was already indirectly proven for the PNIPAM solution of 20 mass%, for which the volume expansion coefficients determined by TMOR and dilatometry perfectly coincide. The increase of the specific refractivity, determined at 30 °C, i.e. below Tc, in dependence of the PNIPAM concentration of the aqueous solutions is quantified in the inset of Fig. 4. Obviously, r(c) increases almost linearly from 0.205 to 0.225 for pure water to the most concentrated PNIPAM solution. One might wonder whether due to quantitative or qualitative arguments, the difference between hydrated and bulk water molecules does not significantly affect the r(c)-relationship.
At the demixing transition, the specific refractivity r(T) first steeply decreases in a kink-like manner for all PNIPAM solutions. This clearly shows that the partial dehydration and the accompanying structural reorganization highly affect the evolution of the specific refractivity. Obviously, the bond polarisabilities are highly affected by demixing. The dehydration process probably starts already slightly, but in a measurable manner, in the homogeneous low temperature phase when the quality of the solvent passes from good to bad.24 It might be that the related changes of the specific refractivity are too small in order to be resolved in our experiments.
For the dilute and semi-dilute solutions, the specific refractivity could be calculated from the low temperature phase, through the order parameter-modified range until the demixed high temperature phase. It turns out that the specific refractivity strongly couples to the order parameter of the demixing transition and shows an anomalous behaviour (i.e. influenced by the saturating order parameter) within a temperature range of a few °C above Tc. As soon as the specific refractivity turns again towards constancy, the phase separated high temperature state is established. This temperature behaviour of the specific refractivity just above Tc suggests that pronounced instabilities of the hydrogen bonds and the structure are at its origin. According to Fig. 4 the constant specific refractivities within the established high temperature phase of the 1 to 6 mass% samples are clearly smaller than that of their low temperature phase. As the total number of molecules is conserved during the demixing process this result suggests that the specific refractivity is also sensitive to the modification in the structure and interactions provoked by the demixing transition.
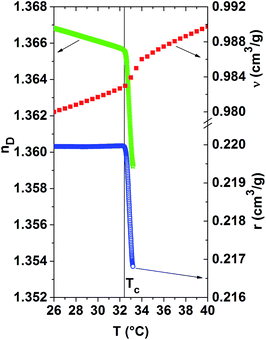
Fig. 5 compares the temperature evolution of the refractive index, the specific refractivity and the specific volume for the 20 mass% PNIPAM solution. This overview shows that the demixing temperature Tc, determined from the position of the kinks of the r(T)-curves and nD(T)-curves, coincide well for this solution. This actually holds also true for the other PNIPAM solutions. In order to assess how much each quantity is affected by the phase separation, their relative changes are calculated in the temperature range between Tc and Tc + 0.8 °C. Remarkably, the relative change of the specific refractivity is largest, namely it amounts to −1.5%. The relative decrease of the refractive index is equal to −0.5%, whereas that of the specific volume is only −0.1%. Thus, the specific refractivity is modified more than ten times stronger than the specific volume by this so-called ‘volume phase transition’.11 As a consequence, local morphological changes, as probed by the specific refractivity, are much more affected by the collapse and partial dehydration of the PNIPAM molecules and their aggregation than the excess volume.
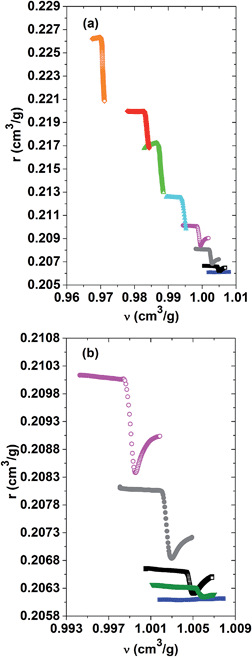
A better understanding of the role of the specific refractivity and the specific volume in the phase separation process can be gained by representing one versus the other for the different PNIPAM solutions. An overview of the r(ν)-relationship for the whole range of investigated PNIPAM concentrations is given in Fig. 6(a). A zoom on the datasets for the dilute to semi-dilute concentrations, for which the refractive indices could be determined across the whole range of the phase separation, is shown in Fig. 6(b). It turns out that the specific refractivity does almost not vary with the specific volume, far away from the demixing transition in the low and high temperature phase. Thus, the change in the refractive index as a function of temperature is almost fully determined by the thermal expansion behaviour, but not due to variations in the structure and interactions. This observation shows in particular that the slight dehydration of the PNIPAM chains accompanying the changeover from a good to a bad solvent when approaching the demixing transition does not affect much the r(ν)-relationship, whereas the subsequent dehydration during the ongoing phase separation does. As depicted in Fig. 6(b), within a narrow range, the specific refractivity first strongly decreases versus the specific volume, before increasing until converging to a similar slope to that observed within the low temperature phase. The unexpected finding that the specific refractivity is more affected by the phase separation than the specific volume gets more pronounced for higher PNIPAM concentrations of the solution. The effect of cooperativity is hence already present on the molecular scale, as expressed by the spatially averaged molecular polarisability probed by the specific refractivity. It is however beyond the scope of the current study to determine what the exact nature of the microscopic order parameters of the LCST-type demixing transition is.
E Conclusion
The evolution of the specific volume and the refractive index was measured independently versus temperature across the LCST-type demixing transition of dilute to concentrated aqueous PNIPAM solutions. Taking advantage of the dual character of the refractive index, the aim of this study is to provide deeper insight into the temperature evolution of the molecular order parameter in comparison to that of the macroscopic one. Whereas the specific volume is known to be strongly related to the macroscopic order parameter, we show for the first time that the molecular order parameter intensely couples to the specific refractivity. Even though we cannot assess the exact nature of the molecular order parameter, it turns out that it is strongly reflected by the spatio-temporally averaged molecular bond polarisabilities, as visualized by the specific refractivity. Far from the demixing temperature, the temperature dependence of the refractive index is indeed dominated by the thermal expansion behaviour of the solutions. In the transition range however, the thermal volume expansion and the specific refractivity interchange their dominance, which demonstrates the eminent role of the changed hydrogen bonding interactions and the ongoing structural reorganization on microscopic and mesoscopic length scales. For the phase-separating 20 mass% PNIPAM solution, the relative change of the specific refractivity is even about seven times stronger than that of the specific volume in the same temperature range. These results provide first insight into the different role played by cooperativity on the molecular and macroscopic scales in the LCST-type demixing transition of PNIPAM solutions.Acknowledgements
We thank O. Astasheva for technical support and C. M. Papadakis for fruitful discussions. M.P. thanks the Fonds National de la Recherche (Luxembourg) for receipt of a Marie Curie co-funded AFR Postdoc grant (FP7-Cofund AFR-PDR 2010-2, 1036107). P.M.-B. acknowledges financial support from the Deutsche Forschungsgemeinschaft DFG, priority program SPP1259 ‘Intelligente Hydrogele’ (grant MU1487/8).Notes and references
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Chem., 1968, 2, 1441–1455 CrossRef CAS.
- V. Aseyev, H. Tenhu and F. M. Winnik, Self Organized Nanostructures of Amphiphilic Block Copolymers II, Adv. Polym. Sci., 2011, 242, 29–89 CrossRef CAS.
- G. Romeo, A. Fernandez-Nieves, H. M. Wyss, D. Acierno and D. A. Weitz, Adv. Mater., 2010, 22, 3441 CrossRef CAS PubMed.
- M. Shibayama, M. Morimoto and S. Nomura, Macromolecules, 1994, 27, 5060–5066 CrossRef CAS.
- F. Tanaka, T. Koga and F. M. Winnik, Prog. Colloid Polym. Sci., 2009, 136, 1–7 CAS.
- Y. Li and T. Tanaka, J. Chem. Phys., 1990, 92, 1365–1371 CrossRef CAS PubMed.
- T. Tanaka, S. T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798 CrossRef CAS.
- A. Meier-Koll, V. Pipich, P. Busch, C. M. Papadakis and P. Müller-Buschbaum, Langmuir, 2012, 28, 8791–8798 CrossRef CAS PubMed.
- P. Kujawa, F. Segui, S. Shaban, C. Diab, Y. Okada, F. Tanaka and F. M. Winnik, Macromolecules, 2006, 39, 341–348 CrossRef CAS.
- P. Kujawa and F. M. Winnik, Macromolecules, 2001, 34, 4130–4135 CrossRef CAS.
- S. Hirotsu, Phase Transitions, 1994, 47, 183–240 CrossRef CAS.
- Y. Satokawa, T. Shikata, F. Tanaka, X.-P. Qiu and F. M. Winnik, Macromolecules, 2009, 42, 1400–1403 CrossRef CAS.
- F. Tanaka, T. Koga, H. Kojima and F. M. Winnik, Macromolecules, 2009, 42, 1321–1330 CrossRef CAS.
- X.-P. Qiu, F. Tanaka and F. M. Winnik, Macromolecules, 2007, 40, 7069–7071 CrossRef CAS.
- D. G. Shchukin, D. O. Grigoriev and H. Möhwald, Soft Matter, 2010, 6, 720–725 RSC.
- J. K. Cho, Z. Meng, L. A. Lyon and V. Breedveld, Soft Matter, 2009, 5, 3599–3602 RSC.
- Y. Liu, Z. Li and D. Liang, Soft Matter, 2012, 8, 4517–4523 RSC.
- O. Boissière, D. Han, L. Tremblay and Y. Zhao, Soft Matter, 2011, 7, 9410–9415 RSC.
- M. A. Molina, C. R. Rivarola, M. F. Broglia, D. F. Acevedo and C. A. Barbero, Soft Matter, 2012, 8, 307–310 RSC.
- B. Sun, Y. Lin, P. Wu and H. W. Siesler, Macromolecules, 2008, 41, 1512–1520 CrossRef CAS.
- Y. Maeda, T. Higuchi and I. Ikeda, Langmuir, 2000, 16, 7503–7509 CrossRef CAS.
- Y. Katsumoto, T. Tanaka, H. Sato and Y. Ozaki, J. Phys. Chem. A, 2002, 106, 3429–3435 CrossRef CAS.
- Y. Katsumoto, T. Tanaka, K. Ihara, M. Koyama and Y. Ozaki, J. Phys. Chem. B, 2007, 111, 12730–12737 CrossRef CAS PubMed.
- H. Kogure, S. Nanami, Y. Masuda, Y. Toyama and K. Kubota, Colloid Polym. Sci., 2005, 283, 1163–1171 CAS.
- Y. Ono and T. Shikata, J. Phys. Chem. B, 2007, 111, 1511–1513 CrossRef CAS PubMed.
- H. Kojima and F. Tanaka, Macromolecules, 2010, 43, 5103–5113 CrossRef CAS.
- Y. Okada and F. Tanaka, Macromolecules, 2005, 38, 4465–4471 CrossRef CAS.
- M. Philipp, K. Kyriakos, L. Silvi, W. Lohstroh, W. Petry, J. K. Krüger, C. M. Papadakis and P. Müller-Buschbaum, J. Phys. Chem. B, 2014, 118, 4253–4260 CrossRef CAS PubMed.
- Y. Ono and T. Shikata, J. Am. Chem. Soc., 2006, 128, 10030–10031 CrossRef CAS PubMed.
- M. Fuellbrandt, E. Ermilova, A. Asadujjaman, R. Hoelzel, F. F. Bier, R. von Klitzing and A. Schoenhals, J. Phys. Chem. B, 2014, 118, 3750–3759 CrossRef CAS PubMed.
- J. Adelsberger, A. Meier-Koll, A. M. Bivigou-Koumba, P. Busch, O. Holderer, T. Hellweg, A. Laschewsky, P. Müller-Buschbaum and C. M. Papadakis, Colloid Polym. Sci., 2011, 289, 711–720 CAS.
- J. Adelsberger, E. Metwalli, A. Diethert, I. Grillo, A. M. Bivigou-Koumba, A. Laschewsky, P. Müller-Buschbaum and C. M. Papadakis, Macromol. Rapid Commun., 2012, 33, 254–259 CrossRef CAS PubMed.
- J. Adelsberger, A. Kulkarni, A. Jain, W. Wang, A. M. Bivigou-Koumba, P. Busch, V. Pipich, O. Holderer, T. Hellweg, A. Laschewsky, P. Müller-Buschbaum and C. M. Papadakis, Macromolecules, 2010, 43, 2490–2501 CrossRef CAS.
- M. Philipp, U. Müller, R. Aleksandrova, R. Sanctuary, P. Müller-Buschbaum and J. K. Krüger, Soft Matter, 2013, 9, 5034–5041 RSC.
- M. Philipp, U. Müller, R. J. Jiménez Riobóo, R. Sanctuary, P. Müller-Buschbaum and J. K. Krüger, Soft Matter, 2013, 9, 9887–9896 RSC.
- M. Philipp, U. Müller, R. Aleksandrova, R. Sanctuary, P. Müller-Buschbaum and J. K. Krüger, Soft Matter, 2012, 8, 11387–11395 RSC.
- T. Hellweg, C. D. Dewhurst, W. Eimer and K. Kratz, Langmuir, 2004, 20, 4330–4335 CrossRef CAS.
- A. Zaccone, J. J. Crassous and M. Ballauff, J. Chem. Phys., 2013, 138, 104908 CrossRef PubMed.
- A. Zaccone, J. J. Crassous, B. Beri and M. Ballauff, Phys. Rev. Lett., 2011, 107, 168303 CrossRef.
- K. Van Durme, G. Van Assche and B. Van Mele, Macromolecules, 2004, 37, 9596–9605 CrossRef CAS.
- S. Hirotsu, I. Yamamoto, A. Matsuo, T. Okajima, H. Furukawa and T. Yamamoto, J. Phys. Soc. Jpn., 1995, 64, 2898–2907 CrossRef CAS.
- F. Afroze, E. Nies and H. Berghmans, J. Mol. Struct., 2000, 554, 55–68 CrossRef CAS.
- X. Zhou, J. Li, C. Wu and B. Zheng, Macromol. Rapid Commun., 2008, 29, 1363–1367 CrossRef CAS PubMed.
- R. Francesconi and S. Ottani, J. Mol. Liq., 2007, 133, 125–133 CrossRef CAS PubMed.
- H. A. Lorentz, Wied. Ann. Phys., 1880, 9, 641–665 CrossRef PubMed.
- B. J. Hoenders, Proceedings of Light-Activated Tissue Regeneration and Therapy Conference, 2008, vol. 12, pp. 297–305 Search PubMed.
- L. V. Lorenz, Wied. Ann. Phys., 1880, 11, 70–103 CrossRef PubMed.
- U. Müller, M. Philipp, M. Thomassey, R. Sanctuary and J. K. Krüger, Thermochim. Acta, 2013, 555, 17–22 CrossRef PubMed.
- M. Reading, A. Luget and R. Wilson, Thermochim. Acta, 1994, 238, 295–307 CrossRef CAS.
- J. K. Krüger, P. Alnot, J. Baller, R. Bactavatchalou, S. Dorosz, M. Henkel, M. Kolle, S. P. Krüger, U. Müller, M. Philipp, W. Possart, R. Sanctuary and C. Vergnat, in Ageing and the Glass Transition, Springer, 2007 Search PubMed.
- R. K. Krishnaswamy and J. Janzen, Polym. Test., 2005, 24, 762–765 CrossRef CAS PubMed.
Footnote |
| † Present address: Universität des Saarlandes, Werkstoffwissenschaften, Lehrstuhl für Adhäsion und Interphasen in Polymeren, D-66041 Saarbrücken. |
| This journal is © The Royal Society of Chemistry 2014 |