Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Disclination lines at homogeneous and heterogeneous colloids immersed in a chiral liquid crystal
Michael
Melle
a,
Sergej
Schlotthauer
*a,
Carol K.
Hall
b,
Enrique
Diaz-Herrera
c and
Martin
Schoen
ab
aStranski-Laboratorium für Physikalische und Theoretische Chemie, Fakultät für Mathematik und Naturwissenschaften, Technische Universität Berlin, Straße des 17. Juni 135, 10623 Berlin, Germany. E-mail: martin.schoen@tu-berlin.de
bDepartment of Chemical and Biomolecular Engineering, North Carolina State University, Engineering Building I, Box 7905, 911 Partners Way, Raleigh, NC 27695, USA
cDepartamento de Física, Universidad Autónoma Metropolitana-Iztapalapa, Iztapalapa, Mexico
First published on 4th June 2014
Abstract
In the present work we perform Monte Carlo simulations in the isothermal-isobaric ensemble to study defect topologies formed in a cholesteric liquid crystal due to the presence of a spherical colloidal particle. Topological defects arise because of the competition between anchoring at the colloidal surface and the local director. We consider homogeneous colloids with either local homeotropic or planar anchoring to validate our model by comparison with earlier lattice Boltzmann studies. Furthermore, we perform simulations of a colloid in a twisted nematic cell and discuss the difference between induced and intrinsic chirality on the formation of topological defects. We present a simple geometrical argument capable of describing the complex three-dimensional topology of disclination lines evolving near the surface of the colloid. The presence of a Janus colloid in a cholesteric host fluid reveals a rich variety of defect structures. Using the Frank free energy we analyze these defects quantitatively indicating a preferred orientation of the Janus colloid relative to the cholesteric helix.
1 Introduction
It is well-known that liquid-crystal molecules (mesogens) in the nematic phase exhibit no long-range positional order of their centers-of-mass but tend to align their longer axes parallel to a preferred direction specified by the global director![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0.1 If a colloid is immersed in such a homogeneously ordered nematic phase the order is perturbed locally. This is because mesogens in the vicinity of the colloid's surface may orient themselves in such a way that their orientation is in contradiction with
0.1 If a colloid is immersed in such a homogeneously ordered nematic phase the order is perturbed locally. This is because mesogens in the vicinity of the colloid's surface may orient themselves in such a way that their orientation is in contradiction with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0.2 As a consequence of the competition between
0.2 As a consequence of the competition between ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 and the local orientation of mesogens near the surface of a colloid, defects arise in the liquid-crystal host phase. The history of dispersed colloidal particles in ordered liquid-crystalline host fluids started in the late 1990's and is still an active field of research.2–6
0 and the local orientation of mesogens near the surface of a colloid, defects arise in the liquid-crystal host phase. The history of dispersed colloidal particles in ordered liquid-crystalline host fluids started in the late 1990's and is still an active field of research.2–6
Depending on the specific preparation of the colloid the preferred local orientation of mesogens may be either parallel or perpendicular with respect to the colloid's surface normal. These specific ways of orienting mesogens can be realized, for example, by varying the chemical composition of the colloid's surface.7
If more than a single colloidal particle is suspended in the liquid-crystal host phase, their specific defect topologies interact if the separation of the colloids is small enough. This gives rise to an effective interaction between the colloids which may be repulsive or attractive, such that in the latter case specifically structured assemblies can be formed.8 For example, if a chemically homogeneous spherical colloid with locally homeotropic surface anchoring (i.e., anchoring of mesogens parallel with respect to the colloid's local surface normal) is placed in a nematic host phase the well known Saturn ring defect topology forms around the colloid's equator.6 If two such colloids come sufficiently close, the defect lines interact and can entangle the colloidal dimer in several ways.9,10
One may measure these effective intercolloidal forces by trapping them in a certain configuration with optical tweezers which can then be used to move the colloids through the host fluid in a controlled manner.11 More recently, optical tweezers have also been used for reconnecting defects of already linked colloids to achieve a more stable configuration.12 Furthermore, optical tweezers are important tools for analyzing complex defect structures.13 The possibility of formation and controlled manipulation of these structures eventually allows one to fabricate novel ordered arrangements of an assembly of colloidal particles which already opened a wide range of applications in optics and photonics.14
Originally, most research in the field was focused on spherical colloids suspended in nematic liquid crystals but in today's research there is no limit regarding the colloid's shape. These shapes range, for example, from rod-like and polygonal shapes to star- or ring-like structures.8 Nowadays, also inhomogeneous, so-called Janus colloids, or, more generally speaking, patchy colloids are beginning to receive an increasing amount of scientific attention.7,15–18 This is primarily because recent advances in chemical synthesis allow one to prepare inhomogeneous colloids in a controlled fashion even down to particle sizes in the nanometer range.19 Generally speaking, the surface of a Janus colloid is composed of antithetic materials. For example, one may envision a spherical Janus colloid where mesogens are anchored in a locally planar fashion at one hemisphere whereas the anchoring may be locally homeotropic at the other. Clearly, more complex defect topologies are expected if such a Janus colloid is immersed in a nematic host phase.15,16
The complexity of the colloidal suspension may be further enhanced by replacing the nematic host phase by another ordered but structurally more sophisticated one. An interesting candidate in this respect is the cholesteric phase forming if the mesogens are chiral. The cholesteric phase may be thought of as a nematic phase in which the director becomes local and rotates continuously around a distinguished axis. Hence, the director forms a helix characterized by the pitch p which is the distance to be travelled along the preferred axis if the director field rotates by an angle of 2π.
Consequently, to characterize order in the cholesteric phase requires ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 to be replaced by
0 to be replaced by ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) if we take the z-axis as that axis around which the helix evolves. It is then clear that in the cholesteric phase
0(z) if we take the z-axis as that axis around which the helix evolves. It is then clear that in the cholesteric phase ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z)·êz = 0 where êz is a unit vector pointing in the z-direction. Hence, in planes orthogonal to êz the cholesteric phase may be perceived as a stacked sequence of two-dimensional nematics where
0(z)·êz = 0 where êz is a unit vector pointing in the z-direction. Hence, in planes orthogonal to êz the cholesteric phase may be perceived as a stacked sequence of two-dimensional nematics where ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) is rotated in the x–y plane between neighboring nematic planes.
0(z) is rotated in the x–y plane between neighboring nematic planes.
If a colloid is now immersed in such a cholesteric host phase it has been demonstrated20,21 that the ratio of pitch and colloidal size influences the formation of defect structures. Hence, compared with the nematic phase, where defect topologies are usually independent of the colloid's size, the ratio of p and the colloidal size enters as a new parameter in the formation of defect topologies in the cholesteric phase. Hence, more complex topologies are anticipated in a liquid-crystal host phase composed of chiral mesogens. This is even more so if two or more colloids are suspended in a cholesteric host phase. Because of the inherent twist of the cholesteric helix the defect lines have even more possibilities to entangle the colloids.12,13
To obtain a theoretical understanding of defect topologies associated with placing a single, chemically homogeneous colloid in a cholesteric host phase, a chiral version of Landau-de Gennes theory1 has been employed in a few cases.13,20–22 As far as computer simulations of a colloid suspended in a cholesteric phase are concerned, no study exists to date to the best of our knowledge. The reason is perhaps twofold. First, because p is generally quite large, fairly large systems need to be employed in molecular simulations which can quickly render such simulations computationally prohibitive. Second, most standard models for liquid crystals composed of chiral mesogens are rather costly from a computational perspective because of pronounced shape anisotropy of the mesogens. For example, Memmer et al.23 suggested an interaction potential for a pair of chiral Gay-Berne molecules. They could only study fairly small systems comprising a few hundred to a few thousand molecules which casts some doubt on the significance of the results obtained for the cholesteric24 and even more so for the much richer structures characteristic of blue phases.23
In contrast, we have recently demonstrated25 that large systems of up to 4 × 104 chiral mesogens can be studied at moderate computational expense if one employs mesogens with a much smaller aspect ratio of about 1.30.25 Our model consists of a chiral version of the (achiral) Hess–Su potential26 which has been shown to describe nematic liquid crystals sufficiently realistically.26–31 In the achiral Hess–Su model a pair of mesogens interact via a Lennard-Jones potential where the strength of the attraction depends on the orientation of the mesogens. Because the chiral version of this model reproduces cholesteric and even blue phases unambiguously25 we feel that it is timely to apply it to investigate defect topologies arising if a colloid is immersed in a cholesteric phase. Our work is based upon Monte Carlo (MC) simulations in the isothermal-isobaric ensemble.
We organized our manuscript as follows. In Section. 2 we introduce our model system. Section 3 is given to key theoretical quantities and to a presentation of our results which we discuss in the concluding Section. 4.
2 Model system
2.1 The liquid-crystal host phase
In this work we consider a liquid-crystal host phase in which a colloidal particle is immersed. The liquid crystal is composed of N mesogens interacting with each other in a pairwise additive fashion. The interactions are described by the fluid-fluid (ff) potential function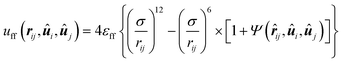 | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij = rij/rij. Unit vectors ûi and ûj specify the orientations of mesogens i and j in space. Hence, uff is a Lennard-Jones potential where the attractive term has been modified to account for different orientations of the mesogens. Accordingly, σ is the “diameter” of a spherical reference molecule and εff is the depth of the attractive well.
ij = rij/rij. Unit vectors ûi and ûj specify the orientations of mesogens i and j in space. Hence, uff is a Lennard-Jones potential where the attractive term has been modified to account for different orientations of the mesogens. Accordingly, σ is the “diameter” of a spherical reference molecule and εff is the depth of the attractive well.
As in our previous work25 we take the anisotropy function to be given by
Ψ(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij,ûi,ûj) = 5ε1P2(ûi·ûj) + 5ε2[P2( ij,ûi,ûj) = 5ε1P2(ûi·ûj) + 5ε2[P2(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij·ûi) + P2( ij·ûi) + P2(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij·ûj)] + ε3[(ûi × ûj)· ij·ûj)] + ε3[(ûi × ûj)·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij](ûi·ûj) ij](ûi·ûj) | (2) |
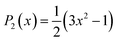 is the second Legendre polynomial. Terms proportional to ε1 and ε2 arise from an expansion of the orientation dependence of the interaction between two achiral mesogens in terms of rotational invariants.32,33 The pseudo-scalar proportional to ε3 accounts for the chirality of the interaction between a pair of mesogens where the degree of chirality is controlled by the magnitude of ε3 and the handedness by its sign. The achiral version of the interaction potential was originally suggested by Hess and Su26 whereas the introduction of chirality by a pseudo-scalar follows in spirit an earlier suggestion by Memmer et al. for a Gay-Berne-like model potential.23 Hence, the anisotropy function preserves the head-tail symmetry of the interaction between pairs of mesogens characteristic of many liquid-crystalline materials, that is the interaction potential in eqn (1) is invariant with respect to a change in sign of ûi and/or ûj.1
is the second Legendre polynomial. Terms proportional to ε1 and ε2 arise from an expansion of the orientation dependence of the interaction between two achiral mesogens in terms of rotational invariants.32,33 The pseudo-scalar proportional to ε3 accounts for the chirality of the interaction between a pair of mesogens where the degree of chirality is controlled by the magnitude of ε3 and the handedness by its sign. The achiral version of the interaction potential was originally suggested by Hess and Su26 whereas the introduction of chirality by a pseudo-scalar follows in spirit an earlier suggestion by Memmer et al. for a Gay-Berne-like model potential.23 Hence, the anisotropy function preserves the head-tail symmetry of the interaction between pairs of mesogens characteristic of many liquid-crystalline materials, that is the interaction potential in eqn (1) is invariant with respect to a change in sign of ûi and/or ûj.1
The model has already been demonstrated to be capable of reproducing properties of liquid crystals in a variety of contexts ranging from the formation of nematic phases27–30 to the development of defect topologies arising near the surface of spherical colloidal particles immersed in a nematic liquid-crystal host phase composed of achiral mesogens.16 In its chiral version, it has recently been shown to correctly reproduce cholesteric and blue phases.25
2.2 Homogeneous and Janus colloid
In this work the N mesogens interact with a colloidal particle via a Yukawa-like potential given by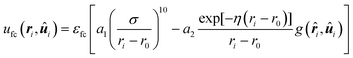 | (3) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i = ri/ri, r0 is the hard-core radius of the colloid, εfc determines the strength of the interaction, η−1 is the screening length of the attraction, and g is the anchoring function that we will discuss further below. Notice that because the colloid is centered at the origin of the coordinate system,
i = ri/ri, r0 is the hard-core radius of the colloid, εfc determines the strength of the interaction, η−1 is the screening length of the attraction, and g is the anchoring function that we will discuss further below. Notice that because the colloid is centered at the origin of the coordinate system, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i points from the center-of-mass of the colloid to the center-of-mass of mesogen i. Parameters
i points from the center-of-mass of the colloid to the center-of-mass of mesogen i. Parameters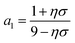 | (4a) |
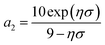 | (4b) |
 | (5) |
| ufc(rmin) = −εfc | (6) |
In this work we also focus on Janus colloids with surfaces composed of antithetic materials. In the present case the conflictive properties of the surface of a Janus colloid are different ways of anchoring a mesogen locally. Anchoring is described by the anchoring function 0 ≤ g ≤ 1 in eqn (3) which serves to discriminate energetically the desired (undesired) local orientation of a mesogen relative to the surface normal of the colloid.
More specifically, we take the anchoring function to be given as16
g(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i,ûi) = w∥( i,ûi) = w∥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i)g∥( i)g∥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i,ûi) + χw⊥( i,ûi) + χw⊥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i)g⊥( i)g⊥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i,ûi) i,ûi) | (7) |
The tendency to align homeotropically at flat surfaces with no specific surface anchoring is known for real liquid crystals34 as well as for model systems i.e. for Gay-Berne35 or Hess–Su29 mesogens. This effect can be explained by the strong side-side attraction of two mesogens and has also been observed for strongly curved surfaces.16 Beacuse of the shape anisotropy homeotropic alignment at a surface enables a higher areal density of mesogens. Because of the stronger side-side attraction this is also reduces the configurational potential energy compared with a planar arrangement of mesogens at the surface plane. Even though the latter would be entropically favored, the energatically favored homeotropic alignment apparently wins. In eqn (7),
g∥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i,ûi) = (1 − |ûi· i,ûi) = (1 − |ûi·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i|)2 i|)2 | (8a) |
g⊥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i,ûi) = (ûi· i,ûi) = (ûi·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i)2 i)2 | (8b) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i) whereas g⊥ serves to align mesogen i in a locally homeotropic fashion (i.e., parallel to
i) whereas g⊥ serves to align mesogen i in a locally homeotropic fashion (i.e., parallel to ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i).
i).
Associated with g‖ and g⊥ are weighting functions
w∥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i) = 1−γ∥(1 − i) = 1−γ∥(1 − ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i·êx)2 i·êx)2 | (9a) |
w⊥(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i) = 1 − γ⊥(1 + i) = 1 − γ⊥(1 + ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i·êx)2 i·êx)2 | (9b) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i·êx = +1 whereas w⊥ assumes its maximum at the colloid's South Pole where
i·êx = +1 whereas w⊥ assumes its maximum at the colloid's South Pole where ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) i·êx = −1. To be physically meaningful both weighting functions in eqn (9) have to be positive semidefinite which is guaranteed if γ‖,
i·êx = −1. To be physically meaningful both weighting functions in eqn (9) have to be positive semidefinite which is guaranteed if γ‖, 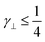 . Specific values of γ‖ and γ⊥ control the sharpness of the transition between the antithetic surface parts of the colloid.
. Specific values of γ‖ and γ⊥ control the sharpness of the transition between the antithetic surface parts of the colloid.
Notice also that our model is capable of describing a chemically homogeneous colloid where mesogens are aligned either parallel or homeotropically at each point on the colloid's surface. To that end one needs to set one of the two weighting functions in eqn (9) equal to one and the other one equal to zero depending on the desired anchoring scenario (see also Table 1).
| Defect topology | Anchoring | η | ε fc | γ ⊥ | γ || | χ |
|---|---|---|---|---|---|---|
| Boojum | Planar | 1.0 | 3.5 | 0.00 | 0.00 | 0.0 |
| Saturn ring | Homeotropic | 0.5 | 1.0 | 0.00 | 1.00 | 1.0 |
| Boojum ring | Planar/homeotropic | 0.5 | 4.0 | 0.05 | 0.25 | 0.6 |
2.3 Fixing the far-field directors
To study experimentally defect topologies evolving around colloidal particles in an ordered liquid-crystal host phase, it is customary to place the colloid and its host between solid substrates.36 Through a specific anchoring scenario at the substrates, this setup allows one to fix the (nonlocal) far-field director![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (k)0 in regions of the liquid crystal that are unperturbed by the presence of the colloid. Superscript k indicates that the far-field director at the lower substrate (k = 1) may differ from its counterpart at the upper substrate (k = 2).
(k)0 in regions of the liquid crystal that are unperturbed by the presence of the colloid. Superscript k indicates that the far-field director at the lower substrate (k = 1) may differ from its counterpart at the upper substrate (k = 2).
In the vicinity of the colloid, the mismatch between the local alignment at the colloid's surface and the alignment of mesogens at the solid substrates will generally give rise to a local director field ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) where
0(r) where ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) does not necessarily coincide with
0(r) does not necessarily coincide with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (k)0. Therefore, we follow the experimental setup in spirit and place our liquid-crystalline host phase plus the dissolved colloid between plane parallel, structureless solid surfaces separated along the z-axis by a distance sz. This distance is always chosen large enough so that a direct interaction with the colloid is precluded and such that in the cholesteric host phase a helix of a certain pitch can be realized based upon earlier experience (see below for specific values of sz employed here).25
(k)0. Therefore, we follow the experimental setup in spirit and place our liquid-crystalline host phase plus the dissolved colloid between plane parallel, structureless solid surfaces separated along the z-axis by a distance sz. This distance is always chosen large enough so that a direct interaction with the colloid is precluded and such that in the cholesteric host phase a helix of a certain pitch can be realized based upon earlier experience (see below for specific values of sz employed here).25
Henceforth, we assume the substrates to be located at z = −sz/2 (k = 1) and sz/2 (k = 2). The interaction between a mesogen and the substrate is described by the potential function
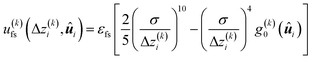 | (10) |
To fix the far-field directors in space we introduce the anchoring function
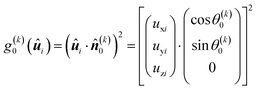 | (11) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (k)0 onto the x- and y-axes, respectively (see Section. 3.2 for specific choices of θ(k)0).
(k)0 onto the x- and y-axes, respectively (see Section. 3.2 for specific choices of θ(k)0).
Fixing the in-plane unidirectional alignment at the surface is a widely used operational technique in the experimental setup.6,13,22 For example, a thin layer of polyimide on flat glass substrates may be “rubbed unidirectionally to obtain an excellent planar alignment”.13 In this spirit we are following the experimental approach by anchoring the mesogens in the plane of the surfaces.
3 Results
3.1 Properties and numerical details
In this work we employ MC simulations carried out predominantly in a specialized isothermal-isobaric ensemble. As explained elsewhere16 in this ensemble the thermodynamic state of the liquid crystal is specified by N, volume szA, the ratio sx/sy (sα is the side length of the simulation cell in α-direction), and the transverse component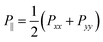 of the pressure tensor P where Pαα (α = x or y) is a diagonal element of P; off-diagonal elements of P vanish as we do not expose the liquid crystal to any shear strain. For fixed values of these variables we generate a distribution of configurations in the 5N-dimensional space spanned by the 3N Cartesian coordinates of the N centers of mass and the 2N orientations of the N linear mesogens. This distribution is proportional to exp[−β(U + P‖szA − Nβ−1
of the pressure tensor P where Pαα (α = x or y) is a diagonal element of P; off-diagonal elements of P vanish as we do not expose the liquid crystal to any shear strain. For fixed values of these variables we generate a distribution of configurations in the 5N-dimensional space spanned by the 3N Cartesian coordinates of the N centers of mass and the 2N orientations of the N linear mesogens. This distribution is proportional to exp[−β(U + P‖szA − Nβ−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A)] where β = 1/kBT (T denotes the temperature and kB is Boltzmann's constant) and A = sxsy.
A)] where β = 1/kBT (T denotes the temperature and kB is Boltzmann's constant) and A = sxsy.
Numerically, this distribution can be realized by employing a standard Metropolis algorithm adapted to the specialized isothermal-isobaric ensemble.37 This algorithm proceeds in a sequence of two steps. Initially, one of the N mesogens is picked sequentially and it is decided with equal probability whether to displace its center-of-mass or to rotate it around one of the three axes of the space-fixed Cartesian coordinate system. The specific axis is also picked randomly with equal probability for each of the axes. Once a displacement or a rotation has been attempted for all mesogens, one attempt is made to change the area A = sxsy. The sequence of N displacement or rotation attempts plus the one attempt to change A constitutes an MC cycle. Our results are typically based upon MC simulations employing 5.0 × 104 cycles for equilibration followed by 1.5–3.0 × 105 cycles during which ensemble averages are computed.
Throughout this work we use the customary dimensionless (i.e., “reduced”) units, that is lengths are given in units of σ, energy in units of εff, temperature in units of εff/kB, and pressure in units of εff/σ3. Based upon previous work16,25 we fix T = 0.95 and P‖ = 1.80 because under these thermodynamic conditions a Boojum and a Saturn ring defect topology is stable if a homogeneous colloid with respective planar and homeotropic surface anchoring is immersed in a nematic phase of the achiral version of our liquid crystal.16 Using instead a Janus colloid, a Boojum ring defect topology would form under the same thermodynamic conditions.16
Our systems typically accommodate 2 × 104 to 7 × 104 mesogens interacting with the various components of the model viaeqn (1), (3), and (10) where we set ε1 = −ε2/2 = 0.04 throughout this work. Under these conditions the liquid crystal is in the nematic phase if ε3 = 0.00 and in the cholesteric phase if ε3 = −0.10.25 These are the only values of the chirality parameter considered in this work unless otherwise stated.
In selecting this value of the coupling constant ε3 some caution is advisable. First, one wishes to make |ε3| as large as possible in order to minimize the pitch of the cholesteric phase. This is because we focus on a high ratio of the colloid's size to p. One could, of course, maximize the ratio d0/p (d0 = 2r0) by increasing the size of the colloid. However, this would not be sensible as it would require host phases comprising many more mesogens. Consequently, this would render the MC simulations computationally more demanding. Second, it is known38 and also observed in our simulations (not shown here) that in the presence of a colloid a transition to a blue phase is favored even before this transition occurs in the absence of the colloid, i.e. in a bulk liquid crystal.25 Hence, to avoid the transition, an upper threshold exists for |ε3| in our model which is slightly larger than the value chosen.
To ensure that effects caused by the presence of the colloidal particle vanish at the boundaries of the simulation cell we calculated the local density profile
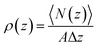 | (12) |
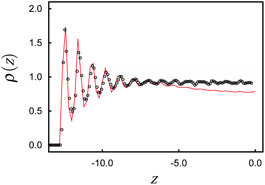 | ||
Fig. 1 Plot of the local density ρ(z) as a function of position z in the lower part (z ≤ 0) of our system; ( ) without and ( ) without and ( ) with a colloidal particle. ) with a colloidal particle. | ||
The key property analyzed in this work is the local director field ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) which we obtain as a numerical solution of the eigenvalue equation16,39
0(r) which we obtain as a numerical solution of the eigenvalue equation16,39
Q(r)![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (r) = λ(r) (r) = λ(r)![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (r) (r) | (13) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (r) and
(r) and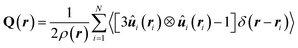 | (14) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 from the nonlocal analogues of eqn (13) and (14).
0 from the nonlocal analogues of eqn (13) and (14).
Topological defects, which are the main subject of this work are singularities of the local director field ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r). However, singularities in the mathematical sense cannot arise in practice but are instead signalled by finite regions of lower order. In the subsequent sections we are particularly interested in identifying such regions characterized by small values of λ+(r). To that end we discretize our simulation cell into small cubic boxes of side length δs = 0.3 and for all visualizations, mark a box with a blue dot if λ+(r) ≤ 0.25. Whereas the choice of this threshold is admittedly somewhat arbitrary, it turned out in practice to optimize the visibility of the rather complex three-dimensional variation of disclination lines.
0(r). However, singularities in the mathematical sense cannot arise in practice but are instead signalled by finite regions of lower order. In the subsequent sections we are particularly interested in identifying such regions characterized by small values of λ+(r). To that end we discretize our simulation cell into small cubic boxes of side length δs = 0.3 and for all visualizations, mark a box with a blue dot if λ+(r) ≤ 0.25. Whereas the choice of this threshold is admittedly somewhat arbitrary, it turned out in practice to optimize the visibility of the rather complex three-dimensional variation of disclination lines.
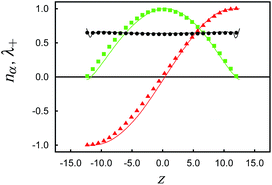
In the cholesteric phase the characteristic helix evolves along the z-axis as shown in Fig. 3. Fixing sz = 27, we obtain a stable helical structure comprising half a pitch in the z-direction of length p ≃ 50 as can be inferred from Fig. 2. Because of the excluded volume near the substrate sz − 2δz ≃ p/2 (see Fig. 1). The helix is stabilized through the anchoring of mesogens at the solid substrate where we choose θ(1)0 = θ(2)0 = 0° in eqn (11). The other case considered in this work is a system in which sz = 40 such that about three quarters of an unstrained full pitch are accommodated. In this case, θ(2)0 = 0° as before but θ(1)0 = 90°. Other parameters of our model system are summarized in Table 1.
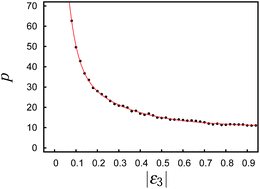 | ||
| Fig. 2 Pitch p as a function of the magnitude of the chiral coupling constant, |ε3|. The red line is intended to guide the eye. The transition from the cholesteric to the blue phase occurs at |ε3| = 0.2.25 | ||
At this stage it seams noteworthy that the cholesteric helix can withstand quite a substantial strain upon compressing or stretching it p/4. For example, in a system in which an unstrained helix of total length p would form this helix can be compressed all the way down to a total length of p/4 by reducing sz before the helix is destroyed. Destruction of the helix is signalled by a decay of λ+(z) to a value close to zero at z = 0 in the middle between the substrates. Were the helix still intact, λ+(z) would be constant across the pore at a relatively high value of about 0.4.
The problem with straining the cholesteric helix on account of an improperly chosen value of sz can in principle be avoided by replacing the monostable directional anchoring conditions (one easy axis) by degenerate planar conditions (infinitely many easy axes) so that ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (1)0 and
(1)0 and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (2)0 are free to adjust themselves in the x–y plane so as to remove the spurious strain. In this case an unstrained helix of a total length corresponding to some fraction of p can be accommodated irrespective of sz.
(2)0 are free to adjust themselves in the x–y plane so as to remove the spurious strain. In this case an unstrained helix of a total length corresponding to some fraction of p can be accommodated irrespective of sz.
However, in view of the Janus colloid, where the angle between its orientation and the direction of the local director field enters as a new parameter, the monostable directional anchoring of mesogens at both substrates is to be preferred over the degenerate planar one. This is because in the later case any orientation of ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (1)0 and
(1)0 and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (2)0 on the unit circle in the x–y plane is energetically permissible as long as the angle between
(2)0 on the unit circle in the x–y plane is energetically permissible as long as the angle between ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (1)0 and
(1)0 and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (2)0 remains fixed such that at any given sz an unstrained helix of constant length can be accommodated. Unfortunately, this way one loses control over the orientation of the local director field at the position of the Janus colloid.
(2)0 remains fixed such that at any given sz an unstrained helix of constant length can be accommodated. Unfortunately, this way one loses control over the orientation of the local director field at the position of the Janus colloid.
To ensure that the cholesteric order at the boundaries is not perturbed by the presence of the colloid we compute the local director field ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) as a function of z. Plots of the components nx(z) and ny(z) of
0(z) as a function of z. Plots of the components nx(z) and ny(z) of ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) and of the local nematic order parameter λ+(z) reveal that an unperturbed helix exists in the host phase (see Fig. 3). This helix is apparently affected only negligibly by the presence of the colloid at the simulation cell's boundaries as one concludes from Fig. 3.
0(z) and of the local nematic order parameter λ+(z) reveal that an unperturbed helix exists in the host phase (see Fig. 3). This helix is apparently affected only negligibly by the presence of the colloid at the simulation cell's boundaries as one concludes from Fig. 3.
With ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) from MC we also compute the Frank free energy as a quantitative measure of deformation of the local director field. In the one-constant approximation, the Frank free energy can be cast as41
0(r) from MC we also compute the Frank free energy as a quantitative measure of deformation of the local director field. In the one-constant approximation, the Frank free energy can be cast as41
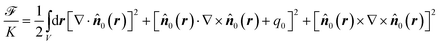 | (15) |
In eqn (15), the constant q0 ≡ 2π/p is the wave number of the cholesteric helix and K ≃ 1.6εff/σ (ref. 42) is a material-specific constant, for our model turns out to be of the same order of magnitude as that characteristic of the Gay-Berne model.43 Moreover, assuming T = 285 K and a particle size of σ = 3.4 × 10−10 m we obtain εff ≈ 3.9 × 10−21 J. With these numbers the elastic constant for our model turns out to be K ≈ 19pN in SI units. Thus, this order of magnitude is realistic for a typical liquid crystal such as p-azoxyanisole.44 In ref. 42 it was also shown that the one-constant approximation is valid here on account of the small aspect ratio of the mesogens. As one can see from eqn (15)q0 modifies the twist contribution to ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) . In the nematic phase, where q0 = 0 because p → ∞, eqn (15) reduces to the standard form1 such that
. In the nematic phase, where q0 = 0 because p → ∞, eqn (15) reduces to the standard form1 such that ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is composed of the usual splay, twist, and bend contributions.
is composed of the usual splay, twist, and bend contributions.
In general, the contribution of each term in eqn (15) is weighted separately by material-specific constants K1, K2, and K3 which can be attributed to bend, splay, and twist deformations of the director field, respectively. However, the one-constant approximation K1 ≃ K2 ≃ K3 = K is very well satisfied for the Hess–Su model.42 This is because of the relatively small aspect ratio of 1.30 of mesogens in the Hess–Su model. In practice, we compute ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) numerically by differentiating
numerically by differentiating ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (r) according to eqn (15).
(r) according to eqn (15).
At this stage it seems noteworthy that the approach taken here is different from the one usually applied in that we obtain ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) as an ensemble average corresponding either to a state at thermodynamic equilibrium or to a rather stable, ”long lived“ metastable state. That is we obtain
0(r) as an ensemble average corresponding either to a state at thermodynamic equilibrium or to a rather stable, ”long lived“ metastable state. That is we obtain ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) as result of intermolecular interactions. The conventional procedure is to take a mean-field expression for the free energy and minimize this functional with respect to
0(r) as result of intermolecular interactions. The conventional procedure is to take a mean-field expression for the free energy and minimize this functional with respect to ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) in principle. Both approaches should provide consistent results as long as the mean-field approximation remains valid.
0(r) in principle. Both approaches should provide consistent results as long as the mean-field approximation remains valid.
3.2 Homogeneous colloid in a cholesteric host phase
To validate the model system as being sufficiently realistic we begin our presentation of results by considering a chemically homogeneous colloid suspended in a cholesteric host phase. In this case the resulting defect topology is well known both theoretically using lattice Boltzmann calculations20,21 and experimentally.13The cholesteric phase is characterized by a helix evolving along the z-axis. As shown in Fig. 3 the unperturbed helix (i.e., sufficiently far away from the surface of the colloid) is characterized by a local director field that can be fitted almost perfectly by the expression
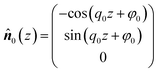 | (16) |
To accommodate a helix of the desired length between the substrates we introduce the phase shift φ0 which can be obtained by simply fitting the MC data in Fig. 3 with eqn (16). Alternatively, φ0 can be dertermined as follows.
Because of the form of the fluid-substrate potential function given in eqn (10) the minimum of that potential is located at zmin = ±sz/2 ∓ δz depending on whether the upper or lower substrate is considered. To accommodate a helix of pitch p between substrates separated by a distance sz we need to have
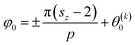 | (17) |
The mesogens are anchored directionally at the lower substrate such that their longer axes point along the y-axis, and hence 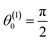 in eqn (11). Under these conditions
in eqn (11). Under these conditions 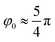 is obtained from eqn (17) for sz = 40. Because we have chosen both p and sz such that three quarters of a full pitch can be accommodated without exposing the helix to any spurious strain, we also anchor our mesogens at the upper substrate directionally such that their longer axes now point along the x-axis which is realized by setting θ(2)0 = 0 in eqn (11) leading, of course, to the same φ0 from eqn (17).
is obtained from eqn (17) for sz = 40. Because we have chosen both p and sz such that three quarters of a full pitch can be accommodated without exposing the helix to any spurious strain, we also anchor our mesogens at the upper substrate directionally such that their longer axes now point along the x-axis which is realized by setting θ(2)0 = 0 in eqn (11) leading, of course, to the same φ0 from eqn (17).
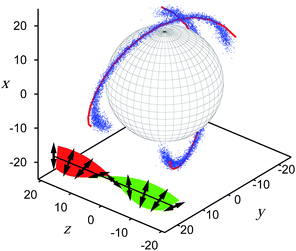
We begin our discussion of results by considering a chemically homogeneous colloid with r0 = 15 (d0/p = 0.6) which anchors the mesogens in a locally homeotropic fashion. If this colloid were immersed in a nematic rather than a cholesteric host phase the well-known Saturn ring defect topology would evolve.16 It consists of a closed disclination line encircling the colloid in the vicinity of its equator if the line connecting the colloid's North and South Pole is parallel to the far-field director.
Because of a possible mismatch between ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) in a cholesteric phase and the local orientation of the mesogens at the surface of the colloid, defects also arise in this case. However, in the present case their topology is much more complex than for a nematic host fluid. For the visualization of this topology we adopt the procedure already described in Section. 3.1. The plot in Fig. 4 shows resulting disclination lines entangling a colloid suspended in a cholesteric host phase. The change of
0(z) in a cholesteric phase and the local orientation of the mesogens at the surface of the colloid, defects also arise in this case. However, in the present case their topology is much more complex than for a nematic host fluid. For the visualization of this topology we adopt the procedure already described in Section. 3.1. The plot in Fig. 4 shows resulting disclination lines entangling a colloid suspended in a cholesteric host phase. The change of ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) along the z-axis is indicated by the small double arrows rotating around a line parallel to the z-axis in the x–y plane. The resulting disclination line is closed and wrapped around the colloid in a rather complex fashion. In particular, the plot in Fig. 4 agrees very nicely with earlier lattice Boltzmann studies21 and experimental results13 and thus validates the model used here.
0(z) along the z-axis is indicated by the small double arrows rotating around a line parallel to the z-axis in the x–y plane. The resulting disclination line is closed and wrapped around the colloid in a rather complex fashion. In particular, the plot in Fig. 4 agrees very nicely with earlier lattice Boltzmann studies21 and experimental results13 and thus validates the model used here.
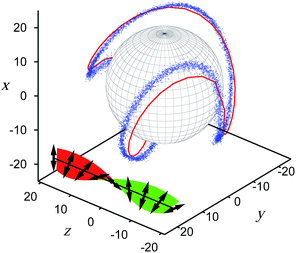 | ||
| Fig. 4 Disclination line represented by a set of blue dots (see text) in the vicinity of a spherical colloidal particle of radius r0 = 15 (d0/p = 0.6) suspended in a cholesteric host phase. Mesogens are anchored in a locally homeotropic fashion at each point of the colloid's surface. The red line is the fit of the expression in eqn (19) to the MC data taking reff ≃ 20 as a fit parameter. The little double arrows indicate the local director and the coloured plane visualizes their continuous variation along the z axis. The colors green and red indicate one or the other side of this plane. | ||
To rationalize the complex spatial variation of the disclination line one may invoke a simple geometrical argument. Consider a vector r pointing from the center of the colloid in an outward direction such that locally r is collinear to the orientation of a mesogen that is homeotropically aligned. Hence, for an ideal defect to arise, r needs to be orthogonal to the local director field satisfying the expression
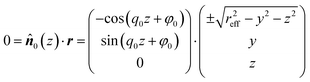 | (18) |
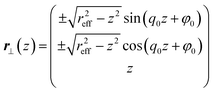 | (19) |
However, if the spherical, chemically homogeneous colloid anchors the mesogens in a locally planar fashion, the defect topology changes dramatically. Instead of one closed disclination loop as in Fig. 4 we observe two individual disclination lines of finite length wrapped around the colloid as shown in Fig. 5. Again, our results are in accord with earlier lattice Boltzmann results.20
 | ||
| Fig. 5 As Fig. 4, but for a planar anchoring. The fit of eqn (22) to the MC data is obtained for reff = 22 and δr = 0.2reff. | ||
The geometric concept behind eqn (18) can also be applied to the case of planar anchoring but requires additional modifications. In this case, the ideal defect arises if the preferred, planar anchoring is perpendicular to the local director, thus ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) is parallel to r and satisfies the expression
0(z) is parallel to r and satisfies the expression
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z)·r = reff 0(z)·r = reff | (20) |
The solution of this expression leads to two defect points due to the fact that ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) is rotating in the x–y plane and can only be parallel to r if its z-components vanish. For that reason one expects the formation of these defect points at z = 0.
0(z) is rotating in the x–y plane and can only be parallel to r if its z-components vanish. For that reason one expects the formation of these defect points at z = 0.
However, our simulation data reveal two line defects instead. In this case, one may wonder how the plot in Fig. 5 depends on our criterion to identify disclination lines. To that end we varied our threshold. It turned out that the length of the disclination lines depicted in Fig. 5 is independent of the threshold used for λ+(r); however, the thickness of the blue lines vanishes completely (and thus the disclination lines) if one uses λ+(r) ≤ 0.05 to identify regions of lower order in the cholesteric host phase. Because the threshold value for λ+(r) does not affect the length of the disclination lines shown in Fig. 5, we propose the following line of arguments to unravel the apparent discrepancy between MC data and the point defects that would form ideally.
In general, the formation of topological defects (which in a mathematical sense are singularities in the director-field) costs free energy. However, it is conceivable that in comparison with the formation of point defects, a strong local deformation of the (continuous) director field is even more costly in terms of free energy. If that is so, the formation of defects is advantageous and entire lines of defects may form. Eventually, however, the deformation of the director field wins energetically such that the disclination lines must end and therefore be of finite length.
Based upon this qualitative energetic argument one would also argue that a disclination line forms as long as the mismatch between ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) and the local alignment of mesogens at the colloid's surface is maximized. Mathematically speaking, the disclination lines satisfy
0(z) and the local alignment of mesogens at the colloid's surface is maximized. Mathematically speaking, the disclination lines satisfy
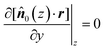 | (21) |
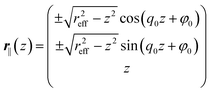 | (22) |
Notice though that r∥(z) in eqn (22) again turns out to encircle the colloid in a closed loop as compared to eqn (19), only sine and cosine functions are interchanged. However, to rationalize that disclination lines are of finite extent in reality, we argue that the largest mismatch between ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z) and the locally planar alignment of mesogens at the surface of the colloid arise at z = 0. The mismatch then decreases with increasing |z|, vanishing eventually at |z| = reff. However, there has to exist a certain threshold value
0(z) and the locally planar alignment of mesogens at the surface of the colloid arise at z = 0. The mismatch then decreases with increasing |z|, vanishing eventually at |z| = reff. However, there has to exist a certain threshold value ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z)·r∥ = δr for the formation of topological defects. Beyond this value an elastic deformation of the director field is energetically favored compared to the defect formation. Clearly, the value of the threshold is a priori unknown but may be adjusted like reff to obtain an optimal representation of the MC data. This representation is possible for reff ≃ 22 and δr ≃ 0.8reff as the plot in Fig. 5 illustrates where again the “++” and “−−” combinations of the components of r∥ in the interval [−reff, reff] have been used.
0(z)·r∥ = δr for the formation of topological defects. Beyond this value an elastic deformation of the director field is energetically favored compared to the defect formation. Clearly, the value of the threshold is a priori unknown but may be adjusted like reff to obtain an optimal representation of the MC data. This representation is possible for reff ≃ 22 and δr ≃ 0.8reff as the plot in Fig. 5 illustrates where again the “++” and “−−” combinations of the components of r∥ in the interval [−reff, reff] have been used.
The similarity between eqn (19) and (22) can be rationalized as follows. Consider a cross section of the colloid in the x–y plane that is located at some z = z′. With respect to the local director ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z′) but irrespective of both the actual anchoring of mesogens at the surface of the colloid and the direction of
0(z′) but irrespective of both the actual anchoring of mesogens at the surface of the colloid and the direction of ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z′), four distinguished points exist (see Fig. 6). At two of them
0(z′), four distinguished points exist (see Fig. 6). At two of them ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z′) is locally parallel to the cross section whereas at the other two
0(z′) is locally parallel to the cross section whereas at the other two ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z′) is locally orthogonal to it. Hence, at the latter two one anticipates the formation of defects. The position of defects alternates with position of the other two points at which the local orientation of the cross section agrees perfectly with
0(z′) is locally orthogonal to it. Hence, at the latter two one anticipates the formation of defects. The position of defects alternates with position of the other two points at which the local orientation of the cross section agrees perfectly with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(z′). Because of eqn (16) all four points rotate in the x–y plane in a counter clockwise fashion with increasing z.
0(z′). Because of eqn (16) all four points rotate in the x–y plane in a counter clockwise fashion with increasing z.
3.3 The twisted nematic cell
In the preceding section an intrinsic cholesteric host phase could form because of the chirality of the interactions between a pair of mesogens. However, a quasi-cholesteric phase may be induced if one places achiral mesogens (ε3 = 0) between planar solid surfaces with hybrid anchoring for which the energetically most favorable alignment of mesogens at one substrate differs from that at the other one.Consider first a homogeneous anchoring scenario realized by setting θ(1) = θ(2) in eqn (11), such that ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (1)0 =
(1)0 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (2)0. If thermodynamic conditions have been chosen properly, a nematic phase will form between the substrates characterized by
(2)0. If thermodynamic conditions have been chosen properly, a nematic phase will form between the substrates characterized by ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (1)0 =
(1)0 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (2)0 =
(2)0 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0. If one now maintains θ(2)0 but changes θ(1)0 the mesogens have to change their orientation from the one imposed by the lower substrate to the favorable one at the upper substrate. This is possible by gradually switching the local director field from
0. If one now maintains θ(2)0 but changes θ(1)0 the mesogens have to change their orientation from the one imposed by the lower substrate to the favorable one at the upper substrate. This is possible by gradually switching the local director field from ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(−sz/2) =
0(−sz/2) = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (1)0 to
(1)0 to ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(sz/2) =
0(sz/2) = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) (2)0 along the z-axis normal to the substrates' planes. As a result a helical structure evolves along the z-axis similar to the one formed when the mesogens themselves are chiral.
(2)0 along the z-axis normal to the substrates' planes. As a result a helical structure evolves along the z-axis similar to the one formed when the mesogens themselves are chiral.
However, in the present case the quasi-cholesteric phase is induced solely by the substrates: The important difference is that in the case of intrinsic chirality, the pitch of the cholesteric helix can be modified by changing ε3 in the mesogen–mesogen interaction potential. A similar tuning of interactions is, of course, impossible in real materials. Here the pitch is a quantity characteristic of any given material. In the quasi-cholesteric phase, however, p is a function of the angle increment Δθ0 ≡ θ(1)0 − θ(2)0 and the handedness of the helix is determined by the sign of Δθ0 (see Fig. 7). Notice, in particular, the different pitch in the quasi-cholesteric helix (see Fig. 7) compared with typical values of p in an intrinsically cholesteric liquid crystal (see Fig. 2).
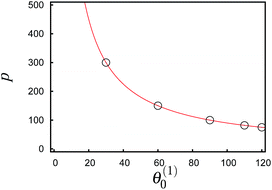 | ||
| Fig. 7 The red line represents the pitch of a TNC with sz = 27 as a function of the angle θ(1)0 at constant θ(2)0 = 0° (see eqn 11) whereas the circles mark the relevant pitches used in Fig. 8 and 9 in a TNC. | ||
The formation of a quasi-cholesteric, substrate-induced phase can also be realized experimentally in a so called twisted nematic cell (TNC). However, experimentally it is generally impossible to gradually vary the anchoring at one substrate relative to the other. In an experimental setup one would simply employ homogeneously anchoring substrates where one of them is rotated in the x–y plane relative to the other.
If a chemically homogeneous colloid is immersed in a quasi-cholesteric phase, one anticipates the formation of disclination lines. Starting with a colloid anchoring mesogens in a locally homeotropic fashion, we see in Fig. 8(a) that the well-known Saturn ring defect topology arises for the case θ(1)0 = θ(2)0 = 0° where the host phase is nematic with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 pointing in the x-direction. Because of the direction of
0 pointing in the x-direction. Because of the direction of ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 the maximum mismatch between
0 the maximum mismatch between ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 and the local alignment of mesogens at the colloidal surface arises around the equator of the colloid as one can see from Fig. 8(a).
0 and the local alignment of mesogens at the colloidal surface arises around the equator of the colloid as one can see from Fig. 8(a).
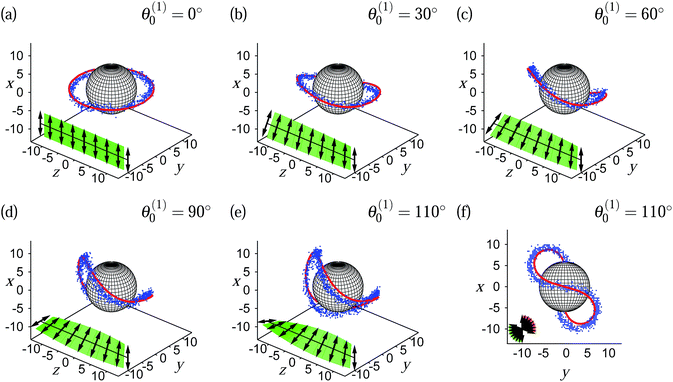 | ||
| Fig. 8 As Fig. 4, but for a spherical colloid of radius r0 = 6 suspended in a TNC. The angle θ in the top-right corner of the plots (a)–(f) indicates the rotation of the directional anchoring vector in eqn (11) and is used for calculation of the pitch. The ratio d0/p in parts (a)–(e) is 0.00, 0.04, 0.08, 0.12, and 0.15 respectively. | ||
Increasing now θ(1)0 in steps of 10° sequentially from one MC run to the next one realizes from Fig. 7 that p decreases from infinity (nematic phase) to a large but finite value in the quasi-cholesteric phase. Plots in Fig. 8(b)–(f) show that in the quasi-cholesteric phase the initial Saturn ring [see Fig. 8(a)] becomes increasingly deformed as p decays (i.e., as θ(1)0 increases). However, it is particularly noteworthy from the plots in Fig. 8 that both undeformed and deformed disclination lines can be represented by the simple analytic expression given in eqn (19). The projection of disclination lines onto the x–y plane in Fig. 8(f) in conjunction with its full three-dimensional representation in Fig. 8(e) reveals that the disclination line is a closed loop wrapped around the colloid for θ(1)0 = 110°.
At this point another feature of a quasi-cholesteric helix in a TNC setup should perhaps be emphasized. For θ(1)0 > 90° the helix has two options of responding to a further increase of θ(1)0. On the one hand, p may decrease further such that the already metastable quasi-cholesteric helix becomes more twisted or, on the other hand, the handedness of the helix may flip at the expense of an increase of p. The latter is possible because of the head-tail symmetry of the achiral mesogens in our model. In practice, we observe in our MC simulations that the change in helix handedness and a simultaneous sudden increase of p occur under TNC conditions if θ(1)0 > 110°.
At this stage another important difference between a quasi-cholesteric phase in a TNC setup and a true cholesteric phase in a liquid crystal with intrinsic mesogenic chirality arises. Starting with a quasi-cholesteric and a cholesteric phase of the same p we are able to reduce p continuously in the latter case by increasing ε3. At some critical value of ε3 the cholesteric phase undergoes a phase transition to a blue phase as we demonstrated elsewhere.25 This blue phase is distinguished from the cholesteric phase structurally because it exhibits double- instead of single-twist helices. A similar phase transition is impossible in the TNC with a liquid crystal composed of achiral mesogens.
Turning now to a discussion of a TNC where a colloid with planar local surface anchoring is immersed in a quasi-cholesteric host phase, we investigate in Fig. 9 the effect of gradually decreasing p as θ(1)0 increases. Starting again with the nematic phase of infinite p (e.g., θ(1)0 = θ(2)0 = 0°) we see from Fig. 9(a) that the well-known Boojum defect topology forms where two defects are located at the North and South Pole of the colloid. Again, as θ(1)0 increases from its initial value of 0° the localized defects of the Boojum topology become short lines which are stretched the larger θ(1)0 (the smaller p) becomes [see Fig. 9(b)–(e)]. For θ(1)0 = 120° the three-dimensional representation in Fig. 9(e) and its projection onto the x–y plane in Fig. 9(f) show that the disclination lines are partially wrapped around the colloid but remain disconnected. This is apropos of the situation depicted in Fig. 5 for a colloid suspended in a cholesteric phase composed of intrinsically chiral mesogens. However, compared with the plot in Fig. 5 the disclination lines depicted in Fig. 9(f) are shorter, which is primarily ascribed to the smaller size of the colloid in the latter case. However, the reader should realize that it is not the absolute value of the colloid's size that matters but only the ratio between this size and the pitch. Typical values for this ratio in the present case [see Fig. 8(f)] are 0.16 as opposed to, for instance, 0.6 for data presented in Fig. 4 or 5.
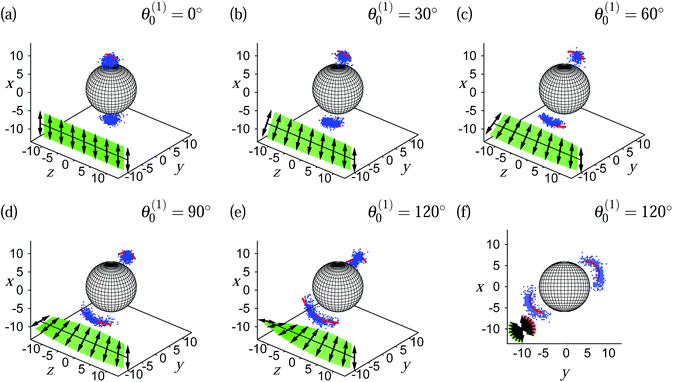 | ||
| Fig. 9 As Fig. 8, but for planar anchoring and d0/p = 0.16 in part (e). | ||
For anchoring angles θ(1)0 > 120° the same sudden change in handedness of the already metastable quasi-cholesteric helix and increase of p occurs that was already described above for a colloid with locally homeotropic surface anchoring of the mesogens. Nevertheless, the plots presented in Fig. 9(a)–(f) also show that the simple analytic expression for disclination lines given in eqn (22) is capable of representing the MC data very well. Hence we conclude that as far as disclination lines are concerned there is essentially no difference between a cholesteric phase formed by intrinsically chiral mesogens and a quasi-cholesteric phase composed of achiral mesogens in a TNC.
3.4 Janus colloid
If, instead of a colloid with homogeneous surface anchoring, a Janus colloid is immersed in a cholesteric phase, the already quite complex spatial variation of disclination lines becomes even more complicated. This is because in the case of a Janus colloid the orientation of its antithetic surfaces with respect to the local orientation of the director field at the position of the colloid's center of mass enters the analysis as a new parameter ϑ which we introduce via![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(0)·ûJ = cos
0(0)·ûJ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ where ûJ is a unit vector describing the orientation of the Janus colloid. Hence, we focus on the rotation of the Janus colloid around the z-axis, such that ûJ·êz = 0.
ϑ where ûJ is a unit vector describing the orientation of the Janus colloid. Hence, we focus on the rotation of the Janus colloid around the z-axis, such that ûJ·êz = 0.
For all the results presented below we fix the position of the Janus colloid such that its center of mass coincides with the origin of the Cartesian coordinate system located at the center of the simulation cell. To analyze the effect of different orientations of the Janus colloid with respect to the cholesteric helix we proceed as follows.
We fix ûJ such that is parallel to the x-axis. By changing the angles θ(k)0 (k = 1, 2) in eqn (11) simultaneously one can then expose the Janus colloid to different orientations of the director field. Therefore, disclination lines form over different parts of the Janus colloid as ϑ is varied. Moreover, because we fix the substrate distance sz = 27 and maintain the coupling constant ε3 = −0.10 the pitch is always fixed such that half a pitch fits between the substrates without spurious strain.
Results plotted in Fig. 10 illustrate the rather complex spatial variation of disclination lines as ϑ varies between 0° and 90°. In all cases we have only a single line of disclinations with disconnected ends such that the line neither forms a closed loop as in the case of a chemically homogeneous colloid with homeotropic surface anchoring nor form two disconnected lines as is the case for locally planar surface anchoring. However, as before in the case of a chemically homogeneous colloid with planar anchoring the disclination line we are dealing with here is of finite length. The fact that we are dealing only with a single disclination line emphasizes the interplay between the locally planar and homeotropic surface anchoring over two hemispheres of the Janus colloid. Generally speaking, the plots in Fig. 10(a) and (b) show that the way in which the disclination line is wrapped around the Janus colloid changes significantly with ϑ.
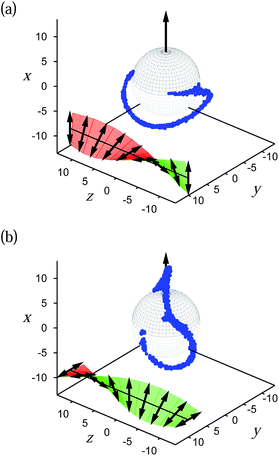 | ||
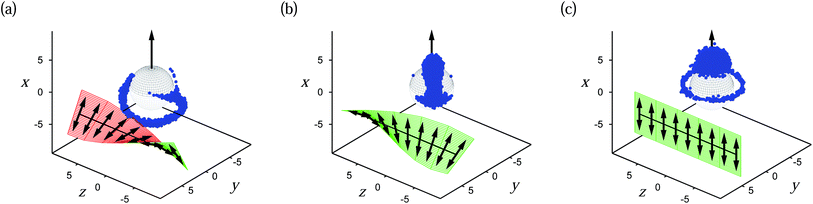
| Fig. 10 As Fig. 4, but for a Janus colloid (r0 = 6, d0/p = 0.24) with planar surface anchoring at the upper (black) hemisphere and a homeotropic anchoring at the lower (grey) hemisphere. The arrow through the colloid indicates its orientation ûJ. The configurations are related to (a) ϑ = 90° and (b) ϑ = 0°. | ||
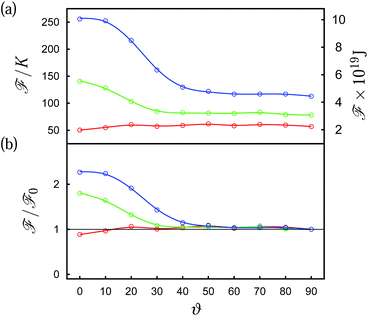
This variation of disclination lines with ϑ also has another interesting consequence which becomes apparent as one changes the size of the Janus colloid. As it is mainly ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0(r) that changes as ϑ is varied, it seems plausible to discriminate energetically between states for different ϑ via the Frank free energy which is a quantitative measure of the free energy density associated with different defect topologies. Based upon a quantitative analysis of the Frank free energy [see eqn (15)] plots in Fig. 11 illustrate the effect. Starting with a small colloid of hard-core radius r0 = 3 (d0/p = 0.12) we see in Fig. 11(a) that the Frank free energy is apparently insensitive to a variation of ϑ except the weak minimum at ϑ = 0. Comparing Fig. 10(a) and 12(a) reveals the size independence of the defect structure at ϑ = 90° as far as the overall topology of the disclination line is concerned. This changes dramatically at ϑ = 0°. The disclination line in Fig. 12(b) is much closer to the surface and is less curved than the one shown in Fig. 10(b). These differences between disclination lines presented in Fig. 10(b) and 12(b) might be the reason for the different behavior of
0(r) that changes as ϑ is varied, it seems plausible to discriminate energetically between states for different ϑ via the Frank free energy which is a quantitative measure of the free energy density associated with different defect topologies. Based upon a quantitative analysis of the Frank free energy [see eqn (15)] plots in Fig. 11 illustrate the effect. Starting with a small colloid of hard-core radius r0 = 3 (d0/p = 0.12) we see in Fig. 11(a) that the Frank free energy is apparently insensitive to a variation of ϑ except the weak minimum at ϑ = 0. Comparing Fig. 10(a) and 12(a) reveals the size independence of the defect structure at ϑ = 90° as far as the overall topology of the disclination line is concerned. This changes dramatically at ϑ = 0°. The disclination line in Fig. 12(b) is much closer to the surface and is less curved than the one shown in Fig. 10(b). These differences between disclination lines presented in Fig. 10(b) and 12(b) might be the reason for the different behavior of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (ϑ). For a vanishing ratio d0/p (p → ∞, nematic host phase) one anticipates the formation of a Boojum ring defect topology as confirmed by plots in Fig. 10(c) and in agreement with experiments, Landau-de Gennes theory, and molecular simulations.7,15,16 Thus, the defect topology in a cholesteric phase, where d0/p = 0.12 [see Fig. 12(b)] is intermediate between the one shown in Fig. 10(b) (d0/p = 0.24) and the Boojum ring topology shown Fig. 12(c).
(ϑ). For a vanishing ratio d0/p (p → ∞, nematic host phase) one anticipates the formation of a Boojum ring defect topology as confirmed by plots in Fig. 10(c) and in agreement with experiments, Landau-de Gennes theory, and molecular simulations.7,15,16 Thus, the defect topology in a cholesteric phase, where d0/p = 0.12 [see Fig. 12(b)] is intermediate between the one shown in Fig. 10(b) (d0/p = 0.24) and the Boojum ring topology shown Fig. 12(c).
 | ||
| Fig. 12 As Fig. 10, but for r0 = 3, (d0/p = 0.12). (a) ϑ = 90°, (b) ϑ = 0°, and (c) Boojum ring defect topology forming in a nematic host fluid (d0/p = 0.). Notice that only a fraction of the entire system is shown. Therefore, the local director fields at the upper and lower boundary of the z-axis are not orthogonal as they would be at z = ±sz/2 on account of the anchoring at the substrates. | ||
Returning now to a more detailed analysis of the Frank free energy in Fig. 11, we notice that for d0/p = 0.16 the plot of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) in Fig. 11(a) reveals that
in Fig. 11(a) reveals that ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) becomes a monotonically decaying function of ϑ with the largest values arising at small angles. However,
becomes a monotonically decaying function of ϑ with the largest values arising at small angles. However, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) quickly levels off as ϑ increases beyond 30°. Going finally to a Janus colloid of r0 = 6 (d0/p = 0.24) we notice that the plot of F in Fig. 11(a) exhibits a maximum at ϑ = 0° and then decays monotonically until a constant value is assumed. The different values in the plateaus of all three curves in Fig. 11(a) are related to the increase in the length of the disclination lines as the colloid becomes bigger. Dividing the curves plotted in Fig. 11(a) by the respective plateau value
quickly levels off as ϑ increases beyond 30°. Going finally to a Janus colloid of r0 = 6 (d0/p = 0.24) we notice that the plot of F in Fig. 11(a) exhibits a maximum at ϑ = 0° and then decays monotonically until a constant value is assumed. The different values in the plateaus of all three curves in Fig. 11(a) are related to the increase in the length of the disclination lines as the colloid becomes bigger. Dividing the curves plotted in Fig. 11(a) by the respective plateau value ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0 reveals that the width of the free energy barrier as well as the relative height of this barrier increases the larger the colloid becomes. This can be seen in Fig. 11(b) where the plot of
0 reveals that the width of the free energy barrier as well as the relative height of this barrier increases the larger the colloid becomes. This can be seen in Fig. 11(b) where the plot of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /
/![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) 0 approaches the common value of 1 at increasingly larger ϑ as the radius of the colloid increases. The same results are expected for a fixed size of the Janus colloid but increasingly shorter pitch. The crucial quantity here is, again, the ratio between the colloid's size and the pitch and not individual values of these quantities.
0 approaches the common value of 1 at increasingly larger ϑ as the radius of the colloid increases. The same results are expected for a fixed size of the Janus colloid but increasingly shorter pitch. The crucial quantity here is, again, the ratio between the colloid's size and the pitch and not individual values of these quantities.
Because of the periodicity of the cholesteric helix the results shown in Fig. 11 will also be repeated periodically. For example, for the curves shown in Fig. 11 there will be another free-energy barrier at angles approaching 180°. These observations offer the possibility for the following Gedankenexperiment. Suppose, one were able to fix the orientation of a Janus colloid which might be conceivable by using a homogeneous magnetic field.45 For Janus colloids much bigger then the ones that could be studied here on account of computational limitations most angles would correspond to energetically unfavorable regions because the width of the free-energy barrier increases with d0/p. Hence, the Janus colloid would be more or less restricted to positions somewhere in the x–y plane so that it might be feasible to form a quasi two-dimensional layer of Janus colloids all with the same orientation through orientational self-assembly.
4 Conclusions
In this work we employ MC simulations carried out in the isothermal-isobaric ensemble to calculate the local director field of a cholesteric liquid-crystal host phase in the presence of an immersed spherical particle. We employ a simple, modified Lennard-Jones model for the liquid crystal following earlier suggestions by Hess and Su.26 To form a cholesteric phase the mesogens need to be chiral. We introduce chirality through a pseudo-scalar coupling in addition to the other orientation dependent terms in the Hess–Su potential. This follows in spirit a suggestion by Memmer et al. for the interaction between a mesogenic pair in the classical Gay-Berne model.23By considering homogeneous colloids with either locally planar or homeotropic surface anchoring of the mesogens we determine disclination lines that had already been obtained earlier in either experiments or in lattice-Boltzmann calculations.13,20,21 Besides the validation of our model through this agreement with earlier works we also offer a simple geometrical argument that explains the complex spatial variation of disclination lines quite nicely.
Based upon the present study one might consider a system with two colloids immersed in a cholesteric host to study the effective pair-wise interactions. This has already been done in experiments22 and lattice-Boltzmann calculations46,47 and could, in principle, also be realized in our model system. In another work we disperse two homogeneous colloids with planar anchoring in a nematic phase and obtain the Frank free energy as a function of the distance between two colloids and the angle formed by the distance vector connecting their centers and the nematic director.48 It turns out that the Frank free energy is well-suited to study the effective interactions between a colloidal pair that are mediated by a nematic host phase. The Frank free energy allowed us48 to explain quantitatively the “magic angle” of about 30° formed between the center-of-mass distance vector of the colloidal pair and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) 0 which is obtained experientially6,11 for a stable configuration of the colloids. From this agreement we conclude that
0 which is obtained experientially6,11 for a stable configuration of the colloids. From this agreement we conclude that ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (ϑ) is equally well-suited to determine the stability of a Janus colloid immersed in a cholesteric host phase.
(ϑ) is equally well-suited to determine the stability of a Janus colloid immersed in a cholesteric host phase.
However, to apply the approach of ref. 48 to study effective interactions between a pair of Janus colloids in such a cholesteric phase comprehensively would be much more demanding. Here the Frank free energy is a function of all three coordinates (e.g. spherical coordinates) and the ratio of d0/p. In the case of Janus colloids one has to take into account the relative orientation of the Janus colloid with respect to the cholesteric helix in addition. Given large and sufficient computational resources one can, of course, use this model system to study a colloidal interactions mediated by the cholesteric phase. However, at least at present the dimension of the parameter space corresponding to such a setup seems prohibitive.
In addition to the Hess–Su potential, where the intrinsic chirality is introduced via the interaction potential, we also study a quasi-cholesteric phase where the mesogen–mesogen interaction is achiral and the formation of a cholesteric helix is introduced through the anchoring of mesogens at two planar solid substrates. This setup follows in spirit that characteristic of a TNC. By comparing disclination lines arising in the intrinsically cholesteric and the quasi-cholesteric liquid crystal, we demonstrate that the topology of the disclination lines apparently only depends on the presence of a helically varying director field irrespective of the precise origin of the helix. Again, the analytic expression derived here from a geometrical argument is capable of describing the complex topology of the resulting disclination lines.
Although the topology of disclination lines evolving around a spherical colloid with homogeneous surface anchoring is quite complex, even more complicated structures occur in the vicinity of a Janus colloid consisting of two hemispheres at which the mesogens are anchored in a locally planar and homeotropic fashion, respectively. Because of the presence of the two hemispheres of antithetic surface anchoring, the orientation of the Janus colloid relative to the local director field of the cholesteric phase matters. Depending on this orientation the topology of disclination lines varies.
Associated with these different topologies is a higher (or lower) free energy which we determine by calculating the Frank free energy in the one-constant approximation. The one-constant approximation is nearly exact because of the small aspect ratio of mesogens in the Hess–Su model.26
By varying the size of the colloid or the pitch of the cholesteric helix, we show that barriers in free energy arise for certain orientations of the Janus colloid relative to the local director field. These barriers increase in magnitude with growing size of the Janus colloids. Simultaneously, the range of angles over which the free-energy barriers are observed becomes wider as the colloid becomes larger (or the pitch smaller). As the size of the colloid as well as the pitch are controllable parameters in corresponding experiments,7,13,49 it seems conceivable that similar free-energy barriers might be used to form self-assembled quasi two-dimensional layers of Janus colloids experimentally, provided the orientation of the Janus colloid can be maintained. The latter may be possible by using homogeneous magnetic fields such that orientationally ordered quasi two-dimensional arrays of Janus colloids could be formed that might have interesting properties. However, at this stage more in-depth research is clearly required to investigate the potential usefulness of the effect reported here for future applications.
Finally, it seems worthwhile emphasizing that the disclination lines obtained in this work have been computed as ensemble averages from relatively long Markov chains of configurations. In none of these individual simulations we observed “jumps” between structurally or thermodynamically distinct states similar to what is occasionally encountered in MC simulations of coexisting phases near the coexistence line. Hence, we conclude that the data presented here correspond to thermodynamically stable or metastable states of a lifetime exceeding that of the simulations considerably.
We are grateful for insightful and very helpful comments by an anonymous referee. Financial support from the Deutsche Forschungsgemeinschaft via the International Graduate Research Training Group 1524 is gratefully acknowledged. It was supported in part by the National Science Foundation's Research Triangle MRSEC (DMR – 1121107). Two of us (EDH and MS) gratefully acknowledge additional financial support from CONACYT-Mexico [Project no. 178963].
References
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon, Oxford, 1995 Search PubMed.
- H. Stark, Phys. Rep., 2001, 351, 387–474 CrossRef CAS.
- E. M. Terentjev, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1330–1337 CrossRef CAS.
- R. W. Ruhwandl and E. M. Terentjev, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 2958–2961 CrossRef CAS.
- P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Science, 1997, 275, 1770–1773 CrossRef CAS.
- P. Poulin and D. A. Weitz, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 626–637 CrossRef CAS.
- M. Conradi, M. Ravnik, M. Bele, M. Zorko, S. Žumer and I. Muševič, Soft Matter, 2009, 5, 3905–3912 RSC.
- U. Tkalec and I. Muševič, Soft Matter, 2013, 9, 8140–8150 RSC.
- M. Ravnik, M. Škarabot, S. Žumer, U. Tkalec, I. Poberaj, D. Babič, N. Osterman and I. Muševič, Phys. Rev. Lett., 2007, 99, 247801 CrossRef CAS.
- M. Ravnik and S. Žumer, Soft Matter, 2009, 5, 269–274 RSC.
- I. I. Smalyukh, O. D. Lavrentovich, A. N. Kuzmin, A. V. Kachynski and P. N. Prasad, Phys. Rev. Lett., 2005, 95, 157801 CrossRef CAS.
- U. Tkalec, M. Ravnik, S. Čopar, S. Žumer and I. Muševič, Science, 2011, 333, 62–65 CrossRef CAS PubMed.
- V. S. R. Jampani, M. Škarabot, M. Ravnik, S. Čopar, S. Žumer and I. Muševič, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2011, 84, 031703 CrossRef CAS.
- I. Muševič, Phil. Trans. R. Soc. A, 2013, 371, 20120266 CrossRef PubMed.
- M. Conradi, M. Zorko and I. Muševič, Opt. Express, 2010, 18, 500–506 CrossRef CAS PubMed.
- M. Melle, S. Schlotthauer, M. G. Mazza, S. H. L. Klapp and M. Schoen, J. Chem. Phys., 2012, 136, 194703 CrossRef PubMed.
- S. Gangwal, A. Pawar, I. Kretzschmar and O. D. Velev, Soft Matter, 2010, 6, 1413–1418 RSC.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- J. Hu, S. Zhou, Y. Sun, X. Fang and L. Wu, Chem. Soc. Rev., 2012, 41, 4356–4378 RSC.
- J. S. Lintuvuori, D. Marenduzzo, K. Stratford and M. E. Cates, J. Mater. Chem., 2010, 20, 10547 RSC.
- J. S. Lintuvuori, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2010, 105, 178302 CrossRef CAS.
- V. S. R. Jampani, M. Škarabot, S. Čopar, S. Žumer and I. Muševič, Phys. Rev. Lett., 2013, 110, 177801 CrossRef CAS.
- R. Memmer, H. G. Kuball and A. Schönhofer, Liq. Cryst., 1993, 15, 345 CrossRef CAS.
- R. Memmer, Mol. Phys., 1996, 89, 1633–1649 CAS.
- M. Melle, M. Theile, C. K. Hall and M. Schoen, Int. J. Mol. Sci., 2013, 14, 17584 CrossRef CAS PubMed.
- S. Hess and B. Su, Z. Naturforsch, 1999, 54a, 559 Search PubMed.
- H. Steuer, S. Hess and M. Schoen, Physica A, 2003, 328, 322 CrossRef.
- H. Steuer, S. Hess and M. Schoen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 69, 031708 CrossRef.
- M. Greschek, M. Melle and M. Schoen, Soft Matter, 2010, 1898 RSC.
- M. Greschek and M. Schoen, Soft Matter, 2010, 6, 4931 RSC.
- M. Greschek and M. Schoen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2011, 83, 011704 CrossRef.
- A. J. Stone, Mol. Phys., 1978, 36, 241 CrossRef CAS.
- C. G. Gray and K. E. Gubbins, Theory of Molecular Fluids, Clarendon, Oxford, 1984, vol. 1 Search PubMed.
- A. A. Sonin, The Surface Physics of Liquid Crystals, Gordon & Breach, Amsterdam, 1995 Search PubMed.
- D. Andrienko, G. Germano and M. P. Allen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2001, 63, 041701 CrossRef CAS.
- U. Ognysta, A. Nych, V. Nazarenko, M. Škarabot and I. Muševic, Langmuir, 2013, 25, 12092 CrossRef PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn, 2001 Search PubMed.
- M. Ravnik, G. P. Alexander, J. M. Yeomans and S. Žumer, PNAS, 2011, 108, 5188–5192 CrossRef CAS PubMed.
- R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303–1334 CrossRef CAS.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes, Cambridge University Press, Cambridge, 3rd edn, 2007 Search PubMed.
- O. D. Lavrentovich and M. Kleman, in Cholesteric Liquid Crystals: Defects and Topology, ed. H.-S. Kitzerow and C. Bahr, Springer-Verlag, New York, 2001, ch. 5 Search PubMed.
- T. Stieger, M. Schoen and M. G. Mazza, J. Chem. Phys., 2014, 140, 054905 CrossRef PubMed.
- M. P. Allen and D. Frenkel, Phys. Rev. A, 1988, 37, 1813 CrossRef.
- A. Srivastava and S. Singh, J. Phys.: Condens. Matter, 2004, 16, 7169–7182 CrossRef CAS.
- S.-H. Hu and X. Gao, J. Am. Chem. Soc., 2010, 132, 7234–7237 CrossRef CAS PubMed.
- J. C. Lintuvuori, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2011, 107, 267802 CrossRef CAS.
- F. E. Mackay and C. Denniston, Europhys. Lett., 2011, 94, 66003 CrossRef.
- M. Melle, S. Schlotthauer, M. G. Mazza and M. Schoen, unpublished, arXiv preprint:1402.7165.
- T. Hegmann, H. Qi and V. Marx, J. Inorg. Organomet. Polym., 2007, 17, 483–508 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |