Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling the assembly of CdS nanorods via solvent and acidity†
L. J. A.
Koster
*ab,
S.
Khodabakhsh
ac and
N. C.
Greenham
a
aCavendish Laboratory, University of Cambridge, J. J. Thomson Avenue, Cambridge CB3 0HE, UK
bZernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: l.j.a.koster@rug.nl
cMelville Laboratory for Polymer Synthesis, Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
First published on 21st July 2014
Abstract
We report control over the phase behavior of CdS nanorods via the solvent and acidity. CdS nanorods were synthesized using alkane phosphonic acid ligands, which were replaced after synthesis by a series of aromatic ligands. Change of ligand enabled us to cast films from different solvents. By replacing toluene with ethanol or water the rod–rod interactions dominate over rod–substrate interactions, thereby favoring simple hexagonal ordering (2D). When dispersed in water, a net electrostatic charge on the nanorods could be induced by deprotonating the ligands at high pH. This net charge favors 2D nematic ordering over homeotropic ordering of the nanorods on a substrate. A calculation of the van der Waals and electrostatic interactions is presented that explains the observed influence of solvent and pH.
Introduction
Many types of nanoparticles have been receiving increasing interest because of their unique tunable properties that enable their use in various optoelectronic applications. The synthesis of cadmium chalcogenide nanoparticles has reached a high degree of sophistication: impressive levels of control over shape and size have been reported for cadmium chalcogenide nanodots, nanorods and branched structures.1–4 The ability to order nanorods in particular orientations will present unique opportunities for the nanorods of a specific chemical composition to be used in a wide variety of different applications. For example, nanorods which in an out-of-plane orientation are suitable for photovoltaic/diode applications could be used in field effect transistors when ordered in-plane between two electrodes. To this end, several groups have reported nanorods with lyotropic behavior.5–15 Over the past decade there has been a great deal of interest in developing a deeper understanding of what governs the ordering of the nanorods and which parameters could play a role in influencing this.16Recently, it has been shown that semiconductor nanorods could be made to assemble in 1D or 2D structures depending on the surface charge.17 Singh et al. found that replacing part of the ligands on CdSe nanorods by pyridine a net charge could be induced which changes the self-assembly process.17 As the nanorods interact via the solvent, its properties are crucial for the phase behavior.18
Here, we use the ability to attach different functional ligands onto CdS nanorods after their synthesis to modify their phase behavior. By using suitable ligands, the nanorods could be transferred from non-polar solvents (such as toluene) to polar solvents such as ethanol or water. This results in a change from nematic to simple hexagonal packing on a substrate. Additionally, we show that a net charge on the nanorods could be induced by changing the acidity of aqueous dispersions which deprotonates part of the ligands. When deposited on a substrate, the resulting Coulomb repulsion forced the nanorods to lie down in a nematic orientation instead of standing up in a simple hexagonal packing. The present work offers a simple approach to control the phase behavior of nanorods via solvent acidity.
Experimental
CdS nanorods (approximately 25 × 6 nm) were synthesized by a hot injection method adapted from ref. 19 (see ESI† for details). In brief, 115 mg CdO is decomposed at 320 °C in the presence of a mixture of 3.50 g trioctylphosphine oxide and 0.62 g tetradecylphosphonic acid (TDPA) under an inert atmosphere. The resulting solution is allowed to cool to 300 °C and kept at this temperature during the remainder of the synthesis. Separately, a solution of 90 mg elemental sulfur in 8 mL trioctylphosphine is prepared. This solution is injected drop-wise over a time span of 80 minutes into the decomposed CdO mixture. When the injection is finished, the reaction mixture is cooled to 80 °C when toluene is added to this mixture in order to avoid solidification, before it is further cooled down to room temperature. The nanorods are washed by repeated precipitation with methanol, followed by centrifugation, decanting the solution and redispersing the nanorods in toluene.Results and discussion
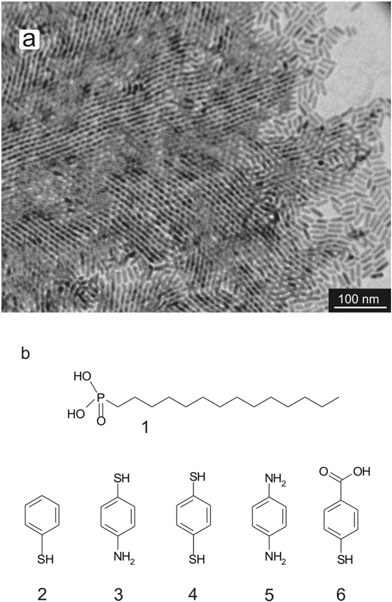
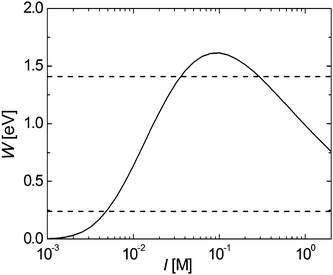
When the resulting TDPA-coated CdS (TDPA–CdS) nanorods were drop-cast onto a carbon-coated transmission electron microscopy (TEM) grid, they adopted a partial ordering (see Fig. 1a). Nanorods near the perimeter of such assemblies display some smectic phases, but the bulk consists of (multi-layered) nematic phases. These assemblies are observed over large scales of over tens of microns.In order to study the effect of intermolecular forces and solvents, several aromatic ligands were employed. In this paper, we treat each ligand as a molecule comprising three different parts; the anchoring group, the auxiliary group and the terminal functional group. The anchoring group is the part of the molecule that is responsible for the assembly of the ligands onto the nanorods, and the auxiliary group, which is the benzene ring in the set of molecules studied here, is responsible for the interactions between the adjacent ligands. The terminal functional group is the functional group which is positioned on the para-position of the benzene ring with respect to the anchoring group. In this report we focus on short aromatic ligands, to keep the inter-ligand interactions constant whilst changing the anchoring and terminal functional groups to investigate the binding of the ligand onto the nanorods, as well the effect of electrostatic forces on the ordering of the nanorods. In order to replace the original ligands (TDPA, see Fig. 1b structure 1) used in the nanorod synthesis, the nanorods were refluxed for 4 hours in the presence of the aromatic ligands, see Fig. 1b for chemical structures of the ligands (details can be found in the Experimental section). It should be noted, that for structures 3, 4, and 5 (see Fig. 1b) no strict distinction between terminal group and anchoring group is possible as it is not clear whether the thiol group or the amine group binds to the nanorods.
Benzenethiol (BT) was used as a reference for studying the effect of the terminal functional group; when cast from a toluene dispersion the resulting nanorods showed locally ordered smectic A phases and tracks of up to approximately 100 nanorods were found, see Fig. 2. Whilst the main image in Fig. 2 shows the extent of the large scale over which these tracks are formed, the inset focuses on these tracks and shows individual nanorods more clearly. These observations show that the phase behavior of CdS nanorods can be influenced by using simple aromatic ligands.
Simple hexagonal ordering of the nanorods perpendicular to the substrate could be achieved by exchanging the original TDPA ligands for 4-aminothiophenol (ATP) (see Fig. 3a). In this case either toluene or ethanol was used to disperse the nanorods. The presence of a terminal functional group appears to have a dramatic effect on the phase behavior, as can be seen by comparing BT–CdS (Fig. 2) with ATP–CdS (Fig. 3a). This raises the issues of which group is on the CdS surface, either the amino- or the thiol group. To assess this, p-benzenedithiol (BDT) and p-benzenediamine (BDA) were used. Interestingly, BDA–CdS nanorods did not show any ordering upon drop casting (see Fig. 3c), whereas BDT–CdS nanorods showed the same behavior as the ATP–CdS ones (see Fig. 3b). If the phase behavior is determined by the terminal functional group, then we suggest that for the ATP-covered nanorods the amine group is bound to the CdS surface whilst the thiol group is the terminal functional group.
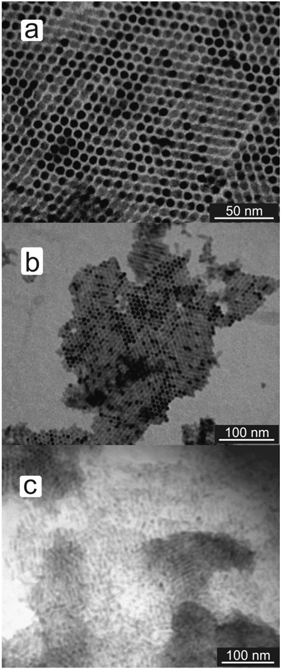 | ||
| Fig. 3 Homeotropic simple hexagonal ordering of ATP–CdS nanorods (a) and BDT–CdS nanorods (b). BDA–CdS nanorods did not show any ordering (c). These nanorods were all drop cast from ethanol. | ||
The results depicted in Fig. 3 imply that the terminal functional group is of great importance. As the thiol group in ATP and BDT is easily deprotonated, we thought it prudent to study the influence of acidity on the ordering of CdS nanorods. The acid dissociation constant of the thiol groups in BDT was estimated from benzenethiol, which has a dissociation constant pKa = 7.78.20 This value is only approximate as monolayers of organic molecules adsorbed at solid surfaces can show significant changes in dissociation constants of functional groups compared to their dissociation in solution. BDT–CdS nanorods were dispersed in aqueous solutions buffered at pH = 4.0 and pH = 9.2. At pH = 4.0, it was found that virtually all the nanorods were aligned in a homeotropic, simple hexagonal fashion (see Fig. 4a). At pH = 9.2, a mixture of nematic and simple hexagonal patterns was observed.
 | ||
| Fig. 4 BDT–CdS nanorods cast from aqueous solutions at pH = 4.0 (a) and pH = 12 (b). MBA–CdS nanorods at pH = 4.0 (c) and pH = 9.2 (d). | ||
To fully deprotonate the ligands, an aqueous KOH solution was used to obtain pH = 12. Under these basic conditions, the vast majority of BDT–CdS nanorods aligned in nematic phases (see Fig. 4b). ATP–CdS nanorods displayed similar behavior (data not shown), again exemplifying the importance of the terminal functional group. To further investigate the influence of acidity, 4-mercaptobenzoic acid (MBA) was used as ligand. The behavior of MBA–CdS was found to be exactly the same: at pH = 4.0 hexagonal ordering was found, while at pH = 9.2 nematic phases resulted (see Fig. 4c and d). Since the acid dissociation constant of MBA in densely packed monolayers is approximately 4.79,21 pH = 9.2 is sufficient to fully deprotonate all the acid groups in the MBA ligand molecules. So, by dispersing the nanorods in a solution of different acidity, we can induce a change in the phase behavior of CdS nanorods.
How can the influence of pH on phase behavior be understood? Onsager has shown that ideal high-aspect-ratio hard rods can assemble in liquid crystalline phases due to a reduction in entropy.22 This reduction is caused by a decrease in excluded volume for the solvent molecules. However, our nanorods have a modest aspect ratio (∼4) and interact with other nanorods and the substrate. These enthalpic contributions to the free energy are of great importance in many nanorod systems as both entropic and energetic factors drive nanorod assembly.23,24 Although entropic effects may certainly contribute to the stability of a specific phase, we do not expect the difference in free energy of the ordered phases due to entropy to be significant: for hard spheres this difference between face-centered cubic and hexagonal close-packed phases is only ∼10−3 kT per particle,25 which is orders of magnitude smaller than the energies considered here. In a recent publication, Titov and Král have discussed the roles van der Waals and Coulombic interactions between CdSe nanorods and between nanorods and the substrate.26 They predicted that hexagonal phases are stable only for low-aspect-ratio CdSe nanorods (L/D < 2–3), which is in good agreement with previous experimental findings. For higher aspect ratios, they predict the existence of nematic and smectic phases. We believe that the framework Titov and Král provide is highly suited to explain our results.
To calculate the van der Waals interactions between the nanorods and between the nanorods and the substrate, we consider coupling between CdS, the solvent and the substrate. These interactions are dominant except at small separations where the ligands start to play a role, both due to their van der Waals interactions,27 as well as entropic and steric repulsion. In the assembly process, nanorods initially separated by large distances are brought into close proximity while interacting via the solvent. The potential energy of the assembly, therefore, should include the effect of the solvent even if there is very little solvent left in the final film. Let VSF and VSS be the potential energies related to substrate-to-face and substrate-to-side interaction, respectively. Similarly, let VRS and VRF be the coupling terms for nanorod side-to-side and nanorod face-to-face van der Waals interactions, respectively. The orientation of the nanorods on a substrate now depends on the relative magnitude of these interactions: for example, strong side-to-side attractive interactions will favor maximizing the number of direct neighbors, as found in simple hexagonal packing. These energies can be calculated from the Hamaker constants (see ESI† for details) and are listed in Table 1. As the Hamaker constants depend on solvent and materials, these energies will be different from the values obtained by Titov and Král since we focus on CdS rather than CdSe nanorods. When the nanorods are electrically neutral, the average energy per nanorod in a simple hexagonal monolayer is given by
| EH = 3VRS + VSF, | (1) |
| EN/SA=VRS + VRF + VSS. | (2) |
| Solvent | V SF (eV) | V SS (eV) | V RS (eV) | V RF (eV) |
|---|---|---|---|---|
| Toluene | −0.092 | −0.348 | −0.122 | −0.036 |
| Ethanol | −0.157 | −0.592 | −0.256 | −0.076 |
| Water | −0.174 | −0.679 | −0.566 | −0.168 |
These expressions do not incorporate any effects arising due to nanorods on the boundary having fewer neighbors. So, we limit the present discussion to large clusters only.
For the MBA–CdS, BDT–CdS or ATP–CdS nanorods in water we compute that the hexagonal phase is lower in energy than the nematic phase: ESH = −1.87 eV and EN/SA = −1.41 eV in the absence of a net charge on the nanorods, in full agreement with the experimental results (see Fig. 4a and c). Since the Hamaker constant for ethanol (0.26 eV)28 is similar to the Hamaker constant for water, it is not surprising that ATP–CdS and BDT–CdS in ethanol display simple hexagonal ordering as well (see Fig. 3a and b). Upon solvent evaporation, the ordering is preserved, which, in addition to the van der Waals interactions, might be aided by interdigitation of the ligands.26 For nanorods in toluene, the nematic phase is lower in energy than the hexagonal phase, again in accordance with the experimental data. The observed trend can be rationalized as a consequence of a decrease in the solvent's Hamaker constant when going from toluene to ethanol and water. This makes the side-to-side attraction between the nanorods dominant over the other terms (see Table 1), which makes it energetically favorable for the nanorods to adopt a hexagonal packing, which increases the number of neighbors over a nematic ordering.
When studying the effect of pH, the electrostatic interactions will become more prominent. Any electrostatic interactions will change the expressions for ESH and EN/SA: VRS will be replaced by VRS + VElecRS, where VElecRS is the electrostatic potential energy of two adjacent nanorods in accord with the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory.27 Note that face-to-face electrostatic interactions can be neglected since only one of the two faces of the nanorods has exposed cadmium atoms that bind the ligands. To estimate the electrostatic energy VElecRS, two adjacent nanorods are treated as two charged planes in an electrolyte. Our calculations show that nematic ordering is favored over hexagonal packing between 0.24 and 1.41 eV coulombic interaction.
To estimate the Coulomb interaction W per unit area between the nanorods in water and in the presence of an electrolyte, the following relation is used27
W = 2σ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Kd)/Kεrε0, exp(−Kd)/Kεrε0, | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes (such as KOH), the inverse Debye length K (in nm−1) is given by27
1 electrolytes (such as KOH), the inverse Debye length K (in nm−1) is given by27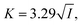 | (4) |
Conclusions
In conclusion, we report control over the phase behaviour of CdS nanorods via the ligand and acidity. By replacing the original TDPA ligands with the shorter BT, smectic A ordering was obtained. This was attributed to enhanced dipolar interactions due to the smaller rod–rod distance. By using ligands with an amino, thiol, or carboxylic acid terminal function group homeotropic simple hexagonal ordering could be obtained. When dispersed in water, this ordering could be turned into nematic ordering under basic conditions. A calculation of the van der Waals and electrostatic interactions was used to explain the observed influence of pH: at low pH, when there is no net charge on the nanorods, enhanced rod side-to-side interactions make possible the occurrence of a simple hexagonal phase. At high pH, electrostatic repulsive forces cause the nanorods to order in nematic patterns so as to reduce the number of nearest-neighbours. This pH control offers a means of changing the phase behaviour of lyotropic nanorods without using an external stimulus.Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council, UK [Grant number EP/C015401/1].Notes and references
- L. Carbone, S. Kudera, E. Carlino, W. J. Parak, C. Giannini, R. Cingolani and L. Manna, J. Am. Chem. Soc., 2006, 128, 748 CrossRef CAS PubMed.
- S. Asokan, K. M. Krueger, V. L. Colvin and M. S. Wong, Small, 2007, 3, 1 CrossRef PubMed.
- S. Sapra, J. Poppe and A. Eychmüller, Small, 2007, 3, 1886 CrossRef CAS PubMed.
- Y. Li, H. Zhong, R. Li, Y. Zhou, C. Yang and Y. Li, Adv. Funct. Mater., 2006, 16, 1705 CrossRef CAS.
- F. Dumestre, B. Chaudret, C. Amiens, M. Respaud, P. Fejes, P. Renaud and P. Zurcher, Angew. Chem., Int. Ed., 2003, 42, 5213 CrossRef CAS PubMed.
- L. Carbone, C. Nobile, M. De Giorgi, F. Della Sala, G. Morello, P. Pompa, M. Hutch, E. Snoeck, A. Fiore, I. R. Franchini, M. Nadasan, A. F. Silvestre, L. Chiodo, S. Kudera, R. Cingolani, R. Krahne and L. Manna, Nano Lett., 2007, 7, 2942 CrossRef CAS PubMed.
- C.-C. Kang, C.-W. Lai, H.-C. Peng, J.-J. Shyue and P.-T. Chou, ACS Nano, 2008, 2, 750 CrossRef CAS PubMed.
- D. V. Talapin, E. V. Shevchenko, C. B. Murray, A. Komowski, S. Förster and H. Weller, J. Am. Chem. Soc., 2004, 126, 12984 CrossRef CAS PubMed.
- L. Li, J. Walda, L. Manna and A. P. Alivisatos, Nano Lett., 2002, 2, 557 CrossRef CAS.
- L. Li and A. P. Alivisatos, Adv. Mater., 2003, 15, 408 CrossRef CAS.
- S. Ahmed and K. M. Ryan, Nano Lett., 2007, 7, 2480 CrossRef CAS PubMed.
- A. Ghezelbash, B. Koo and B. A. Korgel, Nano Lett., 2006, 6, 1832 CrossRef CAS PubMed.
- A. Dessombz, D. Chiche, P. Davidson, P. Panine, C. Chanéac and J.-P. Jolivet, J. Am. Chem. Soc., 2007, 129, 5904 CrossRef CAS PubMed.
- A. Singh, R. D. Gunning, S. Ahmd, C. A. Barrett, N. J. English, J.-A. Garate and K. M. Ryan, J. Mater. Chem., 2012, 22, 1562 RSC.
- J. L. Baker, A. Widmer-Cooper, M. F. Toney, P. L. Geissler and A. P. Alivisatos, Nano Lett., 2010, 10, 195 CrossRef CAS PubMed.
- Z. Quan and J. Fang, Nano Today, 2010, 5, 390 CrossRef CAS PubMed.
- A. Singh, R. D. Gunning, A. Sanyal and K. M. Ryan, Chem. Commun., 2010, 46, 7193 RSC.
- A. Singh, R. D. Gunning, S. Ahmed, C. A. Barrett, N. J. English, J.-A. Garate and K. M. Ryan, J. Mater. Chem., 2012, 22, 1562 RSC.
- A. E. Saunders, I. Popov and U. Banin, J. Phys. Chem. B, 2006, 110, 25421 CrossRef CAS PubMed.
- J. P. Danehy and C. J. Noel, J. Am. Chem. Soc., 1960, 82, 2511 CrossRef CAS.
- H. Hiramatsu and F. E. Osterloh, Langmuir, 2003, 19, 7003 CrossRef CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627 CrossRef CAS PubMed.
- F. Kim, S. Kwan, J. Akana and P. Yang, J. Am. Chem. Soc., 2001, 123, 4360 CrossRef CAS.
- D. V. Talapin, E. V. Shevchenko, C. B. Murray, A. V. Titov and P. Král, Nano Lett., 2007, 7, 1213 CrossRef CAS PubMed.
- P. G. Bolhuis, D. Frenkel, S.-C. Mau and D. A. Huse, Nature, 1997, 388, 235 CrossRef CAS PubMed.
- A. V. Titov and P. Král, Nano Lett., 2008, 8, 3605 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular & Surface Forces, Academic Press, San Diego, CA, USA, 1991 Search PubMed.
- J. Ren, S. Song, A. Lopez-Valdivieso, J. Shen and S. Lu, J. Colloid Interface Sci., 2001, 238, 279 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, calculation of the van der Waals interactions, calculation of the dipole–dipole interactions. See DOI: 10.1039/c4sm00728j |
| This journal is © The Royal Society of Chemistry 2014 |