Open Access Article
Open Access ArticleExperimental verification of fracture mechanism for polymer gels with controlled network structure
Takamasa
Sakai
*,
Yuki
Akagi
,
Shinji
Kondo
and
Ungil
Chung
Department of Bioengineering, Graduate School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan. E-mail: sakai@tetrapod.t.u-tokyo.ac.jp
First published on 9th June 2014
Abstract
Recently, polymer gels have drawn much attention as scaffolds for regenerative medicines, soft actuators, and functional membranes. These applications need tough and robust polymer gels as represented by the double network gels. To fully understand this mechanism and develop further advanced polymer gels, we need to fully understand the molecular origin of fracture energy for conventional polymer gels, which is inhibited by the inherent heterogeneity. In this paper, we show the experimental results on the fracture of model polymer gels with controlled network structure, and discuss the mechanism of the fracture of polymer gels.
I. Introduction
Elastomers are important materials for a variety of applications, including tires, shock absorbing materials, soft actuators, and biomaterials. To tailor the physical properties for each application, the molecular understanding of physical properties is of particular importance. However, at this point, we do not have definite pictures for the molecular origin of physical properties. For example, the elastic modulus (G) is explained by the relationship with the number density of elastically effective chains.1,2 We have two popular models for the elastic modulus, including the affine network1 and phantom network3 models; however, their validity or applicability has not been clarified. This problem is caused by the difficulty in the control of the network structures and in the direct observation of the network structure. Because the elastomers have complicated and heterogeneous structure,4 including heterogeneous distribution of crosslinking, chain entanglements, dangling ends, and loops, we cannot estimate the structural parameters of elastomers from the feed condition. In addition, we cannot observe these complicated substructures with direct visualization by TEM and SEM. To understand the molecular origin of physical properties, as a first step, we need to perform a series of studies on elastomers with controlled network structure.Recently, we succeeded in fabricating homogeneous polymer network system from a novel molecular design in prepolymer architecture and reaction system.5,6 We synthesized two kinds of tetra-armed prepolymers with mutually reactive end groups, which are amine and activated ester. We can fabricate polymer gels by mixing two aqueous solutions of the prepolymers at around the physiological condition. The unique tetra-armed prepolymers completely inhibit the self-biting reaction, and form the elastically effective chains efficiently. The ionic equilibrium of amine species allows us to control the reaction rate and to mix two prepolymer solutions, resulting in homogeneous network structure.7 We named this polymer network swollen in aqueous solution as Tetra-PEG gel, and validated the homogeneity by means of the small angle neutron scattering8,9 and nuclear magnetic resonance.10 These measurements clarified that the heterogeneity of Tetra-PEG gel was strongly suppressed over the other structure-controlled polymer networks, including “model networks.” Using Tetra-PEG gel as a model system, we observed for the first time, the crossover of elastic modulus from the phantom to the affine network models with an increase in the polymer volume fraction,11 which was originally predicted by Flory in 1977.12 These experimental results strongly suggest that Tetra-PEG gel is a promising model system contributing to the molecular understanding of the physical properties of elastomeric materials.
In this paper, we focus on the fracture of polymer gels. In general, the most important parameter related to the fracture is the fracture energy (T0), which is the energy required to propagate a unit length of crack. The Lake–Thomas theory describes T0 as the energy needed to break the chemical bonds per unit cross-section on the fracture surface as follows:13
 | (1) |
 | (2) |
The value of k strongly depends on the system and is in the range from unity to thousands. Notably, the popular double network gels with extremely high fracture toughness have high k up to thousands.18–20 Because the effect of k is so strong, the molecular origin of k is of great importance for designing the advanced materials.
To investigate the fracture energy, we prepared Tetra-PEG gels with variable degree of strand polymerization between crosslinks (Nc), polymer volume fraction (ϕ0), connectivity (p), and heterogeneous distribution in strand length. Through the analysis of Tetra-PEG gels, we discuss the effects of structural parameters on fracture energy based on the Lake–Thomas model, and finally discuss the enhancement factor.
II. Experimental procedure
A. Synthesis and characterization of prepolymers
Tetra-PEG gel consists of two kinds of prepolymers: tetra poly(ethylene glycol)-succinimidyl carbonate (TetraPEG-OSu) and tetra poly(ethylene glycol)-amine (TetraPEG-NH2). These prepolymers were synthesized from tetra poly(ethylene glycol) (TetraPEG-OH). Each prepolymer was characterized by 1H NMR (JEOL JNM-AL 300 MHz) and gel permeation chromatography (TOSOH HLC-8220) system.11,22,23B. Fabrication of Tetra-PEG gels
We fabricated four kinds of Tetra-PEG gels: (i) conventional Tetra-PEG gel, (ii) p-tuned Tetra-PEG gel, (iii) hetero Tetra-PEG gel, and (iv) bimodal Tetra-PEG gel.Equimolar quantities of TetraPEG-NH2 and TetraPEG-OSu (ϕ0: 0.034–0.12) were dissolved in phosphate buffer (pH 7.4) and phosphate-citric acid buffer (pH 5.8), respectively. The ionic strength of buffer solution was varied to maintain the pH of the solution. In order to tune p, the TetraPEG-OSu solution was incubated at 25 °C for a series of times (tdeg). After the incubation time, TetraPEG-NH2 and TetraPEG-OSu solutions were mixed, and the resultant solution was poured into the mold. At least 12 hours were allowed for the completion of the reaction before the following experiment was performed. The detailed experimental conditions are listed in Tables 1–3.
| Combination of TetraPEG's (g mol−1) | ϕ 0 | Ionic strength of buffers (mM) | Incubation time of TetraPEG-OSu (min) |
|---|---|---|---|
| 5k–5k | 0.034 | 50 | 0 |
| 0.050 | |||
| 0.066 | |||
| 0.081 | 100 | ||
| 0.12 | |||
| 10k–10k | 0.034 | 25 | 0 |
| 0.050 | |||
| 0.066 | |||
| 0.081 | 50 | ||
| 0.12 | |||
| 20k–20k | 0.034 | 50 | 0 |
| 0.050 | |||
| 0.066 | |||
| 0.081 | 100 | ||
| 0.12 | |||
| 40k–40k | 0.034 | 25 | 0 |
| 0.050 | |||
| 0.066 | |||
| 0.081 | 50 | ||
| 0.12 | |||
| 20k–20k | 0.081 | 100 | 20 |
| 80 | |||
| 120 | |||
| 160 | |||
| 200 | |||
| 240 | |||
| 320 | |||
| 400 |
| Combination of TetraPEG's (g mol−1) | ϕ 0 | Ionic strength of buffers (mM) |
|---|---|---|
| 5k–10k | 0.034 | 50 |
| 0.050 | ||
| 0.066 | ||
| 0.081 | 100 | |
| 0.12 | ||
| 5k–20k | 0.034 | 25 |
| 0.050 | ||
| 0.066 | 50 | |
| 0.081 | ||
| 0.12 | 100 | |
| 10k–20k | 0.034 | 25 |
| 0.050 | ||
| 0.066 | ||
| 0.081 | 50 | |
| 0.12 |
| Combination of TetraPEG's (g mol−1) | 20 kg mol−1 Tetra-PEG mol fraction (r) | ϕ 0 | Ionic strength of buffers (mM) | |||
|---|---|---|---|---|---|---|
| TetraPEG-NH2 [mM] | TetraPEG-OSu [mM] | |||||
| 5k | 20k | 5k | 20k | |||
| 4.0 | 0 | 4.0 | 0 | 0 | 0.034 | 25 |
| 4.0 | 0 | 3.0 | 1.0 | 0.125 | 0.046 | |
| 4.0 | 0 | 2.0 | 2.0 | 0.25 | 0.058 | |
| 4.0 | 0 | 1.0 | 3.0 | 0.375 | 0.070 | |
| 4.0 | 0 | 0 | 4.0 | 0.5 | 0.081 | 50 |
| 3.0 | 1.0 | 0 | 4.0 | 0.675 | 0.092 | |
| 2.0 | 2.0 | 0 | 4.0 | 0.75 | 0.103 | 100 |
| 1.0 | 3.0 | 0 | 4.0 | 0.875 | 0.113 | |
| 0 | 4.0 | 0 | 4.0 | 1 | 0.124 | |
C. Infrared (IR) measurement
The gel samples were prepared as cylinder shape (diameter: 15 mm, height: 7.5 mm), and immersed in H2O for 2 days in order to remove the sol fraction.After drying in air, the samples were cut into thin films (thickness: 40 μm) using a microtome (SM2000R, Leica). These dried samples were swollen in D2O, and then soaked in a mixture solvent of D2O and oligo-PEG (Mw = 0.40 kg mol−1) (v/v = 1/1). The IR measurements for these samples were performed using a JASCO FT-IR-6300 equipped with a deuterated triglycine sulfate (DTGS) detector, in which 128 scans were co-added at a resolution of 4 cm−1 for the samples.
D. Tearing test
The tearing test was performed in air using a stretching machine (Tensilon RTC-1150A, Orientec Co.). The samples were cut into the shape, which has standardized JIS-K 6252 as 1/2 sizes (width: 50 mm, length: 7.5 mm, thickness: 1 mm, the length of initial notch is 20 mm) using a gel cutting machine (Dumb Bell Co., Ltd.). The two arms of the test sample were clamped and one arm was pulled upward at a constant velocity (40 and 500 mm min−1), while the other arm was maintained stationary; moreover, the tearing force F was also recorded.III. Results and discussion
A. Fabrication of Tetra-PEG gels
We fabricated four kinds of Tetra-PEG gels: (i) conventional Tetra-PEG gel, (ii) p-tuned Tetra-PEG gel, (iii) hetero Tetra-PEG gel, and (iv) bimodal Tetra-PEG gel.(i) Conventional Tetra-PEG gel (Fig. 1a):21 Equimolar amounts of TetraPEG-NH2 and TetraPEG-OSu with the same molecular weight were used as prepolymers. The molecular weights of prepolymers (Mw) were tuned in 5, 10, 20 and 40 kg mol−1 and resultant gels were named as named as 5k, 10k, 20k and 40k Tetra-PEG gel, respectively. The polymer volume fraction (ϕ0) was tuned from 0.034 to 0.12.
(ii) p-tuned Tetra-PEG gel (Fig. 1b):21p-tuned Tetra-PEG gels are fabricated by using partially hydrolyzed TetraPEG-OSu as a prepolymer. Prior to the reaction, Tetra-PEG-OSu was dissolved in the aqueous buffer solution and allowed to hydrolyze for a certain period of time (tdeg = 0, 20, 80, 120, 160, 200, 240, 320 and 400 min). The values of Mw and ϕ0 were fixed as 20 kg mol−1 and 0.081, respectively.
(iii) Hetero Tetra-PEG gel (Fig. 1c):22 Equimolar amounts of TetraPEG-NH2 and TetraPEG-OSu with different molecular weights were used as prepolymers. The polymer gels formed from the combinations of prepolymers with 5k–10k, 5k–20k and 10k–20k were named as 5k–10k, 5k–20k and 10k–20k Tetra-PEG hetero gel, respectively. The value of ϕ0 was tuned from 0.034 to 0.12.
(iv) Bimodal Tetra-PEG gel (Fig. 1d):23 We mixed 5k and 20k Tetra-PEG prepolymers with the molar ratio being tuned (r = (20k Tetra-PEG prepolymer)/(total prepolymer)) while maintaining the equimolar condition of amine and activated ester. The molar concentration of prepolymers was fixed to 8.0 × 10−3 mol L−1. We started from the mixing of 5k TetraPEG-NH2 and 5k TetraPEG-OSu, which forms Tetra-PEG unimodal gel with molecular weight of network strand of 2.5k g mol−1 (r = 0), and then we gradually exchanged 5k TetraPEG-OSu to 20k TetraPEG-OSu. It should be noted that Tetra-PEG gel formed from 5k TetraPEG-NH2 and 20k TetraPEG-OSu (r = 0.5) corresponds to Tetra-PEG unimodal gel with molecular weight of network strand of 6.25k g mol−1. Then, we gradually exchanged 5k TetraPEG-NH2 to 20k TetraPEG-NH2, which finally resulted in Tetra-PEG unimodal gel with molecular weight of network strand of 10k g mol−1 (r = 1.0).
p was estimated by FT-IR measurement for gel samples.11p was estimated from the peak intensity of ionized carboxyl group (1555 cm−1) and that of amide bond (1624 cm−1) as follows:
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0. The values of p were almost constant against ϕ0 in all Tetra-PEG gels, and they were 0.82–0.95 for 5k, 10k and 20k Tetra-PEG gels, 5k–10k, 5k–20k and 10k–20k Tetra-PEG hetero gels and Tetra-PEG bimodal gels, whereas p was 0.71–0.81 for 40k Tetra-PEG gel (Fig. 2).
1.0. The values of p were almost constant against ϕ0 in all Tetra-PEG gels, and they were 0.82–0.95 for 5k, 10k and 20k Tetra-PEG gels, 5k–10k, 5k–20k and 10k–20k Tetra-PEG hetero gels and Tetra-PEG bimodal gels, whereas p was 0.71–0.81 for 40k Tetra-PEG gel (Fig. 2).
B. Estimation of fracture energy
To investigate the fracture energy (T0), we performed the tearing measurement for trouser-shaped specimens.11 The gel specimens were used in as-prepared state, not in equilibrium-swollen state. The two legs of a sample were cramped and the upper leg was pulled upward at a constant velocity of 40 mm min−1, while the other leg was maintained stationary, and the load (F) was recorded. We performed the tearing measurements at a different velocity of 500 mm min−1, and confirmed the rate-independent tearing behavior in this experimental condition. The similar rate-independent tearing behavior was observed for other gel systems.Fig. 3 shows the tearing behavior of conventional Tetra-PEG gels. In the beginning, the load value monotonously increased with an extension, where crack did not propagate. After starting the crack propagation, the load fluctuated with an extension. In the whole region of 5k and 10k, and the low ϕ0 region of 20k and 40k Tetra-PEG gel, the steady tearing, where the degree of fluctuation is relatively small, was observed. On the other hand, the stick-slip tearing, where the degree of fluctuation is large and clear peaks were observed, was observed for 20k and 40k Tetra-PEG gel with the higher ϕ0 region, and the tendency became prominent with increases in Mw and ϕ0.
 | ||
| Fig. 3 Tearing force-extension relationships in (a) 5k, (b) 10k, (c) 20k, (d) 40k Tetra-PEG gel (fine line, ϕ0 = 0.034; bold line, ϕ0 = 0.1). | ||
We estimated different values of T0 from the average of local maximum, the simple average and the average of local minimum values of F as,
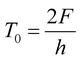 | (4) |
C. p-tuned Tetra-PEG gels
Prior to the investigation on conventional Tetra-PEG gels, we focus on the p-tuned Tetra-PEG gels.21 This is because the connectivity defects of the network can influence the structural parameters including ν and N. When we accept the above-mentioned scaling relationships G ∼ ν and G ∼ N−1, the decrease in p will decrease ν, leading to an increase in N. If the value of N was influenced by p, we could not use the values of N directly calculated from the molecular weight of prepolymers as| N = Mw/ 2mPEG | (5) |
By hydrolyzing the activated ester prior to the reaction, the values of p were successfully tuned from 0.55 to 0.92 (Fig. 4). The effect of p on ν can be directly predicted according to the tree-like approximation as follows:24,25
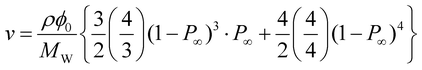 | (6) |
| P∞ = pP3∞ + (1 − p) | (7) |
 is the usual notation for the number of combinations of x items taken y at a time: x!/y!(x − y)!. Notably, in the previous reports, we have checked the validity of ν calculated by the tree-like approximation through the experimental study on elastic modulus of the p-tuned Tetra-PEG gels.26
is the usual notation for the number of combinations of x items taken y at a time: x!/y!(x − y)!. Notably, in the previous reports, we have checked the validity of ν calculated by the tree-like approximation through the experimental study on elastic modulus of the p-tuned Tetra-PEG gels.26
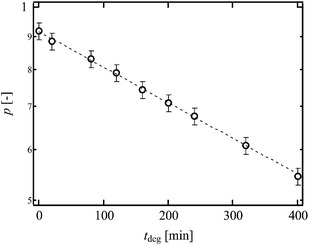 | ||
| Fig. 4 p as a function of tdeg. The dashed line is the guideline shows the relationship, p ∼ exp( − tdeg). (Reproduced from Akagi et al.21 with permission from the American Institute of Physics.) | ||
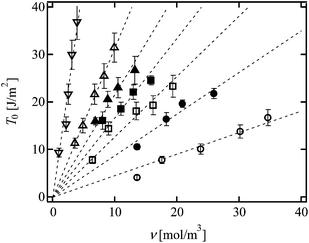
Fig. 5 shows the values of T0 against ν. As mentioned above, the change in ν was purely originated from the change in p. The dashed line represents the scaling prediction of the Lake–Thomas model, T0 ∼ ν. As clearly shown in Fig. 5, the experimental data obeyed the Lake–Thomas prediction in the region ν > 4.0 (p > 0.65). This agreement in this region indicates that ν calculated by the tree-like approximation is applicable to the Lake–Thomas model, and that the term LNU does not depend on p. In the region p > 0.65, we can use the values of N and U calculated from eqn (5) and (8), respectively.
| U = 357 (C–C bond) + 2 × 329 (C–O bond) = 1.0 × 106 J mol−1 | (8) |
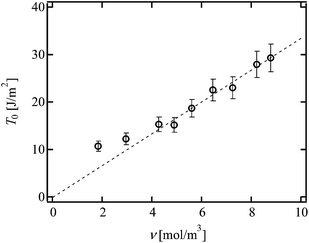 | ||
| Fig. 5 T 0 as a function of ν in p-tuned Tetra-PEG gel. (Reproduced from Akagi et al.21 with permission from the American Institute of Physics.) | ||
On the other hand, in the region of ν < 4.0, T0 deviated upward from the guideline. This region corresponds to the region where the elastic modulus cannot be predicted by ν calculated under the tree-like approximation. A massive amount of dangling chains may inhibit the mean-field-like treatment in this region. In the following analyses, we use the N and U calculated from eqn (5) and (8), because all the values of p shown in Fig. 2 are higher than 0.65.
D. Conventional Tetra-PEG gels and hetero Tetra-PEG gels
In order to investigate the effects of N and ϕ0 on T0, we evaluated T0 of the conventional Tetra-PEG gels with different N and ϕ0.21Fig. 6 (open symbols) shows the values of T0 as a function of ν; the values of T0 of the same N were on the same line proportional to ν. Because the difference in ν for Tetra-PEG gels with each N was purely originated from ϕ0, these data indicate that the slope (LNU) is independent of ϕ0, but dependent on N. From the linear fit, the slopes are estimated to be 0.45, 1.28, 3.15 and 9.18 for 5k, 10k, 20k and 40k Tetra-PEG gels, respectively. Here, we show the data of hetero Tetra-PEG gels (Fig. 1c).22 Notably, each hetero Tetra-PEG gel has a monomodal network strand length defined by the molecular weights of prepolymers (M1 and M2) as N = (M1 + M2)/4mPEG (e.g. for 5k–10k Tetra-PEG hetero gel, N = (5000 + 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)/4/44 = 85.2). As shown in Fig. 6 (filled symbols), we can observe the linear relationships for hetero Tetra-PEG gels, and the slopes increased with an increase in N; the slopes were 0.88, 1.68 and 2.17 for 5k–10k, 5k–20k and 10k–20k hetero Tetra-PEG gels, respectively. Using the constant values of N and U calculated from eqn (5) and (8), we estimated the values of L from the slopes according to eqn (1).
000)/4/44 = 85.2). As shown in Fig. 6 (filled symbols), we can observe the linear relationships for hetero Tetra-PEG gels, and the slopes increased with an increase in N; the slopes were 0.88, 1.68 and 2.17 for 5k–10k, 5k–20k and 10k–20k hetero Tetra-PEG gels, respectively. Using the constant values of N and U calculated from eqn (5) and (8), we estimated the values of L from the slopes according to eqn (1).
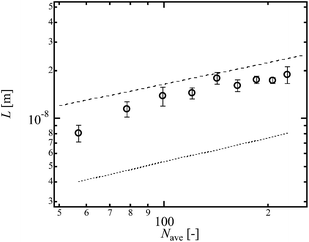
Fig. 7 shows L of conventional Tetra-PEG gels (open circles) and Tetra-PEG hetero gels (filled circles) against N. L increased from 13 to 34 nm with an increase in N. In the original Lake-Thomas model, L corresponds to R0 (≈aN1/2) of virtual network chains with polymerization degree of N (dotted line in Fig. 7). R0 is calculated as bkNk1/2, where bk (0.65 nm) and Nk are the length and number of Kuhn segments, respectively.27–29 The values of Nk are derived as Nk = 0.68 N, where we assume that the bond angles are 109.5°, and bond length of C–C and C–O are 0.154 and 0.145 nm, respectively. The values of L and R0 have similar magnitude and N-dependence, but are different from each other. According to eqn (2), we estimated k for each N and plotted it against N (Fig. 8). The values of k were almost constant and approximately 3 in the range examined. These data indicate that network strands within 3R0 from the crack tip are extended at the fracture, and the length is determined only by N, regardless of p and ϕ0.
 | ||
| Fig. 7 L as a function of N in Tetra-PEG gel (open circles) and hetero Tetra-PEG gel (filled circles). | ||
 | ||
| Fig. 8 k as a function of N in Tetra-PEG gel (open circles) and hetero Tetra-PEG gel (filled circles). | ||
E. Bimodal Tetra-PEG gels
Finally, we investigated effect of another heterogeneity, i.e., heterogeneous distribution in strand length.23 This heterogeneity was introduced by mixing three kinds of 5k and 20k Tetra-PEG prepolymers with the molar ratio being tuned (Fig. 1d, r = (20k Tetra-PEG prepolymer)/(total prepolymer)). We tuned r with fixing the molar concentration of prepolymers to 8.0 × 10−3 mol L−1 (Fig. 1d). The molecular weight of shorter strands is 2.5 kg mol−1, whereas that of longer strands is 10 kg mol−1. Although the difference in the molecular weight is not so large, we can assess the effect of heterogeneous distribution in strand length on T0. Fig. 9 shows the T0 of the bimodal Tetra-PEG gels. As shown in Fig. 9, T0 increased with r. The calculated values of ν were almost constant against r, reflecting the constant p. Considering the constant ν against r, the increase in T0 is originated from other parameters such as N and L. Here, we assume that the value of N in the bimodal Tetra-PEG gels is represented by the number-average degree of polymerization of prepolymers (Nave = (5000 (1 − r) + 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000r)/2mPEG). Fig. 10 shows the Nave-dependence of L and guide of R0 calculated from Nave (dotted line). The values of L and R0 have similar Nave-dependence, but are different from each other. We also estimated k using eqn (2), and plotted against N in Fig. 11. Although the values of k were slightly smaller than those for conventional and hetero Tetra-PEG gels, the values were similar with each other. These data indicate that the heterogeneous distribution in strand length does not significantly influence T0 in the range of this study.
000r)/2mPEG). Fig. 10 shows the Nave-dependence of L and guide of R0 calculated from Nave (dotted line). The values of L and R0 have similar Nave-dependence, but are different from each other. We also estimated k using eqn (2), and plotted against N in Fig. 11. Although the values of k were slightly smaller than those for conventional and hetero Tetra-PEG gels, the values were similar with each other. These data indicate that the heterogeneous distribution in strand length does not significantly influence T0 in the range of this study.
IV. Conclusions
In this paper, we discussed the fracture energy of polymer gels with controlled network structure. The fracture energies of Tetra-PEG gels with tuned structural parameters are fully explained by the Lake–Thomas model with k = 3. The value of k is universal in the range of this study, and both the changes in ϕ0 and N and the connective heterogeneity and heterogeneous distribution in strand length did not affect the value of k. These data suggest that the enhancement factor estimated in this study can be applicable to the conventional polymer gels with the similar concentration range regardless of the degree of heterogeneity, although there is a possibility that the macroscopic heterogeneity (∼μm), which was not observed in Tetra-PEG gel system, affects the fracture toughness. In other words, the network homogeneity does not strongly contribute to the enhancement of fracture toughness. The constant k also suggests that it is difficult for conventional polymer gels to achieve the enhanced fracture toughness. As proposed by Gong, chain entanglements may play an important role for enhanced k.19,20,30–32Here, we must point out the limitation of this study; i.e., we investigated T0 computed from the minimum values of F in the tearing measurements. We ignored the effect of tearing behavior: steady state or stick-slip. Because fracture starts at the maximum values of F, the molecular understanding of T0 calculated from the maximum value of F is also important. Thus, to fully understand the fracture behavior, we also need further investigate the tearing behavior.
Acknowledgements
This work was supported by the Japan Society for the Promotion of Science (JSPS) through the Grants-in-Aid for Scientific Research, the Center for Medical System Innovation (CMSI), the Graduate Program for Leaders in Life Innovation (GPLLI), the International Core Research Center for Nanobio, Core-to-Core Program, A. The Advanced Research Networks and the Funding Program for World-Leading Innovative R&D on Science and Technology (FIRST program); the Ministry of Education, Culture, Sports, Science, and Technology in Japan (MEXT) through the Center for NanoBio Integration (CNBI) and Grants-in-Aid for Scientific Research from MEXT (23700555 to T.S. and 24240069 to U.C.); the Japan Science and Technology Agency (JST) through the S-innovation program and COI STREAM.References
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, ITHACA and LONDON, 1953 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- H. M. James and E. Guth, J. Chem. Phys., 1943, 11, 455–481 CrossRef CAS PubMed.
- M. Shibayama, Macromol. Chem. Phys., 1998, 199, 1–30 CrossRef CAS.
- T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U. I. Chung, Macromolecules, 2008, 41, 5379–5384 CrossRef CAS.
- T. Sakai, React. Funct. Polym., 2013, 73, 898–903 CrossRef CAS PubMed.
- K. Nishi, K. Fujii, M. Chijiishi, Y. Katsumoto, U. Chung, T. Sakai and M. Shibayama, Macromolecules, 2012, 45, 1031–1036 CrossRef CAS.
- T. Matsunaga, T. Sakai, Y. Akagi, U. Chung and M. Shibayama, Macromolecules, 2009, 42, 1344–1351 CrossRef CAS.
- T. Matsunaga, T. Sakai, Y. Akagi, U. I. Chung and M. Shibayama, Macromolecules, 2009, 42, 6245–6252 CrossRef CAS.
- F. Lange, K. Schwenke, M. Kurakazu, Y. Akagi, U. I. Chung, M. Lane, J. U. Sommer, T. Sakai and K. Saalwachter, Macromolecules, 2011, 44, 9666–9674 CrossRef CAS.
- Y. Akagi, J. P. Gong, U. Chung and T. Sakai, Macromolecules, 2013, 46, 1035–1040 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1977, 66, 5720–5729 CrossRef CAS PubMed.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CrossRef CAS.
- A. N. Gent and R. H. Tobias, J. Polym. Sci., Polym. Phys. Ed., 1982, 20, 2051–2058 CrossRef CAS.
- A. N. Gent, Langmuir, 1996, 12, 4492–4496 CrossRef CAS.
- P. G. deGennes, Langmuir, 1996, 12, 4497–4500 CrossRef CAS.
- K. Okumura, Europhys. Lett., 2004, 67, 470–476 CrossRef CAS.
- Y. Tanaka, R. Kuwabara, Y. H. Na, T. Kurokawa, J. P. Gong and Y. Osada, J. Phys. Chem. B, 2005, 109, 11559–11562 CrossRef CAS PubMed.
- M. Huang, H. Furukawa, Y. Tanaka, T. Nakajima, Y. Osada and J. P. Gong, Macromolecules, 2007, 40, 6658–6664 CrossRef CAS.
- S. M. Liang, Z. L. Wu, J. Hu, T. Kurokawa, Q. M. Yu and J. P. Gong, Macromolecules, 2011, 44, 3016–3020 CrossRef CAS.
- Y. Akagi, H. Sakurai, J. P. Gong, U. Chung and T. Sakai, J. Chem. Phys., 2013, 139 Search PubMed.
- S. Kondo, U. Chung and T. Sakai, Polym. J., 2014, 46, 14–20 CrossRef CAS.
- S. Kondo, H. Sakurai, U. I. Chung and T. Sakai, Macromolecules, 2013, 46, 7027–7033 CrossRef CAS.
- D. R. Miller and C. W. Macosko, Macromolecules, 1976, 9, 206–211 CrossRef CAS.
- Y. Akagi, T. Matsunaga, M. Shibayama, U. Chung and T. Sakai, Macromolecules, 2010, 43, 488–493 CrossRef CAS.
- K. Nishi, M. Chijiishi, Y. Katsumoto, T. Nakao, K. Fujii, U. Chung, H. Noguchi, T. Sakai and M. Shibayama, J. Chem. Phys., 2012, 137, 224903 CrossRef PubMed.
- F. Oesterhelt, M. Rief and H. E. Gaub, New J. Phys., 1999, 1, 6.1–6.6 CrossRef.
- F. Kienberger, V. Ph. Pastushenko, G. Kada, H. J. Gruber, C. Riener, H. Schindler and P. Hinterdorfer, Single Mol., 2000, 1, 123–128 CrossRef CAS.
- S. Zou, H. Schonherr and G. J. Vancso, Angew. Chem., Int. Ed., 2005, 44, 956–959 CrossRef CAS PubMed.
- Y. Tanaka, Europhys. Lett., 2007, 78, 56005 CrossRef.
- H. R. Brown, Macromolecules, 2007, 40, 3815–3818 CrossRef CAS.
- T. Nakajima, Y. Fukuda, T. Kurokawa, T. Sakai, U. Chung and J. P. Gong, ACS Macro Lett., 2013, 2, 518–521 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |