Effects of coordination and pressure on sound attenuation, boson peak and elasticity in amorphous solids
Abstract
Connectedness and applied stress strongly affect elasticity in solids. In various amorphous materials, mechanical stability can be lost either by reducing connectedness or by increasing pressure. We present an effective medium theory of elasticity that extends previous approaches by incorporating the effect of compression, of amplitude e, allowing one to describe quantitative features of sound propagation, transport, the boson peak, and elastic moduli near the elastic instability occurring at a compression ec. The theory disentangles several frequencies characterizing the vibrational spectrum: the onset frequency 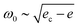 where strongly-scattered modes appear in the vibrational spectrum, the pressure-independent frequency ω* where the density of states displays a plateau, the boson peak frequency ωBP found to scale as
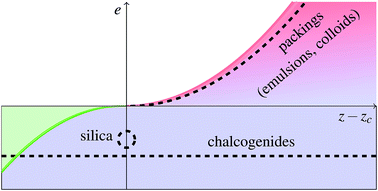
where strongly-scattered modes appear in the vibrational spectrum, the pressure-independent frequency ω* where the density of states displays a plateau, the boson peak frequency ωBP found to scale as 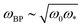 , and the Ioffe–Regel frequency ωIR where scattering length and wavelength become equal. We predict that sound attenuation crosses over from ω4 to ω2 behaviour at ω0, consistent with observations in glasses. We predict that a frequency-dependent length scale ls(ω) and speed of sound ν(ω) characterize vibrational modes, and could be extracted from scattering data. One key result is the prediction of a flat diffusivity above ω0, in agreement with previously unexplained observations. We find that the shear modulus does not vanish at the elastic instability, but drops by a factor of 2. We check our predictions in packings of soft particles and study the case of covalent networks and silica, for which we predict ωIR ≈ ωBP. Overall, our approach unifies sound attenuation, transport and length scales entering elasticity in a single framework where disorder is not the main parameter controlling the boson peak, in agreement with observations. This framework leads to a phase diagram where various glasses can be placed, connecting microscopic structure to vibrational properties.
, and the Ioffe–Regel frequency ωIR where scattering length and wavelength become equal. We predict that sound attenuation crosses over from ω4 to ω2 behaviour at ω0, consistent with observations in glasses. We predict that a frequency-dependent length scale ls(ω) and speed of sound ν(ω) characterize vibrational modes, and could be extracted from scattering data. One key result is the prediction of a flat diffusivity above ω0, in agreement with previously unexplained observations. We find that the shear modulus does not vanish at the elastic instability, but drops by a factor of 2. We check our predictions in packings of soft particles and study the case of covalent networks and silica, for which we predict ωIR ≈ ωBP. Overall, our approach unifies sound attenuation, transport and length scales entering elasticity in a single framework where disorder is not the main parameter controlling the boson peak, in agreement with observations. This framework leads to a phase diagram where various glasses can be placed, connecting microscopic structure to vibrational properties.

 Please wait while we load your content...
Please wait while we load your content...