Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oil-in-water microemulsion droplets of TDMAO/decane interconnected by the telechelic C18-EO150-C18: clustering and network formation†
Paula
Malo de Molina
*ac,
Marie-Sousai
Appavou
b and
Michael
Gradzielski
*a
aStranski-Laboratorium für Physikalische und Theoretische Chemie, Institut für Chemie, Straße des 17. Juni 124, Sekr. TC7, Technische Universität Berlin, D-10623 Berlin, Germany
bForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science JCNS, Outstation at MLZ, Lichtenbergstr. 1, 85747 Garching, Germany
cDepartment of Chemical Engineering, University of California Santa Barbara, 3357 Engineering II, Santa Barbara, CA, USA
First published on 14th May 2014
Abstract
The effect of a doubly hydrophobically end-capped water soluble polymer (C18-PEO150-C18) on the properties of an oil-in-water (O/W) droplet microemulsion (R ∼ 2.85 nm) has been studied as a function of the amount of added telechelic polymer. Macroscopically one observes a substantial increase of viscosity once a concentration of ∼5 hydrophobic stickers per droplet is surpassed and effective cross-linking of the droplets takes place. SANS measurements show that the size of the individual droplets is not affected by the polymer addition but it induces attractive interactions at low concentration and repulsive ones at high polymer content. Measurements of the diffusion coefficient by DLS and FCS show increasing sizes at low polymer addition that can be attributed to the formation of clusters of microemulsion droplets interconnected by the polymer. At higher polymer content the network formation leads to an additional slow relaxation mode in DLS that can be related to the rheological behaviour, while the self-diffusion observed in FCS attains a lower plateau value, i.e., the microemulsion droplets remain effectively fixed within the network. The combination of SANS, DLS, and FCS allows us to derive a self-consistent picture of the evolution of structure and dynamics of the mixed system microemulsion/telechelic polymer as a function of the polymer content, which is not only relevant for controlling the macroscopic rheological properties but also with respect to the internal dynamics as it is, for instance, relevant for the release and transport of active agents.
Introduction
Microemulsions are a thermodynamically stable way of having homogeneous and very finely dispersed mixtures of oil and water. They may occur in the form of oil-in-water (O/W) and water-in-oil (W/O) droplets, or as bicontinuous structures.1,2 Their formation is facilitated by the presence of surfactant3,4 and the extent of structuring depends on the strength of the amphiphile present at the oil–water interface.5,6 Accordingly, they are attractive formulations for many applications where such highly interdispersed systems are required, for instance, when a hydrophobic active agent, substrate, or enzyme has to be present in an aqueous environment. However, for many applications of microemulsions the control of their rheological properties is a crucial question, which is not easily accomplished. Typically dilute microemulsions possess the viscosity of its continuous component (or the average of the both for the case of bicontinuous systems)7,8 irrespective of their structure. Water-based droplet microemulsions typically are water viscous and higher viscosities are only achieved for dense packing of droplets, i.e., above 30 vol%, and then for still somewhat higher concentrations microemulsion gels (cubic phases) are formed.9–13 However, the latter is a phase transition, going from a rather low viscous solution directly to a gel-like behaviour. This might be interesting for some applications, but in many situations having higher but continuously tuneable viscosities would be preferred, and without having to resort to go to very high surfactant concentrations.One way in which the viscosity of droplet microemulsions can be enhanced largely is by addition of a telechelic polymer with hydrophobic stickers (for instance, an alkyl chain) that adheres to the droplets and which is able to bridge the individual droplets. Depending on the number of polymer molecules contained, a physical network forms with corresponding rheological properties. For this approach a number of examples have been published14–20 and such systems have also been studied theoretically.21,22 The effectiveness of bridging is mainly controlled by the end-to-end distance of the polymer and the surface-to-surface separation of neighbouring droplets. MC simulations have shown that interactions become quite effective once both lengths become similar,21 leading to substantial changes of the pair distribution functions of the droplets.22 Once there is on average more than one bridging polymer per droplet, a network with viscoelastic behaviour is formed. The elasticity of the network depends on the number of polymers per droplet, and the viscosity depends on the structural relaxation time, which is determined by the exit time of the hydrophobic sticker from the microemulsion droplets and it is strongly related to the length of the sticker.23 Recently also the role of the number of telechelic arms has been addressed and it has been shown that the polymer architecture can play an important role in the control of the rheological properties; even more so with respect to the internal dynamics of the physically cross-linked microemulsions, where the dynamics, as seen by dynamic light scattering, becomes increasingly complex and slower with increasing number of telechelic arms.24
The dynamic properties of microemulsion and telechelic polymer mixtures are not completely understood despite their impact on the rheological properties or the kinetics of solubilisate exchange. So far, most of the work regarding the dynamics was concerned with DLS experiments, which for the case of highly viscous networks showed two or three relaxation modes.23,25–27 The fastest mode (diffusive) was associated with the concentration fluctuations of the microemulsion droplets, the intermediate mode (independent of q) with the network relaxation of the gel that is related to the terminal relaxation time and the self-diffusion of the polymer, and the slowest mode with the droplets in the surrounding network. Depending on the relaxation time of the stickers the intermediate mode may drop out of the experimental window for the case for too long hydrophobic stickers.23 Alternatively, FRAPP (fluorescence recovery after patterned photobleaching) has been employed to complement DLS measurements, where FRAPP showed a monoexponential relaxation that corresponds to the slowest mode observed in DLS.28 In this respect there is quite a bit known regarding the dynamic properties of networks of interconnected O/W microemulsion droplets, but the picture is yet far from being complete.
Accordingly, the aim of this work is to study such a structurally well characterized microemulsion network in a comprehensive fashion by combining dynamic light scattering (DLS) and fluorescence correlation spectroscopy (FCS) measurements, which yield complementary information, as the first method measures collective diffusion, the second self-diffusion. For that purpose we chose a microemulsion based on a surfactant frequently employed in formulations, tetradecyl dimethyl amine oxide (TDMAO),29 decane as oil (similar to paraffin oil), and the commercial rheological modifier Rewopal 6000 DS (a polyethylene oxide (PEO) with an average number of 150 EO units and having two stearate moieties at its ends). TDMAO has been shown to be able to solubilize hydrocarbons, where the solubilisation capacity is higher the shorter the chain of the solubilized alkane.30,31 TDMAO microemulsions with decane have been studied in some detail before and it was observed that the saturated microemulsion droplets have an almost identical size (R = 3.0 nm) over a large concentration range,10,32 which makes it a well-defined system to be studied. The comprehensive dynamic picture obtained by combining DLS and FCS measurements for microemulsion networks as a function of the amount of added polymer (quantified by the number of stickers per microemulsion droplet: r) combined with the structural and rheological information then shall allow for a systematic understanding of their dynamic properties. This is especially relevant for instance for molecular transport and delivery within such systems, as it is important for pharmaceutical or cosmetic formulations.
Experimental section
Materials
Tetradecyl dimethyl amine oxide (TDMAO, C14H29N(CH3)2O; Aromox 4D-W970, 24–26%) was obtained from Julius Hoesch (Düren, Germany) as a gift. The solutions were freeze-dried until no further water could be removed, at which point one had a water content of 2.5 wt%, as determined via Karl-Fischer-titration, which was taken into account during all sample preparations. n-Decane (∼98%) was obtained from Sigma Aldrich and used as supplied. Water was either of Millipore grade or for the case of SANS experiments we employed D2O obtained from Eurisotop (99.9% isotopic purity). The telechelic polymer was Rewopal 6000DS, which is a polyethylene oxide distearate and was a gift from Evonik Industries. In all our calculations we assumed a chemical formula of (C17H35COO)2EO150 (MW = 7157 g mol−1) for this polymer.The samples were prepared by taking the required amount of a stock solution of 200 mM of surfactant. The appropriate amount of oil and water was added to achieve the final composition of the microemulsion (100 mM TDMAO/35 mM decane–water). The polymer containing microemulsions were prepared by mixing weighted amounts of microemulsions with varying amounts of polymer and mixing with a vortex mixer under heat (∼60 °C) to ensure complete dissolution of the polymer. The polymer addition thereby led to a variation of the droplet volume fraction, which however is rather small (always being less than 5%, see ESI†).
Methods
 | (1) |
| g(2)(t) = 1 + B|g(1)(t)|2 | (2) |
The correlation function g(1)(t) can be written as the Laplace transform of the distribution of relaxation rates G(Γ):
 | (3) |
G(Γ) was obtained by a regularized inverse Laplace transformation of the DLS data using the CONTIN algorithm36 implemented in the ALV software.
An alternative way of analysing multimodal relaxation processes is by fitting g(1)(τ) to a multiexponential function. For the cases discussed here a very suitable functional form was found to be a monoexponential decay for the fast relaxation process together with a stretched exponential decay describing the slower relaxation, which is given by:
g(1)(t) = Af![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τf) + Asl exp(−t/τf) + Asl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τsl)βsl exp(−t/τsl)βsl | (4) |
 | (5) |
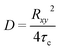 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) was applied at a constant angular frequency, ω, and with an amplitude, γ0. As a result a sinusoidal strain σ (with an amplitude σ0) was recorded, which was shifted by a constant phase angle δ. The complex dynamic shear modulus G*(ω) defined by G′(ω) + iG′′(ω) is given by (G′: storage modulus; G′′: loss modulus):
sin(ωt) was applied at a constant angular frequency, ω, and with an amplitude, γ0. As a result a sinusoidal strain σ (with an amplitude σ0) was recorded, which was shifted by a constant phase angle δ. The complex dynamic shear modulus G*(ω) defined by G′(ω) + iG′′(ω) is given by (G′: storage modulus; G′′: loss modulus): | (7) |
The linear viscoelastic regime was ascertained for all measurements by an amplitude sweep at 10 rad s−1.
Viscosity measurements were carried out using previously calibrated Schott micro-Ubbelohde viscometers of type Ic and IIc (diameter Ic: 0.84+/−0.01 mm; IIc: 1.50+/−0.01 mm, capillary constants: Ic: 0.03 mm2 s−1; IIc: 0.3 mm2 s−1). The viscosity was calculated from the fluid flow time as
| η0 = ρKt | (8) |
Results and discussion
In our work we concentrated on an O/W microemulsion consisting of 100 mM TDMAO/35 mM decane in water (∼3.3 vol%), which is close to the emulsification boundary of this microemulsion system.33 Increasing amounts of Rewopal 6000DS were added to this base formulation. The added polymer amounts are given in g/g (total solution) and alternatively by the number of hydrophobic stearate stickers per microemulsion droplet, r, where the latter was calculated assuming an unchanged radius of the microemulsion droplets of 2.85 nm and a polymer formula of (C17H35COO)2EO150. This size had been deduced similarly before from SANS experiments31,33 and was confirmed in this study to be independent of the polymer admixture (see 3.1). The most relevant parameter for the polymer is its end-to-end distance ree, i.e., the average distance between the hydrophobic stickers. The end-to-end distance of the pure PEO chain free in solution can be estimated via: | (9a) |
 | (9b) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) EO the length of a monomer segment (
EO the length of a monomer segment (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) EO = 0.2928 nm). With these numbers we arrive at an end-to-end distance ree of 8.2 nm, which then should be the relevant distance over which the Rewopal 6000DS can easily lead to a bridging of droplets. This then can be compared to the average spacing of the microemulsion droplets. Assuming a primitive packing for the given radius of 2.85 nm we can calculate the mean distance dss (eqn (9b)) between neighbouring surfaces of droplets to be 8.6 nm (10.4 nm would be the value for fcc packing). This means that the average spacing of the microemulsion droplets is very similar to the end-to-end distance ree of the stickers. Therefore an effective bridging is to be expected and repulsive interaction between the droplets is expected due to the fact that, on average, the stickers might be placed more closely together than they would like to be in an equilibrium polymer conformation (an additional repulsion will be introduced by the presence of the water-soluble PEO units in between the microemulsion droplets).
EO = 0.2928 nm). With these numbers we arrive at an end-to-end distance ree of 8.2 nm, which then should be the relevant distance over which the Rewopal 6000DS can easily lead to a bridging of droplets. This then can be compared to the average spacing of the microemulsion droplets. Assuming a primitive packing for the given radius of 2.85 nm we can calculate the mean distance dss (eqn (9b)) between neighbouring surfaces of droplets to be 8.6 nm (10.4 nm would be the value for fcc packing). This means that the average spacing of the microemulsion droplets is very similar to the end-to-end distance ree of the stickers. Therefore an effective bridging is to be expected and repulsive interaction between the droplets is expected due to the fact that, on average, the stickers might be placed more closely together than they would like to be in an equilibrium polymer conformation (an additional repulsion will be introduced by the presence of the water-soluble PEO units in between the microemulsion droplets).
In the following we studied this mixed microemulsion/telechelic polymer system as a function of the amount of added polymer, described by the number of stickers per microemulsion droplet (r), by means of structural, dynamical and rheological experiments. All the samples investigated were homogeneous and long-time stable but varied very pronouncedly with respect to their viscosity, which increases largely upon the addition of the telechelic polymer. The aim is to correlate the change of the macroscopic properties with the mesoscopic structure and the dynamics of polymer bridged microemulsion systems, with a particular emphasis on the local structure and dynamics.
Small-angle neutron scattering (SANS)
In order to obtain a refined structural picture SANS measurements were performed. We investigated how the structure of the microemulsion is affected by the addition of Rewopal 6000DS. Fig. 1 shows the scattering intensity against the magnitude of the wave vector, q, for O/W microemulsions with Rewopal 6000DS concentrations between 0 and 3 wt% (corresponding to r = 0–15). At first look, the unchanged position of the minimum at high q (≈1.5–1.6 nm−1) and the very similar appearance of the scattering curves for q > 1 nm−1 is a sign that the average size and shape of the droplets are not influenced by the polymer. However, upon increasing the polymer concentration a weak correlation peak arises, i.e., there is an increasing repulsion between the droplets. In addition, there is also a slight upturn of the intensity at low q that indicates either the presence of larger objects or an attractive interaction between the droplets that is most pronounced at intermediate concentration of polymer, i.e., for 1–2 wt% Rewopal 6000DS. | ||
| Fig. 1 SANS scattering intensity as a function of the magnitude q of the scattering vector for aggregates of the pure microemulsion (black squares) and with increasing polymer concentrations between 0 and 3 wt% at a temperature of 25 °C (subsequent curves are shifted by a factor 2n for better clarity). Solid lines: fits with eqn (11) and (13). | ||
A first model-free information was obtained by extrapolating the SANS data by the Guinier-approximation to q = 0 (eqn (10a)), from which the molecular weight MW was deduced (according to eqn (10b), where we used a density d of 0.86 g ml−1 and for the contrasts Δρ see ESI†). The obtained values are summarized in Table 1.
 | (10a) |
 | (10b) |
| C pol/wt% | r | c g/g L−1 | I(0)/cm−1 | S(0) | M W/g mol−1 |
|---|---|---|---|---|---|
| 0 | 0 | 30.73 | 14.62 | 0.73 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
| 0.25 | 1.28 | 30.84 | 17.96 | 0.91 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 0.5 | 2.56 | 30.95 | 14.84 | 0.98 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| 0.75 | 3.82 | 31.07 | 17.61 | 1.02 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 1 | 5.08 | 31.19 | 18.03 | 1.09 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| 1.25 | 6.31 | 31.30 | 18.66 | 1.07 | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| 1.5 | 7.55 | 31.42 | 19.02 | 1.06 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
| 1.75 | 8.77 | 31.54 | 18.55 | 1.01 | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 2 | 9.98 | 31.65 | 19.83 | 0.91 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| 2.25 | 11.18 | 31.77 | 17.95 | 0.86 | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 2.5 | 12.37 | 31.88 | 17.96 | 0.81 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| 2.75 | 13.55 | 32.00 | 16.53 | 0.75 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 3 | 14.72 | 32.11 | 16.21 | 0.69 | 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
A quantitative analysis of the scattering data was done by means of a model of polydisperse spheres interacting with an attractive potential. The neutrons are scattered predominantly by the microemulsion droplets and only for the higher q-range some contribution from the scattering of the polymer chains may be expected.40 We neglected the polymer contribution after verifying that its effect was not significant for a quantitative description of the experimental data. The scattered intensity for polydisperse spheres as a function of the magnitude q of the wave vector is expressed as follows:
| I(q) = ΦP(q,R)S(q,RHS) + Iinc | (11) |
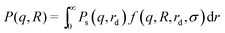 | (12) |
 | (12a) |
 | (12b) |
 | (12c) |
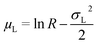 | (12d) |
 | (13) |
The resolution function R(q′,q,Δq) describes the distribution of the q-vectors at a given instrumental configuration. Assuming a Gaussian function for the resolution function,41eqn (13) yields:
 | (14) |
The q-resolution at a given q has three contributions: the finite size of the incident beam, the wavelength resolution and the pixel size on the detector.41 If we neglect the pixel size due to its small dimension (7.5 × 7.5 mm2), Δq is described by:
 | (15) |
For the structure factor S(q) the model of sticky hard spheres (SHS) was employed. Baxter's SHS model42 employs a hard sphere model with an infinitesimally narrow and infinitely deep square well described by the stickiness parameter α, that is a measure of the attractiveness of the spheres at contact. The real interaction potential is more complex. Numerical calculations of the interaction potential for chains between two spheres show an attraction in the order of kT, occurring at a separation less than the end to end distance of the polymer and an increasing repulsion with the polymer length and concentration.43,44 However, if the range of the potential is not too large, a Baxter model can be used instead and the effective hard sphere radius (RHS) will give information about the repulsion and the stickiness parameter (α) about the net attraction.
The details for this model and the corresponding SSHS(q) are given in the ESI.†
The model has as adjustable parameters:
- mean particle radius R.
- standard deviation σ of the size distribution function
- hard sphere radius RHS
- attractive interaction parameter α (stickiness parameter)
- hard sphere volume fraction, although not entirely. We fitted for the lowest and highest polymer concentration, and then in the remaining fits forced the hard sphere volume fraction to increase linearly with the polymer concentration (based on the fact that the volume of the shell increases linearly). See ESI† for more details.
This model allows us to extract the size of the microemulsion droplets and information regarding their interaction potential (Table 2).
| C pol/wt% | r | Φ/% | σ | R/nm | R HS/nm | Φ HS/% | α | B 2 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3.57 | 0.109 | 2.82 | 3.68 | 4.0 | ∞ | 10.57 |
| 0.25 | 1.28 | 3.59 | 0.113 | 2.77 | 4.6 | 3.8 | 0.349 | 5.21 |
| 0.5 | 2.56 | 3.60 | 0.102 | 2.82 | 5.93 | 4.8 | 0.254 | 0.59 |
| 0.75 | 3.82 | 3.62 | 0.114 | 2.82 | 6.09 | 5.7 | 0.226 | −4.26 |
| 1 | 5.08 | 3.63 | 0.120 | 2.83 | 6.3 | 6.6 | 0.203 | −10.20 |
| 1.25 | 6.31 | 3.65 | 0.128 | 2.84 | 6.31 | 7.5 | 0.208 | −8.88 |
| 1.5 | 7.55 | 3.66 | 0.128 | 2.86 | 6.42 | 8.4 | 0.212 | −8.09 |
| 1.75 | 8.77 | 3.68 | 0.129 | 2.88 | 6.57 | 9.1 | 0.225 | −5.30 |
| 2 | 9.98 | 3.70 | 0.136 | 2.88 | 6.6 | 10.4 | 0.250 | 0.19 |
| 2.25 | 11.2 | 3.71 | 0.148 | 2.87 | 6.6 | 11.2 | 0.270 | 3.60 |
| 2.5 | 12.4 | 3.73 | 0.155 | 2.88 | 6.75 | 12.1 | 0.280 | 5.50 |
| 2.75 | 13.6 | 3.74 | 0.157 | 2.87 | 6.81 | 13.0 | 0.300 | 8.86 |
| 3 | 14.7 | 3.76 | 0.149 | 2.94 | 6.83 | 14.0 | 0.320 | 10.92 |
The fit curves are included in Fig. 1 and show very good agreement with the experimental data. The results for the fit parameters are summarized in Table 2. The radius of the microemulsion droplets remains basically unchanged. The pure microemulsion has a radius of 2.82 nm (somewhat less than the fully saturated microemulsion that has an average radius of 3.12 nm32), and then increases slightly with increasing polymer concentration to about 2.94 nm for the maximum polymer content. This increase can be attributed to introducing a significant amount of C18 chains into the microemulsion droplets at the high polymer concentration (for 3 wt% r = 14.7, corresponds to 0.074 stearyl chains per TDMAO molecule). In addition, we observe a slight increase of the polydispersity of the microemulsion droplets with increasing polymer content.
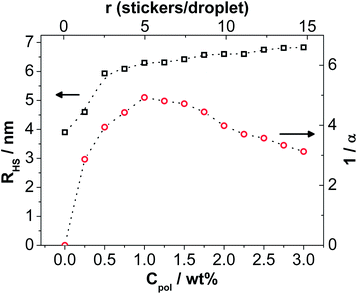
A very interesting observation is that there is a pronounced attractive interaction introduced into the system by the addition of the telechelic polymer. This attraction describes the upturn at low q by the stickiness parameter α, which is a quantitative measure for the attractive component of the interaction potential (and directly related to the second virial coefficient B2viaeqn (16)) and also allows to predict the attractive phase separation of such systems. The inverse 1/α is proportional to the attractive interaction, and first increases rapidly upon polymer addition, goes over a maximum of attractive interaction for r ∼ 5 and then becomes smaller again (Fig. 2). At the same time we observe a pronounced increase of the hard sphere radius RHS that increases continuously from 3.9 to 6.8 nm (Fig. 2). This is also seen directly in the curves via the appearance of a correlation peak for increasing polymer concentration. This means that the presence of the polymer chains makes the microemulsion droplets bulkier (more repulsive). Apparently the presence of the water soluble polymer chains enhances the repulsive interaction between the microemulsion droplets, thereby leading to the correlation peak. It is interesting to note that the extra volume effectively occupied by the polymer, that should be proportional to (RHS3 − R3) increases linearly with the amount of polymer contained (see Fig. S2, ESI†), thereby confirming the picture that the repulsion is directly linked to the amount of water soluble polymer chains.
Similar results were already observed for microemulsion droplets, when the distance between the droplets is larger than Ree the net interaction is attractive and when the polymer is longer, the net interaction is repulsive.17 Theory predicts that attraction dominates the second virial coefficient when chains are less stretched, while repulsion controls the highly stretched limit.43,44 For constant ree and d, the addition of polymer contributes both to an increase of attraction and repulsion.
These counterbalancing factors in the interdroplet interaction can be summarized with respect to their total effect by looking at the second virial coefficient B2 (eqn (16)), which is a very good average measure for the effective attractive/repulsive interaction between the droplets. This is very useful as the two parameters describing the structure factor S(q), the hard sphere radius RHS and the stickiness parameter α, describe opposite effects but are not fully decoupled in their effect on the scattering curves. The dimensionless second virial coefficient can be calculated from:
 | (16) |
The variation of the second virial coefficient is given in Fig. 3 and shows a very interesting behaviour. It starts for the pure microemulsion at a value of about 10 which is well above the value for a simple hard sphere. This can be explained by the fact that in our calculation we took the radius of the microemulsion droplet without considering the hydration shell, which is taken into account by RHS in the analysis. Upon polymer addition the attractive interactions increase dramatically and B2 becomes markedly negative, reaching a minimum around 1 wt% Rewopal 6000 DS, which corresponds to 4–5 stickers per droplet. Apparently for this condition the formation of interconnected clusters is maximized. Upon further addition of polymer, B2 increases again and this repulsive interaction can be ascribed to the action of the water-soluble polymer molecules which are located between the microemulsion droplets and thereby lead to an effective repulsion between the latter. For concentrations above 2.2 wt% (r ∼ 10) it then is higher again than for a simple hard sphere system.
 | ||
| Fig. 3 Dimensionless second virial coefficient as a function of the added polymer concentration calculated with eqn (16) with the structural parameters obtained from the SANS data. Solid line: B2 = 4 (pure hard sphere). | ||
Rheology
The most obvious change of the microemulsions upon addition of the telechelic polymer is the viscosity increase. The original microemulsion is basically water viscous, while upon addition of the polymer an increase of viscosity by more than four orders of magnitude is observed. The zero-shear viscosity is given in Fig. 4 and shows that this marked viscosity increase occurs rather sharply in the range of polymer concentrations of 1.5–2 wt%, which corresponds to a number of stickers per droplet r of 7–10, i.e., well beyond the concentration where the maximum of the attractive interaction between the droplets has been observed (Fig. 2 and 3). It is interesting to note that below this concentration, the increase of viscosity is rather small, which is in agreement with the SANS data, where up to this value only an attractive clustering of the particles is seen. This means that initially individual clusters form (until r ∼ 4–5) that do not lead to a substantial viscosity enhancement and only for a higher polymer content (r ∼ 6) a space-filling viscous network starts to be formed. Such a sharp viscosity increase has been seen before for the case of similar microemulsion droplets but for a much shorter interconnecting polymer and correspondingly higher microemulsion concentrations14 and in similar fashion has also been reported for other mixtures of microemulsions and doubly hydrophobically modified polymer.25The sharp increase of the viscosity can be ascribed to a percolation transition induced by the effective interconnecting of the microemulsion droplets by the telechelic polymer. Such a percolation typically leads to a power law behaviour of the viscosity which can be described as: η ∼ (cp – c)−k1 below the percolation concentration cp and η ∼ (cp − c)k2 above the percolation concentration.45 The power laws fit very well to our experimental data as shown in Fig. 4 and from these fits we obtain a cp of 1.54 wt% (r = 7.4) and k1 = 0.7 and k2 = 1.7, respectively. Here it might be noted that slightly lower values of 1.4–1.6 for k2 have been found for other microemulsions upon the addition of a bifunctional telechelic polymers,16,25,46i.e., here the viscosity increase appears to occur in a slightly more cooperative fashion.
The samples with more than 1.5 wt% Rewopal 6000 DS are sufficiently viscous to be measured by means of oscillating rheological measurements, where they show viscoelastic behaviour that is close to that of a Maxwellian fluid. There are some systematic deviations as shown for example in Fig. 5, where the slopes for the storage modulus G′ and loss modulus G′′ are systematically lower than the theoretically predicted values of −2 and −1, respectively.
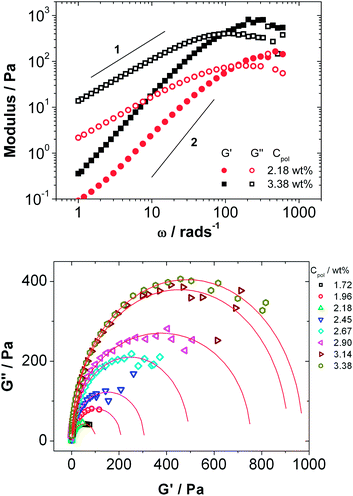 | ||
| Fig. 5 (a) Storage (G′) and loss (G′′) moduli as a function of angular frequency (ω) for microemulsion with 2.16 and 3.38 wt% of C18-EO150-C18 (b) Cole–Cole plot of the loss modulus G′′ as a function of the storage modulus G′ for mixtures of microemulsion consisting of 100 mM TDMAO/35 mM decane–water with different amounts of C18-EO150-C18 added. The lines in (b) represent fits with eqn (17). Measurements were done with the instrument AR-G2 at a constant temperature of 25 °C. | ||
Fig. 5b shows the Cole–Cole plot, which is the representation of the loss modulus G′′ as a function of the elastic modulus G′ that allows for detailed observation of viscoelastic systems.48 For the Maxwell model the data for G′ and G′′ should lie on a semicircle described by a generalized Maxwell model (eqn (17)):49
| G′′/Pa = ((G′G0 − G′2)/Pa2)m | (17) |
The fits of eqn (17) to the experimental data were consistently found to be best described for m = 0.482 (m would be 0.5 for perfect Maxwellian behaviour), which means that there is some systematic but not too large deviation from Maxwellian behaviour. We could deduce reliably the shear modulus G0 of the samples from the fits to eqn (17) and the relaxation time τR from the angular frequency at which G′ = G′′, τR = 1/ωR.
The structural relaxation time τR is rather constant at ∼10 ms irrespective of the polymer concentration. This indicates that this relaxation might be related to the residence time of the stearyl moieties in the microemulsion droplets that can be estimated to be ∼20 ms from relaxation kinetics.47
The obtained G0 is given in Fig. 6 and shows a pronounced increase from about 100 to 1000 Pa (see Table 3) with increasing polymer concentration which sets in beyond a threshold concentration of ∼1.3 wt% (r ∼ 6.2) Rewopal 6000 DS. Empirically the evolution of G0 with the concentration cp of the polymer (in wt%) can be described by a power law of the form: G0 = (307/Pa)((cp − 1.32)/wt%)1.7 (see Fig. S3, ESI†). This critical concentration value of 1.32 wt% is somewhat lower than that observed in the viscosity measurements (1.54 wt%). The exponent 1.7 is somewhat higher than the 1.42 found by Appell et al. for a similar system25 but close to the 1.8 found for a polymer bridged W/O microemulsion.50 In contrast, for the viscosity increase also much higher exponents of 3.6–5.2 have been reported for W/O microemulsions.50 It can also be noted that for higher polymer concentrations the increase is rather linear and one might expect that simply every telechelic polymer contributes equally to the viscosity. This may be explained by the fact that in the viscosity analysis one only sees a rather substantial viscosity, which requires an effective interconnection of the droplets, while the analysis of the viscoelastic moduli gives the value for the onset of elastic properties.
| C pol/wt% | 1.72 | 1.96 | 2.18 | 2.44 | 2.67 | 2.9 | 3.14 | 3.38 |
| r | 8.4 | 9.4 | 10.4 | 11.7 | 12.8 | 13.8 | 15.0 | 16.2 |
| G 0/Pa | 103 | 170 | 209 | 306 | 496 | 754 | 912 | 974 |
| τ R/ms | 16.7 | 9.1 | 8.3 | 8.9 | 10.3 | 9.5 | 10.2 | 10.0 |
| G 0/1NpolkBT | 0.017 | 0.025 | 0.028 | 0.037 | 0.054 | 0.076 | 0.085 | 0.084 |
The experimental G0 can also be compared to the theoretical value for a simple network model given by:51
| G0 = 1NelkT | (18) |
Collective diffusion – dynamic light scattering (DLS)
In order to gain further insight into the mesoscopic dynamic behaviour of the investigated polymer bridged microemulsions, we performed DLS measurements. Fig. 7 shows the intensity autocorrelation functions g(2)(t) for various concentrations of Rewopal 6000DS added to the microemulsion. The pure microemulsion shows a monoexponential relaxation, which corresponds to the simple diffusion of microemulsion droplets with a hydrodynamic radius of 2.43 nm. This is slightly smaller than the value obtained by SANS but might be attributed to the finite concentration and even more to a slight charging of the microemulsion droplets due to protonation of the TDMAO (there is no salt contained to screen the charges). The corresponding repulsive interaction leads to an increase of the apparent diffusion coefficient, as it has been observed before for such microemulsion droplets52. Upon addition of polymer, the correlation function shows a slower relaxation, which indicates the formation of bigger objects. At still higher polymer concentration the curves start deviating from a simple monoexponential relaxation, and a second relaxation mode is observed. The second mode appears at the concentration where the solutions become highly viscous (∼1.75 wt%, r = 7). Its amplitude and characteristic time increase with increasing polymer concentration. This second relaxation mode has to be associated with structural relaxations of an interconnected network of microemulsion droplets. | ||
| Fig. 7 Intensity autocorrelation function g(2)(t) of microemulsions with several concentrations of C18-EO150-C18 added measured at a scattering angle of θ = 90° and a temperature of 25 °C. The lines are the fits with eqn (19). | ||
In order to analyse the relaxation process and verify the number of relaxation modes, the decay time distributions were obtained by inverse Laplace transformation. The evolution of these distribution functions is presented in Fig. S4† and one observes that the slower mode increases in intensity and moves to longer times with increasing concentration of the Rewopal 6000DS, and the slow mode is always much wider than the fast mode. One can distinguish two regimes of polymer concentration. First, below 1 wt% the distribution is monomodal. Then at higher polymer concentration the relaxation process is apparently bimodal and may well be described by two relaxation processes, where the slower one is a rather broad one. Accordingly, we analyzed the autocorrelation curves quantitatively in terms of a sum of a normal and a stretched exponential decay of g(1)(t) as described by eqn (19) (f: fast mode; sl: slow mode), where the amplitudes and the stretching parameter β provide useful information regarding the dynamical behavior of the systems.
g(1)(t) = Af![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Γft) + (1 − Af)exp(−Γslt)β exp(−Γft) + (1 − Af)exp(−Γslt)β | (19) |
 | (20) |
| C pol/wt% | r | A f | D eff/10−11 m2 s−1 | τ sl/ms | 〈τsl〉/ms | n sl | β sl |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1.0 | 9.77 | ||||
| 0.25 | 1.19 | 1.0 | 9.04 | ||||
| 0.5 | 2.39 | 1.0 | 6.39 | ||||
| 0.75 | 3.59 | 0.98 | 4.88 | 0.33 | 0.36 | 1.93 | 0.83 |
| 1 | 4.79 | 0.87 | 4.52 | 0.81 | 0.98 | 2.39 | 0.74 |
| 1.25 | 5.98 | 0.73 | 4.37 | 1.98 | 2.98 | 2.79 | 0.60 |
| 1.5 | 7.17 | 0.73 | 3.49 | 27.0 | 61.0 | 2.17 | 0.47 |
| 1.77 | 8.44 | 0.72 | 3.8 | 18.6 | 30.0 | 1.05 | 0.57 |
| 2.04 | 9.75 | 0.62 | 3.73 | 20.1 | 35.3 | 1.51 | 0.54 |
| 2.3 | 11.0 | 0.67 | 4.09 | 45.8 | 59.6 | 0.58 | 0.68 |
| 2.56 | 12.3 | 0.5 | 4.23 | 86.7 | 116 | 0.38 | 0.66 |
| 3.09 | 14.8 | 0.5 | 5.02 | 102 | 128 | 0.21 | 0.71 |
Eqn (19) fits the experimental data very well. This analysis is complementary to having two or three relaxation modes as the stretched exponential can effectively mimic a biexponential decay for a not too large difference between the two relaxation rates. Actually, it might be noted that in our g(2)(t) curves the presence of a third relaxation mode is less clearly visible than in the case of PEO-distearate investigated by Appell et al.23
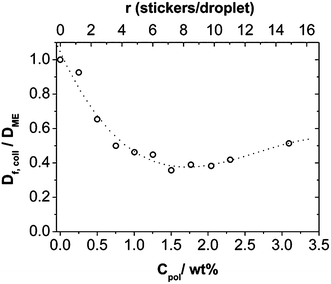
An important question is whether the relaxation processes are diffusive or not. The q-dependence of the relaxation rates was analyzed and showed that the fast mode has a q−2 dependence (see Fig. S5†) and therefore can be associated with the collective diffusion coefficient Df,coll of the microemulsion droplets or clusters formed by them. Its value decreases with increasing polymer concentration (Fig. 8) and reaches a rather constant value at ∼1 wt% Rewopal 6000DS. An interpretation would be that in this concentration regime bigger agglomerates (clusters) of the microemulsion droplets are formed, as already indicated by the SANS measurements and, in agreement with the rheological observations, these clusters are effectively 2–3 times bigger in size than the individual microemulsion droplets. For higher polymer content Df,coll increases again slightly, which means that the collective diffusion of the smaller structural units is not further reduced by the presence of the polymer and the formation of an interconnected network of microemulsion droplets. Here it should be noted that collective diffusion does not really mean the actual transport of individual droplets but is related to the relaxation of the density fluctuations in that system (further information regarding the self-diffusion can be deduced from the FCS experiments described in 3.4.).
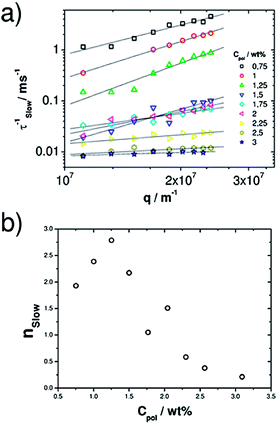
The slow mode is more complex and not purely diffusive. From the log–log representation (Fig. 9) it becomes clear that the power law (Γ ∼ qnslow) dependence of the relaxation rate changes markedly with increasing polymer concentration. The slow relaxation process becomes much slower (Fig. 7 and 9 and Table 4) with increasing polymer concentration. For low polymer content, nslow is approximately 2, thereby indicating diffusive relaxation, then first increases up to a value of almost 3 for ∼1.25 wt% Rewopal 6000DS, and then for still higher a polymer content nslow decreases substantially and approaches 0 around 2.5 wt% Rewopal 6000DS (see Fig. 9b), i.e., the relaxation becomes independent of the size scale considered. Higher q dependencies than q−2 have been observed for crowded systems, where the slower relaxation time arises from caging or obstruction effect of neighboring particles or clusters.53
Relaxation times that are q independent are observed in transient networks, where the slow relaxation time is correlated to the structural relaxation time.23,26,28 In our system at low polymer concentrations the polymer induces the formation of droplet clusters with the corresponding increase in effective volume fraction and viscosity (see Fig. 4) and the q dependence of the slow relaxation increases. Once the network is fully formed, the slower relaxation becomes q independent. Such a transition of the q dependence upon gelation has already for instance been reported for the thermoresponsive gelling of nonionic cellulose ether in the presence of ionic surfactants.54
For this higher polymer concentration the slow relaxation time is in the range of 20–100 ms (Table 4) in the same order of magnitude of the rheological relaxation time (Table 3), but, in contrast to the rheological times, one finds a systematic increase of τslow with increasing polymer concentration.
Another interesting property is the stretching parameter βsl, which is close to 1 for low polymer content but then becomes smaller with increasing polymer content (Table 4). This is consistent with the observation that the second relaxation rate is still diffusive at low polymer content. However, for the range of higher polymer content the stretching parameter βsl deviates increasingly from unity, while at the same time the exponent nsl deviates increasingly from the diffusive value of 2, i.e., this mode is due to a more complex relaxation, that can be ascribed to the viscoelastic network formed in the microemulsion copolymer systems. Once the network is formed, βsl goes to a rather constant value.
The q dependance nslow first increases in the range of cluster formation, where B2 goes to a minimum, and then rapidly goes to zero for the highly viscous systems of an interconnected network of O/W droplets. A further confirmation of the relation between the slow mode and the elastic properties of the network was asserted by the direct proportionality of Aslow and G0 (Fig. S6†).
Self-diffusion – fluorescence correlation spectroscopy (FCS)
While DLS gives information about collective diffusion, FCS measurements yield a complementary insight into the dynamic behavior of the polymer bridged microemulsion systems as FCS measures exclusively self-diffusion of the labeled domains. The droplets were selectively fluorescently labeled with Nile Red at a concentration of 2.5 nM. Then FCS was measured as a function of the concentration of added Rewopal 6000DS. These measurements show for the pure microemulsion droplets a diffusion coefficient very similar to that seen by DLS (9.77, DLS vs. 8.99 10−11 m2 s−1 for FCS; compare Table 4 and S2,† but it should be noted that due to the typical calibration uncertainty of the confocal volume the precision of the FCS diffusion coefficient is not better than 20% in absolute units).Upon adding the bridging polymer Rewopal 6000DS, there is a rapid increase of the relaxation time in the fluorescence correlation functions (Fig. 10 and Table S2†), that occurs in the range of 0 to 2 wt% Rewopal 6000DS. The self-diffusion coefficient Ds is correspondingly reduced (Fig. 11 and Table S2†) in a similar fashion as seen by DLS. However, the reduction of the self-diffusion coefficient Ds is much more pronounced (see Fig. 8 and S5†), which means that the self-diffusion is much more frozen in by the network formation. The fast decrease of the self-diffusion coefficient Ds confirms the idea of the formation of clusters of microemulsion droplets interconnected by the polymer, which is similarly seen in FCS and DLS. Upon further increase of r, Ds remains almost constant and low, thereby indicating that the O/W droplet are largely reduced in their mobility. This is different to DLS, where the network formation leads to a slight increase of Deff (as the network formation allows for faster collective diffusion), while Ds describing the movement of individual droplets remains low, as they are basically fixed in space (it might be noted that here we cannot exclude molecular diffusion of the Nile red by a hopping process, due to its solubility of 0.2 mg ml−1 in water).
 | ||
| Fig. 10 FCS decay curves of microemulsion with C18-EO150-C18 of different concentrations. The lines are the fits with eqn (6) yielding the parameters listed in Table S2.† The inset plots the characteristic diffusion time τD as a function of the polymer concentration. | ||
 | ||
| Fig. 11 Reduced self diffusion coefficient Ds/Ds,ME (squares) calculated as Ds = w02/(4τDγ) and anomalous diffusion exponent γ (circles) as a function of the concentration of C18-EO150-C18 (obtained by analysis with eqn (6)). Ds,ME is the self diffusion coefficient of the microemulsion without polymer. The dotted line is a guide to the eye. | ||
At the same time with increasing r the relaxation mechanism becomes less uniform, which was quantified by fitting the experimental relaxation data by eqn (6) and deducing the parameter γ, which describes the deviation from simple diffusion (that would correspond to γ = 1). Accordingly, the dynamic behavior of the polymer/surfactant mixtures depends largely on their mixing ratio and on their total concentration.
Fig. 11 shows the anomalous diffusion exponent γ that describes the monodispersity of the relaxation mechanism (both the characteristic diffusion time τD and the anomalous diffusion exponent γ are also given in Table S3†). γ is constant up to a value of 1.0 wt% (r ∼ 5) and then decreases linearly with increasing r, which is exactly in the range where the percolation in the samples, i.e., the formation of a highly viscous network, takes place. Accordingly, the appearance of an anomalous diffusion is related to the formation of this network in solution, which means that the arrest of the individual microemulsion droplets is directly seen by FCS. It might be noted here that our FCS observations differ substantially from those reported by Cipelletti et al. obtained by FRAPP on a principally similar O/W droplet system bridged by a PEO-DS. In their case the diffusion observed by FRAPP was related to the slowest relaxation time seen by DLS,28 while in our case it is originally the same as the fast mode of DLS and it then differs increasingly for higher r values. The hydrodynamic radius Rh calculated from the self-diffusion coefficient Ds (Table S2†) of the microemulsion without polymer yields a value of 2.66 nm and the subsequent change of Ds with increasing polymer concentration is first quite similar to that seen by DLS. Only for high polymer content it then is substantially lower. In that context it should also be noted that FCS probes diffusion over a distance of ∼1 μm, which is comparable to the distances probed by DLS, but much smaller than those of the FRAPP experiment.
Conclusions
Our comprehensive structural, dynamical and rheological investigation of a diluted O/W microemulsion allows to derive a detailed structural and dynamical picture of the changes occurring upon adding increasing amounts of a telechelic polymer able to bridge different microemulsion droplets and how this is related to the macroscopically observed increase of viscosity.At low polymer concentration the bridging polymer simply introduces an attractive interaction between the droplets, which leads to the formation of interconnected clusters of droplets (see Fig. 12), as also predicted by MC simulations.22,55 This is evidenced from SANS and also from DLS and FCS, where a much slower diffusion of these clusters is observed. The maximum clustering is observed for a number of about 5 hydrophobic stickers per microemulsion droplet (r = 5), as seen by the minimum of the second virial coefficient, that is a good measure for the effective interaction in this complex self-assembled system. However, at this point the viscosity of the samples is still rather low.
Only for a somewhat higher polymer concentration of r = 7, one observes a rather sharp increase of viscosity that can be attributed to a space-filling formation of a polymer-mediated network of microemulsion droplets (Fig. 12), i.e., here percolation takes place. At this point also a much slower relaxation mode starts to be seen in DLS (and as similarly observed before for cross-linked microemulsion systems23,25–28 that increases with further increasing polymer content, and at this point FCS shows the onset of anomalous diffusion. The amplitude of the slower relaxation mode seen by DLS is directly proportional to the shear modulus G0. For this completely interconnected network of microemulsion droplets one has a largely enhanced viscosity and pronounced viscoelastic properties of the systems, where the collective diffusion seen by DLS is increasing again (due to the interaction between the droplets introduced by the presence of the polymer), whereas the self-diffusion seen by FCS remains very low as the individual droplets are effectively frozen in the viscoelastic network. In that context it might also be interesting to note that dynamic investigations on a related microemulsion/telechelic star polymer system by means of neutron spin-echo (NSE), which probes dynamics over the 1–20 nm range, showed that on that time scale the apparent diffusion coefficient was only reduced by a relatively small extent and network formation, and was more efficient for a 2-arm bridging polymer compared to ones with more bridging arms.56 This is opposite to the trend observed for the rheology, where rheological parameters increase with the number of arms,24 but demonstrates the complexity of the dynamic details in such interconnected microemulsion networks.
Accordingly, the dynamic behaviour of the polymer/surfactant mixtures depends largely on their mixing ratio and on their total concentration and the structural evolution is described by the structural picture given in Fig. 12. First, at low polymer content, interconnected clusters are formed and only for higher content of telechelic polymer a space-filling network with elastic properties appears. Very interesting in that context are the results from FCS, that describe the self-diffusion of the microemulsion droplets and show a very slow internal dynamics for higher polymer content, while at the same time collective diffusion increases again. These findings are very interesting as they show in detail how the internal dynamics, that are correlated for instance to the transport and release of active agents from such a system, are controlled by the amount of telechelic polymer contained. The macroscopic rheological properties can directly be related to the amplitude and relaxation time of the slow mode of DLS. The combination of DLS and FCS results with the rheological observations then allows for a comprehensive understanding of these mixed systems, as it is essential for an optimized formulation of such microemulsion systems, which is important for many applications.
Acknowledgements
This work was funded by the DFG grant GR1030/9-1. For the rheological measurements we are grateful to Prof. M. Solero and the DAAD for funding this exchange program (D/07/10253). The EU is thanked for funding the confocal microscope and its attached FCS unit (EFRE 20072013 2/18). We acknowledge the JCNS for granting beamtime as well as for funding of the SANS experiments. Furthermore we would like to thank S. Prevost, K. Bressel and R. Joksimovic for help with the SANS measurements. P.M.M. gratefully acknowledges a grant from DAAD-La Caixa. Evonik is thanked for the gift of Rewopal 6000 DS.Notes and references
- W. Jahn and R. Strey, J. Phys. Chem., 1988, 92, 2294–2301 CrossRef CAS.
- D. Langevin, Annu. Rev. Phys. Chem., 1992, 43, 341–369 CrossRef CAS.
- T. P. Hoar and J. H. Schulman, Nature, 1943, 152, 102–103 CrossRef CAS.
- M. Gradzielski, Curr. Opin. Colloid Interface Sci., 2008, 13, 263–269 CrossRef CAS PubMed.
- G. Gompper and M. Schick, Phys. Rev. Lett., 1990, 65, 1116–1119 CrossRef CAS.
- M. Gradzielski, D. Langevin, T. Sottmann and R. Strey, J. Chem. Phys., 1996, 104, 3782–3787 CrossRef CAS PubMed.
- M. Gradzielski and H. Hoffmann, Handbook of Microemulsion Science and Technology, Marcel Dekker Inc., New York, 1999, pp. 357–386 Search PubMed.
- J. Peyrelasse, M. Moha-Ouchane and C. Boned, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 4155–4161 CrossRef CAS.
- K. Fontell, Colloid Polym. Sci., 1990, 268, 264–285 CAS.
- M. Gradzielski, H. Hoffmann and G. Oetter, Colloid Polym. Sci., 1990, 268, 167–178 CAS.
- M. Gradzielski, H. Hoffmann, J.-C. Panitz and A. J. Wokaun, J. Colloid Interface Sci., 1995, 169, 103–118 CrossRef CAS.
- E. Nürnberg and W. Pohler, Prog. Colloid Polym. Sci., 1984, 69, 64–72 Search PubMed.
- C. Provost and R. Kinget, Int. J. Pharm., 1988, 44, 75–85 CrossRef CAS.
- M. Gradzielski, A. Rauscher and H. Hoffmann, J. Phys. IV, 1993, 3, 65–79 CrossRef CAS.
- M. Odenwald, H.-F. Eicke and W. Meier, Macromolecules, 1995, 28, 5069–5074 CrossRef CAS.
- H. Bagger-Jörgensen, L. Coppola, K. Thuresson, U. Olsson and K. Mortensen, Langmuir, 1997, 13, 4204–4218 CrossRef.
- M. Filali, R. Aznar, M. Svenson, G. Porte and J. Appell, J. Phys. Chem. B, 1999, 103, 7293–7301 CrossRef CAS.
- F. E. Antunes, K. Thuresson, B. Lindman and M. G. Miguel, Colloids Surf., A, 2003, 215, 87–100 CrossRef CAS.
- S. Maccarrone, H. Frielinghaus, J. Allgaier, D. Richter and P. Lindner, Langmuir, 2007, 23, 9559–9562 CrossRef CAS PubMed.
- A. Zilman, J. Kieffer, F. Molino, G. Porte and S. A. Safran, Phys. Rev. Lett., 2003, 91, 015901 CrossRef CAS PubMed.
- V. Testard, J. Oberdisse and C. Ligoure, Macromolecules, 2008, 41, 7219–7226 CrossRef CAS.
- J. M. G. Sarraguca, A. A. C. C. Pais and P. Linse, Soft Matter, 2009, 5, 140–147 RSC.
- E. Michel, G. Porte, L. Cipelletti and J. Appell, Langmuir, 2004, 20, 984–990 CrossRef CAS.
- P. Malo de Molina, C. Herfurth, A. Laschewsky and M. Gradzielski, Langmuir, 2012, 28, 15994–16006 CrossRef CAS PubMed.
- E. Michel, M. Filali, R. Aznar, G. Porte and J. Appell, Langmuir, 2000, 16, 8702–8711 CrossRef CAS.
- M. Schwab and B. Stühn, J. Chem. Phys., 2000, 112, 6461–6471 CrossRef CAS PubMed.
- T. Blochowicz, C. Gögelein, T. Spehr, M. Müller and B. Stühn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041505 CrossRef CAS.
- E. Michel, L. Cipelletti, E. d'Humieres, Y. Gambin, W. Urbach, G. Porte and J. Appell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031402 CrossRef.
- Kirk-Othmer, Encyclopedia of Chemical Technology, John Wiley & Sons, Inc., New York, 2004, vol. 2, p. 463 Search PubMed.
- G. Oetter, Dissertation, Universität Bayreuth, 1989.
- M. Gradzielski and H. Hoffmann, Adv. Colloid Interface Sci., 1992, 42, 149–173 CrossRef CAS.
- M. Gradzielski, H. Hoffmann and D. Langevin, J. Phys. Chem., 1995, 99, 12612–12623 CrossRef CAS.
- A. Radulescu, V. Pipich, H. Frielinghaus and M.-S. Appavou, J. Phys.: Conf. Ser., 2012, 351, 012026 CrossRef.
- U. Keiderling, Appl. Phys. A: Mater. Sci. Process., 2002, 74, S1455–S1457 CrossRef CAS.
- B. J. Berne and R. Pecora, Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics, Courier Dover Publications, 2000 Search PubMed.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef.
- D. S. Banks and C. Fradin, Biophys. J., 2005, 89, 2960–2971 CrossRef CAS PubMed.
- P.-O. Gendron, F. Avaltroni and K. J. Wilkinson, J. Fluoresc., 2008, 18, 1093–1101 CrossRef CAS PubMed.
- S. Kawaguchi, G. Imai, J. Suzuki, A. Miyahara, T. Kitano and K. Ito, Polymer, 1996, 38, 2885–2891 CrossRef.
- J. S. Pedersen and M. C. Gerstenberg, Macromolecules, 1996, 29, 1363–1365 CrossRef CAS.
- J. S. Pedersen, D. Posselt and K. Mortensen, J. Appl. Crystallogr., 1990, 23, 321–333 CrossRef.
- R. J. Baxter, J. Chem. Phys., 1968, 49, 2770–2774 CrossRef CAS PubMed.
- S. R. Bhatia and W. B. Russel, Macromolecules, 2000, 33, 5713–5720 CrossRef CAS.
- X.-X. Meng and W. B. Russel, J. Rheol., 2006, 50, 169 CrossRef CAS.
- D. Stauffer, A. Coniglio and M. Adam, Adv. Polym. Sci., 1982, 44, 103–158 CrossRef CAS.
- N. Puech, S. Mora, V. Testard, G. Porte, C. Ligoure, I. Grillo, T. Phou and J. Oberdisse, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 13–24 CrossRef CAS PubMed.
- E. A. G. Aniansson, S. N. Wall, M. Almgren, H. Hoffmann, I. Kielmann, W. Ulbricht, R. Zana, J. Lang and C. Tondre, J. Phys. Chem., 1976, 80, 905–922 CrossRef CAS.
- F. Kern, F. Lequeux, R. Zana and S. J. Candau, Langmuir, 1994, 10, 1714–1723 CrossRef CAS.
- T. Annable, R. Buscall, R. Ettelaie and D. Whittlestone, J. Rheol., 1993, 37, 695–726 CrossRef CAS.
- U. Zölzer and H.-F. Eicke, J. Phys. II, 1992, 2, 2207–2219 CrossRef.
- P. J. Flory, J. Chem. Phys., 1950, 18, 108–111 CrossRef CAS PubMed.
- M. Gradzielski and H. Hoffmann, J. Phys. Chem., 1994, 98, 2613–2623 CrossRef CAS.
- K. L. Ngai, A. K. Rajagopal and S. Teitler, J. Chem. Phys., 1988, 88, 5086–5094 CrossRef CAS PubMed.
- B. Nystroem and B. Lindman, Macromolecules, 1995, 28, 967–997 CrossRef CAS.
- J. M. G. Sarraguca, A. A. C. C. Pais and P. Linse, Langmuir, 2008, 24, 11153–11163 CrossRef CAS PubMed.
- I. Hoffmann, P. Malo de Molina, B. Farago, P. Falus, C. Herfurth, A. Laschewsky and M. Gradzielski, J. Chem. Phys., 2014, 140, 034902 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Analysis of the SANS data and additional plots. See DOI: 10.1039/c4sm00501e |
| This journal is © The Royal Society of Chemistry 2014 |