Open Access Article
Open Access ArticleTunable photonic crystals with partial bandgaps from blue phase colloidal crystals and dielectric-doped blue phases
Mitja
Stimulak
and
Miha
Ravnik
*
Faculty of Mathematics and Physics, University of Ljubljana, 1000 Ljubljana, Slovenia. E-mail: miha.ravnik@fmf.uni-lj.si
First published on 23rd June 2014
Abstract
Blue phase colloidal crystals and dielectric nanoparticle/polymer doped blue phases are demonstrated to combine multiple components with different symmetries in one photonic material, creating a photonic crystal with variable and micro-controllable photonic band structure. In this composite photonic material, one contribution to the band structure is determined by the 3D periodic birefringent orientational profile of the blue phases, whereas the second contribution emerges from the regular array of the colloidal particles or from the dielectric/nanoparticle-doped defect network. Using the planewave expansion method, optical photonic bands of the blue phase I and II colloidal crystals and related nanoparticle/polymer doped blue phases are calculated, and then compared to blue phases with no particles and to face-centred-cubic and body-centred-cubic colloidal crystals in isotropic background. We find opening of local band gaps at particular points of Brillouin zone for blue phase colloidal crystals, where there were none in blue phases without particles or dopants. Particle size and filling fraction of the blue phase defect network are demonstrated as parameters that can directly tune the optical bands and local band gaps. In the blue phase I colloidal crystal with an additionally doped defect network, interestingly, we find an indirect total band gap (with the exception of one point) at the entire edge of SC irreducible zone. Finally, this work demonstrates the role of combining multiple – by symmetry – differently organised components in one photonic crystal material, which offers a novel approach towards tunable soft matter photonic materials.
1 Introduction
Photonic crystals attract attention today as advanced optical materials because they can be used to control the flow-of-light.1–3 One of the key characteristics of the photonic crystals is the emergence of photonic bandgaps if illuminated by light, where light of distinct frequencies is reflected from some (local bandgap materials) or all directions (full bandgap materials).4,5 Today typically, materials are designed to achieve full bandgaps;6 however, also photonic crystals with only local band gaps show interesting applications, like for example a notable increase in the efficiency of solar cells, where the predicted enhancement reaches up to 30%.7 Search for ways to produce photonic crystals that are also cheap, easy to make, and have few structural defects is an important field of research in advanced optical materials science.8There are multiple methods to fabricate photonic crystals. Roughly, they can be divided into two approaches: (i) the top down approach with the typical method of nanolithography9–13 and (ii) the bottom up approach typically based on the self-assembly of colloidal crystals.14–18 Various top-down photonic crystalline structures are fabricated today, including first-made complete band gap yablonovite,19 woodpile9 and recently also an inverted yablonovite,20 allowing for the manipulation of light in the infrared or visible spectrum. In the bottom up approach, the self-assembly is typically achieved by gravity sedimentation, vertical deposition, electrophoresis, spin coating, crystallization in physically confined cells and other methods.21 It is a promising route, but it can be affected by the formation of various structural defects, such as stacking faults and macroscopic cracks, which can emerge in the self organization of structures.22,23 These defects distort the flow-of-light; therefore, typically, multiple parameters are optimised to achieve optimal conditions for the self-assembly, including air pressure, humidity, temperature, and solvent.
Special types of photonic crystals are those which include solid24,25 or liquid crystalline birefringent components.26–31 For example, it was shown that highly birefringent photonic crystal fibers can be used for sensing applications, such as curvature,32 torsion33 and pressure sensors.34 The important generalization of the variety of produced photonic crystal structures is that their elementary band structure inherently originates from the symmetry of the material structure (e.g. FCC, BCC, diamond and others), making it the center-piece in the design of new materials.
Special liquid birefringent photonic crystals are cubic liquid crystalline blue phases.35–37 Blue phases (BP) form in highly chiral nematic liquid crystals, where depending on temperature and chirality, the rod molecules align into two distinct periodic three-dimensional orientational textures with body-centred cubic or simple cubic symmetry, called blue phase I (BPI) or blue phase II (BPII), respectively. These liquid crystalline phases appear in a temperature range between a chiral nematic phase and an isotropic liquid phase, and can be stable over a temperature range of 60 K and more, including room temperature, if doped by polymers38 or if using bi-mesogenic molecule based materials.39 Blue phases are explored in various photonic applications, including blue-phase cored optical fiber arrays,40 photonic materials with optically tunable band gaps,41 and as a three-dimensional photonic crystal for lasing.42 The detailed structure of blue phase photonic bands has also been already studied, finding distinct band structures with local and no complete bandgaps37,43 (see also Fig. 1A and B).
 | ||
| Fig. 1 Photonic bands of no-particle blue phases and structures of blue phase colloidal crystals. Calculated photonic bands of (A) (no-particle) blue phase I and (B) (no-particle) blue phase II on the edge of the simple cubic irreducible Brillouin zone. Note that these results agree well with the band structures reported in ref. 37. (C) BP I colloidal crystals combine FCC symmetry of the particle lattice and BCC symmetry of the blue phase fluid. (D) BP II colloidal crystals combine BCC symmetry of the particles and SC symmetry of the fluid. Particle radius is r = 120 nm in (C) and (D). Yellow lines represent the network of −1/2 defect lines (disclinations). The purple lines show the variation of the optical axis of the birefringent blue phase in the given cross-section, corresponding to the eigenvectors of a dielectric tensor with the largest eigenvalue; equivalent also to the nematic director. | ||
Recent research shows that the network of topological defects in blue phases provides a three-dimensional template of trapping sites for colloidal particles.44,45 It was demonstrated by numerical modeling that colloidal particles can be trapped in several stable lattices forming three-dimensional colloidal crystals, each characterized by different free energy per unit cell. It was also shown that colloidal particles with weak surface anchoring substantially increase the thermal stability range of the blue phases, for a factor of two and more. In BPI, the lowest free energy lattice of particles with homeotropic surface anchoring is FCC (Fig. 1c), whereas in BPII it is the BCC particle lattice (Fig. 1d). Importantly, the symmetries of these particle lattices are different from the inherent symmetries of the blue phase liquid: the BPI fluid with BCC symmetry stabilizes the FCC particle lattice, and the BPII fluid with SC symmetry stabilizes the BCC particle lattice. This interesting combination of symmetries brings forward the central idea of this manuscript, i.e. to create a single photonic crystal material which incorporates two underlying ’elementary’ material symmetries (in our case the symmetry of the particle lattice on one hand and the symmetry of the fluid birefringent profile on the other hand). Furthermore, the relevance of either of the symmetry components can be tuned and changed by simple material or system parameters. Indeed, in blue phase colloids, these parameters can be particle size, temperature, or refractive indices of the blue phase or the particles. An important distinction of blue phase-based colloidal crystals, e.g. compared to hard-core colloidal crystals, is that rheologically, they are an effective elastic material where the network of topological defect lines binds the structure.46 The second distinction is that blue phase-based materials are easily switchable with external electric fields at fast switching times, even sub milliseconds, where changes in the blue phase molecular alignment directly affect the optical properties.47,48
In this paper, we report on the optical properties of blue phase I and blue phase II colloidal crystals, identifying them as materials which have their photonic response conditioned by the interplay of two symmetries of the two material components, i.e. the particle lattice and the blue phase unit cells. We compare the photonic bands of the blue phase colloidal crystals with the photonic bands of (no-particle) blue phases and photonic bands of the FCC–BCC lattice of particles in isotropic background, showing that photonic bands and local band gaps can be easily tuned and even created by changing the size of the particles. The changes in the bands and the emergence of the local band gaps are shown to be a joint effect, caused – in different regions of the Brillouin zone – either by the lattice of the particles or by the birefringent profile of the blue phase. Particularly using larger particles leads to larger local band gaps. In the BPI FCC colloidal crystal, we also consider additional filling of the defect lines with another dielectric material, e.g. a polymer, having now a three-component system, which interestingly gives a total indirect band gap (except for one point) between the 7th and 8th band on the entire edge of the SC irreducible zone.
2 Model and method
Blue phases are anisotropic complex fluids with a spatially varying optical axis that follows the direction of the average molecular orientational order called the director. The director texture in blue phases can be thought to be made of stacked cylindrical tubes, called the double twist cylinders, which are permeated by a network of topological defects, where the average molecular order breaks and the material becomes locally isotropic. This complex molecular orientational ordering is typically described by a mesoscopic order parameter tensor Qij, which is calculated by free energy minimisation techniques and can well describe also the locally optically isotropic topological defect regions (for more on blue phases, please see ref. 35 and 36). The order parameter tensor Qij is related to the director ni and the nematic degree of order S as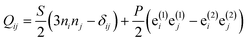 , where P is the biaxiality, e(1)i is the secondary director and e(2) = n × e(1).49,50 From the photonics perspective, the order parameter tensor Qij is directly related to the dielectric tensor of the materials εij as:
, where P is the biaxiality, e(1)i is the secondary director and e(2) = n × e(1).49,50 From the photonics perspective, the order parameter tensor Qij is directly related to the dielectric tensor of the materials εij as: | (1) |
| εij = εpδij, | (2) |
Optical properties of photonic crystals are usually described by band diagrams, representing photonic eigenstates at the edges of the irreducible Brillouin zone.6 Photonic states are given as a solution of Maxwell equations, subjected to assumptions about the material properties. In blue phase colloids, one can typically assume that the structures are stable in time, that there is no charge (ρ = 0), no current (j = 0) and that the material is magnetically isotropic (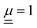 ). We also assume the linear response of the material, giving linear relationships between the applied electric and magnetic field E(r, t) and H(r, t), and the response of the material
). We also assume the linear response of the material, giving linear relationships between the applied electric and magnetic field E(r, t) and H(r, t), and the response of the material  ,
, 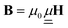 . Further, we assume no absorption losses of the material, which gives us a real, symmetric and positive definite dielectric tensor (
. Further, we assume no absorption losses of the material, which gives us a real, symmetric and positive definite dielectric tensor ( ). And finally, we are interested in the photonic response at primarily optical frequencies, taking the dielectric function not to depend on the frequency of the applied electric field.
). And finally, we are interested in the photonic response at primarily optical frequencies, taking the dielectric function not to depend on the frequency of the applied electric field.
Following classical references to obtain the master equation for calculations of photonic bands (e.g.ref. 6), the linearity of Maxwell equation allows us to separate space and time variable, by taking E(r, t) = E(r)eiωt and H(r, t) = H(r)eiωt. Then we can write Maxwell equations as:
| ∇ × E − iωμ0H = 0, | (3) |
 | (4) |
| ∇·H = 0, | (5) |
 | (6) |
We decouple the first two equations in a way that only the magnetic field strength H remains in the equation, finally writing:
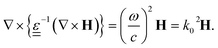 | (7) |
This equation is the master equation for calculations of photonic bands, effectively, being an eigenvalue problem. In order to get photonic states, it has to be solved for distinct dielectric tensor profiles  . The master equation can be formulated also as a function of the electric field E, but using the magnetic field H gives an eigenvalue problem with a Hermitian operator, which simplifies calculations.37
. The master equation can be formulated also as a function of the electric field E, but using the magnetic field H gives an eigenvalue problem with a Hermitian operator, which simplifies calculations.37
Blue phase colloidal crystals have periodic dielectric function; therefore, Bloch theorem and Fourier transformation are used to expand the magnetic field and the inverse of the dielectric tensor in reciprocal space:
 | (8) |
 | (9) |
 is the tensor Fourier coefficient of the dielectric tensor.
is the tensor Fourier coefficient of the dielectric tensor.
Since ∇·H = 0, H is a transverse wave. This is incorporated directly into the master equation. At every point of reciprocal space we define two perpendicular unit vectors, ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) 1 and
1 and ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) 2, that are also perpendicular to vector (k + G). This is achieved by taking some arbitrary unit vector û, that is not parallel to (k + G) and making the following cross-products:
2, that are also perpendicular to vector (k + G). This is achieved by taking some arbitrary unit vector û, that is not parallel to (k + G) and making the following cross-products:  and
and  in every point of reciprocal space. Then one writes hG =
in every point of reciprocal space. Then one writes hG = ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b9.gif) 1H1G +
1H1G + ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b9.gif) 2H2G. This way the transversality is implicitly incorporated throughout the calculation. Effectively, one simplifies the problem, but the rank of eigenproblem is raised by a factor of two.
2H2G. This way the transversality is implicitly incorporated throughout the calculation. Effectively, one simplifies the problem, but the rank of eigenproblem is raised by a factor of two.
If we consider previous expansions in reciprocal space and transversality constraint we can simply solve the eigenvalue problem with standard algorithms that require O(n3) time and n2 space in memory, where n is the rank of the eigenvalue problem. This method is sometimes used,37 but it is very computer time-consuming for our resolution of the unit cell (typically 60 × 60 × 60 points). Instead, we rather use much more efficient iterative algorithm given in ref. 51: one takes some arbitrary initial vector h and multiply it by  until convergence. Time complexity of this algorithm is O(n
until convergence. Time complexity of this algorithm is O(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n). As a result we get first n converged eigenvectors with corresponding eigenvalues-photonic states. Indeed, in our calculations we used both algorithms for solving the eigenvalue problem, finding full agreement between the two approaches.
n). As a result we get first n converged eigenvectors with corresponding eigenvalues-photonic states. Indeed, in our calculations we used both algorithms for solving the eigenvalue problem, finding full agreement between the two approaches.
To construct the photonic bands, we take wave vectors from the edge of the simple cubic (SC) irreducible Brillouin zone (as commonly done in the photonic literature1), following distinct paths and end points labelled G, X, M and R, where the different locations along the path correspond to different magnitudes and directions of the wave-vector k (see Fig. 2). For each chosen k, the corresponding eigenvalues are calculated, forming an ascending set of n eigenvalues. By grouping the eigenvalues and plotting them as a function of k, the band diagrams are generated. Typically, the bands are numbered in an ascending order, with the lowest band (close to the origin Γ point) staring as band 1.
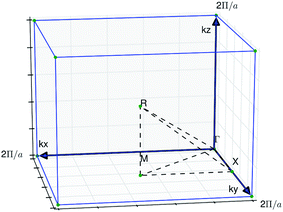 | ||
| Fig. 2 Simple cubic Brillouin zone. The black dashed lines indicate wavevectors used for representing the photonic bands. | ||
Blue phase colloidal crystals are newly predicted materials, not being (yet) demonstrated in experiments. Therefore, for the calculations, we had to choose the dielectric constant of both colloidal particles and the ordinary and extraordinary dielectric constants of the blue phase liquid crystal. We chose blue phase dielectric constants that are in the limits of realizable values, maximising on the dielectric anisotropy, to achieve stronger dielectric contrast. If not stated otherwise, we take εo = 3.6 and εex = 1.7. The dielectric constant of colloidal particles has to be chosen carefully. Some contrast between the particles and BP medium is desired, but not as much that background would appear isotropic compared to particles. That is why we choose the dielectric constant of particles to be εp = 5. For calculations of bands of particle crystals in isotropic background, we set the dielectric constant of the background fluid as εi,j(r) = (2εo + εe)/3δi,j. Finally, we should comment that the demonstrated results, of course, quantitatively strongly depend on the chosen material parameters, in particular on the dielectric constants (refractive indices), but qualitatively we find very similar photonic band responses also at other parameter values.
3 Photonic bands in blue phase I and blue phase II colloidal crystals
Photonic bands are calculated on the edges of the simple cubic (SC) irreducible Brillouin zone to allow for direct comparison between different configurations. Effectively, to identify the role of particles on one hand, and the (no-particle) blue phase in the blue phase colloidal photonic crystals, we separately calculate the photonic bands of three configurations (see Fig. 3 and 4): (i) colloidal crystal (FCC or BCC) in isotropic background, (ii) blue phase I or II with no particles, and (iii) the blue phase colloidal crystals (BPC). Indeed, photonic bands of the BP colloidal crystal appear as an effective combination of the blue phase and the crystal of colloidal particles in isotropic medium. For example, see the inset in Fig. 3 showing a distinct region of the Brillouin zone, where by adding the particles to the blue phase I a local band gap has opened: clearly, blue phase I has no local band gap in this region of the Brillouin zone but the particle lattice has, and the result is a combined photonic band. More specifically, the inset in Fig. 3 demonstrates a local relative gap of size Δω/ω = 0.02 at the point R for BPC I with 120 nm particles. As the second example of the photonic interplay between the blue phase and the particles, note that some photonic bands of the colloidal crystal in isotropic background are degenerate in distinct regions of the Brillouin zone (e.g. in the M–Γ–R region at ωa/2πc ∼ 0.35–0.55), but become nondegenerate when combined into the blue phase colloidal crystal. An exactly similar effective combination of photonic bands and of similar widths, only in different regions of the Brillouin zone, is observed also in blue phase II colloidal crystals as shown in Fig. 4.Photonic bands of blue phase colloidal crystals can be tuned by changing the size of the colloidal particles, as shown in Fig. 5. Relatively small particles (r ∼ 40 nm) have an almost negligible effect on the band structure, which is determined by the birefringent profile of the blue phase; however, interestingly, if the particles are large enough they can cause opening of local band gaps. For particles of radius r = 80 nm, the local band gap (Δω/ω ≈ 0.006) opens at point R in the BPC I crystal, which for particles of size 120 nm the size further increases to Δω/ω ≈ 0.02. Also for the BPC II crystal we see that larger particles cause larger gaps, and there is a local gap of size Δω/ω ≈ 0.02 between the 4th and 5th band for 100 nm colloids in BPC II at point M and a gap of size Δω/ω ≈ 0.03 between the same bands for 120 nm colloids. The photonic bands of blue phase colloidal crystals are a combination of particle bands and blue phase bands that are conditioned by the limiting examples of either of them. For example, particles with the dielectric constant equal to the dielectric constant of the blue phase in the isotropic phase ( ) show almost no effect on photonic bands, because they effectively behave as isotropic blobs (defect regions) of the blue phase. However, qualitatively, if the dielectric constant of the particles is much larger than the eigenvalues of the anisotropic part of the blue phase dielectric tensor, the blue phase appears isotropic and optical properties of the BP crystal become the same as optical properties of a colloidal crystal in an isotropic medium with the symmetry of the particle lattice.
) show almost no effect on photonic bands, because they effectively behave as isotropic blobs (defect regions) of the blue phase. However, qualitatively, if the dielectric constant of the particles is much larger than the eigenvalues of the anisotropic part of the blue phase dielectric tensor, the blue phase appears isotropic and optical properties of the BP crystal become the same as optical properties of a colloidal crystal in an isotropic medium with the symmetry of the particle lattice.
Very recently functionalised blue phase materials are produced, where blue phase I and II defect networks are used to trap polymers38 and nanoparticles (<10 nm).45,52 Effectively, both polymers and nanoparticles fill the network of defect lines throughout the defect core, effectively replacing the blue phase material.53 Indeed, these materials could act as photonic crystals in an exactly analogous way as shown above for the blue phase colloidal crystals, with now blobs of polymers or clustered nanoparticles spread along the blue phase defect networks acting as effective colloidal particles.
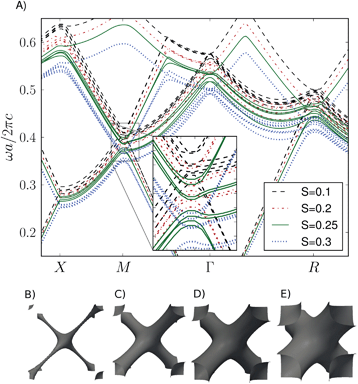
We simulate such polymer or nanoparticle filled blue phases by assuming that defect lines are filled with a new dielectric material, up to cutoff thickness determined by the nematic degree of order S, as shown in Fig. 6b–e. Inside the defect-filled region, we assume the dielectric tensor to be isotropic, εi,j = 5δi,j, whereas outside, we take the dielectric tensor to be unperturbed blue phase II. Fig. 6a shows photonic bands calculated for blue phases II with its defect network filled up to different defect thickness cutoff. Experimentally, this would correspond to a different volume fraction of the polymer (or nanoparticle) dopant. The cutoff value S ≤ 0.1 corresponds to the polymer volume fraction of ∼0.06, S ≤ 0.2 to ∼0.23, S ≤ 0.25 to ∼0.36, and S ≤ 0.3 to ∼0.60. Indeed, we see that for small filling S ≤ 0.1 there is little effect on photonic bands; however, for S ≤ 0.3 the local band gap opens, exactly in an analogous way as demonstrated for blue phase colloidal crystals (Fig. 5). More quantitatively, the size of the band-gap for S ≤ 0.3 filled blue phase is similar to the band gap generated by r = 100 nm particles in blue phase II colloidal crystals. Clearly, this demonstrates that polymer-templated or nanoparticle templated blue phases could also act as photonic crystals with tunable band structure, with the degree of defect network filling being a possible tuning parameter.
Trying to generate a full band-gap photonic crystal, we now combine the two approaches and assume a blue phase colloidal crystal, where – in addition – the defects are filled with polymers or nanoparticles. The effective filling of the blue phase defects relies on the processes of phase separation and particle dispersion in the complex blue phase fluid,52–58 which strongly depends on the used materials.59 Such combination creates a three-component photonic material with photonic bands subjected to the properties of (i) blue phase, (ii) particles and their FCC lattice, and (iii) the dielectric which fills the defect networks. In calculations, we assume an isotropic dielectric tensor of the defect network εi,idef = 4 filled up to S ≤ 0.25 cutoff, and the FCC colloidal crystal with particles of εi,ip = 5. Also, we assume that the interactions, i.e. surface anchoring, at the interfaces between the blue phase and the other two components are weak, meaning that there is no effect of the other two components on the birefringent profile of the blue phases. Interestingly, such three-component system creates an indirect total band gap between the 7-th and 8-th band of the whole edge of SC irreducible Brillouin zone, with the exception of one point on the line M–Γ, as shown in Fig. 7. At this point bands seem to cross each other and no gap appears, not even for different combinations of the dielectric constants of the three components. The band structure of the dielectric defect filled blue phase I FCC colloidal crystal is further visualised in Fig. 8 where an electromagnetic field energy density (|H|2 + ε|E|2) for the 8th and 9th band at point Γ is presented. Similar to the one-dimensional case in the report by Joannopoulos et al. (page 48, ref. 6) we can see that the lower optical band corresponds to high energy density in regions of higher dielectric constant (colloid particles) and the upper band to regions of lower dielectric constant (background). Finally, this new structure of the photonic bands shows that blue phases offer further possibilities for engineering their photonic bands by doping them with multiple optically different guest components, including colloidal particles, polymers, and nanoparticles.
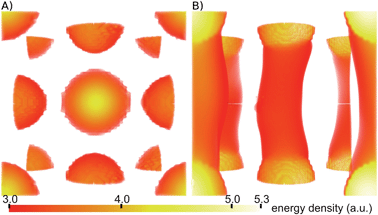 | ||
| Fig. 8 Regions of a high electromagnetic field energy density (|H|2 + |εE|2) within the (real) unit cell of BPC I for the (A) 8th band and (B) 9th band calculated at point Γ. There exists a local band gap between these two bands. Energy in the 8th band is concentrated within dielectric particles, but in the 9th band high energy regions form cylindrical shapes through the unit cell. Units for the energy density are taken following ref. 60. | ||
4 Conclusions
This work proposes soft matter photonic crystals which effectively join components with two different inherent symmetries into one photonic crystal material, creating a complex photonic crystal material with tunable photonic band structure. This combined photonic response is demonstrated by numerical modelling in blue phase colloidal crystals, where blue phase liquid crystalline fluid generates a periodic array of trapping sites for colloidal particles with the symmetry different from the symmetry of the blue phase itself. The relevance of either the particle component or the blue-phase-liquid component can be tuned by simple material parameters, including particle size, temperature, or refractive indices of blue phases or particles.Using Bloch formalism combined with numerical solving of the eigen-equations, we calculate (i) the photonic bands of blue phase colloidal crystals, (ii) the photonic bands of (no-particle) blue phases, and (iii) photonic bands of FCC and BCC lattices of particles in isotropic background. Such comparison of bands reveals that photonic bands and local band gaps can be easily tuned and even created by changing the size of the particles, with larger particles generally leading to larger local band gaps.
To make a link towards related recent experiments, we consider also photonic bands of defect-doped blue phases, where defect cores of blue phases are assumed to be replaced with another dielectric material – like polymer or nanoparticle doped blue phases – also showing opening and tuning of local band gaps by e.g. dopant concentration or dielectric permittivity. For example, in blue phase II based materials, we get roughly equivalent gap size for blue phase defects filled with a dielectric dopant up to a nematic degree of order S = 0.3 cut-off and the blue phase colloidal crystal with particles of size r = 100 nm. As the second analogous material, we consider a three-component system of blue phase colloidal crystals, which have all the defect networks additionally doped with a different dielectric, finding a total indirect band gap (except for one point) between the 7th and 8th band on the entire edge of the SC irreducible zone.
Finally, the demonstrated results show that controlling and combining the symmetries of multiple components in soft matter could be used as a novel route towards tunable soft matter photonics.
Acknowledgements
Authors acknowledge the financial support from the SLO ARRS program P1-0099, SLO ARSS grant Z1-5441 and EU FP7 Marie Curie CIG grant FREEFLUID.References
- J. D. Joannopoulos, P. R. Villeneuve and S. H. Fan, Nature, 1997, 386, 143–149 CrossRef CAS.
- T. Baba, Nat. Photonics, 2008, 2, 465–473 CrossRef CAS.
- M. Eichenfield, et al. , Nature, 2009, 459, 550–U79 CrossRef CAS PubMed.
- E. Yablonovitch, Phys. Rev. Lett., 1987, 58, 2059 CrossRef CAS.
- H. O. Everitt, Optics & Photonics News, 1992, vol. 3, pp. 20–23 Search PubMed.
- J. D. Joannopoulos, S. G. Johnson, J. N. Winn and R. D. Meade, Photonic Crystals: Molding the Flow of Light, Princeton University Press, Princeteon, 2nd edn, 2008 Search PubMed.
- R. B. Wehrspohn and J. Üpping, J. Opt., 2012, 14, 024003 CrossRef.
- S. John, Nat. Mater., 2012, 11, 997–999 CrossRef CAS PubMed.
- V. Mizeikis, K. Seet, S. Juodkazis and H. Misawa, Opt. Lett., 2004, 29, 2061–2063 CrossRef.
- M. Qi, E. Lidorikis, P. T. Rakich, S. G. Johnson, J. D. Joannopoulos, E. P. Ippen and H. I. Smith, Nature, 2004, 429, 538 CrossRef CAS PubMed.
- M. Miyake, Y. C. Chen, P. V. Braun and P. Wiltzius, Adv. Mater., 2009, 21, 3012–3015 CrossRef CAS.
- M. Campbell, D. N. Sharp, M. T. Harrison, R. G. Denning and A. J. Turberfield, Nature, 2000, 404, 53–56 CrossRef CAS PubMed.
- M. Deubel, G. von Freymann, M. Wegener, S. Pereira, K. Busch and C. M. Soukoulis, Nat. Mater., 2004, 3, 444–447 CrossRef CAS PubMed.
- P. Jiang, K. S. Hwang, D. M. Mittleman, J. F. Bertone and V. L. Colvin, J. Am. Chem. Soc., 1999, 121, 11630–11637 CrossRef CAS.
- R. C. Schroden, M. Al-Daous, C. F. Blanford and A. Stein, Chem. Mater., 2002, 14, 3305 CrossRef CAS.
- G. I. N. Waterhouse and M. R. Waterland, Polyhedron, 2007, 26, 356–368 CrossRef CAS PubMed.
- K. A. Arpin, et al. , Nat. Commun., 2013, 4, 2630 Search PubMed.
- A. P. Hynninen, J. H. J. Thijssen, E. C. M. Vermolen, M. Dijkstra and A. van Blaaderen, Nat. Mater., 2007, 6, 202–205 CrossRef CAS PubMed.
- E. Yablonovitch, T. J. Gmitter and K. M. Leung, Phys. Rev. Lett., 1991, 67, 2295 CrossRef CAS.
- I. I. Shishkin, K. B. Samusev, M. V. Rybin, M. F. Limonov, Yu. S. Kivshar, A. Gaidukeviciute, R. V. Kiyan and B. N. Chichkov, JETP Lett., 2012, 95, 457–461 CrossRef CAS.
- J. Zhang, Z. Sun and B. Yang, Curr. Opin. Colloid Interface Sci., 2009, 14, 103–114 CrossRef CAS PubMed.
- J. Hilhorst, et al. , Langmuir, 2009, 25, 10408–10412 CrossRef CAS PubMed.
- M. A. McLachlan, N. P. Johnson, R. M. De La Rue and D. W. McComb, J. Mater. Chem., 2004, 14, 144–150 RSC.
- R. P. Zaccaria, et al. , Opt. Express, 2008, 16, 14812–14820 CrossRef CAS.
- T. Ritari, et al. , Opt. Express, 2004, 12, 5931–5939 CrossRef.
- D. C. Zografopoulos, et al. , Lab Chip, 2012, 12, 3598–3610 RSC.
- J. Beeckman, K. Neyts and P. J. M. Vanbrabant, Opt. Eng., 2011, 50, 081202 CrossRef PubMed.
- Z.-Y. Xie, et al. , Adv. Mater., 2008, 20, 3601 CrossRef CAS.
- S. Ertman, et al. , Opt. Express, 2009, 17, 19298–19310 CrossRef CAS PubMed.
- D.-H. Ko, et al. , Appl. Phys. Lett., 2013, 103, 051101 CrossRef PubMed.
- M. A. Dundar, et al. , Appl. Phys. Lett., 2009, 95, 181111 CrossRef PubMed.
- H. Gong, H. Song, X. Li, J. Wang and X. Dong, Sens. Actuators, A, 2013, 195, 139–141 CrossRef CAS PubMed.
- H.-M. Kim, et al. , IEEE Photonics Technol. Lett., 2010, 22, 1539–1541 CrossRef.
- C. M. Jewart, et al. , Opt. Express, 2010, 18, 25657–25664 CrossRef CAS PubMed.
- D. C. Wright and N. D. Mermin, Rev. Mod. Phys., 1989, 61, 385–432 CrossRef CAS.
- H. Kikuchi, Struct. Bonding, 2008, 128, 99 CrossRef CAS.
- R. M. Hornreich and S. Shtrikman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 2067–2072 CrossRef CAS.
- H. Kikuchi, M. Yokota, Y. Hisakado, H. Yang and T. Kajiyama, Nat. Mater., 2002, 1, 64–68 CrossRef CAS PubMed.
- H. J. Coles and M. N. Pivnenko, Nature, 2005, 436, 997–1000 CrossRef CAS PubMed.
- I. C. Khoo, et al. , Opt. Express, 2013, 21, 4319–4327 CrossRef CAS PubMed.
- H.-Y. Liu, et al. , Appl. Phys. Lett., 2010, 96, 121103 CrossRef PubMed.
- W. Y. Cao, et al. , Nat. Mater., 2002, 1, 111–113 CrossRef CAS PubMed.
- Y. Ogawa, J. Fukuda, H. Yoshida and M. Ozaki, Opt. Lett., 2013, 38, 3380–3383 CrossRef PubMed.
- M. Ravnik, G. P. Alexander, J. M. Yeomans and S. Zumer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5188–5192 CrossRef CAS PubMed.
- A. Sharma, M. Worden and T. Hegmann, Ferroelectrics, 2012, 431, 154–163 CrossRef CAS.
- A. Dupuis, D. Marenduzzo, E. Orlandini and J. M. Yeomans, Phys. Rev. Lett., 2005, 95, 097801 CrossRef CAS.
- H.-S. Kitzerow, Mol. Cryst. Liq. Cryst., 1991, 202, 51 CrossRef CAS.
- Y. Chen, D. Xu, S. T. Wu, S. Yamamoto and Y. Haseba, Appl. Phys. Lett., 2013, 102, 141116 CrossRef PubMed.
- M. Ravnik, G. P. Alexander, J. M. Yeomans and S. Zumer, Faraday Discuss., 2010, 144, 159–169 RSC.
- M. Ravnik and S. Zumer, Liq. Cryst., 2009, 36, 1201–1214 CrossRef CAS.
- S. Johnson and J. Joannopoulos, Opt. Express, 2001, 8, 173–190 CrossRef CAS.
- H. Yoshida, Y. Tanaka, K. Kawamoto, H. Kubo, T. Tsuda, A. Fujii, S. Kuwabata, H. Kikuchi and M. Ozaki, Appl. Phys. Express, 2009, 2, 121501 CrossRef.
- J. Fukuda, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061702 CrossRef.
- J.-M. Wong, J.-Y. Hwang and L.-C. Chien, Soft Matter, 2011, 7, 7956–7959 RSC.
- H. Yoshida, K. Inoue, H. Kubo and M. Ozaki, Opt. Mater. Express, 2013, 3, 842 CrossRef CAS.
- J. S. Lintuvuori, A. C. Pawsey, K. Stratford, M. E. Cates, P. S. Clegg and D. Marenduzzo, Phys. Rev. Lett., 2013, 110, 187801 CrossRef CAS.
- F. Castles, et al. , Nat. Mater., 2012, 11, 599603 CrossRef PubMed.
- B. Senyuk, J. S. Evans, P. Ackerman, T. Lee, P. Manna, L. Vigderman, E. R. Zubarev, J. van de Lagemaat and I. I. Smalyukh, Nano Lett., 2012, 12, 955–963 CrossRef CAS PubMed.
- H. Tanaka, J. Phys.: Condens. Matter, 2000, 12, R207–R264 CrossRef CAS.
- S. G. Johnson, M. Ibanescu, M. A. Skorobogatiy, O. Weisberg, J. D. Joannopoulos and Y. Fink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 066611 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |