In situ observation of a hydrogel–glass interface during sliding friction

Abstract

Direct observation of hydrogel contact with a solid surface in water is indispensable for understanding the friction, lubrication, and adhesion of hydrogels under water. However, this is a difficult task since the refractive index of hydrogels is very close to that of water. In this paper, we present a novel method to in situ observe the macroscopic contact of hydrogels with a solid surface based on the principle of critical refraction. This method was applied to investigate the sliding friction of a polyacrylamide (PAAm) hydrogel with glass by using a strain-controlled parallel-plate rheometer. The study revealed that when the compressive pressure is not very high, the hydrogel forms a heterogeneous contact with the glass, and a macro-scale water drop is trapped at the soft interface. The pre-trapped water spreads over the interface to decrease the contact area with the increase in sliding velocity, which dramatically reduces the friction of the hydrogel. The study also revealed that this heterogeneous contact is the reason for the poor reproducibility of hydrogel friction that has been often observed in previous studies. Under the condition of homogeneous full contact, the molecular origin of hydrogel friction in water is discussed. This study highlights the importance of direct interfacial observation to reveal the friction mechanism of hydrogels.

---

I. Introduction

To reveal the low friction mechanism of bio-tissues, the frictional behaviors of hydrogels are drawing increasing attention. It has been revealed that the frictional coefficient of hydrogels, μ, changes over a wide range and exhibits very low values under certain conditions.^1–3 The recent inventions of mechanically tough hydrogels^4–6 have changed the stereotype of weak and brittle synthetic hydrogels. Tough hydrogels with a low surface friction have demonstrated the high potential of these materials for use in engineering and bio-industries such as low friction bearings and artificial cartilages.^7,8

Studies on the surface sliding friction of various types of bulk hydrogels revealed very rich and complex frictional behavior.^1,9–16 In our previous study, the friction of gels against solid substrates in water was studied using a strain-controlled parallel-plate rheometer.^13–16 We observed the complicated velocity dependence of the frictional stress, depending strongly on the interfacial interaction between the gel and the counter surface. For a repulsive combination, we observed a monotonic increase in the friction with velocity.^13,14 For an adhesive combination, we observed, quite often but not always, a distinct transition from high friction to low friction with the increase in velocity.^15,16 The friction transition behavior was influenced by the adhesive strength of the gel to the substrate,¹⁵ and the normal strain (pressure) applied on the gel.¹⁶ This friction transition in liquids was assumed to be due to the decrease in the contact of the hydrogel to the counter surface with the increase in the sliding velocity, similar to the transition of the boundary lubrication to the elastohydrodynamic lubrication (EHL) observed for elastomers in liquids. The latter is explained by a slight tilting of the sliding elastomer with respect to the substrate so that the liquid can invade the interface from the leading edge.^17–19 However, in the parallel-plate geometry, where disc-shaped gels are coaxially rotated on the flat counter surfaces, this water invasion mechanism should not work, as there is no leading edge for water invasion. A similar transition was also observed for an elastomer sliding on a glass substrate in a viscous liquid with the parallel-plate rheometer.²⁰

We assumed that this friction transition of hydrogels originates from the heterogeneous contact of hydrogels in water.^15,16 When a soft material makes contact with an adhesive hard surface in liquid, the liquid is easily trapped at the interface to form heterogeneous contact.¹⁹ At low velocity, the elastic deformation of the adhered part dominates the friction (elastic friction). At high velocity, a continuous water film is formed at the interface due to the forced wetting of the trapped water, and the friction is governed by hydrodynamic lubrication. So, the increase of velocity induces the friction transition from elastic friction to hydrodynamic lubrication.

Direct observation of the hydrogel contact is indispensable to confirm this hypothesis and to understand the friction transition mechanism. In the case of an elastomer sliding on the solid, the contact can be directly observed and the thickness of the lubrication layer formed can be measured by using the principle of the reflection interference contrast microscopy (RICM) technique.²¹ However, this method cannot be applied to hydrogels in water since the refractive index of the gel is very close to that of water. Visualization of hydrogel contact in water remains a difficult task.

In this paper, we present a novel method based on the principle of critical refraction, to observe the macroscopic contact of hydrogels in water prior to and during the sliding motion. As an adhesive combination, sliding friction of polyacrylamide (PAAm) hydrogels with the glass counter surface was investigated. From the relationship between the frictional stress and the macroscopic contact area at various sliding velocities, the friction transition mechanism is revealed.

II. Experimental section

Sample preparation

Hydrogel. Acrylamide (AAm) was purchased from Junsei Chemical Co., Ltd. N,N′-dimethenebis(acrylamide) (MBAA) as a crosslinker was provided by Tokyo Kasei Kogyo Co., Ltd. and 2-oxoglutaric acid as an initiator was provided by Wako Pure Chemical Industries, Ltd. They were used without further purification.

To obtain a gel specimen tough enough for friction measurement, we used a PAAm hydrogel with an interpenetrating polymer network (IPN) structure, based on the double network concept.⁵ PAAm/PAAm IPN gels were synthesized by a two-step sequential free-radical polymerization method, following the step of double network hydrogels.⁵ In the first step, 4 mol% cross-linking agent of MBAA and 0.01 mol% initiator of 2-oxoglutaric acid, with respect to AAm, were added to 1 M AAm solution. Under an argon gas atmosphere, the solution was poured into the space between two glass plates separated by using a 2 mm silicone rubber spacer. Photo-polymerization was carried out with an UV lamp for 6 hours. In the second step, after the gelation of the first PAAm gel was completed, the gel was immersed into a large amount of aqueous solution containing 4 M AAm, 0.02 mol% MBAA, and 0.01 mol% 2-oxoglutaric acid for a day. By irradiation with the UV lamp for 6 hours under an argon gas atmosphere, the second network was subsequently synthesized in the presence of the first PAAm network. The gel at an equilibrium swelling state was obtained by immersing the sample in pure water for a week.

The water content of the gel was 86 wt%, corresponding to a polymer volume fraction of 0.1. The Young's modulus E of the gel was 41.0 kPa, obtained by compression measurement. We assume that the relationship E = 3k_BT/ξ³ for single network hydrogels is also applicable to the IPN gel, and the average mesh size of the gel ξ was estimated to be 7 nm.

Counter substrates. The thin cover glasses (Matsunami Glass ind., Ltd.) of rectangular-shaped (40 mm × 50 mm) and 0.15 mm in thickness were used as counter substrates of friction without any treatment. The contact angle to water of the glass θ* was measured using a Drop Master 300 (Kyowa Interface Science Co., Ltd.) and the average value of θ* was 45°.

In situ observation of a frictional interface

Principle. The principle for the observation of a gel–glass interface, based on the critical refraction,²² is shown in Fig. 1. Owing to the higher refractive index of the glass than that of the gel, the light from the gel side refracts at angles less than the critical refraction angle θ^c_gel that is determined by the relationship sin θ^c_gel = n_gel/n_glass.

Fig. 1 Schematic illustration for the observation of gel–glass contact based on the principle of critical refraction using a trapezoidal prism. In (a), where the gel is in contact with the glass prism, the light comes from the gel refracts at the angle less than θ^c_gel. On the other hand, in (b), where a water film exists at the gel–glass interface, the light coming from the water film refracts at the angle less than θ^c_water. Here, θ^c_gel and θ^c_water are critical refraction angles of the gel and water, respectively, and θ^c_gel > θ^c_water. So, when one observes at an angle θ_r (θ^c_water < θ_r < θ^c_gel), a bright image of the gel is observed in (a), and a black image is observed in (b).

On the other hand, when there is a water layer at the interface of the gel and the glass, the critical refraction angle θ^c_water is determined by sin θ^c_water = n_water/n_glass. Here, n_glass, n_gel, and n_water are the refractive index of the glass, gel, and water, respectively. Since the refractive index of the hydrogel is slightly larger than that of water, θ^c_gel > θ^c_water. So, from an angle θ_r between these two critical angles, that is, θ^c_water < θ_r < θ^c_gel, one can observe the contact of the hydrogel. When the gel is in contact with the substrate, one observes a bright image (Fig. 1a), while a black image is observed when a water film exists at the interface (Fig. 1b). Based on this principle, we built a novel system to in situ observe the frictional interface by combining the prism with the rheometer as shown in Fig. 2.

Fig. 2 Schematic illustration of the set up for the in-situ observation of macroscopic contact of a hydrogel on a glass counter surface. The trapezoidal prism (2) was attached to the upper jig of the rheometer (1), and a cover glass (3), as a counter surface of friction, was fixed to the prism. The hydrogel (4) was fixed to the lower jig (5) of the rheometer and was compressed in water (6) by the upper jig. The lower jig was kept rotating in the clock-wise direction at a steady angular velocity, which leads to sliding of the hydrogel against the cover glass.

In situ observation. The refractive indices of the materials used are shown in Table 1, where n_water was measured using a refractometer (Anton Paar), n_PAAm by ellipsometry (alpha-SE, J.A Woollam Co., Inc.), and n_glass was provided by the manufacturer (Matsunami Glass ind., Ltd.). Critical refraction angles of water and the gel against glass (θ^c_water, θ^c_gel) were calculated from the refractive indices of these materials. The images of the frictional interface were recorded by using a digital video camera (HDR CX550, Sony). The video camera was located 1.5 m away from the friction specimen so that the whole specimen could be observed at the angles θ_r that satisfy the condition θ^c_water < θ_r < θ^c_gel.

Table 1 Optical properties of the materials used in this study

Wavelength λ (nm)	Refractive index, n			Critical refraction angle θ^c (°)		θ ^cgel − θ^cwater (°)
	Water	PAAm gel	Glass	Water	PAAm gel
436	1.340	1.356	1.527	61.34	62.91	1.57
589	1.333	1.348	1.517	61.45	63.02	1.57
656	1.331	1.346	1.514	61.51	63.05	1.54

---

Table 1 shows that in the visible range, the observable angle range is about 1.5° between the two critical angles of water and the gel. The frictional interface was irradiated with white light to obtain clear photographic images. The angle θ_r was experimentally determined by gradually increasing the observation angle (normal to the friction interface) upto a position that the water image disappeared and the gel image was still observable.

The zoom function of the camera was used to get close images. Adjustments of focus and exposure were set in automatic mode while recording the real time video and the raw images were captured from the video file later on. The disc-shaped specimen was observed as an ellipse shape in the raw images due to the observation from a large angle (about 62°) to the sample normal surface. The ellipse shape was converted back into the circle shape by processing the raw images. The contact area ratio ϕ_macro in relation to the whole disc area (the nominal area) was calculated from the corrected images. Here, we add the subscript “macro” to ϕ in order to distinguish this macroscopic level contact from the micro level contact. Image-Pro (Media Cybernetics, Inc.) and the software of TMPGEnc4.0Xpress (Pegasys, Inc.) were used in the image data analysis.

Friction measurement. The friction of the PAAm gel in pure water was measured by using a rheometer (ARES-2kFRT, TA Instruments) that has parallel-plates geometry and operates in a compressive strain-controlled mode. The top surface of a trapezoidal prism made of BK-7 glass (Chuou Seiki Co., Ltd.) was attached to the upper plate of the rheometer using double-faced tape (Nichiban Co., Ltd.). Cover glass was used as the frictional counter surface, and its edge was firmly fixed to the bottom of the trapezoidal prism using adhesive vinyl tape (Nichiban Co., Ltd.). The possible air gap between the prism and the cover glass was filled with a few drops of immersion oil (refractive index 1.515, Olympus) to match with the refractive index. Disk-shaped PAAm gels, which were 15 mm in diameter and 2.6 mm in thickness, were glued onto the lower plate of the rheometer. The separated gel–glass interface was immersed in pure water for 15 min before experiments, and the temperature of the system was controlled by using the water bath cooling system at 20 °C. The frictional counter surface (cover glass) was then allowed to approach the PAAm gel surface slowly until the initial normal pressure P reached appropriate values. P was varied in the range of 1.1–11 kPa. The corresponding normal strain ε, estimated from ε = P/E, was in the range of 2.7–27%. Before starting the rotation of the lower plate, the gel was equilibrated under compression for 15 min. To eliminate hysteresis in the mechanical tests, all the samples were subjected to a friction pre-run test upto a sliding velocity of 1.0 × 10⁻² m s⁻¹. The data were collected during the second run. Between the first and second runs, the gel was separated from the substrate for 30 min for relaxation in water. Each frictional stress–velocity curve was generated by the Step Rate Sweep Test (SRST) mode, which can change the rotation rate ω from low to high values stepwise. Each rotation rate lasted for 40 seconds, and the average torque at the last 20 seconds was used. The frictional force is calculated using F = 4T(ω)/3R. Here, T(ω) is the frictional torque at the rotation rate ω, and R (=7.5 mm) is the radius of the disc-shaped gel specimen. The average frictional stress σ was calculated using σ = F/πR². Although the sliding velocity varies along the radial direction in parallel-plate geometry, most of the frictional torque comes from the region of large R. So we adopted the sliding velocity at the periphery of the disc-shaped samples, v = ωR, in the σ–v plot.

III. Results and discussion

Contact observation under static conditions

The novel observation system permits us to clearly visualize the hydrogel contact in water. Fig. 3a shows photographic images of contact of the PAAm hydrogel with glass in water. The observation was performed after 15 min loading of various compressive pressures. The bright region of the images indicates the area that the gel is in contact with the glass substrate and the black area indicates trapped water at the interface, as illustrated in Fig. 3b. Fig. 3a clearly shows that the flat gel forms heterogeneous contact with the flat glass substrate even under a normal pressure P of 2.8–5.5 kPa, corresponding to an average normal strain ε as high as 6.8–13%. Homogeneous full contact is reached at a very large pressure of 11 kPa, corresponding to a normal strain of 27%. Here we call such heterogeneous contact as “hetero-contact”.

Fig. 3 (a) Photo images showing the hetero-contact of the PAAm hydrogel with glass in water under various compressive pressures. The images were taken after 15 min of equilibrated time. Dotted circles represent the overall area of the disc-shaped gel. The bright regions are in contact with the glass and the dark regions are trapped with water. (b) An illustration of gel–glass heterogeneous contact. A soft hydrogel forms heterogeneous contact with the adhesive surface, and a water drop was trapped at the interface.

Generally, there are two possible reasons accounting for the formation of the macroscopic “hetero-contact”. One is the “tilting between two surfaces”. When two flat surfaces come close to each other, a slight misalignment always exists to form partial contact. This misalignment effect will be cancelled at a high normal strain. In the present study, the normal strain is larger than several percent. This normal strain range is large enough to cancel the misalignment effect in this study.

Another reason is “trapped water” due to deformation of the soft hydrogel on the adhesive surface. When the normal compression is not very large, the entrapment of water is governed by the energy balance between the elastic deformation of the soft gel and the gel–glass adhesion. According to the elastic dewetting theory,¹⁹ the competition between the surface adhesion energy and the elastic deformation energy is characterized by the elastic length h₀ = −S/E. Here S is the spreading constant of water at the gel/glass interface, and E the modulus of the hydrogel. For adhesive case, S has a negative value, and −S corresponds to the adhesion energy of the hydrogel on glass in water. Assuming S ∼ −1 mN m⁻¹⁶, and using E = 41 kPa, h₀ is estimated to be ∼25 nm. The thickness of the trapped liquid h is related to the radius of trapped liquid R by the relationship¹⁹

h² ∼ Rh₀ (1)

From the contact images shown in Fig. 3a, the size of trapped liquid is in the order of several mm. Using R ∼ 4 mm, h is about ∼10 μm. This estimation indicates that the trapped water drop is ca. 10 μm in thickness. Due to the nucleation mechanism of this elastic dewetting process, the hetero-contact has a random nature. That is, the volume and the position of the trapped water could not be well controlled.^19,23

Friction behaviors at hetero-contact

The hetero-contact formed prior to the sliding friction test greatly influences the friction behavior of the hydrogel. Fig. 4a shows the velocity dependence of the dynamic frictional stress σ of the PAAm gel in hetero-contact against the glass substrate. The friction stress σ decreases slightly with the velocity increase in the low velocity region until v = 10⁻³ m s⁻¹. At v > 10⁻³ m s⁻¹, σ decreases rapidly as the v increases. At high velocity (v > 7 × 10⁻² m s⁻¹), σ increases again.

Fig. 4 (a) Velocity dependence of the dynamic frictional stress σ of the PAAm gel against the glass substrate at hetero-contact and (b) photographic images of the friction interface at each velocity. The contact area ratio ϕ_macro at each velocity was calculated by image analysis (c). The initial pressure was 2.8 kPa.

Fig. 4b shows the corresponding photographic images of the frictional interface. These images show that, the contact area was about 70% under the static condition (v = 0).

The contact shape and area are almost the same under the static conditions at the low velocity range (images 1 and 2). Above the velocity (2.6 × 10⁻³ m s⁻¹) that the frictional stress starts to decrease, the contact area starts to decrease and the trapped water spreads around the interface (images 3 and 4). As shown in image 4, the water spreads to the whole area except the central part of the sample at large velocity. However, as the velocity further increases, part of the periphery region forms contact again with the substrate (image 5), and this is consistent with the friction stress increase.

Thus, the friction and contact area showed a clear correlation with the velocity changes. Fig. 4c shows the velocity dependence of the macroscopic contact area ratio ϕ_macro obtained from the photographic images of Fig. 4b. Since the frictional torque is mostly contributed by the periphery region of the specimen, the contact in this region strongly influences the friction stress.

To observe the spreading process of trapped water with the increase of velocity, the time evolution of the photographic images at the on-set velocity of 2.6 × 10⁻³(m s⁻¹) is shown in Fig. 5. With the rotation of the hydrogel in the clock-wise direction, the area of the water film increases, with the leading edge of the water (indicated by small arrows) spreading along the rotating direction of the hydrogel. At 60 s, the water forms a continuous circular path. This result confirms the forced wetting of the trapped water.¹⁹

Fig. 5 Images of the frictional interface with different times at friction transition velocity (2.6 × 10⁻³ m s⁻¹). The large arrow indicates the direction of the hydrogel rotation, and the small arrow indicates the leading edge of water. The normal pressure was 1.1 kPa.

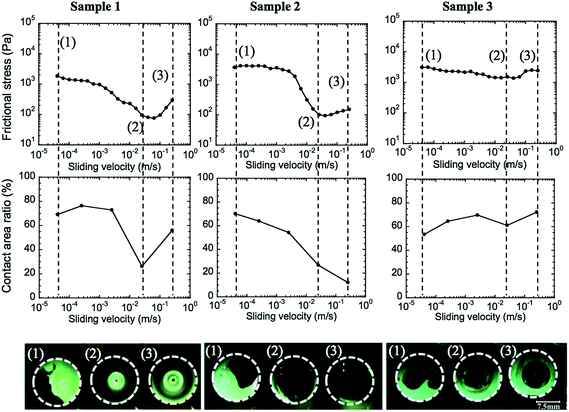
As the hetero-contact is formed via the nucleation process, the volume and the position of the trapped water could not be well controlled. We consider that the poor reproducibility of hydrogel friction often observed is due to this reason.¹⁶ By using this in situ interface observation, we confirm this assumption. Fig. 6 shows the friction behaviors of 3 similar samples. Although the 3 samples were loaded under the same conditions, they formed different initial contacts. By applying sliding motion, spreading of the trapped water occurred at high velocity for all these samples. However, the evolution of the contact varied with the initial position and the shape of trapped water as well as its relationship with the sliding direction. In sample 1, the center of the plane was in contact, so the outer non-contact areas only propagated into the peripheral region along with the sliding direction. But in sample 2, a part of the center was not in contact, and the water propagated into the whole interface. This contact area diminishing, especially in the outside region of the sample, leads to a dramatic reduction in the friction of samples 1 and 2. In contrast, in the case of sample 3 that showed weak velocity dependence of the friction, the trapped water gathered in the central region of the specimen, and the outside region maintained the contact even at high velocity. As the friction is dominated by the outside region, the elastic friction generated at this region appeared as a high friction, so that the friction showed weak velocity-dependence.

Fig. 6 Relationship between frictional behavior and macroscopic contact. The friction strongly depends on the initial contact. Clear water spreading was observed in samples 1 and 2, which leads to dramatic friction reduction at high velocity. Re-adsorption was observed for sample 1 at high velocity. However, in sample 3, the whole periphery was in contact, and no dramatic friction reduction was observed. The pressure was 2.8 kPa.

Furthermore, although the forced wetting occurred in the periphery region both for samples 1 and 2, the contact reforming occurred at the high velocity in sample 1 but not in sample 2. Therefore, friction-strengthening behaviors in the high velocity region (v > 2.6 × 10⁻² m s⁻¹) have different mechanisms for samples 1 and 2. For sample 1, it is due to the increase in the contact area, and for sample 2, it is attributed to the increase in the viscous resistance of the hydrodynamic lubrication. The contact reforming may be due to the pressure-induced squeezing or discharge of the water from the periphery region by centrifugal force.

Considering the partial contact of the gel with the counter surface in water, the total friction stress σ comes from two contributions, the elastic friction from the contact region σ_E and the hydrodynamic lubrication σ_H from the non-contact region.

σ = ϕ_macroσ_E + (1 − ϕ_macro)σ_H (2)

Here, ϕ_macro is the macroscopic contact area ratio, and it is strongly velocity-dependent, as revealed by Fig. 4 and 6. For the friction geometry used in the present study, σ_H = (2/3)ηv/h, where 2/3 is the geometry factor, η is the viscosity of water, and h is the water film thickness. h in this case should depend on the amount of water trapped. In Fig. 6, the sample 2 almost lost the contact at the high velocity end of 2 × 10⁻¹ m s⁻¹. So at this velocity, the gel was isolated from the glass by forming a continuous water film (ϕ_macro = 0), and the friction was only from the hydrodynamic term σ_H. Taking σ = σ_H = 100 Pa, v = 2 × 10⁻¹ m s⁻¹ from Fig. 6, and η = 10⁻³ Pa s for water, we get an average water film thickness h = 1 μm. This value is one order lower in magnitude than the water drop thickness estimated in the previous section from eqn (1). Considering the spreading and possible discharge of the water from the periphery region, this result is reasonable.

Thus, the contact observation confirmed the assumption that the friction reduction of the hydrogel is due to the decrease of the contact area at high velocity by the forced wetting of water pre-trapped at the soft interface.^15,16 However, as shown by sample 1, re-contact may occur with the further increase of velocity, so the friction-strengthening behaviors at the high velocity end may be also due to the increased contact area, in addition to the increased viscous dissipation. Direct interfacial observation is necessary to identify these differences in the friction mechanism. As the hetero-contact is formed based on a nucleation mechanism, the friction behavior observed under the hetero-contact conditions has a poor reproducibility. A recent study has demonstrated that by using a rough surface, well reproducible friction behaviors of hydrogels can be obtained.¹⁶

Friction behaviors at homo-contact

At the hetero-contact, the contact area ϕ_macro changes with sliding velocity, which makes it difficult to observe the behavior of σ_E. In order to reveal that the friction behavior only comes from the elastic friction σ_E, we need to remove the second term σ_H. For this purpose, we make the gel in full contact with the substrate (ϕ_macro = 1) under the static conditions. This, called as homo-contact, can be obtained by applying a large load of 11 kPa at first to the sample to squeeze the trapped water out and then lower the load to the level required. Under these homo-contact conditions, one can discuss the friction in terms of the molecular interaction between the PAAm hydrogel and the glass.^15,24

Fig. 7 shows the friction behavior and the contact images for the sample with an initial homogeneous contact. Different from the hetero-contact, the friction of the sample with homo-contact slowly decreases as the velocity increases in the low velocity region upto 2.6 × 10⁻³ m s⁻¹, and then the friction increases, exhibiting a much larger value than that of the hetero-contact at the high velocity. The homogeneous contact was maintained over the whole velocity range studied. The friction with homo-contact does not show abrupt friction reduction. This result further confirmed that, in the parallel-plates geometry, in which no water invasion from the outside, the friction reduction observed in Fig. 6 is caused by the spreading of trapped water of hetero-contact.

Fig. 7 Velocity dependence on the dynamic frictional stress of the PAAm gel (a) and photographic images of the friction interface at each velocity (b) at homo-contact. The initial pressure was 11 kPa, but when the interface gets full contact the pressure was reduced to 2.8 kPa for friction measurement. The arrow in (b) indicates the rotation direction of the hydrogel.

Fig. 8a shows the frictional behaviors for 3 different normal pressures under homo-contact conditions. Similar to the result shown in Fig. 7, the gel maintains full contact with the counter surface for all the velocities studied (contact images are omitted), and the friction hardly changes with the normal pressure. This result suggests that under these homo-contact conditions, the elastic friction of the PAAm hydrogel is hardly influenced by the pressure applied. These results are in full agreement with our recent study on a zwitterionic hydrogel system.²⁵

Fig. 8 (a) Velocity dependence on the dynamic frictional force of the PAAm gel in homo-contact under 3 different normal pressures. (b) The total observed frictional stress (open circles), the viscous stress (dotted line) estimated from σ_vis, and the elastic stress (closed circles) calculated from the difference between the total stress and the viscous stress. Normal pressure: 2.8 kPa.

Since there is no change in the macroscopic contact area during the sliding process, we could discuss the results shown in Fig. 7 and 8 in terms of hydrogel molecular dynamics. According to the polymer chain adsorption–desorption model,²⁴σ_E is obtained from two contributions: elastic stretching of the adsorbed polymer chain, σ_el, and the viscous dissipation of the hydrated layer of the polymer network, σ_vis.

σ_E = σ_el + σ_vis (3)

Roughly, the hydrated layer thickness is in the order of the mesh size ξ of the hydrogel, so σ_vis = (2/3)ηv/ξ, here we omitted the microscopic contact area ratio ϕ_micro since it is very small. It should be mentioned that the hydrated layer is much thinner than the trapped water layer thickness discussed in the previous section. Using ξ = 7 nm, and η = 10⁻³ Pa s, the magnitude of σ_vis is estimated, and the result is shown as the dotted line in Fig. 8b. From the difference of the observed frictional stress and the viscous stress, one can estimate the elastic stress σ_el. As shown in Fig. 8b, σ_el shows velocity dependence, which is related to the adsorption–desorption dynamics of the polymer chains.^15,24 According to the adsorption adsorption–desorption model, at low velocity, σ_el is independent of the sliding velocity. When v is high enough to perturb the adsorption time of the polymers but still much lower than a characteristic velocity v_f, the frictional stress slightly increases with the velocity. On the other hand, when v is higher than v_f, the desorbed polymers do not have sufficient time to re-adsorb, and then σ_el decreases with v. So around v_f, the σ_el shows a peak. Assuming that one partial chain of the hydrogel forms one adsorption point, the characteristic velocity v_f related to the relaxation time of the partial chains, v_f ∼ (k_BT)^1/3E^2/3/η. For a hydrogel of modulus E = 41 kPa, v_f is estimated in the order of 0.1 m s⁻¹. This value is higher but quite close to the velocity at which σ_el shows a local maximum in Fig. 8b, which justifies the above discussion. However, the friction weakening below the velocity of 2.6 × 10⁻³ m s⁻¹ could not be explained by the single chain dynamics model. The collective adsorption and desorption of polymer chains should be taken into account in such a low velocity region.

Finally we should notice that the present optical set up could only identify a relatively thick water film, approximately in the order of 0.1–1 μm but could not identify changes in the nano-scale contact dynamics. This is because although the polymer chain adsorption and desorption dynamics change with the velocity, as observed by the frictional stress changes (Fig. 7a), the bright images in Fig. 7b hardly change with the sliding velocity.

IV. Conclusions

Based on the critical refraction principle, the macroscopic contact of the hydrogel with glass in water was successfully observed in situ for the first time. A water film of an irregular shape and area was found to be pre-trapped at the interface to form a heterogeneous contact. The macroscopic contact (contact area, shape, and the amount of trapped water at the interface) at the initial states, prior to the sliding motion, strongly affects the friction behaviors over velocity changes. The heterogeneous contact may cause the dramatic friction reduction due to the forced wetting of the pre-trapped water. When the gel has a homogeneous contact with the counter surface, the friction of the gel is almost independent of the normal pressure, and shows gradual friction weakening and then strengthens with velocity increase. Thus, the observation clearly shows that the macroscopic contact and the microscopic interfacial interaction are usually intertwined which makes the friction of hydrogels complicated. Separation of these two effects at different scales is necessary to elucidate the true friction mechanism of hydrogels and to control the hydrogel friction. A study focusing on the interfacial molecular interaction is going to be published in a separate paper.²⁵

Acknowledgements

This research was financially supported by a Grant-in-Aid for Scientific Research (S) (no. 124225006) from the Japan Society for the Promotion of Science (JSPS).

References and notes

1. J. P. Gong, Soft Matter, 2006, 7, 544.
2. J. P. Gong, M. Higa, Y. Iwasaki, Y. Katsuyama and Y. Osada, J. Phys. Chem. B, 1997, 101, 5487.
3. J. P. Gong, T. Kurokawa, T. Narita, K. Kagata, Y. Osada, G. Nishimura and M. Kinjo, J. Am. Chem. Soc., 2001, 123, 5582.
4. Y. Okumura and K. Ito, Adv. Mater., 2001, 13, 485.
5. J. P. Gong, Y. Katsuyama, T. Kurokawa and Y. Osada, Adv. Mater., 2003, 15, 1155.
6. J. Y. Sun, X. H. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Nature, 2012, 489, 133.
7. D. Kaneko, T. Tada, T. Kurokawa, J. P. Gong and Y. Osada, Adv. Mater., 2004, 17, 535.
8. K. Yasuda, J. P. Gong, Y. Katsuyama, A. Nakayama, Y. Tanabe, E. Kondo, M. Ueno and Y. Osada, Biomaterials, 2005, 26, 4468.
9. J. P. Gong, Y. Iwasaki, Y. Osada, K. Kurihara and Y. Hamai, J. Phys. Chem. B, 1999, 103, 6001.
10. T. Charitat and J. F. Joanny, Eur. Phys. J. E, 2000, 3, 369.
11. T. Baumberger, C. Caroli and O. Ronsin, Phys. Rev. Lett., 2002, 88, 075509.
12. M. Takata, T. Yamaguchi and M. Doi, J. Phys. Soc. Jpn., 2010, 79, 063701.
13. J. P. Gong, G. Kagata and Y. Osada, J. Phys. Chem. B, 1999, 103, 6007.
14. S. Oogaki, G. Kagata, T. Kurokawa, Y. Osada and J. P. Gong, Soft Matter, 2009, 5, 1879.
15. T. Tominaga, H. Biederman, H. Furukawa, Y. Osada and J. P. Gong, Soft Matter, 2008, 4(5), 1033.
16. S. Yashima, N. Takase, T. Kurokawa and J. P. Gong, Soft Matter, 2014, 10(18), 3192–3199.
17. B. N. J. Presson, Sliding Friction: Physical Principles and Applications, NanoScience and Technology Series, Springer, Berlin, 2nd edn, 1998.
18. A. Martin, J. Clain, A. Buguin and F. Brochard-Wyart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031605.
19. P. G. de Gennes, F. Brochard-Wyart and D. Quere, Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, Springer, New York, 2003.
20. D. Kaneko, M. Oshikawa, T. Yamaguchi, J. P. Gong and M. Doi, J. Phys. Soc. Jpn., 2007, 76, 043601.
21. P. Martin, P. Silberzan and F. Brochard, Langmuir, 1997, 18, 4910.
22. M. Katz, Introduction to Geometrical Optics, World Scientific Publishing Co. Pte. Ltd., 2002.
23. B. N. J. Persson and F. Mugele, J. Phys.: Condens. Matter, 2004, 16, R295.
24. J. P. Gong and Y. Osada, J. Chem. Phys., 1998, 109, 8062.
25. J. Ahmed, H. L. Guo, T. Yamamoto, T. Kurokawa, M. Takahata, T. Nakajima and J. P. Gong, Macromolecules, 2014, 47(9), 3101–3107.

---

Footnote

† Present address: Faculty of Engineering, Yamagata University, Japan.

---