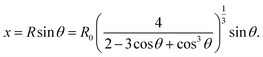Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibro-levitation and inverted pendulum: parametric resonance in vibrating droplets and soft materials†
Rahul
Ramachandran
and
Michael
Nosonovsky
*
College of Engineering & Applied Science, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA. E-mail: nosonovs@uwm.edu; Fax: +1-414-229-6958; Tel: +1-414-229-2816
First published on 1st May 2014
Abstract
The phenomenon of liquid droplets “levitating” or bouncing off a liquid vibrating surface has attracted attention of scientists due to its possible application in microfluidics and novel nanostructured superhydrophobic materials. Several models have been suggested in the literature, and the effect is usually attributed to non-linear viscosity. Here we suggest a simple model relating the effect to the parametric resonance as described by the Mathieu equation, which explains stabilization of an inverted pendulum with vibration foundation. Small fast vibrations can be substituted by an effective “levitation” force. We present modeling and experimental results for oil droplets and discuss how the mathematical separation of the slow and fast motion provides insights on the relation of vibro-levitation of oil droplets and soft materials with the vibro-stabilization of an inverted pendulum, and the “Indian rope” and “Cornstarch monster” tricks.
1 Introduction
Levitation (from Latin levitas lightness) is the process by which an object is suspended by a physical force against gravity. While levitation was claimed by many ancient spiritual and occult teachings and studied by scholars including Sir Isaac Newton, who investigated the possibility of levitation as an opposite force to gravitation,1 physics investigates several ways of levitation including magnetic, electrostatic, acoustic, aerodynamic and others.2 Acoustic levitation is one possibility of a particular interest. The phenomenon is based on the non-linear nature of intense sound waves which results in acoustic radiation pressure creating an average positive force on a suspended object which resists the weight of the object.3Droplets, despite their apparent simplicity, constitute quite complex objects involving such properties and effects as the surface tension, Laplace pressure, capillary waves, and non-linear viscosity. Droplet transport, coalescence, and bouncing off solid and liquid surfaces is still not completely understood, since it involves complex interactions and can lead to complicated scenarios of droplet evolution. This complexity of droplet behavior makes them suitable for various applications in novel smart nanostructured materials, ranging from superhydrophobicity and icephobicity to microfluidic applications where droplets can serve as micro-reactors for various chemical compounds carried by coalescent water droplets.4–16 It has been shown that droplet coalescence can realize the Boolean logic and thus a “droplet computer” can in principle be created.17–19
Recent studies showed experimentally that incoming droplets can bounce-off from a vibrating liquid surface thus leading to the “walking droplets” which, in a sense, combine the properties of waves and particles thus serving an illustration of the particle-wave duality.20–22 The effect of bouncing droplets is thought to be similar to the acoustic levitation due to non-linear viscosity in a thin film which leads to hysteresis. However, a detailed model of such effects remains quite complex and several ideas have been suggested in the literature.23–25
It was suggested26 that the classical stability problem of an inverted pendulum on vibrating foundation has relevance to a diverse class of non-linear effects involving dynamic stabilization of statically unstable systems ranging from the vibrational stabilization of beams, to novel “dynamic materials,” the transport and separation of granular material, soft matter, bubbles and droplets, to synchronization of rotating machinery. In these problems, the small fast vibrational motion can be excluded from the consideration and substituted by effective slow forces acting on the system causing the stabilizing effect.
In this paper we suggest a simple analogy between levitating droplets over a vibrating liquid surface and a well known mechanical system consisting of an inverted pendulum on a vibrating foundation. This analogy sheds light on the necessary conditions for droplet levitation. We further discuss the relation of the phenomenon to other non-linear vibration-caused effects, such as the vibro-levitating “Indian rope” magic trick,27,28 the “cornstarch monster” trick, vibration-induced phase transitions,29 as well as possible applications for “smart” dynamic nanocomposite materials.30
2 Model
2.1 The separation of slow and fast motion and the inverted pendulum
The stabilization of an inverted pendulum on a vibrating foundation is a classical dynamic problem, which has been studied by Stephenson in 1908 using the Mathieu equation approach.31,32 Kapitsa suggested in 1951 a different approach using the separation of the fast vibrational motion over slow oscillations.33 The equation of motion for such a general system can be written in the form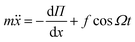 | (1) |
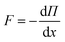 is a “slow” force and f
is a “slow” force and f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt is a fast oscillating force of constant amplitude f. The solution is sought as a sum of the slow and fast oscillating motions x = X(t) + ξ(t). The fast component ξ is assumed to be periodic with the average
Ωt is a fast oscillating force of constant amplitude f. The solution is sought as a sum of the slow and fast oscillating motions x = X(t) + ξ(t). The fast component ξ is assumed to be periodic with the average 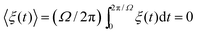 .
.
The “fast” component of motion disappears on the “slow” time scale. To compensate for this an additional effective force is introduced into the equation of motion for the slow component X yielding the equation of motion  , where
, where
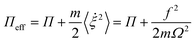 | (2) |
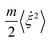 .
.
As an example, consider a system of an inverted pendulum being stabilized in the upside down equilibrium position by the harmonic vibration of its foundation (Fig. 1). The length of the pendulum is L and mass is m. The harmonic oscillation of the foundation is in the form A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt where A is the amplitude of vibration and Ω is the frequency of vibration
Ωt where A is the amplitude of vibration and Ω is the frequency of vibration 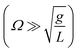 . Its equation of motion is given by
. Its equation of motion is given by
L![[greek psi with two dots above]](https://www.rsc.org/images/entities/i_char_e1af.gif) = g = g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ − AΩ2 ψ − AΩ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ ψ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt Ωt | (3) |
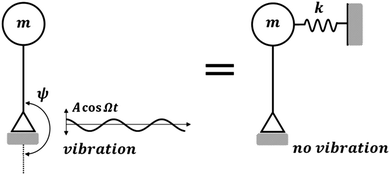 | ||
Fig. 1 An inverted pendulum on a foundation vibrating with a periodic displacement A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt can be represented as an inverted pendulum stabilized by a spring k. Ωt can be represented as an inverted pendulum stabilized by a spring k. | ||
Substituting f = AΩ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ into eqn (2), the effective potential energy is given by
ψ into eqn (2), the effective potential energy is given by
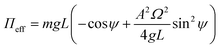 | (4) |
The effective stabilizing force is now given by
 | (5) |
For small angles, the stabilizing force is equivalent to the action of a linear elastic spring force V = −kψ that keeps an inverted pendulum in equilibrium with the effective spring constant 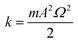 . The stability criterion is given by the condition in eqn (4) being a positive-definite function near the state of equilibrium
. The stability criterion is given by the condition in eqn (4) being a positive-definite function near the state of equilibrium
| A2Ω2 > 2gL | (6) |
Note also that eqn (3) can be presented in the form of Mathieu equation,
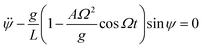 | (7) |
The stability of motion governed by eqn (7) can be studies by the standard methods, which are valid in the assumption of small values of AΩ2/g.
2.2 Liquid droplet levitating on a vibrating foundation
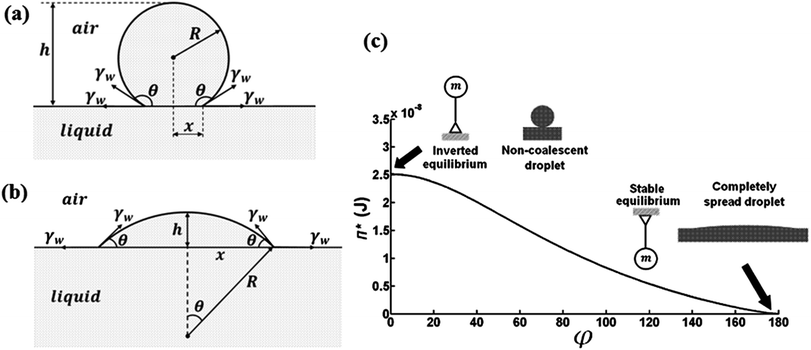
Consider a liquid droplet with the mass m above a flat surface. We assume that the droplet has the shape of a truncated sphere and thus is characterized by the radius R, height h, and the radius of the foundation x (Fig. 2(a) and (b)). The total energy of the droplet involves the gravitational potential energy mgz, where z is the position of the center of mass, and the free surface energy AsγL, where As is the droplet's surface area and γL is the surface free energy per unit area. We assume that the droplet is small enough in comparison with the capillary length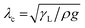 , where ρ is the density; therefore, the capillary contribution prevails over the gravitational one. The capillary length for water (γL = 0.07 N m−1, ρ = 103 kg m−3) at standard temperature and pressure is about λc = 2.6 mm, whereas for corn oil (γL = 0.032 N m−1, ρ = 900 kg m−3) λc = 1.9 mm.
, where ρ is the density; therefore, the capillary contribution prevails over the gravitational one. The capillary length for water (γL = 0.07 N m−1, ρ = 103 kg m−3) at standard temperature and pressure is about λc = 2.6 mm, whereas for corn oil (γL = 0.032 N m−1, ρ = 900 kg m−3) λc = 1.9 mm.
The volume, surface area, and the position of the center of mass above the foundation of the truncated sphere are given by34
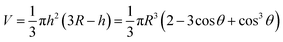 | (8) |
| As = 2πRh = π(x2 + h2) | (9) |
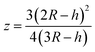 | (10) |
| x2 = 2Rh − h2 | (11) |
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = x/R θ = x/R | (12) |
We now consider spreading of the droplet from the initial spherical shape along the flat surface (Fig. 2(b)). The total volume of the droplet remains constant, so that
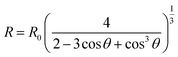 | (13) |
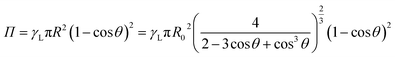 | (14) |
The plot of energy as a function of θ for a corn oil droplet of R0 = 0.25 mm and γL = 0.032 N m−1 is shown in (Fig. 2(c)), and it is observed that θ = 180° corresponds to the unstable equilibrium, similar to an inverted pendulum. Therefore, it is convenient to introduce the variable φ = 180° − θ to characterize the shape of the droplet so that φ = 0 at equilibrium.
Consider now the flat surface vibrating as u = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt. The dynamic equation of motion of the droplet in the vicinity of the unstable equilibrium is
Ωt. The dynamic equation of motion of the droplet in the vicinity of the unstable equilibrium is
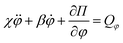 | (15) |
![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) and squared velocity
and squared velocity ![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) 2. The latter term is present due to hysteresis, i.e., the viscous force during the forward motion is different from that during the backward motion
2. The latter term is present due to hysteresis, i.e., the viscous force during the forward motion is different from that during the backward motionQφ = 2πR0φ[α1AΩ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt + α2(AΩ Ωt + α2(AΩ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt)2] Ωt)2] | (16) |
To estimate the values of the parameters χ, β and k we use the following considerations. When the droplet is deformed, the work done per unit time is proportional to the momentum of droplet and thus 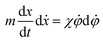 , where m is the mass of the droplet. From Fig. 2(a),
, where m is the mass of the droplet. From Fig. 2(a),
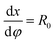 . This gives
. This gives| χ = mR0 | (17) |
Similarly, one can argue that the viscosity of the liquid, μ is related to β as
| β = μR0 | (18) |
For θ close to 180° (or φ → 0°),
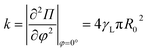 | (19) |
Using in eqn (16), (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt)2 = (1 − cos
Ωt)2 = (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2Ωt)/2 and substituting the amplitudes f1 = 2πR0φα1AΩ and f2 = 2πR0φα2A2Ω2 into eqn (1) yields for the effective “levitating” force
2Ωt)/2 and substituting the amplitudes f1 = 2πR0φα1AΩ and f2 = 2πR0φα2A2Ω2 into eqn (1) yields for the effective “levitating” force
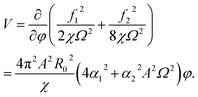 | (20) |
For a corn oil droplet (density ∼ 900 kg m−3, γL = 0.032 N m−1) with R0 = 0.25 mm we can estimate χ = 1.86 × 10−11 kg m, and k = 2.51 × 10−8 N m. It is difficult to estimate the coefficients α1 and α2 involving the linear and non-linear components of viscosity in the thin air layer. However, the values of α1 and α2 are not of interest by themselves, but due to the fact that the viscous force in the form of eqn (16) results in a stabilizing force linearly proportional to φ as given by eqn (20), which is also dependent on Ω.
We note the parallelism between these two systems: the inverted pendulum and the droplet on vibrating foundation. Thus, for a non-vibrating foundation, the position of the spherical drop on top of the liquid surface corresponds to maximum energy and therefore it is similar to the unstable equilibrium of the inverted pendulum. Vibrating foundation can stabilize the inverted pendulum. In the following sections, we will consider other systems with a somewhat similar behavior.
2.3 The “Indian rope” trick
Another interesting phenomenon related to the vibro-levitation is the “Indian rope” trick. The famous trick involves a magician (an Indian fakir) holding a flexible rope, which under certain conditions levitates like a vertical rod. While accounts for the trick remain controversial, Mullin et al.27 suggested that the rope, modeled as a flexible beam, levitates due to vibrating foundation causing the parametric excitation similar to the inverted pendulum.Shishkina et al.28 investigated a rope treated as a flexible Euler beam with the stiffness k subjected to the gravity and an axial load oscillating near the constant value of c2 with the amplitude εa2 and frequency Ω. The transversal deflection of the beam u(x,t) is governed by
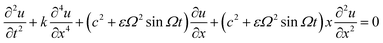 | (21) |
They showed that effect of the oscillating load is equivalent to the increase of the effective flexural stiffness of the rope, k, which becomes equal to  , where x is the distance along the rope. This increase can be significant to exceed the critical value of the stiffness and prevent buckling of the beam (Fig. 3).
, where x is the distance along the rope. This increase can be significant to exceed the critical value of the stiffness and prevent buckling of the beam (Fig. 3).
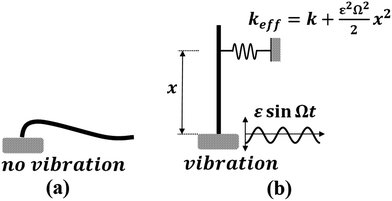 | ||
| Fig. 3 (a) A rope which is under no vibration, buckles under its own weight (b) vertical vibrations results in an increased effective stiffness which prevents buckling. | ||
The same result can be obtained directly by setting the amplitude in eqn (1) as
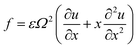 | (22) |
The effective force is then calculated, using 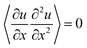 and
and 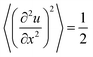 as
as
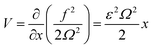 | (23) |
2.4 Cornstarch monsters and other effects
Colloidal suspension of cornstarch in water is a common example of dilatant or shear-thickening fluid. If the cornstarch suspension is taken in hand and squeezed, it can be observed that the suspension turns solid and its surface feels powdery. As soon as the pressure is released, it returns back to its initial flowing state.Peclet number (Pe) which is the ratio of hydrodynamic to diffusion transport rates governs the behavior of colloids.  , where r is the particle radius, D is the diffusion coefficient, and
, where r is the particle radius, D is the diffusion coefficient, and 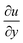 is the shear rate. At high Pe (high shear rates) the hydrodynamic forces are too strong for the diffusion transport to restore the equilibrium of colloidal particles in the suspension. This non-equilibrium state consists of particles clustering together, called hydroclusters.35
is the shear rate. At high Pe (high shear rates) the hydrodynamic forces are too strong for the diffusion transport to restore the equilibrium of colloidal particles in the suspension. This non-equilibrium state consists of particles clustering together, called hydroclusters.35
The hydroclusters are a non-equilibrium state, returning to the equilibrium state of randomness and fluidity once the shear stress is removed. For the system of cornstarch colloidal suspension in water, it is observed that the “cornstarch monsters” levitate on a vibrating surface like an inverted pendulum or the rope in the “Indian rope trick” (Fig. 4(a)). The harmonic vibration of foundation again is seen to stabilize this system in its far-from-equilibrium state.
The hydroclusters formed in cornstarch on application of stress can be simplified into a system of multiple pendulums as shown in Fig. 4(b). High strain rates due to the harmonically vibrating foundation causes formation of hydroclusters of cornstarch particles in water. The hydroclusters of masses m1, m2…, mn (separated by distances l1, l2…, ln) are assumed to be held together by the viscous forces in the surrounding medium. This reduces the phenomenon of cornstarch monsters into a problem of stability of chain of inverted pendulums.
The idea of correlating systems having non-linear vibration induced effects can be generalized in several ways. First, dynamic composite materials with tunable stiffness of reinforcement fibers have already been proposed in the literature.30 Second, vibration-induced stabilization and destabilization can be used for effective phase transition control leading to effective “freezing” (in the case of vibrating droplets), “melting” (in the case of the granular material), or “strengthening” of a flexible fiber. Third, in the case of vibro-levitation, a “levitating force” (denoted by V) is introduced, which is a slow effective force corresponding to the fast small vibrations of the foundation. In the next section we will investigate three types of vibro-levitation.
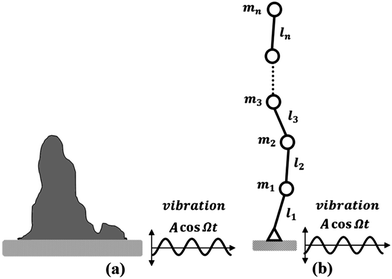
3 Experimental set-up
We investigated experimentally three different types of levitation, induced by vibrating foundation: levitating oil droplets over a vibrating oil bath, the “cornstarch monster” protrusions over a vibrating non-newtonian liquid (cornstarch suspension), and the “levitating Indian rope trick”. A 6.5 inch speaker cone (Pyle Company) formed the vibrating foundation in this study. Sinusoidal waves at a desired frequency (10 Hz < Ω < 1000 Hz) were generated using a Matlab code, which were then amplified using a 20 W amplifier (Lepai) and fed to the speaker (Fig. 5). The vibration of the speaker cone was of the form x = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωt. Since the amplitude of the sound wave was not a controlled parameter, the loudness setting was kept constant during the experiment.
Ωt. Since the amplitude of the sound wave was not a controlled parameter, the loudness setting was kept constant during the experiment.
Liquids used were water, corn oil, SAE 30 engine oil, and 10W40 engine oil. We also used two samples of cornstarch suspension in water, with the starch-to-water volume proportions of 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (sample A) and 2
1 (sample A) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (sample B). The working liquid was placed at the center of the speaker cone to form a bath. Once the speaker was excited by the sound wave, a small drop (typically about 0.1 μL) of the same liquid was dropped on to the surface of the liquid bath using a syringe. This produced satellite droplets which levitated at certain frequencies of vibration of the speaker cone. Levitating droplets could also be produced by pinching and lifting off the liquid surface using a pipette tip/needle. A similar simple experiment was conducted to test the levitation of a rope under harmonic excitation of the foundation. A piece of plastic rope 7 mm long, 4 mm wide and 1 mm thick was affixed to the center of the speaker cone using adhesive tape. Then the sound was turned on so that the speaker cone started to vibrate harmonically and the motion of the rope was observed.
1 (sample B). The working liquid was placed at the center of the speaker cone to form a bath. Once the speaker was excited by the sound wave, a small drop (typically about 0.1 μL) of the same liquid was dropped on to the surface of the liquid bath using a syringe. This produced satellite droplets which levitated at certain frequencies of vibration of the speaker cone. Levitating droplets could also be produced by pinching and lifting off the liquid surface using a pipette tip/needle. A similar simple experiment was conducted to test the levitation of a rope under harmonic excitation of the foundation. A piece of plastic rope 7 mm long, 4 mm wide and 1 mm thick was affixed to the center of the speaker cone using adhesive tape. Then the sound was turned on so that the speaker cone started to vibrate harmonically and the motion of the rope was observed.
4 Results and discussions
In the first experiment, pure water did not produce levitating droplets in the frequency range that it was tested for. However, the higher viscosity liquids, corn oil (Fig. 6(a)), SAE 30, and 10W40 all produced levitating drops in the frequency ranges listed in Table 1, which is consistent with eqn (20). Note, however, that in each case a certain frequency range was observed. In other words, besides a lower frequency limit corresponding to the stability onset there was an upper frequency limit above which the droplet was not stable. Using the analogy with the inverted pendulum, this may be due to the fact that for high frequency the assumptions of small vibration may not be valid. | ||
| Fig. 6 (a) A droplet of corn oil levitating on the surface of corn oil vibrating at 150 Hz, (b) ‘cornstarch monsters’ in sample A at 30 Hz, (c) rope on a foundation vibrating at 130 Hz (movies provided in the ESI†), and (d) Ince–Strutt diagram showing shaded stable region, and the frequency range where levitating droplets are observed. | ||
| Liquid | Viscosity (Pa s) | Surface tension (N m−1) | Frequency range (Hz) |
|---|---|---|---|
| Water | 0.001 | 0.072 | NA |
| Corn oil | 0.052 | 0.032 | 35–350 |
| 10W40 | 0.160 | 0.031 | 30–400 |
| SAE 30 | 0.400 | 0.031 | 30–400 |
The droplets were seen to levitate for several minutes. However, the droplets coalesced with the bath as soon as the sound generation stopped. Outside the specified frequency range the levitating droplets were highly unstable, coalescing with the bath after a short while. At low frequencies it was clearly visible that the interaction between the levitating droplet and the bulk liquid surface created a surface wave. It was also possible to have multiple droplets levitating at the same time. The dependence of the stability of multiple levitating droplets on the frequency was not conclusive from the experiments conducted. Increasing the amplitude of vibration by increasing the loudness resulted in the levitating droplet ‘walking’ on the surface of the liquid bath in seemingly random paths as previously seen by Couder et al.21 Again, the dependency of horizontal motion of droplets to the amplitude could not be conclusively studied since the loudness could not be precisely regulated.
In the second experiment, samples A and B of cornstarch suspensions formed so-called “cornstarch monsters” (or “figurines” with long “fingers”) within a certain range of frequencies (Fig. 6(b)). The typical figurines were visible in both the samples from 15 Hz to around 200 Hz after which they slowly disappeared. The visible difference between the samples was that sample A produced longer cornstarch figurines than sample B.
In the third experiment with the rope, it was seen that rope became unstable from its static equilibrium position when the foundation was vibrated at certain frequencies (Fig. 6(c)). Instabilities were seen to set in at around 17 Hz. The rope became highly unstable in the frequency range 50 Hz to 130 Hz. The instabilities slowly disappeared around 200 Hz and the rope returned to its static equilibrium (buckled) state, which is consistent with eqn (23).
The standard approach to the stability analysis often involves the so-called Ince–Strutt diagram (Fig. 6(d)) for the Mathieu equation (eqn (7)), which can be more conveniently presented as
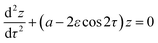 | (24) |
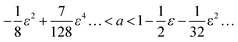 | (25) |
The effective “levitating” force method provides an alternative approach. For vibrating oil droplets, the stabilizing force is given by eqn (20). For cornstarch, which is a strongly non-newtonian liquid, the non-linear effects, such as the increase of the viscosity with flow velocity, can be responsible for the raise of the “fingers”. However, the system is similar to a chain of inverted pendulums on a vibrating foundation. For the “Indian rope”, the mechanism is similar to the stabilization of the inverted pendulum on a vibrating foundation, and the force is given by eqn (23). From the qualitative results described above, it is apparent that the stability of levitating droplets has a dependence on the frequency of vibration of the foundation. This can be considered analogous to the stability of an inverted pendulum. The lower and upper limits of the stable region are determined by the frequency range in which indefinitely stable levitating droplets are observed.
5 Conclusion
In summary, we investigated the effect of vibration on the liquid droplets. Theoretical analysis showed that the effect of vibrating substrate can result in parametric excitation of the droplet leading to the stability of its maximum energy state on top of the vibrating liquid surface. The effect is similar to the stabilization of the inverted pendulum with vibrating foundation and can be interpreted as the action of an effective stabilizing force (“levitation force”) caused by fast vibrations with small amplitude. Similar effects are observed in other experiments involving levitation, such as the “cornstarch monster” and “Indian rope trick”.Notes and references
- J. D. Black, Comparative Literature, 1980, 32, 42–62.
- E. H. Brandt, Science, 1989, 243, 349–355 CAS.
- A. Marmur and R. H. A. Ras, Soft Matter, 2011, 7, 7382–7385 RSC.
- D. Quéré, Rep. Prog. Phys., 2005, 68, 2495–2532 CrossRef.
- E. Bormashenko, R. Pogreb, T. Stein, G. Whyman, M. Erlich, A. Musin, V. Machavariani and D. Aurbach, Phys. Chem. Chem. Phys., 2008, 10, 4056–4061 RSC.
- M. Nosonovsky and B. Bhushan, J. Phys.: Condens. Matter, 2008, 20, 395005 CrossRef.
- R. Tadmor, P. Bahadur, A. Leh, H. E. N'guessan, R. Jaini and L. Dang, Phys. Rev. Lett., 2009, 103, 266101 CrossRef.
- R. Tadmor, Soft Matter, 2011, 7, 1577–1580 RSC.
- H. Kwon, A. T. Paxson, K. K. Varanasi and N. A. Patankar, Phys. Rev. Lett., 2011, 106, 036102 CrossRef.
- M. Nosonovsky, Nature, 2011, 477, 412–413 CrossRef CAS PubMed.
- V. Hejazi, K. Sobolev and M. Nosonovsky, Sci. Rep., 2013, 3, 2194 Search PubMed.
- J. S. Sharp, Soft Matter, 2012, 8, 399–407 RSC.
- X. Liu, Z. Liu, Y. Liang and F. Zhou, Soft Matter, 2012, 8, 10370–10377 RSC.
- J. Wu, W. Wen and P. Sheng, Soft Matter, 2012, 8, 11589–11599 RSC.
- P. d. Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, Springer, New York, 2004 Search PubMed.
- E. Y. Bormashenko, Wetting of Real Surfaces, De Gruyter, Berlin, 2013 Search PubMed.
- I. R. Epstein, Science, 2007, 315, 775–776 CrossRef CAS PubMed.
- M. Prakash and N. Gershenfeld, Science, 2007, 315, 832–835 CrossRef CAS PubMed.
- H. Mertaniemi, R. Forchheimer, O. Ikkala and R. H. A. Ras, Adv. Mater., 2012, 24, 5738–5743 CrossRef CAS PubMed.
- Y. Couder, E. Fort, C. H. Gautier and A. Boudaoud, Phys. Rev. Lett., 2005, 94, 177801 CrossRef CAS.
- Y. Couder, S. Protière, E. Fort and A. Boudaoud, Nature, 2005, 437, 208 CrossRef CAS PubMed.
- Y. Couder, A. Boudaoud, S. Protière and E. Fort, Europhys. News, 2010, 41, 14–18 CrossRef PubMed.
- F. Blanchette and T. P. Bigioni, Nat. Phys., 2006, 2, 254–257 CrossRef CAS.
- S. Dorbolo, D. Terwagne, N. Vandewalle and T. Gilet, New J. Phys., 2008, 10, 113021 CrossRef.
- T. Gilet, D. Terwagne, N. Vandewalle and S. Dorbolo, Phys. Rev. Lett., 2008, 100, 167802 CrossRef CAS.
- I. I. Blekhman, Vibrational Mechanics, World Scientific, Singapore, 2000 Search PubMed.
- T. Mullin, A. Champneys, W. B. Fraser, J. Galan and D. Acheson, Proc. R. Soc. A, 2003, 459, 539–546 CrossRef.
- E. V. Shishkina, I. I. Blekhman, M. P. Cartmell and S. N. Gavrilov, Nonlinear Dyn., 2008, 54, 313–331 CrossRef PubMed.
- J. P. D. Clewett, K. Roeller, R. M. Bowley, S. Herminghaus and M. R. Swift, Phys. Rev. Lett., 2012, 109, 228002 CrossRef.
- K. Lurie, An Introduction to the Mathematical Theory of Dynamic Materials, Springer, New York, 2007 Search PubMed.
- A. Stephenson, Philos. Mag., 1908, 15, 233–236 CrossRef.
- A. Stephenson, Mem. Proc. – Manchester Lit. Philos. Soc., 1908, 52, 1–10 Search PubMed.
- P. L. Kapitza, Usp. Fiz. Nauk, 1951, 44, 7–15 Search PubMed.
- E. W. Weisstein, “Spherical Cap” From MathWorld–A Wolfram Web Resource, http://mathworld.wolfram.com/SphericalCap.html.
- N. J. Wagner and J. F. Brady, Phys. Today, 2009, 62, 27–32 CrossRef CAS PubMed.
- L. Meirovitch, Elements of vibrational analysis, McGraw-Hill, New York, 1986 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm00265b |
| This journal is © The Royal Society of Chemistry 2014 |