(Ir)reversibility in dense granular systems driven by oscillating forces

Abstract

We use computer simulations to study highly dense systems of granular particles that are driven by oscillating forces. We implement different dissipation mechanisms that are used to extract the injected energy. In particular, the action of a simple local Stokes' drag is compared with non-linear and history-dependent frictional forces that act either between particle pairs or between particles and an external container wall. The Stokes' drag leads to particle motion that is periodic with the driving force, even at high densities around close packing where particles undergo frequent collisions. With the introduction of inter-particle frictional forces this “interacting absorbing state” is destroyed and particles start to diffuse around. By reducing the density of the material we go through another transition to a “non-interacting” absorbing state, where particles independently follow the force-induced oscillations without collisions. In the system with particle–wall frictional interactions this transition has signs of a discontinuous phase transition. It is accompanied by a diverging relaxation time, but not by a vanishing order parameter, which rather jumps to zero at the transition.

---

1 Introduction

Driven colloidal or granular systems represent important models for the study of non-equilibrium processes. The competition between energy-injection from the driving and energy-extraction from thermal or non-thermal dissipative processes leads to non-equilibrium stationary states that may be quite different from their thermal counterparts. Frequently, the driving force consists of periodically repeating signals. Especially for granular systems many different driving mechanisms have been invented that belong to this category, for example oscillatory shear,^1–3 temperature oscillations^4,5 or shaking.⁶

Non-Brownian particles immersed in high-viscosity fluid formally obey the Stokes' equation and thus should present time-reversible dynamics under periodic driving forces. A recent study⁷ shows that this reversibility can be broken when driving amplitude or particle density gets too high. The breaking of time-reversibility must be due to additional forces that are not accounted for in the Stokes' equation, for example in the form of direct particle–particle frictional interactions. A simple model⁸ to capture this irreversibility is obtained by adding random displacements on genuinely reversible particle trajectories. With the relaxation time diverging at the transition it is believed to be a critical point that belongs to the universality class of conserved directed percolation.⁹

This reversible–irreversible transition has also been looked at by simulations in the context of the yielding transition of amorphous solids.^10,11 Cyclic shear with amplitudes below a critical value leads to particle trajectories that are periodic with the external force. Larger amplitudes lead to irreversible dynamics. Apparently, below yielding the system self-organizes in such a way as to trap itself deep down in the energy landscape, where barriers are too large to be overcome for the given strain.

In this contribution we obtain yet another view on the reversible (or irreversible) motion of periodically driven particle systems. We ask about the role of frictional interactions in this self-organization. To this end we define different model systems that allow assessment of the interplay between the periodic driving force and different dissipative processes using fast computer simulations. In particular, we will test a simple linear Stokes' drag force against non-linear and history-dependent (dry) friction forces.

2 Model

We simulate a monolayer (xy-plane) bi-disperse system of N = 2500 particles each with a mass density of ρ. One half of the particles have radius R_s = 0.5d (small particles), the other half have radius R_l = 0.7d (large particles). The masses are accordingly m_s,l = (4πρ/3)R_s,l³. We choose the simulation box length L such that we have a fixed packing fraction . In order to minimize finite-size effects, we use periodic boundary conditions in both directions.

Two particles i and j are in contact, if their distance is smaller than the sum of their radii, r < R_i + R_j. Contacting particles interact via the pair force:

F⃑_ij = (F_n + F_n,d)n̂_ij + (F_t + F_t,d)t̂_ij (1)

where n̂_ij and t̂_ij are unit vectors between the pair in normal and in tangential directions, respectively. F_n = k_n (r − (R_i + R_j)) models a harmonic spring with a spring constant of k_n. F_n,d = −γ_nυ_ij,n is a damping term in the normal direction proportional to the velocity difference with the normal damping constant γ_n. F_t introduces a shear force modelling dry frictionwhich sums up the tangential displacement since formation of the contact at time t₀. k_t is the tangential spring constant. Finally, F_t,d = −γ_tυ_ij,t describes a damping term in the tangential direction analogous to the one in the normal direction: . 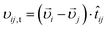In addition, the tangential force is limited by the Coulomb condition F_t ≤ μF_n (μ is the friction constant).

The main dissipative forces are modelled in two ways: A ”viscous” system and a ”surface” system. In the viscous system a velocity dependent damping force affects each particle: (γ_υ is the viscous damping constant). This models a viscous liquid, in which the particles experience a volume independent drag. In the surface system the particles are placed on a surface. The surface–particle interactions are the same as between two particles. Due to the shear force with the surface, the particles experience friction while moving.

With the following driving force energy is injected directly into the bulk of the system. The small particles are driven with an oscillating force F(t) = F₀ sin(ωt) along the plane in the y-direction (as sketched in Fig. 1), possibly leading to collisions with the passive big particles. In case of collisions, small and big particles do not return to their initial position. Without collisions active particles, after a full force cycle, do return to their initial position.

In the simulation and in the following we measure lengths in units of diameters of small particles (d = 1), densities in units of ρ (ρ = 1) and times in units of driving force period (T = 1 and ω = 2π). The parameters for the forces are given in Table 1. Unless stated explicitly, the driving force amplitude is set to F₀ = 1.6 in the surface system, and to F₀ = 100 in the viscous system. Newton's equations of motion are integrated with a time-step of Δt = 0.001 and using the LAMMPS program.^12,13

Table 1 Parameters for the forces as used in the simulations of the surface system. Whenever different values are used for the viscous system they are given in brackets. The particle–surface forces are only used in the surface system. For the viscous system the parameter γ_υ acts equivalently to the parameter γ_t in the surface system. Frictional forces may be turned off by setting the friction coefficient μ = 0

Parameter	Particle–particle	Particle–surface
k n	1000	1000 (−)
k t	2/7kn	2/7kn (−)
γ n	0.5	100 (−)
γ t	0	5 (50)
μ	0 (1)	1 (−)

---

3 Results

To quantify the inter-cycle motion of the particles we define the mean-square displacement (MSD) after an integer number of force cycles (“stroboscobic imaging”)where x_i(t) is the x-coordinate of particle i at time t and t_n = nT represents integer multiples of the driving period. With this definition the intra-cyclic motion of the particles is naturally masked and only the inter-cyclic motion is picked up. If the MSD turns out to be zero, then this indicates that particle motion is periodic with the driving force. Such a state is called absorbing, as there are no fluctuations that can drive the system away from it. In a stationary state, the MSD is independent of n, Δ²(n,m) ≡ Δ_s²(m). We will also be interested in how the stationary state is approached. To this end, we define the following “activity”

A(n) = Δ²(n, 1)/Δ²(0, 1) (4)

which measures the MSD after just one cycle, taken relative to the start of the simulation.

We start by considering systems at density ϕ = 0.82, which is close to the critical jamming density ϕ_J = 0.843.

3.1 Stokes' drag

Let us first consider the case where dissipation is governed by a simple Stokes' drag force , and no frictional forces are present (μ = 0). By choosing γ_υ large enough we arrive at a dynamics that is overdamped and where the particle mass m plays no role.

Note, that at the level of two interacting particles this drag force does not lead to reversible trajectories. Particles will simply push each other out of their way until there is no interaction any more. This is different, therefore, from the hydrodynamic interactions of the Stokes' equation which lead to fully reversible trajectories.

Fig. 1 Sketch of the modeled system. All small particles are driven periodically in the y-direction. The boundaries are periodic in both x- and y-directions.

Perhaps surprising, we nevertheless find that the N-particle system evolves into a stationary state where particles show no inter-cycle motion and Δ_s²(m) ≡ 0. As shown in Fig. 2, the intra-cycle motion in this stationary state is non-trivial, with the particles tracing complex loops. This indicates that particles permanently interact with their neighbors, but these interactions are such that periodic trajectories result.

Fig. 2 Without friction particle motion is periodic with the external driving and trajectories form closed loops (ϕ = 0.82). (a) x-coordinate vs. time t. (b) x(t) vs. y(t).

This is quite different from the situation encountered in the colloidal experiments and simulations of ref. 7 and 8. There, the particles can arrange in such a way as to avoid any particle interactions. Once this is achieved, a non-interacting absorbing state is reached. The intra-cycle trajectories for this scenario would correspond to straight lines (and not loops) that are traced out by going back and forth.

The presence of these loops has been noted previously¹⁴ and discussed extensively by Schreck et al.,¹⁵ where the name “loop-reversible states” has been introduced.

3.2 Frictional interactions

Let us now ask how far frictional interactions affect these loop-reversible states. We will study two different scenarios, where friction either acts between particles or between particles and an exterior container, e.g. a horizontal plate on which the particles are placed in a two-dimensional experiment.^3,6,16,17

3.2.1 Inter-particle friction. We start by discussing the case of inter-particle friction. The acting forces are as before, just now we consider the case of a finite friction coefficient μ = 1. With this choice, forces between contacting particles also act in the tangential direction. Moreover, these forces cannot be derived from a potential energy and depend on the particle history.

It is known that frictional forces can have a rather strong influence on the rheological behavior of dense particle systems. In granular suspensions, for example, inter-particle friction leads to the dramatic effect of discontinuous shear thickening,^18,19 where suspension viscosity increases by orders of magnitude.

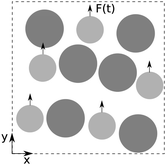
Here, friction destroys loop-reversibility, as is readily apparent from Fig. 3. Depicted is the trajectory of a test particle over a few hundreds of cycles. We clearly see the slow evolution of nearly periodic cycles. Thus, with the introduction of a history-dependent frictional force, the particle motion is irreversible.

Fig. 3 By adding inter-particle friction the loops are not closed but slowly evolve over time. As a result the particles diffuse around.

Interestingly, at long times it is also diffusive. There is no glass-like regime, where particles would be confined to cage-like regions. At first sight this is unexpected, as the particle density is rather high and way above the usual hard-sphere glass transition density. However, it should be remembered that we are dealing with an overdamped and non-thermal system. There can therefore be no entropic confinement, characteristic of the hard-sphere glass. This will become clearer in the next section, where we discuss the effect of particle–wall friction. It will turn out that one can go through a fluid–glass transition by increasing the amplitude F₀ of the driving force.

3.2.2 Frictional plate. In the following we will assume no inter-particle friction, i.e. μ = 0. Instead, we introduce a friction coefficient μ_s = 1 between particles and a horizontal plate, on which the particles are assumed to be placed.

Here, we choose the surface-friction μ_s to act only on the driven small particles, while the Stokes' drag γ_υ is assumed to act only on the passive large particles. Different combinations of μ_s and γ_υ are possible, leading to qualitatively similar results.¹⁴

In this setting the driving amplitude F₀ becomes an important control parameter. This role is highlighted in Fig. 4a, where we plot the MSD Δ_s²(m) for three different values of F₀.

Fig. 4 (a) MSD Δ_s²vs. lag time for different driving amplitudes (ϕ = 0.825). For high driving forces particles are efficiently trapped in their neighboring cages. For small forces the MSD evidences intermediate super-diffusive and terminal diffusive regimes. (b and c) Velocity vs. time for a typical undriven particle for a small (b) and large (c) driving force, respectively.

First, a finite MSD indicates irreversible dynamics. Thus, reversibility is destroyed just as with inter-particle friction (here, due to the inertial dynamics of the driven particles). At short times, increasing the driving amplitude increases the particle activity as is to be expected. At long times, however, the roles are reversed. Small driving amplitudes lead to strongly diffusing particles, while for large amplitudes, particles are trapped in nearest-neighbor cages, like in a glass. Thus, the system undergoes an inverted glass-transition, namely by increasing the driving amplitude. Noticeable is the pronounced super-diffusive particle motion on intermediate timescales before the diffusive regime sets in. This has been the subject of our previous publication.¹⁴ There, we have argued that this transition can be understood in terms of a competition between frictional dissipation and randomization via collisions (Fig. 4b and c).

Consider the passive (large) particles. As they are not driven themselves, they only move because they are kicked around by the driven (small) particles. For small driving amplitudes these kicks are very weak and only temporarily mobilize the passive particles. The particles undergo some small slip displacement and quickly come to rest before the next kick occurs. Thus, all the momentum from the kick is immediately lost to the surface. This is evident in Fig. 4b as the intermittent behavior of the velocity of a typical large particle.

By way of contrast, at high driving amplitudes (in the glassy phase) this momentum is first redistributed (via collisions) to other particles before it is dissipated away. As a consequence the associated particle velocity is strongly fluctuating and never goes to zero (Fig. 4c). It is this randomization which leads to the caging of the particles.

3.3 ϕ-dependence

Up to now we have considered systems at rather high densities close to the critical jamming density ϕ_J = 0.843. For these dense systems not much space is available for particle motion. Driven by an external force, particles therefore necessarily come into contact and strongly interact.

In the following we want to discuss the effects of lowering the density away from the jamming threshold. This will generate more space for particle motion and self-organization into an absorbing and non-interacting state will be possible. We start with the overdamped viscous system of Section 3.2.1, where interparticle friction introduces activity into an otherwise loop-reversible system.

Fig. 5 displays the evolution of the particle activity A (as defined in eqn (4)) with the simulation time for different packing densities ϕ. For small densities the activity quickly decays to very small values. The system thus reaches an absorbing state, and particles can arrange in such a way as to go out of each other's way (during their cyclic motion). As density is increased the time-scale for this decay increases. Above a critical density, a quasi-plateau is formed at intermediate times (“active state”, 500 ≲ n ≲ 10⁴), and a terminal relaxation occurs at very long times n ≳ 10⁴.

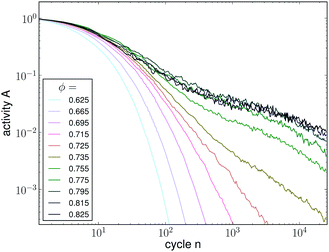Fig. 5 Activity A as a function of simulation time for different packing fractions ϕ; an overdamped viscous system with inter-particle friction and no wall.

It is this slow process which makes a quantitative analysis of these results not very meaningful. For example, the relaxation time-scale shows complex behavior depending on the scale of the activity that one is interested in.

The presence of the quasi-plateau and the terminal relaxation in the active state are worrisome also from the point of view that no real stationary state is formed. The snapshots, Fig. 6, make clear what is happening. As time proceeds the active particles (black) segregate from the passive particles (orange/gray) forming stripes in the direction perpendicular to the driving. This pattern formation is the reason for the absence of a real plateau in the activity. The slow terminal relaxation of the activity then corresponds to the coarsening of the pattern.

Fig. 6 Snapshots of the particle configuration of the viscous system taken at different times (ϕ = 0.775). Active particles are depicted in black, passive particles in orange/gray. After a few thousand force cycles particles segregate into stripes oriented perpendicular to the driving direction.

Fig. 7 displays the structure factor S(q) of this pattern at times corresponding to the snapshots in Fig. 6. The segregation is particularly evident in the y-direction with q_x = 0. Similar segregation phenomena have been observed in different granular systems, in experiments^6,20 as well as in simulations.^21–23

Fig. 7 (a) Structure factor S(q_x = 0, q_y) (SF) for the three different times displayed in Fig. 6. The stripe pattern is evident as a peak at small q_y that increases with simulation time.

By simulating a mono-disperse system with Gaussian distributed particle radii, we checked that the stripe formation is not dependent on the bi-dispersity of the system, but the segregation is a consequence of driving a fraction of the particles differently, which is also supported by the work of Pooley and Yeomans.²¹

Interestingly, we do not observe the stripe-formation when we consider the surface system, where friction only acts between a particle and the container wall (see Fig. 8‡). This second system is closest to the simulations in ref. 21, where stripe-formation is indeed seen. Parameters are quite different, however, and we work at a much higher oscillation frequency. This leads to much smaller oscillation amplitudes which, in our case, are quite small as compared to the particle diameter. We have checked that by decreasing the frequency to appropriate values the stripes quickly form. This is compatible with the phase diagram presented in that study. The driving frequency primarily determines the maximum distance over which particles move during force oscillations. Smaller frequencies meaning larger distances, and therefore a stronger tendency to demix.

Fig. 8 Snapshots of the particle configuration of the surface system taken at different times (ϕ = 0.795). No structure formation is observed.

Fig. 9 displays the activity as a function of time. As before a transition from an absorbing to active state is observed at a critical packing fraction ϕ★. With the slow processes of structure formation absent in this system, we do observe a real stationary state at high densities. No terminal relaxation of the activity is noticeable.

Fig. 9 Activity as a function of simulation time for different volume fractions increasing from left to right; surface system with inertial dynamics and particle–wall friction.

Interestingly, the behavior of the activity shows signs of a discontinuous transition between the absorbing and active state. At the critical packing fraction the activity in the stationary state is finite, . For given ϕ < ϕ^★ the activity follows the critical line for a while before it eventually decays to zero. The closer the transition is approached, the longer it takes to eventually relax. This scenario is quite similar to mode-coupling theories for the glass transition.^24,25

We quantify the relaxation timescale by fixing the MSD to Δ²(τ, 1) = 10⁻¹. An order parameter OP of the transition can be defined from the MSD in the stationary state OP = Δ_s²(1). Both quantities are displayed in Fig. 10 which show the expected behavior: the transition (at ϕ★ ≈ 0.80) is accompanied by an increasing time-scale and the order-parameter shows a very rapid decay from the active to the absorbing state.

Fig. 10 (right axis) OP Δ_s²(1) as a function of ϕ defined as the MSD in the stationary state. (left axis) Relaxation time-scale τ as a function of ϕ defined via Δ²(τ, 1) = 10⁻¹.

Interestingly, the order parameter is non-monotonic in the active state and also decays towards higher densities. This signals the vicinity of random close packing ϕ_rcp, where packing constraints inhibit particle motion. It would be tempting to speculate that this onset is related to the second characteristic packing fraction observed in ref. 16.

4 Conclusions

In conclusion, we have studied different densely packed driven particle systems by computer simulations. We focused on cyclic driving forces that directly act on a subset of the particles, thereby injecting energy into the bulk of the system. Energy is extracted from the system via different dissipation mechanisms. We studied a simple local Stokes' drag force as well as frictional forces that act either between particle pairs or between particles and an external container wall.

We find a surprising wealth of physical phenomena. The local Stokes' drag leads to periodic particle motion even at high densities around close packing. This represents a special kind of absorbing state, where particles continually interact with their nearest neighbors. Introducing inter-particle frictional forces destroys this absorbing state and allows particles to diffuse around. No glassy state is observed, however, which we explain by the fact that particle motion is overdamped and no temperature-like randomization is present.

In agreement with this argument we do observe a glassy regime when particle inertia is important. By considering a system with particle–wall friction we observe an inverted fluid-to-glass transition, where the glass is entered by increasing the driving amplitude. In the fluid phase particle motion is markedly superdiffusive. We argued that for large driving amplitudes the injected momentum (in combination with the Newtonian dynamics) is randomized by collisions with neighboring particles. This randomization leads to entropic caging. By way of contrast, for small driving forces, the momentum is quickly lost to the surface. No confinement is possible and particles can diffuse around.

Finally, by reducing the packing fraction of the material we go through a transition to an absorbing state, where particles independently follow the force-induced oscillations, but without interactions. We find that this transition is accompanied by particle segregation in the case of viscous interactions, but not in the case of inertial dynamics. This latter situation allows quantitative determination of the properties of the transition. In contrast to the continuous transition scenario proposed in ref. 7 and 8 we observe signs of a discontinuous transition. It is accompanied by a diverging relaxation time, but not by a vanishing order parameter, which rather jumps to zero at the transition.

Some of these different features have readily been observed in experiments, like the super-diffusive dynamics¹⁶ or the segregation.⁶ A discontinuous transition into an absorbing state has just recently been described in the work of Neel et al.²⁶ A more theoretical analysis on the discontinuous transition is given by Xu and Schwarz in ref. 27, accompanied by simulations.

Our work suggests a close link to the action of frictional forces. It would be interesting to explore this link in more detail, both with simulations as well experiments.

Acknowledgements

We acknowledge fruitful discussions with J. Yeomans as well as financial support by the Deutsche Forschungsgemeinschaft, Emmy Noether program: He 6322/1-1.

References

1. O. Pouliquen, M. Belzons and M. Nicolas, Phys. Rev. Lett., 2003, 91, 014301.
2. O. Dauchot, G. Marty and G. Biroli, Phys. Rev. Lett., 2005, 95, 265701.
3. J. Zhang, T. S. Majmudar, A. Tordesillas and R. P. Behringer, Granular Matter, 2010, 12, 159.
4. K. Chen, J. Cole, C. Conger, J. Draskovic, M. Lohr, K. Klein, T. Scheidemantel and P. Schiffer, Nature, 2006, 442, 257.
5. T. Divoux, H. Gayvallet and J.-C. Géminard, Phys. Rev. Lett., 2008, 101, 148303.
6. T. Mullin, Phys. Rev. Lett., 2000, 84, 4741–4744.
7. D. J. Pine, J. P. Gollub, J. F. Brady and A. M. Leshansky, Nature, 2005, 438, 997.
8. L. Corte, P. M. Chaikin, J. P. Gollub and D. J. Pine, Nat. Phys., 2008, 4, 420.
9. G. I. Menon and S. Ramaswamy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061108.
10. I. Regev, T. Lookman and C. Reichhardt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062401.
11. D. Fiocco, G. Foffi and S. Sastry, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 020301.
12. S. J. Plimpton, J. Comput. Phys., 1995, 117, 1.
13. http://lammps.sandia.gov/index.html .
14. J. Plagge and C. Heussinger, Phys. Rev. Lett., 2013, 110, 078001.
15. C. F. Schreck, R. S. Hoy, M. D. Shattuck and C. S. O'Hern, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052205.
16. F. Lechenault, O. Dauchot, G. Biroli and J.-P. Bouchaud, Europhys. Lett., 2008, 83, 46003.
17. D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Nature, 2011, 480, 355.
18. E. Brown and H. Jaeger, J. Rheol., 2012, 56, 875.
19. C. Heussinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 050201.
20. P. Sánchez, M. R. Swift and P. J. King, Phys. Rev. Lett., 2004, 93, 184302.
21. C. M. Pooley and J. M. Yeomans, Phys. Rev. Lett., 2004, 93, 118001.
22. G. C. M. A. Ehrhardt, A. Stephenson and P. M. Reis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 041301.
23. M. P. Ciamarra, A. Coniglio and M. Nicodemi, Phys. Rev. Lett., 2005, 94, 188001.
24. W. T. Kranz, M. Sperl and A. Zippelius, Phys. Rev. Lett., 2010, 104, 225701.
25. M. Fuchs and M. E. Cates, J. Rheol., 2009, 53, 957.
26. B. Neel, et al., 2014, arXiv:1401.1839.
27. S.-L.-Y. Xu and J. M. Schwarz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052130.

---

Footnotes

† Contribution to the web-theme of the International Soft Matter Conference ISMC 2013.

‡ For this figure we have switched off the Stokes' drag completely and assumed surface friction to act on both types of particles.

---