DOI:
10.1039/C4SM00145A
(Paper)
Soft Matter, 2014,
10, 3938-3949
Viscoelasticity of nematic liquid crystals at a glance
Received
19th January 2014
, Accepted 3rd March 2014
First published on 4th March 2014
Abstract
Polarised microscopy is shown to be a powerful alternative to light scattering for the determination of the viscoelasticity of aligned nematic liquid crystals. We perform experiments in a wide range of temperatures by using an adapted version of the recently introduced differential dynamic microscopy technique, which enables us to extract scattering information directly from the microscope images. A dynamic analysis of the images acquired in different geometries provides the splay, twist and bend viscoelastic ratios. A static analysis allows a successful determination of the bend elastic constant. All our results are in excellent agreement with those obtained with the far more time-consuming depolarised light scattering techniques. Remarkably, a noteworthy extension of the investigated temperature-range is observed, owing to the lower sensitivity of microscopy to multiple scattered light. Moreover, we show that the unique space-resolving capacities of our method enable us to investigate nematics in the presence of spatial disorder, where traditional light scattering fails. Our findings demonstrate that the proposed scattering-with-images approach provides a space-resolved probe of the local sample properties, applicable also to other optically anisotropic soft materials.
1 Introduction
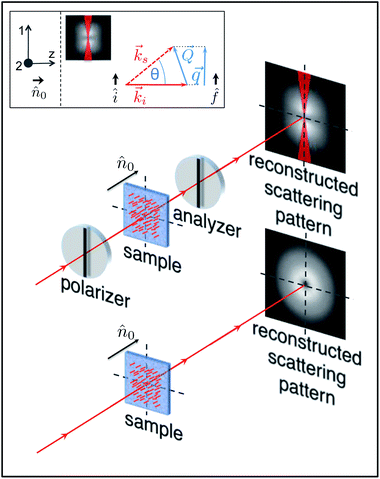
Devices based on nematic liquid crystals (LC) are very common and include displays for TVs, computers and phones, optical shutters and modulators, and 3D glasses for cinema or television.1–4 One of the most important properties for all these devices is the characteristic time of collective reorientation after the application of external fields, which sets the time scale of the device. The relaxation of LC can be interpreted as a viscoelastic response to a distortion of the director field and the reorientation time is mostly determined by the so-called viscoelastic ratios, which quantify the importance of the LC viscosity compared to its elasticity.5 Nematics have relatively low viscosities and even small external forces such as thermal agitation can locally distort their order. One of the classical means to study the lifetime of these thermally excited orientational fluctuations is small-angle Depolarised Dynamic Light Scattering (DDLS). DDLS exploits the fact that temporal intensity fluctuations in the depolarised scattered light are a direct consequence of the orientational fluctuations of the LC director. By studying the lifetime of the scattering intensity fluctuations, one can thus access the three viscoelastic ratios that correspond to splay, twist and bend deformations of the LC director, provided that suitable scattering geometries are used.5,6 Small-angle DDLS measurements are quite demanding, requiring very clean sample cells and optical surfaces to minimise the unwanted scattered light (stray light). In addition, measurements at several scattering angles are often necessary, which increases substantially the overall measurement time to achieve the sample characterisation. Another possible – although scantily explored – route for the characterisation of the LC viscoelasticity exploits the fact that the director fluctuations can be easily visualised in real space by means of depolarised microscopy and recorded with a pixel detector (camera) for subsequent analysis. This idea was originally used in ref. 7, where spatial Fourier transforms of microscope images of nematic LC were analysed in time to extract the twist viscoelastic ratio. While the latter was found to be in agreement with previous DDLS measurements, no information about the bend and splay viscoelastic rations could be retrieved, leaving the full potential of dynamic microscopy experiments still unexpressed. A particularly promising technique for the full characterisation of the LC viscoelasticity is represented by the recently introduced Differential Dynamic Microscopy (DDM).8 In its simplest implementation, DDM allows performing Dynamic Light Scattering (DLS) experiments with a camera-equipped microscope, by recording a short movie of the sample and processing it through a combination of subtraction of images acquired at different times and a spatial Fourier analysis. The sample dynamics is then recovered by looking at the increase of the square amplitude of each Fourier mode as the time separation between the two subtracted images is made larger, which provides the intermediate scattering function for the corresponding wave vector.9 This approach has been successfully demonstrated with a variety of samples including colloids and bacteria, both in bright field,8–10 phase contrast,11–13 and fluorescence wide-field14 or confocal15 microscopy. We shall prove here that DDM in combination with properly oriented polarisers – hereinafter named polarised differential dynamic microscopy or pDDM – allows performing DDLS experiments with a microscope and permits the full characterisation of LC viscoelastic ratios in nematics. To this aim we first develop a theoretical description of dynamic microscopy experiments with optically anisotropic samples. We then succeed in measuring experimentally the three viscoelastic ratios in a nematic LC sample with suitable alignment, thereby demonstrating pDDM as a powerful tool for the rapid characterisation of nematics. The use of pDDM for the extraction of the elastic constants necessitates alignment-dependent theoretical expressions describing the effect of the light propagation in a distorted medium on the image intensity. Even though deriving such expressions is beyond the aim of this work, we adapt recent results developed in ref. 16, primarily for the description of electroconvection patterns, for one of the experimental geometries used in this study. As a result we could extract the bend elastic constant at various temperatures and find it to be in excellent agreement with literature data. We also show that our imaging-based approach allows extracting the viscoelastic parameters in a heterogeneous planar nematic, by means of a space-resolved experiment that would be practically impossible with DDLS. Our results suggest a routine use of microscopes for the determination of the viscoelastic properties of various optically anisotropic fluids, such as for instance lyotropic liquid crystals made of anisotropic macromolecules or colloids.17–20
2 Nematodynamics
The relaxation of orientational fluctuations of the director is usually described in the framework of nematodynamics theory.5,21 The elastic cost of deformation of the nematic order is expressed by the free-energy volume density| | 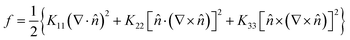 | (1) |
where the unit vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) =
) = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 + δ
0 + δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) provides the local orientation of the director. In fact, eqn (1) defines the three elastic constants K11, K22 and K33 that are associated with splay, twist and bend deformations, respectively.
) provides the local orientation of the director. In fact, eqn (1) defines the three elastic constants K11, K22 and K33 that are associated with splay, twist and bend deformations, respectively.
Nematodynamics uses eqn (1) as a starting point to write equations that account for conservation of the linear and angular momentum, suitably complemented by the constitutive equations for the material.5,21 Exact solutions of such equations can be obtained by their linearization for small fluctuations of velocity (δ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ) and direction (δ
) and direction (δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ) around the equilibrium solution (
) around the equilibrium solution (![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0 and
= 0 and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) =
= ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0). By introducing the Fourier transform δ
0). By introducing the Fourier transform δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) = ∫δ
) = ∫δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )exp(−i
)exp(−i![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ·
·![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )d
)d![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and by choosing an orthonormal reference system (ê1, ê2, ê3 =
and by choosing an orthonormal reference system (ê1, ê2, ê3 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0), such that for each wave vector
0), such that for each wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) the unit vector ê2 is perpendicular to
the unit vector ê2 is perpendicular to ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) and ê1 is perpendicular to ê2, the free energy density in eqn (1) assumes the particularly useful diagonal form
and ê1 is perpendicular to ê2, the free energy density in eqn (1) assumes the particularly useful diagonal form
| | 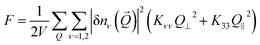 | (2) |
in the reciprocal space. For each
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif)
=
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ∥
∥ +
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥
⊥ =
Q∥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0
0 +
Q⊥ê1 fluctuations of the nematic director are accordingly decomposed in two collective normal modes (
v = 1, 2), defined by the relative orientation of
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0
0 and
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif)
, and schematically depicted in
Fig. 1. Mode 1 describes director fluctuations δ
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif)
perpendicular to
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0
0 in the (
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0
0,
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif)
) plane, which are due to splay and bend deformations. Fluctuations perpendicular to the (
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0
0,
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif)
) plane define mode 2, which is a combination of twist and bend deformations. Relaxation of the modes occurs exponentially with a rate
| | 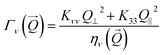 | (3) |
where
ην(
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif)
) denotes two
Q-dependent viscosities defined in terms of the Leslie viscosities
5αi (
i = 1, 2, 3, 4, 5, 6) as
| | 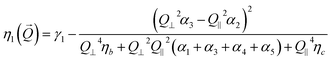 | (4) |
and
| | 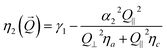 | (5) |
where
γ1 =
α3 −
α2,
ηα =
α4/2,
ηb = (
α2 +
α4 +
α6)/2, and
ηc = (−
α2 +
α4 +
α5)/2.
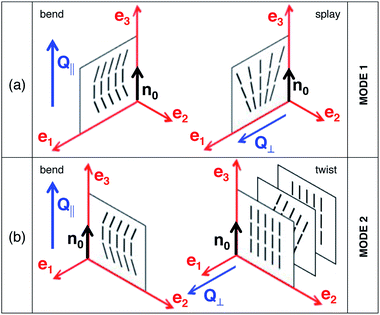 |
| | Fig. 1 Cartesian reference system (ê1, ê2, ê3 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0) used to decompose the director fluctuations in mode 1 and mode 2. The wave vector 0) used to decompose the director fluctuations in mode 1 and mode 2. The wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) of the fluctuations (not shown) and the director of the fluctuations (not shown) and the director ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 form a plane. The unit vector ê2 is perpendicular to that plane. With this choice 0 form a plane. The unit vector ê2 is perpendicular to that plane. With this choice ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) lies in the ( lies in the (![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, ê1) plane and can be seen as the sum of 0, ê1) plane and can be seen as the sum of ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ∥ and ∥ and ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥. (a) Mode 1 corresponds to bend and splay distortions of the director. (b) Mode 2 accounts for bend and twist. The vector δ ⊥. (a) Mode 1 corresponds to bend and splay distortions of the director. (b) Mode 2 accounts for bend and twist. The vector δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) (not shown) is oriented along ê1 for mode 1 (a) and along ê2 for mode 2 (b). ) (not shown) is oriented along ê1 for mode 1 (a) and along ê2 for mode 2 (b). | |
These rather complex expressions can be simplified in some limit cases. For the cases of interest in the present work, one has:
| | 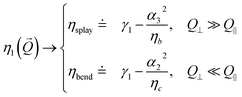 | (6) |
| | 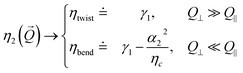 | (7) |
which define
ηsplay,
ηtwist,
ηbend, and in turn result in the following expressions for the relaxation rates of the two modes:
| | 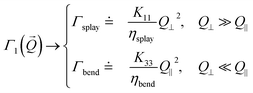 | (8) |
| | 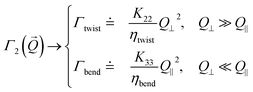 | (9) |
For each of the three deformations, the viscoelastic ratio is thus in the form K/η where K is a deformation-dependent elastic constant (measured in newton) and η is the corresponding viscosity (measured in Pa s). In the next paragraph we will show how it is possible to exploit the limits in eqn (8) and (9) in DDM experiments.
3 Dynamic microscopy of fluctuating nematics
In this paragraph we first briefly recall the working principles of bright-field DDM, as introduced in ref. 8 and 9. In addition, we describe DDM in the presence of polarising elements, which are the essence of the pDDM method. Our description includes the outline of novel experimental geometries that are used here for the characterisation of the viscoelasticity of nematics.
Bright-field DDM
DDM is a near-field (or deep-Fresnel) scattering technique22 that allows the recovery of scattering information about the sample by analysing sequences of images (movies) acquired close to the sample (deep-Fresnel regime) rather than in the sample far-field (Fig. 2). The main idea of DDM is to extract from microscope images a signal that is proportional to the density fluctuations within the sample. In this way, by means of Fourier transform analysis, it is possible to quantify relevant statistical quantities such as the static and the dynamic structure factor, for comparison with suitable theoretical models or with analogous quantities extracted from far-field scattering experiments.9
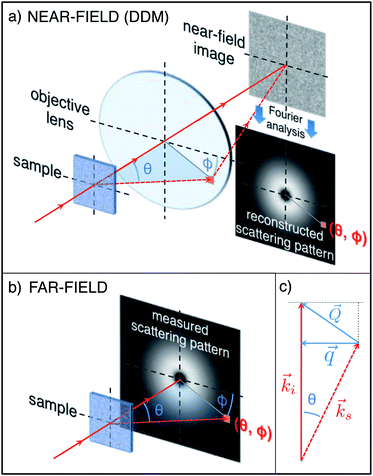 |
| | Fig. 2 In a DDM experiment (a) light impinging on the sample is scattered at various angles and is collected by the objective lens. Two-dimensional microscope images of the sample are Fourier analysed and information equivalent to a traditional far-field scattering experiment (b) is recovered. A generic scattered ray (wave propagating) with polar angle θ and azimuthal angle ϕ (dashed line), which corresponds to the point (θ, ϕ) in the far-field scattering pattern (b), is collected by the lens in a DDM experiment (a) and contributes to the images. The contribution of each scattered ray (wave) can be isolated by means of a two dimensional Fourier analysis, which is based on the two-dimensional projection ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) (defined in eqn (12)) of the wave vector (defined in eqn (12)) of the wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) transferred during the scattering process (c). The length ks of the scattered wave vector transferred during the scattering process (c). The length ks of the scattered wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s may differ in general from the length ki of the incident wave vector s may differ in general from the length ki of the incident wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i (inelastic scattering). i (inelastic scattering). | |
In bright-field DDM experiments such a task is easily tackled for weakly scattering samples i.e. whenever the intensity of the transmitted beam I0 = E*0E0 is way larger than the intensity of the scattered light Is = E*sEs, where E0 and Es are the incident and scattered fields, respectively. Indeed, fulfillment of the heterodyne condition Is ≪ I0 guarantees that the intensity of each microscope image can be written as
| | | I(x, y, t) = |E0 + Es(x, y, t)|2 ≃ I0 + 2Re[E*0Es(t)] | (10) |
where the homodyne term
Is has been neglected and where Re[…] is the real part of the argument.
Eqn (10) shows that a measure of the intensity
I(
x,
y,
t) enables one to access the real part of the fluctuating scattering field
Es(
x,
y,
t), a consequence of the intrinsic interferometric nature of the method. This fact can be exploited if an effective procedure for removing the transmitted light intensity
I0 is found. Among the possible choices,
9 a very common one is to calculate the algebraic difference between two images acquired at different times
t0 and
t0 + Δ
t to obtain the
difference image| | | d(x, y, t0, Δt) ≐ I(x, y, t0 + Δt) − I(x, y, t0) ≃ 2Re{E*0[Es(t0 + Δt) − Es(t0)]}. | (11) |
For stationary ergodic samples the dependence on the reference time t0 can be neglected since all the images obtained by subtracting pairs separated in time by the same value of Δt are statistically equivalent. This allows averaging of the spatial Fourier power spectra of all difference images with the same Δt to obtain the image structure function
| | | D(qx, qy, Δt) = 〈|∫dqxdqxexp[−i(xqx + yqy)d(x, y, t0, Δt)]|2〉t0. | (12) |
The image structure function is studied for each ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) as a function of Δt by fitting the trend of the experimental data points with the theoretical expression
as a function of Δt by fitting the trend of the experimental data points with the theoretical expression
| | D(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt) = A( , Δt) = A(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) )[1 − g( )[1 − g(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt)] + B( , Δt)] + B(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) ) | (13) |
where
B(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
) is a background term that accounts for the noise of the detection chain,
A(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
) =
T(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
)
I(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
),
I(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
) is the intensity scattered by the sample and
T(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
) is a transfer function that depends on the microscope.
9 It is particularly relevant that
g(
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
, Δ
t), the so-called
intermediate scattering function, is the quantity normally accessible in DLS experiments and this provides the link between DDM and DLS.
9 For most of the systems previously analysed with DDM
8–12,14,15 the image structure function bore a circular symmetry (like in
Fig. 2a and b), such that an azimuthal average for
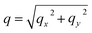
was performed. The structure function
D(
q, Δ
t) was thus typically studied as a function of Δ
t by fitting the trend of the experimental data points with the theoretical expression
| | | D(q, Δt) = A(q)[1 − g(q, Δt)] + B(q). | (14) |
It is worth noting that the wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) accessible in DDM experiments is a two-dimensional projection of the wave vector
accessible in DDM experiments is a two-dimensional projection of the wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i −
i − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s transferred during a scattering process, where
s transferred during a scattering process, where ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i and
i and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s are the incident and the scattered wave vector, respectively (see Fig. 2c). As a consequence of the small wave vectors accessible in DDM experiments, typically well below 10 µm−1, the difference between
s are the incident and the scattered wave vector, respectively (see Fig. 2c). As a consequence of the small wave vectors accessible in DDM experiments, typically well below 10 µm−1, the difference between ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) and
and ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) is usually negligible, as is a common practice for camera-based far-field small angle elastic scattering experiments.23,24
is usually negligible, as is a common practice for camera-based far-field small angle elastic scattering experiments.23,24
DDM with polarising elements (pDDM)
Orientational fluctuations of the nematic director can change the polarisation state of incident light. The two modes decomposing the fluctuations of the nematic director introduced in eqn (2) can be easily probed in a scattering experiment, where a nematic liquid crystal slab is illuminated by a plane wave with wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i and polarisation direction î. The scattered light is then collected in a direction specified by the wave vector
i and polarisation direction î. The scattered light is then collected in a direction specified by the wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) f and the polarisation direction
f and the polarisation direction ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) . The polarisation directions î and
. The polarisation directions î and ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) are usually selected by use of linear polarising elements placed before and after the LC sample, respectively. The scattering differential cross-section σd in such experiments is given by
are usually selected by use of linear polarising elements placed before and after the LC sample, respectively. The scattering differential cross-section σd in such experiments is given by| | 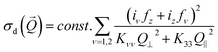 | (15) |
where iν = î·êν, iz = î·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, fν =
0, fν = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) ·êν, fz =
·êν, fz = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) ·
·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0. The dynamics is described by the intermediate scattering function, which is given by
0. The dynamics is described by the intermediate scattering function, which is given by| | g(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) , Δt) = g1( , Δt) = g1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )exp[−Γ1( )exp[−Γ1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )Δt] + g2( )Δt] + g2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )exp[−Γ2( )exp[−Γ2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )Δt] )Δt] | (16) |
where the relaxation rates Γν(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) have been already defined in eqn (3) and where g1(
) have been already defined in eqn (3) and where g1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) + g2(
) + g2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) = 1, with g1(
) = 1, with g1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) and g2(
) and g2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) depending on σd(
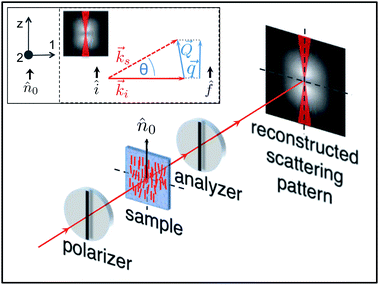
) depending on σd(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ). The presence of the term (ivfz + izfv)2 in eqn (15) shows that the relative contribution of each mode to the scattered light can be suppressed by a careful choice of the orientation of the director and of the polarising elements. As recently reviewed in ref. 6, several far field scattering geometries have been proposed and reported in the literature to take advantage of this possibility. One of the main advantages of pDDM is that we can exploit known results from light scattering theory and we do not need ad hoc calculations, at least if we want to extract dynamic information. In principle, the investigation with DDM of the depolarised scattering of light from orientational fluctuations of the director requires thus a simple strategy: equipping the microscope with two linear polarising elements and performing a DDM analysis without resorting to an azimuthal averaging of the image structure function in the Fourier space. However, the ostensible simplicity of the experimental strategy can be misleading. Indeed, validity of eqn (10) is based on the assumption that the transmission of light through the sample remains large enough that the homodyne term Is = E*sEs can be safely neglected. An immediate consequence of such requirement is that typical geometries employed in DDLS experiments, where the sample is sandwiched between crossed polarisers and the signal of interest is a small intensity contribution superimposed to an ideally zero background, cannot be used directly with DDM. Indeed, under these conditions the homodyne term is dominant, eqn (10) becomes a bad approximation and the easy connection between DDM and far-field scattering experiments is lost. However, this difficulty can be overcome by identifying experimental geometries with orientation of the director and of the polarising elements that allow for the presence of a sufficiently intense transmitted beam. This problem is somehow similar to the one encountered in ref. 25, where the dynamics of randomly oriented colloidal particles was studied with near-field scattering. However, in the present case, it is possible to take advantage of well established procedures to fix the alignment of the director at the cell surfaces, as sketched in Fig. 3.
). The presence of the term (ivfz + izfv)2 in eqn (15) shows that the relative contribution of each mode to the scattered light can be suppressed by a careful choice of the orientation of the director and of the polarising elements. As recently reviewed in ref. 6, several far field scattering geometries have been proposed and reported in the literature to take advantage of this possibility. One of the main advantages of pDDM is that we can exploit known results from light scattering theory and we do not need ad hoc calculations, at least if we want to extract dynamic information. In principle, the investigation with DDM of the depolarised scattering of light from orientational fluctuations of the director requires thus a simple strategy: equipping the microscope with two linear polarising elements and performing a DDM analysis without resorting to an azimuthal averaging of the image structure function in the Fourier space. However, the ostensible simplicity of the experimental strategy can be misleading. Indeed, validity of eqn (10) is based on the assumption that the transmission of light through the sample remains large enough that the homodyne term Is = E*sEs can be safely neglected. An immediate consequence of such requirement is that typical geometries employed in DDLS experiments, where the sample is sandwiched between crossed polarisers and the signal of interest is a small intensity contribution superimposed to an ideally zero background, cannot be used directly with DDM. Indeed, under these conditions the homodyne term is dominant, eqn (10) becomes a bad approximation and the easy connection between DDM and far-field scattering experiments is lost. However, this difficulty can be overcome by identifying experimental geometries with orientation of the director and of the polarising elements that allow for the presence of a sufficiently intense transmitted beam. This problem is somehow similar to the one encountered in ref. 25, where the dynamics of randomly oriented colloidal particles was studied with near-field scattering. However, in the present case, it is possible to take advantage of well established procedures to fix the alignment of the director at the cell surfaces, as sketched in Fig. 3.
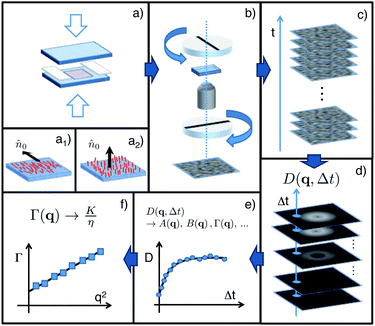 |
| | Fig. 3 Sketch of the pDDM experimental and data analysis procedure. (a) The sample is confined between two glass slides whose surfaces are treated in order to promote the planar (a1) or the homeotropic (a2) alignment of the director. (b) The sample cell is positioned on the microscope stage between two polarising elements. The polarisers are mutually oriented according to the modes to be probed (see text). (c) A stack of digital images of the sample is acquired with a fixed frame rate. (d) For each Δt, the 2D image structure function D(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt) is calculated by averaging the Fourier power spectrum of the difference of images separated in time by the same time delay Δt. (e) The fit of D( , Δt) is calculated by averaging the Fourier power spectrum of the difference of images separated in time by the same time delay Δt. (e) The fit of D(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt) as a function of Δt allows the estimation of the q-dependent amplitudes A, the rates Γ and the camera noise B (see eqn (13) and (16)). (f) The linear fit of each Γ as a function of q2 in selected geometry-dependent directions allows the estimation of the corresponding viscoelastic ratio, according to eqn (3). , Δt) as a function of Δt allows the estimation of the q-dependent amplitudes A, the rates Γ and the camera noise B (see eqn (13) and (16)). (f) The linear fit of each Γ as a function of q2 in selected geometry-dependent directions allows the estimation of the corresponding viscoelastic ratio, according to eqn (3). | |
We have thus decided to first study LC samples with homeotropic and (homogeneous) planar alignment of the director at the cell surfaces (Fig 3a1 and a2), which represent two cases often encountered in the literature. The general scheme of our pDDM experiments is sketched in Fig. 3 where we describe the common features of all the experiments that we have conducted. The specific features of each experimental geometry can be instead appreciated by inspecting Fig. 4–7, where we have dropped the objective lens and the microscope image to focus the attention on the reconstructed scattering pattern A(qx, qy) = D(qx, qy, Δt → ∞) and its symmetries. For all these geometries we will also specify the correct relations between the amplitude Q of the three-dimensional wave vector of the fluctuations and the amplitude q of the two-dimensional wave vector associated with the image Fourier transform. We note that light scattering from liquid crystals is in general inelastic (ks ≠ ki) with Δq = |ki − ks|max = k0Δm, where Δm = |me − mo| is the difference between the extraordinary and ordinary refractive indices of the sample and k0 is the incident wave vector in the vacuum.
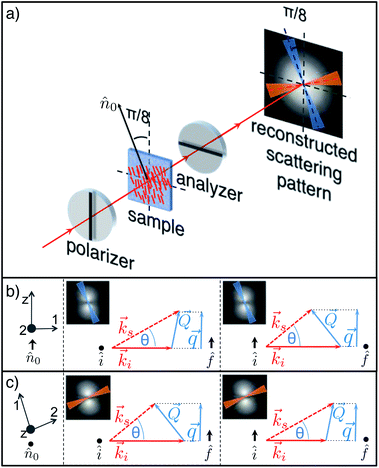 |
| | Fig. 4 (a) Sketch of a pDDM experiment in the P1 geometry. Unpolarised light crosses a linearly polarising element (polariser) and interacts with the nematic sample, whose director is placed at π/8 with respect to the polariser axis. Both the transmitted beam and the scattered light encounter a second polarising element (analyser), perpendicular to the first one. Microscope images (not shown) are acquired and processed as described in the text to recover information equivalent to a traditional far-field scattering experiment. If the scattering pattern is analysed along the direction parallel (blue online) or perpendicular (red online) to the director, the contribution of polarised scattering is negligible. (b) For ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ∥ ∥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 (corresponding reference system on the left) the two combinations of interest are: incident ordinary light and scattered extraordinary light (centre); incident extraordinary light and scattered ordinary light (right). (c) For 0 (corresponding reference system on the left) the two combinations of interest are: incident ordinary light and scattered extraordinary light (centre); incident extraordinary light and scattered ordinary light (right). (c) For ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ⊥ ⊥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 (corresponding reference system on the left) the two combinations of interest are: incident extraordinary light and scattered ordinary light (centre); incident ordinary light and scattered extraordinary light (right). 0 (corresponding reference system on the left) the two combinations of interest are: incident extraordinary light and scattered ordinary light (centre); incident ordinary light and scattered extraordinary light (right). | |
Planar alignment – geometry P1.
In this geometry the polariser and the analyser are crossed and the director forms an angle π/8 with the polariser (Fig. 4). This choice for the angle guarantees not only a fairly intense transmitted beam intensity but also the linearity between the change in intensity and the (small) local orientational fluctuation of the director. As customarily done in optics, the linearly polarised incident light can be decomposed into two components, one with the polarisation direction of the electric field perpendicular to the director (ordinary light) and the other one parallel to it (extraordinary light). A similar decomposition can be made for the scattered light where both the elastic and inelastic scattering processes contribute to the scattering pattern. However, if the scattering pattern is analysed in the two directions (bow-ties in Fig. 4a) that are parallel (centre in Fig. 4b and c) and perpendicular (right in Fig. 4b and c) to the director, the contribution of polarised scattering is negligible. The use of eqn (15) with the proper reference system allows the estimation of the contribution of the two modes by recalling that the scattering of each mode is proportional to (ivfz + izfv)2, with v = 1, 2.
• for director orientation modulations with wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to
parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 the suitable reference system is drawn on the left side of panel b in Fig. 4. In this direction, only mode 2 can be thus probed. Indeed, for ordinary incident light and extraordinary scattered light (Fig. 4, panel b, centre) one has i1 = iz = f1 = f2 = 0, which implies (i1fz + izf1)2 = 0 and
0 the suitable reference system is drawn on the left side of panel b in Fig. 4. In this direction, only mode 2 can be thus probed. Indeed, for ordinary incident light and extraordinary scattered light (Fig. 4, panel b, centre) one has i1 = iz = f1 = f2 = 0, which implies (i1fz + izf1)2 = 0 and 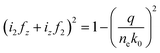 , whereas for extraordinary incident light and ordinary scattered light (Fig. 4, panel b, right) one has i1 = i2 = f1 = fz = 0, which leads to (i1fz + izf1)2 = 0 and (i2fz + izf2)2 = 1. Considering that Q|| = q and Q⊥ ≃ Δq, we have the following expression for the relaxation rate of mode 2:
, whereas for extraordinary incident light and ordinary scattered light (Fig. 4, panel b, right) one has i1 = i2 = f1 = fz = 0, which leads to (i1fz + izf1)2 = 0 and (i2fz + izf2)2 = 1. Considering that Q|| = q and Q⊥ ≃ Δq, we have the following expression for the relaxation rate of mode 2:
| | 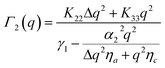 | (17) |
which can be expanded for
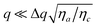
to give
| | 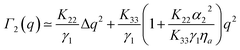 | (18) |
The rate Γ2(q) has a rather complex dependence on q. The intercept for q → 0 provides the twist viscoelastic ratio. The bend ratio can be extracted only for large q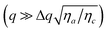 where
where
| | 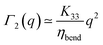 | (19) |
It appears that, in the absence of prior information about the value of 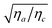 , it is not easy to know a priori whether the bend viscoelastic ratio in eqn (19) is experimentally accessible or one rather accesses the more complex combination in eqn (18).
, it is not easy to know a priori whether the bend viscoelastic ratio in eqn (19) is experimentally accessible or one rather accesses the more complex combination in eqn (18).
• for ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 the reference system is depicted on the left side of panel c in Fig. 4. Both for extraordinary incident light and ordinary scattered light (Fig. 4, panel c, centre) and ordinary incident light and extraordinary scattered light (Fig. 4, panel c, right) one has (i1fz + izf1)2 = q2/(Δq2 + q2) and (i2fz + izf2)2 = q2/(Δq2 + q2), which implies that both modes show-up in the scattering intensity. In addition, we have Q|| = 0 and
0 the reference system is depicted on the left side of panel c in Fig. 4. Both for extraordinary incident light and ordinary scattered light (Fig. 4, panel c, centre) and ordinary incident light and extraordinary scattered light (Fig. 4, panel c, right) one has (i1fz + izf1)2 = q2/(Δq2 + q2) and (i2fz + izf2)2 = q2/(Δq2 + q2), which implies that both modes show-up in the scattering intensity. In addition, we have Q|| = 0 and 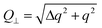 , which leads to
, which leads to
| | 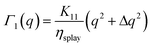 | (20) |
| | 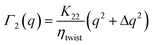 | (21) |
for the relaxation rates of the two modes. For
q ≪ (
K11/
K22)Δ
q the scattering from mode 2 dominates over mode 1 and the splay and twist contributions can be easily separated
via double-exponential fitting of the structure function by using
eqn (16) or, when this is not possible, by inspecting the low-
q and the high-
q limits of the system dynamics, where a single exponential behaviour is a good approximation. It has to be mentioned that for low-
q the scattering is due to twist fluctuations as expected also from the fact that refractive index modulations with
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif)
≃ 0 are characterised by
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif)
parallel to the
z-axis. Modulations of this kind can only be originated by twist deformation of the LC director, which thereby act as Bragg diffraction grating with transmission coefficient peaked around
Q ≃ Δ
q.
Planar alignment – geometry P2.
In this configuration the polariser, the analyser and the director are all parallel to each other (Fig. 5). In contrast with the previous case, scattering is elastic here and Q ≃ Δq. Along the direction described by the bow-tie region in Fig. 5 (inset) the dynamics is due to mode 1 and in particular to bend fluctuations of the director. Indeed, (i1fz + izf1)2 = q2/(nek0)2 and (i2fz + izf2)2 = 0 and the relaxation rate is given by| | 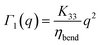 | (22) |
which, at variance with geometry P1, allows for an unambiguous determination of the bend viscoelastic ratio. In practice, a combination of P1 and P2 experiments allows always a full characterisation of the splay, twist and bend viscoelastic ratios, even though for some samples P2 experiments could prove to be unnecessary. For this geometry, a detailed theoretical treatment of the deep Fresnel diffraction from periodic modulations of the nematic LC was presented recently.16 In particular, we can make use of the expression for the intensity I given in eqn (48) of ref. 16 to write:| | 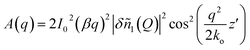 | (23) |
where β = 1 − (mo/me)2, z′ is the observation distance and |δñ1(Q)|2 is the 3D power spectrum of the director fluctuations within the scattering plane (mode 1). For q ≫ π/h (about 0.06 µm−1 for a sample thickness h = 50 µm) one can safely assume that Q ≃ q and application of the equipartition theorem to eqn (23) gives the simple result| | 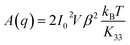 | (24) |
where V = L2h is the probed sample volume, and L is the length of the image side. Finally, even though the analysis in ref. 16 does not account for the effects of limited coherence of the light source and of the transfer function of the objective, such effects can be safely neglected at small enough q,9 which enables us to make use of eqn (24) to extract the bend elastic constant K33 from our pDDM images acquired in the P2 geometry. We note here that in contrast to the case of non-absorbing colloidal particles, periodic modulations of the director in the P2 geometry do not behave as a simple phase grating, as it can be appreciated from eqn (23) that contains a cos2 term instead of the usual sin2 term.9 Quite interestingly, this shows that the birefringence of LC brings in additional ingredients to the problem of deep Fresnel scattering and in turn to the description of Differential Dynamic microscopy experiments. While these ingredients do not affect the determination of the LC dynamics, they need to be carefully accounted for when static scattering information is of interest.
 |
| | Fig. 5 Sketch of a pDDM experiment in the P2 geometry. Unpolarised light crosses the polariser and interacts with the nematic sample, whose director is parallel to the polariser axis. The analyser is oriented parallel to the polariser. In the inset we draw the reference system used for mode decomposition (left) and the scattering diagram (right) describing elastic scattering processes with ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ∥ ∥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0. 0. | |
Homeotropic alignment – geometry H2.
In this geometry, the polariser is not perpendicular to the analyser but it is rotated by an angle β (for instance, for the experiments reported here we used β = 30°) with respect to that condition (Fig. 7). This configuration guarantees the fulfilment of the heterodyne condition and the validity of eqn (10). With respect to H1 geometry, here we have an additional depolarised scattering contribution. Indeed, similar to geometry P1, the incident light can be considered as the sum of two components, one with polarisation parallel to the polariser and the other one perpendicular to it. Because of the presence of the analyser both components can now interfere with the transmitted beam.
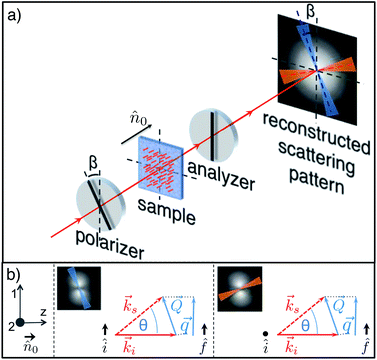 |
| | Fig. 7 (a) Sketch of a pDDM experiment in the H2 geometry. Unpolarised light crosses the polariser and interacts with the nematic sample, whose director is parallel to the optical axis. The analyser is oriented at β = 30° with respect to the polariser. If the scattering pattern is analysed along the direction parallel (blue online) to the polariser the contribution of depolarised scattering is negligible and only polarised scattering is of interest. If the scattering pattern is analysed along the direction perpendicular (red online) to the polariser the only relevant contribution comes from depolarised scattering. (b) Reference system used for mode decomposition (left), the scattering diagram (centre) describing elastic scattering processes within the plane of the analyser and the scattering diagram (left) describing elastic scattering process within the plane perpendicular to the analyser. | |
• for director modulations with wave vector along the polariser direction, mode 1 is probed and, in analogy with geometry H1, splay-induced polarised scattering is observed. Indeed, one has (i1fz + izf1)2 = q2/(nok0)2 and (i2fz + izf2)2 = 0, with ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥. The relaxation rate of such fluctuations is
⊥. The relaxation rate of such fluctuations is
| | 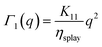 | (26) |
• in the direction perpendicular to the polariser, depolarised scattering is sensitive to mode 2 and (i1fz + izf1)2 = 0, (i2fz + izf2)2 = q2/(nok0)2 with ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥. Twist fluctuations with wave vector
⊥. Twist fluctuations with wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) act thus as a diffraction grating with wavelength 2π/q and the relaxation rate of such fluctuations is thus given by
act thus as a diffraction grating with wavelength 2π/q and the relaxation rate of such fluctuations is thus given by
| |  | (27) |
It appears that a combination of P1 and P2 measurements always allows for a complete characterisation of the LC viscoelasticity, with geometry P1 being sufficient under some circumstances. By contrast, measurements on a homeotropically aligned LC can not provide access to the bend viscoelastic ratio.
4 Experimental
For our experiments we use the thermotropic liquid crystal 4-hexyl-4′-cynanobiphenyl (6CB, Sigma-Aldrich), whose nematic phase is in the temperature range 14.5–28.8 °C. We consider two samples that are confined in cells made of optical-quality glass windows and that differ only in the alignment of the LC molecules at the cell surface. To that purpose the cell surfaces in contact with the LC sample are treated so as to favour either parallel (planar or P) or perpendicular (homeotropic or H) alignment. H alignment is obtained by depositing a layer of polyimide (polymer 0626 from Nissan Chemistry Industries) with spin coating (3000 rpm for 2 minutes), whereas for P alignment, spin coating of a 0.5% water solution of polyvinyl-alcohol (3000 rpm for 2 minutes) is followed by rubbing. By using Mylar® spacers, the cell thickness is set to h = 50 ± 3 µm, as checked with optical Fabry–Perot interferometry in reflection. The cell is then filled with 6CB in the isotropic phase at T = 40 °C and sealed with epoxy glue. The sample is subsequently cooled at a low rate from the isotropic to the nematic phase and eventually kept for at least one hour at 10 °C (or 12 °C for some of the experiments) below the nematic–isotropic transition temperature TNI = 28.8 °C. Measurements are performed at different temperatures in the nematic phase after careful thermalisation of the sample. Thermalisation takes place inside an INSTEC-HCS301I hot stage mounted on a NIKON Eclipse Ti-U microscope, which is also used for the sample observation. At each temperature, images of the fluctuations are acquired with a fast camera (IDT M3), with the image pixel size corresponding to dpix = 1.2 µm in real space (magnification 10×). A typical dataset consists of a sequence of 8000 images, acquired with a sampling rate of 2500 images per s and an exposure time of 400 µs. The total measurement time is thus 3.2 s for each temperature and geometry. The acquired images are stored on a disk for subsequent pDDM analysis, which is performed by using MATLAB®. In contrast with bright field DDM experiments, the 2D structure functions of LC do not bear in general an azimuthal symmetry, as it can be appreciated in Fig. 4–7. As a consequence, instead of azimuthally averaging the data with the same q but different (qx, qy) over 2π, we limit the angular size of the region over which the averaging is performed by using bow-tie shaped regions, as shown in Fig. 8 (panels a and b) and 11, for the planar and homeotropic samples, respectively.
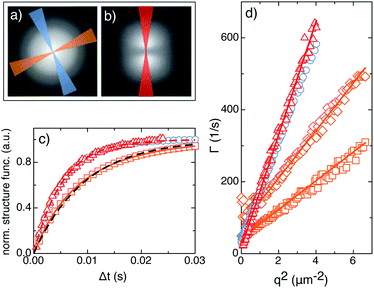 |
| | Fig. 8 (a) Reconstructed scattering pattern A(qx, qy) for the P1 geometry. The two shaded bow-tie areas, centred, respectively, around a direction parallel (blue) and perpendicular (orange) to the nematic director ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, indicate the regions where the azimuthal averages are performed. (b) Reconstructed scattering pattern for the P2 geometry. The red shaded area, oriented along the direction of the nematic director, indicates the region used for the azimuthal average. (c) Normalised structure functions for the P1 and P2 geometries at q = 1.0 µm−1. Blue circles (orange squares) correspond to 0, indicate the regions where the azimuthal averages are performed. (b) Reconstructed scattering pattern for the P2 geometry. The red shaded area, oriented along the direction of the nematic director, indicates the region used for the azimuthal average. (c) Normalised structure functions for the P1 and P2 geometries at q = 1.0 µm−1. Blue circles (orange squares) correspond to ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel (perpendicular) to parallel (perpendicular) to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 in the P1 geometry. Red triangles correspond to 0 in the P1 geometry. Red triangles correspond to ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 in the P2 geometry. The dashed line is the best fitting single exponential curve for 0 in the P2 geometry. The dashed line is the best fitting single exponential curve for ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ∥ ∥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, while the continuous blue line is the best fitting double exponential curve for 0, while the continuous blue line is the best fitting double exponential curve for ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ⊥ ⊥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0. (d) q-dependent relaxation rates Γ obtained with the P1 (circles, squares and diamonds) and the P2 (triangles) geometries. 0. (d) q-dependent relaxation rates Γ obtained with the P1 (circles, squares and diamonds) and the P2 (triangles) geometries. | |
5 Results and discussion
Planar alignment
At each temperature, data for planar samples are acquired first in the P1 geometry (polariser ⊥ analyser) and immediately after in the P2 geometry (polariser || analyser) by rotating the sample and the polariser. According to the expectations from theory (Section 3), the reconstructed scattering patterns A(qx, qy) for the P1 (Fig. 8a) and P2 (Fig. 8b) geometries have quite different symmetry properties. As far as the pDDM analysis is concerned, for the P1 geometry, the two shaded bow-tie areas (angular width π/32) in Fig. 8a indicate the two regions used for azimuthal averaging, one (blue) with the scattering wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to the director
parallel to the director ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, whereas the other (orange) with
0, whereas the other (orange) with ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0. It can be noticed that the two highlighted regions are rotated by π/8 with respect to the image axes as a consequence of the fact that in this geometry the director forms an angle π/8 with the polariser (Fig. 4a). By contrast, the scattering pattern for the P2 geometry is almost concentrated in a direction parallel to the director (Fig. 8b), as scattering vanishes perpendicularly to it. The region used for the pDDM analysis is highlighted in blue and has an angular width of π/16. In Fig. 8c we plot three structure functions measured at T − TNI = 0.2 °C and for q = 1.0 µm−1 in the P1 and in the P2 geometries. It appears that relaxation of the director fluctuations when
0. It can be noticed that the two highlighted regions are rotated by π/8 with respect to the image axes as a consequence of the fact that in this geometry the director forms an angle π/8 with the polariser (Fig. 4a). By contrast, the scattering pattern for the P2 geometry is almost concentrated in a direction parallel to the director (Fig. 8b), as scattering vanishes perpendicularly to it. The region used for the pDDM analysis is highlighted in blue and has an angular width of π/16. In Fig. 8c we plot three structure functions measured at T − TNI = 0.2 °C and for q = 1.0 µm−1 in the P1 and in the P2 geometries. It appears that relaxation of the director fluctuations when ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is perpendicular to
is perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 (orange squares in Fig. 8c for the P1 geometry) are slower than fluctuations in the parallel direction (blue circles for the P1 geometry and red triangles for the P2 geometry in Fig. 8c). According to the theoretical expectation, the P2 geometry is the easiest case to analyse. Indeed, a single mode (mode 1) of pure bend is probed with a rate given by eqn (22). Fitting the structure function with a single exponential curve (red dashed line in Fig. 8c) provides the rate Γ1, which is plotted as a function of q2 in Fig. 8d (red triangles). For each temperature, the obtained results are well fitted with a linear function, from which the bend ratio K33/ηbend can be extracted. Results for different temperatures are reported in Fig. 9a (full red circles) and are in excellent agreement with previous experiments on the same sample with DDLS.28 The situation is more complex for the P1 geometry. For
0 (orange squares in Fig. 8c for the P1 geometry) are slower than fluctuations in the parallel direction (blue circles for the P1 geometry and red triangles for the P2 geometry in Fig. 8c). According to the theoretical expectation, the P2 geometry is the easiest case to analyse. Indeed, a single mode (mode 1) of pure bend is probed with a rate given by eqn (22). Fitting the structure function with a single exponential curve (red dashed line in Fig. 8c) provides the rate Γ1, which is plotted as a function of q2 in Fig. 8d (red triangles). For each temperature, the obtained results are well fitted with a linear function, from which the bend ratio K33/ηbend can be extracted. Results for different temperatures are reported in Fig. 9a (full red circles) and are in excellent agreement with previous experiments on the same sample with DDLS.28 The situation is more complex for the P1 geometry. For ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to
parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, scattering is originated only from mode 2 and thus the dynamics is again well described by a single exponential function (blue circles in Fig. 8c). The rate Γ2 extracted from the single exponential fitting is plotted in Fig. 8d (blue circles) as a function of q2. In principle, these data should be fitted with eqn (17). However, this fit becomes very challenging because of the large number of fitting parameters and the limited q-range of the experiments. In addition, the possible use of the simpler expression in eqn (19) to extract the bend ratio is based on prior knowledge of ηa, ηc and Δq to ensure that the condition
0, scattering is originated only from mode 2 and thus the dynamics is again well described by a single exponential function (blue circles in Fig. 8c). The rate Γ2 extracted from the single exponential fitting is plotted in Fig. 8d (blue circles) as a function of q2. In principle, these data should be fitted with eqn (17). However, this fit becomes very challenging because of the large number of fitting parameters and the limited q-range of the experiments. In addition, the possible use of the simpler expression in eqn (19) to extract the bend ratio is based on prior knowledge of ηa, ηc and Δq to ensure that the condition 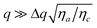 is met. Literature data for ηa and ηc relative to our sample could not be retrieved. However, data for 5CB26 and MBBA27 in a T−TNI range similar to the one explored here show that
is met. Literature data for ηa and ηc relative to our sample could not be retrieved. However, data for 5CB26 and MBBA27 in a T−TNI range similar to the one explored here show that 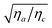 remains in the range 1–1.7. Based on this estimate, we can expect the condition
remains in the range 1–1.7. Based on this estimate, we can expect the condition 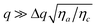 to be met only in a narrow range close to the critical temperature TNI, where in principle it should be possible to extract the bend viscoelastic ratio. In fact, even quite close to TNI, the approximation of eqn (17) with eqn (19) is still not fully satisfactory, as it can be appreciated in Fig. 8d, by comparing the rates obtained in this condition (blue circles) with the ones obtained in the P2 geometry (red triangles). For
to be met only in a narrow range close to the critical temperature TNI, where in principle it should be possible to extract the bend viscoelastic ratio. In fact, even quite close to TNI, the approximation of eqn (17) with eqn (19) is still not fully satisfactory, as it can be appreciated in Fig. 8d, by comparing the rates obtained in this condition (blue circles) with the ones obtained in the P2 geometry (red triangles). For ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, the structure function is the sum of two exponential functions due to the superposition of modes 1 and 2 (eqn (16)). A double exponential fit (continuous line) thus provides the corresponding relaxation rates Γ1(q) and Γ2(q) (diamonds and squares in Fig. 8d, respectively). For small q, where scattering from mode 2 dominates, data for Γ1(q) appear quite noisy, as the small amplitude of mode 1 translates into a large uncertainty in determining Γ1(q). Nevertheless, data for both modes can be well fitted to eqn (20) and (21) to extract the splay and twist viscoelastic ratios, respectively and Δq. The results for different temperatures are shown as orange down-triangles in Fig. 9b and c, respectively. Again the agreement with previous experiments in ref. 28 is very good.
0, the structure function is the sum of two exponential functions due to the superposition of modes 1 and 2 (eqn (16)). A double exponential fit (continuous line) thus provides the corresponding relaxation rates Γ1(q) and Γ2(q) (diamonds and squares in Fig. 8d, respectively). For small q, where scattering from mode 2 dominates, data for Γ1(q) appear quite noisy, as the small amplitude of mode 1 translates into a large uncertainty in determining Γ1(q). Nevertheless, data for both modes can be well fitted to eqn (20) and (21) to extract the splay and twist viscoelastic ratios, respectively and Δq. The results for different temperatures are shown as orange down-triangles in Fig. 9b and c, respectively. Again the agreement with previous experiments in ref. 28 is very good.
 |
| | Fig. 9 Viscoelastic ratios of 6CB measured as a function of the temperature difference from the transition temperature TNI. Full symbols are obtained with pDDM in different geometries (P1 geometry – red circles, P2 geometry – orange down-triangles, H1 geometry – green diamonds, H2 geometry – blue up-triangles). Empty symbols are literature data (from ref. 28) obtained with DDLS. | |
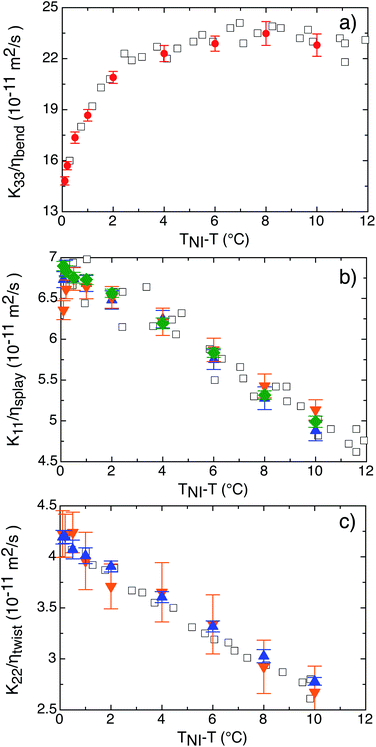
As a by-product of the analysis in the P1 geometry, the birefringence Δm can be obtained from the experimentally determined Δq, by using the relationship Δq = k0Δm = (2π/λ0)Δm, where we used λ0 = 580 nm for the peak wavelength of our light source.9 Results obtained in this way for Δm at different temperatures are reported in Fig. 10a (black circles) together with the literature data obtained with traditional refractometry (red squares).27
 |
| | Fig. 10 Experimentally determined birefringence (panel a) and bend elastic constant (panel b) of 6CB as a function of the temperature difference from the transition temperature TNI. Black circles are data obtained with pDDM. Red squares are literature data from ref. 27. | |
Finally, by making use of eqn (24) it is also possible to calculate the bend elastic constant from the amplitude A(q) of the structure functions for ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to
parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 obtained for each temperature in the P2 geometry. A reliable estimate of the low-q limit A0 of the amplitude is obtained as the average of A(q) over the interval [0.39, 0.49] µm−1, where A(q) is essentially flat. According to eqn (24), the bend elastic constant K33 is estimated as K33 = 2I02Vβ2kBT/A0. As shown in Fig. 10, the obtained values compare remarkably well with the literature data obtained by light scattering.27 Most remarkably, we are able to extend the existing data-range by almost a decade with pDDM approaching further towards TNI. This is because pDDM is less sensitive to multiple scattering as compared to traditional light scattering methods. We note that in principle the good result obtained for K33 could be extended also to the other two elastic constants, provided that some expressions analogous to eqn (24) are available for the corresponding geometries. Given the complexity of the calculations involved, the derivation of such expressions is well beyond the purpose of the present article, but it should be a priority for further developing the full potential of the method.
0 obtained for each temperature in the P2 geometry. A reliable estimate of the low-q limit A0 of the amplitude is obtained as the average of A(q) over the interval [0.39, 0.49] µm−1, where A(q) is essentially flat. According to eqn (24), the bend elastic constant K33 is estimated as K33 = 2I02Vβ2kBT/A0. As shown in Fig. 10, the obtained values compare remarkably well with the literature data obtained by light scattering.27 Most remarkably, we are able to extend the existing data-range by almost a decade with pDDM approaching further towards TNI. This is because pDDM is less sensitive to multiple scattering as compared to traditional light scattering methods. We note that in principle the good result obtained for K33 could be extended also to the other two elastic constants, provided that some expressions analogous to eqn (24) are available for the corresponding geometries. Given the complexity of the calculations involved, the derivation of such expressions is well beyond the purpose of the present article, but it should be a priority for further developing the full potential of the method.
Homeotropic alignment
At each temperature we have performed measurements first in the H1 geometry (no polarisers, Fig. 11b) and successively in the H2 geometry (polariser and analyser mutually oriented at 60°). In H1 geometry (mode 1) the splay ratio can be obtained by taking advantage of the azimuthal symmetry of the scattering pattern (Fig. 11b) whereas both splay and twist ratios can be extracted in H2 geometry (mode 1 and 2) by analysing the dynamics in two perpendicular directions in the q-space.
 |
| | Fig. 11 (a) Reconstructed scattering pattern for the H1 geometry (parallel polarisers). The red shaded bow-tie area, oriented along the direction of the axis of the polarising elements, indicates the region where the azimuthal average is performed. (b) Reconstructed scattering pattern for the H1 geometry (no polarisers). (c) Reconstructed scattering pattern for the H2 geometry. The two shaded bow-tie areas are oriented, respectively, along a direction parallel (blue) and perpendicular (orange) to the axis of the polariser and indicate the regions where the azimuthal averages are performed. | |
The results are reported in Fig. 9b and c, where green diamonds are obtained in the H1 geometry, whereas blue up-triangles in the H2 geometry. All the results are in excellent agreement with both the literature data and the measurements are performed in the P1 geometry. We note that the quality of the results obtained with the H1 geometry, where azimuthal averaging of the structure functions over 2π was performed, is appreciably higher than that obtained in other geometries. This also shows that polarising elements are not always needed for the characterisation of the viscoelastic behaviour of LC.
Heterogeneous planar alignment
To explore the novel possibilities offered by this imaging-based scattering method, a last set of experiments was performed with a sample of 6CB confined in a cell whose glass surfaces were kept untreated, to obtain a heterogeneous planar alignment that occurs with many samples for which alignment procedures are not available or known, such as for instance biological LC formers.17 The alignment of the LC molecules at the surfaces is spontaneously planar but does not remain uniform across the cell width. This alignment is also known in the literature as random planar alignment. Images acquired between crossed polarisers under this condition have the typical Schlieren texture appearance (Fig. 12a). However, it is still possible to identify small domains inside which the planar alignment is approximately uniform even though different domains are characterised by different orientations of the director.
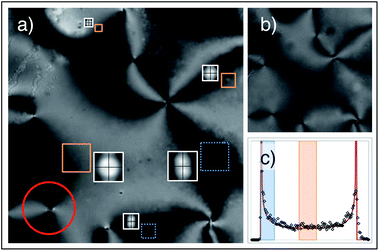 |
| | Fig. 12 Portion of a heterogeneous planar sample of 6CB observed between crossed (a) and parallel (b) polarisers. (c) Intensity histogram (symbols) of the area enclosed in the red circle in panel (a), centred around a point-like defect. The continuous line is the best fitting curve of the form: P(I) = (1/π)(I − Imin)−1/2(Imax − I)−1/2, expected from theory. The intensity range outlined in blue (orange) with dotted (continuous) contour corresponds to regions where the nematic director is approximately parallel (tilted by π/8 + nπ/4, with n integer) with respect to the polarising element. In panel (a) some representative regions of interest are shown, corresponding to these orientations; dotted blue squares were analysed with pDDM in the P1 geometry, while orange squares in the P2 geometry. The corresponding reconstructed scattering patterns are also shown close to each region of interest. | |
To investigate the amount of quantitative information that can be extracted in this condition we have prepared a sample of 6CB with heterogeneous planar alignment that was characterised at the fixed temperature T = 22.7 ± 0.2 °C. Two movies of the same region (8000 images with 512 × 512 resolution) were acquired, respectively, at 800 and 1000 frames per second. The first movie was taken with the sample placed between perpendicular polarisers (Fig. 12a), while for the second the polarisers were kept parallel (Fig. 12b). Such double acquisition enabled us to identify proper sub-regions for the pDDM analysis as follows. A point-like defect and the corresponding region of interest such as the one outlined with a red circle in Fig. 12a is chosen under the assumption that the orientation of the director around it is uniformly distributed. The image intensity histogram of the region of interest similar to the one in Fig. 12a is calculated and fitted with the theoretical expression: P(I) = (1/π)(I − Imin)−1/2(Imax − I)−1/2 derived under the hypothesis of uniform distribution of the director orientation to obtain a correspondence between intensity levels in the image and director angle (modulo π/4). Once such correspondence is obtained (Fig. 12a) the analysis proceeds differently according to the viscoelastic ratio of interest.
Splay and twist.
For the determination of the splay and twist viscoelastic ratios we select an intensity range at the centre of the histogram and determine the corresponding regions in the image, where the director is oriented at π/8 + nπ/4 (n integer), with respect to the polarising elements. Inside these regions small square regions of interest (ROI) (64 × 64 or 32 × 32 or 16 × 16 pixels) are selected and a pDDM analysis is run in parallel for all of them. The actual orientation of the director within each ROI can be easily determined by exploiting the asymmetry displayed by the 2D structure function, as shown in Fig. 11a. The structure functions with ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 are analysed and fitted with a single exponential, since the limited size of the square regions of interests prevents a double exponential fit. Nevertheless, the twist and splay viscoelastic ratios can be extracted from the Γ(q) data in Fig. 13. The results for the two ratios (K11/ηsplay = (5.9 ± 0.3) × 10−11 m2 s−1, K22/ηtwist = (2.6 ± 0.6) × 10−11 m2 s−1) are in fair agreement with those obtained with uniformly aligned samples, reported in Fig. 9.
0 are analysed and fitted with a single exponential, since the limited size of the square regions of interests prevents a double exponential fit. Nevertheless, the twist and splay viscoelastic ratios can be extracted from the Γ(q) data in Fig. 13. The results for the two ratios (K11/ηsplay = (5.9 ± 0.3) × 10−11 m2 s−1, K22/ηtwist = (2.6 ± 0.6) × 10−11 m2 s−1) are in fair agreement with those obtained with uniformly aligned samples, reported in Fig. 9.
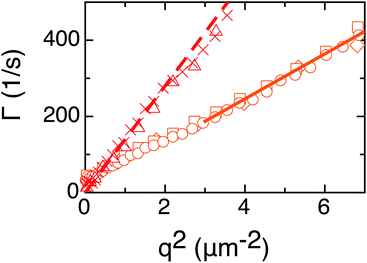 |
| | Fig. 13
q-dependent relaxation rates Γ obtained for a heterogeneous planar sample of 6CB at T = 22.7 ± 0.2 °C. Different symbols correspond to the different regions of interest in the sample, as shown in Fig. 12. Circles, squares and diamonds correspond to regions of interest equivalent to a P1 geometry experiment. Crosses and empty triangles are equivalent to a P2 geometry experiment. The shown fitting lines allow extraction of the bend (dashed line) and the splay (continuous line) ratios, whereas the extrapolated q = 0 limit of the P1 data provides an estimate of the twist ratio. | |
Bend.
An intensity range in the lower part of the image histogram is selected and the corresponding regions in the image are determined, where the director is parallel or perpendicular to the polarising elements. Since we are interested only in the regions with the director parallel to the polarisers, we focus on the regions where the intensity is larger and select small square regions of interest (32 × 32 or 16 × 16 pixels) for the pDDM analysis. The analysis proceeds in each region of interest by using the same method used for the P2 geometry. The bend ratio obtained from the slope of the Γ(q) curves in Fig. 13 is K33/ηbend = (1.3 ± 0.3) × 10−10 m2 s−1, which is about 70% smaller than the result obtained with homogeneously planar samples. This discrepancy can be attributed to a large, unknown pre-tilt angle at the surfaces, as independently verified with experiments performed on homogenous planar samples confined between glass plates rubbed in opposite directions, or to an unavoidable twist29 due to the possibly different orientation of the director on the two cell surfaces.
6 Conclusions
Our experiments demonstrate the versatile use of pDDM for the characterisation of the dynamics of liquid crystals and, in perspective, of other optically anisotropic fluids. It is worth stressing that the differential algorithm provides a very effective solution to the stray light problem, which makes DDLS measurements at small angles very challenging. Our method could thus be used as a robust analytical tool that would function in harsh environments as those typically found in production plants. More theoretical work will be needed to exploit the full potential of the method, not only for the characterisation of the three viscoelastic ratios but also for the corresponding elastic constant.
Acknowledgements
We acknowledge funding by the Italian Ministry of Education and Research, “Futuro in Ricerca” Project ANISOFT (RBFR125H0M), from the CARIPLO grant 2008-2413 and from the Swiss National Science Foundation grant 200020-140908.
References
- S. S. Choi, S. M. Morris, W. T. S. Huck and H. J. Coles, Soft Matter, 2009, 5, 354 RSC.
- F. Serra, K. C. Vishnubhatla, M. Buscaglia, R. Cerbino, R. Osellame, G. Cerullo and T. Bellini, Soft Matter, 2011, 7, 10945 RSC.
- Y. D. Liu and H. J. Choi, Soft Matter, 2012, 8, 11961 RSC.
-
S. M. Kelly and M. O'Neill, Liquid crystals for electro-optic applications, in Handbook of Advanced Electronic and Photonic Materials and Devices, ed. H. S. Nalwa, vol. 7, Liquid Crystals, Display and Laser Materials, 2001 Search PubMed.
-
P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, London, 2001 Search PubMed.
-
H. F. Gleeson, in Handbook of Liquid Crystals, ed. D. Demus, J. Goodby, G. W. Gray and H.-W. Spiess, Wiley-VCH, Halle, 2008, pp. 699–718 Search PubMed.
- H. Orihara, A. Sakai and T. Nagaya, Mol. Cryst. Liq. Cryst., 2001, 366, 143 CrossRef CAS.
- R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102 CrossRef.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031403 CrossRef.
- F. Ferri, A. D'Angelo, M. Lee, A. Lotti, M. C. Pigazzini, K. Singh and R. Cerbino, Eur. Phys. J.: Spec. Top., 2011, 199, 139 CrossRef CAS.
- L. G. Wilson, V. A. Martinez, J. Schwarz-Linek, J. Tailleur, G. Bryant, P. N. Pusey and W. C. K. Poon, Phys. Rev. Lett., 2011, 106, 018101 CrossRef CAS.
- V. A. Martinez, R. Besseling, O. A. Croze, J. Tailleur, M. Reufer, J. Schwarz-Linek, L. G. Wilson, M. A. Bees and W. C. K. Poon, Biophys. J., 2012, 103, 1637 CrossRef CAS PubMed.
- M. Reufer, V. A. Martinez, P. Schurtenberger and W. C. Poon, Langmuir, 2012, 28, 4618 CrossRef CAS PubMed.
- K. He, M. Spannuth, J. C. Conrad and R. Krishnamoorti, Soft Matter, 2012, 8, 11933 RSC.
- P. J. Lu, F. Giavazzi, T. E. Angelini, E. Zaccarelli, F. Jargstorff, A. B. Schofield, J. N. Wilking, M. B. Romanowsky, D. A. Weitz and R. Cerbino, Phys. Rev. Lett., 2012, 108, 218103 CrossRef.
- W. Pesch and A. Krekhov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052504 CrossRef.
- M. Nakata, G. Zanchetta, B. D. Chapman, C. D. Jones, J. O. Cross, R. Pindak, T. Bellini and N. A. Clark, Science, 2007, 318, 1276 CrossRef CAS PubMed.
- G. Zanchetta and R. Cerbino, J. Phys.: Condens. Matter, 2010, 22, 323102 CrossRef PubMed.
- S. Chakraborty, J. T. Gleeson, A. Jakli and S. Sprunt, Soft Matter, 2013, 9, 1817 RSC.
- A. S. Poulos, D. Constantin, P. Davidson, B. Pansu, E. Freyssingeas, A. Madsen and J. Chanac, J. Chem. Phys., 2012, 132, 091101 CrossRef PubMed.
-
P. Oswald and P. Pieranski, Nematic and Cholesteric Liquid Crystals, CRC Press, Boca Raton, 2005 Search PubMed.
- R. Cerbino and A. Vailati, Curr. Opin. Colloid Interface Sci., 2009, 14, 416 CrossRef CAS PubMed.
- F. Ferri, Rev. Sci. Instrum., 1997, 68, 2265 CrossRef CAS PubMed.
- L. Cipelletti and D. A. Weitz, Rev. Sci. Instrum., 1999, 70, 3214 CrossRef CAS PubMed.
- D. Brogioli, D. Salerno, V. Cassina, S. Sacanna, A. P. Philipse, F. Croccolo and F. Mantegazza, Opt. Express, 2009, 17, 1222 CrossRef CAS.
-
C. P. Lapointe, Elastic Interactions and Manipulation of Wire-shaped Inclusions in Nematic Liquid Crystals, PhD thesis, The Johns Hopkins University, 2009.
-
Physical properties of liquid crystals: nematics, ed. D. A. Dunmur, A. Fukuda and G. R. Luckhurst, INSPEC, 2001 Search PubMed.
- J. Hirakata, G. Chen, T. Toyooka, S. Kawamoto, H. Takezoe and A. Fukuda, Jpn. J. Appl. Phys., 1986, 25, L607 CrossRef CAS.
- M. Buscaglia, G. Lombardo, L. Cavalli, R. Barberi and T. Bellini, Soft Matter, 2010, 6, 5434 RSC.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article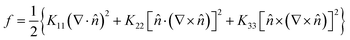
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) =
) = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 + δ
0 + δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) provides the local orientation of the director. In fact, eqn (1) defines the three elastic constants K11, K22 and K33 that are associated with splay, twist and bend deformations, respectively.
) provides the local orientation of the director. In fact, eqn (1) defines the three elastic constants K11, K22 and K33 that are associated with splay, twist and bend deformations, respectively.
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ) and direction (δ
) and direction (δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ) around the equilibrium solution (
) around the equilibrium solution (![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0 and
= 0 and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) =
= ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0). By introducing the Fourier transform δ
0). By introducing the Fourier transform δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) = ∫δ
) = ∫δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )exp(−i
)exp(−i![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ·
·![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )d
)d![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and by choosing an orthonormal reference system (ê1, ê2, ê3 =
and by choosing an orthonormal reference system (ê1, ê2, ê3 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0), such that for each wave vector
0), such that for each wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) the unit vector ê2 is perpendicular to
the unit vector ê2 is perpendicular to ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) and ê1 is perpendicular to ê2, the free energy density in eqn (1) assumes the particularly useful diagonal form
and ê1 is perpendicular to ê2, the free energy density in eqn (1) assumes the particularly useful diagonal form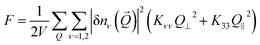
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) =
= ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ∥ +
∥ + ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥ = Q∥
⊥ = Q∥![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 + Q⊥ê1 fluctuations of the nematic director are accordingly decomposed in two collective normal modes (v = 1, 2), defined by the relative orientation of
0 + Q⊥ê1 fluctuations of the nematic director are accordingly decomposed in two collective normal modes (v = 1, 2), defined by the relative orientation of ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 and
0 and ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) , and schematically depicted in Fig. 1. Mode 1 describes director fluctuations δ
, and schematically depicted in Fig. 1. Mode 1 describes director fluctuations δ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 in the (
0 in the (![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0,
0, ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) plane, which are due to splay and bend deformations. Fluctuations perpendicular to the (
) plane, which are due to splay and bend deformations. Fluctuations perpendicular to the (![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0,
0, ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) plane define mode 2, which is a combination of twist and bend deformations. Relaxation of the modes occurs exponentially with a rate
) plane define mode 2, which is a combination of twist and bend deformations. Relaxation of the modes occurs exponentially with a rate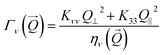
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) denotes two Q-dependent viscosities defined in terms of the Leslie viscosities5αi (i = 1, 2, 3, 4, 5, 6) as
) denotes two Q-dependent viscosities defined in terms of the Leslie viscosities5αi (i = 1, 2, 3, 4, 5, 6) as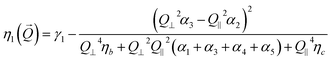
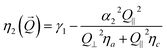
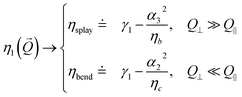
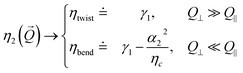
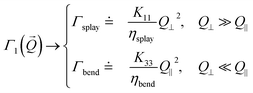
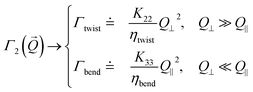

![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) (defined in eqn (12)) of the wave vector
(defined in eqn (12)) of the wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) transferred during the scattering process (c). The length ks of the scattered wave vector
transferred during the scattering process (c). The length ks of the scattered wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s may differ in general from the length ki of the incident wave vector
s may differ in general from the length ki of the incident wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i (inelastic scattering).
i (inelastic scattering).![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) as a function of Δt by fitting the trend of the experimental data points with the theoretical expression
as a function of Δt by fitting the trend of the experimental data points with the theoretical expression![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt) = A(
, Δt) = A(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) )[1 − g(
)[1 − g(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt)] + B(
, Δt)] + B(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) )
)![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is a background term that accounts for the noise of the detection chain, A(
) is a background term that accounts for the noise of the detection chain, A(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) = T(
) = T(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) )I(
)I(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ), I(
), I(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is the intensity scattered by the sample and T(
) is the intensity scattered by the sample and T(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is a transfer function that depends on the microscope.9 It is particularly relevant that g(
) is a transfer function that depends on the microscope.9 It is particularly relevant that g(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt), the so-called intermediate scattering function, is the quantity normally accessible in DLS experiments and this provides the link between DDM and DLS.9 For most of the systems previously analysed with DDM8–12,14,15 the image structure function bore a circular symmetry (like in Fig. 2a and b), such that an azimuthal average for
, Δt), the so-called intermediate scattering function, is the quantity normally accessible in DLS experiments and this provides the link between DDM and DLS.9 For most of the systems previously analysed with DDM8–12,14,15 the image structure function bore a circular symmetry (like in Fig. 2a and b), such that an azimuthal average for 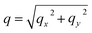 was performed. The structure function D(q, Δt) was thus typically studied as a function of Δt by fitting the trend of the experimental data points with the theoretical expression
was performed. The structure function D(q, Δt) was thus typically studied as a function of Δt by fitting the trend of the experimental data points with the theoretical expression![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) accessible in DDM experiments is a two-dimensional projection of the wave vector
accessible in DDM experiments is a two-dimensional projection of the wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i −
i − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s transferred during a scattering process, where
s transferred during a scattering process, where ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i and
i and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) s are the incident and the scattered wave vector, respectively (see Fig. 2c). As a consequence of the small wave vectors accessible in DDM experiments, typically well below 10 µm−1, the difference between
s are the incident and the scattered wave vector, respectively (see Fig. 2c). As a consequence of the small wave vectors accessible in DDM experiments, typically well below 10 µm−1, the difference between ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) and
and ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) is usually negligible, as is a common practice for camera-based far-field small angle elastic scattering experiments.23,24
is usually negligible, as is a common practice for camera-based far-field small angle elastic scattering experiments.23,24![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i and polarisation direction î. The scattered light is then collected in a direction specified by the wave vector
i and polarisation direction î. The scattered light is then collected in a direction specified by the wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) f and the polarisation direction
f and the polarisation direction ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) . The polarisation directions î and
. The polarisation directions î and ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) are usually selected by use of linear polarising elements placed before and after the LC sample, respectively. The scattering differential cross-section σd in such experiments is given by
are usually selected by use of linear polarising elements placed before and after the LC sample, respectively. The scattering differential cross-section σd in such experiments is given by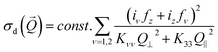
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, fν =
0, fν = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) ·êν, fz =
·êν, fz = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) ·
·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0. The dynamics is described by the intermediate scattering function, which is given by
0. The dynamics is described by the intermediate scattering function, which is given by![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) , Δt) = g1(
, Δt) = g1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )exp[−Γ1(
)exp[−Γ1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )Δt] + g2(
)Δt] + g2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )exp[−Γ2(
)exp[−Γ2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) )Δt]
)Δt]![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) have been already defined in eqn (3) and where g1(
) have been already defined in eqn (3) and where g1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) + g2(
) + g2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) = 1, with g1(
) = 1, with g1(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) and g2(
) and g2(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) depending on σd(
) depending on σd(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ). The presence of the term (ivfz + izfv)2 in eqn (15) shows that the relative contribution of each mode to the scattered light can be suppressed by a careful choice of the orientation of the director and of the polarising elements. As recently reviewed in ref. 6, several far field scattering geometries have been proposed and reported in the literature to take advantage of this possibility. One of the main advantages of pDDM is that we can exploit known results from light scattering theory and we do not need ad hoc calculations, at least if we want to extract dynamic information. In principle, the investigation with DDM of the depolarised scattering of light from orientational fluctuations of the director requires thus a simple strategy: equipping the microscope with two linear polarising elements and performing a DDM analysis without resorting to an azimuthal averaging of the image structure function in the Fourier space. However, the ostensible simplicity of the experimental strategy can be misleading. Indeed, validity of eqn (10) is based on the assumption that the transmission of light through the sample remains large enough that the homodyne term Is = E*sEs can be safely neglected. An immediate consequence of such requirement is that typical geometries employed in DDLS experiments, where the sample is sandwiched between crossed polarisers and the signal of interest is a small intensity contribution superimposed to an ideally zero background, cannot be used directly with DDM. Indeed, under these conditions the homodyne term is dominant, eqn (10) becomes a bad approximation and the easy connection between DDM and far-field scattering experiments is lost. However, this difficulty can be overcome by identifying experimental geometries with orientation of the director and of the polarising elements that allow for the presence of a sufficiently intense transmitted beam. This problem is somehow similar to the one encountered in ref. 25, where the dynamics of randomly oriented colloidal particles was studied with near-field scattering. However, in the present case, it is possible to take advantage of well established procedures to fix the alignment of the director at the cell surfaces, as sketched in Fig. 3.
). The presence of the term (ivfz + izfv)2 in eqn (15) shows that the relative contribution of each mode to the scattered light can be suppressed by a careful choice of the orientation of the director and of the polarising elements. As recently reviewed in ref. 6, several far field scattering geometries have been proposed and reported in the literature to take advantage of this possibility. One of the main advantages of pDDM is that we can exploit known results from light scattering theory and we do not need ad hoc calculations, at least if we want to extract dynamic information. In principle, the investigation with DDM of the depolarised scattering of light from orientational fluctuations of the director requires thus a simple strategy: equipping the microscope with two linear polarising elements and performing a DDM analysis without resorting to an azimuthal averaging of the image structure function in the Fourier space. However, the ostensible simplicity of the experimental strategy can be misleading. Indeed, validity of eqn (10) is based on the assumption that the transmission of light through the sample remains large enough that the homodyne term Is = E*sEs can be safely neglected. An immediate consequence of such requirement is that typical geometries employed in DDLS experiments, where the sample is sandwiched between crossed polarisers and the signal of interest is a small intensity contribution superimposed to an ideally zero background, cannot be used directly with DDM. Indeed, under these conditions the homodyne term is dominant, eqn (10) becomes a bad approximation and the easy connection between DDM and far-field scattering experiments is lost. However, this difficulty can be overcome by identifying experimental geometries with orientation of the director and of the polarising elements that allow for the presence of a sufficiently intense transmitted beam. This problem is somehow similar to the one encountered in ref. 25, where the dynamics of randomly oriented colloidal particles was studied with near-field scattering. However, in the present case, it is possible to take advantage of well established procedures to fix the alignment of the director at the cell surfaces, as sketched in Fig. 3.

![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt) is calculated by averaging the Fourier power spectrum of the difference of images separated in time by the same time delay Δt. (e) The fit of D(
, Δt) is calculated by averaging the Fourier power spectrum of the difference of images separated in time by the same time delay Δt. (e) The fit of D(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , Δt) as a function of Δt allows the estimation of the q-dependent amplitudes A, the rates Γ and the camera noise B (see eqn (13) and (16)). (f) The linear fit of each Γ as a function of q2 in selected geometry-dependent directions allows the estimation of the corresponding viscoelastic ratio, according to eqn (3).
, Δt) as a function of Δt allows the estimation of the q-dependent amplitudes A, the rates Γ and the camera noise B (see eqn (13) and (16)). (f) The linear fit of each Γ as a function of q2 in selected geometry-dependent directions allows the estimation of the corresponding viscoelastic ratio, according to eqn (3).![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to
parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 the suitable reference system is drawn on the left side of panel b in Fig. 4. In this direction, only mode 2 can be thus probed. Indeed, for ordinary incident light and extraordinary scattered light (Fig. 4, panel b, centre) one has i1 = iz = f1 = f2 = 0, which implies (i1fz + izf1)2 = 0 and
0 the suitable reference system is drawn on the left side of panel b in Fig. 4. In this direction, only mode 2 can be thus probed. Indeed, for ordinary incident light and extraordinary scattered light (Fig. 4, panel b, centre) one has i1 = iz = f1 = f2 = 0, which implies (i1fz + izf1)2 = 0 and 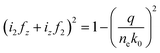 , whereas for extraordinary incident light and ordinary scattered light (Fig. 4, panel b, right) one has i1 = i2 = f1 = fz = 0, which leads to (i1fz + izf1)2 = 0 and (i2fz + izf2)2 = 1. Considering that Q|| = q and Q⊥ ≃ Δq, we have the following expression for the relaxation rate of mode 2:
, whereas for extraordinary incident light and ordinary scattered light (Fig. 4, panel b, right) one has i1 = i2 = f1 = fz = 0, which leads to (i1fz + izf1)2 = 0 and (i2fz + izf2)2 = 1. Considering that Q|| = q and Q⊥ ≃ Δq, we have the following expression for the relaxation rate of mode 2: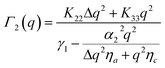
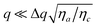 to give
to give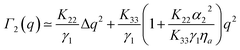
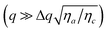 where
where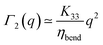
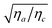 , it is not easy to know a priori whether the bend viscoelastic ratio in eqn (19) is experimentally accessible or one rather accesses the more complex combination in eqn (18).
, it is not easy to know a priori whether the bend viscoelastic ratio in eqn (19) is experimentally accessible or one rather accesses the more complex combination in eqn (18).![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 the reference system is depicted on the left side of panel c in Fig. 4. Both for extraordinary incident light and ordinary scattered light (Fig. 4, panel c, centre) and ordinary incident light and extraordinary scattered light (Fig. 4, panel c, right) one has (i1fz + izf1)2 = q2/(Δq2 + q2) and (i2fz + izf2)2 = q2/(Δq2 + q2), which implies that both modes show-up in the scattering intensity. In addition, we have Q|| = 0 and
0 the reference system is depicted on the left side of panel c in Fig. 4. Both for extraordinary incident light and ordinary scattered light (Fig. 4, panel c, centre) and ordinary incident light and extraordinary scattered light (Fig. 4, panel c, right) one has (i1fz + izf1)2 = q2/(Δq2 + q2) and (i2fz + izf2)2 = q2/(Δq2 + q2), which implies that both modes show-up in the scattering intensity. In addition, we have Q|| = 0 and 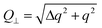 , which leads to
, which leads to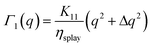
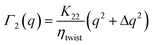
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ≃ 0 are characterised by
≃ 0 are characterised by ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) parallel to the z-axis. Modulations of this kind can only be originated by twist deformation of the LC director, which thereby act as Bragg diffraction grating with transmission coefficient peaked around Q ≃ Δq.
parallel to the z-axis. Modulations of this kind can only be originated by twist deformation of the LC director, which thereby act as Bragg diffraction grating with transmission coefficient peaked around Q ≃ Δq.
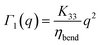
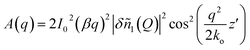
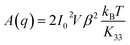
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to the polarising elements behave as a diffraction grating with wavelength 2π/q and in fact, only polarised scattering due to splay fluctuations is probed. Indeed, one has for the two modes (i1fz + izf1)2 = q2/(nok0)2 and (i2fz + izf2)2 = 0, with
parallel to the polarising elements behave as a diffraction grating with wavelength 2π/q and in fact, only polarised scattering due to splay fluctuations is probed. Indeed, one has for the two modes (i1fz + izf1)2 = q2/(nok0)2 and (i2fz + izf2)2 = 0, with ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥. The relaxation rate of such fluctuations is thus given by
⊥. The relaxation rate of such fluctuations is thus given by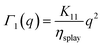
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥. The relaxation rate of such fluctuations is
⊥. The relaxation rate of such fluctuations is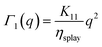
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ⊥. Twist fluctuations with wave vector
⊥. Twist fluctuations with wave vector ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ≃
≃ ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) act thus as a diffraction grating with wavelength 2π/q and the relaxation rate of such fluctuations is thus given by
act thus as a diffraction grating with wavelength 2π/q and the relaxation rate of such fluctuations is thus given by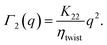
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to the director
parallel to the director ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, whereas the other (orange) with
0, whereas the other (orange) with ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0. It can be noticed that the two highlighted regions are rotated by π/8 with respect to the image axes as a consequence of the fact that in this geometry the director forms an angle π/8 with the polariser (Fig. 4a). By contrast, the scattering pattern for the P2 geometry is almost concentrated in a direction parallel to the director (Fig. 8b), as scattering vanishes perpendicularly to it. The region used for the pDDM analysis is highlighted in blue and has an angular width of π/16. In Fig. 8c we plot three structure functions measured at T − TNI = 0.2 °C and for q = 1.0 µm−1 in the P1 and in the P2 geometries. It appears that relaxation of the director fluctuations when
0. It can be noticed that the two highlighted regions are rotated by π/8 with respect to the image axes as a consequence of the fact that in this geometry the director forms an angle π/8 with the polariser (Fig. 4a). By contrast, the scattering pattern for the P2 geometry is almost concentrated in a direction parallel to the director (Fig. 8b), as scattering vanishes perpendicularly to it. The region used for the pDDM analysis is highlighted in blue and has an angular width of π/16. In Fig. 8c we plot three structure functions measured at T − TNI = 0.2 °C and for q = 1.0 µm−1 in the P1 and in the P2 geometries. It appears that relaxation of the director fluctuations when ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is perpendicular to
is perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 (orange squares in Fig. 8c for the P1 geometry) are slower than fluctuations in the parallel direction (blue circles for the P1 geometry and red triangles for the P2 geometry in Fig. 8c). According to the theoretical expectation, the P2 geometry is the easiest case to analyse. Indeed, a single mode (mode 1) of pure bend is probed with a rate given by eqn (22). Fitting the structure function with a single exponential curve (red dashed line in Fig. 8c) provides the rate Γ1, which is plotted as a function of q2 in Fig. 8d (red triangles). For each temperature, the obtained results are well fitted with a linear function, from which the bend ratio K33/ηbend can be extracted. Results for different temperatures are reported in Fig. 9a (full red circles) and are in excellent agreement with previous experiments on the same sample with DDLS.28 The situation is more complex for the P1 geometry. For
0 (orange squares in Fig. 8c for the P1 geometry) are slower than fluctuations in the parallel direction (blue circles for the P1 geometry and red triangles for the P2 geometry in Fig. 8c). According to the theoretical expectation, the P2 geometry is the easiest case to analyse. Indeed, a single mode (mode 1) of pure bend is probed with a rate given by eqn (22). Fitting the structure function with a single exponential curve (red dashed line in Fig. 8c) provides the rate Γ1, which is plotted as a function of q2 in Fig. 8d (red triangles). For each temperature, the obtained results are well fitted with a linear function, from which the bend ratio K33/ηbend can be extracted. Results for different temperatures are reported in Fig. 9a (full red circles) and are in excellent agreement with previous experiments on the same sample with DDLS.28 The situation is more complex for the P1 geometry. For ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to
parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, scattering is originated only from mode 2 and thus the dynamics is again well described by a single exponential function (blue circles in Fig. 8c). The rate Γ2 extracted from the single exponential fitting is plotted in Fig. 8d (blue circles) as a function of q2. In principle, these data should be fitted with eqn (17). However, this fit becomes very challenging because of the large number of fitting parameters and the limited q-range of the experiments. In addition, the possible use of the simpler expression in eqn (19) to extract the bend ratio is based on prior knowledge of ηa, ηc and Δq to ensure that the condition
0, scattering is originated only from mode 2 and thus the dynamics is again well described by a single exponential function (blue circles in Fig. 8c). The rate Γ2 extracted from the single exponential fitting is plotted in Fig. 8d (blue circles) as a function of q2. In principle, these data should be fitted with eqn (17). However, this fit becomes very challenging because of the large number of fitting parameters and the limited q-range of the experiments. In addition, the possible use of the simpler expression in eqn (19) to extract the bend ratio is based on prior knowledge of ηa, ηc and Δq to ensure that the condition 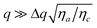 is met. Literature data for ηa and ηc relative to our sample could not be retrieved. However, data for 5CB26 and MBBA27 in a T−TNI range similar to the one explored here show that
is met. Literature data for ηa and ηc relative to our sample could not be retrieved. However, data for 5CB26 and MBBA27 in a T−TNI range similar to the one explored here show that 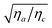 remains in the range 1–1.7. Based on this estimate, we can expect the condition
remains in the range 1–1.7. Based on this estimate, we can expect the condition 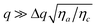 to be met only in a narrow range close to the critical temperature TNI, where in principle it should be possible to extract the bend viscoelastic ratio. In fact, even quite close to TNI, the approximation of eqn (17) with eqn (19) is still not fully satisfactory, as it can be appreciated in Fig. 8d, by comparing the rates obtained in this condition (blue circles) with the ones obtained in the P2 geometry (red triangles). For
to be met only in a narrow range close to the critical temperature TNI, where in principle it should be possible to extract the bend viscoelastic ratio. In fact, even quite close to TNI, the approximation of eqn (17) with eqn (19) is still not fully satisfactory, as it can be appreciated in Fig. 8d, by comparing the rates obtained in this condition (blue circles) with the ones obtained in the P2 geometry (red triangles). For ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0, the structure function is the sum of two exponential functions due to the superposition of modes 1 and 2 (eqn (16)). A double exponential fit (continuous line) thus provides the corresponding relaxation rates Γ1(q) and Γ2(q) (diamonds and squares in Fig. 8d, respectively). For small q, where scattering from mode 2 dominates, data for Γ1(q) appear quite noisy, as the small amplitude of mode 1 translates into a large uncertainty in determining Γ1(q). Nevertheless, data for both modes can be well fitted to eqn (20) and (21) to extract the splay and twist viscoelastic ratios, respectively and Δq. The results for different temperatures are shown as orange down-triangles in Fig. 9b and c, respectively. Again the agreement with previous experiments in ref. 28 is very good.
0, the structure function is the sum of two exponential functions due to the superposition of modes 1 and 2 (eqn (16)). A double exponential fit (continuous line) thus provides the corresponding relaxation rates Γ1(q) and Γ2(q) (diamonds and squares in Fig. 8d, respectively). For small q, where scattering from mode 2 dominates, data for Γ1(q) appear quite noisy, as the small amplitude of mode 1 translates into a large uncertainty in determining Γ1(q). Nevertheless, data for both modes can be well fitted to eqn (20) and (21) to extract the splay and twist viscoelastic ratios, respectively and Δq. The results for different temperatures are shown as orange down-triangles in Fig. 9b and c, respectively. Again the agreement with previous experiments in ref. 28 is very good.

![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) parallel to
parallel to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 obtained for each temperature in the P2 geometry. A reliable estimate of the low-q limit A0 of the amplitude is obtained as the average of A(q) over the interval [0.39, 0.49] µm−1, where A(q) is essentially flat. According to eqn (24), the bend elastic constant K33 is estimated as K33 = 2I02Vβ2kBT/A0. As shown in Fig. 10, the obtained values compare remarkably well with the literature data obtained by light scattering.27 Most remarkably, we are able to extend the existing data-range by almost a decade with pDDM approaching further towards TNI. This is because pDDM is less sensitive to multiple scattering as compared to traditional light scattering methods. We note that in principle the good result obtained for K33 could be extended also to the other two elastic constants, provided that some expressions analogous to eqn (24) are available for the corresponding geometries. Given the complexity of the calculations involved, the derivation of such expressions is well beyond the purpose of the present article, but it should be a priority for further developing the full potential of the method.
0 obtained for each temperature in the P2 geometry. A reliable estimate of the low-q limit A0 of the amplitude is obtained as the average of A(q) over the interval [0.39, 0.49] µm−1, where A(q) is essentially flat. According to eqn (24), the bend elastic constant K33 is estimated as K33 = 2I02Vβ2kBT/A0. As shown in Fig. 10, the obtained values compare remarkably well with the literature data obtained by light scattering.27 Most remarkably, we are able to extend the existing data-range by almost a decade with pDDM approaching further towards TNI. This is because pDDM is less sensitive to multiple scattering as compared to traditional light scattering methods. We note that in principle the good result obtained for K33 could be extended also to the other two elastic constants, provided that some expressions analogous to eqn (24) are available for the corresponding geometries. Given the complexity of the calculations involved, the derivation of such expressions is well beyond the purpose of the present article, but it should be a priority for further developing the full potential of the method.![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) perpendicular to
perpendicular to ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0 are analysed and fitted with a single exponential, since the limited size of the square regions of interests prevents a double exponential fit. Nevertheless, the twist and splay viscoelastic ratios can be extracted from the Γ(q) data in Fig. 13. The results for the two ratios (K11/ηsplay = (5.9 ± 0.3) × 10−11 m2 s−1, K22/ηtwist = (2.6 ± 0.6) × 10−11 m2 s−1) are in fair agreement with those obtained with uniformly aligned samples, reported in Fig. 9.
0 are analysed and fitted with a single exponential, since the limited size of the square regions of interests prevents a double exponential fit. Nevertheless, the twist and splay viscoelastic ratios can be extracted from the Γ(q) data in Fig. 13. The results for the two ratios (K11/ηsplay = (5.9 ± 0.3) × 10−11 m2 s−1, K22/ηtwist = (2.6 ± 0.6) × 10−11 m2 s−1) are in fair agreement with those obtained with uniformly aligned samples, reported in Fig. 9.