Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Particle segregation in a sedimenting bidisperse soft sphere system†
Matthias
Kohl
* and
Michael
Schmiedeberg
Institut für Theoretische Physik II: Weiche Materie, Heinrich-Heine-Universität Düsseldorf, D-40225 Düsseldorf, Germany. E-mail: mkohl@thphy.uni-duesseldorf.de
First published on 21st March 2014
Abstract
We study the sedimentation process of a binary colloidal soft sphere system where significant overlaps of the particles are possible. We employ estimates of the equation of states in the small and large pressure limit in order to predict the final states of the sedimentation process. Furthermore, Brownian dynamics simulations were performed in order to confirm the predictions and to explore the dynamics of the sedimentation. We observe that the segregation process due to gravity usually consists of multiple steps. Instead of single particles moving upwards or downwards we usually observe that first local segregation occurs, then clusters consisting of particles of one species are formed that finally sink towards their equilibrium position within the final sedimentation profile. The possible final states include complex phases like a phase consisting of large particles on the top and the bottom of the system with small particles in between. We also observe metastable network-like structures.
1 Introduction
Due to the ubiquitous presence of gravity sedimentation processes immediately play an important role in a huge number of common situations. Controlling the sedimentation process is important in order to regulate the growth of crystals or amorphous phases1,2 and in order to support or avoid separation effects in mixtures of different types of particles. Such separation effects are of great interest in many technical applications. Therefore the sedimentation of colloids1–8 and the behavior of granular materials under gravity9–18 have been a subject of research for a long time.For example, the rise dynamics of large particles in shaken granular systems, also known as the Brazil nut effect, has been studied extensively.9–19 Furthermore, the reverse effect, i.e., large particles sinking to the bottom for a different choice of parameters, has also been described theoretically12,14,15 and observed in experiments.12,16,19 Explanations for the segregation of large particles to the top or bottom are based on e.g. buoyancy,13,17,18 filling of voids by small particles,10,12 convective motion,11,17 condensation effects,14 or inertia effects.12,17
For the sedimentation of colloidal particles, the inertia effects can be neglected. A detailed theory has been developed and compared to simulations for the segregation of charged colloidal particles due to gravity.3–6 The sedimentation in soft sphere systems with small particle overlaps was reported to mainly depend on the bulk properties of random mixtures and of phases that only consist of one particle species.7 However, also a more complex behavior has been observed.8 Besides colloids that are close to the hard sphere limit, in recent years, there is a large amount of interest in soft particles that allow for significant large overlaps and therefore might possess a special phase behavior,20–26 complex glassy dynamics,27–33 and non-trivial jamming properties.34 Such soft colloids correspond to star-polymers,35–37 polymer coils,38 or soft microgel particles28,39 and are therefore in principle accessible in experiments.
In this article, we use Brownian dynamics simulations in order to study the segregation process in a binary system of such soft spheres. We show that the overlaps of the particles significantly influence the effective buoyancy and therefore the sedimentation process. As a consequence, the sedimentation process might lead to complex configurations, e.g., in some cases large particles might rise at small pressures due to a lower mass density while they might also sink at large pressures because of large particle overlaps. Thus, the large particles might assemble both at the top of the system as well as at the bottom, where the pressure is larger. Furthermore, the dynamics of the segregation process consists of multiple steps. First, we observe local demixing, then clusters of the same particle species form, and finally these clusters rise or sink towards their equilibrium position.
The paper is organized as follows: in Section 2 we introduce a model system and describe the simulation details. In Section 3 we discuss the theoretical background that enables us to predict the sedimentation behavior. The resulting equilibrium states are presented and compared to the final states of our Brownian dynamics simulation in Section 4, whereas Section 5 illuminates the dynamical process in approaching the equilibrium. Finally, we conclude in Section 6.
2 Binary soft sphere system
2.1 Model system
We consider a binary mixture consisting of Ns small particles with diameter σs and mass ms and Nl large particles with diameter σl and mass ml. Throughout the whole paper we fix σl = 2σs but vary the masses. As a control parameter, we employ the ratio of the mass densities, i.e., | (1) |
The particles interact according to a finite-ranged purely repulsive harmonic pair potential
 | (2) |
We study particles in a gravitational field in the z-direction. Moreover, there is a plane wall at the bottom of the simulation box. This corresponds to an additional external field acting on every sphere
| uext(ri) = migzi + uw(zi) | (3) |
 | (4) |
The stiffness of the wall is given by a dimensionless constant ε*w = εw/ε and the strength of the gravitational field by g* = msgσs/(ξkBT) where g is the gravitational acceleration.
In the following we use the particle diameter σs of the smaller particles as a suitable length scale and the prefactor ε of the interaction potential as an energy scale. Furthermore, we usually employ the Brownian time τB = σs2/D0 as a time scale, with D0 = kBT/γs denoting the short-time self-diffusion coefficient where γs is the friction coefficient of a small sphere. We also introduce the dimensionless temperature T* = kBT/ε and the dimensionless pressure P* = Pσs3/ε. The total bulk number density of the system is given by ρ = N/V where N = Ns + Nl is the total number of particles and V denotes the volume of the system.
2.2 Simulation details
We perform Brownian dynamics simulations,40i.e., we simulate the particle trajectories given by the overdamped Langevin equation| γiṙi(t) = Fi(r1, …, rN) + fi(t), | (5) |
In our simulation we consider Ns = 2000 small and Nl = 2000 large particles. We employ periodic boundary conditions perpendicular to the gravitational force. The length of the simulation box in x and y-directions is Lx = Ly = 10σs. We use finite time steps with Δt = 10−4τB or below. In the beginning we place all the particles randomly into the simulation box at a low packing fraction of ϕ = 0.1. After an initial relaxation time without gravity of 200τB, the external field is instantaneously switched on.
We choose an almost hard wall with a stiffness ε*w = 100, which makes it rather impenetrable for the particles. The strength of the gravitational field is g* = 1.5.
3 Theory
3.1 Bulk equation of state: limiting cases
In equilibrium we observe a segregation of the two particle species. In order to predict which species is forced to the top and which one to the bottom, we first consider the low and high number density limits of the bulk equation of state of demixed phases that consist of only one particle species.For low densities, the equation of state can be estimated by truncating the virial expansion after the second term, i.e.,
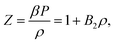 | (6) |
 | (7) |
For large densities, we employ the so-called Mean Spherical Approximation (MSA).41 The MSA is a well-established approximation for soft particle systems at large densities.20,42–44 Note that sometimes the MSA is also called random phase approximation (RPA).20,44 For soft penetrable spheres, the hard core becomes negligibly small and the overall approximate closure relation is43
| c(r) = −βu(r). | (8) |
The equation of state is determined by integrating over the compressibility factor
 | (9) |
 | (10) |
In summary, for our soft sphere systems we can use the limiting approximations
 | (11) |
The prefactor in the low number density case is calculated by eqn (7). For the high number density regime an analytical estimate for the prefactor is given by the MSA (see eqn (8)).
For our system, we introduce the dimensionless packing fraction ϕ = ρV(σi), with V(σi) = πσi3/6 being the three-dimensional volume of a sphere with diameter σi. In Fig. 1 the bulk equations of state for monodisperse soft spheres at different temperatures are presented theoretically for the limiting cases of high and low densities together with data from Brownian dynamics simulations. Note that the packing fraction can be larger than one.29,33,34 In order to prevent crystallization effects at very high densities in our simulations, we have introduced a small bidispersity for the diameters, which is equivalent to a variance of 0.04. The approximations for small and large packing fractions describe our simulation results very well. Apparently, at low packing fractions the pressure increases with increasing temperature. However, at large packing fractions, the pressure approximately is independent of the temperature. Therefore, the slopes in the intermediate regime must also become larger. Since the equation of state is typically not analytically known in an intermediate number density regime, we will later approximate the intermediate regime by a polynomial interpolation of the two limiting cases.
 | ||
| Fig. 1 Double logarithmic plot of the equation of state of a system consisting of one particle species with only a small amount of bidispersity in order to avoid crystallization. The different colors denote cases with different temperatures. The points show the simulation data. Additionally, the limiting cases of the analytical approximations from eqn (11) are plotted (solid lines). All curves converge against a limiting line at large packing fractions. | ||
3.2 Sedimentation profiles
To introduce gravity it is necessary to also incorporate the masses ms and ml into the discussion. As mentioned before, we investigate the particular case, where small and large particles have a size ratio σl/σs = 2. The masses are set by the dimensionless mass density ratio ξ defined in eqn (1). The sedimentation profiles will strongly depend on this mass density ratio.For hard particles with a ratio ξ = 1 no phase separation due to buoyant forces is expected. Inertia effects that are important for the Brazil nut effect in granular systems12,17 can be neglected because the dynamics is overdamped.
However, in our case particles are very soft and as a consequence their thermodynamic properties strongly depend on the temperature and pressure (see Fig. 1). As we will show in the following, especially the compressibility will determine the buoyant forces, which for soft particles also depend on temperature and pressure. We will use estimates of the buoyancy in order to predict the segregation of sedimenting soft colloids. The buoyancy of the large particles for a given temperature T* and pressure P* depends on the ratio of the mass densities, i.e., the ratio of the number densities ρl(P*, T*)/ρs(P*, T*) weighted by the corresponding masses ml and ms. We introduce a buoyancy function
 | (12) |
If bl(P*, T*, ξ) is positive, the larger particles will be lifted up with respect to the smaller ones. On the other hand they sink to the ground as soon as bl(P*, T*, ξ) becomes negative.
In Fig. 2(a) we show the equations of state for small and large particles with ξ = 2.4 and T* = 0.005. Note that we have weighted the packing fraction of the small particles with the mass density ratio ξ. In Fig. 2(b) we plot the buoyancy function as a function of P*. As it turns out, for ξ = 2.4 the buoyancy function has two zeros corresponding to the two intersecting points of the weighted equations of state in Fig. 2(a). The zeros of the buoyancy function denote the pressures for which the directions of the buoyant forces on large particles reverse. Consequently, at intermediate pressures the larger particles are lifted up in a bath of smaller particles, whereas for small and large pressures they sink. In the further discussion we will focus on the second zero, because in our simulations the pressure due to gravity is usually larger than the one at the first zero of bl. In the next section, we will focus on the final states that we expect from considering the buoyancy function and compare these predictions to the final states we find in the simulations.
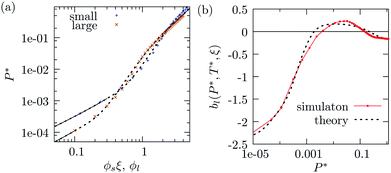 | ||
| Fig. 2 (a) Equations of state of large and small particles with a mass density ratio of ξ = 2.4 and at temperature T* = 0.005. Note that the packing fraction for the larger particles is not weighted, whereas for the small particles it is multiplied by ξ for the visualization of the corresponding impact of gravity. Points indicate simulation data, the solid lines are the limiting approximations of eqn (11). In order to obtain the dashed lines, the limiting cases are interpolated by a polynomial function. The curves have two intersection points. (b) The buoyancy function bl(P*, T*, ξ) denoting the buoyancy of the larger particles. For small and large pressures the function is negative indicating that large particles sink while for intermediate pressure bl(P*, T*, ξ) is positive and therefore large particles rise. The red points and line denote the simulation results, the black dashed line corresponds to a theoretical prediction obtained by the interpolation of the analytical limiting cases of the equation of state (cf. dashed line in (a)). | ||
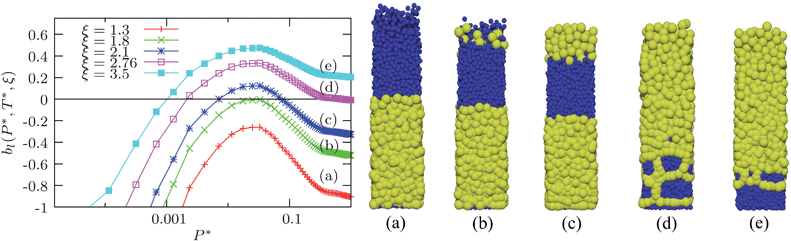
4 Final states
In this section we discuss the final states of the sedimentation process for different values of the mass density ratio ξ defined in eqn (1). For hard particles from considerations of buoyancy one expects that large particles reside on top of the small ones for ξ > 1 or the other way around for ξ < 1. In our case of soft particles, buoyancy also depends on the pressure. Gravity induces a monotonic increase in pressure from the top to the bottom of the system and therefore the pressure depends on the height. As a consequence, we find equilibrium phases, where large particles gather both on the top and at the bottom of the system.In Fig. 3 the buoyancy function bl(P*, T*, ξ) together with final states of simulations are shown for a constant temperature T* = 0.005. For ξ = 1.3 the function bl(P*, T*, ξ) is negative at any pressure. Therefore, smaller particles are always expected to lie above the larger ones. The corresponding simulated final state is shown in Fig. 3(a). For ξ ≈ 1.8 there is one zero, for ξ > 1.8 even two zeros are possible. In the case of two zeros, i.e., 1.8 < ξ < 2.76, an intermediate pressure regime exists, where the large particles move upwards. As a consequence, for a simple sedimentation with a randomly distributed mixture at the beginning, one will always obtain a 3-phase-stacking. These states are mainly governed by large particles that are lifted up for the intermediate pressure in the upper part of the system and large particles that sink due to sufficiently high pressure in the lower part of the system. The small particles gather in the center part of the system. It is important to note that the thickness of the top slice of larger particles is limited. If one adds more particles at the top of the box, the pressure at the upper interface will increase and therefore the threshold for the uplift of larger particles will be exceeded. Then, some of the larger particles will aggregate into a cluster and sediment cooperatively to the bottom basin. This procedure may appear several times until the condition of positive buoyancy is recovered. We will describe the dynamics of this process in more detail in the next section.
For ξ ≈ 2.76 the buoyancy function is only negative for very low pressures, then it becomes positive and converges roughly towards zero for very high pressures. For this value no preferred stacking is expected at high pressures. In the simulations (cf.Fig. 3(d)), particles segregate into a network structure in high pressure regions at the bottom of the simulation box. Despite the network-like segregation no net flow of one of two species can be observed over the whole time of the simulation and we cannot discriminate from our simulations whether a further segregation process takes place only very slowly or whether the networks depict some kind of metastable state. For intermediate pressures towards the top of the system the uplift of the larger particles becomes significant. A further increase of the mass density ratio, i.e., ξ > 2.76, again leads to segregation into two phases with opposite stacking to that for small ξ. Except for the small pressures in the top layer, for all other pressures within the sedimentation profile bl(P*, T*, ξ) > 0 and therefore the large particles move to the top. In principle, this behavior is confirmed by our simulations (see Fig. 3(e)). However, in the simulations, we also observe an unexpected non-equilibrium behavior at the interface of the two phases. Particles at the interface are arranged in bubble-like objects, where the shell consists of large and the core of small particles. Though these structures are very stable over the whole simulation run of 500τB, the behavior probably does not denote the equilibrium case. We suppose that the occurrence of these bubbles stems from the different effective softness of the particle species. Due to the fact that all particles have the same maximum potential, larger particles can easily have more absolute overlap with each other. Therefore, a shell of larger particles that forms during the sedimentation process is quite stable and hardly penetrable for a cluster of smaller particles. A shell of large particles forms when a cluster of small particles moves through the bath of large particles until the basin of small spheres is attained. However, the shell of large particles does not break up in order to release the small particles. Instead a protuberance is formed at the interface.
In Fig. 3 we have considered the final states for constant temperature, constant relative softness of the particles, and varying relative mass densities. In order to investigate how the buoyancy function and therefore the final states depend on the temperature or on the relative softness of the particles, we also consider systems with a fixed mass density ratio of ξ = 2.5 but with varying temperature (cf.Fig. 4(a)) or relative softness (cf.Fig. 4(d)). While at a small temperature the buoyancy function possesses two zeros and therefore we observe a 3-phase-stacking (see also Fig. 4(b)), for a larger temperature the buoyancy function is negative for all pressures and as a consequence for a large temperature the small particles always end up on top of the large particles (see the final state shown in Fig. 4(c)).
Particles of distinct species may not have the same softness. Therefore, for the buoyancy functions shown in Fig. 4(d) we again fixed the temperature at T* = 0.005, where the 3-phase-stacking has been found, but now vary the relative softness of the particle species. The relative softness is given by the fraction εl/εs, where εi denotes the prefactors of the interaction potentials of small and large particles in eqn (2). Here, the temperature has been normalized with respect to the energy scale of the small particles. Our theoretical calculations predict a 3-phase-stacking in the case of εl ≈ εs or εl > εs. However, for εl < 0.5εs, the buoyancy functions are negative for all pressures and therefore, we only expect 2-phase stackings with the softer large particles at the bottom and the small particles on top. Note that the buoyancy functions do not depend on the softness prefactor εls for the interaction between a small sphere and a large sphere. However, our considerations are only valid if mixing of the particles is not artificially supported, e.g., by a prefactor εls that is much smaller than εl or εs.
5 Dynamics
In the following we discuss the dynamics of the sedimentation processes. Fig. 5 shows the evolution of the sedimentation for a mass density ratio ξ = 2.5. At time zero the particles are randomly mixed. While they sink to the ground the pressure is increased at any point within the already sedimented particles. High densities cause a segregation of large and small particles, where the larger particles either sink at high pressure or rise in low pressure regions. The final state after 500τB is shown in the last snapshot and consists of a clear 3-phase-stacking. | ||
| Fig. 5 Sedimentation of small and large particles with ξ = 2.5 from an initial system with randomly distributed spheres with ϕ = 0.1. The snapshots only show the bottom of the simulation box. In the final state large particles can be found below and above the smaller ones. A fully time resolved visualization of this exemplary sedimentation process is included in the ESI.† | ||
The segregation process consists of different steps. First the particles locally segregate. This is due to the fact that the gain in volume fraction for overlaps between particles of the same species is larger than the volume gain of overlaps between small and large particles. In order to quantify this effect, we plot the relative gain in free volume ΔVij/(Vi + Vj) due to an overlap of spheres of species i and j as a function of the overlap energy Eij in Fig. 6. The overlap energy Eij is given by the respective pair interaction potentials as in eqn (2). The relative gain in volume for overlaps of spheres of the same kind is energetically preferred in comparison to the volume gained by overlaps of two spheres of distinct species. The effect becomes even larger at higher energies, i.e., large overlaps. Therefore, the segregation of particle species will occur faster if the overlaps become large. For this reason the segregation process in colder systems is slowed down mainly because of two influences, one being the dynamical slowdown due to the lower temperature and the other being the less significant volume gain due to smaller overlaps. Indeed, in some of our simulations we could observe that at lower temperatures segregation does not take place within the whole simulation time. Unfortunately, from finite simulation time one cannot discriminate between real asederotrope phases (as in the experiments by Serrano et al.7) and a very slow separation process. Nevertheless, one can conclude that particles in cold systems with less overlaps stay mixed at least for very long times.
At the temperatures that we usually consider in most of our simulations, in the first step the particles locally segregate and we observe the formation of clusters of the particles that are unstable in the region they are located. In the next step these clusters rise or sink. Finally the clusters merge with the phase consisting of the same particles at the top or bottom of the system. Note that the merging process can take a long time and might include the formation of protuberances as we have already mentioned at the end of the previous section.
In order to study the cluster formation and movements, we perturb final states by adding additional small or large particles such that we can observe the relaxation process of the additional particles in detail. We first consider the situation that corresponds to the reverse Brazil nut state for granular systems. There, small particles lay on top of the larger ones. We choose ξ = 1.8, which is the threshold value for such a stacking (cf.Fig. 3(b)). Now we add a small amount of large particles and let them sediment on top of the small particles. In Fig. 7 the resulting relaxation process is shown. First, larger particles stay segregated from the small ones on the top. Then they form a cluster, which subsequently is able to pass through the barrier formed by the small particles. The cluster sinks downwards and finally merges with the lower phase of large particles. The process repeats several times with other clusters until a stable final state is recovered.
 | ||
| Fig. 7 Snapshots of a system with small particles (blue) sitting on large particles (yellow) at a mass density ratio of ξ = 1.8 (cf.Fig. 3(b)). The system is perturbed by additional large particles that are placed on top of the final state. The snapshots (b)–(e) show the resulting relaxation process. The small particles have been faded out for better insight into the large spheres. First, a cluster of large particles (for better visibility colored magenta) emerges from the unstable top layers of larger particles, then the cluster sinks through the basin of small particles until it merges again with the stable ensemble of the larger particles. A movie is available in the ESI.† | ||
If the initial state is the other way around, i.e., large particles are on top of the small ones (as in a Brazil nut system), we observe how additional small particles also pass the central zone of large spheres by forming clusters. In Fig. 8 we show the dynamics of such a relaxation process for ξ = 3.5 (see also Fig. 3(e) for the corresponding final state). Interestingly, the cluster formation of small particles only occurs at sufficiently high pressures and densities. While in the diluted regions close to the top of the system the small particles slip through voids between the large particles and therefore penetrate the central zone of large particles one by one, this is no longer possible if the particles are further away from the top region, i.e., when the pressure becomes larger and overlaps between large particles become more pronounced. At a depth, where the motion of single small colloids through the voids of large particles no longer is efficient, formation of clusters of small particles sets in. Subsequently these clusters pass through the large particle zone. When the clusters reach the interface, they usually remain stable for a long time while they are still surrounded by a shell of large particles (cf. description at the end of the previous section).
 | ||
| Fig. 8 Snapshots of a system with large particles on top of small particles at ξ = 3.5 (cf.Fig. 3(e)). Additional small particles are added on the top. The relaxation process is displayed in (b)–(e) where the larger particles are faded out and clusters of small particles are marked by different colors. The newly added small particles first penetrate the zone of large particles where they form clusters. The clusters then sink to the interface, where they may remain in bubbles or form protuberances that are metastable and stay for a long time. A movie is available in the ESI.† | ||
6 Conclusions
We have presented theoretical predictions for the final states of a sedimentation process within a binary colloidal soft sphere system and confirmed them by Brownian dynamics simulations. The results turned out to differ significantly from the behavior of sedimenting hard spheres. For example, we observe 3-phase-stackings as well as metastable or long-lasting network-like structures. Furthermore, the sedimentation process also is more comprehensive. In order to demonstrate the relaxation process, we have perturbed sedimented states by adding particles on top of already finished sedimentation profiles. We observe that particles do not sediment homogeneously through the zone of the other species in order to re-establish the equilibrium state, but they rather aggregate into clusters and sink to the ground cooperatively.We want to mention that, if the buoyancy function bl that we introduced in Section 3.2 possesses two zeros, our theory will even allow for a 4-phase-stacking with small particles on top followed by large particles, then small particles again, and finally large particles at the bottom. The reason we did not observe such a stacking is that the first zero occurs at very small pressures such that for our gravitational strength the uppermost small particle phase only is stable within a very small layer. However, further investigations with other pair interactions or other parameters might lead to situations where the 4-phase-stacking is stable.
For our analysis we employed a harmonic model pair potential. However, we expect that our method and the reported mechanisms of separation are also valid for other soft particle systems whenever significant overlaps between the particles occur. Furthermore it would be interesting to study the particle separation process in a system of a soft granular material, where in addition to the buoyancy effects studied here inertia effects might also be important.
Acknowledgements
This work was supported by the DFG within the Emmy-Noether programme (Schm 2657/2).References
- P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- Z. Cheng, W. B. Russel and P. M. Chaikin, Nature, 1999, 401, 893–895 CrossRef CAS PubMed.
- J.-P. Simonin, J. Phys. Chem., 1995, 99, 1577–1581 CrossRef CAS.
- R. van Roij, J. Phys.: Condens. Matter, 2003, 15, S3569 CrossRef CAS.
- A. Cuetos, A.-P. Hynninen, J. Zwanikken, R. van Roij and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061402 CrossRef CAS.
- A. Torres, A. Cuetos, M. Dijkstra and R. v. Roij, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041405 CrossRef.
- C. G. Serrano, J. J. McDermott and D. Velegol, Nat. Mater., 2011, 10, 716–721 CrossRef CAS PubMed.
- A. P. Philipse, Curr. Opin. Colloid Interface Sci., 1997, 2, 200–206 CrossRef CAS.
- A. Rosato, K. J. Strandburg, F. Prinz and R. H. Swendsen, Phys. Rev. Lett., 1987, 58, 1038–1040 CrossRef.
- R. Jullien, P. Meakin and A. Pavlovitch, Phys. Rev. Lett., 1992, 69, 640–643 CrossRef.
- J. B. Knight, H. M. Jaeger and S. R. Nagel, Phys. Rev. Lett., 1993, 70, 3728–3731 CrossRef.
- T. Shinbrot and F. J. Muzzio, Phys. Rev. Lett., 1998, 81, 4365–4368 CrossRef CAS.
- N. Shishodia and C. R. Wassgren, Phys. Rev. Lett., 2001, 87, 084302 CrossRef CAS.
- D. C. Hong, P. V. Quinn and S. Luding, Phys. Rev. Lett., 2001, 86, 3423–3426 CrossRef CAS.
- J. A. Both and D. C. Hong, Phys. Rev. Lett., 2002, 88, 124301 CrossRef.
- A. P. J. Breu, H.-M. Ensner, C. A. Kruelle and I. Rehberg, Phys. Rev. Lett., 2003, 90, 014302 CrossRef CAS.
- D. A. Huerta and J. C. Ruiz-Suárez, Phys. Rev. Lett., 2004, 92, 114301 CrossRef CAS.
- D. A. Huerta, V. Sosa, M. C. Vargas and J. C. Ruiz-Suárez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031307 CrossRef CAS.
- M. Schröter, S. Ulrich, J. Kreft, J. B. Swift and H. L. Swinney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 011307 CrossRef.
- A. A. Louis, P. G. Bolhuis and J. P. Hansen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 7961–7972 CrossRef CAS.
- C. N. Likos, M. Watzlawek and H. Löwen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 3135–3144 CrossRef CAS.
- M. Watzlawek, C. N. Likos and H. Löwen, Phys. Rev. Lett., 1999, 82, 5289–5292 CrossRef CAS.
- S. Prestipino, F. Saija and P. V. Giaquinta, J. Chem. Phys., 2005, 123, 144110 CrossRef PubMed.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051501 CrossRef CAS.
- B. M. Mladek, D. Gottwald, G. Kahl, M. Neumann and C. N. Likos, Phys. Rev. Lett., 2006, 96, 045701 CrossRef.
- G. Malescio, J. Phys.: Condens. Matter, 2007, 19, 073101 CrossRef CAS PubMed.
- L. Berthier and T. A. Witten, EPL, 2009, 86, 10001 CrossRef.
- J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83–86 CrossRef CAS PubMed.
- L. Berthier, A. J. Moreno and G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 060501 CrossRef.
- M. Schmiedeberg, T. K. Haxton, S. R. Nagel and A. J. Liu, Europhys. Lett., 2011, 96, 36010 CrossRef.
- C. Zhao, K. Tian and N. Xu, Phys. Rev. Lett., 2011, 106, 125503 CrossRef.
- L. Wang, Y. Duan and N. Xu, Soft Matter, 2012, 8, 11831–11838 RSC.
- M. Schmiedeberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052310 CrossRef.
- M. P. Ciamarra and P. Sollich, Soft Matter, 2013, 9, 9557–9561 RSC.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
- C. N. Likos, Soft Matter, 2006, 2, 478–498 RSC.
- C. Mayer, E. Zaccarelli, E. Stiakakis, C. N. Likos, F. Sciortino, A. Munam, M. Gauthier, N. Hadjichristidis, H. Iatrou, P. Tartaglia, H. Löwen and D. Vlassopoulos, Nat. Mater., 2008, 7, 780–784 CrossRef CAS PubMed.
- A. A. Louis, P. G. Bolhuis, J. P. Hansen and E. J. Meijer, Phys. Rev. Lett., 2000, 85, 2522–2525 CrossRef CAS.
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. Weitz, Microgel Suspensions: Fundamentals and Applications, Wiley, 2011 Search PubMed.
- M. Allen and D. Tildesley, Computer simulation of liquids, Clarendon Press, 1999 Search PubMed.
- J. P. Hansen and I. R. McDonald, Theory of simple liquids, Academic Press, London, 1976 Search PubMed.
- B. Mladek, M. Fernaud, G. Kahl and M. Neumann, Condens. Matter Phys., 2005, 8, 135 CrossRef.
- C. N. Likos, B. M. Mladek, D. Gottwald and G. Kahl, J. Chem. Phys., 2007, 126, 224502 CrossRef PubMed.
- S. D. Overduin and C. N. Likos, J. Chem. Phys., 2009, 131, 034902 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Movies of dynamic sedimentation processes. See DOI: 10.1039/c4sm00140k |
| This journal is © The Royal Society of Chemistry 2014 |